
Interpreting Xor Intuitionistic Fuzzy Connectives from
Quantum Fuzzy Computing
Anderson Avila, Renata Reiser, Maurício Pilla and Adenauer Yamin
PPGC - CDTEC, UFPEL, Pelotas, Brazil
Keywords:
Intuitionistic Fuzzy, Quantum Computing, Xor Operator.
Abstract:
Computer systems based on intuitionistic fuzzy logic are capable of generating a reliable output even when
handling inaccurate input data by applying a rule based system, even with rules that are generated with im-
precision. The main contribution of this paper is to show that quantum computing can be used to extend the
class of intuitionistic fuzzy sets with respect to representing intuitionistic fuzzy Xor operators. This paper
describes a multi-dimensional quantum register using aggregations operators such as t-(co)norms based on
quantum gates allowing the modeling and interpretation of intuitionistic fuzzy Xor operations.
1 INTRODUCTION
Fuzzy logic (FL) and its extensions as the Atanassov’s
fuzzy intuitionistic logic (A-IFL)(Atanassov and Gar-
gov, 1998; Atanassov, 2017) together with quantum
computing (QC) are relevant research areas consoli-
dating the analysis and the search for new solutions
for difficult problems faster than the classical logi-
cal approach by extending results from conventional
computing.
Similarities between these areas in the represen-
tation and modelling of uncertainty have been ex-
plored (Pykacz, 1993; Kreinovich et al., 2009; Man-
nucci, 2006). The uncertainty of human being’s rea-
soning can be modelled in A-IFL as a mathemati-
cal model inheriting the indeterminacy from mem-
bership and non-membership degrees which are not
necessarily complementary. It provides techniques
helping physicists and mathematicians to transform
their uncertainty ideas into new computational pro-
grams (Kosheleva et al., 2015).
The uncertainty of the real world is concerned
with fundamental concepts of QC by making use of
properties of quantum mechanics as the superposition
which suggest an improvement in the efficiency re-
garding complex tasks. In addition, simulations using
classical computers improve the development and val-
idation of basic quantum algorithms, anticipating the
knowledge related to their behaviours when executed
in a quantum computer.
In spite of quantum computers being restricted to a
few research centers and laboratories, the studies from
quantum information and quantum computation are a
reality nowadays.
In this context, new methods dealing with fuzzy
approaches to quantum computational logics have
been proposed (Chiara et al., 2018). Moreover, it
contributes to increase the interest in quantum algo-
rithm applications representing fuzzy and intuitionis-
tic fuzzy systems.
1.1 Synergy between FL and QC
Potentialities from quantum parallelism and superpo-
sition of quantum states are explored by new method-
ologies. See, e.g. providing a model for humanoid be-
haviours based on FL (Raghuvanshi and Perkowski,
2010) and using a density operator and logical con-
nectives defined by quantum gates (Bertini and Lep-
orini, 2017). In other areas, QC is used to im-
prove computations as Econometric Modeling (Sri-
boonchitta et al., 2019) and to integrate concepts
from quantum genetic algorithm and fuzzy neural net-
work (Li et al., 2010) as a model employed to control
an inverted pendulum system.
From a logical perspective, many-valued fuzzy
approach is a consolidated research area (Hájek,
1998) and recent efforts integrating the quantum com-
putational logic are considered (Chiara et al., 2018).
See, e.g. (Freytes et al., 2010) making use of quantum
states to represent information processing in QC.
In (Rigatos and Tzafestas, 2002), a parallel control
fuzzy algorithm is proposed showing that both QC
and fuzzy learning algorithms are relevant research
288
Avila, A., Reiser, R., Pilla, M. and Yamin, A.
Interpreting Xor Intuitionistic Fuzzy Connectives from Quantum Fuzzy Computing.
DOI: 10.5220/0008169702880295
In Proceedings of the 11th International Joint Conference on Computational Intelligence (IJCCI 2019), pages 288-295
ISBN: 978-989-758-384-1
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

areas which can profit from each other.
In this work, the modelling and interpretation of
A-IFL via QC provides the description of intuitionis-
tic fuzzy connectives by using quantum registers and
quantum transformations from the traditional model
of quantum circuits.
The information regarding each intuitionistic
fuzzy set is represented by pairs of quantum registers,
guaranteeing the inherent unitarity of quantum states
and quantum transformations well as the flexibility
of the complementarity relation of membership and
non-membership functions characterizing intuitionis-
tic fuzzy sets.
Some results of such research area are mainly re-
lated to interpretation of fuzzy connectives via QC, as
negation, conjunction, disjunction, implications and
xor operators (Avila et al., 2015) and to intuitionistic
fuzzy connectives (Reiser et al., 2016).
This work extends that approach by the interpreta-
tion of two classes of intuitionistic fuzzy Xor connec-
tives via QC, the ⊗
I
and ⊕
I
intuitionistic fuzzy Xor
operators, which can be expressed as composition of
conjunctions (S
I
), disjunctions (T
I
) and the comple-
mentary operators (N
I
). But different from other rep-
resentable intuitionistic fuzzy connectives, an intu-
itionistic fuzzy Xor connective cannot be expressed
as an N-dual pair of Xor and EXor fuzzy connectives.
So, quantum states and quantum operators provide
interpretation for intuitinistic fuzzy values and con-
nectives, respectively. In particular, Xor and EXor
can be applied to explore regular applications based
on symmetric functions by making use of reversible
logic (He et al., 2017) and can be also extended to
QC (Perkowski et al., 2001).
1.2 Paper Outline
The remainder of this paper is organized as follows.
Section 2 presents the foundations on A-IFL. Sec-
tion 3 brings the main concepts of QC. In Section 4,
the study and modeling of intuitionistic fuzzy Xors
using QC is described. An interpretation of classi-
cal A-IFS (Atanassov, 2016; Mannucci, 2006) from
quantum states is also considered, presenting the op-
erations on A-IFS modelled from quantum transfor-
mations, relating the Atanassov’s intuitionistic fuzzy
approach(Atanassov, 1986) to two classes of Xor op-
erators and also considering representable Xor con-
nectives obtained by composition of standard nega-
tion together with the Product and Algebraic Sum.
Finally, conclusions and further work are discussed
in Section 5.
2 FUZZY LOGIC APPROACH
The A-IFL is a type-2 fuzzy logic conceived as a gen-
eralization of FL overcoming the limitations related to
fuzzy sets for dealing with problems where the rules
applied to the system could not be defined with preci-
sion, mainly related to non-membership degree which
cannot be defined as a complement of its membership
degree.
An element x∈X belongs to the subset A such that
0 ≤µ
A
(x) + ν
A
≤1, meaning that a non-membership
degree ν
A
(x) is not necessary the complement of its
membership degree µ
A
(x). Thus, A is given as:
A = {(x, µ
A
(x), ν
A
(x)) : x ∈ X ,0 ≤ µ
A
(x) + ν
A
≤ 1} (1)
Taking µ
A
(x) = x
1
, ν
A
(x) = x
2
∈ [0, 1] for an element
x ∈ χ, the set of all Atanassov’s intuitionistic fuzzy
values is given as
˜
U = {(x
1
, x
2
) : x
1
+ x
2
≤ 1}. The
least and greatest element on
˜
U are given as
˜
0 = (0, 1)
and
˜
1 = (1, 0), respetively.
Considering the research of A-IFL, it makes pos-
sible to extend the usual logic connectives, as follows:
1. Conjunction, usually modelled by a triangular
norm (t-norm) operator (Klement et al., 2013),
which is an additive aggregation used in the
framework of intersection in A-IFL;
2. Disjunction which is frequently modelled by a tri-
angular conorm (Klement et al., 2013) (t-conorm)
representing the t-norm dual operation;
3. Complement as a negation, a non-increasing
function, defined in the Atanassov’s seminal
work (Atanassov, 2006), reverting the extremes of
the unit interval [0, 1].
4. Xor operators, considering in this work two rep-
resentable classes ⊕
I
P
and ⊗
I
P
(Bedregal et al.,
2013), both defined by composition of the above
connectives verifying the symmetry, associativity,
neutral element and boundary conditions.
Now, the connectives used to make the correlation
between QC and A-IFL will be described in terms
of representability based on fuzzy negations and
aggregations.The standard intuitionistic fuzzy nega-
tion (Atanassov, 2006) is expressed as follows:
N
I
S
( ˜x) = (x
2
, x
1
), ∀˜x = (x
1
, x
2
) ∈
˜
U. (2)
Meanwhile, for all ˜x = (x
1
, x
2
), ˜y = (y
1
, y
2
) ∈
˜
U, the
intersection and union can be defined, respectively, in
terms of a t-norm T and a t-conorm S, given as:
T
I
( ˜x, ˜y) = T
I
((x
1
, x
2
), (y
1
, y
2
)) = (T (x
1
, y
1
), S(x
2
, y
2
));
S
I
( ˜x, ˜y) = S
I
((x
1
, x
2
), (y
1
, y
2
)) = (S(x
1
, y
1
), T (x
2
, y
2
)).
We consider the Product t-norm T
I
P
and Algebraic
Sum S
I
P
, respectively described as follows:
T
I
P
( ˜x, ˜y)=(T
P
(x
1
, y
1
), S
P
(x
2
, y
2
))=(x
1
y
1
, x
2
+ y
2
+ x
2
y
2
);
S
I
P
( ˜x, ˜y)=(S
P
(x
1
, y
1
), T
P
(x
2
, y
2
))=(x
1
+ y
1
+ x
1
y
1
, x
2
y
2
)).
Interpreting Xor Intuitionistic Fuzzy Connectives from Quantum Fuzzy Computing
289

The classical xor expressions considered for this
work are described as follows:
A ⊕B ≡ (¬A ∧B) ∨(A ∧¬B);
A ⊗B ≡ (A ∨B) ∧(¬A ∨¬B).
Definition 2.1. The Atanassov’s intuitionistic fuzzy
Xor operator is a function E
I
:
˜
U
2
→
˜
U verifying:
E1: E
I
(
˜
0,
˜
0) = E
I
(
˜
1,
˜
1) =
˜
0 and E
I
(
˜
0,
˜
1) = E
I
(
˜
1,
˜
0) =
˜
1;
E2: E
I
( ˜x, ˜y) = E
I
( ˜y, ˜x);
E3: ˜y
1
≤ ˜y
2
⇒ E
I
(
˜
0, ˜y
1
) ≤ E
I
(
˜
0, ˜y
2
);
E4: ˜y
1
≤ ˜y
2
⇒ E
I
(
˜
1, ˜y
1
) ≥ E
I
(
˜
1, ˜y
2
).
Proposition 2.1. The functions ⊕
I
, ⊗
I
:
˜
U
2
→
˜
U
given as follows:
⊕
I
( ˜x, ˜y) = S
I
(T
I
(N
S
I
( ˜x), ˜y), T
I
( ˜x, N
S
I
( ˜y))) (3)
⊗
I
( ˜x, ˜y) = T
I
(S
I
( ˜x, ˜y), S
I
(N
S
I
( ˜x), N
S
I
( ˜y))) (4)
are intuitionistic fuzzy Xor operators.
Proof. Consider ⊕
I
operator. It holds that:
E
I
1: The following boundary conditions are
verified in the endpoints of unit interval:
⊕
I
(
˜
0,
˜
0)=S
I
(T
I
(N
S
I
(
˜
0),
˜
0), T
I
(
˜
0, N
S
I
(
˜
0)))=S
I
(
˜
0,
˜
0)=
˜
0;
⊕
I
(
˜
1,
˜
1)=S
I
(T
I
(N
S
I
(
˜
1),
˜
1), T
I
(
˜
1, N
S
I
(
˜
1)))=S
I
(
˜
0,
˜
0)=
˜
0;
⊕
I
(
˜
0,
˜
1)=S
I
(T
I
(N
S
I
(
˜
0),
˜
1), T
I
(
˜
0, N
S
I
(
˜
1)))=S
I
(
˜
1,
˜
0)=
˜
1;
⊕
I
(
˜
1,
˜
0)=S
I
(T
I
(N
S
I
(
˜
1),
˜
0), T
I
(
˜
1, N
S
I
(
˜
0)))=S
I
(
˜
0,
˜
1)=
˜
1;
E
I
2 : ∀˜x, ˜y ∈
˜
U the following is verified
E
I
( ˜x, ˜y) = S
I
(T
I
(N
S
I
( ˜x), ˜y), T
I
( ˜x, N
S
I
( ˜y)))
= S
I
(T
I
( ˜y, N
S
I
( ˜x)), T
I
(N
S
I
( ˜y), ˜x)) = E
I
( ˜y, ˜x);
E
I
3 : If ˜y
1
≤ ˜y
2
then the following is verified
⊕
I
(
˜
0, ˜y
1
) = S
I
(T
I
(N
S
I
(
˜
0), ˜y
1
), T
I
(
˜
0, N
S
I
( ˜y
1
)))
≤ S
I
(T
I
(N
S
I
(
˜
0), ˜y
2
), T
I
(
˜
0, N
S
I
( ˜y
2
))) = E
I
(
˜
0, ˜y
2
);
E
I
4 : If ˜y
1
≤ ˜y
2
then the following is verified
⊕
I
(
˜
1, ˜y
1
) = S
I
(T
I
(N
S
I
(
˜
1), ˜y
1
), T
I
(
˜
1, N
S
I
( ˜y
1
)))
≥ S
I
(T
I
(N
S
I
(
˜
1), ˜y
2
), T
I
(
˜
1, N
S
I
( ˜y
2
))) = E
I
(
˜
1, ˜y
2
);
Therefore, Proposition 2.1 is verified.
Based on those expressions, one can use the oper-
ators T
I
, S
I
, N
I
S
to construct the Atanassov’s intuition-
istic fuzzy xor (⊕
I
, ⊗
I
) respectively given as follows:
⊕
I
( ˜x, ˜y) =
=S
I
(T
I
(N
S
I
( ˜x), ˜y), T
I
( ˜x, N
S
I
( ˜y)))
=S
I
(T
I
((x
2
, x
1
), (y
1
, y
2
)), T
I
((x
1
, x
2
), (y
2
, y
1
))))
=S
I
((T (x
2
, y
1
), S(x
1
, y
2
)), (T (x
1
, y
2
), S(x
2
, y
1
))))
=(S(T (x
2
, y
1
), T (x
1
, y
2
)), T (S(x
1
, y
2
), S(x
2
, y
1
))) (5)
⊗
I
( ˜x, ˜y) =
=T
I
(S
I
( ˜x, ˜y), S
I
(N
S
I
( ˜x), N
S
I
( ˜y)))
=T
I
(S
I
((x
1
, x
2
), (y
1
, y
2
)), S
I
((x
2
, x
1
), (y
2
, y
1
)))
=T
I
((S(x
1
, y
1
), T (x
2
, y
2
)), (S(x
2
, y
2
), T (x
1
, y
1
)))
=(T (S(x
1
, y
1
), S(x
2
, y
2
)), S(T (x
2
, y
2
), T (x
1
, y
1
))) (6)
By considering T
I
P
and S
I
P
in Eqs. (5) and (6), the
xor (⊕
I
, ⊗
I
) operators can be respectively expressed
as follows:
⊕
I
( ˜x, ˜y) = ((x
1
y
2
+ x
2
y
1
−x
1
x
2
y
1
y
2
),
= (x
1
x
2
+ x
1
y
1
+ x
2
y
2
+ y
1
y
2
−x
1
x
2
y
1
−
x
1
x
2
y
2
−x
1
y
1
y
2
−x
2
y
1
y
2
+ x
1
x
2
y
1
y
2
)). (7)
⊗
I
( ˜x, ˜y) = ((x
1
x
2
+ x
1
y
2
+ x
2
y
1
+ y
1
y
2
−x
1
x
2
y
1
= −x
1
x
2
y
2
−x
1
y
1
y
2
−x
2
y
1
y
2
+ x
1
x
2
y
1
y
2
),
= (x
1
y
1
+ x
2
y
2
−x
1
x
2
y
1
y
2
)). (8)
According to (Mannucci, 2006), fuzzy sets can be
obtained by quantum superposition of classical fuzzy
states associated with a quantum register.
3 QUANTUM COMPUTING
In QC, the qubit is the basic information unit, being
the simplest quantum system, defined by a unitary and
bi-dimensional state vector.
Qubits are generally described, in Dirac’s nota-
tion (Nielsen and Chuang, 2003), by the following
expression
|ψi = α|0i+β|1i
when the coefficients α and β are complex numbers
for the amplitudes of the corresponding states in the
computational basis (state space), respecting the con-
dition |α|
2
+|β|
2
= 1, which guarantees the unitary of
the state vectors of the quantum system, represented
by (α, β)
t
(Kaye et al., 2007).
The state space of a quantum system with mul-
tiple qubits is obtained by the tensor product of the
space states of its subsystems. Considering a quan-
tum system with two qubits, |ψi = α|0i+ β|1i and
|ϕi = γ|0i + δ|1i, the state space comprehends the
tensor product given by
|Πi= |ψi⊗|ϕi = α ·γ|00i+ α ·δ|01i+β ·γ|10i+ β ·δ|11i.
The state transition of a quantum systems is per-
formed by controlled and unitary transformations as-
sociated with orthogonal matrices of order 2
N
, with
N being the number of qubits within the system, pre-
serving norms, and thus, probability amplitudes (Imre
and Balázs, 2005). For instance, the NOT opera-
tor (Pauli-X transformation) and its application over
1-dimensional and 2-dimensional quantum systems
are presented in the following.
X|ψi =
0 1
1 0
α
β
=
β
α
; (9)
X
⊗2
|Πi=
0 0 0 1
0 0 1 0
0 1 0 0
1 0 0 0
α ·γ
α ·δ
β ·γ
β ·δ
=
α ·γ
α ·δ
β ·δ
β ·γ
(10)
FCTA 2019 - 11th International Conference on Fuzzy Computation Theory and Applications
290

Furthermore, the action of a Toffoli QT is also
shown in next Eq. (11), describing a controlled op-
eration for a 3-dimensional quantum system
T |χi = T (ψ ⊗ϕ ⊗σ).
In this case, the NOT operator is applied to the
third qubit |σi when the current states of the first two
qubits |ψi and |ϕi are both |1i:
Similarly to QTs of multiple qubits which were
obtained by the tensor product performed over unitary
transformations, Eq.(11) presents the matrix structure
of such QT, when |X i is the initial state:
T|X i=
1 0 0 0 0 0 0 0
0 1 0 0 0 0 0 0
0 0 1 0 0 0 0 0
0 0 0 1 0 0 0 0
0 0 0 0 1 0 0 0
0 0 0 0 0 1 0 0
0 0 0 0 0 0 0 1
0 0 0 0 0 0 1 0
α
β
γ
δ
ε
θ
υ
σ
=
α
β
γ
δ
ε
θ
σ
υ
(11)
In order to obtain information from a quantum
system, it is necessary to apply measurement opera-
tors, defined by a set of linear operators M
m
, called
projections. The index m refers to the possible mea-
surement results. If the state of a 1-dimensional quan-
tum system is |ψi immediately before the measure-
ment, the probability of an outcome occurrence is
given by p(|ψi) =
M
m
|ψi
q
hψ|M
†
m
M
m
|ψi
. When measuring
a qubit |ψi with α, β 6= 0, the probability of observ-
ing |0i and |1i are, respectively, given by the follow-
ing expressions:
p(0) = hφ|M
†
0
M
0
|φi = hφ|M
0
|φi = |α|
2
;
p(1) = hφ|M
†
1
M
1
|φi = hφ|M
1
|φi = |β|
2
.
After the measuring process, the quantum state
|ψi has |α|
2
as the probability to be in the state |0i
and |β|
2
as the probability to be in the state |1i.
In multidimensional systems, the operators M
n
m
and p
N
(m) denote the m-projection and correspond-
ing probability measure, both performed on the n-
qubit.
4 INTERPRETING XOR
OPERATORS BASED ON QC
The description of intuitionistic fuzzy sets from the
QC viewpoint extends the work in (Mannucci, 2006)
by modeling an element ˜x = (x
1
, x
2
) by a pair of one-
dimensional qubit quantum states (|x
1
i, |x
2
i) where:
|x
1
i =
p
1 −x
1
|0i+
√
x
1
|1i; (12)
|x
2
i =
p
1 −x
2
|0i+
√
x
2
|1i. (13)
By modeling fuzzy operators in QC(Avila et al.,
2015), the Product t-norm T
P
and Algebriac Sum t-
conorm can be represented through the Toffoli gate
(T) and the standard negation through the Pauli-X
gate (N).
So the first step to generate the quantum represen-
tation for both Xor operators ⊕
I
P
and ⊗
I
P
is to ap-
ply De Morgan’s law related to t-(co)norms T (S) and
fuzzy negation N as present in Eqs. (5) and (6), result-
ing on the following expressions for their membership
and non-membership degrees when considering ( ˜x, ˜y)
as input:
µ
⊕
I
= N(T (N(T (x
2
, y
1
)), N(T (x
1
, y
2
)))) (14)
ν
⊕
I
= T (N(T (N(x
1
), N(y
2
))), N(T (N(x
2
), N(y
1
)))) (15)
µ
⊗
I
= T (N(T (N(x
1
), N(y
1
))), N(T (N(x
2
),N(y
2
)))) (16)
ν
⊗
I
= N(T (N(T (x
2
, y
2
)), N(T (x
1
, y
1
)))) (17)
Taking ˜x = (x
1
, x
2
), ˜y = (y
1
, y
2
), the initial quan-
tum stated |φiis the 10-dimensional quantum register:
|φi = |x
1
i⊗|x
2
i⊗|y
1
i⊗|y
2
i⊗|0i⊗|0i⊗|0i⊗|0i.
Then, the quantum representation of the Xor op-
erator ⊕
I
P
can be obtained by translating Eqs. (14)
and (15), respectively resulting in the following QT
compositions:
µ
⊕
I
=M
9
1
◦N
5,6,9
◦T
5,6
9
◦N
5,6
◦T
1,4
6
◦T
2,3
5
(18)
ν
⊕
I
=M
10
1
◦T
7,8
10
◦N
2,3,8
◦T
2,3
8
◦N
2,3
◦N
1,4,7
◦T
1,4
7
◦N
1,4
(19)
Analogously, considering the initial quantum state
|φi, the quantum representation of the Xor operator
⊗
I
P
can be obtained by translating Eqs. (16) and (17),
respectively resulting in QT compositions given as
follows:
µ
⊗
I
=M
9
1
◦T
5,6
9
◦N
2,4,6
◦T
2,4
6
◦N
2,4
◦N
1,3,5
◦T
1,3
5
◦N
1,3
(20)
ν
⊗
I
=M
10
1
◦N
10,7,8
◦T
7,8
10
◦N
7,8
◦T
1,3
8
◦T
2,4
7
(21)
For both quantum representations of membership
functions, it is used 10 qubits: 2 pairs for the in-
puts ( ˜x, ˜y), 4 ancillaries qubits to store intermediate
results and 1 pair for the final result. The member-
ship degree obtained is stored on qubit 9 and the non-
membership degree on qubit 10.
Interpreting Xor Intuitionistic Fuzzy Connectives from Quantum Fuzzy Computing
291
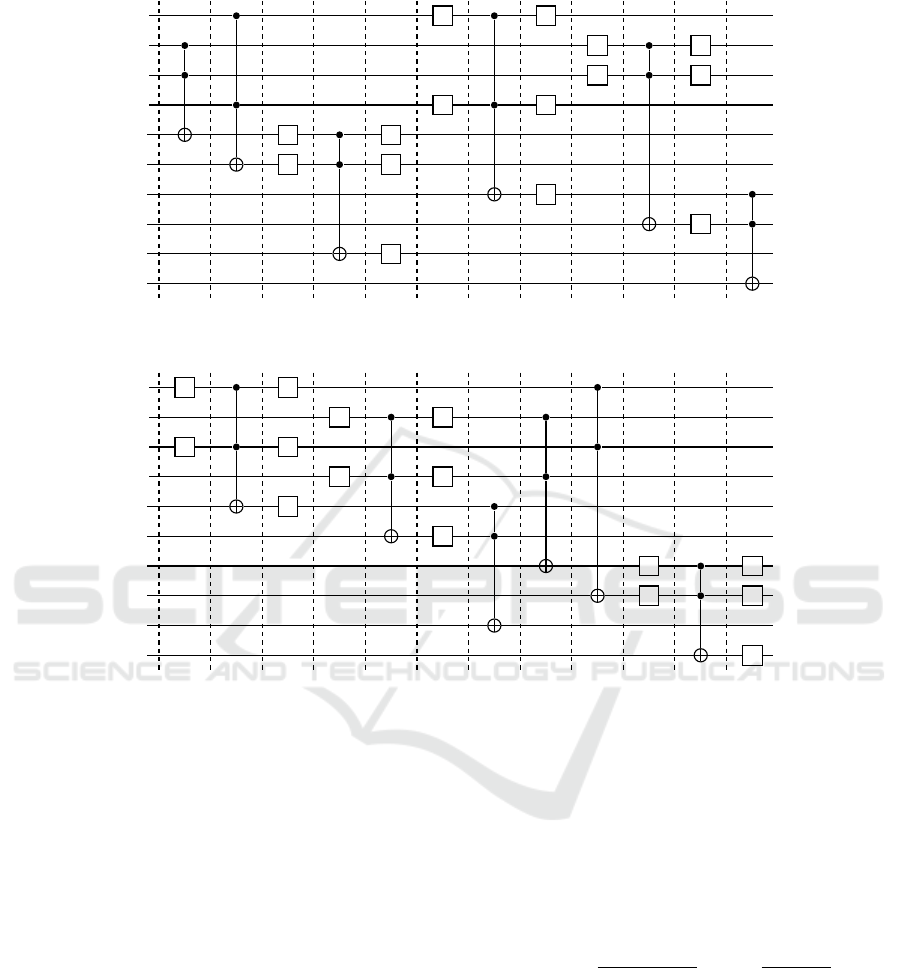
|x
1
i
|x
2
i
|y
1
i
|y
2
i
|0i
|0i
|0i
|0i
|0i
|0i
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
T0
T1 T2
T3
T4
T5 T6
T7
T8
T9
T10
T11 T12
Figure 1: Quantum circuit modelling ⊕
I
P
( ˜x, ˜y).
|x
1
i
|x
2
i
|y
1
i
|y
2
i
|0i
|0i
|0i
|0i
|0i
|0i
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
T0
T1 T2
T3
T4
T5 T6
T7
T8
T9
T10
T11 T12
Figure 2: Quantum circuit modelling ⊗
I
P
( ˜x, ˜y).
4.1 Modelling ⊕
I
P
Quantum Operator
See in Fig. 1 the quantum circuit for the ⊕
I
P
Xor oper-
ator, resulting from the composition of Eq.(18) (from
T1 to T5) and Eq. (19) (from T6 to T12) which is an-
ticipating the measure operations.
Columns in Table 1 show the non-void amplitude
evolution for the most relevant points of this quantum
circuit, with T0 denoting the initial quantum state and
T12 is the final quantum state resulting on ⊕
I
P
Xor
operator obtained from the application of all compo-
sition quantum operators. And, in such columns, the
changed qubits are highlighted.
After performing the circuit in Fig. 1, the measure
operator M
9
1
is applied, that is, on the 9
th
qubit and
related to |1i, it has probability
p
9
⊕
I
(1) = x
1
y
2
+ x
2
y
1
−x
1
x
2
y
1
y
2
,
corresponding to the membership degree of ⊕
I
P
Xor
operator, obtained by the µ
⊕
I
expression. Therefore,
p
9
⊕
I
(1) = µ
⊕
I
P
( ˜x, ˜y)
.
Analogous, the resulting measure operator M
9
0
has
the probability expressed as follows
p
9
⊕
I
(1)(0) = 1 −x
1
y
2
−x
2
y
1
+ x
1
x
2
y
1
y
2
,
corresponding to the complement of the membership
degree of ⊕
I
P
( ˜x, ˜y), meaning that
p
9
⊕
I
(1)(0) = 1 −µ
⊕
I
( ˜x, ˜y).
Thus, the 9
th
qubit is given by the following ex-
pression:
|µ
⊕
I
i =
q
1 −µ
⊕
I
( ˜x, ˜y)|0i+
q
µ
⊕
I
( ˜x, ˜y)|1i.
In addition, by applying the measure operator
M
10
1
, that is, on the 10
th
qubit and related to |1i, the
result quantum state has probability
p
10
⊕
I
(1) = x
1
x
2
+ x
1
y
1
+ x
2
y
2
+ y
1
y
2
−x
1
x
2
y
1
−x
1
x
2
y
2
−x
1
y
1
y
2
−x
2
y
1
y
2
+ x
1
x
2
y
1
y
2
,
corresponding to the non-membership degree of
⊕
I
P
( ˜x, ˜y). Then, it means that
p
10
⊕
I
(1) = ν
⊕
I
( ˜x, ˜y).
FCTA 2019 - 11th International Conference on Fuzzy Computation Theory and Applications
292

Table 1: Evolution of superposition quantum registers in modelling quantum circuit: ⊕
I
P
( ˜x, ˜y).
non-void amplitudes T 0 T 1 T 2 T 5 T 8 T 11 T 12
(1 −x
1
)(1 −x
2
)(1 −y
1
)(1 −y
2
) 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000
(1 −x
1
)(1 −x
2
)(1 −y
1
)y
2
0001000000 0001000000 0001000000 0001000000 0001001000 0001001000 0001001000
(1 −x
1
)(1 −x
2
)y
1
(1 −y
2
) 0010000000 0010000000 0010000000 0010000000 0010000000 0010000100 0010000100
(1 −x
1
)(1 −x
2
)y
1
y
2
0011000000 0011000000 0011000000 0011000000 0011001000 0011001100 0011001101
(1 −x
1
)x
2
(1 −y
1
)(1 −y
2
) 0100000000 0100000000 0100000000 0100000000 0100000000 0100000100 0100000100
(1 −x
1
)x
2
(1 −y
1
)y
2
0101000000 0101000000 0101000000 0101000000 0101001000 0101001100 0101001101
(1 −x
1
)x
2
y
1
(1 −y
2
) 0110000000 0110100000 0110100000 0110100010 0110100010 0110100110 0110100110
(1 −x
1
)x
2
y
1
y
2
0111000000 0111100000 0111100000 0111100010 0111101010 0111101110 0111101111
x
1
(1 −x
2
)(1 −y
1
)(1 −y
2
) 1000000000 1000000000 1000000000 1000000000 1000001000 1000001000 1000001000
x
1
(1 −x
2
)(1 −y
1
)y
2
1001000000 1001000000 1001010000 1001010010 1001011010 1001011010 1001011010
x
1
(1 −x
2
)y
1
(1 −y
2
) 1010000000 1010000000 1010000000 1010000000 1010001000 1010001100 1010001101
x
1
(1 −x
2
)y
1
y
2
1011000000 1011000000 1011010000 1011010010 1011011010 1011011110 1011011111
x
1
x
2
(1 −y
1
)(1 −y
2
) 1100000000 1100000000 1100000000 1100000000 1100001000 1100001100 1100001101
x
1
x
2
(1 −y
1
)y
2
1101000000 1101000000 1101010000 1101010010 1101011010 1101011110 1101011111
x
1
x
2
y
1
(1 −y
2
) 1110000000 1110100000 1110100000 1110100010 1110101010 1110101110 1110101111
x
1
x
2
y
1
y
2
1111000000 1111100000 1111110000 1111110010 1111111010 1111111110 1111111111
In analogous way, the resulting measure operator
M
10
0
has the probability
p
10
⊕
I
(0) = 1 −x
1
x
2
−x
1
y
1
−x
2
y
2
−y
1
y
2
+ x
1
x
2
y
1
+ x
1
x
2
y
2
+ x
1
y
1
y
2
+ x
2
y
1
y
2
−x
1
x
2
y
1
y
2
,
corresponding to the complement of the non-
membership degree of ⊕
I
P
( ˜x, ˜y), that is,
p
10
⊕
I
(0) = 1 −ν
⊕
I
( ˜x, ˜y).
Thus, the 10
th
qubit is given as follows:
|ν
⊕
I
i =
q
1 −ν
⊕
I
( ˜x, ˜y)|0i+
q
ν
⊕
I
( ˜x, ˜y)|1i.
Concluding, the interpretation of intuitionistic
fuzzy values related to the ⊕
I
P
Xor connective is pro-
vided by the pair (|µ
⊕
I
i, |ν
⊕
I
i) of quantum registers.
Remark 4.1. As a relevance, the entanglement of
such qubits makes the fuzzy quantum circuits differ-
ent from circuits modeling other logical approaches.
For instance, by taking the results from ⊕
I
P
Xor
operator one can easily observe that when the mea-
surement applied to the 10
th
qubit is related to |1i,
then it returns 7
th
and 8
th
qubits also related to |1i,
meaning that these three qubits collapse to value 1.
This is a phenomenon that does not occur in stan-
dard fuzzy set theory: the result of measurement (ob-
servation) affects the state of other arguments.
So, these values can be used in next calculations
performed by other functions but involving such qubit
systems, independently of the reuse of circuit inputs,
which are also restored from 1
rs
to 4
th
qubits.
4.2 Modelling ⊗
I
P
Quantum Operator
Fig. 2 shows the ⊗
I
P
quantum circuit related to com-
position of Eq.(20) (from T1 to T7) and Eq.(21) (from
T8 to T12) without the measure operations.
Analogously, based on the entanglement of such
qubits, one can easily observe that when the measure-
ment 10
th
qubit is related to |0i simultaneously, the
5
th
and 6
th
qubits are also related to |0i, meaning that
these three qubits collapse to value 0.
Moreover, see columns in Table 2 presenting the
evolution of the non-void amplitudes for the most rel-
evant points of this circuit, with T0 being the initial
quantum state and T12 is the final quantum state, ie,
the quantum state resulting after the application of all
the quantum operators related to the ⊗
I
P
( ˜x, ˜y).
After executing this circuit, applying the measure
operator M
9
1
, that is, on the 9
th
qubit and related to
|1i, it has the following distribution of probability:
p
9
⊗
I
P
(1) = x
1
x
2
+ x
1
y
2
+ x
2
y
1
+ y
1
y
2
−x
1
x
2
y
1
−
x
1
x
2
y
2
−x
1
y
1
y
2
−x
2
y
1
y
2
+ x
1
x
2
y
1
y
2
,
corresponding to the membership degree of ⊗
I
P
( ˜x, ˜y),
then we obtain that
p
9
⊗
I
(1) = µ
⊗
I
P
( ˜x, ˜y)
. (22)
Analogously, the measure M
9
0
has the following
probability
p
9
⊗
I
(0) = 1 −x
1
x
2
−x
1
y
2
−x
2
y
1
−y
1
y
2
+ x
1
x
2
y
1
+
x
1
x
2
y
2
+ x
1
y
1
y
2
+ x
2
y
1
y
2
−x
1
x
2
y
1
y
2
,
which means that the complement of the membership
degree of ⊗
I
P
Xor operator is given as follows
p
9
⊗
I
(0) = 1 −µ
⊗
I
P
( ˜x, ˜y). (23)
Thus, By Eqs. (22) and (23) we have that the 9
th
qubit can be given as follows:
|µ
⊗
I
i =
q
1 −µ
⊗
I
( ˜x, ˜y)|0i+
q
µ
⊗
I
( ˜x, ˜y)|1i.
Interpreting Xor Intuitionistic Fuzzy Connectives from Quantum Fuzzy Computing
293

Table 2: Evolution of superposition quantum registers in modelling quantum circuit: ⊗
I
P
( ˜x, ˜y).
non-void amplitudes T 0 T 3 T 6 T 7 T 8 T 11 T 12
(1−x
1
)(1−x
2
)(1−y
1
)(1−y
2
) 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000
(1 −x
1
)(1 −x
2
)(1 −y
1
)(1 −y
2
) 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000
(1 −x
1
)(1 −x
2
)(1 −y
1
)y
2
0001000000 0001000000 0001010000 0001010000 0001010000 0001010000 0001010000
(1 −x
1
)(1 −x
2
)y
1
(1 −y
2
) 0010000000 0010100000 0010100000 0010100000 0010100000 0010100000 0010100000
(1 −x
1
)(1 −x
2
)y
1
y
2
0011000000 0011100000 0011110000 0011110010 0011110010 0011110010 0011110010
(1 −x
1
)x
2
(1 −y
1
)(1 −y
2
) 0100000000 0100000000 0100010000 0100010000 0100010000 0100010000 0100010000
(1 −x
1
)x
2
(1 −y
1
)y
2
0101000000 0101000000 0101010000 0101010000 0101011000 0101011000 0101011001
(1 −x
1
)x
2
y
1
(1 −y
2
)
0110000000 0110100000 0110110000 0110110010 0110110010 0110110010 0110110010
(1 −x
1
)x
2
y
1
y
2
0111000000 0111100000 0111110000 0111110010 0111111010 0111111010 0111111011
x
1
(1 −x
2
)(1 −y
1
)(1 −y
2
) 1000000000 1000100000 1000100000 1000100000 1000100000 1000100000 1000100000
x
1
(1 −x
2
)(1 −y
1
)y
2
1001000000 1001100000 1001110000 1001110010 1001110010 1001110010 1001110010
x
1
(1 −x
2
)y
1
(1 −y
2
) 1010000000 1010100000 1010100000 1010100000 1010100000 1010100100 1010100101
x
1
(1 −x
2
)y
1
y
2
1011000000 1011100000 1011110000 1011110010 1011110010 1011110110 1011110111
x
1
x
2
(1 −y
1
)(1 −y
2
) 1100000000 1100100000 1100110000 1100110010 1100110010 1100110010 1100110010
x
1
x
2
(1 −y
1
)y
2
1101000000 1101100000 1101110000 1101110010 1101111010 1101111010 1101111011
x
1
x
2
y
1
(1 −y
2
) 1110000000 1110100000 1110110000 1110110010 1110110010 1110110110 1110110111
x
1
x
2
y
1
y
2
1111000000 1111100000 1111110000 1111110010 1111111010 1111111110 1111111111
Moreover, applying the measure operator M
10
1
,
that is, measurement on the 10
th
qubit and related to
|1i, the resulting probability is given as follows:
p
10
⊗
I
P
(1) = x
1
y
1
+ x
2
y
2
−x
1
x
2
y
1
y
2
,
which corresponds to the non-membership degree of
⊗
I
( ˜x, ˜y), therefore, we obtain that
p
10
⊗
I
(1) = ν
⊗
I
( ˜x, ˜y). (24)
Analogous, the measure M
10
0
has the probability
p
10
⊗
I
(0) = 1 −x
1
y
1
−x
2
y
2
+ x
1
x
2
y
1
y
2
,
corresponding to the complement of the non-
membership degree of ⊗
I
P
( ˜x, ˜y), that is,
p
10
⊗
I
(0) = 1 −ν
⊗
I
( ˜x, ˜y). (25)
And finally, by Eqs. (24) and (25) we have that the
10
th
qubit is given by:
|ν
⊗
I
i =
q
1 −ν
⊗
I
( ˜x, ˜y)|0i+
q
ν
⊗
I
( ˜x, ˜y)|1i.
Concluding, the interpretation of intuitionistic
fuzzy values related to the ⊗
I
P
Xor connective is pro-
vided by the pair (|µ
⊗
I
i, |ν
⊗
I
i) of quantum registers.
5 CONCLUSIONS
This paper describes the interpretation of two classes
of Xor operations on A-IFS through concepts of QC.
It was modelled using a quantum register using oper-
ations over fuzzy sets described by QTs.
Therefore, the presented approach to interpreta-
tion of intuitionistic fuzzy valued from quantum reg-
isters and quantum states shows another basic con-
struction in the specification of fuzzy expert systems
from QC, in order to obtain new information tech-
nologies based on intuitionistic fuzzy approach.
Computer systems based on A-IFL and performed
over quantum computers may be able to generate
an output considering the manipulation of inaccurate
data and also dealing with imprecision in the model of
rule-based system, by taking advantage of properties
as quantum parallelism.
Further work aims at consolidation of this specifi-
cation including not only other fuzzy connectives but
also constructors (e.i. automorphisms and reductions)
and the corresponding extension of (de)fuzzyfication
methodology from formal structures provided by QC.
ACKNOWLEDGEMENTS
This work is partially supported by the Brazil-
ian grants: 309533/2013-9 (CNPq), 448766/2014-
0 (MCTI/CNPQ), PROCAD/CAPES/Brasil Finance
Code 001, and PqG-FAPERGS Edital 02/2017
(17/2551-0001207-0).
REFERENCES
Atanassov, K. and Gargov, G. (1998). Elements ofintuition-
istic fuzzy logic. Fuzzy Sets and Systs., 9(1):39–52.
Atanassov, K. T. (1986). Intuitionistic fuzzy sets. Fuzzy
Sets and Systems, 20:87–96.
Atanassov, K. T. (2006). On intuitionistic fuzzy negations.
In Computational Intelligence, Theory and Applica-
tions, pages 159–167. Springer.
Atanassov, K. T. (2016). Mathematics of intuitionistic fuzzy
sets. In Fuzzy Logic in Its 50th Year - New Develop-
ments, Directions and Challenges, pages 61–86.
FCTA 2019 - 11th International Conference on Fuzzy Computation Theory and Applications
294

Atanassov, K. T. (2017). Intuitionistic Fuzzy Logics, vol-
ume 351 of Studies in Fuzziness and Soft Computing.
Springer.
Avila, A., Schmalfuss, M., Reiser, R., and Kreinovich, V.
(2015). Fuzzy xor classes from quantum computing.
In International Conference on Artificial Intelligence
and Soft Computing, pages 305–317. Springer.
Bedregal, B., Reiser, R., and Dimuro, G. (2013).
Revising XOR–implications: Classes of fuzzy
(Co)implications based on fuzzy XOR (XNOR) con-
nectives. International Journal of Uncertainty, Fuzzi-
ness and Knowlegde– Based Systems, 14(6):1–29.
Bertini, C. and Leporini, R. (2017). A fuzzy approach to
quantum logical computation. Fuzzy Sets and Sys-
tems, 317:44–60.
Chiara, M. L. D., Giuntini, R., Sergioli, G., and Leporini, R.
(2018). A many-valued approach to quantum compu-
tational logics. Fuzzy Sets and Systems, 335:94–111.
Freytes, H., Giuntini, R., Sergioli, G., and Aricò, A. (2010).
Representing fuzzy structures in quantum computa-
tion with mixed states. In 40th IEEE International
Symposium on Multiple-Valued Logic, ISMVL 2010,
Barcelona, Spain, 26-28 May 2010, pages 162–166.
Hájek, P. (1998). Metamathematics of fuzzy logic, volume 4.
Springer Science & Business Media.
He, X., Li, Y., Qin, K., and Meng, D. (2017). On the char-
acterizations of fuzzy xnor connectives. Journal of
Intelligent and Fuzzy Systems, 32(3):2733–2745.
Imre, S. and Balázs, F. (2005). Quantum Computing and
Communications An Engineering Approach. Johm
Wiley & Sons, Ltd.
Kaye, P., Laflamme, R., and Mosca, M. (2007). An Intro-
duction to Quantum Computing. Oxford University
Press.
Klement, E. P., Mesiar, R., and Pap, E. (2013). Triangu-
lar norms, volume 8. Springer Science & Business
Media.
Kosheleva, O., Reiser, R., and Kreinovich, V. (2015).
Formalizing the informal, precisiating the imprecise:
How fuzzy logic can help mathematicians and physi-
cists by formalizing their intuitive ideas. In Trillas, E.,
Seising, R., and Kacprycz, J., editors, Fuzzy Logic:
Towards the Future, volume 325 of LNCS, pages 301–
321. Springer International Publishing, Netherlands,
2015.
Kreinovich, V., Kohout, L., and Kim, E. (2009). Similarity
between quantum logic and fuzzy logic.
Li, P., Song, K., and Yang, E. (2010). Quantum genetic
algorithm and its application to designing fuzzy neu-
ral controller. In Sixth International Conference on
Natural Computation, ICNC 2010, Yantai, Shandong,
China, 10-12 August 2010, pages 2994–2998.
Mannucci, M. (2006). Quantum fuzzy sets: Blending
fuzzy set theory and quantum computation. CoRR,
abs/cs/0604064.
Nielsen, M. and Chuang, I. (2003). Quantum Computa-
tion and Quantum Information. Cambridge University
Publisher, Cambridge.
Perkowski, M. A., Chrzanowska-Jeske, M., Mishchenko,
A., Song, X., Al-Rabadi, A., Massey, B., Kerntopf,
P., Buller, A., Józwiak, L., and Coppola, A. J. (2001).
Regular realization of symmetric functions using re-
versible logic. In Euromicro Symposium on Digital
Systems Design 2001 (Euro-DSD 2001), 4-6 Septem-
ber 2001, Warsaw, Poland, pages 245–253.
Pykacz, J. (1993). Fuzzy quantum logic i. International
Journal of Theoretical Physics, 32:1691–1708.
Raghuvanshi, A. and Perkowski, M. A. (2010). Fuzzy
quantum circuits to model emotional behaviors of hu-
manoid robots. In Proceedings of the IEEE Congress
on Evolutionary Computation, CEC 2010, Barcelona,
Spain, 18-23 July 2010, pages 1–8.
Reiser, R., Lemke, A., de Avila, A. B., Vieira, J., Pilla,
M. L., and Bois, A. R. D. (2016). Interpretations on
quantum fuzzy computing: Intuitionistic fuzzy opera-
tions ×quantum operators. Electr. Notes Theor. Com-
put. Sci, 324:135–150.
Rigatos, G. G. and Tzafestas, S. G. (2002). Parallelization
of a fuzzy control algorithm using quantum computa-
tion. IEEE Trans. Fuzzy Systems, 10(4):451–460.
Sriboonchitta, S., Nguyen, H. T., Kosheleva, O.,
Kreinovich, V., and Nguyen, T. N. (2019). Quantum
approach explains the need for expert knowledge: On
the example of econometrics. In Structural Changes
and their Econometric Modeling, pages 191–199.
Interpreting Xor Intuitionistic Fuzzy Connectives from Quantum Fuzzy Computing
295
