
Playing Iterated Rock-Paper-Scissors with an Evolutionary Algorithm
R
´
emi B
´
edard-Couture
1
and Nawwaf Kharma
2
1
Department of Software Engineering,
´
Ecole de Technologie Sup
´
erieure, Montreal, Canada
2
Department of Electrical and Computer Engineering, Concordia University, Montreal, Canada
Keywords:
Evolutionary Algorithms, Learning Algorithms, Game Theory, Game Playing Agents, Rock-Paper-Scissors,
RoShamBo.
Abstract:
Evolutionary algorithms are capable offline optimizers, but are usually left out as a good option for a game-
playing artificial intelligence. This study tests a genetic algorithm specifically developed to compete in a
Rock-Paper-Scissors competition against the latest opponent from each type of algorithm. The challenge is
big since the other players have already seen multiple revisions and are now at the top of the leaderboard. Even
though the presented algorithm was not able to take the crown (it came second), the results are encouraging
enough to think that against a bigger pool of opponents of varying difficulty it would be in the top tier of
players since it was compared only to the best. This is no small feat since this is an example of how a carefully
designed evolutionary algorithm can act as a rapid adaptive learner, rather than a slow offline optimizer.
1 INTRODUCTION
Game-playing artificial intelligence has always been
of great interest to the research community. Games
like chess and poker are the subjects of many publi-
cations and competitions, but the game of RPS (short
for Rock-Paper-Scissors, also known as RoShamBo)
never had much interest because it seems so trivial.
Many people think that always playing random is the
best strategy, but that is necessarily true when the
game is repeated multiple times with the same op-
ponent. The first official RPS competition (Billings,
1999a), led to a very innovative algorithm that em-
ployed a meta-strategy (Egnor, 2000). Over the years,
game predictors based on different algorithms such
as history matching, statistical methods or neural net-
works, were improved so much that they can now
win more than 75% of their matches (Knoll, 2011).
Among popular artificial intelligence techniques, evo-
lutionary algorithms (EAs) are competent offline opti-
mizers, but to compete against the others in this game,
they will need to become fast on-line learners, adapt-
ing quickly to the changing strategies of the opponent.
This is the main challenge we faced, one that neces-
sitated a highly customized EA, a competitive player
whose architecture and performance are described in
this paper.
It is common belief that always playing random
is the best strategy (also known as the Nash equilib-
rium). This is true if all the opponents also use that
strategy, however as soon as one player is not purely
random, it is possible to exploit, thus gaining advan-
tage over the rest of the population. This is further
studied in (Bi and Zhou, 2014; Wang et al., 2014).
Due to the nature of the game being highly ran-
dom, any algorithm using history matching tech-
niques will be prone to detection by other intelligent
algorithms. The method proposed in the paper is sim-
ilar to an LCS (Learning Classifier System) which
might be more applicable to other real-world prob-
lems such as workload scheduling or data mining.
2 A BRIEF HISTORY OF RPS
COMPETITIONS
Competitions are good to drive progress and often
help to bring novel ideas to existing algorithms. There
is currently a popular website (Knoll, 2011) hosting
an ongoing competition for RPS algorithms, where
bots (algorithms able to play a game similarly to hu-
mans) go against each others for matches of a thou-
sand rounds. In this context, a round consists of one
action from each opponent, drawing from the set of
Rock, Paper or Scissors. The final score of a match is
the difference between rounds won and rounds lost.
Bédard-Couture, R. and Kharma, N.
Playing Iterated Rock-Paper-Scissors with an Evolutionary Algorithm.
DOI: 10.5220/0008175902050212
In Proceedings of the 11th International Joint Conference on Computational Intelligence (IJCCI 2019), pages 205-212
ISBN: 978-989-758-384-1
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
205

2.1 First International RoShamBo
Competition
In 1999, Darse Billings, a researcher at the Uni-
versity of Alberta organized the First International
RoShamBo Competition. The format of the compe-
tition and the results can be found on his website
(Billings, 1999a). In this competition, every player
competes against every other player in matches of a
thousand rounds each. If the score is between minus
fifty and plus fifty, it is a tie. The results are reported
using two ranking systems. The first one is Open
Ranking where the rank is determined by the sum of
the scores of all matches played, while the Best of the
Best considers only the number of matches won. An
analysis of the participating algorithms revealed that
all the techniques used could be grouped under two
main families of algorithms. Programs either used a
direct history method where the predictor is looking
at the history for matching patterns or alternatively
used statistical methods such as Markov Models or
frequency counters.
The winner of the first competition was a pro-
gram named Iocaine Powder, developed by Dan Eg-
nor (Egnor, 2000). The source code can be found on-
line in the compilation of all the participants (Billings,
1999b). This bot uses a direct history method along
with a meta-strategy called Sicilian reasoning. The
concept of Sicilian reasoning comes from the movie
The Princess Bride. It is a meta-strategy that incorpo-
rates the level of prediction the opponent is using and
allows the algorithm to evaluate which degree of pre-
diction (simple-guessing, second-guessing or triple-
guessing) is best performing. It also allows the al-
gorithm to evaluate if the opponent is using a similar
meta-strategy. On top of that, the Iocaine Powder bot
also uses multiple strategies and a meta-meta-strategy
and shows full understanding of the complexity of
this game. Full description of the algorithm with its
source code can be found online (Billings, 1999b).
2.2 Second International RoShamBo
Competition
A second competition was held the following year
(Billings, 2000a) based on the same rules. It also in-
cluded a test suite were participants could test their
algorithm against the winners of the previous com-
petition, hoping to raise the level of the new submis-
sions. Although this new generation saw some im-
provement, most algorithms were inspired by the pre-
vious winner, Iocaine Powder. However, even with
access to its source code, the new entries did not im-
prove much on its idea (except for the new winner)
since Iocaine Powder still managed to finish in third
place, overall.
The winner of the second event was Greenberg by
Andrzej Nagorko which is a direct descendant of Io-
caine Powder. Although its source code is available
online, it is not documented nor described so it is hard
to understand the improvements executed on its pre-
decessor, but it appears to use the same idea of multi-
ple strategies along with Sicilian reasoning.
2.3 RPSContest
Eleven years later, Byron Knoll reopened the compe-
tition through an online platform known as RPSCon-
test (Knoll, 2011). Although there has not been any
update since 2012, the platform still works today and
the leader board is automatically kept up to date. The
format of the competition is slightly different from the
two previous ones. The programs must be submitted
in Python and the CPU limit is set to five seconds per
match. The ranking is also less representative than
the previous ranking schemes since it is based on the
average win ratio of random matches. The win ratio
is the number of victories divided by the total number
of matches, weighted more heavily on recent matches.
There is also no limit placed on the number of submis-
sions or their content. It is common to see an author
submitting more than ten versions of the same algo-
rithm. It is obvious that duplicating a better than av-
erage bot a hundred times will have a negative effect
on the ranking of all the other algorithms.
Daniel Lu provided a comprehensive summary of
the most common strategies and meta-strategies for
playing RPS (Lu, 2011). Following the two Interna-
tional RoShamBo Competitions, bots based on his-
tory matching or statistical methods were proven to
work well, but having an ongoing online tournament
allowed new ideas to emerge. Notably, some of the
top players are now using neural networks to analyze
the emerging history of a game and hence, predict the
opponent’s next move. Surprisingly, only two bots in
the leader board are using EAs and they are ranked
below average.
We reviewed the bots on the first page of the leader
board (top 50) to include only the best (usually latest)
version of an algorithm and exclude all other versions.
This gave us a succinct list of the latest versions of
the best performing algorithms. The rest of the list
(comprising of weaker algorithms) was skipped over
except for any EA-based program.
At the time of this study, the number one bot
on the leader board was Tweak the best. This bot
uses multiple strategies and meta-strategies with a
Markov Model to make its prediction. The next bot to
ECTA 2019 - 11th International Conference on Evolutionary Computation Theory and Applications
206

use a different type of algorithm is dllu1 randomer.
Ranked second, it is very similar to Iocaine Pow-
der (based on direct history) but with a higher level
of meta-strategies. It is really amazing to see that
Iocaine Powder is still one of the best performing
strategies for this game, even though its rank might
be the result of a greater popularity within the RPS-
playing community. The best neural network bot,
NN2 10 0.99 0.25, is ranked 39
th
and the rest of the
top 50 bots are all based on either Markov Models
(such as Context Tree Weighting) or history matching
(mostly described as DNA sequencers). Lastly, the
best bot using an EA is X-Gene v4 and sits at position
1989 in the leader board.
3 REVIEW OF ACADEMIC
LITERATURE
The academic literature related specifically to genetic
algorithms applied to Rock-Paper-Scissors is rather
limited. In 2000, researchers from Japan conducted
a similar experiment by constructing a genetic algo-
rithm to play RPS (Ali et al., 2000). The results they
reported were positive against systematic and human
players, but did not show the performance of their al-
gorithm against advanced strategies and other algo-
rithms. Some papers will study different aspects of
the game (Wang et al., 2014; Lebiere and Anderson,
2011; Billings, 2000b), while others apply EAs to
game theory (Xavier et al., 2013; Kojima et al., 1997).
Iterated Rock-Paper-Scissors is a unique problem that
can not be assimilated in general game theory or other
popular games such as chess.
A history matching predictor based on an evolu-
tionary algorithm was used for reservoir simulation in
the oil industry (Xavier et al., 2013), but their contri-
bution is not applicable to the problem of competing
predictors.
In a recent study of social behaviour in Rock-
Paper-Scissors tournaments (Wang et al., 2014), re-
searchers demonstrated that in a small population, the
strategies used to play the game follow a cyclic mo-
tion to shift between the available actions. Their study
also shows that the strategies in a population are af-
fected by the magnitude of the reward. Understanding
how humans play in a variety of contexts adds valu-
able insights to those working on artificial intelligence
algorithms, as models are often inspired by solutions
found in nature.
Another research paper about decision making
(Lebiere and Anderson, 2011) explains how humans
play in sequential decision making and how they are
able to learn and recognize multiple patterns at once.
The human players make decisions that are similar to
those recommended by statistical models. The human
players balanced safe and risky choices by taking into
account both the recency of events as well as their fre-
quency.
More related to the game of Rock-Paper-Scissors,
a group of researchers published a paper demonstrat-
ing the effectiveness of a simple statistical predictor
(Valdez et al., 2014). They used the Beat Frequent
Method predictor and developed a framework to op-
timize it. Since there is a strong bias with meta-
strategies based on Iocaine Powder in the Second In-
ternational RoShamBo Competition, they focused on
the test suite of the First International RoShamBo
Competition. Their results were successful in improv-
ing the basic predictor and demonstrated that using
a shorter history is more effective, especially against
weak opponents. Still, their predictor was unable to
beat strong bots such as Iocaine Powder. Despite
its lackluster performance, another paper on the same
predictor was published in 2015 (Valdez et al., 2015).
The literature on EAs is vast and rich, and cover-
ing the latest advances in this field is out of the scope
of this study. The reader should refer to (Eiben et al.,
2003) and (Koza, 1992) for a proper introduction to
both evolutionary and genetic algorithms. There is
also a vast number of publications on AI in games,
but the focus of this paper is on the development and
utilization of EA techniques in the playing of iterated
Rock-Paper-Scissors.
4 METHODOLOGY
The evolutionary algorithm described in this section
is somewhat similar to a Pittsburgh-style LCS algo-
rithm, but designed to be highly adaptive, with fitness
values used both for the rules and the individuals. See
(Urbanowicz and Moore, 2009) for a complete intro-
duction to LCS algorithms.
An overview of our algorithm is presented in fig-
ure 1; it illustrates the steps the EA takes, at every
round, to make a prediction. For the first hundred
rounds, the algorithm executes random moves, to al-
low the EA population to be at least partially molded
by information about the opponent’s play style. This
could be circumvented by reusing prior knowledge of
good strategies established in our experiments.
4.1 Exploration
The exploration phase is governed by a genetic algo-
rithm, which its main components are described in the
following sections.
Playing Iterated Rock-Paper-Scissors with an Evolutionary Algorithm
207

Figure 1: Diagram of the Algorithm.
4.1.1 Representation
An individual consists of a set of rules and has its own
fitness value and learning rate. A rule is defined by a
context, an action and a target round, along with a
separate fitness value and learning rate. The match-
ing of a rule is done on the history string, which is
stored from the opponent’s point of view. This repre-
sentation was chosen because it allows an individual
to capture the dependencies between the transitions of
played rules by using a separate fitness value.
Context. The context is a sequence of the length
of the window size that represents a possible history
of plays, using the characters W (Win), L (Lose), D
(Draw) and a wildcard character. Using wild cards al-
lows the EA to capture simple strategies easily. It is
important to analyze the history from a win, lose or
draw perspective since the actions have a cyclical de-
pendency (R < P < S < R ...). The outcome is what
is important for this algorithm.
Action. The three possible actions are win (W), lose
(L) or draw (D). The win action means play the move
that would have won for the target round; similarly
for lose and draw.
Target. The target range is between one and the size
of the window, since round zero is the current round
(the round the EA is trying to predict).
4.1.2 Initialization
The population is initialized randomly. For each con-
text, both action and target are selected randomly us-
ing a uniform distribution.
4.1.3 Parent Selection
A new population is created at every round of the
game. The parent selection process uses tournament
selection without replacement and with a tournament
size of 3. The algorithm also uses a tolerance of
5% when comparing fitness values; two individuals
whose fitness values are within tolerance are consid-
ered equally fit. When two or more individuals are
equally fit, one of them is chosen randomly. It is pos-
sible to wait a few rounds before generating a new
population, but the algorithm reported better results
by evolving every round.
4.1.4 Genetic Operators
Crossover. Two-point crossover is performed twice
on the parents, producing 4 children. Generating
more children by crossover is helpful for exploring
the search space. The implementation follows the
standard two-point crossover: pick two position ran-
domly and swap the middle part between both par-
ents. The learning rate and winning rate of the chil-
dren are initialized the same way as new individuals
(set to 0).
ECTA 2019 - 11th International Conference on Evolutionary Computation Theory and Applications
208
Mutation. Every child is run through the mutation
operation. The overall mutation probability is 0.4.
Since every individual has 256 rules and the mutation
distribution is uniformly random over the rules, the
probability of rule mutation is 0.4/256. If a mutation
is applied to a rule, it will either change its action or
target to any other action or target, respectively, with
equal probability.
4.1.5 Survivor Selection
Crowding. In deterministic crowding with multiple
children, the distances between all the children and
both parents are measured, using both the action and
target parts of rules to compute distance. Children
are divided into two groups, each comprising a parent
and the children that are closer to it than the other par-
ent. The fittest child in each group competes with the
parent of that group and the fitter individual is passed
on to the next generation. This way of implementing
crowding allows exploring more of the search space
by generating more than two children while ensuring
that the size of the population stays constant through-
out the generations. Equations 1 and 2 describe how
the distance between two individuals is measured. In
equation 1, the values of pairwise distances are de-
scribed along with their condition. a
i
and a
j
refer to
the actions and t
i
and t
j
to the targets of the two rules.
A distance value of 1 is given when a feature is dif-
ferent, without comparing the actual values since they
are independent. A higher distance value of 3 is given
when both the actions and targets are different to em-
phasize the double mutation that would be required to
make them identical (only one of the two can be mu-
tated per generation). Finally, the distance measure
presented in equation 2 is simply the sum of the dis-
tances between every pair of corresponding rules, in
the two individuals.
d(i, j) =
3 if a
i
6= a
j
and t
i
6= t
j
1 else if a
i
6= a
j
or t
i
6= t
j
0 otherwise
(1)
D(i, j) =
∑
i, j
d(i, j) (2)
Injection. The EA uses injection to help maintain
diversity. The injection rate is set at 5% of population
size. When creating the population of the next gen-
eration, the worst 5% of the current generation is re-
placed by new, randomly initialized individuals. The
fitness of the newly created individuals is initialized
by replaying the last 16 rounds, which was found to
give a good approximation of their fitness value, as if
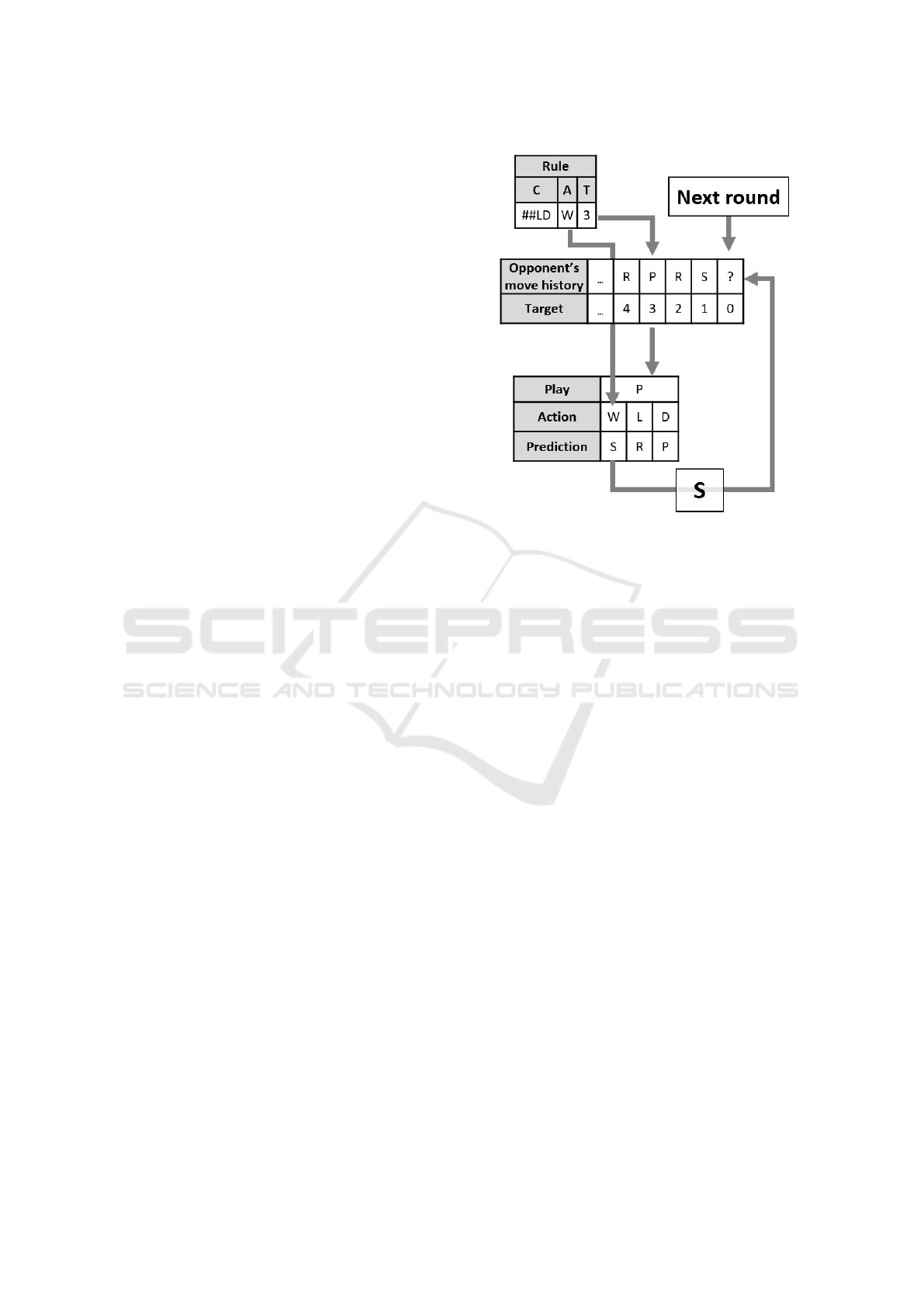
Figure 2: Computing the Prediction of a Rule.
they had been in the population from the beginning of
the match.
Elitism. The algorithm also uses elitism by copying
the current hero into the new population.
4.2 Context Matching
The context matching step consist of identifying
which rules are applicable given the current history
by comparing the history string with all the contexts,
taking into account wildcards.
4.3 Prediction Calculation
Each applicable rule computes the prediction of the
opponent’s next move. The target of the rule is used
to extract the move played by the opponent at that spe-
cific round of the game (the target value is relative to
the most recently played round, where a target value
of 1 represents the latest round played). The action of
the rule can be read like this: play the move that will
[win/lose/draw] against move [Rock/Paper/Scissors],
given the opponent’s move history. In the example il-
lustrated in figure 2, the targeted move is P (Paper)
and action is W (Win), so the move that would win
against Paper is Scissors. Thus, the prediction is that
the opponent will play Scissors on the next round.
Playing Iterated Rock-Paper-Scissors with an Evolutionary Algorithm
209

4.4 Rule Selection
Once all applicable rules have made their prediction
on the opponent’s next move, the individual will se-
lect the one with the highest fitness value for its final
prediction. Fitness values of the rules are compared
using a tolerance and in case of a tie, a random se-
lection is made. This selection has an impact on the
fitness of the individual as a whole.
4.5 Hero Selection
The individual with the highest fitness value is se-
lected as the hero and the algorithm will use its pre-
diction to counter the opponent’s next move. The fit-
ness evaluation process is the same one as the rule
selection process (see section 4.4). In order to capture
the relationships between context as the match pro-
ceeds, the selection of a new hero only happens every
4 rounds (synchronized with the window size).
The final step of the EA is to determine if the hero
is good enough to play by comparing its fitness to a
predefined threshold (set to 0.75). This is a defensive
measure that instructs our player to make a random
move if the fitness of the hero is too low.
4.6 Fitness Update
The algorithm has two levels of fitness values, rep-
resented by the symbol Ω, and calculated using the
same formula (equation 3) shown below. Each rule
has its own fitness value, and each individual (con-
sisting of a set of rules) also has its own fitness value.
Once the round is played, the opponent’s move is
compared to the predictions of both the matching
rules and the individuals of the population, and their
fitness values are updated following equation 3. The
initial fitness value is 0 and β is the learning rate,
which is set to 0.4 for the entire algorithm. One would
think that in order to be highly adaptive, a high learn-
ing rate would be required, but anything greater than
0.5 induces overfitting. Self-adaptation of the learn-
ing rate, at the individual level, might yield better re-
sults. With this equation, the range of possible fitness
values is between 0 and 1 inclusively.
Ω(t +1) =
(
Ω(t) · (1 − β) + 1 · β, if predicted right
Ω(t) · (1 − β) + 0 · β, otherwise
(3)
4.7 Termination Criteria
The algorithm is active throughout the whole match.
The only termination criteria is the end of the match,
or equivalently a thousand rounds.
Table 1: Summary of the Evolutionary Algorithm for RPS.
Representation Integer
Recombination Two point crossover
Recombination probability 80%
Mutation Random variation
Mutation probability 40%
Parent selection Tournament(k=3)
Survival selection Deterministic crowding
Injection 5%
Elitism 1
Population size 500
Number of offspring 4
Initialization Random
Termination condition 1000 rounds
Window size 4
4.8 Algorithm Parameters
Table 1 presents the different parameters required to
run the algorithm, which were determined empiri-
cally, except for the termination condition that is set
by the context of the competition. As EAs are gener-
ally robust, changes to those values did not have a sig-
nificant impact on the results. The exceptions to that
were the population size and window size, which have
a larger impact on the search space. A population of
500 was found to be optimal as lower values would
degrade the performance too much while higher val-
ues would only bring marginal benefits. Smaller win-
dow sizes did not seem to capture complex strategies
and bigger window sizes had too much impact on the
computational cost of the algorithm.
5 RESULTS
The results are summarized in table 2 and two match
examples are illustrated in figure 3. The metric used
to rank a bot is the percentage of matches won over
all the matches played. This gives the overall per-
formance but hides the details of performance against
each specific opponent. The percentage of rounds
won over all the rounds played gives a second layer of
detail as to the efficiency of the algorithm, but suffers
the same problem of hiding the specific one-on-one
performance.
In any EA, the diversity of the population is criti-
cal to its success, thus it is important to have an accu-
rate measurement method to ensure equilibrium be-
tween exploitation and exploration. Every time the
population is evolved, the diversity of individuals is
measured by sampling 10% of the population. For
instance, if the population is made from a hundred
individuals, ten are selected randomly and compared
to each other. The distance measure is the same as
ECTA 2019 - 11th International Conference on Evolutionary Computation Theory and Applications
210

Figure 3: Outcomes and diversity measurements of one match (out of ten) against two opponents. These examples were care-
fully selected to demonstrate the differences in behavior of a completely random opponent as opposed to a more predictable
strategy. The top part of the graph shows the win ratio (
Wins
Losses
) and percentage(
Wins
Rounds
) of the algorithm and the grey zones
mark the rounds that it played random. The dark lines identify short sequences where the algorithm took action. In order
to win, the win ratio of the algorith should be above 1 at the end of the match. The bottom part of the figure shows the
mean and standard deviation of the diversity measurements. Crowding and injection help to maintain such high diversity and
occasionally the diversity would collapse but only for a few rounds.
that used for the deterministic crowding (presented at
equation 2). The distances between every pair of in-
dividuals in the sample are calculated and hence, the
mean and standard deviation of those distance values
are used as approximate, but on average accurate, re-
flections of population diversity. Further explanations
of the performance measures are provided within the
legend of figure 3.
Table 2: Results of a 10 matches tournament.
Rank Bot
Matches
Won(%)
Rounds
Won(%)
1 dllu1 randomer 74 34.4
2 GAiRPS 60 33.3
3 NN2 10 0.99 0.25 56 36
4 Tweak the best 52 37.1
5 Random 38 33.1
6 X-Gene v4 14 27.2
To measure the quality of the algorithm, an of-
fline tournament was held against the best bots for
each category of algorithm. The four opponents are
Tweak the best (Markov model), dllu1 randomer (his-
tory matching), NN2 10 0.99 0.25 (neural networks)
and X-Gene V4 (genetic algorithm). An extra bot
always playing random was also included as a con-
trol. Each algorithm played ten matches against every
other one and the results are reported in tables 2. Ta-
ble 3 reports the number of games won (out of 10)
against each of the other types of algorithm, provid-
ing additional information on the performance of the
proposed algorithm.
The results are quite positive, as our customized
Evolutionary Algorithm (named GAiRPS) beat the
other EA and took second place. The ranking is
Table 3: Number of matches won against each opponent.
Opponent Wins (out of 10)
dllu1 randomer 4
NN2 10 0.99 0.25 6
Tweak the best 8
Random 6
X-Gene v4 6
close to the official leader board with only X-Gene
V4 placed below the random bot, but the top three al-
gorithms have swapped places. Again, the bot using a
history matching approach similar to Iocaine Powder
has a definitive edge over others.
We were able to demonstrate that an EA could
perform better than a random bot, and compete with
other types of artificial intelligence methods in play-
ing RPS. Still, to achieve this result, the algorithm had
to play a lot more random than originally planned, and
the difference in computational resources is consider-
able in comparison to the opponents.
The complexity of GAiRPS could be greatly im-
proved by borrowing ideas from opponents. The com-
plete source code will be provided upon request.
6 CONCLUSION
This study demonstrates that a carefully designed
Evolutionary Algorithm can be competitive in a tour-
nament of Rock-Paper-Scissors, where rapid adap-
tation (learning) and exploitation of temporal pat-
terns are essential for winning. Obtaining the sec-
ond place in a custom tournament against only the
Playing Iterated Rock-Paper-Scissors with an Evolutionary Algorithm
211

top performing algorithms of the online competition
(Knoll, 2011) is a notable feat and demonstrates that
EAs should not be automatically excluded for on-line
learning algorithms. In this specific case, the robust-
ness of the algorithm comes from playing random
very often, a popular technique among the other com-
petitors as well. In order to achieve these good re-
sults, the restriction on computational resources has
been removed.
In our EA, the search space was limited to (4 ×
3)
256
possibilities, but chances are that the optimal
solutions lay outside this space. Hence, one way to
improve the algorithm would be to make the window
size a self-adaptive parameter of individual predic-
tors, although it would probably increase complex-
ity. To gain popular traction, the efficiency should
be hugely improved, to the point where it could be
submitted online for an official ranking on the rp-
scontest leader board. Also, the introduction of meta-
strategies might well have a positive impact on EA
performance.
The meta-strategies developed by the community
for this game (notably the Sicilian reasoning from
Iocaine Powder) are extremely efficient; the best of
them are able to win more than 75% of their matches.
Such good predictors would be great candidates for
performing other tasks such as predicting the trend of
a stock market or other multi-agent games.
REFERENCES
Ali, F. F., Nakao, Z., and Chen, Y.-W. (2000). Playing the
rock-paper-scissors game with a genetic algorithm.
In Proceedings of the 2000 Congress on Evolution-
ary Computation. CEC00 (Cat. No. 00TH8512), vol-
ume 1, pages 741–745. IEEE.
Bi, Z. and Zhou, H.-J. (2014). Optimal cooperation-trap
strategies for the iterated rock-paper-scissors game.
PloS one, 9(10):e111278.
Billings, D. (1999a). The first international roshambo pro-
gramming competition. https://webdocs.cs.ualberta.
ca/
∼
darse/rsbpc1.html [Accessed on 2018-06-09].
Billings, D. (1999b). First roshambo tournament test
suite. https://webdocs.cs.ualberta.ca/
∼
darse/rsb-ts1.c
[Accessed on 2018-06-10].
Billings, D. (2000a). The second interna-
tional roshambo programming competition.
https://webdocs.cs.ualberta.ca/
∼
darse/rsbpc.html
[Accessed on 2018-06-09].
Billings, D. (2000b). Thoughts on roshambo. ICGA Jour-
nal, 23(1):3–8.
Egnor, D. (2000). Iocaine powder. ICGA Journal, 23(1):33–
35.
Eiben, A. E., Smith, J. E., et al. (2003). Introduction to
evolutionary computing, volume 53. Springer.
Knoll, B. (2011). Rock paper scissors programming compe-
tition. http://www.rpscontest.com [Accessed on 2018-
05-27].
Kojima, T., Ueda, K., and Nagano, S. (1997). An evolu-
tionary algorithm extended by ecological analogy and
its application to the game of go. In IJCAI (1), pages
684–691.
Koza, J. R. (1992). Genetic programming: on the program-
ming of computers by means of natural selection, vol-
ume 1. MIT press.
Lebiere, C. and Anderson, J. R. (2011). Cognitive con-
straints on decision making under uncertainty. Fron-
tiers in psychology, 2:305.
Lu, D. L. (2011). Rock paper scissors algorithms. https:
//daniel.lawrence.lu/programming/rps/ [Accessed on
2018-06-03].
Urbanowicz, R. J. and Moore, J. H. (2009). Learning clas-
sifier systems: a complete introduction, review, and
roadmap. Journal of Artificial Evolution and Applica-
tions, 2009:1.
Valdez, S. E., Barayuga, V. J. D., and Fernandez, P. L.
(2014). The effectiveness of using a historical
sequence-based predictor algorithm in the first inter-
national roshambo tournament. International Jour-
nal of Innovative Research in Information Security
(IJIRIS), 1(5):59–65.
Valdez, S. E., Siddayao, G. P., and Fernandez, P. L. (2015).
The effectiveness of using a modified” beat frequent
pick” algorithm in the first international roshambo
tournament. International Journal of Information and
Education Technology, 5(10):740.
Wang, Z., Xu, B., and Zhou, H.-J. (2014). Social cycling
and conditional responses in the rock-paper-scissors
game. Scientific reports, 4:5830.
Xavier, C. R., dos Santos, E. P., da Fonseca Vieira, V., and
dos Santos, R. W. (2013). Genetic algorithm for the
history matching problem. Procedia Computer Sci-
ence, 18:946–955.
ECTA 2019 - 11th International Conference on Evolutionary Computation Theory and Applications
212
