
Lyapunov Functions for Linear Stochastic Differential Equations:
BMI Formulation of the Conditions
Sigurdur Hafstein
Science Institute and Faculty of Physical Sciences, University of Iceland, Dunhagi 5, 107 Reykjav
´
ık, Iceland
Keywords:
Stochastic Differential Equation, Lyapunov Function, Bilinear Matrix Inequalities.
Abstract:
We present a bilinear matrix inequality (BMI) formulation of the conditions for a Lyapunov functions for
autonomous, linear stochastic differential equations (SDEs). We review and collect useful results from the
theory of stochastic stability of the null solution of an SDE. Further, we discuss the It
ˆ
o- and Stratonovich
interpretation and linearizations and Lyapunov functions for linear SDEs. Then we discuss the construction
of Lyapunov functions for the damped pendulum, wihere the spring constant is modelled as a stochastic
process. We implement in Matlab the characterization of its canonical Lyapunov function as BMI constraints
and consider some practical implementation strategies. Further, we demonstrate that the general strategy is
applicable to general autonomous and linear SDEs. Finally, we verify our findings by comparing with results
from the literature.
1 INTRODUCTION
For a linear deterministic system
˙
x = Ax, A ∈ R
d×d
,
with a globally asymptotically stable (GAS) equilib-
rium, one can compute a quadratic Lyapunov func-
tion V (x) = x
T
Qx by solving a particular type of
the Sylvester equation (Sylvester, 1884), the so-called
continuous-time Lyapunov equation,
Q
T
A + AQ = −P, (1)
for any given symmetric and (strictly) positive defi-
nite P. In the spirit of linear matrix inequalities (LMI)
(Boyd et al., 1994) this is sometimes written:
compute Q 0, such that Q
T
A + AQ ≺ 0,
although there is no need to solve an LMI problem be-
cause (1) is just a linear equation that has a symmetric
and positive definite solution Q for any given symmet-
ric and positive definite P, if and only if A is Hurwitz
(the real-parts of all eigenvalues are strictly less than
zero). For efficient algorithms to solve it cf. e.g. (Bar-
tels and Stewart, 1972; Mikkelsen, 2009). However, if
one wants to compute a common quadratic Lyapunov
function V (x) = x
T
Qx for a collection of linear sys-
tems
˙
x = A
i
x, i = 1, 2,... ,m, cf. e.g. (Filippov, 1988;
Aubin and Cellina, 1984; Liberzon, 2003; Sun and
Ge, 2011), one must resort to solve the LMI:
Q 0 and Q
T
A
i
+ A
i
Q ≺ 0 for i = 1,2, ...,m.
The stability theory of stochastic differential equa-
tions (SDEs) is a much less mature subject and al-
gorithms or general procedures to compute Lyapunov
functions, even for autonomous, linear SDEs, are not
available. In this paper we will show that there is a
canonical form for such functions and we will for-
mulate the conditions for a Lyapunov function as a
bilinear matrix inequality (BMI) feasibility problem
(VanAntwerp and Braatz, 2000).
The organization of the paper is as follows: after
fixing the notation we recall the basic theory of SDEs,
their stability, and Lyapunov functions for SDEs in
Section 2. In Section 3 we study the autonomous,
linear case in more detail, before we derive our BMI
problem in Section 4, both in general and, as a demon-
stration, for an important example from the literature.
In Section 5 we give a short verification of our re-
sults and then conclude the paper with some finish-
ing remarks on future research. We give several code
examples of how to efficiently define the BMI prob-
lem, but we do not consider in this paper how to solve
it. Computing a solution to a BMI problem is a chal-
lenging task, cf. e.g. (Kheirandishfard et al., 2018b;
Kheirandishfard et al., 2018a) that will be tackled for
our particular BMI problem in the future.
Notation: We denote by kxk the Euclidian norm of
a vector x ∈ R
d
. Vectors are assumed to be column
vectors. For a symmetric matrix Q ∈ R
d×d
we write
Q 0 and Q if Q is (strictly) positive definite and
Hafstein, S.
Lyapunov Functions for Linear Stochastic Differential Equations: BMI Formulation of the Conditions.
DOI: 10.5220/0008192201470155
In Proceedings of the 16th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2019), pages 147-155
ISBN: 978-989-758-380-3
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
147

semi-positive definite, respectively, and similarly for
≺ and . For a symmetric Q 0 we define the ener-
getic norm kxk
Q
:=
p
x
T
Qx. We write and for
probability and expectation respectively. The under-
lying probability spaces should always be clear from
the context. The abbreviation a.s. stands for almost
surely, i.e. with probability one, and
a.s.
= means equal
a.s.
2 SDEs AND LYAPUNOV
STABILITY
In this section we describe the class of problems we
are concerned with and recall and collect some defini-
tions and useful results. For a more detailed descrip-
tion of the problems cf. (Gudmundsson and Hafstein,
2018, §2) and the books (Mao, 2008) and (Khasmin-
skii, 2012), to which we will frequently refer.
Stochastic differential equations (SDEs) are or-
dinary differential equations with some added ran-
dom distribution or noise. The noise is usually as-
sumed to be “white noise” and is modelled with a U-
dimensional Wiener process W = (W
1
,W
2
,. .. ,W
U
)
T
,
where the W
i
, i = 1, 2,. .. ,U, are independent 1-
dimensional Wiener processes. The general au-
tonomous d-dimensional SDE of It
ˆ
o type is given by
dX(t) = f(X(t))dt + g(X(t))·dW(t)
or equivalently
dX(t) = f(X(t))dt +
U
∑
u=1
g
u
(X(t)) ·dW
u
(t) (2)
for i = 1,2,. .. ,d. Thus f = ( f
1
, f
2
,. .. , f
d
)
T
, g =
(g
1
,g
2
,. .. ,g
U
), and g
u
= (g
u
1
,g
u
2
,. .. ,g
u
d
)
T
, where
f
i
,g
u
i
: R
d
→ R. We consider strong solutions to the
SDE (2), which are given by
X
x
(t) = x +
Z
t
0
f(X(s))ds +
Z
t
0
g(X(s))dW(s)
for deterministic initial value solutions X
x
(t) fulfill-
ing X
x
(0) = x ∈R
d
a.s., where the second integral is
interpreted in the It
ˆ
o sense.
Another much used type of SDEs is given by the
Stratonovich approach
dX(t) = f(X(t))dt + g(X(t))◦dW(t), (3)
with strong solutions for deterministic initial values
X
x
(0) = x ∈R
d
a.s. given by
X
x
(t) = x +
Z
t
0
f(X(s))ds +
Z
t
0
g(X(s)) ◦dW(s),
where the second integral is interpreted in the
Stratonovich sense.
It is adequate or even instrumental to use It
ˆ
o’s
stochastic integral if the noise has no autocorrelation.
This is the case, for example, when modelling finan-
cial markets. When the noise is a model of some un-
known or complicated dynamic sub-system, then it is
more naturally represented using the Stratonovich ap-
proach. Fortunately, for our purposes it is enough to
study the SDE (2), because the Stratonovich SDE (3)
is equivalent to the It
ˆ
o type SDE
dX(t) =
e
f(X(t))dt +
U
∑
u=1
g
u
(X(t)) ·dW
u
(t), (4)
with
e
f(x) := f(x) +
1
2
U
∑
u=1
Dg
u
(x)g
u
(x),
where Dg
u
is the Jacobian of g
u
. The term added to
f(x) is often referred to as “noise-induced drift” for
obvious reasons.
Hence, we will in the following concentrate on the
It
ˆ
o SDE (2), but we will also interpret some of our re-
sults for the Stratonovich SDE (3) too. Further, we
will from now on assume that the origin is an equi-
librium of the system (2), i.e. f(0) = 0 and g
u
(0) = 0
for u = 1,2,...,U. Note that if the origin is an equi-
librium of the Stratonovich SDE (3), then it is also an
equilibrium of the equivalent It
ˆ
o SDE (4). As shown
in (Mao, 2008) it suffices to consider deterministic
initial value solutions when studying the stability of
an equilibrium.
A great number of concepts are used for classi-
fying stability of equilibria of SDEs and the nomen-
clature is far from uniform. For our needs global
asymptotic stability in probability of the zero so-
lution (Khasminskii, 2012, (5.15)), also referred to
as stochastic asymptotic stability in the large (Mao,
2008, Definition 4.2.1 (iii)), is the most useful. How-
ever, we need many other concepts in intermediate
steps. For a more detailed discussion of the stability
of SDEs see the books by Khasminskii (Khasminskii,
2012) or Mao (Mao, 2008).
We recall a few definitions of stability that we use
later:
Definition 2.1 (Stability in Probability (SiP)). The
null solution X(t)
a.s.
= 0 to the SDE (2) is said to be sta-
ble in probability (SiP) if for every r > 0 and 0 < ε < 1
there exists a δ > 0 such that :
kxk ≤ δ implies
sup
t≥0
kX
x
(t)k ≤ r
≥ 1 −ε.
Definition 2.2 (Asymptotic Stability in Probability
(ASiP)). The null solution X(t)
a.s.
= 0 to the SDE (2) is
said to be asymptotically stable in probability (ASiP)
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
148

if it is SiP and in addition for every 0 < ε < 1 there
exists a δ > 0 such that :
kxk ≤ δ implies
n
lim
t→∞
kX
x
(t)k = 0
o
≥ 1 −ε.
Definition 2.3 (Global Asymptotic Stability in Prob-
ability (GASiP)). The null solution X(t)
a.s.
= 0 to the
SDE (2) is said to be globally asymptotically stable in
probability (GASiP) if it is SiP and for any x ∈ R
d
we
have
n
lim
t→∞
kX
x
(t)k = 0
o
= 1.
Definition 2.4 (Exponential p-Stability (p-ES)). The
null solution X(t)
a.s.
= 0 to the SDE (2) is said to be
exponentially p-stable (p-ES) for a constant p > 0, if
there exist constants A,α > 0 such that
{
kX
x
(t)k
p
}
≤ Akxk
p
e
−αt
holds true for all x ∈ R
d
and all t ≥ 0.
Since we are concerned with autonomous SDEs
the concepts of SiP and GASiP automatically include
uniform stability in probability and stability in the
large uniformely in t > 0 respectively, cf. (Khasmin-
skii, 2012, Remark 5.3, §6.5). The conditions for SiP
and ASiP are more commonly stated
lim
kxk→0
{
sup
t>0
kX
x
(t)k ≤ r
}
= 1 for all r > 0
for SiP and additionally
lim
kxk→0
limsup
t→∞
kX
x
(t)k = 0
= 1
for ASiP. This is clearly equivalent to our definitions
as can be seen by fixing r > 0 and writing down the
definition of a limit: for every ε > 0 there exists a
δ > 0. Our formulation is more natural when studying
the stochastic counterpart of the basin of attraction
(BOA) in the stability theory for deterministic sys-
tems, cf. (Gudmundsson and Hafstein, 2018). Instead
of the limit kxk → 0 we consider: Given some confi-
dence 0 < γ ≤ 1 how far from the origin can sample
paths start and still approach the equilibrium as t →∞
with probability greater than or equal to γ. The exact
definition is:
Definition 2.5 (γ-Basin Of Attraction (γ-BOA)).
Consider the system (2) and let 0 < γ ≤ 1. The set
n
x ∈ R
d
:
n
lim
t→∞
kX
x
(t)k = 0
o
≥ γ
o
(γ-BOA)
is called the γ-basin of attraction (γ-BOA) of the equi-
librium at the origin.
Any sample path started in γ-BOA will tend to-
wards the origin with probability γ or greater.
Just as for deterministic differential equations, the
various stability properties for SDEs can be character-
ized by the existence of so-called Lyapunov functions.
The stochastic counterpart to the orbital derivative of
V : R
d
→ R for deterministic systems, i.e. the deriva-
tive along solution trajectories of
˙
x = f(x), x(0) = ξ,
given by
d
dt
V (φ(t,ξ))
t=0
= ∇V (ξ)
•
f(ξ),
is the generator, where one has to add a term account-
ing for the stochastic drift:
Definition 2.6 (Generator of an SDE). For the SDE
(2) the associated generator for some appropriately
differentiable V : U → R with U ⊂ R
d
is given by
LV (x) := ∇V (x)
•
f(x)
+
1
2
d
∑
i, j=1
U
∑
u=1
g
u
i
(x)g
u
j
(x)
∂
2
V
∂x
i
∂x
j
(x).
Note that LV is the drift term in the expres-
sion for the stochastic differential of the process t 7→
V (X
x
(t)). Accordingly, the Stratonovich SDE (3) has
the generator
LV (x) := ∇V (x)
•
"
f(x) +
1
2
U
∑
u=1
Dg
u
(x)g
u
(x)
#
(5)
+
1
2
d
∑
i, j=1
U
∑
u=1
g
u
i
(x)g
u
j
(x)
∂
2
V
∂x
i
∂x
j
(x).
When defining Lyapunov functions for SDEs it
is convenient to introduce the function class K
∞
of
strictly increasing continuous functions µ : R → R,
such that µ(0) = 0 and lim
x→∞
µ(x) = ∞.
Definition 2.7 (Lyapunov function for a SDE). Con-
sider the system (2). A function
V ∈C(U) ∩C
2
(U \{0}),
where 0 ∈ U ⊂ R
d
is a domain, is called a (local)
Lyapunov function for the the system (2) if there are
functions µ
1
,µ
2
,µ
3
∈K
∞
, such that V fulfills the prop-
erties :
(i) µ
1
(kxk) ≤V (x) ≤ µ
2
(kxk) for all x ∈ U
(ii) LV (x) ≤ −µ
3
(kxk) for all x ∈ U \{0}
If U = R
d
the function V is said to be a global Lya-
punov function.
It is instrumental that one does not demand that
a Lyapunov function V for an SDE is differentiable
at the origin, cf. (Khasminskii, 2012, Remark 5.5);
Lyapunov Functions for Linear Stochastic Differential Equations: BMI Formulation of the Conditions
149

see also (Bjornsson and Hafstein, 2018) for similar re-
sults for almost sure exponential stability introduced
in (Mao, 2008, Def. 4.3.3.1).
We conclude this section with the following gen-
eral theorem:
Theorem 2.8. If there exists a Lyapunov functions for
the system (2), then the null solution is ASiP. Further,
let V
max
> 0 and assume that V
−1
([0,V
max
]) is a com-
pact subset of the domain U of the Lyapunov function.
Then, for every 0 < β < 1 the set V
−1
([0,βV
max
]) is a
subset of the (1 −β)-BOA of the origin. In particular,
if the Lyapunov function is global, i.e. U = R
d
, then
the origin is GASiP.
For these results see (Bjornsson et al., 2018,
Th. 2.6) and (Khasminskii, 2012, Th. 5.5, Cor. 5.1).
3 LINEAR AUTONOMOUS SDEs
We will now consider equations (2) and (3) assuming
that f and the g
u
are linear, i.e. there exists matrices
F,G
u
∈ R
d×d
such that f(x) = Fx and g
u
(x) = G
u
x
for all x ∈ R
d
and u = 1,2, .. .,U. The SDE (2) can
then be written
dX(t) = FX(t)dt +
U
∑
u=1
G
u
X(t) ·dW
u
(t) (6)
and its generator, with F
i j
and G
u
i j
as the components
of the matrices F and G
u
respectively, as
LV (x) =
d
∑
i, j=1
F
i j
x
j
∂V
∂x
i
(x) (7)
+
1
2
d
∑
i, j,k,`=1
U
∑
u=1
x
k
x
`
G
u
ik
G
u
j`
∂
2
V
∂x
i
∂x
j
(x).
Similarly, for the Stratonovich SDE (3) the generator
is given by
LV (x) =
d
∑
i, j=1
F
i j
x
j
+
1
2
d
∑
k=1
U
∑
u=1
G
u
i j
G
u
jk
x
k
!
∂V
∂x
i
(x)
+
1
2
d
∑
i, j,k,`=1
U
∑
u=1
x
k
x
`
G
u
ik
G
u
j`
∂
2
V
∂x
i
∂x
j
(x). (8)
For the autonomous linear SDE with constant co-
efficients (6) the relations between the stability con-
cepts in the last section are much simpler than in the
nonlinear case; for a proof of the following theorem
see (Hafstein et al., 2018, Prop. 1).
Theorem 3.1. The following relations hold for the
null solution of system (6) :
i) ASiP is equivalent to GASiP.
ii) p-ES for some p > 0 implies GASiP.
iii) ASiP/GASiP implies p-ES for all small enough
p > 0.
Unsurprisingly, the GASiP of the null solution of
the linearization of the SDE (2) implies the ASiP of
the null solution of the original system. Just as for de-
terministic systems, this can be shown by construct-
ing a global Lyapunov function for the linearized sys-
tem, which then is a local Lyapunov function for
the original nonlinear system. In the stochastic case
cf. e.g. (Bjornsson et al., 2018, Th. 3.4), where ex-
plicit bounds are given on the area where the Lya-
punov function is valid for the original nonlinear sys-
tem.
Just as quadratic Lyapunov functions V (x) =
x
T
Qx, Q 0, are a natural candidate for determinis-
tic, linear, autonomous systems, Lyapunov functions
of the algebraic form V (x) = kxk
p
Q
:= (x
T
Qx)
p
2
, with
Q 0 and p > 0, are the natural candidate for stochas-
tic, linear, autonomous systems (6). This is justified
by the following theorem, where Q ∈ R
d×d
is an arbi-
trary symmetric and positive definite matrix.
Theorem 3.2. The origin is GASiP for the linear sys-
tem (6), if and only if for all small enough p > 0 there
exist constants c
1
,c
2
,c
3
,c
4
,c
5
> 0 and a (Lyapunov)
function V ∈C(R
d
) ∩C
2
(R
d
\{0}) such that :
i) c
1
kxk
p
Q
≤V (x) ≤c
2
kxk
p
Q
for all x ∈ R
d
.
ii) LV (x) ≤ −c
3
kxk
p
Q
for all x ∈ R
d
\{0}.
iii) V is positively homogenous of degree p.
iv)
∂V
∂x
r
(x)
≤c
4
kxk
p−1
Q
for all r = 1,2,...,d and all
x ∈ R
d
\{0}.
v)
∂
2
V
∂x
r
∂x
s
(x)
≤ c
5
kxk
p−2
Q
for all r,s = 1, 2,. .. ,d
and all x ∈ R
d
\{0}.
Proof. Follows by (Bjornsson et al., 2018, Thms. 3.2,
3.3) and the fact that for all x ∈ R
d
we have
λ
1
2
Q,min
kxk ≤ kxk
Q
≤ λ
1
2
Q,max
kxk,
where λ
Q,min
> 0 and λ
Q,max
> 0 are the smallest and
largest eigenvalues of Q respectively.
The function V (x) = kxk
p
Q
:= (x
T
Qx)
p
2
automati-
cally fulfills the condition i) of the last theorem with
c
1
= c
2
= 1 and with α > 0 we have V (αx) = α
p
V (x),
i.e. condition iii) is fulfilled. Further, routine calcula-
tions give
∂V
∂x
r
(x) = pkxk
p−2
Q
d
∑
i=1
Q
ir
x
i
(9)
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
150

and
∂
2
V
∂x
r
∂x
s
(x) =
pkxk
p−4
Q
Q
sr
kxk
2
Q
+ (p −2)
d
∑
i, j=1
Q
is
Q
jr
x
i
x
j
!
,
which together with |x
i
| ≤ kxk ≤ λ
−
1
2
Q,min
kxk
Q
deliver
conditions iv) and v) with
c
4
= pλ
−
1
2
Q,min
d
∑
i=1
|Q
ir
|
and
c
5
= p
|Q
sr
|+ |p −2|λ
−1
Q,min
d
∑
i, j=1
|Q
is
Q
jr
|
!
.
Hence, the only condition for a Lyapunov function re-
maining for V (x) = kxk
p
Q
is condition ii), i.e. whether
LV (x) ≤ −c
3
kxk
p
Q
. Note that this is the case for both
the It
ˆ
o and the Stratonovich interpretation of the solu-
tions, only the generator LV is defined differently.
In (Hafstein et al., 2018) this problem was stud-
ied and a linear matrix inequality (LMI) was derived,
which verified condition ii) for a given and fixed
Q 0. This essentially implies that one has to “guess”
an appropriate Q 0 for a Lyapunov function candi-
date and then verify if the candidate actually is a Lya-
punov function. Even in this quite restrictive setup the
authors were able to obtain considerably better results
for the interesting example of a damped harmonic os-
cillator with noise (Khasminskii, 2012, Example 6.6)
than previous attempts.
In the next section we will show how the prob-
lem of generating a Lyapunov function of the form
V (x) = kxk
p
Q
for this system can be formulated as a
BMI and how the long and tedious routine compu-
tations can be considerably simplified by using the
Symbolic Math Toolbox in Matlab. Further, we use
the results obtained to verify some of the results ob-
tained in (Hafstein et al., 2018). The important step,
however, of solving the BMI, will be dealt with later.
4 BMI FOR THE LYAPUNOV
FUNCTION
To derive a bilinear matrix inequality (BMI) feasibil-
ity problem for the conditions of a Lyapunov function
for an autonomous, linear SDE, we will consider a
concrete example, namely, the damped harmonic os-
cillator
¨x + k ˙x + ω
2
x = 0
from (Khasminskii, 2012, Ex. 6.6) and (Hafstein
et al., 2018, Ex. 5.1). Setting x
1
= ωx and x
2
= ˙x we
get the linear system of equations
˙
x = Fx, with x =
x
1
x
2
and F =
0 ω
−ω −k
.
The eigenvalues of F are λ
±
= (−k ±
√
k
2
−4ω
2
)/2
and the origin is globally asymptotically stable for k >
0.
We add white noise to the damping and consider
the SDE
dX(t) = FX(t)dt + G
1
X(t)dW
1
(t), (10)
where
X =
X
1
X
2
and G
1
=
0 0
0 −σ
.
Here W
1
is a one-dimensional Wiener-process and σ
quantifies the noise.
As show in (Hafstein et al., 2018, Lemma 4.1)
the generator from Definition 2.6 using the Lyapunov
functions candidate V (x) = kxk
p
Q
and for the system
(6) interpreted in the It
ˆ
o sense, can be written
LV (x) = −
p
2
kxk
p−4
Q
H(x) (11)
with
H(x) = −x
T
F
T
Q + QF +
U
∑
u=1
(G
u
)
T
QG
u
!
xkxk
2
Q
+
2 − p
4
U
∑
u=1
x
T
(QG
u
+ (G
u
)
T
Q)x
2
.
Similarly, by comparing (7) and (8) and taking for-
mula (9) into account, one sees that by adding the fol-
lowing term on the right-hand-side of (11), one gets
the generator (8) for the system (6) interpreted in the
Stratonovich sense:
d
∑
i, j=1
1
2
d
∑
k=1
U
∑
u=1
G
u
i j
G
u
jk
x
k
!
∂V
∂x
i
(x)
= kxk
p−2
Q
p
2
U
∑
u=1
d
∑
i, j,k,`=1
G
u
i j
G
u
jk
x
k
Q
`i
x
`
= kxk
p−2
Q
p
2
U
∑
u=1
d
∑
j,k,`=1
[QG
u
]
` j
G
u
jk
x
k
x
`
= kxk
p−2
Q
p
2
U
∑
u=1
d
∑
k,`=1
[QG
u
G
u
]
`k
x
k
x
`
= kxk
p−2
Q
p
2
U
∑
u=1
x
T
Q[G
u
]
2
x
= kxk
p−2
Q
p
4
U
∑
u=1
x
T
Q[G
u
]
2
+ [(G
u
)
T
]
2
Q
x
Lyapunov Functions for Linear Stochastic Differential Equations: BMI Formulation of the Conditions
151

In the preceding computations [QG
u
]
` j
denotes the
(`, j)-entry of the matrix QG
u
etc. Alternatively, one
can add
e
H(x) = −
1
2
U
∑
u=1
x
T
Q[G
u
]
2
+ [(G
u
)
T
]
2
Q
xkxk
2
Q
to H(x) in (11), i.e. the generator in the Stratonovich
interpretation can be written
LV (x) = −
p
2
kxk
p−4
Q
H(x)+
e
H(x)
. (12)
Note that both the H(x) and
e
H(x) are homogenous
polynomials in x ∈ R
d
of degree 4. In the following
we will consider the It
ˆ
o interpretation, but note that
the adaptation to the Stratonovich is straight forward.
The condition ii) from Theorem 3.2 becomes
LV (x) = −
p
2
kxk
p−4
Q
H(x) ≤ −c
3
kxk
p
Q
or
H(x) ≥
2c
3
p
kxk
4
Q
. (13)
We need to fix the parameter p > 0 in H(x) and (13)
to proceed. If c
3
> 0 is now also fixed we can work
further with inequality (13) directly. If, however, we
want c
3
> 0 to be a parameter in our BMI problem,
it is preferable to take advantage of the norm equiv-
alence of k·k and k·k
Q
and consider the stricter in-
equality
H(x) ≥ ckxk
4
with c =
2c
3
λ
2
Q,max
p
, (14)
that implies (13) and we will do this in the following.
Now we are ready to write the conditions for a
Lyapunov function for our ansatz V (x) = kxk
p
Q
for our
equation (10) as a BMI. First we fix p > 0 and define
P
c
(x,y) = H(x,y) −c(x
2
+ y
2
)
2
.
Note that P
c
(x,y) ≥ 0 for all x,y ∈ R is equivalent to
(14).
The objective is to find a parameter c > 0, a sym-
metric and positive definite matrix Q ∈ R
2×2
, and
a symmetric and positive semi-definite matrix P ∈
R
3×3
, such that for Z = (x
2
xy y
2
)
T
we have
P
c
(x,y) = Z
T
PZ =: P
Z
. (15)
More detailed, we want to determine values for the
variables
c,Q
1
,Q
2
,Q
3
,P
1
,P
2
,P
3
,P
4
,P
5
,P
6
such that c > 0,
Q =
Q
1
Q
2
Q
2
Q
3
0,
P =
P
1
P
2
P
3
P
2
P
4
P
5
P
3
P
5
P
6
0,
and, additionally, such that P
c
is the same polynomial,
in x and y, as the expression P
Z
:= Z
T
PZ. If we suc-
ceed in doing this, then V (x) = kxk
p
Q
automatically
fulfills all the conditions in Theorem 3.2, except pos-
sibly condition ii), just because Q 0. Further, the
condition ii) is also fulfilled because P
c
= P
Z
, as a
polynomial in x and y, is easily seen to be the sum of
squared polynomials and thus nonnegative; namely
P
c
(x,y) = P
Z
=
3
∑
i=1
√
D
i
[OZ]
i
2
,
where P = O
T
DO is the factorization of P using an
orthogonal matrix O ∈R
3×3
and diagonal matrix D ∈
R
3×3
, the D
i
≥ 0 are the eigenvalues of P, or equiva-
lently the diagonal elements of D, and [OZ]
i
is the ith
element in the vector OZ, a polynomial in x and y.
To obtain the relations between the variables we
have to equate the coefficients of the polynomials P
c
and P
Z
. This can be done by equating all fourth-order
partial derivatives of P
c
and P
Z
with respect to x and
y, i.e.
∂
4
P
c
∂x
4
=
∂
4
P
Z
∂x
4
,
∂
4
P
c
∂x
3
∂y
=
∂
4
P
Z
∂x
3
∂y
,
∂
4
P
c
∂x
2
∂y
2
=
∂
4
P
Z
∂x
2
∂y
2
∂
4
P
c
∂x∂y
3
=
∂
4
P
Z
∂x∂y
3
,
∂
4
P
c
∂y
4
=
∂
4
P
Z
∂y
4
This is most conveniently achieved by using a com-
puter algebra system (CAS). In the following Listing
1 we use Matlab’s Symbolic Toolbox to set up the
problem as explained above. Note that we keep p as
well as the constants ω = w,k,σ = s of our example
SDE (10) as parameters:
Listing 1: Setting up the problem.
sy ms Q1 Q2 Q3 P1 P2 P3 P4 P5 P6 c
sy ms w k s p
Q =[ Q1 Q2;Q2 Q3 ]
G =[0 0;0 - s]
F =[0 w ; -w -k]
sy ms x y
xv =[x y].'
Pc = -xv. ' *( F. '* Q+Q *F+ G. '* Q*G )* xv ...
* xv. ' *Q* xv ...
+(2 -p )/4*( xv. ' *( Q *G + G. '* Q )* xv )ˆ2 ...
-c *(xv. '* xv )ˆ2
P =[ P1 P2 P3; P2 P4 P5; P3 P5 P6]
Z =[ x ˆ2 x*y y ˆ2] .'
PZ = Z. '*P* Z
Obtaining the relations between the vari-
ables is now easy using symbolic differentiation,
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
152

e.g. diff(PZ,x,4) gives 24*P1 and diff(Pc,x,4)
gives 48*Q1*Q2*w - 24*c and we obtain the relation
P
1
= 2Q
1
Q
2
ω − c from ∂
4
P
c
/∂x
4
= ∂
4
P
Z
/∂x
4
.
This procedure, however, becomes tedious for
obtaining the coefficients for Q
1
Q
1
, Q
2
Q
2
, Q
3
Q
3
,
Q
1
Q
2
, Q
1
Q
3
, Q
2
Q
3
, c from P
c
; in terms of
the parameters p,ω,k,σ. A more automated
process is given in Listing 2 and one can imme-
diately read from its output diff(P_Z,x,4)=P1
and Q1*Q1 Q2*Q2 Q3*Q3 Q1*Q2 Q1*Q3 Q2*Q3 c =
0, 0, 0, 2*w, 0, 0, -1 the same information,
i.e. P
1
= 2ω ·Q
1
Q
2
+ (−1) ·c
Listing 2: Obtaining the relations: ∂
4
/∂x
4
.
eq = diff ( PZ , x ,4)/ f ac to ri al (4);
fp ri nt f (' \ ndiff ( P_Z ,x ,4 )=% s\ n' , ch ar ( eq ))
eq = diff ( Pc , x ,4)/ f ac to ri al (4);
fp ri nt f (' diff (P_c ,x ,4)= % s\n' , c har (eq ))
eq1= diff ( eq ,Q1 , 2) /2;
eq2= diff ( diff ( eq , Q1) , Q2 );
eq3= diff ( eq ,Q2 , 2) /2;
eq4= diff ( eq ,c);
eq5= diff ( eq ,Q3 , 2) /2;
eq6= diff ( diff ( eq , Q1) , Q3 );
eq7= diff ( diff ( eq , Q2) , Q3 );
fp ri nt f (' Q1* Q1 Q2*Q2 Q3*Q3 Q1*Q2 ...
Q1 * Q3 Q2 * Q3 c = %s , %s , %s , % s , ...
%s , %s , %s \ n\ n' , ch ar ( eq1 ) , . ..
ch ar ( eq3 ), c har ( eq5 ) , ch ar ( eq2 ), . ..
ch ar ( eq6 ), c har ( eq7 ) , char ( eq4 ))
The other cases are similar and can be im-
plemented by adapting the code in Listing 2,
e.g. for the case ∂
4
P
c
/∂x
2
∂y
2
= ∂
4
P
Z
/∂x
2
∂y
2
just change eq=diff(PZ,x,4)/factorial(4);
to eq=diff(diff(PZ,x,2),y,2)/(2*2); and
similarly eq=diff(Pc,x,4)/factorial(4); to
eq=diff(diff(Pc,x,2),y,2)/(2*2);
The results from this procedure are the following
relations between the variables:
Variable Relations:
P
1
= 2ωQ
1
Q
2
−c
P
2
= −ωQ
2
1
+ 2ωQ
2
2
+ kQ
1
Q
2
+ ωQ
1
Q
3
2P
3
+ P
4
= (4k −pσ
2
+ 2σ
2
)Q
2
2
−6ωQ
1
Q
2
+ (2k −σ
2
)Q
1
Q
3
+ 6ωQ
2
Q
3
−2c
P
5
= −2ωQ
2
2
+ ωQ
2
3
−ωQ
1
Q
3
+ (3k −pσ
2
+ σ
2
)Q
2
Q
3
P
6
= (2k −pσ
2
+ σ
2
)Q
2
3
−2ωQ
2
Q
3
−c.
We now come to writing our BMI problem.
One formulation of a BMI feasibility problem is
to determine values for the variables q
1
,q
2
,. .. ,q
M
,
given symmetric matrices A
i j
,B
i
,C ∈ R
N×N
, i, j =
1,2, .. ., M, such that
M
∑
i=1
M
∑
j=i
q
i
q
j
A
i j
+
M
∑
i=1
q
i
B
i
+C 0. (16)
Our problem has the variables
q
1
= Q
1
,q
2
= Q
2
,q
3
= Q
3
,q
4
= P
3
,q
5
= P
4
,q
6
= c,
because the original variables P
1
, P
2
, P
5
, P
6
can be
written in terms of q
1
= Q
1
, q
2
= Q
2
, q
3
= Q
3
, q
6
= c.
To define the appropriate matrices let us first de-
fine the matrices E
ii
= e
i
e
T
i
and E
i j
:= e
i
e
T
j
+ e
j
e
T
i
for
i < j. Here e
i
is the usual ith unit vector in R
8
.
The constraints of our BMI feasibility problem for
the SDE (10) can be written
6
∑
i=1
6
∑
j=i
q
i
q
j
A
i j
+
6
∑
i=1
q
i
B
i
+C 0 (17)
with the following nonzero matrices and where ε > 0
is a small parameter.
Matrix Definitions:
A
11
= −ωE
12
,
A
12
= 2ωE
11
+ kE
12
−6ω(E
44
−E
55
)
A
13
= ωE
12
+ (2k −σ
2
)(E
44
−E
55
) −ωE
23
A
22
= 2ωE
12
+ (4k −pσ
2
+ 2σ
2
)(E
44
−E
55
) −2ωE
23
A
23
= 6ω(E
44
−E
55
) + (3k −pσ
2
+ σ
2
)E
23
−2ωE
33
A
33
= ωE
23
+ (2k −pσ
2
+ σ
2
)E
33
B
1
= E
66
B
2
= E
67
B
3
= E
77
B
4
= E
13
+ 2(E
55
−E
44
)
B
5
= E
22
+ E
55
−E
44
B
6
= −E
11
−2(E
44
−E
55
) −E
33
+ E
88
C = −ε(E
66
+ E
77
+ E
88
)
All other matrices are set to the zero 8 ×8 matrix.
Note that one can also consider the left-hand-side of
(17) as matrix M ∈ R
8×8
, whose entries are quadratic
functions in the variables q
i
.
A few comments are in order. First, since the BMI
problem (16) is written in terms of semi-definiteness,
i.e. rather than , conditions like c > 0 and Q 0
must be written as c −ε ≥ 0 and Q −εI 0 respec-
tively, for a fixed, small parameter ε > 0.
Second, the constraints P 0 are implemented in
the principal submatrix M
1:3,1:3
:= (M
i j
)
i, j=1,2,3
, the
constraints Q 0 in the principal submatrix M
6:7,6:7
,
and the constraints c > 0 in the principal submatrix (or
Lyapunov Functions for Linear Stochastic Differential Equations: BMI Formulation of the Conditions
153
element) M
8,8
. The principal submatrices (elements)
M
4,4
and M
5,5
are used to force the equality
2P
3
+ P
4
= (4k −pσ
2
+ 2σ
2
)Q
2
2
−6ωQ
1
Q
2
(18)
+ (2k −σ
2
)Q
1
Q
3
+ 6ωQ
2
Q
3
−2c.
Apart from these principal submatrices the entries of
M are zero. Lets go through the constraints in more
detail:
Principal Submatrix M
1:3,1:3
:
From the Matrix Definitions and (17) we see, by look-
ing for E
11
in the Matrix Definitions, that
M
1,1
= 2ωq
1
q
2
−q
6
.
From the definitions of the variables q
i
and the Vari-
able Relations this implies M
1,1
= 2ωQ
1
Q
2
−c = P
1
.
In exactly the same way we get M
2,1
= M
1,2
= P
2
,
M
2,3
= M
3,2
= P
5
, M
3,3
= P
6
, where P
2
, P
5
, P
6
,
just as P
1
, are written in terms of the q
1
= Q
1
,
q
2
= Q
2
, q
3
= Q
3
, q
6
= c. The variables q
4
= P
3
and q
5
= P
4
cannot be written directly in terms of
the other variables, and are thus put into M
1:3,1:3
as
M
1,3
= M
3,1
= q
4
= P
3
and M
2,2
= q
5
= P
4
.
Principal Submatrices M
4,4
,M
5,5
,M
8,8
:
Since we only have ≥ and not = in the BMI feasi-
bility problem (17) at our service, we implement the
equality (18) through
M
4,4
= rhs −lhs ≥0 and M
5,5
= lhs −rhs ≥0,
where “lhs” and “rhs” denote the left-hand-side and
the right-hand-side of equation (18), respectively.
Further,
c = q
6
= M
8,8
−ε ≥ 0.
Principal Submatrix M
6:7,6:7
:
The implementation is obvious:
M
6:7,6:7
=
q
1
−ε q
2
q
2
q
3
−ε
=
Q
1
Q
2
Q
2
Q
3
−εI 0.
5 VERIFICATION
We verified numerically our construction of the BMI
feasibility problem (17) for the SDE (10) for some
sets of parameters k, ω,σ, p,c,Q that were used in the
sum-of-squared (SOS) approach in (Hafstein et al.,
2018, Ex. 5.1). For example, with
ω = 2.75, k = 0.9, σ = 2, p = 0.1, Q =
3 1/3
1/3 3
one can fix
q
1
= 3, q
2
= 1/3, q
3
= 3, q
6
= 0.05 = c,
and find values for the variables q
4
and q
5
such that
the BMI feasibility problem (17) has a solution; in-
deed, with q
4
= −12.126111 and q
5
= 5.596667 the
minimum eigenvalue of M
1:3,1:3
is greater than 0.02.
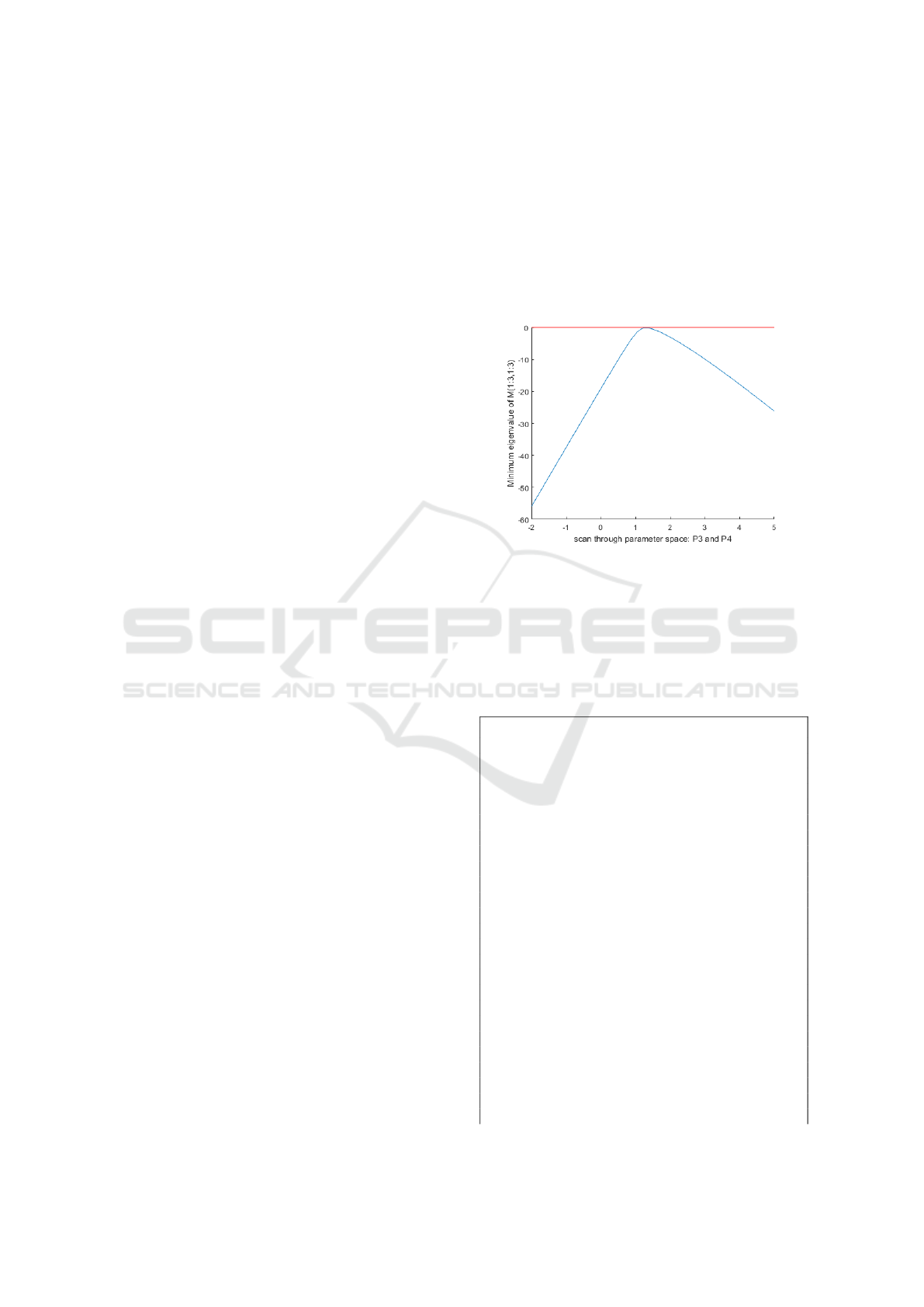
If ω is changed from ω = 2.75 to ω = 2.5 it is not
possible to find values for q
4
and q
5
such that the BMI
feasibility problem (17) has a solution; even with q
6
=
c = 0 the minimum eigenvalue of M
1:3,1:3
is always
negative (less than −0.15), see Figure 1.
Figure 1: The minimum eigenvalue of M
1:3,1:3
= P for a
scan through values for the variables q
4
= P
3
and q
5
= P
4
.
For no admissible values for q
4
and q
5
is the minimum pos-
itive.
These results fully conform to the findings ob-
tained in (Hafstein et al., 2018, Ex. 5.1). The code
for producing these results is given in Listing 3.
Listing 3: Verification.
% ma ke the Eij
E= eye (8);
E11=E ( : ,1 )* E (1 ,:);
E22=E ( : ,2 )* E (2 ,:);
E33=E ( : ,3 )* E (3 ,:);
E44=E ( : ,4 )* E (4 ,:);
E55=E ( : ,5 )* E (5 ,:);
E66=E ( : ,6 )* E (6 ,:);
E77=E ( : ,7 )* E (7 ,:);
E88=E ( : ,8 )* E (8 ,:);
E12=E ( : ,1 )* E (2 ,:)+ E (: ,2)*E (1 , :);
E13=E ( : ,1 )* E (3 ,:)+ E (: ,3)*E (1 , :);
E23=E ( : ,2 )* E (3 ,:)+ E (: ,3)*E (2 , :);
E67=E ( : ,6 )* E (7 ,:)+ E (: ,7)*E (6 , :);
% wo rk s
w =2 . 75 ; k =0 .9 ; s =2 .0; p =0 .1 ; c =0 .0 5 ;
q1 =3 .0 ; q2 =1 /3 .0; q3 =3 .0 ; q6 =c;
% w =2 .5 ; c =0 .05 ; q6 = c; % does not work
V =( 4* k - p* s ˆ2+2* s ˆ2)* q2 ˆ2 -6* w * q1 * q2 ...
+( 2* k -s ˆ2) * q1 * q3 +6* w * q2 * q3 -2* c ;
eps =0 . 05 ;
% ma ke A, B , C as p os si bl e
A11=- w * E12 ;
A12 =2* w* E 11 + k* E12 -6* w *( E44 - E55 );
A13=w * E12 +(2* k - s ˆ2 )*( E44 - E55)- w*E23 ;
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
154

A22 =2* w* E 12 + (4*k- p *s ˆ2+2* s ˆ2) ...
*( E44 - E55 ) -2* w * E2 3 ;
A23 =6* w*( E44 - E55 )+(3 * k-p *s ˆ2+ s ˆ 2) ...
* E23 -2 * w* E33 ;
A33=w * E23 +(2* k - p* s ˆ2 + s ˆ2 )* E33 ;
B1 = E6 6 ; B2 = E67 ;B3 = E 77 ;
B4 = E1 3 +2*( E55 - E44 );
B5 = E2 2 +E55 - E44 ;
B6 = -E11 -2*( E44 - E5 5 )-E33 + E88 ;
C=- e ps *( E66 +E77 + E88 );
% 2* P3 + P4 = V
xm in = -2; xmax =5; st ep s = 10 00 ;
x= ze ros ( step s ,1);
me = z eros ( steps ,1);
for i = 1: steps
x(i )= xmin + i/steps *( xmax - xmin );
q4 = x( i )* V /2 ; q5 =V -2* q4 ;
M=q1 ˆ2 * A1 1 +q1 *q2 * A12 + q1*q3*A13 . ..
+ q2 ˆ 2* A 22 + q2 * q3 * A2 3 + q3 ˆ2* A33 .. .
+ q1 * B1 + q2 * B2 + q3 * B3 + q4 * B4 ...
+ q5 * B5 + q6 * B6 + C;
me ( i )= mi n ( eig (M ( 1: 3 ,1:3))) ;
end
fp ri nt f (' max - min ei g = %d\ n' , max(me ))
ho ld on
pl ot ( x,me )
pl ot ( x, zeros ( le ng th ( x ) ,1) ,' r' )
6 CONCLUSIONS
We presented a bilinear matrix inequality (BMI) ap-
proach for the computation of Lyapunov functions for
autonomous, linear stochastic differential equations
(SDE). For a concrete example we showed how to
derive the BMI problem and we verified the results
of our approach by comparing with previous findings.
Future work will be aimed at writing software to gen-
erate the BMI problem automatically for a general au-
tonomous, linear SDE and solving the BMI problem
numerically.
ACKNOWLEDGEMENT
The research done for this paper was supported by the
Icelandic Research Fund (Rann
´
ıs) in the project ‘Lya-
punov Methods and Stochastic Stability’ (152429-
051), which is gratefully acknowledged.
REFERENCES
Aubin, J.-P. and Cellina, A. (1984). Differential Inclusions.
Springer.
Bartels, R. and Stewart, G. (1972). Solution of the matrix
equation AX+XB=C. Communications of the ACM,
15(9):820–826.
Bjornsson, H., Giesl, P., Gudmundsson, S., and Hafstein,
S. (2018). Local Lyapunov functions for nonlinear
stochastic differential equations by linearization. In
In Proceedings of the 15th International Conference
on Informatics in Control, Automation and Robotics
(ICINCO), pages 579–586.
Bjornsson, H. and Hafstein, S. (2018). Dynamical Systems
in Theoretical Perspective, volume 248 of Springer
Proceedings in Mathematics and Statistics, chapter
Lyapunov functions for almost sure exponential sta-
bility, pages 51–61. Springer.
Boyd, S., El Ghaoui, L., Feron, E., and Balakrishnan,
V. (1994). Linear matrix inequalities in system and
control theory, volume 15 of SIAM Studies in Ap-
plied Mathematics. Society for Industrial and Applied
Mathematics (SIAM), Philadelphia, PA.
Filippov, A. (1988). Differential Equations with Discon-
tinuous Right-hand Side. Kluwer. Translated from
Russian, original book from 1985.
Gudmundsson, S. and Hafstein, S. (2018). Probabilistic
basin of attraction and its estimation using two Lya-
punov functions. Complexity, Article ID:2895658.
Hafstein, S., Gudmundsson, S., Giesl, P., and Scalas,
E. (2018). Lyapunov function computation for au-
tonomous linear stochastic differential equations us-
ing sum-of-squares programming. Discrete Contin.
Dyn. Syst Ser. B, 23(2):939–956.
Khasminskii, R. (2012). Stochastic stability of differential
equations. Springer, 2nd edition.
Kheirandishfard, M., Zohrizadeh, F., Adil, M., and Madani,
R. (2018a). Convex relaxation of bilinear matrix in-
equalities part II: Applications to optimal control syn-
thesis. In Proceedings of 57rd IEEE Conference on
Decision and Control (CDC), pages 75–82.
Kheirandishfard, M., Zohrizadeh, F., and Madani, R.
(2018b). Convex relaxation of bilinear matrix inequal-
ities part I: Theoretical results. In Proceedings of 57rd
IEEE Conference on Decision and Control (CDC),
pages 67–74.
Liberzon, D. (2003). Switching in systems and control.
Systems & Control: Foundations & Applications.
Birkh
¨
auser.
Mao, X. (2008). Stochastic Differential Equations and Ap-
plications. Woodhead Publishing, 2nd edition.
Mikkelsen, C. (2009). Numerical Methods For Large Lya-
punov Equations. PhD thesis: Purdue University,
West Lafayette (IN), USA.
Sun, Z. and Ge, S. (2011). Stability Theory of Switched Dy-
namical Systems. Communications and Control Engi-
neering. Springer.
Sylvester, J. (1884). Sur l’equation en matrices px=xq. C.
R. Acad. Sci. Paris., 99(2):67–71, 115–116.
VanAntwerp, J. and Braatz (2000). A tutorial on linear and
bilinear matrix inequalities. Journal of Process Con-
trol, 10:363–385.
Lyapunov Functions for Linear Stochastic Differential Equations: BMI Formulation of the Conditions
155
