Comparison of Querying Performance of Neo4j on Graph and

Hyper-graph Data Model

Mert Erdemir

1 a

, Furkan Goz

2 b

, Alev Mutlu

2 c

and Pinar Karagoz

1 d

Department of Computer Engineering, Middle East Technical University, Ankara, Turkey

Department of Computer Engineering, Kocaeli University, Kocaeli, Turkey

Keywords:

Graph Database, Graph, Hyper-graph, Performance Analysis, Neo4j.

Abstract:

Graph databases are gaining wide use as they provide ﬂexible mechanisms to model real world entities and

the relationships among them. In the literature, there exists several studies that evaluate performance of graph

databases and graph database query languages. However, there is limited work on comparing performance for

graph database querying under different graph representation models. In this study, we focus on two graph

representation models: ordinary graphs vs. hyper-graphs, and investigate the querying performance of Neo4j

for various query types under each model. The analysis conducted on a benchmark data set reveal what type

of queries perform better on each representation.

1 INTRODUCTION

Graph databases have found wide range of applica-

tions as they provide a powerful mechanism to store,

query, and analyse graph-like data. Such data is al-

ready large in volume and is still been produced as

a result of scientiﬁc research, e.g. computational bi-

ology and chemoinformatics, and social networking

applications such as Facebook and Twitter.

Although graph database technology can be con-

sidered as a new innovation, there are several graph

database implementations and a wide range of studies

comparing their performance with respect to differ-

ent aspects. The work given in (Jouili and Vansteen-

berghe, 2013) compares the performance of different

graph database implementations in terms of data load-

ing, traversal, and capacity to handle simultaneous re-

quests. In (Kolomi

cenko et al., 2013), performance

of different graph database implementations are com-

pared with respect to creating indexes, querying short-

est paths, and ﬁnding nodes/edges with certain prop-

erties. In addition to them, there are studies that focus

on comparing different graph database querying lan-

guages (Holzschuher and Peinl, 2013; Holzschuher

and Peinl, 2016) and on comparing performance

https://orcid.org/0000-0002-8283-8952

https://orcid.org/0000-0002-6726-3679

https://orcid.org/0000-0003-0547-0653

https://orcid.org/0000-0003-1366-8395

of graph databases against relational database sys-

tems (Batra and Tyagi, 2012; Vicknair et al., 2010).

In the literature, there also exists studies that compare

data analytics capabilities of graph databases. For in-

stance, in (Lee et al., 2012; Yan et al., 2005), perfor-

mance of the graph isomorphism algorithms provided

by different graph database systems are compared.

In this study, we focus on querying performance

of graph database when data is represented using

different graph models. More speciﬁcally, we use

Neo4j

as the graph database, and investigate its

querying performance for data that is modeled (i) as

a simple graph, and (ii) as a hyper-graph. A hyper-

graph is a generalization of a simple graph where an

edge can connect zero or more vertices as opposed

to connecting exactly two nodes in simple graphs.

Hyper-graphs are argued to better handle semantics

of data (Bu et al., 2010; Li and Li, 2013) and have

been subject to several studies.

Today there are graph database vendors, such as

HypergraphDB

, that directly support hyper-graph

data model. However, Neo4j is known as world lead-

ing graph database technology (Patil et al., 2018)

and, although not natively, supports modelling data

as hyper-graphs. In this study we model a book data

set under simple graph and hyper-graph models and

investigate querying performance of Neo4j for sev-

https://neo4j.com

http://www.hypergraphdb.org

Erdemir, M., Goz, F., Mutlu, A. and Karagoz, P.

Comparison of Querying Performance of Neo4j on Graph and Hyper-graph Data Model.

DOI: 10.5220/0008214503970404

In Proceedings of the 11th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2019), pages 397-404

ISBN: 978-989-758-382-7

397

eral types of queries. In this paper we also argue what

type of hyper-edges should be formed, which type of

modelling is preferable for which type of queries.

The rest of the paper is organized as follows. In

Section 2, we provide deﬁnitions of simple graph,

hyper-graph and their respective data models, and

brieﬂy introduce graph databases. In Section 3 we in-

troduce the data set used in this study, and the models

proposed. In Section 4 we report the graph query-

ing performances for both models and discuss the ob-

tained results. The last section concludes the paper.

2 PRELIMINARIES

In this section we ﬁrstly deﬁne graph and hyper-graph

data models, then introduce the graph database con-

cept.

2.1 Graph Data Model

Graph is deﬁned as a pair of sets G = (V, E) where V

is ﬁnite set of vertices and E, set of edges, is the set

of 2-element subset of V. In a graph data model, ver-

tices represent entities and edges between them rep-

resent the relationship between the entities. Edges

have direction in order to show the direction of the

relationship. Vertices and edges can be bundled with

properties that represent their features or roles. Data

manipulation is achieved via graph-centric operations

such as traversal.

Graph data model is suitable for modelling sev-

eral real life problems including social networks, col-

laboration networks, transportation networks, and bi-

ological networks. In (Hajian and White, 2011)

an e-commerce social network is modeled within a

graph structure where nodes represent individuals,

posts, and comments and edges indicate the interac-

tions between the nodes. In (Barber and Scherngell,

2013), R&D collaboration is analysed using graph

data model where nodes represent projects and or-

ganizations and edges indicate which organization is

involved in which project. In (Integrating, 2018),

nodes represent road intersections and edges repre-

sent road segments that connect road intersections.

Graph-based approaches have extensively been used

to analyse biological structures (Emmert-Streib et al.,

2016; Frainay and Jourdan, 2016), as well.

2.2 Hyper-graph Data Model

Hyper-graph is a generalization of simple graphs de-

noted as G = (V, E) where V is a ﬁnite set of vertices

and E is the set of k-element (k ≥ 0) subsets of V.

As hyper-edges enable modeling high order relations,

relations that include more than two entities, hyper-

graphs are advocated to better capture semantics of

complex data (Bu et al., 2010; Li and Li, 2013; Lung

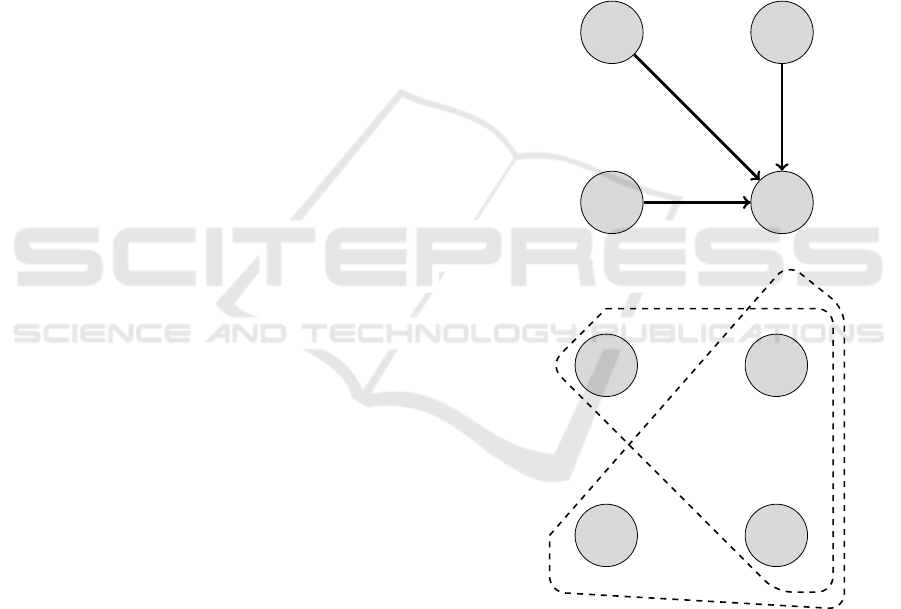
et al., 2018). As an example, suppose there are two

chemicals, namely A and B, that make a bond of type

BT1. Further suppose that chemical A also makes a

bond of type BT1 with chemical C. If these two re-

lations are modeled using a graph model, Figure 1a

will be obtained. From Figure 1 one may also infer

that there is bond between chemicals B and C of type

BT1, which is not the case. If the same relations are

modeled using hyper-graphs, model presented in Fig-

ure 1b will be obtained. This model prevents the mis-

inference done in Figure 1a.

BT1

(a)

BT1

(b)

Figure 1: Graph vs. Hyper-graph model representation.

In hyper-graph data modelling, hyper-edges are

user deﬁned and this arises a challenge in hyper-graph

model construction. In (Bu et al., 2010), a uniﬁed

hyper-graph model is proposed for music recommen-

dation, such that, binary relations such as friendship,

as well as n-ary relations such as hyper-edges con-

necting all songs that belong to an album, or hyper-

edges that connect an artist and all of his/her albums

are deﬁned. In (Li and Li, 2013), a news recommen-

KDIR 2019 - 11th International Conference on Knowledge Discovery and Information Retrieval

398

dation system based on hyper-graphs is presented.

In the study, hyper-edges that deﬁne different high-

order relationships among users (users that read about

the same topic), news articles (articles that belong to

the same topic), user-article-topic hyper-edges (users

that read articles about the same topic) are deﬁned.

In (Lung et al., 2018) a hyper-graph model repre-

senting scientiﬁc research community is constructed,

such that, nodes represent publications and authors,

and hyper-edges that connect (i) an author and his/her

publications; (ii) a publication and authors that con-

tributed in that publication are deﬁned.

2.3 Graph Databases

Graph databases have recently gained increasing pop-

ularity and have found several applications both in in-

dustry and scientiﬁc research. Below we list some of

the popular graph database systems.

• AllegroGraph

: It is implemented as an RDF

database and supports SPARQL, RDFS++, and

Prolog reasoning. It is primarily used for geo-

spatial reasoning and social network analysis.

• DEX

: It is a bitmaps-based graph database. Its

API provides several functionalities including link

analysis, pattern recognition, and keyword search.

• Neo4j: It is among the most popular graph

database systems and built upon a network model.

Its API provides efﬁcient traversals.

• HypergraphDB: It provides high-order relation-

ships between nodes and relational-style queries.

In this work, we choose to use Neo4j as the graph

database due to its widespread use both in academy

and industry. Another important reason for this ra-

tionale is that our analysis is focused on comparing

graph vs. hyper-graph in the same environment by

using basic graph querying capabilities. Hence, the

analysis do not include speciﬁc functionalities such

as RDF modeling or analytics capabilities.

3 DATA SET AND MODELS

In this section we ﬁrstly introduce the data set used in

this study, and then explain the graph and hyper-graph

models constructed in order to represent the data.

https://franz.com/agraph/allegrograph/

http://sparsity-technologies.com/

3.1 Data Set Description

The data set used in study is crawled from an on-

line bookstore. For each book its author(s), publi-

cation year, publisher, and category information are

retrieved. If the same book is published by multiple

publishers in different years, such books are treated

as different books. As indicated in Table 1, there are

71242 books, authored by 36647 authors.

Table 1: Data set properties.

Number of books 71242

Number of authors 36647

Number of categories 34

Number of publication years 57

Number of publishers 1922

3.2 Graph-based Model

In graph model for the book data set, 9 different types

of nodes are created. Nodes are created to store book

titles, author names, publisher names and publication

dates. However, these nodes are not bundled with

properties that indicate the type of the information

they store but instead are connected to special nodes

that indicate the type of information they store. Nodes

that are connected to the special node Writers store

author information. Similarly, nodes connected to

the special node BookCategory store book categories,

nodes connected to the special node Publisher store

publisher names, and nodes connected to special node

Dates store publication dates.

To indicate relationships between nodes, 5 types

of edges are created. In order to indicate authorship

relation, an edge of type WRITTEN

BY is placed be-

tween a book and an author. Similarly, a HAS TYPE

type of edge is placed between a book and its cat-

egory, PUBLISHED BY type of edge is placed be-

tween a book and its publisher, and lastly PUB-

LISHED IN type of edge is placed between a book

and its publication year. Nodes are connected to spe-

cial nodes via IS A edges.

Figure 2 is a visualisation of model described

above for book entitled ”Korku’nun Butun Sesleri”.

Leftmost and rightmost nodes are the special nodes,

and the nodes in between represent the book informa-

tion.

3.3 Hyper-graph Model

Figure 3 includes a sample for the hyper-graph model

proposed to represent the book data set. Similar to

the graph model, hyper-graph model of the book data

set consists of nodes representing book titles, author

Comparison of Querying Performance of Neo4j on Graph and Hyper-graph Data Model

399

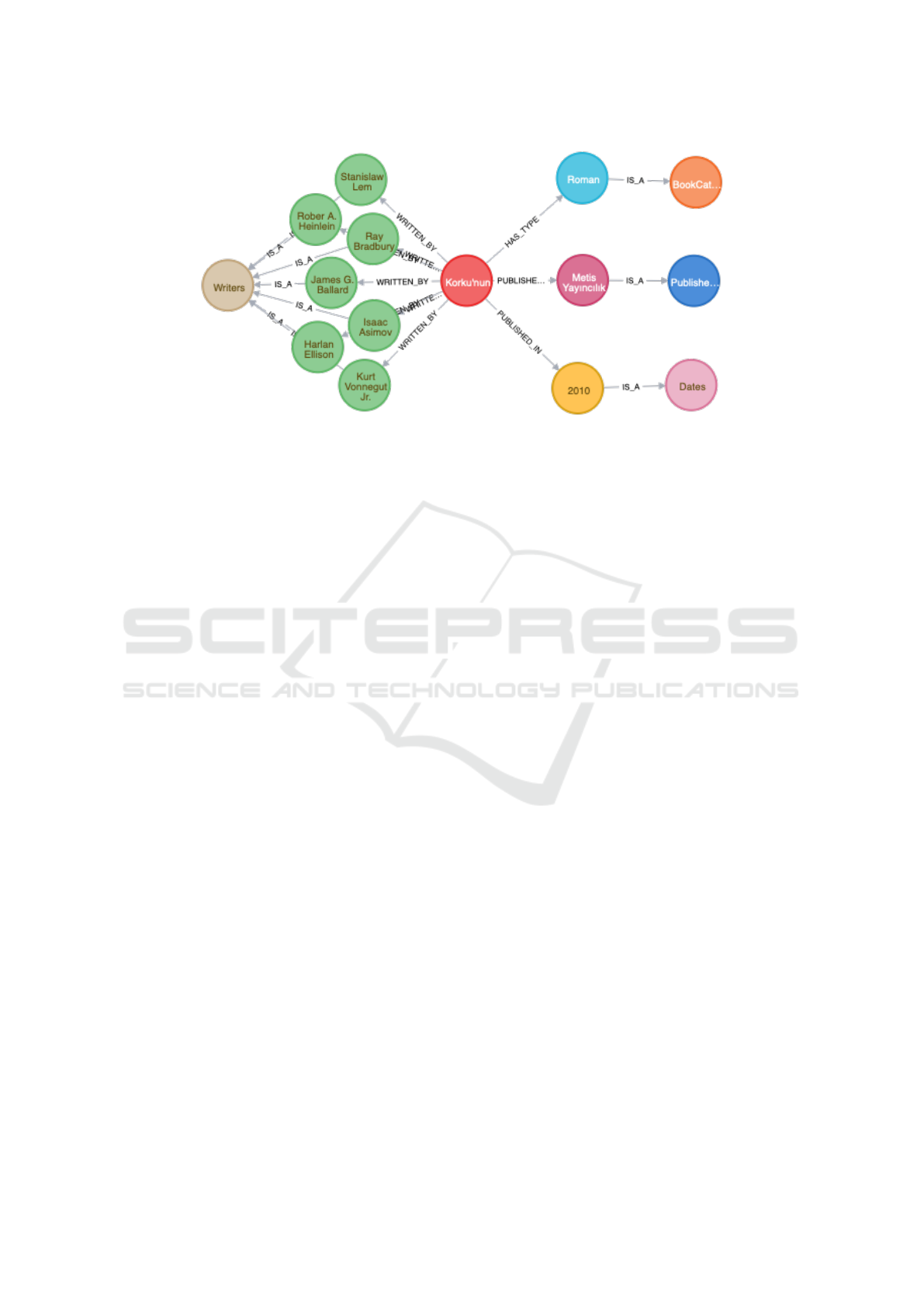
Figure 2: Graph model to represent books.

names, categories, publishers, and publication years.

In order to establish relationships between a book and

its attributes, both binary edges and hyper-edges are

used, hence the hyper-graph model is not homoge-

neous. Bw edge in Figure 3 is binary and establishes

<author, book> relationship. Nodes labeled bpd203,

bcp15, bcd11, and bcpd203 indeed represents hyper-

edges. Node bpd203 is a hyper-edge that connects

node storing the book title, Korku’nun Butun Ses-

leri, its publisher, Metis Yayincilik, and its publication

year, 2010. Also, not all attributes are connected to

book in a similar way, i.e. <author, book> relation-

ship is directly established, while <book, category>,

<book, publication year>, and <book, publisher>

relations are established via hyper-edges.

The hyper-graph model has 12 types of hyper-

edges and 2 types of binary edges, as follows:

• E

bcd

: This hyper-edge is created to capture

<category, publication year, book> relationships.

While creating such type of hyper-edges, each cat-

egory is paired with every publication year.

• E

bdc

: This hyper-edge is similar to E

bcd

in a sense

but this time each publication year is paired with

every category. Although these hyper-edges seem

very similar in structure, they serve for different

purposes. If one is interested in listing all books

that belong to a speciﬁc category, say Novel (Ro-

man in Figure 2.2), the list of the books will be

obtained by traversing E

bcd

type of hyper-edges

where category is Novel. However, if one is in-

terested in listing the books published in a spe-

ciﬁc year, say 2012, this time hyper-edges of type

bdc

where publication date is 2012, would be tra-

versed.

• E

bcp

: This hyper-edge is created to capture

<category, publisher, book> relationships. While

creating this type of hyper-edges each category is

paired with every publisher.

• E

bpc

: This hyper-edge is created to capture

<publisher, category, book> relationships. Dis-

tinction between E

bcp

and E

bpc

is similar to that

of E

bcd

and E

bdc

• E

bpd

: This hyper-edge is created to capture

<publisher, publication year, book> relation-

ships. Creation of such type of hyper-edges is

similar to the ones mentioned above.

• E

bd p

: This hyper-edge is created to capture

<publication year, publisher, book> relation-

ships. Creation of such type of hyper-edges is

similar to the ones mentioned above and distinc-

tion between E

bpd

and E

bd p

type of hyper-edges

is similar to that of E

bcd

and E

bdc

• E

bcpd

: This hyper-edge is created to capture

<category, publisher, publication year, book> re-

lationships. While creating such hyper-edges each

bcp

hyper-edge is extended to include nodes rep-

resenting year information. Hyper-edges that rep-

resent all combinations of <category, publisher,

publication year> are created in a similar fashion

to E

bcpd

and purposes similar to the creation of

bcd

and E

bdc

types of hyper-edges.

• e

: This is a binary edge to indicate <book,

author> relationship. If a book is authored by

multiple authors, several author nodes are con-

nected to the book node.

• e

W b

: This is a binary edge to indicate <author,

book> relationship.

In the proposed hyper-graph model, hyper-edges

are not created for every combination of the attributes.

As an example <author, publication year, book> type

KDIR 2019 - 11th International Conference on Knowledge Discovery and Information Retrieval

400

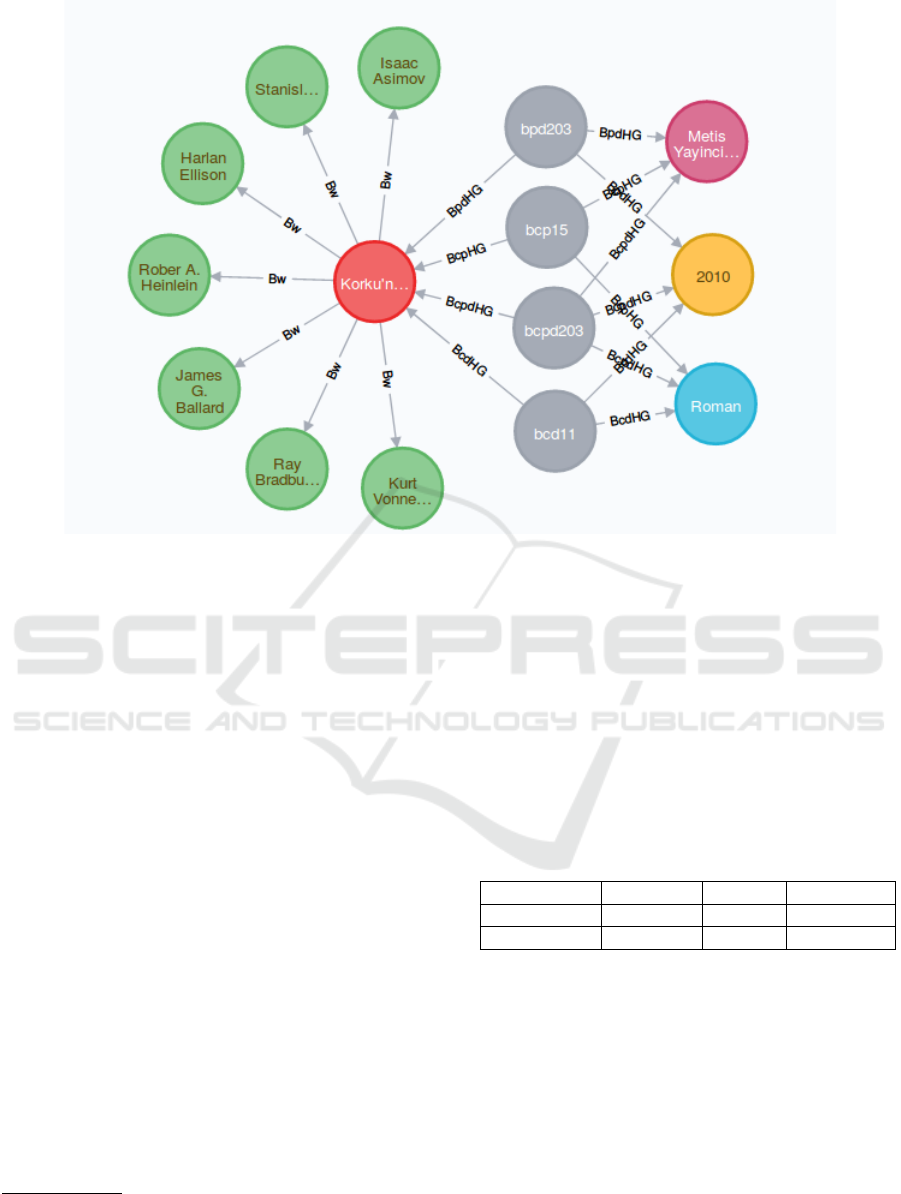
Figure 3: Hyper-graph data model to represent books.

of hyper-edges, which will connect author, publica-

tion year, and book, are not created. Based on the

statistics given in Table 1, for the worst case, 36647

× 57 = 2088879 such type of hyper-edges will be cre-

ated and probably each hyper-edge will connect dis-

tinct <author, publication year, book> triples. How-

ever, for the worst case, only 34×57 = 1938 dis-

tinct E

bcd

type of hyper-edges are created and such

<category, publication year> tuple is associated with

37 distinct books on average.

4 EVALUATION OF THE

MODELS

In this section, we ﬁrstly discuss the storage required

to represent the graph and hyper-graph models. Later,

we provide certain queries and analyse their running

times. Moreover, we also investigate the number of

nodes and relations that form valid paths that connect

starting node of a query to the nodes that represent the

result set

In Table 2, we report the number of nodes, the

number of relations needed to represent each model

and also the required storage. As the table indicates,

One should realize that these numbers are not the total

number of nodes/relations traversed to obtain the result set.

Nodes traversed but failed to reach an element of the result

set are discarded.

the hyper-graph model has larger number of nodes,

relations and requires more storage. This is due to

the fact that Neo4j does not have direct support for

hyper-edges but represents such structures using extra

nodes. To represent a hyper-edge that connects three

nodes, say nodes A, B, and C, Neo4j creates an extra

node, say node D, and places relationships between

A and D, B and D and between C and D. Node D is

then treated as a hyper-edge that connects A, B, and

C. The number of relations is also large due to way

Neo4j manages hyper-edges.

Table 2: Graph properties.

Model Storage #Nodes #Relations

Graph 21.71 MB 109906 329346

Hyper-graph 28.13MB 155959 480373

To evaluate how the different representations ef-

fect the running time of queries, we devised 12

queries, some of which are more suitable for the

graph representation and some more suitable for the

hyper-graph representation, and compared their run-

ning time. These queries are listed in Table 3. Queries

with ids 3 to 8 are more suitable for the hyper-graph

representation.

• Query 3 can be processed by traversing E

ddc

type

of hyper-edges where publication date is ﬁxed to

2017 and category varies.

• Query 4 and Query 5 can be processed by travers-

ing either E

bcd

or E

bdc

type of hyper-edges as both

Comparison of Querying Performance of Neo4j on Graph and Hyper-graph Data Model

401

Table 3: Queries to evaluate performance.

Query ID Query

1 Group name of the authors by their book categories who authored books published by Is

Bankasi Yayinlari.

2 Group name of the authors by their publishers who published a book in category Novel.

3 Group name of authors by their book categories who published a book in 2017.

4 List name of the authors who published a book in category Novel in 2017.

5 List name of the authors who published a book in 2017 in category Novel.

6 List name of the authors who authored books published by Is Bankasi Yayinlari in category

Novel.

7 List name of the authors who authored books published by Is Bankasi Yayinlari in 2017.

8 Group name of the authors by their book categories who published a book by Is Bankasi

Yayinlari in 2017.

9 List name of the books which are published either in 2016 or 2017 or 2018.

10 List name of the books which are published by either Is Bankasi Yayinlari or Cinius or

DoganEgmont Yayincilik

11 List name of the books that belong to either of the following categories, Novel or Poem or

School Age or Children’s Books.

12 List name of the books which are authored either by Kolektif or Stefan Zweig or Franz Kafka.

Table 4: Query evaluation results (time in ms.).

Query Graph based Model Hyper-graph based Model

ID Exec. Time # Nodes # Relations Exec. Time # Nodes # Relations

1 1520 - - 1661 - -

2 8818 - - 9413 - -

3 40922 - - 38533 - -

4 17793 - - 18138 - -

5 595 - - 2490 - -

6 233 - - 248 - -

7 476 - - 187 - -

8 119 - - 49 - -

9 51 283644 252128 67 187218 156015

10 12 44649 39688 16 28962 24135

11 50 283869 252328 69 188316 156930

12 49 55404 49248 47 36648 30540

publication year and category values are ﬁxed.

• Query 6 can be processed by traversing E

bpc

bcp

type of hyper-edges as both publisher and

category values are ﬁxed.

• Query 7 and Query 8 can be processed by travers-

ing E

bpd

or E

bd p

type of hyper-edges as publisher

and publication year values are ﬁxed.

The remaining queries are more suitable for graph

representation as there are direct relationship between

the search criteria and attributes sought for. As an ex-

ample, considering Query 1, in graph model there is

a direct edge between a book and its publisher how-

ever in the hyper-graph model, such a relationship is

established via hyper-edges which contain publisher

information.

The running times of the queries are listed in Ta-

ble 4. Running times are calculated by averaging

ﬁve runs of every query, without caching the queries.

When the running times are examined, it can be seen

that queries have similar running times on both mod-

els but they always have shorter running time for

the graph model, with exception for Query 4. Ob-

taining such results was surprising as we expected

queries suitable for the hyper-graph model to have

shorter running times when executed on the hyper-

graph model compared to graph model. Similarly,

it was unexpected for queries suitable for the graph

model to have shorter running times when run on the

graph model compared to the hyper-graph model. We

believe that obtaining seemingly poor performance

for queries designed for hyper-graph model is due to

the indirect support of Neo4j for hyper-graphs. This

indirect support requires creation of more nodes and

edges and increases the search space.

KDIR 2019 - 11th International Conference on Knowledge Discovery and Information Retrieval

402

For queries 9 to 12 number of nodes and rela-

tions that form valid paths from the starting nodes

to the nodes that represent the result set are given.

From these numbers, one can see that the hyper-graph

model builds shorter paths when compared to the

graph model. These statistics are not provided for the

ﬁrst 8 queries as these these queries are initiated with

more than one node and the search is not a traversal.

5 CONCLUSION

In this paper, we study the querying performance on

graph modeling in graph databases. More speciﬁcally,

given the same data, we compare the querying perfor-

mance under simple graph and hyper-graph models

on Neo4j graph database. The querying performance

is analyzed for 12 different queries. While selecting

the queries, we included both those involve hyper-

edges and those binary edges.

As expected, hyper-graph model leads to higher

storage cost due to the inclusion of additional nodes

to model hyper-edges, which also leads to increase in

number of edges on the overall. However, this brings

an advantage for queries involving multiple type of

nodes. This advantage is most obvious for Query 7

and Query 8 (in Table 4), where the execution time

is considerably reduced, such as to half or quarter.

On the other hand, there are surprising results where

simple graphs perform better for such type of queries,

such as Query 5. For this query, the traversal cost pos-

sibly dominates the execution time for hyper-graph

model due to higher number of nodes.

As a future work, we plan to test the models on

more complex data sets such as news and biological

data sets. These data set contain higher order rela-

tionships compared to the book data set. We also plan

to implement and evaluate the performance of hyper-

graph model on graph database systems that have di-

rect support for hyper-edge construction.

ACKNOWLEDGEMENTS

This work is partially supported by Scientiﬁc and

Technological Council of Turkey (TUBITAK) with

grant number 117E566.

REFERENCES

Barber, M. J. and Scherngell, T. (2013). Is the european

r&d network homogeneous? distinguishing relevant

network communities using graph theoretic and spa-

tial interaction modelling approaches. Regional Stud-

ies, 47(8):1283–1298.

Batra, S. and Tyagi, C. (2012). Comparative analysis of re-

lational and graph databases. International Journal of

Soft Computing and Engineering (IJSCE), 2(2):509–

512.

Bu, J., Tan, S., Chen, C., Wang, C., Wu, H., Zhang, L.,

and He, X. (2010). Music recommendation by uniﬁed

hypergraph: combining social media information and

music content. In Proceedings of the 18th ACM inter-

national conference on Multimedia, pages 391–400.

ACM.

Emmert-Streib, F., Dehmer, M., and Shi, Y. (2016). Fifty

years of graph matching, network alignment and net-

work comparison. Information Sciences, 346:180–

197.

Frainay, C. and Jourdan, F. (2016). Computational meth-

ods to identify metabolic sub-networks based on

metabolomic proﬁles. Brieﬁngs in bioinformatics,

18(1):43–56.

Hajian, B. and White, T. (2011). Modelling inﬂuence in

a social network: Metrics and evaluation. In 2011

IEEE Third International Conference on Privacy, Se-

curity, Risk and Trust and 2011 IEEE Third Interna-

tional Conference on Social Computing, pages 497–

500. IEEE.

Holzschuher, F. and Peinl, R. (2013). Performance of graph

query languages: comparison of cypher, gremlin and

native access in neo4j. In Proceedings of the Joint

EDBT/ICDT 2013 Workshops, pages 195–204. ACM.

Holzschuher, F. and Peinl, R. (2016). Querying a graph

database–language selection and performance consid-

erations. Journal of Computer and System Sciences,

82(1):45–68.

Integrating, A. (2018). Core: Generating a computation-

ally representative road skeleton-integrating aadt with

road structure. In Big Data Analytics and Knowledge

Discovery: 20th International Conference, DaWaK

2018, Regensburg, Germany, September 3–6, 2018,

Proceedings, volume 11031, page 59. Springer.

Jouili, S. and Vansteenberghe, V. (2013). An empirical

comparison of graph databases. In 2013 Interna-

tional Conference on Social Computing, pages 708–

715. IEEE.

Kolomi

cenko, V., Svoboda, M., and Ml

ynkov

a, I. H. (2013).

Experimental comparison of graph databases. In Pro-

ceedings of International Conference on Information

Integration and Web-based Applications & Services,

page 115. ACM.

Lee, J., Han, W.-S., Kasperovics, R., and Lee, J.-H. (2012).

An in-depth comparison of subgraph isomorphism al-

gorithms in graph databases. In Proceedings of the

VLDB Endowment, volume 6, pages 133–144. VLDB

Endowment.

Comparison of Querying Performance of Neo4j on Graph and Hyper-graph Data Model

403

Li, L. and Li, T. (2013). News recommendation via hy-

pergraph learning: encapsulation of user behavior and

news content. In Proceedings of the sixth ACM inter-

national conference on Web search and data mining,

pages 305–314. ACM.

Lung, R. I., Gask

o, N., and Suciu, M. A. (2018). A hyper-

graph model for representing scientiﬁc output. Scien-

tometrics, 117(3):1361–1379.

Patil, N., Kiran, P., Kiran, N., and KM, N. P. (2018). A

survey on graph database management techniques for

huge unstructured data. International Journal of Elec-

trical and Computer Engineering, 8(2):1140.

Vicknair, C., Macias, M., Zhao, Z., Nan, X., Chen, Y., and

Wilkins, D. (2010). A comparison of a graph database

and a relational database: a data provenance perspec-

tive. In Proceedings of the 48th annual Southeast re-

gional conference, page 42. ACM.

Yan, X., Yu, P. S., and Han, J. (2005). Substructure sim-

ilarity search in graph databases. In Proceedings of

the 2005 ACM SIGMOD international conference on

Management of data, pages 766–777. ACM.

KDIR 2019 - 11th International Conference on Knowledge Discovery and Information Retrieval

404