Data Mining Techniques for Early Detection of Breast Cancer

Maria Inês Cruz

and Jorge Bernardino

1,2 a

Polytechnic of Coimbra – ISEC, Rua Pedro Nunes, Quinta da Nora, 3030-199 Coimbra, Portugal

CISUC – Centre of Informatics and Systems of University of Coimbra, Pinhal de Marrocos, 3030-290 Coimbra, Portugal

Keywords: Data Mining, Cancer, Breast Cancer, Biomarkers, Ensemble.

Abstract: Nowadays, millions of people around the world are living with the diagnosis of cancer, so it is very important

to investigate some forms of detection and prevention of this disease. In this paper, we will use an ensemble

technique with some data mining algorithms applied to a dataset related to the diagnosis of breast cancer using

biological markers found in routine blood tests, in order to diagnose this disease. From the results obtained,

it can be verified that the model got an AUC of 95% and a precision of 87%. Thus, through this model it is

possible to create new screening tools to assist doctors and prevent healthy patients from having to undergo

invasive examinations.

1 INTRODUCTION

Cancer is a disease where the cells of our body divide

without control due to the fact that they have

undergone mutations in their DNA, and because of

this, cells acquire properties during this division

process (CUF, 2017).

Today, millions of people around the world living

with the diagnosis of cancer. In Portugal, in 2018

were recorded about 58.199 new cases of cancer in

which about 28.960 of these cases don’t survive

(Global Cancer Observatory, 2018). The constant

investigation on this area is extremely necessary.

Some types of cancer can be detected before they

cause problems, and so it is very important to do

screening tests.

One of these types is the breast cancer, a cancer

that forms in tissues of the breast. The most common

type of breast cancer is ductal carcinoma, which

begins in the lining of the milk ducts (thin tubes that

carry milk from the lobules of the breast to the

nipple). Another type of this cancer is lobular

carcinoma, which begins in the lobules (milk glands)

of the breast. Invasive breast cancer is a cancer that

has spread from where it began to surround normal

tissue. Breast cancer can occur in both men and

women, although male breast cancer is rare. It is the

most common no cutaneous cancer in United States

women, with an estimated 62,930 cases of local

https://orcid.org/0000-0001-9660-2011

disease and 268,600 cases of invasive disease in

2019. Clinical trials have established that screening

asymptomatic women using mammography, with or

without clinical breast examination, decreases breast

cancer mortality (National Cancer Institute, n.d.).

The early detection of cancer is one of the most

efficient methods for the diagnosis of this disease.

“The cancer kills us because we give time to do it”

writes researcher Patrizia Paterlini-Bréchot in her

book “Kill the Cancer”. This researcher discovered a

blood test that allows visualizing the presence of

cancerous cells, of any type of cancer except

leukaemia and lymphomas, “often before the cancer

can be detected”. It further considers that to “kill the

cancer” it is necessary “extend the methods of early

detection” and that “very early diagnosis is the way

to save millions of lives” (Agência Lusa, 2018).

Therefore, the computational tools of data mining

become very important to analyse all of data that

coming of several medical exams. These can be used

in extracted data from blood tests, thus making an

important contribution to the experts, offering more

screening tools.

The purpose of this paper is to apply many

techniques of data mining to a dataset with some

features found in routine blood tests in order to

predict the presence of breast cancer.

In this paper will be made a univariate and

multivariate descriptive analysis for the data pre-

434

Cruz, M. and Bernardino, J.

Data Mining Techniques for Early Detection of Breast Cancer.

DOI: 10.5220/0008346504340441

In Proceedings of the 11th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2019), pages 434-441

ISBN: 978-989-758-382-7

processing. We will build a model based on ensemble

techniques and use the Stacking Ensemble learning

technique which will be explained in the next section.

The algorithms that we will use in our model are

Logistic Regression, Random Forest, Naive Bayes

and Support Vector Machine. To train and validate

the model will be used Validation Set and Cross-

Validation methods. The aim is to evaluate the

performance of the model in terms of accuracy,

precision, recall, false negatives rate and AUC (Area

Under the ROC Curve).

There are some studies regarding the application

of DM techniques to breast cancer diagnostic

datasets. In 2018, a study for create and analyse the

dataset that will be used in this paper was done

(Patrício et al., 2018).

In this study, a univariate analysis was elaborated

where each variable was evaluated as to normality

using some normalization tests. In the end was using

the ROC curve to evaluate each parameter. In

multivariate analysis the Gini coefficient was used,

on average, in all trees of a Random Forest. The

predictive models used logistic regression, support

vector machines and random forest algorithms. The

Monte Carlo Cross-Validation was adopted in the

training set and the models was evaluated in relation

to AUC, specificity and recall. The SVM using

Glucoses, Resistin, Age and IMC as predictors got a

recall between 82% and 88% and a specificity

between 85% and 90%. The confidence interval of

95% to the AUC was [0.87;0.91].

This paper is organized as follows. In section 2 are

introduced some fundamental concepts. In section 3

the dataset is explored in order to understand the data.

In section 4 the model is created and analysed. In

section 5 the results are discussed and evaluated

according to the metrics. Finally, section 6 presents

the conclusions and some ideas for future work.

2 FUNDAMENTAL CONCEPTS

This section describes some of the fundamental

theoretical concepts to understand the study that will

be performed. We explain the data mining concept, as

well as the various steps of this process.

2.1 Data Mining

Data Mining can be considered as the synonymous of

the term Knowledge Discovery from Data, or KDD,

or as merely an essential step in knowledge discovery

process. This process of discovery is a sequence of

the following steps:

 Data Cleaning, to remove the noise and

inconclusive data;

 Data Integration, where many data sources can

be integrated;

 Data Selection, where the relevant data for the

analysis are extracted from data base;

 Data Transformation, where the data are

transformed and consolidated properly to make

the analysis performing summary and aggregation

operations.

 Data Mining, the essential process where is used

methods to extract patterns and correlations of the

data;

 Patterns Evaluation, to identify the real interest

of the patterns that represent knowledge based on

“interest” metrics;

 Knowledge Presentation, where techniques of

visualization and representation of knowledge are

used to present knowledge to users.

This approach shows data mining as a step of the

knowledge discovery process, although essential

because it reveals patterns that are hidden for

evaluation. However, in industry and investigation

the term is frequently used to define all process of

knowledge discovery (Borges, Marques, and

Bernardino, 2013). Therefore, a broad view of data

mining was adopted as the process of discovering

interesting patterns and knowledge from large

amounts of data.

2.2 Data Pre-processing

Typically, the daily data is redundant and

inconsistent, also containing missing values. On the

other hand, there is also the problem of having a large

amount of data or, conversely, a small amount of data.

In order to perform a good analysis of the data, it

is necessary to prepare the data. This process involves

a more in-depth analysis of the attributes and values

of the data.

The starting point for this pre-processing will be

to obtain a statistical description of the data,

identifying its attributes and performing a univariate

and multivariate analysis.

Univariate descriptive analysis involves

describing the central tendency and dispersion of an

attribute. Some measures of the central tendency are

the mean (average number of all values), mode (most

frequent value) and median (number that is in the

middle of the list). The dispersion can be measured

by variance or standard deviation, range of values

(minimum and maximum value), percentiles,

quartiles, and the five-number summary (it involves

Data Mining Techniques for Early Detection of Breast Cancer

435

the minimum, the first quartile, the median, the third

quartile and the maximum).

Multivariate descriptive analysis involves

analysing the correlation between attribute pairs

through scatter plots. After these analyses are

followed the cleaning, transformation and reduction

of the data. This stage is where the outliers and

missing values (attribute values that are missing in

some examples) are treated.

Having thus the data already pre-processed and

prepared for analysis it is possible to move to the

stage of construction of the data mining models.

2.3 Types of Learning

At the stage of model construction, the purpose of the

analysis is to learn to recognize complex patterns and

make intelligent and data-driven decisions. There are

then two types of learning (Kaufmann, Han and

Kamber, 2006): supervised and unsupervised

learning. In this case study, the dataset examples have

an attribute that classifies them, whether the patient

has cancer or not. So, this study will focus on

supervised learning.

In Supervised Learning we find Classification

problems, where the output variable is qualitative (a

class, category or diagnosis), such as the prediction of

a person having or not having a particular disease.

For this type of learning, in the construction of the

model it is necessary to have a training to teach our

method to estimate the model using the available data

examples (Kaufmann, Han and Kamber, 2006). This

training is performed using a learning algorithm, in

this case study will be used Logistic Regression,

Random Forest, Naive Bayes and Support Vector

Machine.

It is then necessary to evaluate the quality of the

model created (Kaufmann, Han and Kamber, 2006),

that is, if the estimate corresponds to the observations.

The goal is for the method to obtain generalization

capability, that is, to be precise in situations that are

not found in the training and not to memorize the

examples. For this evaluation a test set is created with

different examples from those used for training. If

there are examples for testing available, these

examples are used to evaluate the model, if no

examples are available the training set is divided into

two parts, training with one and testing with the other.

For this approach there are two methods of validation:

 Validation Set: this method divides 70% of the

data for training and 30% of the data for test;

 Cross-validation: there are two techniques for

this method, one of which is k-fold Cross-

validation in which the initial data are randomly

divided into k exclusive subsets, each

approximately of the same size. The training and

the test are done k times. In the first iteration,

subset 1 is used for testing and the rest for

training, and so on. Another technique is the

Leave-one-out Cross-validation which is a

special case of k-fold cross-validation where one

example is taken at a time for testing and the rest

are used for training.

2.4 Ensemble Methods

Ensemble methods is a data mining technique that

combines several base models in order to produce one

optical predictive model. These methods can be

divided in two groups:

 Sequential: where the base learners are generated

sequentially (e.g. AdaBoost). The motivation of

these methods is to exploit the dependence

between the base learners. The overall

performance can be boosted by weighing

previously mislabelled examples with higher

weight;

 Parallel: where the base learners are generated in

parallel (e.g. Random Forest). The motivation of

these methods is to exploit independence between

the base learners since the error can be reduced

significantly by averaging.

There are three ways for using ensemble methods,

that are bagging, boosting and stacking. In this study

the stacking method described below is used.

2.4.1 Stacking

Stacking is an ensemble learning technique that

combines multiple classification or regression models

via a meta-classifier or a meta-regressor. The base

level models are trained based on a complete training

set, then the meta-model is trained on the outputs of

the base level model as features (Smolyakov, 2017).

In this study we will use the Stacking method with

Random Forest, Naive Bayes and Logistic

Regression as base algorithms and the Support Vector

Machine as meta-classifier.

2.5 Learning Algorithms

In this section we briefly describe how the learning

algorithms used for this study works.

2.5.1 Bayesian Algorithms (Naive Bayes)

Bayesian algorithms follow probabilistic approaches

that create strong assumptions about how data is

KDIR 2019 - 11th International Conference on Knowledge Discovery and Information Retrieval

436

generated and construct a probabilistic model that

incorporates these assumptions. They use a set of

classified training examples to estimate the model

parameters. Classification in the new examples is

done with the Bayes rule by selecting the class that is

most likely to have generated that example

(McCallum and Nigam, 1998).

The Naive Bayes is a probabilistic algorithm

based on Bayes’ theorem and is the simplest classifier

of these algorithms since it is assumed that all

attributes are independent given the class context.

Although this assumption is false in most real-world

data, this classifier performs well most of the time.

Thanks to this assumption, the parameters for each

attribute can be learned separately, and thus there is a

simplification of learning, especially with many

attributes.

This method works with several probabilities for

each class. These probabilities are reflected in the

conditioned probability of each value of the attribute

given to the class, as well as the probability of the

class (Langley, Iba, and Thompson, 1992).

2.5.2 Random Forest

Random Forest is a supervised learning algorithm,

and as the name implies it creates a forest and makes

it somehow random. The “forest” is an ensemble of

Decision Trees (Loh and Shin, 1997), most of the

time trained with the “bagging” method. The general

idea of this method is that a combination of learning

models increases the overall result. In a simple way,

this algorithm builds multiple decision trees and

merges them together to get a more accurate and

stable prediction.

This method adds additional randomness to the

model, while growing trees. Instead of searching for

the most import feature while splitting a node, it

searches for the best feature among a random subset

of features. This results in a wide diversity that

generally results in a better model.

This algorithm is a collection of Decision Trees

but exist some differences. If we input a training

dataset with features and labels into a decision tree, it

will formulate some rules, which will be used to make

the predictions. In comparison, the Random Forest

randomly selects observations and features to build

several decision trees and then averages the results.

One of the vantages of this algorithm is that it

prevents overfitting (in a simple way, it is when a

model learns too much noise) (Technopedia, n.d.)

most of the time, by creating random subsets of the

features and building smaller trees using them.

Afterwards, it combines the subtrees. With decision

trees, the more we increase the depth of the tree the

more likely there is to be overfitting (Donges, 2018).

2.5.3 Logistic Regression

Logistic regression is used in classification problems

in which the attributes are numerical, it is an

adaptation of linear regression methods. Considering

a dataset where the target is a binary categorical

variable, the value of 0 and 1 is given to each of the

categories respectively, and instead of the regression

executing the response directly, it executes the

probability that the response belongs to a category (0

or 1).

If the model is done following the linear

regression approach, the attributes that have values

close to zero will have a negative probability and if

they have very high values the probability will exceed

the value 1 (James, Witten, Hastie, and Tibshirani,

2013). These predictions are not correct because a

true probability, regardless of the value of the

attribute, must be between 0 and 1. Whenever a

straight line is fitted to a binary response that is coded

as 0 or 1, it always be possible to predict p(X) < 0 and

p(X) > 1 at the outset (unless the X range is limited).

To avoid this problem, one must make the

probability model using a function that provides

outputs between 0 and 1 for all values of X.

2.5.4 Support Vector Machine

The objective of the support vector machine

algorithm is to find a hyperplane (decision boundaries

that help classify the data points) in an N-dimensional

space, when the N is the number of features, that

distinctly classifies the data points. To separate the

two classes of data points, there are many possible

hyperplanes that could be chosen. The main objective

is to find a plane that has the maximum distance

between data points of both classes. Therefore, it is

possible to provide some reinforcement so that future

data points can be classified with more confidence.

Support Vectors are data points that are closer to

the hyperplane and influence the position and

orientation of the hyperplane, using this support

vectors it is possible to maximize the margin of the

classifier. Hyperplanes and support vectors are the

core for building an SVM algorithm (Gandhi, 2018).

2.6 Evaluation Metrics

Finally, it is necessary to evaluate the performance of

the model created. For this, there are several

evaluation metrics (

Sunasra, 2017):

Data Mining Techniques for Early Detection of Breast Cancer

437

 Accuracy: is the degree of proximity of an

amount with the true value of that quantity, that is,

the model hit rate, the number of times the model

hit the forecasts;

 Precision: is the degree to which repeated

measurements under unchanged conditions show

the same results, that is, the generalization ability

of the model;

 Recall: is the rate of values that the model

predicted positive and it is positive in dataset;

 Specificity: is the rate of values that the model

predicted negative and it is negative in dataset;

 False Negatives Rate: is the rate of values that

the model missed, classifying as negatives the

positive values.

Another metric of evaluation is the ROC curve, which

consists of the graphical representation of the pairs,

recall and specificity in all limits of classification

(thresholds) (Google Developers, 2019). This curve

allows you to achieve the AUC (Area Under the

ROC Curve) measurement that measures the entire

area under the ROC curve. The higher the AUC the

better is the model used as it is performing the

predictions correctly. The AUC ranges from 0 to 1. If

a model obtains 100% of missed predictions, will

have an AUC of 0 and vice versa.

3 DATA EXPLORATION

The dataset used for the analysis is called Breast

Cancer Coimbra Dataset and can be consulted

publicly in (Machine Learning Repository, 2018).

This dataset was used for a study at the University of

Coimbra with the objective of constructing a

predictive model that could potentially be used as a

bio marker for breast cancer.

It was created in May of 2018 and contains 10

quantitative attributes and one categorical variable

which indicates the presence or not of breast cancer.

The attributes are anthropometric data and parameters

that can be collected in routine blood tests.

Were collected data of 64 sick women and 52

healthy women. So, the dataset contains 116

examples. The patient data were collected before the

surgery and the treatments (Patrício et al., 2018).

The categorical variable indicates the values 1 and

2, that corresponding, respectively to women healthy

and sick. The dataset is complete, not containing

missing values.

A description of the dataset is given below

(Patrício et al., 2018) (Frazão, 2018):

 Age: Age of the patient (24 to 89);

 BMI: Body Mass Index (18,37 to 38,58 kg/m



);

 Glucose: Quantity of sugar in blood (60 to 201

mg/dL);

 Insulin: Hormone produced by pancreas to

reduce the rate of glucose in blood (2,432 to 58,46

U/mL);

 HOMA: Homeostatic Model Assessment, is a

method used to quantify the insulin resistance

(Lemos, 2018) (0,467 to 25,05);

 Leptin: Protein responsible for the control of food

ingested, send information to the brain (Gunnars,

2018) (4,3 to 90,3 ng/mL);

 Adiponectin: Protein responsible for the

regulation of the glucose in blood (1,66 to 38,04

ng/mL);

 Resistin: Protein responsible for block the

principal action of the leptin (3,21 to 82,1 ng/mL);

 MCP-1: Monocyte Chemoattractant Protein 1,

recruit monocytes and specific cells to spots of

inflammation.

A univariate analysis was performed where the values

of the mean, the standard deviation and the five-

number summary for each attribute were calculated.

The Excel tool was used to perform these

calculations.

Through these values it is possible to create

boxplots. The Orange tool was used to create and

display them. There is greater dispersion of data in the

Age, BMI and Leptin attributes. It is possible to

conclude this by comparing attributes.

Figure 1: Boxplot of attribute Age.

Figure 2: Boxplot of attribute Glucose.

For example, Figure 1 and Figure 2 represent the

boxplots relative to attributes Age and Glucose,

respectively. Note that the interquartile range is

smaller in the Glucose attribute, so the values of this

attribute are mostly close to the mean value.

Therefore, it is concluded that the values of this

attribute are less dispersed compared to age.

In attributes with greater dispersion it becomes

more difficult to find patterns in the data, whereas in

the less dispersed the patterns are found more easily.

KDIR 2019 - 11th International Conference on Knowledge Discovery and Information Retrieval

438

Using the Information Gain method, it is verified

that the attributes most relevant for classification, that

is, for the division of classes are Glucose, HOMA,

Resistin and Insulin.

It is also possible to check the existence of outliers

in all attributes except the Age and BMI attributes by

calculating the upper and lower admissible limits. For

the remaining attributes, it is important to have the

outliers in consideration, since being a medical

dataset, values “out of ordinary” may indicate

important information. It is verified that most of these

values classify diseased patients, which may indicate

that the values have arisen naturally and are important

for the analysis, since they can be a factor of

differentiation in the classification of the problem.

Thus, the same previous analysis was made, but

replacing the outliers with the permissible upper

limit, which showed a single difference in the

dispersion of the data, in which the data became more

dispersed than with the original values. This means

that the outliers do not have great relevance to the

classification of the dataset so they will be kept in the

learning models. We found in Figure 3 that the values

are more dispersed than in Figure 2, with the size

between quartiles increased, which means that the

values are farthest from each other.

Figure 3: Boxplot of attribute Glucose without outliers.

Moving to a multivariate analysis, and through the

visualization of scatter plots, a single correlation

between the HOMA and Insulin attributes is verified,

which is natural since HOMA is a method that

calculates insulin resistance. This correlation is

perceptible because the values form a diagonal line.

The fact that there are two correlated attributes can

mean that it is indifferent whether one exists or not,

since both transmit the same information, and thus

will not interfere in the learning of the model. We

decide to make a prior analysis to verify if the HOMA

attribute when taken from the dataset had a

significance influence on the results and it was

verified that the results did not suffer significant

differences so we will keep all the attributes for the

learning of the model.

4 CONSTRUCTION OF THE

MODEL

In a scenario made previously to this same dataset,

three classification algorithms were analysed:

Decision Tree, Logistic Regression and Naive Bayes.

In this analysis there were no good results, and the

maximum AUC achieved was with logistic regression

with a value of 79% and an accuracy of 74%. The

results are illustrated in Table 1.

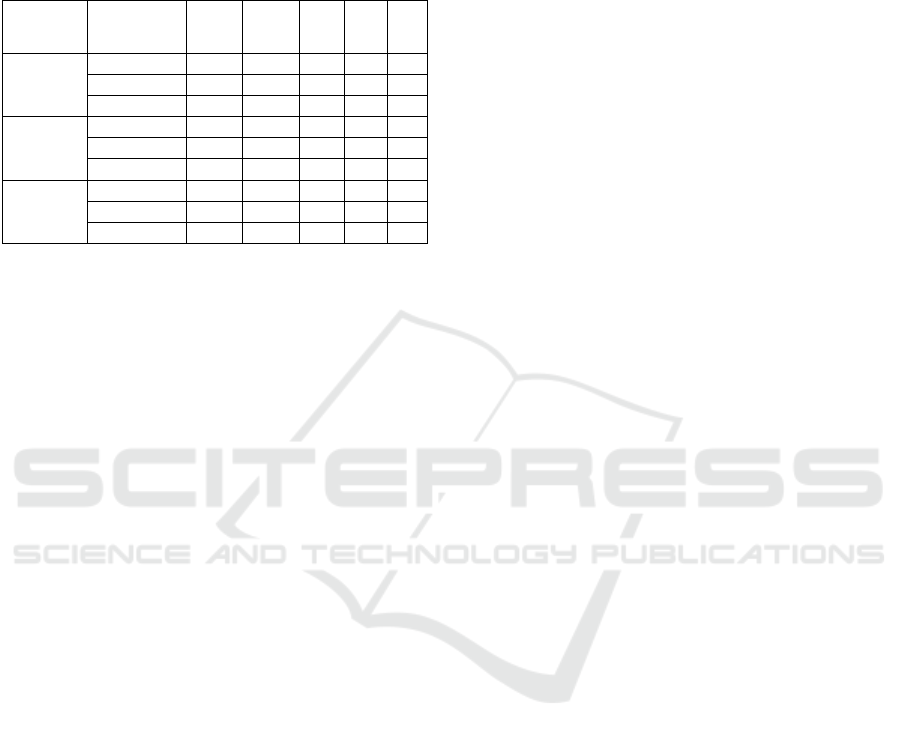
Table 1: Results of the individual classifiers.

Algorithm Accuracy Precision Recall AUC Specificity FNR

Logistic

Regression

0.74 0.74 0.73 0.79 0.64 0.28

Decision

Tree

0.72 0.72 0.71 0.73 0.63 0.32

Naive Bayes 0.68 0.68 0.68 0.74 0.58 0.33

Random

Forest

0.66 0.66 0.66 0.70 0.66 0.30

After this, we decided to try to improve these

results with the model proposed below, using

Ensemble methods.

For our model we will then use the ensemble

stacking method, with Logistic Regression, Random

Forest and Naive Bayes as base models and Support

Vector Machine as final meta-classifier. We used the

Orange tool to evaluate the model. The parameters

used in each algorithm were as follows: in Random

Forest 10 trees are created, with 5 attributes at each

split; in Logistic Regression the Tikhonov

regularization was used (Kringstad, 2019) with a cost

strength of 3; in Naive Bayes has no parameters to

adjust; in SVM the cost (penalty term for loss) of the

minimization of the error function is 1, the kernel

function (is a function that transforms attribute space

to a new feature space to fit the maximum-margin

hyperplane) used was polynomial and the permitted

deviation from the expected value was 0,001 and the

limit iterations was 100.

As validation methods are used, first the

Validation Set and then the Cross-Validation, in order

to analyse the differences of the model between both

methods. In the Validation Set on the base models,

the train/test was repeated ten times and in the meta-

classifier was repeated two times.

In the Table 1 it is possible to visualize the values

of precision, recall, accuracy, AUC and false

negatives rate (FNR on Table 2) for the Validation Set

(70-30 on Table 2) method, with 70% of the dataset

Data Mining Techniques for Early Detection of Breast Cancer

439

for training and 30% for test, Cross-Validation k-

folds (CV1 in Table 2) and Cross Validation Leave-

one-out (CV2 in Table 2) in base models and meta-

classifier.

Table 2: Results of the model.

Validation

Methods in

Base models

Validation

method in

Meta-Classifier

Accuracy Precision Recall AUC FNR

70-30

70-30 0.86 0.87 0.86 0.95 0.14

CV1 0.73 0.79 0.73 0.96 0.27

CV2 0.62 0.71 0.62 0.84 0.38

CV1

70-30 0.77 0.78 0.76 0.87 0.24

CV1 0.73 0.80 0.73 0.86 0.27

CV2 0.71 0.77 0.71 0.83 0.29

CV2

70-30 0.64 0.79 0.64 0.81 0.36

CV1 0.73 0.80 0.73 0.86 0.27

CV2 0.71 0.77 0.71 0.83 0.29

5 RESULTS DISCUSSION AND

EVALUATION

It is possible to verify through the results that this

model obtains better results than the model made in

the previous study, as would be expected.

We can say that the model presented good results

because all the AUC values are superior to 80%. A

significant difference can be noted when using the

Validation Set method in base models and in meta-

classifier. Thus, achieving an AUC of 95%, a

precision 87% and an FNR of 14%.

In our view, the most important metrics in medical

studies are the ability of the model to adapt to new

cases, that is, the generalization capacity of the model

(precision) and especially the false negative rate,

since the worst case scenario can happen is to

diagnose the person as being healthy (negative

diagnosis) and in fact the person having the disease

(positive diagnosis). It is also very important to have

a good AUC value as it means that the model made

most of the prediction correctly.

Good results with 80% precision and 86% AUC

are also found using Cross-Validation k-folds method

in all algorithms.

Worst values are displayed when we use the

Cross-Validation Leave-one-out in base models and

the Validation Set in meta-classifier.

It is verified through the data exploration of data

that the most relevant features for the distinction

between the classes are Age, BMI, Leptin, Resistin

and Adiponectin.

Due to the small dataset, the results are not very

reliable, so it was interesting made a research with

more subjects to test the model.

6 CONCLUSIONS

The first conclusions were withdrawn in the pre-

processing phase of this study through the

visualization of a decision tree and are that all the

subjects of this dataset aged less than or equal to 74,

Leptin values less than or equal to 31.12, Resistin

higher than 13, Adiponectin higher than 2.2, and BMI

lower than 32 have the disease. There are 26 patients

with these conditions, which makes up 41% of the

patients in the dataset.

With this study it was also possible to conclude

that the ensemble methods significantly improve the

models. In our specific case, using the staking method

it was concluded that the more times we train the base

algorithms the better are the results.

On the other hand, the fact that the best validation

method is the validation set means that many times

(randomly) the examples used for testing are used in

the training, which implies a greater accuracy in the

predictions, but not because the model learned the

results but memorized them.

Despite this, using Cross-Validation k-folds in the

base models and meta-classifier also obtains good

results, so it can be concluded that the model

generally shows good results.

This paper can help other investigators to create

an effective predictive model for detecting cancer

through blood routine exams, before the treatment

becomes more complex and the total elimination of

cancer is more difficult to achieve.

For future work, we intend to improve the results

by testing other algorithms and other ensemble

methods. It was interesting to get new features related

to routine blood test and increase the dataset should

be considered in order to get more efficient results.

REFERENCES

CUF. (2017). O que é o cancro? Retrieved from

https://www.saudecuf.pt/oncologia/o-cancro/o-que-e-

o-cancro/.

Global Cancer Observatory. (2018) International Agency

for Research on Cancer. Retrieved from

https://gco.iarc.fr/today/data/factsheets/populations/62

0-portugal-fact-sheets.pdf/.

National Cancer Institute. (n.d.) NCI Dictionary of Cancer

Terms. Retrieved from https://www.cancer.gov/

publications/dictionaries/cancca-terms/search?contains

=false&q=breast+cancer/.

National Cancer Institute. (n.d.) Breast Cancer Treatment

(PDQ)- Health Professional Version. Retrieved from

https://www.cancer.gov/types/breast/hp/breast-treatme

nt-pqd#_551_toc/.

KDIR 2019 - 11th International Conference on Knowledge Discovery and Information Retrieval

440

Agência Lusa. (2018, April 21). Médica defende teste de

sangue de rotina para detetar células tumorais. [News

Post]. Retrieved from https://www.publico.pt/

2018/04/21/sociedade/noticia/medica-defende-teste-de

-sangue-de-rotina-para-detectar-celulas-tumorais-1811

211/.

Borges, L.C., Marques, V.M. and Bernardino, J. (2013).

Comparison of data mining techniques and tools for

data classification. Proceedings of the International C*

Conference on Computer Science and Software

Engineering (C3S2E’13). ACM, USA, 113-116.

Wikipedia. (2019, March 17). Amplitude Interquartil.

Retrieved from https://pt.wikipedia.org/wiki/

Amplitude_interquartil.

Kaufmann, M., Han, J. and Kamber, M. (2006). General

Approach to Classification. Data Mining: Concepts and

Techniques, 8, 328-330.

Kaufmann, M., Han, J. and Kamber, M. (2006). Model

Evaluation and Selection. Data Mining: Concepts and

Techniques, 8, 364-370.

Smolyakov, V. (2017, August 22). Ensemble Learning to

Improve Machine Learning Results. [Blog Post].

Retrieved from https://blog.statsbot.co/ensemble-

learning-d1dcd548e936/.

McCallum, A., Nigam, K. (1998). A comparison of event

models for Naive Bayes text classification. AAAI-98

Work. on Learning for Text Categorization,752, 41-48.

Langley, P., Iba, W. and Thompson, K. (1992). An analysis

of Bayesian classifiers.

Loh, W., Shin, Y. (1997). Split Selection Methods for

Classification Trees. Statistica Sinica, 815-840.

Technopedia. (n.d.). Overfitting. Retrieved from

https://www.technopedia.com/definition/32512/overfit

ting/.

Donges, N. (2018, February 22). The Random Forest

Algorithm. [Blog Post]. Retrieved from

https://towardsdatascience.com/the-random-forest-

algorithm-d457d499ffcd/.

James, G., Witten, D., Hastie, T. and Tibshirani, R. (2013).

Logistic Regression. An Introduction to Statistical

Learning, 4.3.

Gandhi, R. (2018, June 7). Support Vector Machine-

Introduction to Machine Learning Algorithms. [Blog

Post] Retrieved from https://towardsdatascience.com/

support-vector-machine-introduction-to-machine-lear

ning-algorithms-934a444fca47/.

Sunasra, M. (2017). Performance Metrics for

Classification problems in Machine Learning. Retrieved

from https://medium.com/thalus-ai/performance-metri

cs-for-classification-problems-in-machine-learning-par

t-i-b085d432082b.

Google Developers. (2019). Classification: ROC and AUC.

Retrieved from https://developers.google.com/

machine-learnig/crash-course/classification/roc-and-au

c/.

Machine Learning Repository. (2018). Breast Cancer

Coimbra Data Set. Retrieved from

https://archive.ics.uci.edu/ml/Breast+Cancer+Coimbra

#/.

Patrício, M., Pereira, J., Crisóstomo, J., Matafome, P.,

Gomes, M., Seiça, R., Caramelo, F. (2018). Using

resistin, glucose, age and BMI to predict the presence

of breast cancer. BMC Cancer, 18(1), 1-8.

Frazão, A. (2018). Exame da Glicose: como é feito e valores

de referência. Retrieved from https://www.

tuasaude.com/exame-da-glicose/.

Lemos, M. (2018). Para que serve o índice HOMA.

Retrieved from https://www.tuasaude.com/para-que-

serve-o-indice-homa/.

Gunnars, K. (2018). Leptin and Leptin Resistance:

Everything You Need To Know. Retrieved from

https://www.healthline.com/nutrition/leptin-101/.

Kringstad, A. (2019). Tikhonov regularization. Beyond L2.

Retrieved from https://towardsdatascience.com/

tikhonov-regularization-an-example-other-than-l2-892

2ba512/.

Data Mining Techniques for Early Detection of Breast Cancer

441