
Measuring and Avoiding Information Loss During Concept Import from
a Source to a Target Ontology
James Geller
1 a
, Shmuel T. Klein
2 b
and Vipina Kuttichi Keloth
1 c
1
Dept. of Computer Science, New Jersey Institute of Technology, U.S.A.
2
Dept. of Computer Science, Bar Ilan University, Ramat Gan 52900, Israel
Keywords:
Biomedical Ontologies, Concept Import, Information Content, Information Loss.
Abstract:
Comparing pairs of ontologies in the same biomedical content domain often uncovers surprising differences.
In many cases these differences can be characterized as “density differences,” where one ontology describes
the content domain with more concepts in a more detailed manner. Using the Unified Medical Language
System across pairs of ontologies contained in it, these differences can be precisely observed and used as the
basis for importing concepts from the ontology of higher density into the ontology of lower density. However,
such an import can lead to an intuitive loss of information that is hard to formalize. This paper proposes an
approach based on information theory that mathematically distinguishes between different methods of concept
import and measures the associated avoidance of information loss.
1 INTRODUCTION
The field of Medical Informatics has developed a
rich ecosystem for research, development, and appli-
cations of biomedical terminologies and ontologies.
The NCBO BioPortal (NCBO, 2019) provides access
to over 772 such resources, containing, as of May 20,
2019, over 9.4 million classes (which would be called
“concepts” in other repositories). BioPortal keeps a
rich set of statistics about the upload and use of on-
tologies. These statistics allow the analysis of the
quality of ontology maintenance by the curators of in-
dividual BioPortal entries (Geller et al., 2018).
BioPortal takes a “big tent” inclusive approach to-
ward the question of What qualifies as a biomedical
ontology? This is expressed both in the content and
structure of some of the resources accessible through
bioportal. Thus, (Stato, 2019) is a general purpose
statistics ontology that is not specific to medicine.
MeSH, the Medical Subject Headings (MeSH, 2019)
is contained in BioPortal, although it is widely ac-
knowledged that it is structurally not an ontology at
all.
Another major resource for biomedical ontologies
is the Unified Medical Language System (UMLS)
(UMLS, 2019), developed by the National Library of
a
https://orcid.org/0000-0002-9120-525X
b
https://orcid.org/0000-0002-9478-3303
c
https://orcid.org/0000-0001-6919-1122
Medicine (NLM), an institute under the US Govern-
ment National Institutes of Health (NIH). The most
important component of the UMLS is the Metathe-
saurus (Meta, 2019).
A new version of it is released twice a year and
over a long period of time (“decades”), every new
release has expanded on the previous version. Ac-
cording to the most recent release notes (Metanotes,
2019), the UMLS contains 3,848,696 concepts and
12,362,080 concept names from 210 distinct termi-
nology sources. The staff of the NLM integrates the
different terminologies such that each group of terms
with identical meaning is tied together as a single con-
cept and assigned a Concept Unique Identifier (CUI).
However, individual terms are maintained with their
source information.
1.1 Concept Import
The unique richness of the UMLS makes it possible
to compare its subterminologies on a concept basis.
Researchers have observed (He et al., 2014) that paths
between pairs of concepts that are identical by their
CUIs may be different in two different terminologies.
Specifically, if a pair of concepts (A, B) exists in both
terminologies T
1
and T
2
, such that there is a path from
A to B consisting of one or more IS-A links (similar
to subclass links), then the following situations can
arise.
442
Geller, J., Klein, S. and Keloth, V.
Measuring and Avoiding Information Loss During Concept Import from a Source to a Target Ontology.
DOI: 10.5220/0008354904420449
In Proceedings of the 11th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2019), pages 442-449
ISBN: 978-989-758-382-7
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

• There may be direct IS-A links from A to B in T
1
and T
2
, with no intervening concepts. This ex-
presses that A is a more specific concept than B.
• There may be paths of IS-A links and intervening
concepts in T
1
and T
2
that are identical. Thus there
may be a concept Z between A and B in both T
1
and T
2
, such that (A IS-A Z) and (Z IS-A B). This
would be a path of two IS-A links.
• There may be paths of IS-A links and interven-
ing concepts such that the intervening concepts
in T
1
are different from those in T
2
; furthermore
the paths may be of different lengths, including a
length of one in either T
1
or T
2
.
The two concepts A and B are called anchor con-
cepts. Following the literature (Rector et al., 2006),
the difference between paths of different lengths ex-
presses a density difference. As these paths appear
in IS-A paths that are conventionally drawn akin to
the vertical direction, these have been called vertical
density differences.
The above observations raised the following in-
triguing question. If one designates T
1
as a source
terminology and T
2
as a target ontology, and the path
between the anchor concepts in T
1
is longer than that
in T
2
, does this mean that the intervening concepts
from T
1
that are missing in T
2
can or even should be
imported into T
2
? In consultation with ontology cu-
rators and medical experts, it was determined that the
results of an algorithm comparing paths in two on-
tologies may not be used for automated import from
a source ontology into a target terminology. How-
ever, these results could be presented to target ontol-
ogy curator(s) for a decision whether an import would
be useful for improving it. It was furthermore ob-
served that even with the help of such an algorithm,
the actual work of the target ontology curator remains
formidable (He and Geller, 2016). The reasons given
by ontology curators for not importing valid concepts
include that they do not want to clutter up their on-
tology with concepts for which no use case exists or
which no user has ever requested (Curators, 2019).
In contrast to research on vertical density differ-
ences, this paper reports on work on horizontal den-
sity differences (Keloth et al., 2018; Keloth et al.,
2019). Importing concepts from a source into a tar-
get ontology, based on horizontal density differences,
would lead to a loss of information, and in this paper
we analyze how to quantify and avoid this loss.
1.2 Relationship to Data and Ontology
Integration
A rich literature exists on ontology alignment, match-
ing and integration. The extensive work of Shvaiko,
Euzenat, et al. (Shvaiko et al., 2018) may provide an
excellent entry point into this field. Synonym substi-
tution is one tool that can be used for the purpose of
integration; this was proposed by (Huang et al., 2009),
(Huang et al., 2007) using WordNet (WordNet, 2019)
as additional resource besides the UMLS.
Our goals in this paper are more limited in that we
are not attempting automated integration and are also
limiting ourselves to a form of local “point wise” im-
port. On the other hand, we are addressing the ques-
tion of what loss of information occurs and how to
avoid it, if the human curator agrees to an import.
Ontologies can function as tools in (database) schema
integration (Geller et al., 1992; Rahm, 2016).
1.3 Horizontal Density Differences
Figure 1 shows a bare bones example of a horizontal
density difference. Terminology 1 (the source) con-
tains a concept A that also exists in Terminology 2
(the target). Furthermore, by using both Terminol-
ogy 1 and Terminology 2 in the version provided by
the UMLS, because A has the same CUI in Termi-
nology 1 and Terminology 2, we may assert that it is
the same concept (unless the team of the NLM made
a mistake during their integration). Furthermore, we
observe that (X IS-A A) (i.e., X is a subclass or sub-
concept of A) in both the source and the target ontol-
ogy, and again the identity of X is assured by having
the same CUI. The same applies to Y and Z. How-
ever, there is a density difference. Terminology 1 has
an additional concept W that does not exist in Ter-
minology 2. We also assume that W does not exist
anywhere in Terminology 2.
After importing W into Terminology 2, A has the
same children in both terminologies. However, at this
point, the information that X, Y and Z were originally
in Terminology 2 and that W is “a recent addition,” is
completely lost. We note that the situation described
in Figure 1 is not “theoretical.”
In a recent paper (Keloth et al., 2019), we showed
that there are many instances of horizontal density dif-
ferences. This study was based on two popular medi-
cal terminologies, MEDCIN and the National Cancer
Institute thesaurus (NCIt). It was shown that identi-
cal concepts with different sets of children in NCIt
and MEDCIN appear 1966 times. More interestingly,
1049 of these concepts do not have any children in
common in NCIt and MEDCIN. Table 1 shows an ex-
Measuring and Avoiding Information Loss During Concept Import from a Source to a Target Ontology
443

A
X Y Z W
A
X Y Z
Terminology 1 Terminology 2
Figure 1: Horizontal Density Difference.
ample parent concept that appears in NCIt and MED-
CIN and has four common children. The right column
shows an example additional child concept in MED-
CIN. Table 2 shows seven more examples, listing only
the number of common children instead of showing
them, in the column with the header C#.
In (Keloth et al., 2019) the authors examined dif-
ferent approaches of how to use this insight for im-
porting concepts from MEDCIN into NCIt. However,
they did not deal with the issue of potential loss of
information during an import.
Figure 2(a) shows the original situation. Figure
2(b) shows naive import of D and E from the source
ontology into the target ontology. In this case a user
of the target ontology cannot tell that there is a “his-
torical” difference between the concepts X, Y , and Z
versus the concepts D and E. This is a form of infor-
mation loss.
In Figure 2(c) we attempt to avoid this loss of in-
formation by creating an artificial intermediate node
Inter1 which maintains a memory of the fact that D
and E were imported. However, this leads to an imbal-
ance of the structure that is not logical, because in the
source ontology X , Y, Z, D, and E are all at the same
level. As level is commonly used to imply generality
(in tree-structured ontologies), placing two groups of
concepts that were originally at the same level in the
source ontology into two different levels in the target
ontology corresponds to mutating the structure of the
target ontology in an undesirable way. Figure 2(d)
shows an alternative solution with two new interme-
diate nodes. Now the concepts X, Y, Z, D, and E are
back to being at the same hierarchical level while still
maintaining full information of the provenance of the
imported concepts and the original concepts. How-
ever, in solution 2(d) we pay the price of having to
introduce two artificial nodes.
The idea of introducing intermediate structuring
nodes that have little meaning in the ontology might
be objected too. However, it is not totally unprece-
dented. In the NDF-RT (National Drug File - Refer-
ence Terminology) (NDF-RT, 2019) groups of drug
concepts are combined together by similar intermedi-
ate concepts (that, however, have chemical justifica-
tions).
2 MEASURING INFORMATION
We shall try to quantify the rather fuzzy concepts ex-
posed above. The big difficulty is that even if a sin-
gle concept is imported into an ontology of thousands
of concepts, “every concept is now suspect.” In other
words, it is impossible to tell by looking at a concept
whether it was originally in the ontology, or whether
it was imported. Thus, we will use a “backwards ap-
proach,” focusing on the gain of information achieved
by making the structural changes during import that
avoid the original “global” loss.
Measuring information is the main objective of In-
formation Theory and is quite well understood since
Shannon’s pioneering work in 1948 (Shannon, 1948).
The typical scenario is that of a discrete random vari-
able X, taking on a finite number of possible values
x
1
, . . . , x
n
. One also generally assumes that there is
a given probability distribution, assigning the prob-
ability p
i
to the event X = x
i
, for 1 ≤ i ≤ n. The
average amount of information conveyed by the ran-
dom variable X, called its entropy, is then defined
as H(X) = −
∑
n
i=1
p
i
log
2
p
i
, and is measured in bits.
Resnik (Resnik, 1995) has used entropy to measure
semantic similarity between concepts within one sin-
gle ontology, which is a different problem than the
one posted here.
The first obstacle to overcome when trying to ex-
tend the notion of entropy to the concepts of an ontol-
ogy as those in Figures 1 and 2 is that there is no un-
derlying probability distribution. One way to avoid it,
is to assume uniform probabilities, that is, p
i
=
1
n
for
all i, in which case H(X) = log
2
n. Indeed, the infor-
mation amount given in the left hand side ontologies
shown in Figure 2 is log
2
5 = 2.32 bits, which is the
number of bits necessary to encode a possible choice
among the five alternatives X , Y , Z, D and E.
For the purposes of this analysis we will ignore
any connections between concepts that do not imple-
KEOD 2019 - 11th International Conference on Knowledge Engineering and Ontology Development
444
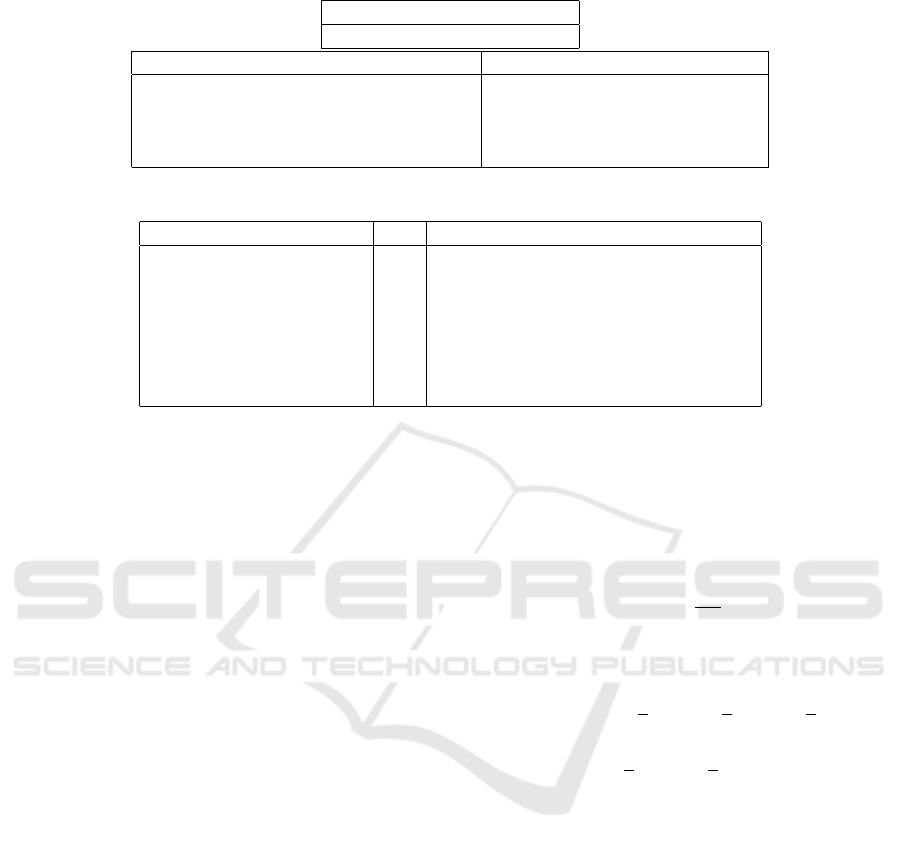
Table 1: Example of Common Children and Extra Child.
Parent
C0149516 : Chronic sinusitis
Common Children Example Extra Child in MEDCIN
C0008712 : Chronic sphenoidal sinusitis C0155827 : Chronic pansinusitis
C0008683 : Chronic frontal sinusitis
C0008698 : Chronic maxillary sinusitis
C0008681 : Chronic ethmoidal sinusitis
Table 2: Examples of Extra Children.
Parent C # Example Extra Child in MEDCIN
Anti-Arrhythmia Agents 13 pilsicainide hydrochloride
Testosterone 4 testosterone methyl
Loop Diuretics 5 Xipamide
Cranial Nerve Neoplasms 15 overlapping neoplasm of cranial nerve
Glycogen Storage Disease 7 GLYCOGEN STORAGE DISEASE Ic
Mastectomy 6 Bilateral mastectomy
Retinoids 4 aliretinoin
ment the concept taxonomy, i.e., we will not consider
any lateral/semantic relationships such as “location.”
Nevertheless, a second complication arises from the
fact that the structures of many important real life
ontologies may be more generally directed acyclic
graphs (DAGs), such as SNOMED CT (SNOMED
CT, 2019), considered the most important clinical on-
tology, and the NCIt (NCIt, 2019) mentioned ear-
lier, rather than the over-simplified approximation as
a tree-like hierarchy dealt with in the example figures
above. We shall, however, restrict this preliminary in-
vestigation only to trees, and tackle the general prob-
lem in future work.
In previous work on structural families of ontolo-
gies in BioPortal (Ochs et al., 2016) over 140 tree-
shaped biomedical ontologies were observed. Ex-
amples include the Healthcare Common Procedure
Coding System (HCPCS) and the Drug Ontology
(DRON).
To deal with the general case, we shall derive our
suggested measure inductively. Assume a tree struc-
ture with r + 1 levels indexed 0 (for the level of the
root) to r, and with n
i
nodes on level i, for 0 ≤ i ≤ r.
Denote the number of nodes on level i that are further
sub-partitioned as m
i
, so that n
i
− m
i
is the number
of leaves at level i. These m
i
nodes have, respectively,
n
i+1,1
, n
i+1,2
, . . . , n
i+1,m
i
children on level i+1, so that
m
i
∑
j=1
n
i+1, j
= n
i+1
for 0 ≤ i < r.
For the example tree displayed in Figure 3, r = 3,
(n
0
, . . . , n
3
) = (1, 4, 8, 7), (m
0
, . . . , m
3
) = (1, 3, 2, 0)
and (n
1,1
; n
2,1
, n
2,2
, n
2,3
; n
3,1
, n
3,2
) = (4; 3, 2, 3; 4, 3).
We define the information content I of the tree T
by summing, within each level and over all the lev-
els, the logarithm of the branching multiplicity of the
nodes, taking a weighted average for the nodes within
each level. Formally
I(T ) =
r
∑
i=1
m
i−1
∑
j=1
n
i, j
n
i
log
2
(n
i, j
). (1)
Returning to the example of Figure 3, we get
I(T ) = log
2
4 +
3
8
log
2
3 +
2
8
log
2
2 +
3
8
log
2
3
+
4
7
log
2
4 +
3
7
log
2
3
= 5.26 bits.
In particular, for a simple ontology with n con-
cepts, represented by a tree of depth 1, that is, with
just one level of n leaf nodes, the information content
will be log
2
n.
Suppose then that we are given an ontology, which
is conveniently represented as a tree structure, and
that we want to refine it by introducing an interme-
diate node R. Assume that this intermediate node is
added between level i − 1 and level i of the tree for
some i > 0, that there are n
i
nodes on level i and that
k of them should now be connected to the new node R.
The passage from the right hand tree in Figure 2(b) to
that of Figure 2(c) is the special case for which i = 1,
n
1
= 5 and k = 2. The general scenario is depicted in
Figure 4. Note that for convenience, we assume that
the k nodes of level i which are connected to R are sib-
lings, in the sense that they were originally children of
the same node on level i − 1.
Measuring and Avoiding Information Loss During Concept Import from a Source to a Target Ontology
445

A
X Y Z
MEDCIN NCIt
(a) Initial Situation
A
X Y Z D E
A
X Y Z D E
(b) Import of D and E with complete loss of information.
A
X Y Z
D E
Inter1
(c) Import of D and E maintaining the information that they
have a common "provenance" from MEDCIN.
A
X Y Z D E
Inter1Inter2
(d) Import of D and E with restructuring, making the provenance of all
children of A explicit in the target ontology.
A
X Y Z D E
A
X Y Z D E
A
X Y Z D E
Figure 2: Different Approaches to Importing Concepts.
KEOD 2019 - 11th International Conference on Knowledge Engineering and Ontology Development
446
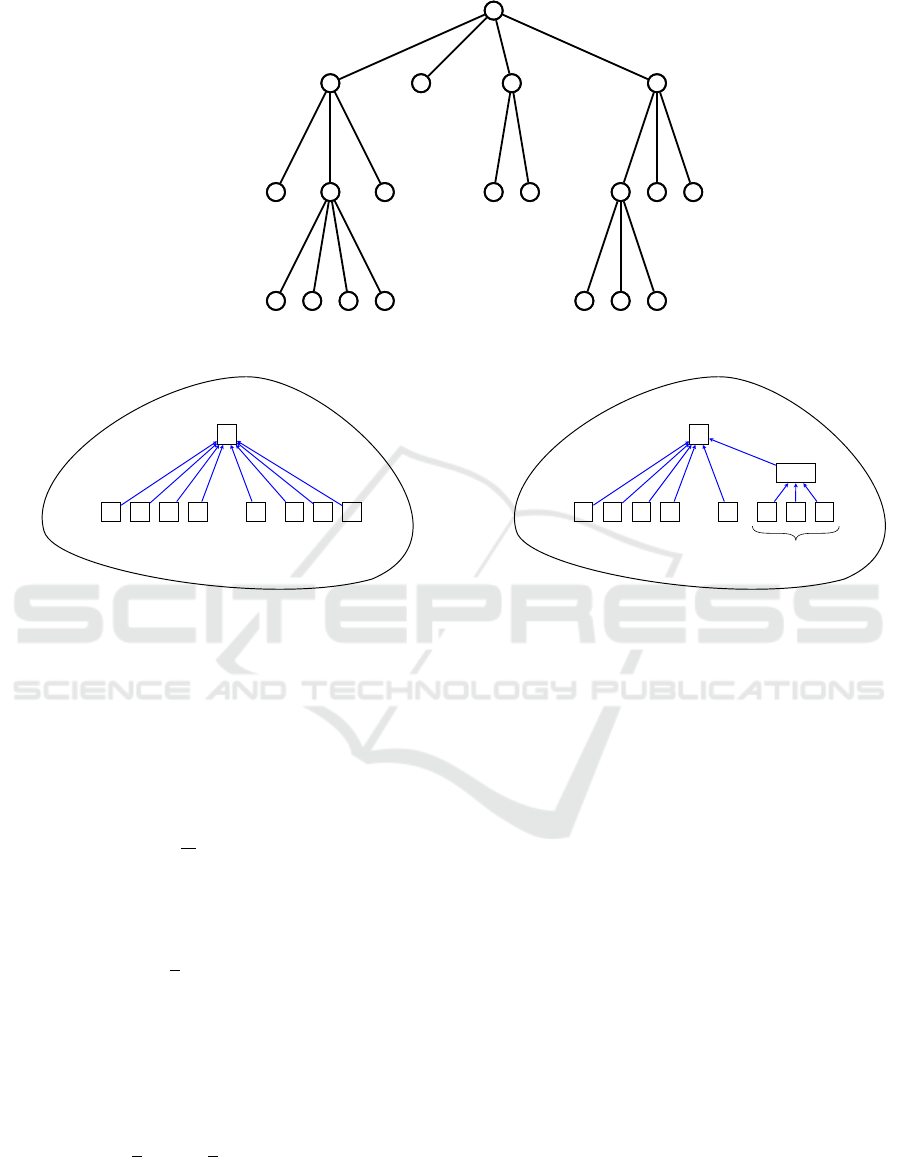
3
2
1
0
Figure 3: Example tree hierarchy.
. . . . . .
. . .. . .
. . .
i
i - 1
. . . . . .
. . .. . .
. . .
i
i - 1
k
Figure 4: Schematic view of the inductive step in the definition of the information measure.
Since the modified tree structure has obviously
added some information, we define the additional
amount of information that has been added by insert-
ing the intermediate node R as follows. A new choice
among k elements has been adjoined, which should
add another log
2
k bits, but only k of the n
i
nodes are
affected, so we define the added information amount
as
k
n
i
log
2
k, (2)
thereby extending the definition in eq. (1). Returning
to the example of Figure 2(c), we get that the infor-
mation at this stage is
log5 +
2
5
log2 = 2.72 bits. (3)
The addition of another intermediate node, as in
the passage from the right hand tree in Figure 2(c)
to that of Figure 2(d) is yet another example of the
same generalization principle, so we get as informa-
tion content of the structure with both intermediate
nodes:
log5 +
2
5
log2 +
3
5
log3 = 3.67 bits. (4)
A technical problem arises from the fact that the
definition of the additional information relies on hav-
ing the levels of the tree well defined. However, the
newly inserted intermediate nodes may disrupt the
level numbering if one considers these nodes as equiv-
alent to the original nodes in the tree. For example,
the nodes D and E in the right hand side tree of Fig-
ure 2(c) would then be on level 2, while their former
siblings X, Y and Z remain on level 1, as in the left
hand side of the figure. As a result, the information
added by the inter2 node would then be biased, be-
cause it would consider all the (remaining) nodes of
level 1 to be affected, and not only 3 of the 5 nodes
that were originally on level 1.
Since a model in which the level of a node is not
influenced by the possible insertion of intermediate
nodes seems more reasonable and closer to the real
life scenario we wish to simulate, we shall ignore in-
termediate nodes for the calculation of the level of a
node. This is consistent with the fact that these nodes
have been artificial additions in the first place, that
they are not content-bearing and are used only for
technical convenience. Applying this new convention
then yields, for our running example, the information
amounts reported in eqs. (3) and (4).
One of the advantages of this approach of defining
the information content as given in eq. (2) is that, by
definition, this information measure is an increasing
function of the complexity of the hierarchical struc-
Measuring and Avoiding Information Loss During Concept Import from a Source to a Target Ontology
447

ture: every newly introduced branching conveys ad-
ditional information, and accordingly, adds a non-
negative amount to the previously defined information
estimate.
It follows that we may define the information loss
mentioned in the title of this work by taking the dif-
ference between the information contents of the hier-
archical structure after and before the import of the
concepts from the source to the target ontology. This
is precisely the amount given in eq. (2), so it is de-
fined as the number of bits lost by not including the
additional intermediate node(s).
Another advantage is that the specific definition
as a precise number of information bits to be derived
from the structure can have a logical interpretation:
the given number of bits is the minimal one, from the
compression point of view, needed to communicate
all the information displayed by the hierarchy, see
any textbook dealing with coding, e.g., (Klein, 2016,
Chapter 11).
As we have argued, the introduction of the inter-
mediate nodes counteracts a hard to quantify global
information loss. Thus, using one or two intermediate
nodes avoids the issue of information loss by main-
taining a record of the ontology from which the im-
ported concepts are taken.
3 EXPERIMENTAL SETUP
The idea of trying to quantify a semantic concept by
assigning it a measure that can be efficiently and pre-
cisely calculated is not new and has been applied in
various fields. An example could be the attraction
factor defined in (Choueka et al., 1983), allowing to
sort the terms of an ontology according to the strength
by which they “attract” the term(s) following them;
thus once upon a has a high factor, being practically
always followed by time, but and has a low factor,
even though and the is very frequent, yet there are
many other combinations starting with and. Another
example would be (Geller et al., 2015), in which a
measure is derived helping to identify term pairs with
strong semantic correlation.
Devising a convincing experimental setup to eval-
uate the usefulness of a proposed measure does not
seem to be a trivial task. The intuition of most read-
ers will hardly differentiate between a structure that
has been assigned, say, 4.8 bits, and one with only 3.6
bits; and it will be even harder to convince ourselves
why the increase should be by precisely 33%.
A reasonable, yet very resource intensive, ap-
proach would be to make use of human informants.
One could then prepare a large set of examples and
ask the informants to classify them according to what
they “feel” their information content should be. In
a second stage, the results, averaged over all infor-
mants, could be compared with what would be ob-
tained by classifying the examples according to the
information measure proposed herein. A high corre-
lation would then be supportive of the usefulness of
our suggestions. The current paper, however, is only
meant to present the basic ideas, and we leave their
evaluation for future work.
4 CONCLUSIONS AND FUTURE
WORK
The UMLS mapping of concepts from different on-
tologies makes it possible to observe potentially miss-
ing concepts by comparing pairs of ontologies. A do-
main expert can then decide whether such concepts
should be imported or not. Many opportunities for
such imports exist. However, when a concept is im-
ported naively, the information that it was not origi-
nally in the target ontology is lost. Quantifying this
loss is difficult, because it affects the whole target on-
tology. We have presented an approach to quantifying
the loss of information by measuring the gain that is
achieved by maintaining the source information dur-
ing import, with the aid of “artificial” parent nodes.
In future work, we plan to extend the presented
model from trees to Directed Acyclic Graphs (DAGs),
which covers a much larger set of biomedical ontolo-
gies. We will also attempt to perform a user study
with human informants. An algorithm for automat-
ically generating intermediate nodes during import
will also be provided.
REFERENCES
Choueka, Y., Klein, S. T., and Neuvitz, E. (1983). Auto-
matic retrieval of frequent idiomatic and collocational
expressions in a large corpus. Journal Association Lit-
erary and Linguistic Computing, 4:34–38.
Curators (2019). Personal communication with ncit and
snomed curators.
Geller, J., Keloth, V. K., and Musen, M. A. (2018). How
sustainable are biomedical ontologies? In AMIA
2018, American Medical Informatics Association An-
nual Symposium, San Francisco, CA, November 3-7,
2018.
Geller, J., Klein, S. T., and Polyakov, Y. (2015). Identifying
pairs of terms with strong semantic connections in a
textbook index. In KEOD 2015 - Proceedings of the
International Conference on Knowledge Engineering
KEOD 2019 - 11th International Conference on Knowledge Engineering and Ontology Development
448

and Ontology Development, Volume 2, Lisbon, Portu-
gal, November 12-14, 2015, pages 307–315.
Geller, J., Perl, Y., Neuhold, E., and Sheth, A. (1992). Struc-
tural schema integration with full and partial corre-
spondence using the dual model. Information Systems,
17(6):443 – 464.
He, Z. and Geller, J. (2016). Preliminary analysis of diffi-
culty of importing pattern-based concepts into the na-
tional cancer institute thesaurus. In Exploring Com-
plexity in Health: An Interdisciplinary Systems Ap-
proach - Proceedings of MIE2016 at HEC2016, Mu-
nich, Germany, 28 August - 2 September 2016., pages
389–393.
He, Z., Geller, J., and Elhanan, G. (2014). Categorizing the
relationships between structurally congruent concepts
from pairs of terminologies for semantic harmoniza-
tion. In AMIA Joint Summits on Translational Science
proceedings, pages 48–53.
Huang, K., Geller, J., Halper, M., and Cimino, J. J. (2007).
Piecewise synonyms for enhanced UMLS source ter-
minology integration. In AMIA 2007, American
Medical Informatics Association Annual Symposium,
Chicago, IL, USA, November 10-14, 2007.
Huang, K., Geller, J., Halper, M., Perl, Y., and Xu, J.
(2009). Using wordnet synonym substitution to en-
hance UMLS source integration. Artificial Intelli-
gence in Medicine, 46(2):97–109.
Keloth, V. K., He, Z., Chen, Y., and Geller, J. (2018). Lever-
aging horizontal density differences between ontolo-
gies to identify missing child concepts: A proof of
concept. In AMIA 2018, American Medical Informat-
ics Association Annual Symposium, San Francisco,
CA, November 3-7, 2018.
Keloth, V. K., He, Z., Elhanan, G., and Geller, J. (2019). Al-
ternative classification of identical concepts in differ-
ent terminologies: Different ways to view the world.
Journal of Biomedical Informatics, in press.
Klein, S. T. (2016). Basic Concepts in Data Structures.
Cambridge University Press.
MeSH (2019). Medical Subject Headings, https://bioportal.
bioontology.org/ontologies/{mesh}.
Meta (2019). The UMLS Metathesaurus, https:
//www.nlm.nih.gov/research/umls/knowledge\
sources/metathesaurus/.
Metanotes (2019). Metathesaurus Release Notes,
https://www.nlm.nih.gov/research/umls/know\-
ledge\ sources/metathesaurus/relea\-se/notes.htm.
NCBO (2019). https://bioportal.bioontology.org/.
NCIt (2019). The National Cancer Institute thesaurus, https:
//ncithesaurus-stage.nci.nih.govncitbrowser/.
NDF-RT (2019). National Drug File Reference Ter-
minology, https://www.nlm.nih.gov/research/umls/
sourcereleasedocs/current/{ndfrt}/.
Ochs, C., He, Z., Zheng, L., Geller, J., Perl, Y., Hripcsak,
G., and Musen, M. A. (2016). Utilizing a structural
meta-ontology for family-based quality assurance of
the bioportal ontologies. Journal of Biomedical Infor-
matics, 61:63–76.
Rahm, E. (2016). The case for holistic data integra-
tion. In Advances in Databases and Information Sys-
tems - 20th East European Conference, ADBIS 2016,
Prague, Czech Republic, August 28-31, 2016, Pro-
ceedings, pages 11–27.
Rector, A. L., Rogers, J., and Bittner, T. (2006). Granularity,
scale and collectivity: When size does and does not
matter. Journal of Biomedical Informatics, 39(3):333–
349.
Resnik, P. (1995). Using information content to evalu-
ate semantic similarity in a taxonomy. In IJCAI’95
Proceedings of the 14th international joint conference
on Artificial intelligence - Volume 1, Montreal, Que-
bec, Canada, August 20 - 25, 1995, pages 448–453.
Morgan Kaufmann Publishers Inc. San Francisco, CA,
USA.
Shannon, C. E. (1948). A mathematical theory of communi-
cation. Bell System Technical Journal, 27(2):379–423.
Shvaiko, P., Euzenat, J., Jim
´
enez-Ruiz, E., Cheatham, M.,
and Hassanzadeh, O., editors (2018). Proceedings of
the 13th International Workshop on Ontology Match-
ing co-located with the 17th International Semantic
Web Conference, OM@ISWC 2018, Monterey, CA,
USA, October 8, 2018, volume 2288 of CEUR Work-
shop Proceedings. CEUR-WS.org.
SNOMED CT (2019). https://www.snomed.org/
Stato (2019). Statistics Ontology, https://bioportal.\-
bioontology.org/ontologies/{stato}.
UMLS (2019). The Unified Medical Language System,
https://www.nlm.nih.gov/research/umls/.
WordNet (2019). https://wordnet.princeton.edu/.
Measuring and Avoiding Information Loss During Concept Import from a Source to a Target Ontology
449
