Enhancements for Sliding Window based Stream Classiﬁcation

Engin Maden

1,2

and Pinar Karagoz

Department of Information Technologies, The Central Bank of the Republic of Turkey, Ankara, Turkey

Department of Computer Engineering, Middle East Technical University (METU), Ankara, Turkey

Keywords:

Streaming Data, Stream Mining, Classiﬁcation, kNN, Naive Bayes, Sliding Window.

Abstract:

In stream mining, there are several limitations on the classiﬁcation process, since the time and resource are

limited. The data is read only once and the whole history of data can not be stored. There are several methods

developed so far such as stream based adaptations of decision trees, nearest-neighbor methods and neural

network classiﬁers. This paper presents new enhancements on sliding window based classiﬁcation methods.

As the ﬁrst modiﬁcation, we use the traditional kNN (K-Nearest Neighbors) method in a sliding window

and include the mean of the previous instances as a nearest neighbor instance. By this, we aim to associate

the behaviour pattern coming from the past and current state of data. We call this method as m-kNN (Mean

extended kNN). As the second enhancement, we generate an ensemble classiﬁer as the combination of our

m-kNN with traditional kNN and Naive Bayes classiﬁer. We call this method CSWB (Combined Sliding

Window Based) classiﬁer. We present the accuracy of our methods on several datasets in comparison to the

results against the state-of-the-art classiﬁers MC-NN (Micro Cluster Nearest Neighbor) and VHT (Vertical

Hoeffding Tree). The results reveal that the proposed method performs better for several data sets and have

potential for further improvement.

1 INTRODUCTION

The amount of data that is obtained from different

sources such as telecommunication, credit card us-

age and social media is getting higher and it has be-

come important to extract valuable information from

such data sources. There are several characteristics of

data streams that can be summarized as follows (Ste-

fanowski and Brzezinski, 2017):

• The ﬂow of data is continuous.

• The volume of data is high.

• The arrival rate of data is rapid.

• The distribution of data may change over time.

Conventional data mining tasks such as classiﬁca-

tion and clustering can be applied on streaming data,

as well. However, as given in (Bifet et al., 2010), there

are several limitations for a stream classiﬁer:

• During streaming, instances can be examined only

one by one, each can be examined only once.

• The memory resource is limited in comparison to

the amount of streaming data, hence it is not fea-

sible to make batch processing.

• It is necessary to process data fast in order to re-

spond (near) real time.

In this paper, we propose an enhancement of kNN

where it is applied in a sliding window approach. To

deal with inﬁnite data streams, windowing is com-

monly used in stream processing. A window can

be deﬁned as a set of stream elements within a cer-

tain time frame. There are two common types of

sliding windows, which are time-based and count-

based. In time-based sliding windows, a time inter-

val is used for specifying the borders of the window

while the count of instances speciﬁes these borders in

count-based ones (Badiozamany, 2016). In this pa-

per, count-based sliding window is used to process

the data streams. Our method is called m-kNN (mean

extended kNN) and in this method traditional kNN is

applied in a sliding window. Additionally, one of the

k-nearest neighbors is obtained among the centroids

(the mean values of the features) of the classes. The

class centroid, which is the most similar to the incom-

ing instance, is considered as the k

nearest neigh-

bor. As the second enhancement, a combined version

of m-kNN, traditional kNN and Naive Bayes is ap-

plied in sliding window mechanism, and this method

is called CSWB (Combined Sliding Window Based)

Maden, E. and Karagoz, P.

Enhancements for Sliding Window based Stream Classiﬁcation.

DOI: 10.5220/0008356501810189

In Proceedings of the 11th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2019), pages 181-189

ISBN: 978-989-758-382-7

181

classiﬁer.

The contribution of this work is as follows:

• m-kNN is presented to associate the behaviour

pattern coming from the past and current state of

data.

• An ensemble classiﬁer called CSWB is developed

as the combination of our m-kNN with traditional

kNN and Naive Bayes classiﬁer.

• These two enhancements are evaluated on several

data sets from different domains. The experiments

reveal that the enhancements provide higher accu-

racy values for several of the data sets, and have

potential for further improvement.

This paper is organized as follows: In Section 2,

the basis technique of the proposed method and the

algorithms used for comparison are described. In Sec-

tion 3, related studies are summarized. In Section

4, proposed enhancements for sliding window based

stream classiﬁcation are described in details. In Sec-

tion 5, experiments and results are presented. Finally,

the paper is concluded with an overview in Section 6.

2 PRELIMINARIES

kNN is one of the well-known algorithms in classiﬁ-

cation task. In kNN, prediction for the new incom-

ing sample is performed by searching through the en-

tire training set. The similarity between the incom-

ing sample and previously classiﬁed instances is de-

termined by distance calculation. In this work, we use

Euclidean Distance in kNN process for similarity cal-

culation.

Once the similarity values are available, the ﬁrst

k instances, which are the nearest neighbors for the

sample to be classiﬁed, are determined. The next step

is to determine the class label of the incoming in-

stance under majority voting among the neighbours.

For accuracy comparison, we implemented the

streaming version of MC-NN as a state-of-the-art

streaming classiﬁer in the literature (Tennant et al.,

2017). MC-NN uses micro-clusters in the nearest

neighbor approach. There are two measures for each

micro cluster in MC-NN as follows:

• Error Count: It is the count of misclassiﬁed

instances for the micro cluster. It is initially 0

and incremented by 1 for incorrect classiﬁcations.

Similarly, it is decremented by 1 for correct clas-

siﬁcations.

• Participation Percentage: It is the degree of re-

cency for the micro-cluster and calculated accord-

ing to the timestamp of the instances in the micro-

cluster when they participate.

The ﬂow of the MC-NN can be summarized as

follows:

• Calculate the centroids of the current micro-

clusters (Each micro-cluster contains instances

belonging to the same class).

• Calculate the Euclidean distance between each

centroid and the new distance.

– Assign the instance to the nearest micro-cluster.

– Check if the assigned value is equal to the ac-

tual class label of the instance.

• If the classiﬁcation is correct, decrease the error

count of the micro-cluster by 1.

• Otherwise, add the instance to the nearest Micro-

Cluster that matches the instance’s class label.

– Increment the error count of both involved

Micro-Clusters.

– If the error count of any of these two micro-

clusters exceeds the error threshold, calculate

the variance value for each attribute and split

the micro-cluster according to this attribute.

– Calculate the participation percentage for each

micro-cluster.

• Delete any micro-cluster having participation per-

centage lower than the performance threshold.

When the error count exceeds the error threshold,

the variance of each feature is calculated. For the fea-

ture having the maximum variance, the mean value is

calculated. According to this mean value, the cluster

is split into two new micro clusters.

Recency of current micro clusters refers to

whether a micro cluster is old, and hence should be

deleted or not. It is determined through participation

percentage, which is the ratio of the sum of times-

tamps of instances in micro cluster to the real triangu-

lar number of micro cluster. The real triangular num-

ber of a micro cluster is calculated as the difference

between the triangular number for current timestamp

and the initial triangular number for the micro cluster.

The initial triangular number is calculated with the

timestamp value for the micro cluster when the micro

cluster is generated and the ﬁrst instance is assigned

to this micro cluster (Tennant et al., 2017). If the par-

ticipation percentage for a micro cluster is lower than

a given threshold, the micro cluster is deleted.

The other method from literature we use for ac-

curacy comparison is Vertical Hoeffding Tree (VHT).

It is implemented in Apache SAMOA (Scalable Ad-

vanced Massive Online Analysis) framework

. VHT

is a distributed classiﬁer and it uses vertical paral-

lelism. Vertical parallelism partitions the instances

https://samoa.incubator.apache.org

KDIR 2019 - 11th International Conference on Knowledge Discovery and Information Retrieval

182

according to the attributes and enables parallel pro-

cessing. The number of attributes in each partition

is decided by the division of the number of total at-

tributes and the number of partitions. The algorithm

is executed in parallel on the attributes in each parti-

tion and the best local attribute for split operation is

selected. Following this, the results of these parallel

computations are combined in order to select the best

global attribute to split, and to grow the tree (Kourtel-

lis et al., 2016).

3 RELATED WORK

In the literature of stream mining, there is a variety

of studies on stream classiﬁcation including nearest

neighbor methods, decision tree based methods and

ensemble classiﬁers. One of such studies is VHT, in

which a vertical parallelism is applied on the features

of streaming data (Kourtellis et al., 2016). Another

one is MC-NN which is a data stream classiﬁer based

on the statistical summary of data (Tennant et al.,

2017). Both of these methods, as described in Section

2, are used for comparison. In (Tennant et al., 2014),

the kNN is applied within sliding windows. We used

this method for accuracy comparison, as well.

Another windowing approach for stream learning

is PAW (Probabilistic Adaptive Window), which in-

cludes a mechanism to include older examples as well

as the most recent ones. Therefore, it is possible to

maintain information on past concept drifts while be-

ing able to adapt quickly to new ones (Bifet et al.,

2013).

Law and Zaniolo propose ANNCAD (Adaptive

Nearest Neighbor Classiﬁcation Algorithm for Data

Streams), which is an incremental classiﬁcation al-

gorithm using a multi-resolution data representation

to ﬁnd adaptive nearest neighbors of a given data in-

stance. As the basic difference from the traditional

kNN method, instead of using a ﬁxed number of

neighbors, they adaptively expand the neighborhood

area until the classiﬁcation reaches a satisfactory level

(Law and Zaniolo, 2005).

ADWIN (ADaptive WINdowing) is a method of-

fered to maintain a window of variable size. In AD-

WIN2, the method is further improved for memory

usage and time efﬁciency. The authors further com-

bine ADWIN2 with the Naive Bayes classiﬁer and

analyse their method using synthetic and real world

data sets (Bifet and Gavalda, 2007).

Stefanowski proposes a new data stream classi-

ﬁer called the AUE2 (Accuracy Updated Ensemble).

The aim of this classiﬁer is reacting equally well to

different types of drift. AUE2 combines accuracy-

based weighting mechanisms and Hoeffding Trees

(Brzezinski and Stefanowski, 2013).

Another ensemble classiﬁcation algorithm is pro-

posed in (Chen et al., 2018) in order to deal with noise

and concept drift in streams. This algorithm is based

on attribute reduction and makes use of sliding win-

dow. It is aimed to reach a high performance in noisy

data streams with low computation complexity.

Fong et al. propose an improved version of VFDT

(Very Fast Decision Tree) that makes use of mis-

classiﬁed results for post-learning. Their approach

is called MR (Misclassiﬁed Recall) and it is a post-

processing step for relearning a new concept. They

apply their method on HAR (Human Activity Recog-

nition) dataset where most misclassiﬁed instances be-

long to ambiguous movements (Fong et al., 2017).

4 PROPOSED METHOD:

ENHANCEMENTS FOR

SLIDING WINDOW BASED

DATA STREAM CLASSIFIERS

In this work, we propose two enhancements for the

use of kNN on stream classiﬁcation under sliding

window. The ﬁrst one is called m-kNN (Mean Ex-

tended kNN), which utilizes traditional kNN with the

addition that one of the neighbors is chosen out of the

current window to reﬂect the past behavior. The sec-

ond one is called CSWB (Combined Sliding Window

Based) and it is a combination of m-kNN, kNN and

Naive Bayes.

4.1 m-kNN Classiﬁer

In m-kNN, we apply kNN within sliding windows

with the difference from the traditional kNN that k-1

instances are selected within the window, whereas the

last instance is used as an average of the history. At

the beginning of the method we ﬁll the current win-

dow with the most recent past instances. After that,

within the current window, by using Euclidean dis-

tance, k-1 nearest neighbors of the incoming instance

are found. Additionally, we also calculate centroids

of the classes by using the past instances. Hence, we

obtain class representatives from the history. Among

the class representatives, we determine the most sim-

ilar one, and this instance is used as the k

nearest

neighbor. As in the conventional kNN, the class la-

bel is determined with majority voting among these k

instances.

Assuming that we learn the actual class of the in-

stance in the next time instance, the representative of

Enhancements for Sliding Window based Stream Classiﬁcation

183

the class is updated. In order to slide the window, this

instance is pushed into the head of the window, and

the oldest instance is removed.

The algorithm for m-kNN can be summarized as

given in Algorithm 1.

In order to further improve the method for a dy-

namic and adaptive nature, a dynamic size for slid-

ing window is elaborated on. Additionally, using a

dynamic number of nearest neighbors obtained class

representatives is included as well. Finally, misclassi-

ﬁed instances in the current window are replaced with

the these instances obtained from the class represen-

tatives.

• Using a Dynamic Size for Sliding Window: For

this approach we have an error count that indicates

the count of misclassiﬁed instances in the cur-

rent window. If this count exceeds a pre-deﬁned

threshold value, we discard the portion of the win-

dow including the ﬁrst misclassiﬁed instance. Af-

ter cutting this portion of window, for the next it-

erations where classiﬁcations are correct, we con-

tinue to extend the sliding window.

• Using a Dynamic Count for the Nearest Neigh-

bors Obtained from Centroids of Classes: For

this approach when the error count exceeds given

threshold, we increment the number of near-

est neighbors obtained from the centroids of the

classes among the K-nearest-neighbors up to a

pre-deﬁned maximum value. As a result, we can

increase the weight of the average values for the

classes. When the error count decreases below the

given threshold, we decrement this count for near-

est neighbors.

• Replacing Misclassiﬁed Instances with Near-

est Centroid of Classes: For this approach, if

the error count exceeds the given threshold, we

replace the ﬁrst occurrences of misclassiﬁed in-

stances with a pre-deﬁned count in the current

window.

4.2 CSWB Classiﬁer

As the second enhancement for sliding window based

classiﬁers, CSWB is proposed. CSWB combines m-

kNN, Naive Bayes and kNN classiﬁers. For voting,

we investigate two alternative approaches:

• Majority Voting with Equal Weights: In this ap-

proach, after each classiﬁer completes its process,

if at least two of them produce the same result, the

instance is assigned to this class. Otherwise, since

Naive Bayes has high accuracy results in general

according to our experiments, it has a higher pri-

ority to determine the class label.

Algorithm 1: m-kNN.

Input : Data stream, parameter for kNN: k, the

size of the sliding window: n

Output: Class label assigned to instance: assCla

f :number of features;

c: number of class labels;

claLab[c][ f ]: Features list for each class label;

w:=i

, i

, ..., i

n−1

;

 Put the ﬁrst n −1 instances into sliding window;

for ( i = 0; i < c; i + + ) {

for ( j = 0; j < f ; j + + ) {

claLab[i][j]:=mean value of feature;

 Calculate the mean values of features

for each class;

}

ins: incoming instance in data stream;

eucDis[n − 1]: Euclidean Distances;

for ( i = 0; i < n −1; i + + ) {

eucDis[i]:=EuclDist(ins,w[i]);

 Calculate Euclidean Distance between each

element in the sliding window and incoming

sample;

}

neaNei[]:=k-1 nearest neighbors to ins;

eucDis[c]: Euclidean Distances;

 Find the k − 1 nearest neighbors of incoming

sample in sliding window;

for ( i = 0; i < c; i + + ) {

eucDis[i]:=EuclDist(ins,claLab[i]);

 Calculate Euclidean Distance between ins

and each class with the previously calculated

average values of attributes

}

neaNei[k]:=Nearest neighbor to ins in claLab[];

 Add the nearest class to the k − 1 neighbors

assCla:=Class label having the majority in

k-nearest neighbors;

 Assume that we learn the actual label of the

instance after classiﬁcation;

for ( i = 0; i < c; i + + ) {

for ( j = 0; j < f ; j + + ) {

Update the mean values of features for

this actual class of the instance;

}

Add ins to the sliding window;

Remove w[0] from sliding window;

 Update the sliding window;

return assCla;

• Voting with Current Accuracy: In this version,

we keep the accuracy values up to the new clas-

siﬁcation step and sum up the accuracy values for

classiﬁers having the same result. Finally, we as-

sign the instance to the class having the highest

total accuracy value.

KDIR 2019 - 11th International Conference on Knowledge Discovery and Information Retrieval

184

5 EXPERIMENTS

5.1 Experiment-1: Analysis on m-kNN

In this experiment we have used four real-world

datasets. The details of data sets used in this exper-

iment can be given as follows:

• KDD Cup 99’: The data set, which is about net-

work intrusion

, includes 42 attributes and con-

tains about 10M instances. In our experiments,

we used a 10% portion containing about 494K in-

stances.

• Electricity Market: The data set contains in-

stances collected from the Australian New South

Wales Electricity Market

. In this electricity mar-

ket, there are not ﬁxed prices and they are affected

by demand and supply. The prices are set ev-

ery ﬁve minutes. The data set contains 45312 in-

stances and the class label identiﬁes the change of

the price relative to a moving average of the last

24 hours.

• Forest Cover Type: The data set contains obser-

vations about forest cover types of 30 x 30 meter

cells in US

. The instances in this data set have

54 attributes such as elevation, aspect and slope.

• Air Quality: It is about the amount of several

chemicals in the air

. We have used the values

for the amounts of chemicals such as tin oxide, ti-

tania, tungsten oxide and indium oxide. We have

clustered the values of indium oxide and deter-

mine the labels for classiﬁcation.

We implemented m-kNN and MC-NN and

also we used Apache SAMOA to execute VHT

method. For m-kNN our parameters are k=10, win-

dow size=100 and for MC-NN error threshold=5,

performance threshold=0.75.

The results of our tests for our m-kNN method,

VHT and MC-NN on KDD Cup 99, Electricity Mar-

ket, Forest Cover Type, and Air Quality datasets are

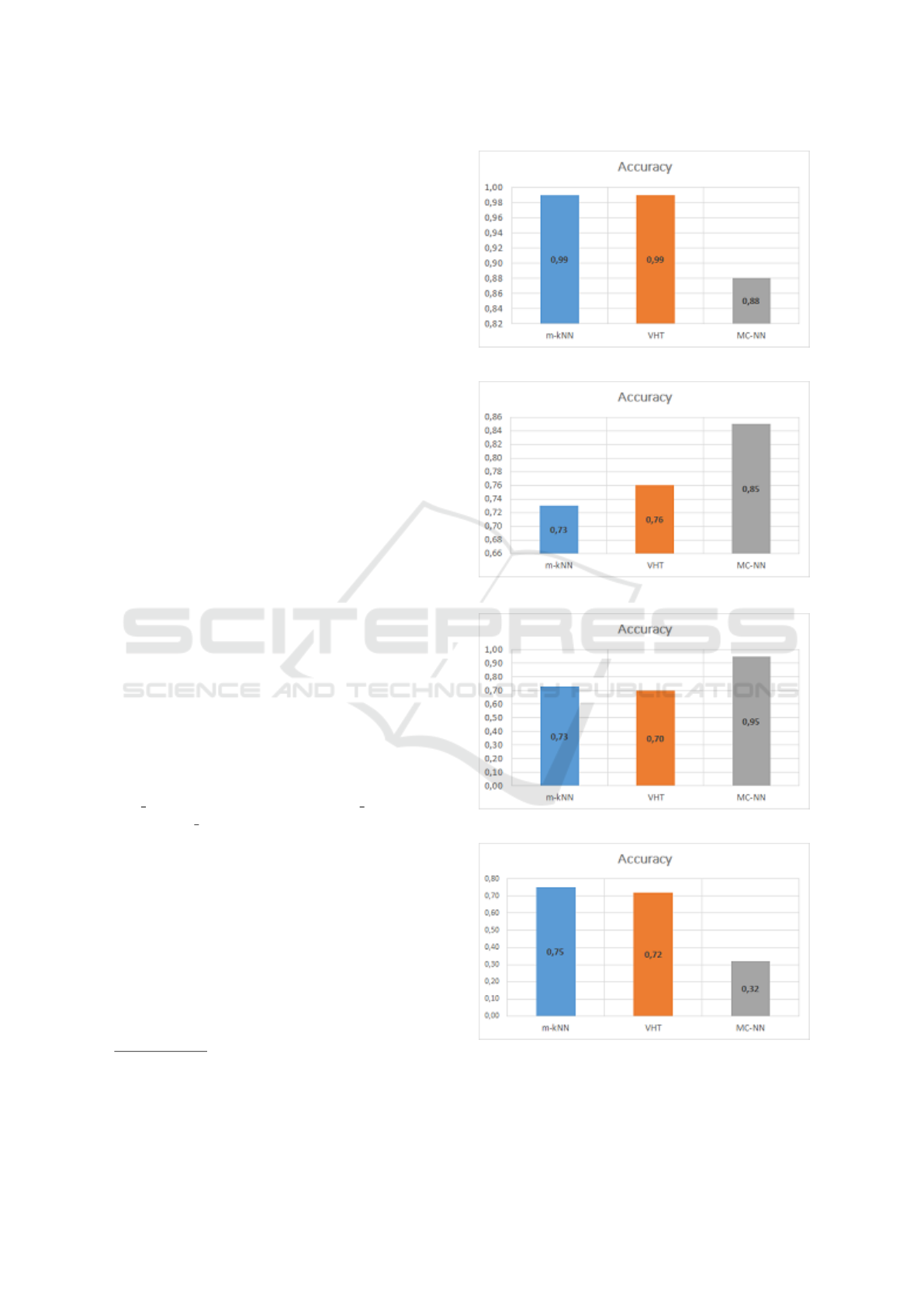
given in Figure 1, 2, 3, and 4, respectively. In these

ﬁgures, the highest accuracy values for each method

among the results obtained with different parameters

are taken into account.

According to the results of our experiments, we

can see that our m-kNN method has a high accuracy

for KDD Cup 99’ data set as 99%. It also has the

best accuracy values for Air Quality data set. On the

other hand, it has lower accuracy values for Electricity

http://kdd.ics.uci.edu/databases/kddcup99/kddcup99

https://www.openml.org/d/151

https://archive.ics.uci.edu/ml/datasets/Covertype

https://archive.ics.uci.edu/ml/datasets/Air+quality

Figure 1: Accuracy for KDD Cup 99’ in Experiment 1.

Figure 2: Accuracy for Electricity Market in Experiment 1.

Figure 3: Accuracy for Forest Cover Type in Experiment 1.

Figure 4: Accuracy for Air Quality in Experiment 1.

Market and Forest Cover Type data sets with respect

to MC-NN.

Enhancements for Sliding Window based Stream Classiﬁcation

185

5.2 Experiment-2: Analysis on CSWB

In this experiment, we used several other data sets

from real-world and also two synthetic data sets.

• Appliances Energy Prediction: The samples in

this data set were collected periodically with an

interval of 10 min for about 4.5 months

. We used

the columns temperature in living room, outside

temperature, outside pressure, wind speed and the

energy consumption in the data set. We clustered

the values of energy consumption and determine

the labels for classiﬁcation .

• Human Activity Recognition (HAR): This data

set is obtained from the recordings of 30 subjects

performing activities of daily living while carry-

ing a waist-mounted smartphone with embedded

inertial sensors

. There are 561 attributes and

10299 instances in this data set .

• ATM Terminal Data Sets: This data set con-

tains amount of money withdrawn from ATM

machines. Each data instance contains an identity

for the ATM machine, a date and an amount.

We used the data of two ATM terminals for one

year period and duplicated this data to a period

of 20 years. We also extracted several features

including month, day of month, day of week and

is work day from the date information. To label

the instances we discretized the amount of money

feature by applying k-Means clustering. This is

the ﬁrst version of our ATM data set (ATM v1).

As the second version we also added several other

features on weather conditions as temperature,

humidity and wind speed by using the location of

ATM terminal (ATM v2).

• SEA: This is a synthetic data set that contains

60,000 examples, 3 attributes and 2 classes

. In

this dataset, the attributes are numeric between 0

and 10 (Street and Kim, 2001).

• Hyperplane: This is another synthetic data set,

which contains 10,000 instances with 10 attributes

and 2 classes

For the ﬁrst part of the analysis we conducted ex-

periments by adding enhancements for making our m-

https://archive.ics.uci.edu/ml/datasets/Appliances+

energy+prediction

https://archive.ics.uci.edu/ml/datasets/human+activity+

recognition+using+smartphones

http://www.liaad.up.pt/kdus/downloads/sea-concepts-

dataset

https://www.win.tue.nl/

∼

mpechen/data/DriftSets/

hyperplane1.arff

kNN method more dynamic and adaptive. In the anal-

ysis, each of the following enhancements is applied

separately:

• Using a dynamic size for sliding window

• Using a dynamic count for the nearest neighbors

obtained from centroids of classes

• Replacing misclassiﬁed instances with nearest

centroid of classes

The results of this experiment are given in Table

1. According to the results we can see that the method

with dynamic number of nearest neighbors lowers the

accuracy values and the other enhancements do not

change the results.

For the second part of this experiment, we applied

m-kNN (without dynamic and adaptive extensions),

Naive Bayes, traditional kNN, and CSWB classiﬁer

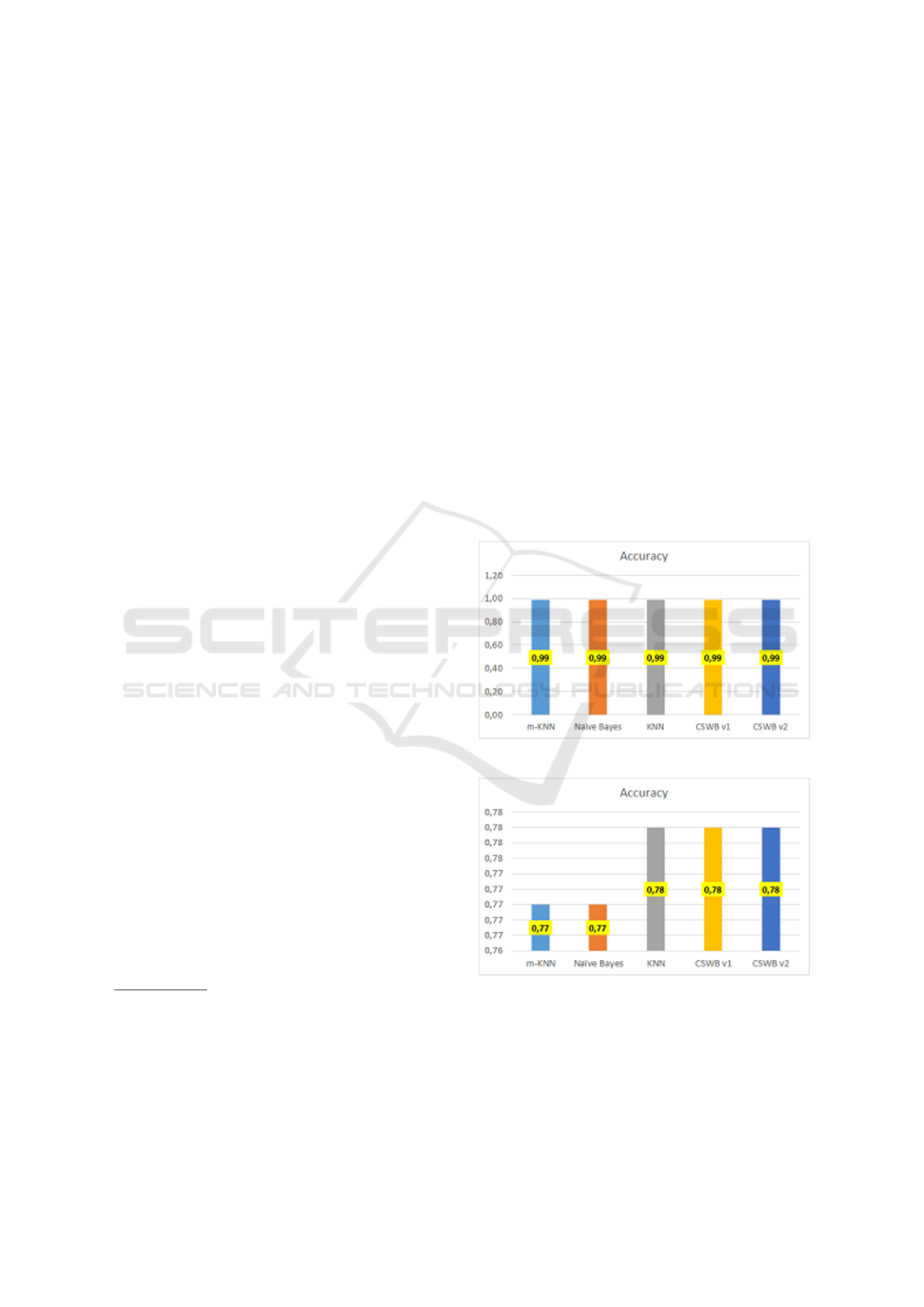
in two versions of voting. The results of our tests on

the data set for our m-kNN method, VHT and MC-

NN are given in Figure 5, 6, 7, 8, 9, 10, 11, 12, 13,

and 14.

Figure 5: Accuracy for KDD CUP 99 in Experiment 2.

Figure 6: Accuracy for Air Quality in Experiment 2.

KDIR 2019 - 11th International Conference on Knowledge Discovery and Information Retrieval

186

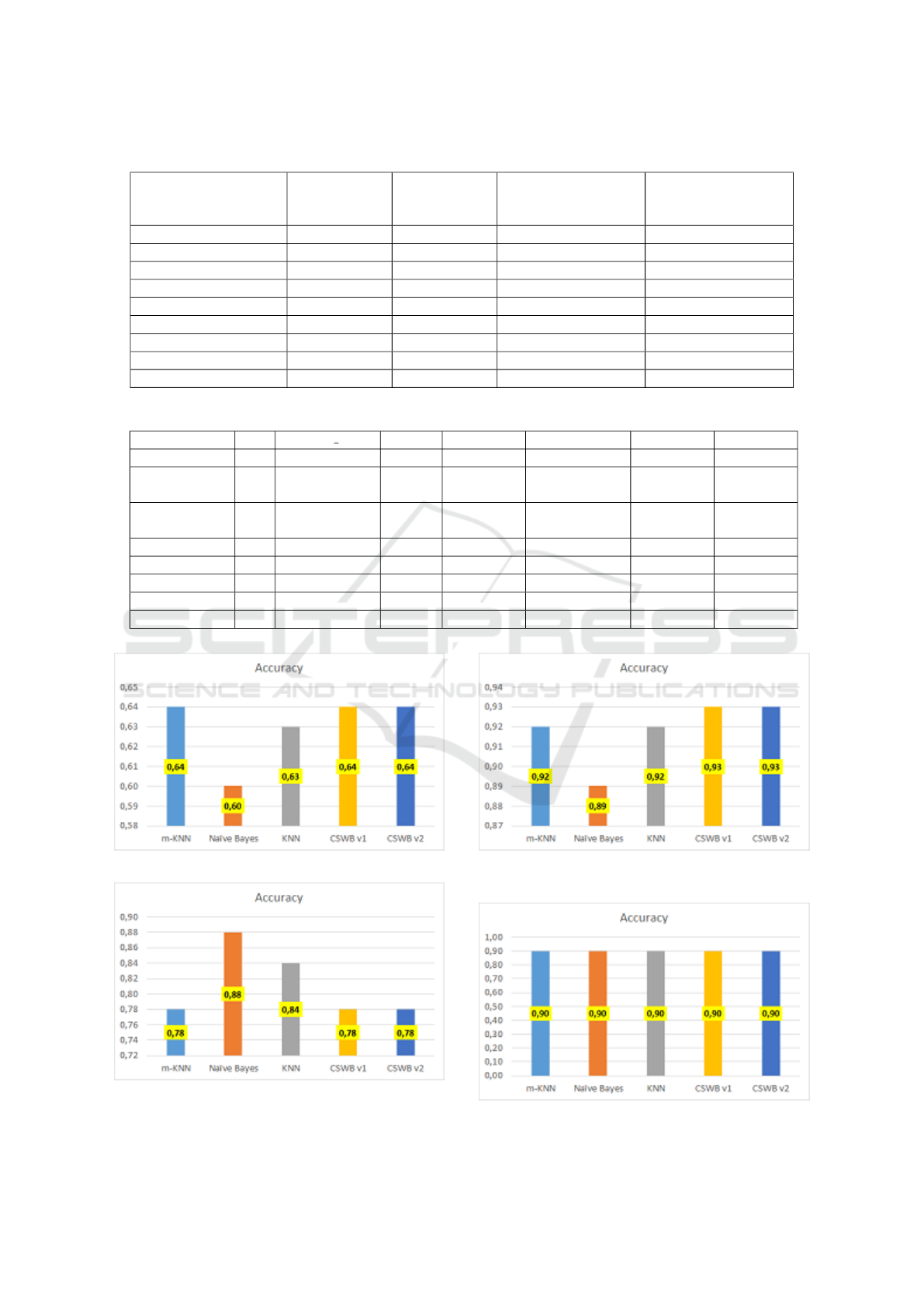
Table 1: Results after enhancements for m-kNN are enabled.

Dataset Original

m-kNN

Dynamic

Window

Enabled

Dynamic count of

nearest mean enabled

Replace with nearest

mean enabled

ATM v1 0.29 0.29 0.14 0.29

KDD CUP 99 0.99 0.99 0.99 0.99

Air Quality 0.75 0.75 0.70 0.75

Appliances Energy 0.61 0.61 0.57 0.61

Electricity 0.73 0.73 0.73 0.73

Hyperplane 0.74 0.74 0.60 0.74

SEA 0.82 0.82 0.77 0.82

HAR 0.81 0.81 0.78 0.81

Forest Cover Type 0.73 0.73 0.72 0.80

Table 2: Summary of the results in Experiment-2.

Dataset k window size mkNN kNN Naive Bayes CSWB v1 CSWB v2

Air Quality 5 100 0.77 0.77 0.76 0.78 0.78

Appliances

Energy

5 25 0.64 0.63 0.63 0.64 0.64

Appliances

Energy

5 500 0.63 0.63 0.51 0.63 0.64

HAR 5 250 0.91 0.91 0.87 0.92 0.92

HAR 5 500 0.92 0.92 0.82 0.93 0.93

ATM v2 5 25 0.30 0.35 0.31 0.36 0.36

ATM v2 5 50 0.32 0.38 0.31 0.39 0.39

ATM v2 5 250 0.30 0.42 0.32 0.43 0.43

Figure 7: Accuracy for Appliances Energy Pred. in Ex.2.

Figure 8: Accuracy for Electricity Market in Experiment 2.

Figure 9: Accuracy for Human Activity Recognition in Ex-

periment 2.

Figure 10: Accuracy for Forest Cover Type in Ex.2.

Enhancements for Sliding Window based Stream Classiﬁcation

187

Figure 11: Accuracy for ATM v1 in Experiment 2.

Figure 12: Accuracy for ATM v2 in Experiment 2.

Figure 13: Accuracy for SEA in Experiment 2.

Figure 14: Accuracy for Hyperplane in Experiment 2.

When we compare the results under equal valued

parameters, we can see that m-kNN and CSWB meth-

ods have better results that the other methods for sev-

eral data sets. These results are given in the Table 2.

In this experiment we have used k values: {5, 10} and

window size values:{25, 50, 100, 250, 500}.

For each method we have taken the highest accu-

racy into account for these varying parameters. Ac-

cording to the results among these 10 data sets we

can see that m-kNN has the highest accuracy for 3

of the data sets and CSWB classiﬁer is the best for 6

of the data sets. When we analyse the results in Ta-

ble 2, we can see that our enhancements give better

results when k=5 with respect to k=10. This may in-

dicate that making k respectively smaller can reveal

the effect of additional nearest instance coming from

the mean values of attributes and increasing k may de-

grade the success of our enhancements.

6 CONCLUSIONS

In this work we focused on streaming data classiﬁca-

tion, which attracts attention as a comparatively new

research problem. We propose new enhancements, m-

kNN and CSWB classiﬁers, for sliding window based

methods in data streams.

Since our enhancements are based on sliding win-

dow approach and we only keep the instances in the

current window from the whole data stream, they are

scalable for data streams with huge sizes. The mem-

ory space required to execute these enhancements are

proportional to the window size plus the number of

class labels, as the instances having the current mean

values for the features are maintained throughout the

execution process of data stream.

We analyzed the performance of the proposed

methods on data sets from different domains. For

the comparison, we implemented MC-NN, and used

VHT implementation in Apache SAMOA. Addition-

ally, we applied Naive Bayes and traditional kNN in

sliding window mechanism for accuracy comparison.

We have also elaborated on several variations for a

more adaptive and dynamic structure, however they

did not improve the accuracy.

According to the results obtained from different

data sets, our approaches have higher accuracy values

with respect to other methods for several data sets.

When we review the results of our experiments we

can see that m-kNN has lower accuracy values for

some datasets such as Electricty Market. This can

be related with the poor assocation between the cur-

rent state of the data and the behaviour pattern coming

from the past.

KDIR 2019 - 11th International Conference on Knowledge Discovery and Information Retrieval

188

As a result it can be concluded that sharp changes

in data streams can lower the accuracy performance

of m-kNN and it can be preferred when there is a

stronger linkage and a slight transition between the

past and current state of the data. For the future work,

we plan to further analyse failure cases to be able de-

vise improvements and for CSWB classiﬁer different

classiﬁers from the literature can be combined with

m-kNN to improve the accuracy performance further.

REFERENCES

Badiozamany, S. (2016). Real-time data stream clustering

over sliding windows. PhD thesis, Acta Universitatis

Upsaliensis.

Bifet, A. and Gavalda, R. (2007). Learning from time-

changing data with adaptive windowing. In Proceed-

ings of the 2007 SIAM international conference on

data mining, pages 443–448. SIAM.

Bifet, A., Holmes, G., Kirkby, R., and Pfahringer, B.

(2010). Moa: Massive online analysis. Journal of

Machine Learning Research, 11(May):1601–1604.

Bifet, A., Pfahringer, B., Read, J., and Holmes, G. (2013).

Efﬁcient data stream classiﬁcation via probabilistic

adaptive windows. In Proceedings of the 28th annual

ACM symposium on applied computing, pages 801–

806. ACM.

Brzezinski, D. and Stefanowski, J. (2013). Reacting to dif-

ferent types of concept drift: The accuracy updated

ensemble algorithm. IEEE Transactions on Neural

Networks and Learning Systems, 25(1):81–94.

Chen, Y., Li, O., Sun, Y., and Li, F. (2018). Ensemble clas-

siﬁcation of data streams based on attribute reduction

and a sliding window. Applied Sciences, 8(4):620.

Fong, S., Hu, S., Song, W., Cho, K., Wong, R. K., and

Mohammed, S. (2017). On recognizing abnormal hu-

man behaviours by data stream mining with misclas-

siﬁed recalls. In Proceedings of the 26th International

Conference on World Wide Web Companion, pages

1129–1135. International World Wide Web Confer-

ences Steering Committee.

Kourtellis, N., Morales, G. D. F., Bifet, A., and Murdopo,

A. (2016). Vht: Vertical hoeffding tree. In 2016 IEEE

International Conference on Big Data (Big Data),

pages 915–922. IEEE.

Law, Y.-N. and Zaniolo, C. (2005). An adaptive nearest

neighbor classiﬁcation algorithm for data streams. In

European Conference on Principles of Data Mining

and Knowledge Discovery, pages 108–120. Springer.

Stefanowski, J. and Brzezinski, D. (2017). Stream classiﬁ-

cation. Encyclopedia of Machine Learning and Data

Mining, pages 1191–1199.

Street, W. N. and Kim, Y. (2001). A streaming ensemble

algorithm (sea) for large-scale classiﬁcation. In Pro-

ceedings of the seventh ACM SIGKDD international

conference on Knowledge discovery and data mining,

pages 377–382. ACM.

Tennant, M., Stahl, F., Di Fatta, G., and Gomes, J. B.

(2014). Towards a parallel computationally efﬁcient

approach to scaling up data stream classiﬁcation. In

International Conference on Innovative Techniques

and Applications of Artiﬁcial Intelligence, pages 51–

65. Springer.

Tennant, M., Stahl, F., Rana, O., and Gomes, J. B. (2017).

Scalable real-time classiﬁcation of data streams with

concept drift. Future Generation Computer Systems,

75:187–199.

Enhancements for Sliding Window based Stream Classiﬁcation

189