Sports Analytics: Maximizing Precision in Predicting MLB Base Hits

Pedro Alceo

and Roberto Henriques

NOVA Information Management School, Campus de Campolide, Lisboa

Keywords: Machine Learning, Data Mining, Predictive Analysis, Classification Model, Baseball, MLB.

Abstract: As the world of sports expands to never seen levels, so does the necessity for tools which provided material

advantages for organizations and other stakeholders. The main objective of this paper is to build a predictive

model capable of predicting what are the odds of a baseball player getting a base hit on a given day, with the

intention of both winning the game Beat the Streak and to provide valuable information for the coaching staff.

Using baseball statistics, weather forecasts and ballpark characteristics several models were built with the

CRISP-DM architecture. The main constraints considered when building the models were balancing, outliers,

dimensionality reduction, variable selection and the type of algorithm – Logistic Regression, Multi-layer

Perceptron, Random Forest and Stochastic Gradient Descent. The results obtained were positive, in which the

best model was a Multi-layer Perceptron with an 85% correct pick ratio.

1 INTRODUCTION

In the past few years the professional sports market

has been growing impressively. Events such as the

Super Bowl, the Summer Olympics and the UEFA

Champions League are fine examples of the

dimension and global interest that can be generated

by this industry currently. As the stakes grow bigger

and further money and other benefits are involved in

the market, new technologies and methods surge to

improve stakeholder success (Mordor Intelligence,

2018).

Nowadays sports, as in many other industries use

data to their advantage in their search for victory. For

most organizations winning is the key factor for good

financial performance since it provides return in the

form of fan attendance, merchandising, league

revenue and new sponsorship opportunities

(Collignon & Sultan, 2014). Sports analytics is a tool

to reach this objective by helping coaches, scouts,

players and other personnel making better decisions

based on data, it leads to short and long-term benefits

for stakeholders of the organization (Alamar, 2013).

The growing popularity of sports and the

widespread of information also resulted in the growth

of betting in sports events. This resulted in a growth

of sports analytics for individuals outside sports

organizations, as betting websites started using

information based analytical models to refine their

odds and gamblers to improve their earnings (Mann,

2018).

In baseball, base hits are the most common way

for a batter to help is team produce runs, both by

getting into scoring position and to help his other

team-mates to score. Therefore, base hits are among

the best outcomes a batter can achieve during his at-

bat to help his team win games.

The objective of this project is to build a database

and a data mining model capable of predicting which

MLB batters are most likely to get a base hit on a

given day. In the end, the output of the work can have

two main uses:

 To give a methodical approach for coach’s

decision making and on what players should have

an advantage on a given game and therefore make

the starting line-up;

 To improve one’s probabilities of winning the

game MLB Beat the Streak.

For the construction of the database, we collected

data from the last four regular seasons of the MLB,

from open sources. Regarding the granularity of the

dataset, a sample consists of the variables of a player

in a game. Additionally, in the dataset, it was not

considered pitchers batting nor players who had less

than 3 plate appearances in the game. Finally, the

main categories of the variables used in the models

are:

 Batter Performance;

 Batter’s Team Performance;

190

Alceo, P. and Henriques, R.

Sports Analytics: Maximizing Precision in Predicting MLB Base Hits.

DOI: 10.5220/0008362201900201

In Proceedings of the 11th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2019), pages 190-201

ISBN: 978-989-758-382-7

 Opponent’s Starting Pitcher Performance;

 Opponent’s Bullpen Performance;

 Weather Forecast;

 Ballpark Characteristics.

The final output of the project should be a

predictive model, which adequately fits the data using

one or multiple algorithms and methods to achieve

the most precision, measured day-by-day. The results

will then be compared with other similar projections

and predictions to measure the success of the

approach.

This paper approaches some relevant work and

concepts that are important for a full understanding of

the topics at hand during Section 2. Section 3, 4 and

5 explain the Data Mining methodology

implemented, from the the creation of the dataset to

the final models achieved. In section 6 it is possible

to understand what were the results and insights that

are of most relevant from the best models. Finally, a

brief conclusion is presented, summarizing the

project and the most important discoveries found

along this paper and limitations on what points could

still be further improved.

2 BACKGROUND AND RELATED

WORK

2.1 Sports Analytics

Sports and analytics have always had a close

relationship as in most sports both players and teams

are measured by some form of statistics, which are

used to provide rankings for both players and teams.

Nowadays, most baseball studies using data

mining tools focus on the financial aspects and

profitability of the game. The understanding of

baseball in-game events is often relegated to

sabermetrics: “the science of learning about baseball

through objective evidence” (Wolf, 2015). Most

sabermetrics studies concentrate on understanding

the value of an individual and once again are mainly

used for commercial and organizational purposes

(Ockerman & Nabity, 2014). The reason behind the

emphasis on the commercial side of the sport is that

“it is a general agreement that predicting game

outcome is one of the most difficult problems on this

field” (Valero, C., 2016) and operating data mining

projects with good results often requires investments

that demand financial return.

Apart from the financial aspects of the game,

predictive modelling is often used to try and predict

the outcome of matches (which team wins a game or

the number of wins a team achieves in a season) and

predicting player’s performance. The popularity of

this practice grew due to the expansion of sports

betting all around the world (Stekler, Sendor, &

Verlander, 2010). The results of these models are

often compared with the Las Vegas betting

predictions, which are used as benchmarks for

performance. Projects like these are used to increase

one's earning in betting but could additionally bring

insights regarding various aspects of the game (Jia,

Wong & Zeng, 2013; Valero, C., 2016).

2.2 Statcast

Statcast is a relatively new data source that was

implemented in 2015 across all MLB parks.

According to MLB.com Glossary (MLB, 2018)

“Statcast is a state-of-the-art tracking technology that

allows for the collection and analysis of a massive

amount of baseball data, in ways that were never

possible in the past. (…) Statcast is a combination of

two different tracking systems -- a Trackman Doppler

radar and high definition Chyron Hego cameras. The

radar, installed in each ballpark in an elevated

position behind home plate, is responsible for

tracking everything related to the baseball at 20,000

frames per second. This radar captures pitch speed,

spin rate, pitch movement, exit velocity, launch angle,

batted ball distance, arm strength, and more.”

2.3 Beat the Streak

The MLB Beat the Streak is a betting game based on

the commonly used term hot streak, which in baseball

is applied for players that have been performing well

in recent games or that have achieved base hits on

multiple consecutive games. The objective of the

game is to pick 57 times correctly in a row a batter

that achieves a base hit on the day that it was picked.

The game is called Beat the Streak since the longest

hit streak achieved was 56 by the hall of fame Joe

DiMaggio, during the 1941 season. The winner of the

contest, wins US$ 5.600.000, with other prizes being

distributed every time a better reaches a multiple of 5

in a streak, for example picking 10 times or 25 times

in a row correctly (Beat the Streak, 2018).

2.4 Predicting Batting Performance

Baseball is a game played by two teams who take

turns batting (offense) and fielding (defence). The

objective of the offense is to bat the ball in play and

score runs by running the bases, whilst the defence

tries to prevent the offense from scoring runs. The

Sports Analytics: Maximizing Precision in Predicting MLB Base Hits

191

game proceeds with a player on the fielding team as

the pitcher, throwing a ball which the player on the

batting team tries to hit with a bat. When a player

completes his turn batting, he gets credited with a

plate appearance, which can have one of the

following outcomes, as seen below:

Figure 1: Breakdown of a plate appearance.

Denotated in green are the events which result on

a base hit and in red the events which are not.

Thereafter, what this paper tries to achieve is to

predict if a batter will achieve a Home Run (HR) or a

Ball hit in play (HIP) among all his plate appearances

(PA) during a game. In contrast it seeks to avoid Base

on Balls (BB), Hit by Pitch (HBP), Strikeouts (SO)

and Outs in Play (OIP). The most common approach

which mostly resembles the model built in this project

is forecasting the batting average (AVG). The main

difference from both approaches is that the batting

average does not account for Base on Balls (BB) and

Hit by Pitches (HBP) scenarios.

There are many systems which predict offensive

player performance including batting averages. These

models range from simple to complex. Henry

Druschel from Beyond the Boxscore identifies that

the main systems in place are: Marcel, PECOTA,

Steamer, and ZiPS (Druschel ,2016):

 Marcel encompasses data from the last three

seasons and gives extra weight to the most recent

seasons. Then it shrinks a player’s prediction to

the league average adjusted to the age using a

regression towards the mean. The values used for

this are usually arbitrary;

 PECOTA uses data for each player using their

past performances, with more recent years

weighted more heavily. PECOTA then uses this

baseline along with the player's body type,

position, and age, to identify various comparison

players. Using an algorithm resembling k-nearest

neighbors, it identifies the closest player to the

projected player and the closer this comparison is

the more weight that comparison player's career

carries.;

 Steamer much like Marcel’s methodology uses a

weighted average based on past performance. The

main difference between the 2 is that Steamer’s

the weight given for each year’s performance and

how much it regresses to the mean is less

arbitrary, i.e. these values vary between statistics

and are defined by performing regression analysis

of past players;

 ZiPS like Marcel and Steamer uses a weighted

regression analysis but specifically four years of

data for experienced players and three years for

newer players or players reaching the end of their

careers. Then, like PECOTA, it pools players

together based on similar characteristics to make

the final predictions.;

Goodman and Frey (2013), developed a machine

learning model to predict the batter most likely to get

a hit each day. Their objective was to win the MLB

Beat the Streak game, to do this they built a

generalized linear model (GLM) based on every game

since 1981. The variables used in the dataset, were

mainly focused on the starting pitcher and batter

performance, but also including some ballpark related

features. The author’s normalize the selected features

but no further pre processing was carried. The results

on testing were 70% precision on correct picks and in

a real-life test achieved a 14-game streak with a peak

precision of 67,78%.

Clavelli and Gottsegen (2013), created a data

mining model with the objective of maximizing the

precision of hit predictions in baseball. The dataset

built was scraped using python achieving over 35.000

samples. The features used in their paper regard batter

and opposing pitcher’s recent performance and

ballpark characteristics, much like the work the

previous work analyzed. The compiled game from

previous seasons were then inputed in a logistic

regression, which achieved a 79,3% precision on its

testing set. In the paper, it is also mentioned the use

of a support vector machine, which ended up heavily

overfitting resulting in a 63% precision in its testing

set.

3 DATASET

The two main software used to develop this project

were Microsoft Excel and Python. In the first stage,

Microsoft Excel was used for data collection, data

integration and variable transformation purposes. In a

second stage, the dataset was imported to Python

where the remaining data preparation, modelling and

evaluation processes were carried out. In Python, the

three crucial packages used were Pandas (dataset

KDIR 2019 - 11th International Conference on Knowledge Discovery and Information Retrieval

192

structure and data preparation), Seaborn (data

visualization) and Sklearn (for modelling and model

evaluation). The elements used in the data collection

and data storage processes are broadly depicted in

Figure 2.

Figure 2: Data partitioning diagram.

The data considered for this project were the games

played in Major League Baseball for the seasons

2015, 2016, 2017 and 2018. The features were

collected from the three open source websites:

 Baseball Reference: Game-by-game player

statistics and weather conditions, which could be

sub-divided into batting statistics, pitching

statistics and team statistics (Baseball Reference,

2018);

 ESPN: Ballpark factor (ESPN, 2018);

 Baseball Savant: Statcast yearly player statistics,

such as average launch angle, average exit

velocity, etc (Baseball Savant, 2018).

In order to build the final dataset, the different

features were saved in Excel Sheets. From Baseball

Reference three sub sections were created: batter box-

scores, pitcher box-scores and team box-scores. From

Sports Savant batter yearly Statcast statistics. From

ESPN the ballpark related aspects.

The chosen features categories will be explained

for a general understanding on what they are and their

potential importance for the models:

The Batter’s Performance category includes

variables that look to describe characteristics,

conditions or the performance of the batter. These

variables translate into data features like the

short/long term performance of the batter, tendencies

that might prove beneficial to achieve base hits or

even if the hand matchup, between the batter and

pitcher, is favourable. The reason behind the creation

of this category is that selecting good players based

on their raw skills is a worthwhile advantage for the

model.

Regarding the Batter’s Team Performance

category, the only aspect that fits this category is the

on-base percentage (OBP) relative to the team’s

batter. Since baseball offense is constituted by a 9-

player rotation if the batter’s team mates perform

well, i.e. get on base, this leads to more opportunities

for the batter and a consequently higher number of at-

bats to get a base hit.

The Opponent’s Starting Pitcher category refers

to the variables that regard the recent performance of

the starting pitcher, from the opposing team of the

batter being taken in consideration. These variables

relate to the pitcher’s performance in the last 3 to 10

games and the number of games played by the starting

pitcher. The logic behind the category is that the

starting pitcher has a big impact on preventing base

hits and the best pitchers tend to allow fewer base hits

than weaker ones.

The Opponent’s Bullpen Performance category is

quite similar to the previous one. Whereas the former

category looks to understand the performance of the

starting pitchers the latter focus on the performance

of the bullpen, i.e. the remaining pitchers that might

enter the game when starting pitcher get injured, get

tired or enter to create tactical advantages. The

reasoning for this category is the same as the previous

one, a weaker bullpen tends to provide a higher

change of base hits than a good one.

The Weather Forecast Category regards some

weather conditions that have an impact on the target

variable. The features that are taken into account are

wind speed and temperature. Firstly, the temperature

affects a baseball game in 3 main aspects: the baseball

physical composition, the player’s reactions and

movements, and the baseball’s flight distance (Koch

& Panorska, 2013). If all other aspects remain

constant higher temperatures lead to a higher chance

of offensive production and thus base hits. Secondly,

wind speed affects the trajectory of the baseball,

which can lead to lower predictability of the ball’s

movement and even the amount of time a baseball

spends in the air (Chambers, Page & Zaidinis, 2003).

Finally, the Ballpark Characteristics category

englobes the ESPN ballpark hit factor, the roof type

and the altitude. The “Park factor compares the rate

of stats at home vs. the rate of stats on the road. A rate

higher than 1.000 favours the hitters. Below favours

the pitcher” meaning that this factor will have into

consideration several aspects from this or other

categories, indirectly (ESPN, 2018). Altitude is

another aspect that is crucial to the ballpark, the

higher the altitude the ballpark is situated the farther

the baseball tends to travel. The previous statement is

important to the Denver’s Coors Field, widely known

Sports Analytics: Maximizing Precision in Predicting MLB Base Hits

193

for its unusually high offensive production (Kraft &

Skeeter, 1995).

Finally, the roof type of the ballpark affects some

meteorological metrics, since a closed roof leads to

no wind and a more stable temperature, humidity, etc

when compared to ballparks with and open roof.

4 PRE-PROCESSING

The dataset built for this project is imbalanced, from

which the total 155.521 samples, around 65,3% are

batters that achieved at least a base hit and the

remaining 34,7% are at batters whose game ended

without achieving a base hit. Although not very

accentuated it possible to determine that the dataset is

imbalanced.

Table 1: Distribution of the dependent variable.

Hit

Count

Percentage

Yes

101.619

65,3%

53.902

34,7%

Total

155.521

100%

Both the under sample and oversample

approaches were taken into consideration for the

project. However, oversampling was not a feasible

solution in the specific context of this paper, since the

objective of the paper is to predict which are the best

players for a given day and, therefore the creation of

random games with random dates would disturb the

analysis. This may have led to players having to play

multiple fictitious games in the same days which

would not make sense in the context of the regular

season of baseball.

In conclusion the only method that will be tested

for balancing the dataset is random under sampling.

This consists on removing random observations from

the majority class until the classes are balanced, i.e.

have a similar number of observations for each of the

dependent variable values.

In this project it is implemented both holdout and

cross-validation methods, since there was enough

data. The initial dataset was firstly divided into

training set (80%) and test set (20%) using a simple

holdout method. Note that to achieve the best

simulation possible, the division was done

chronologically, i.e. the first 80% of the games

correspond to the training set and the remainder to the

test set.

Finally, for the training aspect of the project the

training set was recursively divided into a smaller

training set (60% of the total) and a validation set

(20% of the total). This division implies that for

feature selection, hyper parameter tuning, evaluation

the data was used with a stratified cross-validation

technique with 10-folds. As seen below, figure 2

represents an overview of the partitions and their use

for the project.

Figure 3: Data partitioning diagram.

Regarding normalization, the most common

methods to obtain normalization of the variables is

through normalization, standardization and scaling.

The min-max normalization rescales variables in a

range between 0 and 1, i.e. the biggest value per

variable will assume the form of 1 and the lowest 0.

It is an appropriate method for normalizing datasets

where its variables assume different ranges and, at the

same time, solves the mentioned problem of biased

results for some specific algorithms that cannot

manage variables with different ranges (Larose,

2005). This was the solution applied to normalize the

numeric variables in the dataset:

𝑋

∗

𝑋 − min (𝑋)

𝑟𝑎𝑛𝑔𝑒(𝑋)

𝑋 − min (𝑋)

max

(

𝑋

)

− min (𝑋)

(1)

In contrast, as some algorithms cannot cope with

categorical variables, if it is intended the use of these

types of variables in all models there is a need to

transform these into a numerical form. Binary

encoding was the solution implemented to solve this

issue, where by creating new columns with binary

values it is possible to translate categorical

information into 1’s and 0’s (Larose, 2005).

Regarding missing values, only the Statcast

variables (Average Launch Angle, Average Exit

Velocity, Brls/PA% and Percentage Shift) had

missing values, which comprised around 1% of all the

features. These originated from the difference from

the two data sources, i.e. some players were not in the

Statcast database and therefore did not have a match

when building the final database. To solve this issue

the observations with missing values relative to

Statcast features were deleted due to their immaterial

size.

KDIR 2019 - 11th International Conference on Knowledge Discovery and Information Retrieval

194

Figure 4: Top-down project diagram.

Additionally, some missing values were created

after the variable transformation process. These

missing values are the calculated performance

statistics for the first game of every player in the

dataset (pitcher or batter) and the same for every

matchup pitcher vs batter. In sort, every observation

which comprises the first game of a player its

statistics from the previous “X games” will be NaN

since its their first game in the dataset. These

occurrences represented around 4% of the dataset for

every batter and pitcher.

Finally, there were two main methods used to

detect outliers in this project. In a first phase, it was

calculated the z-score for all features with the

objective of understanding what the variables with the

most extreme values were considering the mean and

standard deviation of the respective features. In this

analysis values that are less than -3 standard

deviations or greater than 3 standard deviations than

the mean are usually considered outliers. In the

context of our problem we cannot simply remove all

observations with features that exceed these values

but are a good start on understanding which variables

have more outliers and their overall dimension in the

context of the whole dataset (Larose, D., & Larose,

C., 2014).

The other method used for outlier detection was

boxplots, to visualize feature values in the context of

their interquartile ranges. In this method any values

that lie under the 1st quartile by more than 1,5 times

the size of the interquartile range or over the 3rd

quartile by more than 1,5 times the size of the

interquartile range is considered an extreme value in

the context of the respective feature (Larose, D., &

Larose, C., 2014).

In the end, the outlier detection of this project

consisted on removing the most extreme values from

feature using both the information from the z-score

analysis and the visualization power of the box-plots.

Note that due to the unknown influence of the outliers

on the project, every model was tested with outliers

and without the identified extreme values. With this

it will be possible to have a good comparison of the

performance of the models for both scenarios.

5 MODELLING

This chapter focus on presenting the methods used for

modelling, feature selection and their respective

hyper parameter tuning. Figure 4 depicts an end-to-

end view of the paper, where it is possible to perceive

the logic behind the processes performed to transform

the initial dataset into insight on the problem in

question.

Beginning in the dataset, various branching paths

are created in order to test several hypotheses. This

method enables the creation of the final 48 models,

which are all evaluated equally and therefore provide

a broader look on all the methods tested and what is

the best final model for this problem.

In short, pre-processing and dimensionality

reduction methods are applied to the initial dataset, as

seen in figure 4. Thereafter the selected variables

already pre-processed are used as inputs to the

Sports Analytics: Maximizing Precision in Predicting MLB Base Hits

195

algorithms, which output a probability estimate i.e.

how likely is a batter to get a base hit in that game.

Thereafter some evaluation metrics are applied to the

models and the final conclusions are reached.

Over the course of this section a deeper look will

be taken for the feature selection (PCA, no PCA, RFE

and RFE without inter-correlated variables), the

algorithms and the respective method used for hyper-

parameter tuning and finally what evaluation metrics

were applied to compare the final models created.

5.1 Algorithms

The logistic regression was developed by David Cox

in 1958. This algorithm is an extension of the linear

regression, which is mainly used in data mining for

the modelling of regression problems. The former

differs from the latter since it looks to solve

classification problems by using a sigmoid function

or similar to transform the problem into a binary

constraint (Cox, 1958). The SAGA algorithm was

chosen during the hyper parameter tuning for the

logistic regression. SAGA follows the path of other

algorithms like SAG, also present in the SKlearn

library, as an incremental gradient algorithm with fast

linear convergence rate. The additional value that

SAGA provides is that it supports non-strongly

convex problems directly, i.e. without much

alterations it better adapts to these types of problems

in comparison with other similar algorithms (Defazio,

Bach & Lascoste-Julien, 2014).

A multi-layer perceptron is a type of neural

network, inspired by the structure of the human brain.

These algorithms make use of nodes or neurons

which connect to one another in different levels with

weights attributed to each connection. Additionally,

some nodes receive extra information through bias

values that are also connected with a certain weight

(Zhang, Patuwo, & Hu, 1997).

The optimization algorithm used for training

purposes was Adam, a stochastic gradient-based

optimization method which works very well with big

quantities of data and provides at the same time low

computational drawbacks (Kingma & Ba, 2015).

Regarding the activation functions, during the hyper

parameter tuning the ones selected were ‘identity’- a

no-op activation, which returns f(x) = x and ‘relu’- the

rectified linear unit functions, which returns f(x) =

max (0, x).

The concept of random forest is drawn from a

collection of decision trees. Decision trees are a

simple algorithm with data mining applications,

where a tree shaped model progressively grows

splitting into branches based on the information held

by the variables. Random forests are an ensemble of

many of these decision trees, i.e. bootstrapping many

decision trees achieves a better overall result, because

decision trees are quite prone to overfitting the

training data (Kam Ho, 1995).

The stochastic gradient descent is a common

method for optimizing the training of several machine

learning algorithms. As mentioned, it is used in both

the multi-layer perceptron and logistic regression

approach available in the SKlearn library. This away

it is possible to use the gradient descent as the method

of learning, where the loss, i.e. the way the error is

calculator during training, is associated with another

machine learning algorithm. This enables more

control on the optimization and less computational

drawbacks for the cost of a higher number of

parameters (Scikit-learn, 2018a, Mei, Montanari &

Nguyen, 2018).

During the parameter tuning, the loss function that

was deemed most efficient was ‘log’ associated with

the logistic regression. Therefore, for this algorithm

the error used for training will resemble a normal

logistic regression, already described previously.

5.2 Feature Selection

In data mining projects where there are high

quantities of variables it is good practice to reduce the

dimensionality of the dataset. Some of the reasons

that make this process worthwhile are a reduction in

computational processing time and, for some

algorithms, overall better results. The latter results

from the elimination of the curse of dimensionality –

the problem caused by the exponential growth in

volume related to adding several dimensions to the

Euclidean space (Bellman, 1957). In conclusion,

feature selection looks to eliminate variables with

reductant information and keeping the ones who are

most relevant to the model (Guyon & Elisseeff,

2003).

The first method used for selection the optimal set

of variables was to use the recursive feature

elimination (RFE) functionality in SKlearn. In a first

instance, all variables are trained, and a coefficient is

calculated for each variable, giving the function a

value on which features are the best contributors for

the model. Thereafter, the worst variable is removed

from the set and the process is repeated iteratively

until there are no variables left (Guyon, Weston,

Barnhill & Vapnik, 2002).

Another method implemented for dimensionality

reduction was the principal component analysis

(PCA). This technique looks to explain the

correlation structure of the features by using a smaller

KDIR 2019 - 11th International Conference on Knowledge Discovery and Information Retrieval

196

set of linear combinations or components. By

combining correlated variables, it is possible to use

the predictive power of several variables in a reduced

number of components.

Finally, the correlation between the independent

features and the dependent variable were visualized

as a tool to understand what the most relevant

variables for the models might be. This analysis was

carried for all variables, i.e. it was calculated the

correlation between all dependent variables as well.

This had the objective of doing a correlation-based

feature selection, meaning that it is desirable to pick

variables highly correlated with the dependent

variable and the same time with low intercorrelation

with the other independent features (Witten, Frank, &

Hall, 2011).

5.3 Hyperparameter Tuning

The method chosen for hyperparameter tuning was

Gridsearch with stratified 10-fold cross validation

implemented using the SKlearn library. The process

is similar to a brute force approach, where Python

runs every possible combination of hyperparameters

assigned and returns as the output the best

combination for the predefined metrics (Scikit-learn,

2018b). This process was performed for every

algorithm twice, once for the PCA and once for the

no PCA formatted dataset. Needing to compare

unbalanced and balanced datasets the metric chosen

was area under curve.

5.4 Evaluation

The final step of the model process was to choose the

metrics that better fitted the problem. The main

constraints of the problem were to find good metrics

that enabled the comparison between balanced and

imbalanced datasets and, of course to achieve the

objective of the project. The most appropriate metric

to fulfil these requirements was precision with the

objective of defining a tight threshold to secure a very

high rate of correct predictions on players that would

get a base hit. Nevertheless, other metrics that adapt

to this type of problem were also calculated in order

to get a better overall view of the final models, such

as:

 Area Under Curve;

 Cohen Kappa;

 Precision and Average Precision.

Finally, for each model it was calculated the

precision for the Top 250 and Top 100 instances, i.e.

the instances with highest probability of being base

hits as predicted by the models. This analysis

resembles the strategy that will be applied in the real

world, for which only the top predictions will be

chosen for the game. Note that this analysis will also

give a very good impression on what threshold should

be used for this point onward.

6 RESULTS

The objective of the paper was to create a model

capable of consistently picking MLB players who

will get a base hit on a given day. A dataset was built

from scratch with variables that, according to the

literature review, proved to have the most potential on

predicting the aforementioned outcome.

During the process of developing the final 48

models, some alternatives were tested or pondered

but later dropped. The main topics approached in such

manner were:

 Some sampling techniques;

 Several machine learning algorithms did not reach

the evaluation stage for various reasons;

 Several metrics were pondered but were dropped

in detriment of the ones illustrated in this paper.

The results of the final 48 models show some

variance when all factors are considered, but overall

it is viable to retain one main insight from the analysis

on the test set metrics. As seen in the figure below,

the use of PCA did not help the models perform better

according to any metric:

Figure 5: Average model performance on test set, by use of

PCA.

Apart from PCA, RFE and correlation-based

feature selection were also used during the process of

selecting the most valuable variables for the models.

Comparing RFE results with the smaller subset of

variables composed by the RFE selected variables

minus the inter-correlated variables from those

selections, it was possible to conclude that more often

than not the smaller subset performs better than the

full subset from the original RFE, thus highlighting

some of the variables that are not so relevant when

considered with the remaining selected variables. The

most predominant variables being cut off, from this

0,00 0,10 0,20 0,30 0,40 0,50 0,60 0,70 0,80

Precision Top 100

Precison Top 250

Precision

Avg Precision

AUC

Cohen Kappa

WO/ PCA W/ PCA

Sports Analytics: Maximizing Precision in Predicting MLB Base Hits

197

process, are batter and pitcher performance statistics

and altitude. RFE selected several variables that

belong to the same subcategory and hence are

somewhat correlated. That way it was possible to

withdraw some of these excess variables to achieve

better overall results, leading to a belief that RFE

alone was not the optimal strategy for feature

selection for the dataset built for this project.

Regarding variable usage, the most used variables

fall under the batter performance statistics category,

additionally the models use at least one variable from

each of the remaining categories, where the most

prevalent are hits per innings for the starting pitcher

(last 10 games), ESPN hit factor, temperature and hits

per innings for the bullpen (last 3 games). The

category with the least representation is the team

batting statistics, as on-base-percentage (OBP) does

not seem to add much prediction value on the

outcome of the dependent variable.

Considering the metrics chosen it was now

possible to select the best models, table 2 presents the

various metrics for the top 3 models selected. The

logic behind the selection was to choose the models

with the highest precision on the Top 100 and 250

instances, giving most attention to those that also

performed well on other metrics.

All in all, balanced datasets work well on this

project and, most of the top performing models came

from sets with random under sampling. When

analysing balanced datasets, these outperform the

unbalanced datasets in every metric except for the top

100 and 250 precision, deeming most of them

irrelevant. Additionally, imbalanced datasets also had

the inconvenience of choosing the most common

label for most instances, during validation, producing

ambiguous results and limiting possible analysis and

conclusions between these results.

Furthermore, methods like outlier’s removal,

inter-correlated variable removal and the choice of

algorithm do not appear to produce dominant

strategies in this project and in the right conditions all

possibilities produce good results, as seen in the

diversity of methods used in the top 3 models.

In a real-life situation, the 1st model in the tables

above would provide the best odds of beating the

streak with an expected rate of correct picks of 85%,

in situations where the model’s probability estimate

is very high. The remaining top models also prove to

be viable, in which models with precision on Top 250

instances higher than the former model give a slight

improvement on expected correct picks at lower

probability estimations.

The information used to rank the instances by

probabilities estimates was further used to calculate

at what threshold can we expect to achieve similar

correct picks. Note that it is not mandatory to pick a

player every single day, therefore it is optimal to wait

and pick only when the models are confident enough

on when a base hit is occurring. For this analysis

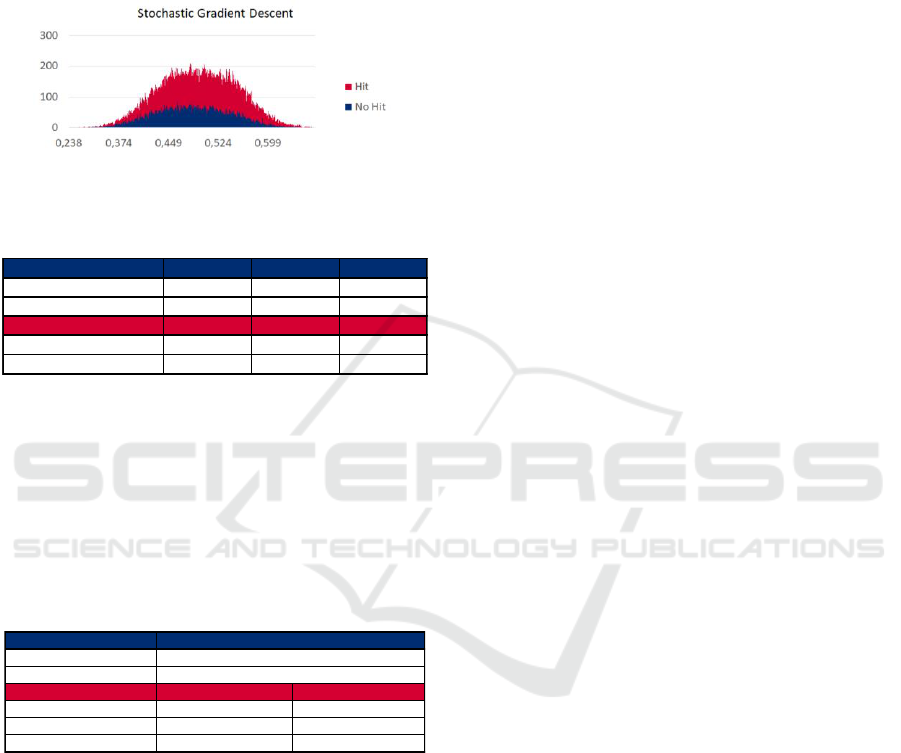
figures 4 to 6 explore the hits and no hits per

probability estimate of each of the top 5 models:

Figure 6: Distribution of probability estimates for the best

Multi-Layered Perceptron.

Figure 7: Distribution of probability estimates for the best

Logistic Regression.

It possible to note a sweet spot in the far right of

each of the figures, where there are areas with no or

very few no-hit instances where the models predict

hit. After a thorough analysis it is impossible to

Table 2: Distribution of the dependent variable.

Validation Set (Stratified 10-Fold CV)

Test Set

AUC

Cohen

Kappa

Avg

Precision

AUC

Cohen

Kappa

Avg

Precision

Top 250

Precision

Top 100

0,566

0,095

0,555

0,550

0,536

0,057

0,664

0,718

0,760

0,850

Random Under Sampling, Without Outliers, Without PCA, No Correlated Variables, Multi-Layered Perceptron

0,567

0,095

0,555

0,548

0,528

0,043

0,660

0,716

0,768

0,820

Random Under Sampling, Without Outliers, Without PCA, All Variables, Logistic Regression

0,562

0,078

0,551

0,539

0,545

0,080

0,668

0,690

0,760

0,800

Random Under Sampling, With Outliers, Without PCA, No Correlated Variables, Stochastic Gradient Descent

KDIR 2019 - 11th International Conference on Knowledge Discovery and Information Retrieval

198

choose a threshold that gives an 100% change of only

picking hit instances that were correctly predicted, for

57 instances. Nevertheless, the top 100 strategy still

works well in this analysis and, in table 15, it is

depicted the different values that are good thresholds

to achieve above 80% expected correct picks.

Figure 8: Distribution of probability estimates for the best

Stochastic Gradient Descent.

Table 3: Threshold analysis on top 3 models.

The models provide different ranges of

probabilities but in the end all thresholds fall under

approximately 80%-90% of the overall distributions,

according to the z-score. Some ensembles techniques

were tried to improve the expected results, such as

majority voting and boosting techniques but none of

these techniques provided any improvement in the

results and were later dropped.

Table 4: Project results versus results of other strategies.

The most basic strategies used for playing a game

like Beat the Streak is to either pick a complete

random player or to pick one of the best batters in the

league. These strategies, as expected, have very low

results compared to any of the models. From the

models identified during the literature review, it is

possible to see improvements and strategies that give

a player an advantage over the simple strategies. The

best and preferred method used by other papers is to

use a type of linear model, that was also tried during

this project. Nevertheless, the multi-layer perceptron,

mentioned in the top 3 algorithms, provides a 5-

percentage point improvement over the best model

from other papers. The improvements over the

previous works, mentioned in Figure 4 and previously

discussed in the end of section 2 of this paper, cannot

be attributed to a single factor. However, the main

differences that, in the end, resulted in a better

outcome of this paper, comparatively to the other two,

are as follow.

A wider scope of variable types. In other works,

the authors focus primarily on the use of variables

regarding the batter’s and pitcher’s performance, as

well as ballpark characteristics. In this paper the focus

shifts to the use to a wider range of variable types,

which in the end proved to be important to provide a

wider understanding on the event being predicted.

The experimentation of several pre-processing

methods, modelling methods and algorithms. In this

paper no method is deemed to be definitive and by

creating a greater number of models it was possible

to test several methods and test combinations of those

in order to get a better understanding on what are the

processes that work and, with this, be more confident

that it was possible to arrive to a good conclusion.

This contrasts with the the more unilinear direction

followed by the other authors who tended not to

experiment several approaches to their problem.

Finally, the overall strategy of evaluation of this

paper better suits the task being presented. In the

papers mentioned the authors focus on standard

metrics to evaluate the results of the models, such as

precision. However, because of the nature of the

game Beat the Streak, it is not crucial to evaluate all

features in the test set, but more importantly we are to

be sure of the picks being made. Therefore, by

wielding the probability estimates in conjunction with

the 100 or 250 precision metrics, one can achieve

more accurate conclusions.

7 CONCLUSIONS

The main objectives of this project were to produce a

model that could predict which players were most

likely to get a base hit on a given day and, in this

sense, provide an estimation of the probability of said

event occurring, for the use of stake holders in MLB

teams.

To achieve these objectives the following steps

were taken:

 Build a database using open-source data including

features from a variety of categories;

 Use descriptive statistics and data visualization

techniques to explore the value of the features

identified during the literature review;

 Build a predictive model using data mining and

machine learning techniques, which predicts the

Probability Estimates

MLP LG1 SGD

Maximum probability 0,658 0,671 0,679

Minimun probabilty 0,242 0,218 0,238

Threshold top 100 0,608 0,616 0,643

Z-score threshold 0,880 0,878 0,918

Expected correct ratio 85% 82% 80%

Paper

Random guessing

Picking best player

Algorithm

Linear Model MLP

Goodman & Frey (2013)

70% -

Clavelli & Gottsegen (2013)

80% -

Best Models (this paper)

82% 85%

Expected Correct Picks

≈ 60%

≈ 67%

Sports Analytics: Maximizing Precision in Predicting MLB Base Hits

199

probability of a base hit occurring for each

instance;

 Apply the model on a test set and analyse the

predictions to select the best models and to find

the optimal thresholds.

Firstly, the data needed for this project was

collected from Baseball Reference, Baseball Savant

and ESPN websites. This data was distributed into

different Microsoft Excel sheets and later integrated

into a single database, displaying the features from

each batter’s game, not including pitchers batting.:

Secondly, the database was imported to Python

and structured using the Pandas library. Several

descriptive statistics and data visualization

techniques were applied to the database, using the

Seaborn package to extract insights on the quality of

the data, to understand what type of transformations

were needed and to gain insights on some the

variables being used. Throughout the latter process it

was possible to find out that the best variables in

terms of correlation to the dependent feature were

mostly batting statistics. At the same the time,

variables from this sub-category suffered from inter-

correlation with one another, which was taken into

consideration during the feature selection.

Using the insights gained from the second step it

was possible to do the pre-processing and

transformations on the dataset, making it ready for the

third step of the project. Thereafter, several models

were built with the main constraints being data set

balancing, the use of outliers, the use of PCA and a

feature selection using RFE or using RFE in

conjunction with a correlation-based feature selection

creating a smaller subset of features from the RFE

selected variables.

From the final 48 models created it was possible

to retain some insights:

 PCA did not perform as well as the other forms of

feature selection;

 Overall, balancing the datasets using random

under sampling obtained better results than no

balancing;

 It was possible to obtain simpler models by

removing inter-correlated variables from the RFE

selected features and obtain similar or better

models.

Finally, after analysing the performance of the

models against the test set, the top 3 models were

chosen as possible candidates for usage in a real-

world situation. With the ability to calculate the

probability estimates for each instance, it was

possible to then find the thresholds for each model.

The best model gave an expected correct pick rate of

85% on the top 100 picks (precision on top 100 most

probable instances), on test set, i.e. half a season

worth of instances.

The model that provides these results is a multi-

layer perceptron, no outliers, no PCA and with the

removal of inter-correlated variables from the

original feature selection. When compared to similar

works, this model has about 20 percentage points gain

on precision over the best basic strategy and a 5

percentage points gain over the best model analyzed

during the literature review.

Nevertheless, a base hit in baseball has a very

close relationship to a player’s ability and other

factors already mentioned during this paper. These

types of events are prone to be random, since there

are a lot of elements that are hard to quantify into

features and, thus cannot be fully translated in a

machine learning model. The influence of luck can be

diminished but it is hard to ever obtain a 100% model

in predicting these events. The project at hand had

some good results but it is unlikely that with an 85%

expected correct pick ratio, it will predict correctly 57

times in a row.

The main points for improvement for this project

would be:

 Collect data from more seasons;

 Experiment with a wider variety of sampling

techniques;

 Identify new variables, especially from factors not

used in this project, for example defensive

performance from the opposing team;

 Experiment with other algorithms and further tune

the hyperparameters used in them;

 Effective use of some form of ensemble

technique.

REFERENCES

Alamar, B., 2013, Sports Analytics: A Guide for Coaches,

Managers, and Other Decision Makers. Columbia

University Press.

Baseball Reference, 2018, Baseball Reference. Retrieved

from Baseball Reference: https://www.baseball-

reference.com

Baseball Savant, 2018, Baseball Savant. Retrieved from

Baseball Savant: https://baseballsavant.mlb.com

Beat the Streak, 2018, Beat the Streak: Official Rules.

Retrieved from Beat the Streak: http://mlb.mlb.com/

mlb/fantasy/bts/y2018/?content=rules

Bellman, R., 1957, Dynamic programming. Princeton, NJ:

Princeton University Press.

Chambers, F., Page, B., & Zaidinjs, C., 2003, Atmosphere,

weather and baseball: How much farther do baseballs

KDIR 2019 - 11th International Conference on Knowledge Discovery and Information Retrieval

200

really fly at Denver’s Coors Field. Prof. Geogr. 55th

edition, 491-504.

Clavelli, J., & Gottsegen, J., 2013, Maximizing Precision of

Hit Predictions in Baseball.

Collignon, H., & Sultan, N., 2014, Winning in the Business

of Sports. ATKearney.

Cox, D., 1958, The Regression Analysis of Binary

Sequences. Journal of the Royal Statistical Society.

Series B, 20(2), 215-242.

Defazio, A., Bach, F., & Lacoste-Julien, S., 2014, SAGA:

A Fast-Incremental Gradient Method with Support for

Non-Strongly Convex Composite Objectives.

Advances in Neural Information Processing Systems,

27, pp. 1-9.

Druschel, H., 2016, Guide to the Projection Systems.

Retrieved from Beyond the Box Score:

https://www.beyondtheboxscore.com/2016/2/22/1107

9186/projections-marcel-pecota-zips-steamer

explained-guide-math-is-fun

ESPN., 2018, ESPN Hit Factor. Retrieved from ESPN:

http://www.espn.com/mlb/stats/parkfactor

Goodman, I., & Frey, E., 2013, Beating the Streak:

Predicting the MLB Players Most Likely to Get a Hit

each Day.

Guyon, I., & Elisseeff, A., 2003, An Introduction to

Variable and Feature Selection. Journal of Machine

Learning Research, 3, 1157-1182.

Guyon, I., Weston, W., Barnhill, S., & Vapnik, V.2002,

Gene Selection for Cancer Classification using Support

Vector Machines. Machine Learning, 46(1-3), 1-3.

Jia, R., Wong, C., & Zeng, D., 2013, Predicting the Major

League Baseball Season.

Kam Ho, T., 1995, Random Decision Trees. Proceedings.

3rd International Conference on Document Analysis

and Recognition, (pp. 278-282).

Kingma, D., & Ba, J., 2015, Adam: A Method for

Stochastic Optimization. 3rd International Conference

for Learning Representations, (pp. 1-15).

Koch, B., & Panorska, A., 2013, The Impact of

Temperature on major League Baseball. Weather,

Climate, and Society journal, 5(4), 359-366.

Kraft, M., & Skeeter, B., 1995, The effect of meteorological

conditions on fly ball distances in north American

Major League Baseball games. Geogr. Bull, 37, 40-48.

Larose, D., & Larose, C., 2014, Discovering Knowledge in

Data: An Introduction to Data Mining (2 ed.). John

Wiley & Sons, Inc.

Larose, D., 2005, Discovering Knowledge in Data: An

Introduction to Data Mining. John Wiley & Sons, Inc.

Mann, R., 2018, The Marriage of Sports Betting, Analytics

and Novice Bettors.

Mei, S., Montanari, A., & Nguyen, P., 2018, A Mean View

of the Landscape of Two-Layers Neural Networks. 1-

103.

MLB., 2018, Glossary / Statcast. Retrieved from MLB:

http://m.mlb.com/glossary/statcast

Mordor Intelligence, 2018, 2018 Sports Analytics Market -

Segmented by End User (Team, Individual), Solution

(Social Media Analysis, Business Analysis, Player

Fitness Analysis), and Region - Growth, Trends and

Forecast (2018 - 2023).

Ockerman, S., & Nabity, M., 2014, Predicting the Cy

Young Award Winner. PURE Insights, 3(1), 9.

Scikit-Learn, 2018a, Stochastic Gradient Descent.

Retrieved from: https://scikit-learn.org/stable/modules/

sgd.html#classification0

Scikit-Learn, 2018b, Grid Search CV. Retrieved from:

https://scikitlearn.org/stable/modules/generated/sklear

n.model_selection.GridSearchCV.html#sklearn.model

_selection.GridSearchCV

Stekler, H., Sendor, D., & Verlander, R., 2010, Issues in

sports forecasting. International Journal of

Forecasting, 26(3), 606-621.

Valero, C., 2016, Predicting Win-Loss outcomes in MLB

regular season games – A comparative study using data

mining methods. International Journal of Computer

Science in Sport, 15(2), 91-112.

Witten, I., Frank, E., & Hall, M., 2011, Data Mining:

Practical Machine Learning Tools and Techniques (2

ed.). Morgan Kaufmanne, Inc.

Wolf, G., 2015, The Sabermetric Revolution: Assessing the

Growth of Analytics in Baseball by Benjamin Baumer

and Andrew Zimbalist (review). Journal of Sport

History, 42(2), 239-241.

Zhang, G., Patuwo, B., & Hu, M., 1997, Forecasting with

artificial Neural Networks: The state of state of the art.

International Journal of Forecasting, 14, 35-62.

Sports Analytics: Maximizing Precision in Predicting MLB Base Hits

201