
Exact and Approximate Rule Extraction from Neural Networks with
Boolean Features
Fawaz A. Mereani
1,2 a
and Jacob M. Howe
1 b
1
City, University of London, London, U.K.
2
Umm AL-Qura University, Makkah, Saudi Arabia
Keywords:
Neural Networks, XSS, Rule Extraction, Explainable AI.
Abstract:
Rule extraction from classifiers treated as black boxes is an important topic in explainable artificial intelligence
(XAI). It is concerned with finding rules that describe classifiers and that are understandable to humans, having
the form of (I f ...T hen...Else). Neural network classifiers are one type of classifier where it is difficult to know
how the inputs map to the decision. This paper presents a technique to extract rules from a neural network
where the feature space is Boolean, without looking at the inner structure of the network. For such a network
with a small feature space, a Boolean function describing it can be directly calculated, whilst for a network with
a larger feature space, a sampling method is described to produce rule-based approximations to the behaviour
of the network with varying granularity, leading to XAI. The technique is experimentally assessed on a dataset
of cross-site scripting (XSS) attacks, and proves to give very high accuracy and precision, comparable to that
given by the neural network being approximated.
1 INTRODUCTION
Artificial intelligence and machine learning, and in
particular neural networks, can produce models that
give high predictive accuracy, leading to excellent
performance in complex tasks such as detecting ob-
jects in the images (He et al., 2016), or understanding
natural language (Cho et al., 2014). The model re-
sulting from a trained neural network is essentially
a black box: the way in which the neural network
reaches a decision from the input data is not ac-
companied by an explanation that can be interpreted
by a user. There is growing interest in being able
to explain the decision making resulting from ma-
chine learning models. That might be by opening up
black box models (Baehrens et al., 2010; Bach et al.,
2015), by developing methods that help to understand
what the model has learned (Mahendran and Vedaldi,
2015; Nguyen et al., 2016), or (as will be done in
the current work) by extracting rules from the net-
works. The term Explainable Artificial Intelligence
(XAI) captures the problem of making artificial intel-
ligence systems understandable to humans (Gunning,
2016). XAI aims to ”produce more explainable mod-
a
https://orcid.org/0000-0003-2832-304X
b
https://orcid.org/0000-0001-8013-6941
els, while maintaining a high level of learning per-
formance (prediction accuracy); and enable human
users to understand, appropriately, trust, and effec-
tively manage the emerging generation of artificially
intelligent partners” (Gunning, 2016).
In previous work, a variety of machine learning
techniques were used to detect JavaScript based cross-
site scripting (XSS) attacks (Mereani and Howe,
2018a; Mereani and Howe, 2018b). The performance
of the resulting classifiers was evaluated and they
achieved high predictive accuracy results in the detec-
tion of XSS attacks using a large real-world data set
of malicious and benign scripts. A curious aspect of
this work is that most of the features used for training
the model are Boolean valued.
The current paper investigates rule extraction from
neural networks trained to detect XSS attacks using a
feature set building on (Mereani and Howe, 2018b).
The work starts from the observation that if the fea-
tures that a neural network is working with are all
Boolean, then the trained neural network precisely de-
fines a Boolean function. That is, for any combination
of (Boolean) inputs, the result of the classification by
the trained neural network is either malicious or be-
nign, a Boolean value. If the number of features is
small, then each possible input combination can be
evaluated, resulting in the enumeration of the truth ta-
424
Mereani, F. and Howe, J.
Exact and Approximate Rule Extraction from Neural Networks with Boolean Features.
DOI: 10.5220/0008362904240433
In Proceedings of the 11th International Joint Conference on Computational Intelligence (IJCCI 2019), pages 424-433
ISBN: 978-989-758-384-1
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

ble for the Boolean function that the neural network
represents. As the number of features increases, the
size of the truth table quickly becomes infeasible to
produce and reduce (in (Mereani and Howe, 2018b),
62 features were used). Hence for neural networks
defined over larger features spaces approximations of
the encoded neural network are considered and a sam-
pling based approach is taken. This approach to rule
extraction treats the neural network as a black box,
and the extracted Boolean function results in a deci-
sion making method that is more explainable to hu-
mans (Gunning, 2016). The approach extends to any
other problem with a Boolean feature set. The contri-
butions of this paper as follows:
• Re-engineering of the features required to use
machine learning techniques to detect JavaScript
based XSS attacks, by reducing and ranking the
features in (Mereani and Howe, 2018b)
• The observation that this feature set is entirely
Boolean, hence a trained classified defines a
Boolean function
• A technique to approximate this Boolean function
when the feature set is large is provided
• An empirical evaluation of rule extraction from,
and approximation of, neural networks for XSS
detection is given.
The rest of this paper is organised as follows: Sec-
tion 2 gives background and related work on methods
for extracting rules and the detection of XSS attacks
in scripts. Section 3 describes the dataset used, in-
cluding how features are selected and ranked, how
neural networks are trained and evaluated using this
data set, and the method used for constructing and
approximating Boolean functions. Section 4 presents
results related to the application of the rule extraction,
and Section 5 discusses the results. Further discussion
and concluding remarks are given in Section 6.
2 BACKGROUND AND RELATED
WORK
2.1 Rule Extraction
Many applications need to build an accurate and
easy to understand classifier by using traditional tech-
niques. These requirements (accuracy, ease) always
work in a paradoxical manner, as (Breiman et al.,
2001) has stated, “Unfortunately, in prediction, ac-
curacy and simplicity (interpretability) are in con-
flict.” Therefore, the extraction of rules is a middle
method between the two requirements by implement-
ing a simple set of rules based on (I f ...T hen...Else)
to simulate the work of the predictions of the model.
Extraction of rules aims to find rules that can be un-
derstood in terms of how the classification models
work. Furthermore, rule extraction techniques pro-
pose to explain the predictive rules that are made in-
side the black box without modification (Craven and
Shavlik, 1996; Martens et al., 2009; Baesens et al.,
2011). Extracted rules are important in the field of
data mining, where they have been described as an
important process to identify useful patterns that can
be understood (Fayyad et al., 1996).
Algorithms for extracting rules from neural net-
works are divided into three main types. The first type
is called the black box or pedagogical, the second is
decompositional, and the third is eclectic. Pedagog-
ical is not interested in the internal structure of the
network, but is interested in extracting the relation-
ship between inputs and outputs without the need to
scrutinise the behaviour of the internal network (Taha
and Ghosh, 1996; Tsukimoto, 2000). An example
of using a pedagogical method is found in (Saito and
Nakano, 1988), where the rules were extracted from a
multilayer medical diagnostic system by monitoring
the effect of network outputs when changing inputs.
Furthermore, the VIA method (Thrun, 1993) is an-
other example which uses a generate and test proce-
dure to extract the rules from neural networks trained
by backpropagation. This method is characterised by
performing the output of the network through the sys-
tematic variation of the pattern of input. Decompo-
sitional is the extraction of the rule directly from the
layers in the network with the customisation of the
linguistic meaning of the layers. The rules are ex-
tracted by analysing activation, outputs of hidden lay-
ers, and the weights that are related to them (Etchells
and Lisboa, 2006). In (Setiono and Liu, 1995) a three
step algorithm to understand neural networks is pro-
posed. The first step is to decrease the weight by
creating a backpropagation network to reflect the im-
portant connections on its larger weights. Second, to
trim the network by deleting irrelevant connections
while maintaining predictive accuracy. In the third
step, the rule is extracted by estimating the values of
the hidden unit activation. In (Setiono and Liu, 1997)
the decompositional technique NeuroLinear is capa-
ble of extracting rules from the oblique classification
of the neural networks with one hidden layer. Eclec-
tic method is the combination of the previous two
methods. An example of this method is (Keedwell
et al., 2000) in which they suggest a method to dis-
cover trends in large datasets using a neural network
as a black box to discover knowledge, but at the same
Exact and Approximate Rule Extraction from Neural Networks with Boolean Features
425

time examines the weights by pruning and clustering
the activation values of the hidden units. Control pa-
rameters have been used to analyse the data for con-
trolling the probability of occurrence and the accuracy
of the rules.
Extracting rules using a decompositional ap-
proach is complex and large, where the time and
computation are the most important constraints of
the method. The pedagogical approach is potentially
faster because it does not analyse the weights or in-
ternal structure of the neural network, but the most
important disadvantage is that it is less likely to find
all the correct rules that describe the behaviour of the
neural network. The eclectic approach is slower but
more precise because it combines the two approaches
(Augasta and Kathirvalavakumar, 2012).
One of the most common methods to extract rules
from non-rule based classifiers is to produce decision
trees, corresponding to rules of the form of i f ...then.
The tree is the model, the leaves are classes, and the
branches represent the sequence of features that lead
to that class (Ardiansyah et al., 2016). The deci-
sion tree family of classifiers can capture rules that
can be represented using several forms that can be
understood by humans as explained in (Bondarenko
et al., 2017). If-Then / If-Then-Else rules contain an
“i f ” condition, potentially over a number of logical
operands such as conjunction, disjunction, and nega-
tion, followed by a “then” that indicates a class. An
example of an “i f ...then...else” rule is: i f (a
11
< x
1
<
a
12
) and (a
21
< x
2
< a
22
) then ClassA else ClassB.
M-of-N rules make a decision for only one class for
which M rules must be covered from a full set of
N rules, and these rules can be more compact than
“i f ...then” rule sets. Oblique rules / multi-surface
method tree have rules which separate a space by us-
ing planes, and this allows a data point to be cat-
egorised as belonging to a specific class. Equation
rules are similar to oblique rules, but using non-linear
equations to separate spaces. Fuzzy rules are sim-
ilar to “i f ...then” rules, but dealing with fuzzy sets
and an underlying many-value fuzzy logic. Here, the
black box, pedagogical approach with Boolean func-
tions acting the role of the decision tree rules is taken.
2.2 Minimising Boolean Expression
It is often useful to find a compact representation
for a Boolean function. A minimal representation of
a Boolean expression is simpler to understand and
write, as well as less prone to error in interpreta-
tion. Importantly, a minimal representation can be
more effective and efficient when implemented in ex-
periments (Rudell, 1986). Therefore, minimising a
Boolean expression to find a representation equiva-
lent to the original expression but of a minimum size,
is considered here.
Minimisation can be done in several ways depend-
ing on the number of variables. There are several
common methods used to minimise expressions. Kar-
naugh Maps (Karnaugh, 1953) are a graphical way
to minimising a Boolean expression. Taking a truth
table of the expression as a matrix, then eliminat-
ing all the complementary pairs, results in a min-
imised Boolean expression. This method is effective
for small number of variables, but becomes more dif-
ficult for larger numbers of variables. Manipulating
expressions using the rules and theories of Boolean
algebra might also be used, but again these methods
do not scale well. The Tabular (or Quine-McCluskey)
Method is a more efficient method of calculating Kar-
naugh Maps and can be practical when minimising
expressions that contain larger numbers of variables
(Manojlovic, 2013). Reduced Ordered Binary Deci-
sion Diagrams (ROBDDs) (Bryant, 1992) place an
order on the variables of a Boolean function, and
then represent this function as a graph structure, giv-
ing a canonical, non-redundant representation of the
Boolean function, given the variable ordering. The
Tabular Method will be used in this approach.
2.3 Cross-Site Scripting
Cross-Site Scripting (XSS) is a type of attack target-
ing web applications, ranked by OWASP as one of
the top 10 attacks (OWASP, 2017). XSS is standardly
prevented from being executed through good coding
practice, using sanitization and escaping to prevent
untrusted content being interpreted as code (Wein-
berger et al., 2011). Parser-level isolation provides an
alternative, confining user input data during the life-
time of the application (Nadji et al., 2009). Black-
lists are viewed as easy to circumvent and these ap-
proaches are preferred (Weinberger et al., 2011).
Machine learning techniques have been applied
to prevent XSS attacks. An early approach (Likar-
ish et al., 2009) evaluates ADTree, SVM, Naive
Bayes, and RIPPER classifiers by tracking the sym-
bols that appear in malicious and benign scripts, and
achieved precision of up to 92%. Another approach,
(Wang et al., 2013), extracts features used in ma-
licious scripts much more than benign, such as the
DOM-modifying functions and the eval function; this
method achieved accuracy rate of up to 94.38%. Fur-
thermore, in (Mereani and Howe, 2018a) a number
classifiers were evaluated: SVM with linear and poly-
nomial kernels, k-NN and Random Forest. Using a
k-NN classifier achieved high accuracy results up to
NCTA 2019 - 11th International Conference on Neural Computation Theory and Applications
426
99.75%, with precision rate up to 99.88%. Here the
extracted features depend on the occurrence or not
of a syntactic element within a script. A neural net-
work classifier was evaluated in (Mereani and Howe,
2018b) to prevent XSS attacks by using ensemble and
cascading techniques and the results gave a very high
accuracy of up to 99.80% in the base level which their
feature groups used directly, and 99.89% at the meta
level where the features are the outputs of base level.
As well as in scripting, there is emerging interest
in using neural networks to detect malware in exe-
cutables, for instance, in (Rhode et al., 2017) a recur-
rent neural network is used to detect malicious exe-
cutables at execution time with 93% accuracy.
3 METHODOLOGY
This section describes the dataset used in the exper-
iments, the approach to selecting features to build
analyses with, and the training of neural networks.
The aim of this work is to find Boolean functions as
rules extracted from the neural networks, which can
be used as classifiers. The approach to extracting a
Boolean function from a neural network is given, both
for exact rule extraction, and for a series of approxi-
mations to a network.
3.1 Datasets
The current work uses the dataset from (Mereani and
Howe, 2018b), with the training set augmented with
addition files from CSIC 2010 (Gim
´
enez et al., 2010)
(with 152 malicious instances and 3971 benign in-
stances). The purpose of increasing the dataset is to
cover more types of scripts to extract more precise
rules. The classifiers are to determine whether or not
text entered into a web application represents a cross-
site script. Hence the dataset consists of 43,218 files,
of which 28,068 labelled as benign and 15,150 la-
belled as malicious. Note that 9,068 of the benign
scripts are plain text from (Wang et al., 2011). These
are then divided into a training set of 19,122 instances
(5,150 malicious and 13,972 benign) and a testing set
of 24,096 instances (10,000 malicious and 14,096 be-
nign), with no overlap between the training and test-
ing datasets.
3.2 Selected Features
The starting point of this work is to abstract the in-
put into the same 62 features as used in (Mereani and
Howe, 2018b). These are divided into two groups,
alphanumeric and non-alphanumeric features. Rather
than working with these features immediately without
further reflection as in (Mereani and Howe, 2018b),
here the features have been ranked by using Algo-
rithm 1 (MathWorks, 2019). The method selects the
most powerful features in a sequential feature selec-
tion. This method works by minimising over all fea-
ture subsets, which uses the deviance and chi-square
to find the most powerful features. The deviance is
twice the difference between the log likelihood of
that model and the saturated model, and the inverse
of the chi-square with degrees of freedom is used to
set the termination tolerance parameter. The applica-
tion of the ranking algorithm on the feature set shows
that only 34 features need be used, and the ranking
of these selected features in order of effectiveness is
given in Table 1. The key observation of these fea-
tures is that they are all Boolean valued, allowing the
exploitation of this additional 0/1 valued structure.
Algorithm 1: Ranking Features Algorithm.
Input: Original features set;
Start with empty features subset;
Feature = Sequential Feature Selection;
while (Deviance > Chi-Square) do
Feature Subset = Add feature to selected
feature subset;
Feature = Sequential Feature Selection;
end
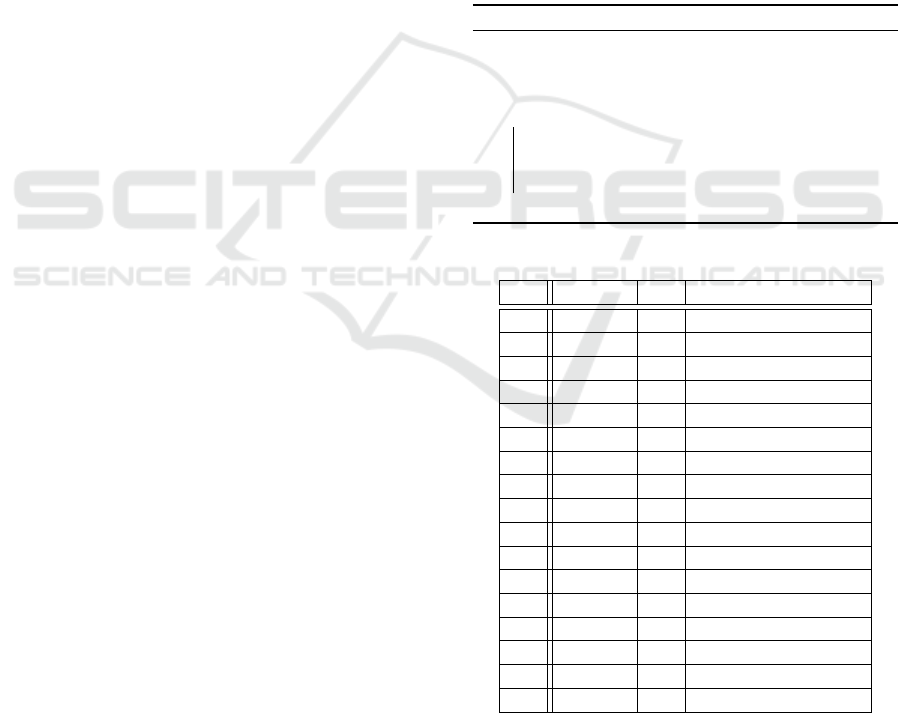
Table 1: Selected Features.
No. Features No. Features
1 Alert 18 %
2 < 19 (<)
3 { 20 @
4 ? 21 Onload
5 ! 22 StringfromCharCode
6 JS File 23 :
7 HTTP 24 \
8 - 25 ]
9 ’ 26 (
10 ; 27 ‘
11 & 28 Img
12 , 29
0
>
13 Src 30 ==
14 Space 31 /
15 &# 32 Onerror
16 Eval 33 //
17 . 34 iframe
3.3 Classifier Optimisation
Feed forward neural network classifiers were built us-
ing the features from Table 1. The classifiers were
Exact and Approximate Rule Extraction from Neural Networks with Boolean Features
427

built using a single hidden layer, and the number of
neurons (units) within the network is set to be 10
hidden units. The train function updates the weight
and bias values and was optimised by setting it to be
”trainbr,” which is used to minimise a combination
of squared errors and weights. Two neural networks
were built: one using all 34 features, which is viewed
as the best network, the one from which rules are to
be extracted, and the other using the top 16 features,
which will be used for comparison, evaluation and
discussion.
3.4 Neural Networks and Boolean
Functions
Observe that a neural network each of whose input
features is Boolean, and whose output is a Boolean
value, is precisely equivalent to a Boolean function.
Enumerating each possible input, and calculating the
corresponding output results in the truth table for this
Boolean function. Hence, the neural network can be
replaced by this Boolean function, resulting in a rule
based system, each of whose decisions is explainable
and auditable. In the current study, the feature set is
Boolean, therefore this approach applies. However,
whilst for a low number of features this rule extrac-
tion technique might be applied directly, the number
of potential inputs grows exponentially, and the prob-
lem quickly becomes infeasible.
3.5 Sampling
The key neural network in this work is the one trained
over a feature space with 34 features. This provides
an exemplar case for where the Boolean function de-
fined is too large to generate from the network. De-
spite this, there is motivation to find a Boolean func-
tion that can be used in place of the neural network.
The approach taken is to sample the neural network
and use this sample to build a Boolean function; this
Boolean function then provides an approximation of
the original function. The idea is to fix a number of
features for which producing Boolean function via a
truth table is feasible and to determine what value the
function should take by interrogating the neural net-
work with the full feature set. For example, suppose
it is determined that considering 4 features will result
in a truth table that can be feasibly constructed. Then
the four highest ranking features (in Table 1) will pro-
vide the entries for the truth table. For a row of the
truth table, the values of these features is fixed, and
then extended with values for the remaining 30 fea-
tures to give an input to the neural network, which is
then queried and the result noted. This is done re-
peatedly and from the resulting sample the most fre-
quently occurring result is the entry in the truth table.
Whilst the training dataset is relatively large, with
19,112 scripts, this is still very small compared to the
2
34
possible inputs to the neural network. This means
that whilst the neural network learns from its training
set, the generalisation is not necessarily great enough
that every input to the neural network is equally mean-
ingful. That is, a random sampling extending the fixed
values might not give a good results, since it might
not match the shape of likely inputs. Indeed, this was
observed in development, with inputs holding the de-
fault value dominating. In order to counteract this,
the extensions were generated from the training set,
with a random selection of instances from the train-
ing set being selected (with the full 34 features), and
these being used for sampling the neural network with
the fixed features replacing the corresponding feature
values.
Algorithm 2 specifies the sampling method. Here,
the input to the algorithm is L (an integer) the number
of fixed features, NN a trained neural network (in this
case with 34 features) and Sample a random selection
from the training set of inputs to the neural network
(in this work consisting of 1024 inputs). A truth ta-
ble, TT, for the fixed features, with undefined output
values, is constructed by buildInitTruthTable. Each
row of this truth table is considered in turn. The val-
ues of the row of TT are substituted into each element
of Sample leading to an input which is passed to the
neural network NN for classification. If the result is
classification as malicious the a counter for malicious
instances, malicious count is incremented, otherwise,
benign count is incremented. Once each element of
Sample has been considered, a comparison between
the two counts is made, and the output column of the
truth table TT is populated with 0 if most instances are
malicious, and 1 otherwise.
This work investigates successive approximations,
with a varying number of fixed features: 1, 2, 4, 8, 10,
12 and 16 features. In order to sample the 34 feature
neural network, 1024 cases from training dataset were
used as the basis for the samples. As described above,
the entry for each row of truth table is simply the most
common verdict returned by the neural network being
approximated.
3.6 Extracting Rules
After labelling all rows in the truth table, each row can
be considered to be a rule that describes one class. To
give a more succinct set of rules, the Boolean func-
tion can be minimised (Schwender, 2007) resulting in
simplified expressions. The minimised Boolean func-
NCTA 2019 - 11th International Conference on Neural Computation Theory and Applications
428

Algorithm 2: Sampling Method Algorithm.
Input: L ∈ N, NN, Sample;
TT = buildInitTruthTable(L);
for row in TT do
malicious count = 0;
benign count = 0;
for s in Sample do
input = substitute(row, s);
result = NN(input) ;
if result == malicious then
malicious count ++;
else
benign count ++;
end
end
if malicious count > benign count then
TT[row] = 0 ; \\Malicious
else
TT[row] = 1 ; \\Benign
end
end
tions are then evaluated as classifiers. For minimising
Boolean functions “Logic Friday” (Rickmann, 2012)
has been used which uses the Tabular Method as a
minimisation algorithm.
4 RESULTS
In the experiments, MatLab 2018b was used to build
the neural networks, and to find the truth tables based
on these neural networks. This was done using vari-
ous numbers of fixed features: 1, 2, 4, 8, 10, 12, and
16. The extracted truth tables defined a set of rules
acting as a classifier approximating the original neu-
ral network, and these rule sets were then reduced to
a more compact representation using “Logic Friday”
(Rickmann, 2012).
4.1 Neural Networks
Table 2 gives the performance of the neural network
classifier, which was trained using the full 34 features,
and tested using the testing dataset. Evaluation uses
the confusion matrix, along with Accuracy, Precision,
Sensitivity, and Specificity measures. This network is
the one from which rules are extracted, giving a series
of approximations.
For later comparison purposes, Table 3 repeats
this evaluation, but this time showing the performance
of a neural network classifier created using just the
16 highest ranked features. For this network, the
Boolean function that the network defines can be pre-
cisely extracted and Table 4 shows the number of the
rules that result from constructing the truth table for
the 16 features, along with the number of rules that
classify scripts as benign after minimisation is applied
(hence any script whose features do not match a rule
for benign is malicious).
Table 2: Neural Network Classifier Performance Using 34
Features.
Accuracy 99.88 Confusion Matrix
Precision 99.98 M B
Sensitivity 99.75 M 9998 8
Specificity 99.98 B 25 14071
Table 3: Neural Network Classifier Performance Using 16
Features.
Accuracy 99.78 Confusion Matrix
Precision 99.94 M B
Sensitivity 99.53 M 9994 6
Specificity 99.95 B 47 14049
Table 4: Classifier Labelling Using 16 Feature.
Features Malicious Benign Minimised
Classifer 41,549 23,987 2,560
4.2 Rule Extraction
The rules were extracted from the neural network
trained on 34 features by applying the sampling
method for each row in the truth table, hence the num-
ber of extracted rules is equal to (2
Features
), where
each row describes one rule. This process was re-
peated for 1, 2, 4, 8, 10, 12, and 16 features. Each of
these gives an approximation to the neural network,
and the purpose of this repetition is to observe the
number of rules that are extracted and the accuracy
of the results on the testing dataset.
Tables 5,..., 11 give the results of testing the rules
extracted from the 34 feature neural network, ap-
proximating with 1, 2, 4, 8, 10, 12 and 16 features.
Again, the evaluation is given in terms of the confu-
sion matrix, and the Accuracy, Precision, Sensitivity
and Specificity measures.
Table 5: Results of Using 1 Feature.
Accuracy 91.96 Confusion Matrix
Precision 80.70 M B
Sensitivity 99.92 M 8070 1930
Specificity 87.95 B 6 14090
Table 12 summarises the number of rules for each
class by using the various numbers of selected fea-
Exact and Approximate Rule Extraction from Neural Networks with Boolean Features
429

Table 6: Results of Using 2 Features.
Accuracy 91.96 Confusion Matrix
Precision 80.70 M B
Sensitivity 99.92 M 8070 1930
Specificity 87.95 B 6 14090
Table 7: Results of Using 4 Features.
Accuracy 98.95 Confusion Matrix
Precision 97.54 M B
Sensitivity 99.92 M 9754 246
Specificity 98.28 B 7 14089
Table 8: Results of Using 8 Features.
Accuracy 98.13 Confusion Matrix
Precision 95.62 M B
Sensitivity 99.87 M 9562 438
Specificity 96.98 B 12 14084
Table 9: Results of Using 10 Features.
Accuracy 99.15 Confusion Matrix
Precision 98.00 M B
Sensitivity 99.96 M 9800 200
Specificity 98.60 B 3 14093
Table 10: Results of Using 12 Features.
Accuracy 99.82 Confusion Matrix
Precision 99.62 M B
Sensitivity 99.96 M 9962 38
Specificity 99.73 B 3 14093
Table 11: Results of Using 16 Features.
Accuracy 99.90 Confusion Matrix
Precision 99.94 M B
Sensitivity 99.82 M 9994 6
Specificity 99.95 B 18 14078
tures. The final column gives the number rules that
classify the input as benign after minimisation (hence,
any input not matching one of these rules is classified
as malicious).
4.3 Timing
The number of extracted rules grows exponentially
with the number of features used for approximation.
Therefore, it is important to take into account the time
taken by the proposed method. Table 13 gives the
time taken for each approximation, including the ex-
traction of the rules, and their minimisation.
Table 12: Number of Rules for Selected Features.
Features Malicious Benign Minimised
1 Feature 1 1 1
2 Features 2 2 1
4 Features 7 9 3
8 Features 100 156 29
10 Features 384 640 62
12 Features 1,560 2,536 229
16 Features 39,792 25,744 2,488
Table 13: Timing of Rule Extraction from the Classifier.
Features Interval
1 Feature 18 sec
2 Features 37 sec
4 Features 120 sec
8 Features 390 sec
10 Features 7,846 sec
12 Features 30,598 sec
16 Features 482,618 sec
5 DISCUSSION
The key result in this paper is that presented in Ta-
ble 11. This table gives the evaluation of a Boolean
function over 16 variables/features as a rule-based
classifier, where the Boolean function has been ex-
tracted from the neural network over 34 features eval-
uated in Table 2. The performance of this rule-based
classifier matches (in fact, slightly betters) that of the
neural network that it is modelling, with 99.90% ac-
curacy and 99.94% precision, demonstrating that rule
extraction has been successfully accomplished. For
comparison, a neural network was training using the
same 16 features, with the results presented in Ta-
ble 3, and again the extracted rule-based Boolean
function classifier in Table 11 performs slightly bet-
ter than this neural network.
A series of approximations have been built and
evaluated in Tables 5,.., 11, using an increasing num-
ber of features. The number of rules both before and
after minimisation is given in Table 12. As might
be expected, as the number of features increases, the
number of rules (after minimisation) increases too,
and the performance of the resulting classifiers im-
proves. The improvements are not necessarily mono-
tonic, but the pattern is clear. The improvements
come at some cost – as can be seen in Table 13, with
the current approach to implementation, the time to
build the Boolean functions increases exponentially,
with the best approximation using 16 features tak-
ing more than five days of computation. If compar-
ing against the Boolean function extracted from the
NCTA 2019 - 11th International Conference on Neural Computation Theory and Applications
430

16 feature neural network, the number of minimised
rules is comparable, but it should be noted that it is
much faster to extract the rules from the small net-
work, since sampling is not required (and also note
that the resulting rules are a precise description of the
neural network).
One motivation for this investigation is to extract
rule-based systems, where some level of explainable
AI is produced. That is, for any classification, the rea-
soning can be described, allowing decision making to
be auditable. The approximations given in this work
give such auditable decisions. The successive approx-
imations show that relatively good performance can
be achieved with the use of only a small number of
features. That the sampling approach gives approx-
imations with some degree of noise is illustrated by
the anomalous 8 feature case, where the introduc-
tion of feature 7, URL addresses, leads to some ad-
ditional misclassifications, compared to the courser 4
feature classifier. It should also be noted that the very
course 1 feature classifier still gives useful result, with
80.70% precision. The reason for this result is that the
highest ranking feature is the use of ”Alert” within
the script and that a high proportion of attacks in the
database use this, whilst it is rarely used in benign
scripts. This first feature is very powerful. This obser-
vation (whilst not surprising to the authors) is a good
illustration of XAI in action, where the rule-based
system has made the explanation explicit. However,
it should be noted that the best approximation still re-
quires thousands of rules even after minimisation, and
whilst this makes decision making auditable, it is less
clear that each individual decision can be interpreted
by a human user, in the context of the larger number
of rules.
As noted in the methodology, the current approach
requires a double use of the training set, firstly to train
the neural network, and secondly to guide the sam-
pling approach used in the approximation of the neu-
ral network by a Boolean function. However, given
the size of the Boolean function described by the
trained neural network, some kind of guidance seems
inevitable in a black box approach to approximation.
The black box approach has worked, resulting in suc-
cessfully extracting rules in form of (i f ...then...else)
in order to distinguish malicious and benign scripts
without delving deeper into the inner structure of the
neural network classifier.
6 CONCLUSION
This paper demonstrates the ability to perform rule
extraction from a neural network classifier, where the
feature space is Boolean, the result being a Boolean
function initially described by a truth table, then min-
imised to a more compact representation. Differ-
ent levels of approximation were investigated. The
rules extracted provide good results in classification
of scripts as malicious or benign, with testing demon-
strating up to 99.94% accuracy and precision rate up
to 99.90% using a 16 feature approximation of the 34
feature neural network. These results are as good as
those for the initial neural network, though the current
implementation takes a long time to compute the ap-
proximation (a single expensive rule extraction is not
in itself problematic, however it limits the scalability
of the approach, and means that it cannot be used for
rapid updates of the rules). The number of rules ex-
tracted grows with the number of features used in the
approximation. As discussed in Section 5, this means
that these rules are auditable – it is easy to look up
the reasoning for any given classification – whilst it
remains to be investigated whether a human user of
the rule set views thousand of rules (each easily inter-
preted by itself) as being humanly intelligible.
It is possible to use the proposed black box
method of extracting rules from the classifiers for
other kinds of classification, and for other problems
where the features are Boolean. Future work is to in-
vestigate this, as well as how this approach might be
generalised to features which are not Boolean valued,
by piecewise approximation, or otherwise. Further re-
ductions of the rules (perhaps using BDDs), in par-
ticularly further approximation to give more compact
rules sets will also be explored.
In conclusion, a process following XAI principles
of giving an interpretation of a black box classifier in
a form of rules that are understandable to humans has
be shown to lead to a successful rule based outcome.
REFERENCES
Ardiansyah, S., Majid, M. A., and Zain, J. M. (2016).
Knowledge of extraction from trained neural network
by using decision tree. In 2016 2nd International Con-
ference on Science in Information Technology (IC-
SITech), pages 220–225. IEEE.
Augasta, M. G. and Kathirvalavakumar, T. (2012). Rule ex-
traction from neural networks—a comparative study.
In International Conference on Pattern Recognition,
Informatics and Medical Engineering (PRIME-2012),
pages 404–408. IEEE.
Bach, S., Binder, A., Montavon, G., Klauschen, F., M
¨
uller,
K.-R., and Samek, W. (2015). On Pixel-Wise Ex-
planations for Non-Linear Classifier Decisions by
Layer-Wise Relevance Propagation. PLoS ONE,
10(7):e0130140.
Exact and Approximate Rule Extraction from Neural Networks with Boolean Features
431

Baehrens, D., Schroeter, T., Harmeling, S., Kawanabe, M.,
Hansen, K., and M
¨
uller, K.-R. (2010). How to Ex-
plain Individual Classification Decisions. Journal of
Machine Learning Research, 11:1803–1831.
Baesens, B., Martens, D., Setiono, R., and Zurada, J. M.
(2011). Guest Editorial White Box Nonlinear Predic-
tion Models. IEEE Transactions on Neural Networks,
22(12):2406–2408.
Bondarenko, A., Aleksejeva, L., Jumutc, V., and Borisov, A.
(2017). Classification Tree Extraction from Trained
Artificial Neural Networks. Procedia Computer Sci-
ence, 104:556–563.
Breiman, L. et al. (2001). Statistical modeling: The two cul-
tures (with comments and a rejoinder by the author).
Statistical Science, 16(3):199–231.
Bryant, R. E. (1992). Symbolic Boolean Manipulation with
Ordered Binary Decision Diagrams. ACM Computing
Surveys, 24:293–318.
Cho, K., Van Merri
¨
enboer, B., Gulcehre, C., Bahdanau,
D., Bougares, F., Schwenk, H., and Bengio, Y.
(2014). Learning Phrase Representations using RNN
Encoder-Decoder for Statistical Machine Translation.
In Empirical Methods in Natural Language Process-
ing, page 1724–1734. Association for Computational
Linguistics.
Craven, M. W. and Shavlik, J. W. (1996). Extracting tree-
structured tepresentations of trained networks. In
Advances in Neural Information Processing Systems,
pages 24–30. MIT Press.
Etchells, T. A. and Lisboa, P. J. (2006). Orthogonal search-
based rule extraction (OSRE) for trained neural net-
works: a practical and efficient approach. IEEE trans-
actions on Neural Networks, 17(2):374–384.
Fayyad, U., Piatetsky-Shapiro, G., and Smyth, P.
(1996). From data mining to knowledge discovery in
databases. AI magazine, 17(3):37–37.
Gim
´
enez, C. T., Villegas, A. P., and Mara
˜
n
´
on, G.
´
A. (2010).
HTTP data set CSIC 2010. Information Security In-
stitute of CSIC (Spanish Research National Council).
Gunning, D. (2016). Explainable Artificial Intelligence
(XAI). Technical Report DARPA/I20, Defense Ad-
vanced Research Projects Agency.
He, K., Zhang, X., Ren, S., and Sun, J. (2016). Deep resid-
ual learning for image recognition. In Computer Vi-
sion and Pattern Recognition, pages 770–778. IEEE.
Karnaugh, M. (1953). The map method for synthesis
of combinational logic circuits. Transactions of the
American Institute of Electrical Engineers, Part I:
Communication and Electronics, 72:593–599.
Keedwell, E., Narayanan, A., and Savic, D. (2000). Creat-
ing rules from trained neural networks using genetic
algorithms. Internation Journal of Computers, System
and Signal, 1(1):30–42.
Likarish, P., Jung, E., and Jo, I. (2009). Obfuscated ma-
licious Javascript detection using classification tech-
niques. In Malicious and Unwanted Software (MAL-
WARE), pages 47–54. IEEE.
Mahendran, A. and Vedaldi, A. (2015). Understand-
ing Deep Image Representations by Inverting Them.
In Computer Vision and Pattern Recognition, pages
5188–5196. IEEE.
Manojlovic, V. (2013). Minimization of Switching Func-
tions using Quine-McCluskey Method. International
Journal of Computer Applications, 82(4):12–16.
Martens, D., Baesens, B., and Van Gestel, T. (2009). De-
compositional rule extraction from support vector ma-
chines by active learning. IEEE Transactions on
Knowledge and Data Engineering, 21(2):178–191.
MathWorks (2019). Feature selection. https://uk.
mathworks.com/help/stats/feature-selection.html.
Accessed: 11/3/2019.
Mereani, F. A. and Howe, J. M. (2018a). Detecting Cross-
Site Scripting Attacks Using Machine Learning. In
International Conference on Advanced Technologies
and Applications Intelligent Systems and Computing,
pages 200–210. Springer.
Mereani, F. A. and Howe, J. M. (2018b). Preventing Cross-
Site Scripting Attacks by Combining Classifiers. In
Proceedings of the 10th International Joint Confer-
ence on Computational Intelligence - Volume 1, pages
135–143. SciTePress.
Nadji, Y., Saxena, P., and Song, D. (2009). Document Struc-
ture Integrity: A Robust Basis for Cross-site Scripting
Defense. In Network and Distributed System Security
Symposium. Internet Society.
Nguyen, A., Yosinski, J., and Clune, J. (2016). Multi-
faceted Feature Visualization: Uncovering the Dif-
ferent Types of Features Learned by Each Neu-
ron in Deep Neural Networks. arXiv preprint
arXiv:1602.03616.
OWASP (2017). OWASP Top 10 - 2017 rc1.
https://www.owasp.org. Accessed: 7/6/2017.
Rhode, M., Burnap, P., and Jones, K. (2017). Early
Stage Malware Prediction Using Recurrent Neural
Networks. Computers and Security, 77:578–594.
Rickmann, S. (2012). Logic Friday (version 1.1.4)[com-
puter software]. https://web.archive.org/web/
20131022021257/http://www.sontrak.com/. Ac-
cessed: 24/11/2018.
Rudell, R. L. (1986). Multiple-valued logic minimiza-
tion for PLA synthesis. Technical Report UCB/ERL
M86/65, University of California, Berkeley.
Saito, K. and Nakano, R. (1988). Medical diagnostic ex-
pert system based on PDP model. In Proceedings of
IEEE International Conference on Neural Networks,
volume 1, pages 255–262.
Schwender, H. (2007). Minimization of Boolean Expres-
sions using Matrix Algebra. Technical report, Tech-
nical Report//Sonderforschungsbereich 475, Kom-
plexit
¨
atsreduktion in Multivariaten Datenstrukturen,
Universit
¨
at Dortmund.
Setiono, R. and Liu, H. (1995). Understanding Neural Net-
works via Rule Extraction. In IJCAI, volume 1, pages
480–485.
Setiono, R. and Liu, H. (1997). NeuroLinear: From neural
networks to oblique decision rules. Neurocomputing,
17(1):1–24.
Taha, I. and Ghosh, J. (1996). Three techniques for extract-
ing rules from feedforward networks. In Intelligent
NCTA 2019 - 11th International Conference on Neural Computation Theory and Applications
432

Engineering Systems Through Artificial Neural Net-
works, pages 23–28. ASME Press.
Thrun, S. B. (1993). Extracting Provably Correct Rules
from Artificial Neural Networks. Technical report,
University of Bonn.
Tsukimoto, H. (2000). Extracting rules from trained neu-
ral networks. IEEE Transactions on Neural Networks,
11(2):377–389.
Wang, H., Lu, Y., and Zhai, C. (2011). Latent aspect rat-
ing analysis without aspect keyword supervision. In
Proceedings of the 17th ACM SIGKDD International
Conference on Knowledge Discovery and Data Min-
ing, KDD ’11, pages 618–626, New York, NY, USA.
ACM.
Wang, W.-H., Lv, Y.-J., Chen, H.-B., and Fang, Z.-L.
(2013). A Static Malicious JavaScript Detection Us-
ing SVM. In Proceedings of the International Confer-
ence on Computer Science and Electronics Engineer-
ing, volume 40, pages 21–30.
Weinberger, J., Saxena, P., Akhawe, D., Finifter, M., Shin,
R., and Song, D. (2011). A Systematic Analysis of
XSS Sanitization in Web Application Frameworks. In
European Symposium on Research in Computer Secu-
rity, volume 6879 of Lecture Notes in Computer Sci-
ence, pages 150–171. Springer.
Exact and Approximate Rule Extraction from Neural Networks with Boolean Features
433
