
CoSky: A Practical Method for Ranking Skylines in Databases
Hana Alouaoui, Lotfi Lakhal, Rosine Cicchetti and Alain Casali
Laboratoire d’Informatique et Syst
`
eme, CRNS UMR 7020, Aix Marseille Universit
´
e, France
Keywords:
Databases, IR, MCDA, Ranking, Skylines.
Abstract:
Discovering Skylines in Databases have been actively studied to effectively identify optimal tuples/objects
with respect to a set of designated preference attributes. Few approaches have been proposed for ranking
the skylines to resolve the problem of the high cardinality of the result set. The most recent approach to
rank skylines is the dp-idp (dominance power- inverse dominance power) which extensively uses the Pareto-
dominance relation to determine the score of each skyline. The dp-idp method is in the very same spirit as tf-idf
weighting scheme from Information Retrieval. In this paper, we firstly make an Enrichment of dp-idp with
Dominance Hierarchy to facilitate the determination of Skyline scores, we propose then the CoSky method
(Cosine Skylines) for fast ranking skylines in Databases without computing the Pareto-dominance relation.
Cosky is a TOPSIS-like method (Technique for Order of Preference by Similarity to Ideal Solution) resulting
from the cross-fertilization between the fields of Information Retrieval, Multiple Criteria Decision Analysis,
and Databases. The innovative features of CoSky are principally: the automatic weighting of the normalized
attributes based on Gini index, the score of each skyline using the Saltons cosine of the angle between each
skyline object and the ideal object, and its direct implementation into any RDBMS without further structures.
Finally, we propose the algorithm DeepSky, a Multilevel skyline algorithm based on CoSky method to find
Top-k ranked Skylines.
1 INTRODUCTION
Skyline computation, previously known as Pareto sets
and maximal vectors (Bentley et al., 1978), has re-
ceived a great attention in the statistical and mathe-
matical fields since many past decades. The skyline
computation is crucial to many multi-criteria deci-
sion making applications. Therefore, skyline queries
have attracted considerable attention in the context of
databases, especially with the introduction of skyline
operator by (Borzsonyi et al., 2001). These queries
are simple and expressive. They do not need user-
defined scoring functions. They only require the user
preferences concerning the minimization or the maxi-
mization of attribute values. Suppose a customer who
wishes to buy a car and he is seeking for a car with
high power, low mileage and low price. Neverthe-
less, these criteria of selecting Cars are complemen-
tary since cars of higher power and lower mileage are
more expensive. In order to find such cars, we must
query the corresponding Cars database relation (Ta-
ble 1). Let price, mileage (klm) and power be the at-
tributes of Cars, the users prefer to minimize the price
and the Mileage (klm) and maximize the power by
selecting items that are better than others regarding
Table 1: Database Relation Cars.
idcar price klm power
C
1
25 10 8
C
2
20 30 6
C
3
25 15 7
C
4
5 40 7
C
5
25 45 5
C
6
45 15 6
C
7
35 40 5
C
8
45 45 4
these three attributes.
Here is an example of a skyline query (with sky-
line operator) on the relation Cars:
SELECT ∗ FROM C a rs SKYLINE OF p r i c e MIN, klm MIN , pow er MAX;
The associated SQL query without skyline opera-
tor is:
SELECT ∗ FROM C a rs C ar1
WHERE NOT EXISTS (
SELECT ∗ FROM C a rs C ar2
WHERE (
Ca r2 . p r i c e =< Car1 . p r i c e
AND C ar 2 . klm =< Car1 . klm
508
Alouaoui, H., Lakhal, L., Cicchetti, R. and Casali, A.
CoSky: A Practical Method for Ranking Skylines in Databases.
DOI: 10.5220/0008363005080515
In Proceedings of the 11th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2019), pages 508-515
ISBN: 978-989-758-382-7
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

AND C ar 2 . po wer >= C ar 1 . po wer )
AND ( Ca r2 . p r i c e < Car1 . p r i c e
OR Car2 . klm < Car1 . klm
OR Car2 . power > C ar1 . power ) ) ;
As a result, a set of good cars is returned (C
1
, C
2
,
C
4
). Good cars in our case is the set of cars which
are as good or better in all dimensions (price, klm and
power) and better in at least one dimension. This set
of good points (cars) forms the Skylines. The Pareto-
dominance specifies which data points belong to the
skyline and it can be formalized as follows:
Let r be a relational table, with A
1
, . . . , A
m
at-
tributes. A preference over A
j
is an expression of
one of two forms: Pref (A
i
) = min or Pref (A
i
)
= max. Let p and q be two tuples of r. We
say that p dominates q (denoted p≺
d
q) if and
only if p.A1≤q.A1, . . . , p.A
m
≤q.A
m
and ∃ j ∈ [1..m] :
p.A
j
<q.A
j
With:
(, ≺) =
(≤, <) iff pre f (A
j
) = min
(≥, >) iff pre f (A
j
) = max
(1)
In other words, an object (tuple) p dominates an-
other object q if it is as good in all attributes, and is
strictly better in at least one attribute. The Skyline is
a set S of tuples which are not dominated by any other
tuple. S = {t ∈ r|t is not dominated}
One of the major issues of the skyline operator is
the high cardinality of the result set which does not of-
fer any interesting insights. All objects are equally in-
teresting and there is no significant discrimination be-
tween them. In order to face this obstacle, an efficient
ranking of skyline objects has become a compelling
need. This solution is efficient especially in the case
of high dimensional or anti-correlated data and partic-
ipates in reducing the huge size of the result set. Our
contribution lies within this scope. In this paper, we
introduce a novel approach that aims on one hand at
enriching an IR- style ranking mechanism based on
dp-idp scoring scheme. Our enrichment is founded
on the integration of a Dominance Hierarchy (DH) in
order to improve the calculation of skyline scores and
their afterward ranking. And on the other hand, we
propose our CoSky (Cosine Skylines) approach that
handles with skyline objects ranking without favor-
ing any dominance relationship. CoSky is a TOPSIS-
like method (the Technique for Order of Preference
by Similarity to Ideal Solution (Lai et al., 1994)) is a
cross-fertilization between the fields of Information
Retrieval, Multiple Criteria Decision Analysis, and
Databases. CoSky innovations are summarized by
the following steps: the attributes normalization using
Gini index, the automatic weighting of the normalized
attributes: they do not need user-defined weighting at-
tributes as in TOPSIS method (Tscheikner-Gratl et al.,
2017), the calculation of each skyline score using the
Salton’s cosine of the angle between each skyline ob-
ject and the ideal object, and its direct implementation
into SQL without further structures.
The rest of the paper is organized as follows: sec-
tion 2 gives an overview of the methods proposed
in the literature to extract and rank the skyline ob-
jects. In section 3, we explain the dp-idp method
and we point out its weaknesses and the difficul-
ties grasped while calculating the scores and defin-
ing the layers of minima. In section 4, we describe
our proposal of enrichment and extension of dp-idp
Ranking mechanism based on Dominance Hierarchy
pre-computation. In section 5, we present our non-
dominance based approach The Cosky method, we
describe the main steps and we discuss the obtained
results given by a running example. The algorithm
DeepSky, a Multilevel skyline algorithm to find Top-
k ranked Skylines that have k highest scores is de-
scribed in section 6. Finally, we sum up the main
conclusions of this paper as well as point out direc-
tions for future works.
2 RELATED WORK
In addition to the skyline queries, a panoply of al-
gorithms have been proposed in order to meet sky-
line constraints which vary with the studied computa-
tional domain. In (Borzsonyi et al., 2001), the Block
Nested Loop (BNL) algorithm is proposed in database
context; its principle is based on a window (memory
block with limited space) of size w. This window
stores the first points that are undominated in each
pass. Passes are made over the data until obtaining all
the skyline points and each dominated point is elimi-
nated to not be read in the future. In case the window
is full, a temporary disk file is used to hold the can-
didate objects. The BNL algorithm is provided of a
timestamping mechanism allowing it to find out when
a point is in the skyline and when all points it domi-
nates were eliminated. In (Spyratos et al., 2012), au-
thors propose an approach to compute the skyline of
a relational table taking into account preferences ex-
pressed over one or more attributes. This approach
does not consider the table structure or the tuples in-
dexing. It is based on query lattice concept presented
and explained in the paper. An algorithm is developed
to construct the skyline as the union of answers to a
subset of queries from that lattice without directly ac-
cessing the table R. To rank the query, they consider
the maximum path from the root query to another
query q. The higher the rank of a query the less the
tuples in its answer are preferred. Two index-based
CoSky: A Practical Method for Ranking Skylines in Databases
509

algorithms namely; Bitmap and Index are introduced
in (Tan et al., 2001). Bitmap uses the bitmap encod-
ing to determine the dominating points. The Index
approach is based on the partitioning of different ob-
jects into sorted lists. The sorting parameter is the
minimum coordinate. The lists are then indexed by
a B-tree. These algorithms return skyline points in a
fixed order which cannot be adapted to the users pref-
erences. In (Papadias et al., 2005), the Branch and
Bound Skyline (BBS) algorithm is proposed, this al-
gorithm is based on nearest-neighbor search and only
nodes containing skyline points are accessed. BBS
is simple to implement due to its progressiveness and
I/O optimality. The SaLSa algorithm (Bartolini et al.,
2007) is a natural extension of SFS (Chomicki et al.,
2003) algorithm, whose originality is the ability of
computing the result without applying the computa-
tion of the Pareto-dominance relation to all the ob-
jects. This is achieved by pre-sorting the data us-
ing a monotone (as SFS) limiting function, and then
checking that unread data are all dominated by a so-
called stop point (object). A Randomized Skyline al-
gorithm (RAND) is presented in (Das Sarma et al.,
2009). RAND is a multi-pass streaming algorithm
which takes into account randomized I/Os. A compar-
ison between RAND and other known algorithms is
given and shows that it performs in the case of minor
and simple variations in the input (eg. Perturbations
of the data orders) while the other algorithms do not
return significant results with such variations. As we
mentioned above, the huge cardinality of a skyline set
is a main obstacle that a decision maker faces. In or-
der to avoid it, an efficient selection of skyline objects
has to be performed. Numerous works have been de-
voted to study the ranking of skylines. In (Chan et al.,
2006), a metric called skyline frequency is proposed
in order to rank the skyline by retaining the interest-
ing points with high skyline frequency. This method
scales well with dimensionality unlike other ranking
methods. Experiments show that the proposed algo-
rithm runs faster than other algorithms and returns
correct results even when considering a huge number
of dimensions
An alternative to skyline queries is presented in (Yiu
and Mamoulis, 2007); the top-k dominating queries.
These queries are proposed as a ranking method not
based on a scoring function. The top-k dominating
queries are evaluated in a multi-dimensional data con-
text.
In (Bartolini et al., 2007), a ranking approach applied
on an image Database is introduced. The technique is
based on the shaping of what the user is looking for
by specifying user defined regions that dominate all
other regions. Authors show that the obtained results
are as good as those based on scoring functions and
that the proposed approach provides a perfect running
time.
(Vlachou and Vazirgiannis, 2010) propose a ranking
approach of skyline objects for a SKYCUBE (Lakhal
et al., 2017) in order to focus on the most informa-
tive objects. A Skyline graph is built up and captures
the dominance relationships between skyline objects
belonging to different subspaces. In (Chen et al.,
2015), a new operator is introduced in order to find
the most desirable skyline object (MDSO). A ranking
criterion is formalized, it considers the number of the
non-skyline objects dominated by a skyline object s.
The higher this criterion is, the more interesting the
skyline object is. To process MDSO queries, three al-
gorithms are proposed namely; Cell Based algorithm
(CB), Sweep Based algorithm (SB), and Reuse Based
algorithm (RB). They return the most desirable k sky-
line objects.
3 SKYLINE RANKING BASED ON
DP-IDP
The dp-idp (dominance power- inverse dominance
power), is inspired by the tf-idf weighting scheme
from Information Retrieval which assigns to a term
t a weight in a document d. The idea is not to deter-
mine the number of occurrences of each query term
t in d, but instead the tf-idf weight of each term in
d. The aim is to find important keywords in a docu-
ment corpus. In the skyline context, dominated points
impact skyline point differently. Consequently, these
points have not the same importance. Their contri-
bution depends on some local (per skyline point) and
some global characteristics (the entire skyline), simi-
larly to tf-idf.
The explored idea in (Valkanas et al., 2014) is that
a point’s importance has to be inversely proportional
to the number of skyline points that dominate it. The
dp-idp scheme takes into account the relative posi-
tions of the dominated points in order to differentiate
between them. It is centered on points that are not
dominated by many others: e.g. if sp≺
d
p
1
, sp≺
d
p
2
,
and p
1
and p
2
do not dominate each other, they con-
tribute equally to sp. Otherwise, if p
1
≺
d
p
2
, then
score(p
1
) > score(p
2
), consequently the contribution
of p
1
is more considerable. The idp of a point p ∈
D\S) is the number of skyline points which dominate
p. A point p is important if it does not appear fre-
quently in a skylines point dominated set :
id p(p) = log
|S|
|{sp ∈ S : sp ≺
d
p}|
(2)
KDIR 2019 - 11th International Conference on Knowledge Discovery and Information Retrieval
510
To measure the d p of a dominated point p, its rel-
ative position to the skyline point sp is very important
and has to be taken into account. Hence, the same
dominated point may contribute differently to differ-
ent skyline points. For this reason, we have to find the
layer of minimalm(p, sp) where the dominated point
p is located with respect to sp. The dominance power
of p is then given by the inverse of the layer where it
lies : The score (sp) which measures the importance
of a skyline point sp is given by the following for-
mula:
Score(sp) =
∑
p:sp≺
d
p
1
lm(p, sp)
log
|S|
|{sp
0
∈ S : sp
0
≺
d
p}|
(3)
The Baseline algorithm (Valkanas et al., 2014) is
proposed to rank the skyline on the basis of dp-idp
scheme. The main steps of this algorithm are:
1. Extracting the minimal layers of each skyline
point sp;
2. Considering each point (p) in each layer of min-
ima lm (p, sp), the number of skyline points dom-
inating it has to be found. The score sp is then
updated;
3. Sorting the skyline on the basis of the returned
scores.
This algorithm is time consuming and has lots of
shortcomings as mentioned in (Valkanas et al., 2014).
But the most important weakness according to us, is
the difficulty of the calculation of the layer of minima
which may lead to wrong results. For this reason, we
propose an enrichment of this approach in order to
make the Baseline algorithm faster .
At this state, our objective is to ameliorate the
dominance based approach (dp-idp) and to improve
the skyline ranking (Section 4). Further, in this paper,
we will introduce our non-dominance based approach
and we will discuss its performance in ranking sky-
line objects without referring to any dominance rela-
tion calculation (Section 5 and Section 6).
4 ENRICHMENT OF DP-IDP
WITH DOMINANCE
HIERARCHY
The dominance relation can be seen as an hierarchi-
cal sorting, i.e. A skyline point has necessarily a hi-
erarchical position superior to its dominated points.
This assumption motivated us to map the dominance
relationship, studied above, to a graph that we call
Dominance Hierarchy. The integration of DH into the
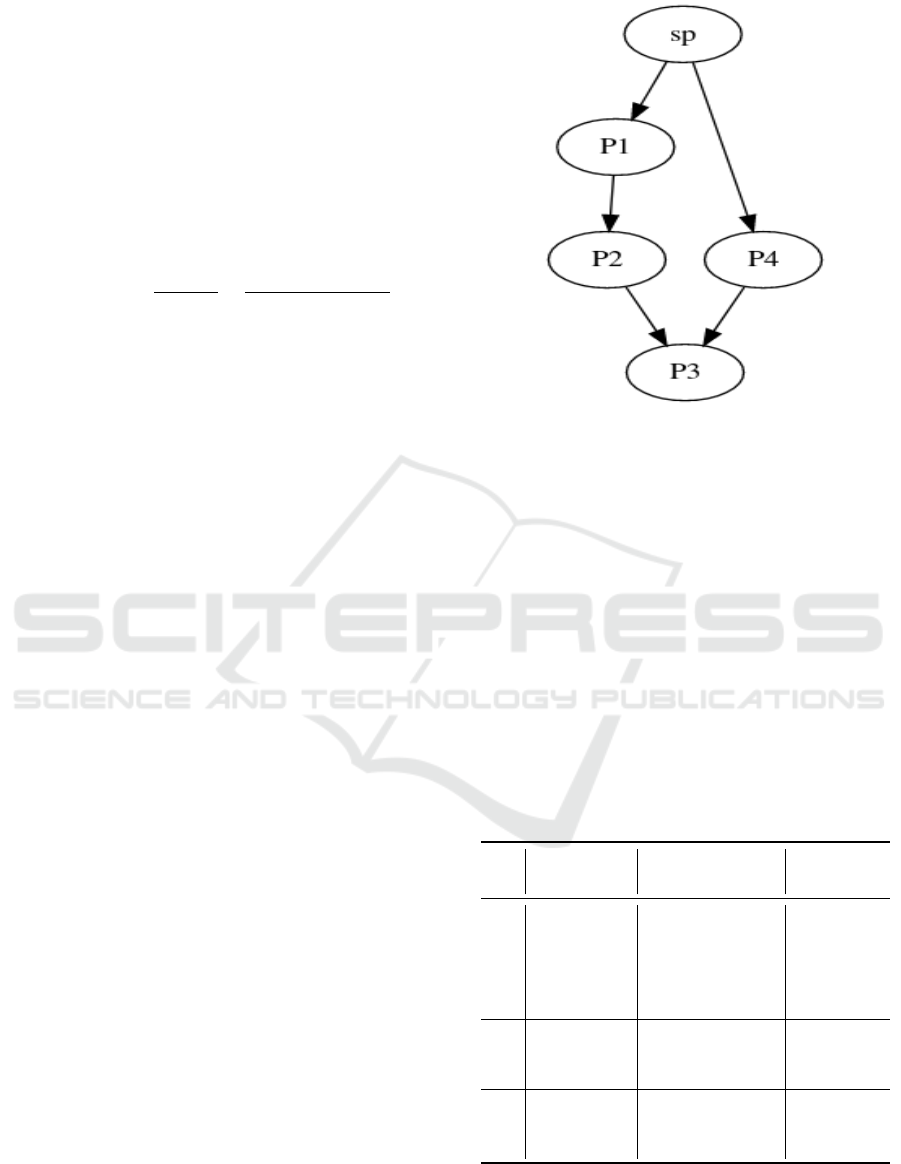
Figure 1: An example of a DH graph.
dp-idp skyline r anking method permits a better com-
putation of layers of minima (first step in the base-
line algorithm) and consequently leads to better rank-
ing results. Our proposed graph is a kind of Directed
Acyclic Graph (DAG) used to give a presentation of
a partially ordered set (poset) by drawing its coverage
graph (i.e, graph which represents the same reacha-
bility relation of the main graph but with the fewest
possible edges). The DAG has a topological ordering
which may give an excellent presentation of the Hi-
erarchy evolution from a skyline point sp to its domi-
nated points.
Given a set of objects (D) and an order of domi-
nance ≺
d
, DH is the coverage graph of the ordered
set (D, ≺
d
).
Table 2: Scores Calculation.
sp Dominated Lm (p, sp) Score (sp)
points p
C
1
C
3
Lm(C
3
,C
1
) = 2 0.297
C
5
Lm(C
5
,C
1
) = 3
C
6
Lm(C
6
,C
1
) = 3
C
7
Lm(C
7
,C
1
) = 3
C
8
Lm(C
8
,C
1
) = 4
C
2
C
5
Lm(C
5
,C
2
) = 2 0
C
7
Lm(C
7
,C
2
) = 2
C
8
Lm(C
8
,C
2
) = 3
C
4
C
5
Lm(C
5
,C
4
) = 2 0
C
7
Lm(C
7
,C
4
) = 2
C
8
Lm(C
8
,C
4
) = 3
The DH is a direct acyclic graph (c f . Figure 1)
contains as vertex the skyline point (sp). The order of
Dominance is illustrated by the edges between sp and
CoSky: A Practical Method for Ranking Skylines in Databases
511
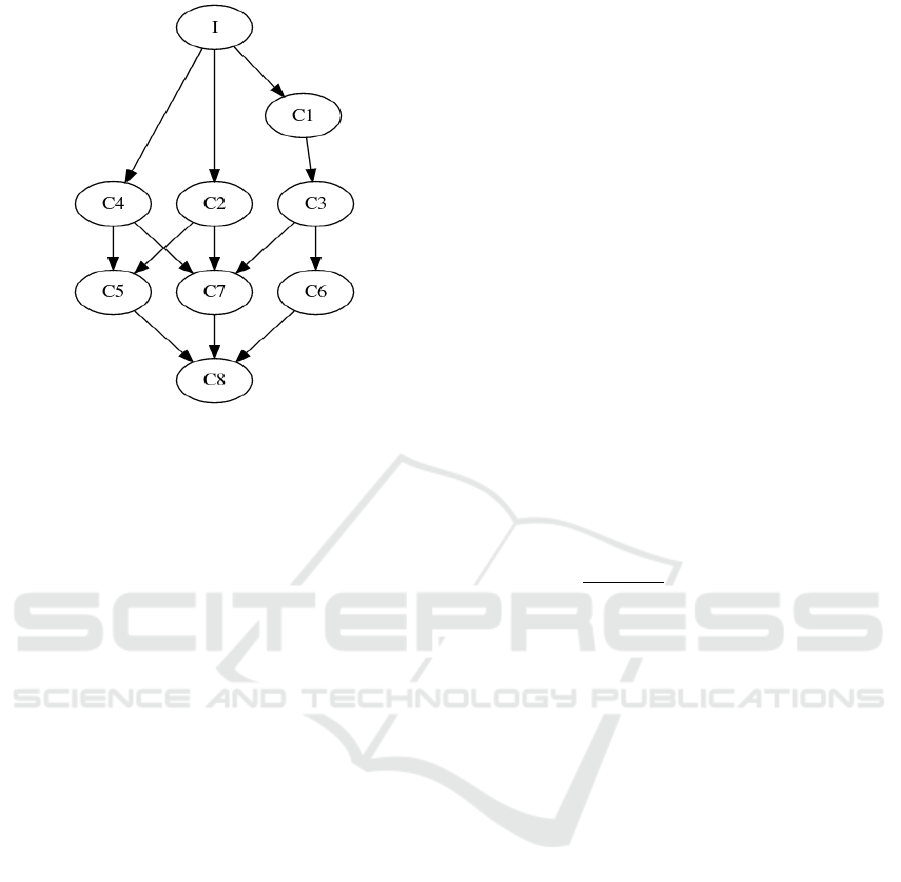
Figure 2: An example of a DH graph.
its dominated points (p
1
, p
2
, p
3
and p
4
).
We define the layer of minima(p,sp) as the num-
ber of vertices of the minimal path from sp to p in
DH. To compute the layer of minima(p3, sp), there
are two paths from sp to p
3
as shown in the graph
(c f . Figure 1):
1. First path: sp→p
1
→p
2
→p
3
‘
2. Second path: sp→p
4
→p
3
The first path contains 4 vertices and the second
one contains 3 vertices, then the minimal path from sp
to p
3
is the second one and lm(p
3
, sp) = 3. Lets con-
sider another example, the DH graph in Figure 2 il-
lustrates the dominance relations between the skyline
points and the dominated points of the Cars database
relation. I is the ideal point dominating all skylines.
To compute the score, we use formula 3. Thus, the
obtained rank is : C
1
,C
2
,C
4
or C
1
,C
4
,C
2
.
On the basis of the obtained results (c f . Table 2),
we conclude that the dp-idp method is unable to dis-
tinguish two skylines dominating objects which are
dominated by all skylines as it is the case here of the
skylines C
2
and C
4
.
5 THE COSKY METHOD
In order to solve the ranking problem, we propose
the CoSky method for ranking skylines in Databases.
CoSky (COsine Skylines) is a multi-steps approach
and it is not based on dominance relation calcula-
tion. CoSky is the first TOPSIS-like method applied
to ranking the skylines. TOPSIS (Lai et al., 1994),
(Behzadian et al., 2012) is based on a vectorial nor-
malisation, a user-weight calculation of each attribute,
and the score of each object uses a geometric calcula-
tion of the distances between each alternative (object)
and the ideal/anti-ideal solutions. In CoSky method,
the normalisation of the attributes is based on the sum,
an automatic weighting of the normalized attributes
based on Gini index, and the score uses the Salton’s
cosine of the angle between each skyline object and
the ideal object. More calculation details are given
later in this section. In the rest of the paper, we con-
sider that i∈[1..n] and j∈[1..m] (where n is the number
of tuples and m is the number of attributes).
5.1 Step 1: Attributes Normalization
based on the Sum
The Skylines are normalized in the range between 0
and 1 to eliminate anomalies with different measure-
ment units and scales. This process transforms differ-
ent scales and units among various attributes (or cri-
terias) into common measurable units to make these
attributes comparables.
Let us consider the tuple p
i
= <v
i1
, v
i2
, .., v
im
> ∈
rSkyNorm (Normalized skylines), then we have :
v
i j
=
t
i
[A
j
]
∑
n
i=1
t
i
[A
j
]
, ∀t
i
∈ rSky(Skylines) (4)
5.2 Step 2: Automatic Weighting of
Normalized Attributes based on
Gini Index
Ranking the skylines aims principally to give an ex-
pressive discrimination between the selected objects.
In order to reach such finality, it is crucial to fix a dis-
criminative measure. In the literature, several mea-
sures were proposed. The entropy concept was used
in various Multi-Attribute Decision Making prob-
lems. In (Huang, 2008) and (Hosseinzadeh Lotfi and
Fallahnejad, 2010), an entropy based method was pro-
posed. This method fits well with our computation
context where we aim at differentiating attribute val-
ues in order to attempt a better decision making re-
lated to the skyline ranking. However, it has many
limits especially related to the entropy calculation.
Entropy requires logarithmic function computation
what presents a computational time issue. Then, it is
generally intended for attributes that occur in classes.
We rather propose another measure ’the Gini in-
dex’ which is faster than entropy and does not use logs
to insure the automatic weighting of attributes. More-
over, it is intended for continuous attributes. The Gini
index is employed to derive the weights of the eval-
uation criteria (attributes) in our proposed method.
KDIR 2019 - 11th International Conference on Knowledge Discovery and Information Retrieval
512

Hence, it determines the degree of divergence of at-
tribute values. The Gini index of A
j
is calculated by
the following equation:
Gini(A
j
) = 1 −
n
∑
i=1
t
i
[A
j
]
2
(5)
The corresponding weight is given by the follow-
ing formula:
W (A
j
) =
Gini(A
j
)
∑
m
j=1
Gini(A
j
)
(6)
Let us consider the tuple p
i
= {a
i1
, a
i2
, . . . , a
im
} ∈
rSkyPond (rsky after attributes weighting), then we
have :
a
i j
= W (A
j
) ×t
i
[A
j
], ∀t
i
∈ rSkyNorm (7)
5.3 Step 3: Determination of the Ideal
Skyline
The ideal, denoted I
+
, is an object that corresponds
optimally to the user preferences. For example, if
we consider the cars table, then searching an ideal
car combines conditions on the price which has to be
the smallest possible, the number of kilometers; the
smallest possible, and the power; the greatest possi-
ble.
Thus, if we consider I
+
=< v
1
, v
2
, .., v
m
>, then
we have:
v
j
=
max(A
j
) iff pre f (A
j
) = max
min(A
j
) iff pre f (A
j
) = min
(8)
5.4 Step 4: Calculation of Skyline
Scores on the Basis of the Salton’s
Cosine
This step aims to determine the score of a skyline ob-
ject on the basis of the Salton’s Cosine (or Similar-
ity Cosine). We calculate the cosine of the angle be-
tween the ideal and the skyline. The more the angle
is little (high cosine), the more the skyline object is
important. The Salton cosine ranges between 0 and
1 and is given in the formula below. Let us con-
sider the tuple p
i
=< x
i1
, x
i2
, .., x
im
>∈ rSkyPond and
I
+
=< y
1
, y
2
, .., y
m
> the ideal object, then we have :
t
i
[Score] = Cosine(p
i
, I
+
) =
p
i
.I
+
||p
i
||.||I
+
||
(9)
t
i
[Score] =
∑
m
j=1
x
i j
.y
j
q
∑
m
j=1
x
2
i j
.
q
∑
m
j=1
y
2
j
, ∀t
i
∈ rSkyScore
(10)
As a consequence of equation 10, t
i
[score] = 1
if and only if the skyline is the best object, and
t
i
[score] = 0 if and only if the skyline is the worst
object.
Remark: We can use the similarity principle of
TOPSIS to calculate the score of each skyline ob-
ject as following: Let us consider t
i
[scoreIdeal] =
Cosine(p
i
, I
+
) and ti[scoreAideal] = Cosine(p
i
, I
−
),
p
i
∈ rSkyPond, I
+
the ideal and I
−
the anti-ideal ob-
ject./ Thus, if we consider I
−
=< v
1
, v
2
, .., v
m
>, then
we have:
v
j
=
max(A
j
) iff pre f (A
j
) = min
min(A
j
) iff pre f (A
j
) = max
(11)
5.5 Step 5 : Ranking the Result by the
Score
This is the final step in the CoSky process, it aims to
sort the skyline objects on the basis of the calculated
scores. The CoSky steps applied to the car database
relation can be calculated using a SQL queries (c f .
Appendix). The obtained results are given in Table 3.
The obtained rank is C
1
, C
4
, C
2
.
Table 3: Skylines ranking with CoSky method.
idcar price klm power score
C
1
25 10 8 0.814
C
4
5 40 7 0.803
C
2
20 30 6 0.769
Unlike dp-idp, the CoSky method distinguishes
clearly the skyline scores. The skyline objects C
4
and
C
2
have explicit scores (score 6= 0 ) while using dp-
idp their score is 0. Thus we can rank them.
6 FINDING TOP-K RANKED
SKYLINES
The notion of Multilevel skylines for finding Top-
k Skylines (not ranked) is introduced in (Preisinger
and Endres, 2015). A Top-k Skyline query Qk on a
Database relation r computes the Top-k tuples with
respect to the skyline preferences. Let us consider
S
0
(r) the classical skyline set and Card(r) > k, then
we have:
1. If Card(S
0
(r)) > k, then Qk returns only k tuples
from S
0
(r);
2. If Card(S
0
(r)) = k, then Qk returns the skylines
(i.e. the set S
0
(r));
CoSky: A Practical Method for Ranking Skylines in Databases
513

3. If Card(S
0
(r))k, then the elements of S
0
(r) are
not enough numerous for an correct answer. A
Multilevel skylines approach has to be applied.
That means, not only all elements of the S
1
(r),
the first level, are returned from (r\S
0
(r)), but also
some of the S
2
(r), the set of skylines result from
(r\(S
0
(r) ∪ S
1
(r)) and if the number of result tu-
ples is still less than k, then we have to build S
3
(r),
and so on . . .
The following algorithm DeepSky uses this multi-
level principle with our ranking method to find Top-k
ranked Skylines. It returns the Multilevel k skylines
that have the k highest scores computed by the CoSky
procedure.
Input: The database relation r, Preferences
on attributes, and k
Output: the Top-k tuples/objects with best
scores : Topk
FS := 0;
rlayer := r;
while FS ≥k or rlayer =
/
0 do
rsky := CoSky(rLayer);
FS := FS + card (rsky);
if FS ¡ k then
Topk := Topk ∪ rsky;
rlayer := rlayer \ rsky;
end
else if FS ≥k then
Topk := the first k skylines of rsky;
return Topk;
end
end
return Topk;
Algorithm 1: Algorithm DeepSky for finding the best Top-k
skylines.
Example: If we consider k = 4, the algorithm Deep-
Sky returns C
1
, C
4
, C
2
, the ranked skylines from level
0 and C
3
the only skyline from level 1.
7 CONCLUSIONS
In this paper, we proposed novel techniques for rank-
ing skyline objects. Three contributions are de-
scribed: The first is an enrichment of dp-idp method
by dominance hierarchy to fast scoring skylines. The
second is the CoSky method based on the renowned
TOPSIS schema from Multiple Criteria Decision
Analysis and Salton’s cosine similarity from Informa-
tion retrieval. An example of an SQL implementa-
tion of the proposed method was also described. Fi-
nally, we presented an algorithm for finding the Top-
k ranked skylines that have k highest scores using
the principle of Multilevel skylines and the CoSky
method. As a short term future work, we will im-
plement our approach in online sales applications in a
Big Data context.
REFERENCES
Bartolini, I., Ciaccia, P., Oria, V., and Ozsu, T. (2007). Flex-
ible integration of multimedia sub-queries with qual-
itative preferences. journal of Multimed Tools Appl,
33:275––300.
Behzadian, M., Otaghsara, S. K., Yazdani, M., and Ignatius,
J. (2012). A Review on state of the art survey of TOP-
SIS applications. Expert Systems with Applications,
39:13051—-13069.
Bentley, J. L., Kung, H. T., mellon Umversuy Putsburgh,
C., Schkolnick, M., and Thompson, C. D. (1978). On
the average number of maxima in a set of vectors and
applications. Journal of the ACM.
Borzsonyi, S., Kossmann, D., and Stocker, K. (2001). The
skyline Operator. In Proceedings of the ICDE Confer-
ence, page 421–430.
Chan, C. Y., Jagadish, H. V., Tan, K., Tung, A., and Zhang,
Z. (2006). On high dimensional skylines. In Pro-
ceedings of the International Conference on Extend-
ing Database Technology (EDBT), pages 478–495.
Chen, L., Gang, C., and Li, Q. (2015). Efficient algorithms
for finding the most desirable skyline objects. Knowl-
edge Based Systems, 89:250–264.
Chomicki, J., Godfrey, P., Gryz, J., and Liang, D. (2003).
Skyline with presorting. pages 717– 719.
Das Sarma, A., Lall, A., Nanongkai, D., and Xu, J. (2009).
Randomized multi-pass streaming skyline algorithms.
PVLDB, 2:85–96.
Hosseinzadeh Lotfi, F. and Fallahnejad, R. (2010). Im-
precise shannon’s entropy and multi attribute decision
making. Entropy, 12.
Huang, J. (2008). Combining entropy weight and TOPSIS
method for information system selection. In Proceed-
ings of International Conference on Automation and
Logistics, pages 1184–1281.
Lai, Y., Liu, T., and Hwang, C. (1994). TOPSIS for MODM.
European Journal of Operational Research, 76:486–
500.
Lakhal, L., Nedjar, S., and Cicchetti, R. (2017). Multi-
dimensional skyline analysis based on agree concept
lattices. Intelligent Data Analysis, 21:1245—-1265.
Papadias, D., Tao, Y., Fu, G., and Seeger, B. (2005).
Progressive skyline computation in database systems.
ACM Trans. Database Syst., 30:41–82.
Preisinger, T. and Endres, M. (2015). Looking for the Best,
but not too Many of Them: Multi-Level and Top-k
Skylines. International Journal on Advances in Soft-
ware, 8:467–480.
KDIR 2019 - 11th International Conference on Knowledge Discovery and Information Retrieval
514

Spyratos, N., Sugibuchi, T., Simonenko, E., and Meghini,
C. (2012). Computing the skyline of a relational table
based on a query lattice. CEUR Workshop Proceed-
ings, 876:145–160.
Tan, K.-L., Eng, P.-K., and Chin Ooi, B. (2001). Efficient
progressive skyline computation. pages 301–310.
Tscheikner-Gratl, F., Egger, P., Rauch, W., and Kleidor-
fer, M. (2017). Comparison of multi-criteria decision
support methods for integrated rehabilitation prioriti-
zation. Water, 9(2).
Valkanas, G., Papadopoulos, A., and Gunopulos, D. (2014).
Skyline ranking
`
a la ir. CEUR Workshop Proceedings,
1133:182–187.
Vlachou, A. and Vazirgiannis, M. (2010). Ranking the
sky: Discovering the importance of SKYLINE points
through subspace dominance relationships. Data and
Knowledge Engineering, 69:943–964.
Yiu, M. and Mamoulis, N. (2007). Efficient Processing of
Top-k Dominating Queries on Multidimensional Data.
In Proceedings of the VLDB conference, pages 483–
494.
APPENDIX
WITH r Sky AS ( SELECT ∗ FROM C a rs C1
WHERE NOT EXISTS
(SELECT ∗ FROM Ca r s C2
WHERE ( C2 . p r i c e <= C1 . p r i c e
AND C2 . klm <= C1 . klm
AND C2 . pow er >= C1 . powe r )
AND ( C2 . p r i c e < C1 . p r i c e
OR C2 . klm < C1 . klm
OR C2 . p ower > C1 . powe r ) )
) ,
rSkyNorm AS (SELECT i d c a r ,
p r i c e / S p r i c e AS pr iceNo rm ,
klm / Sklm AS klmNorm ,
pow er / Spower AS powerNorm
FROM rSky ,
(SELECT SUM ( p r i c e ) AS S p ri c e ,
SUM ( klm ) AS Sklm ,
SUM ( pow er ) AS Sp ower FROM r Sk y )
) ,
r Sk y G in i AS ( SELECT
1− (SUM ( priceN or m ∗ p ri ce No rm ) ) AS p r i c e g i n i ,
1−(SUM ( klmNorm ∗ klmNorm ) ) AS k l mg i ni ,
1− (SUM ( powerNorm ∗ powerNorm ) ) AS p o w e r gin i
FROM rSkyNorm
) ,
rSkyW AS (SELECT
p r i c e g i n i / ( p r i c e g i n i + k l m g i ni + p o w e rg i n i ) AS p ri ce w ,
k l m gi n i / ( p r i c e g i n i + k l mgi n i + p o w e r g in i ) AS klmw ,
p o wer g i n i / ( p r i c e g i n i + k l m gin i + p o wer g i n i )AS powerw
FROM r Sk y G in i
) ,
rS kyP ond AS (SELECT
i d c a r ,
p ri c e w ∗ p ri ce No rm AS p r i ce p o nd ,
klmw ∗ klmNorm AS klmpond ,
powerw ∗ powerNorm AS pow erp ond
FROM rSkyNorm , rSkyW
) ,
i d e a l AS (SELECT
MIN ( p r i c e p o n d ) AS I DL p ri ce ,
MIN ( klmpon d ) AS IDLklm ,
MAX ( powe rpon d ) AS IDLpower
FROM r s ky Po n d
) ,
r Sk y Sco r e AS (SELECT
i d c a r ,
( I D Lp r i ce ∗ p r i c e p o nd + IDLklm ∗ klmpond +
IDLpower ∗ pow erp ond ) /
( s q r t ( p r i c e p o n d ∗ p r i c e p o n d + klmpond ∗ klm pond +
powerp ond ∗ power pond ) ) ∗
( s q r t ( I D Lp r i ce ∗ I DLp r ice + IDLklm ∗ IDLklm +
IDLpower ∗ IDLpower ) ) )
AS s c o r e
FROM i d e a l , r Sky Pon d
)
SELECT ca . i d c a r , p r i c e , klm , power , s c o r e FROM
rS ky ca , r S ky S co r e r s
WHERE c a . i d c a r = r s . i d c a r
ORDER BY s c o r e d es c ;
CoSky: A Practical Method for Ranking Skylines in Databases
515
