Things You Might Not Know about the k-Nearest Neighbors Algorithm

Aleksandra Karpus

, Marta Raczy

nska and Adam Przybylek

Faculty of Electronics, Telecommunications and Informatics, Gda

nsk University of Technology, ul. G. Narutowicza 11/12,

80-233 Gda

nsk, Poland

Keywords:

Recommender Systems, Collaborative Filtering, Similarity Measure, Neighborhood Size.

Abstract:

Recommender Systems aim at suggesting potentially interesting items to a user. The most common kind of

Recommender Systems is Collaborative Filtering which follows an intuition that users who liked the same

things in the past, are more likely to be interested in the same things in the future. One of Collaborative

Filtering methods is the k Nearest Neighbors algorithm which ﬁnds k users who are the most similar to an

active user and then it computes recommendations based on the subset of users. The main aim of this paper is

to compare two implementations of k Nearest Neighbors algorithm, i.e. from Mahout and LensKit libraries,

as well as six similarity measures. We investigate how implementation differences between libraries inﬂuence

optimal neighborhood size k and prediction error. We also show that measures like F1-score and nDCG are

not always a good choice for choosing the best neighborhood size k. Finally, we compare different similarity

measures according to the average time of generating recommendations and the prediction error.

1 INTRODUCTION

Recommender Systems aim at suggesting potentially

interesting items to a user. They are present in ev-

eryday life, e.g. in e-commerce shops, social media,

news portals or media services. The most common

kind of Recommender Systems is Collaborative Fil-

tering which follows an intuition that users who are

similar to each other, i.e. liked the same things in

the past, are more likely to be interested in the same

things in the future. For example, if Alice and Bob

are both fans of fantasy books and Bob read one more

book than Alice and liked the book, then we could

recommend it to her with a big probability that she

would like it too (Jannach et al., 2010).

One of Collaborative Filtering methods is the k

Nearest Neighbors algorithm (kNN). It ﬁrst ﬁnds k

users who are the most similar to an active user and

then it computes recommendations based on the sub-

set of users. Similar users are called the nearest neigh-

bors. The neighborhood size k is given as a parameter

to the algorithm. We deﬁne what we mean by ”simi-

lar” by choosing a similarity measure.

The neighborhood size is very important for the

kNN algorithm. As shown in (Herlocker et al., 1999),

high k value leads to big prediction error and bad rec-

https://orcid.org/0000-0001-6198-1234

https://orcid.org/0000-0002-8231-709X

ommendations. It is also time and memory consum-

ing. However, too small k values leads to the over-

ﬁtting problem. Therefore, it is crucial to choose the

neighborhood size wisely.

The main aim of this paper is to compare two im-

plementations of the kNN algorithm, i.e. from Ma-

hout

and LensKit

libraries, as well as six similar-

ity measures: Pearson correlation coefﬁcient, cosine

distance, euclidean distance, Jaccard similarity, Log-

likelihood ratio and Spearman’s rank correlation co-

efﬁcient. We investigate how implementation differ-

ences between libraries inﬂuence optimal neighbor-

hood size k and prediction error. We also show that

precision, recall, F1-score and nDCG measures are

not always good choice for choosing the best neigh-

borhood size k.

The rest of the paper is organized as follows. Sec-

tion 2 provides background for this paper. In Sec-

tion 3 we describe datasets that we used for experi-

ments. Detailed information about choosing neigh-

borhood size, differences in implementation of the

kNN algorithm and their inﬂuence on k value and pre-

diction error are given in Section 4. In Section 5 we

present average time that the kNN algorithm needs to

generate a list of top-10 recommendations depending

on a library and a similarity measure. Section 6 sum-

https://mahout.apache.org/

https://java.lenskit.org/

Karpus, A., Raczy

nska, M. and Przybylek, A.

Things You Might Not Know about the k-Nearest Neighbors Algorithm.

DOI: 10.5220/0008365005390547

In Proceedings of the 11th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2019), pages 539-547

ISBN: 978-989-758-382-7

539

marizes all experiments and Section 7 concludes the

paper.

2 BACKGROUND

In this section we brieﬂy describe similarity measures

that were used in our experiments. We also report

approaches for choosing the best neighborhood size

for the kNN algorithm that have been presented in the

literature.

2.1 Similarity Measures

The most common similarity measure is the Pearson

correlation coefﬁcient (Pearson, 1895; Soper et al.,

1917) which is presented in the formula (1). This

measure considers the fact that users interpret rating

scale in different ways. Some of them rate just items

that they really like (only ratings 4 and 5) and some

of them use the whole rating scale.

sim(x, y) =

∑

i∈I

x,i

− ¯r

)(r

y,i

− ¯r

)

∑

i∈I

x,i

− ¯r

)

∑

i∈I

y,i

− ¯r

)

(1)

where i indicates an item from the set of items I, r

x,i

is the rating that a user x gave to an item i and the

symbol ¯r

corresponds to the average rating of user x.

Another very popular similarity measure is the co-

sine similarity (Singhal, 2001) given by the formula

(2).

cos(x, y) =

x • y

, (2)

where • indicates vector dot product and

is the

norm of a user vector x.

The euclidean similarity is another distance mea-

sure adapted as similarity. It is deﬁned as a sum of

squares of differences between ratings given by two

different users. It is given by the formula (3).

d(u

, u

) =

∑

iεI(u

)

I(u

)

(r(i, u

) − (r(i, u

))

(3)

where I(u

) indicates a set of all items rated by the

user 1 and r(i, u

) is a rating given to the item i by the

user u

the Jaccard similarity (Jaccard, 1902; Jaccard,

1912) is given by the formula (4).

jacc(A, B) =

A ∩ B

A ∪ B

, (4)

where ∩ indicates the intersection and ∪ the union of

sets A and B.

The Log-likelihood ratio is similar to the Jaccard

similarity. Nevertheless, it is able to capture signiﬁ-

cant co-occurrences. The Log-likelihood similarity of

a user with herself is not equal to 1 (Dunning, 1993).

The Spearman’s rank correlation coefﬁcient is

based on the Pearson correlation coefﬁcient. How-

ever, instead of user ratings it uses ranks of these rat-

ings. The rank is a place on an ordered list of user

ratings (Aggarwal, 2016).

2.2 Neighborhood Size

There are two approaches for the kNN algorithm. One

assumes to choose a threshold for similarity value,

e.g. 0.5. Neighbors that are chosen in this way,

i.e. with a higher similarity to the active user, could

be more valuable as the predictors than those with a

lower similarity (Breese et al., 1998).

The second approach just chooses a ﬁxed number

of neighbors, i.e. neighborhood size k. It has been

proven that this technique performs better than the

one with threshold (Herlocker et al., 1999).

As shown in (Herlocker et al., 1999), too high k

value leads to the big prediction error and the bad

quality of recommendations. It is also time and mem-

ory consuming. However, too small k values leads

to the overﬁtting problem. Therefore, it is crucial to

choose the neighborhood size wisely.

Some papers report that a neighborhood of 20 to

50 users is reasonable, providing enough neighbors to

average out extremes (Herlocker et al., 2002; Good

et al., 1999). Nevertheless, a neighborhood size de-

pends on the data characteristics like sparsity (Syme-

onidis et al., 2014). Thus, the optimal k value should

be determined by a cross-validation (Desrosiers and

Karypis, 2011).

The idea behind a method reported in (Kim and

Cho, 2003) is to check a change in the value of the F1-

score metric depending on the given parameter of the

neighborhood size k. The values analysed are consec-

utive multiples of the number 10 in the range 10-100

and the entire interval 2-9.

The evaluation consists of examining the quality

of generated recommendations for each user from the

input set, from which the 10 best ratings of a given

user were removed. After modifying the input data,

top-10 recommendations are generated. Afterwards,

it is veriﬁed how many of removed items have been

included in the recommendation list. The whole pro-

cedure is repeated for all users and the average is cal-

culated from the outcomes.

KDIR 2019 - 11th International Conference on Knowledge Discovery and Information Retrieval

540

3 DATASETS

We performed our experiments with two publicly

available datasets: MovieLens 1M

and Book-

Crossing

The MovieLens 1M dataset (ML1M) contains

1,000,209 anonymous ratings of approximately 3,900

movies made by 6,040 MovieLens users who joined

MovieLens in 2000. Additionally, it contains demo-

graphic information about users and genres of movies

(Harper and Konstan, 2015).

The Book-Crossing dataset (BX) was collected in

a 4-week crawl from the Book-Crossing community.

It contains 278,858 anonymized users with demo-

graphic information, 1,149,780 ratings and 271,379

books. Ratings are made from users’ implicit and ex-

plicit feedback on books (Ziegler et al., 2005). For

further experiments we used only explicit user ratings.

Basic statistics about both datasets are presented

in Table 1.

Table 1: Basic statistics about MovieLens 1M (ML1M) and

Book-Crossing (BX) datasets.

ML1M BX

Number of users 6040 278858

Number of items 3952 271379

Number of ratings 1000209 1143780

Max number of ratings/user 2314 13602

Min number of ratings/user 20 1

Avg number of ratings/user 165.598 10.921

Rating scale 1-5 1-10

Average rating 3.582 7.601

Sparsity (in %) 4.2 0.0015

4 CHOOSING THE BEST

NEIGHBORHOOD SIZE

Since it is crucial to choose the neighborhood size

wisely, we decided to perform a series of experiments

to do so. In this section we describe two methodolo-

gies that we followed while performing experiments

and we present results obtained with both of them.

4.1 F1-score based Approach

At the beginning of our study, in order to ﬁnd the op-

timal value of k, we followed the approach by (Kim

and Cho, 2003) presented in Section 2.2. We per-

formed an analysis on Book-Crossing and MovieLens

1M datasets. We used the Mahout library and its class

https://grouplens.org/datasets/movielens/1m/

https://grouplens.org/datasets/book-crossing/

GenericRecommenderIREvaluator, which calculates

metrics such as precision, recall, F1-score and nDCG.

The entire input set was taken into account for the

evaluation. The evaluate() method takes a parameter

denoting the relevance threshold, which was calcu-

lated for each set separately as the sum of the arith-

metic mean and the standard deviation of all grades

for each user separately. The Mahout library supports

the generation of this value for a user.

Since we want to compare a performance of dif-

ferent similarity measures, we repeated the procedure

six times - one per each of following measures: Pear-

son correlation coefﬁcient, cosine distance, euclidean

distance, Jaccard similarity, Log-likelihood ratio and

Spearman’s rank correlation coefﬁcient. Results are

presented in Figures 1 and 2 and in Table 2. Due to

the space limits, we report here only representative

subset of obtained plots.

Table 2: Best k-values for both datasets obtained with dif-

ferent similarity measures using the Mahout library and F1-

score.

Similarity ML1M BX

Pearson 2 3

Cosine 3 4

Euclidean 5 5

Jaccard 2 20

Log-likelihood 2 7

Spearman 45 6

We could observe strange curves which differ sig-

niﬁcantly from the shape that was expected. There

is only one plot for the MovieLens dataset and the

Spearman similarity (see Figure 1) which behaves as

expected, i.e. F1-score increases along with the in-

crease of k value to some point and then starts de-

creasing. This point determines the maximum value

of F1 and the optimal neighborhood size.

Table 2 shows that the highest values of the F1-

score are in most cases achieved for small k values.

In the real systems, too low value of this parameter

causes the problem of overﬁtting, while too high val-

ues may contribute to the generation of recommen-

dations which are irrelevant from the user’s point of

view (Herlocker et al., 1999). Usually, the optimal k

value that is chosen for real recommendation systems

is the number from the range 40-60 (Kim and Cho,

2003).

We suspect that the problem is with the method-

ology for choosing the k value presented in (Kim and

Cho, 2003), because it is impossible to determine in

a reliable way whether the recommendations are ac-

curate. Generated recommendation list may contain

offers that the user has not assessed or seen, and yet

could be accurate for a user. The problem of how well

Things You Might Not Know about the k-Nearest Neighbors Algorithm

541

Figure 1: F1-score, Precision, Recall and nDCG depending on the k value computed for the MovieLens 1M dataset.

the generated list of recommendations is suited for a

user can not be properly validated without the partic-

ipation of real users who can give a response if the

list met their expectations after watching a movie or

reading a book from the list.

4.2 MAE based Approach

Because of the reasons mentioned above, we decided

to use the mean absolute error (MAE) for choosing

the k value, as was suggested in (Herlocker et al.,

1999). Due to decreasing MAE values at the end of

the selected interval, experiments were also carried

out on the k value equal to 150, 200, 250, 300, 400,

500, 750, 1000, 1500, 2000, 3000, 4000, 5000 and

10000. After the initial analysis of the results, a reso-

lution was also increased around the minimum MAE

value for each similarity measure separately. Unlike

the approach we followed earlier, this time we used

the 10-fold cross validation and the ﬁnal MAE value

was computed as a mean of obtained results. Tables

3 and 4 present outcomes returned by Mahout and

LensKit libraries respectively. Since the LensKit li-

brary provides only two similarity measures imple-

mentations, i.e. Pearson correlation coefﬁcient and

cosine distance, Table 4 has fewer rows than Table 3.

Please note big differences between the best neighbor-

hood size obtained with different libraries. To explain

this phenomenon we took a closer look into libraries

implementations of the kNN algorithm. We found out

that they differ signiﬁcantly from each other.

The approach in the Mahout library starts with se-

lecting k nearest neighbors of an active user according

to a given similarity measure. The k value is the one

obtained as a parameter. The rating prediction for a

speciﬁc item consists of two stages. Firstly, the library

KDIR 2019 - 11th International Conference on Knowledge Discovery and Information Retrieval

542

Figure 2: F1-score, Precision, Recall and nDCG depending on the k value computed for the Book-Crossing dataset.

Table 3: Best k-values for different similarity measures

received with the Mahout library on MovieLens 1M and

Book-Crossing datasets.

MovieLens 1M Book-Crossing

Similarity best k MAE best k MAE

Pearson 1400 0.760 5000 2.813

Cosine 2800 0.761 1900 1.454

Euclidean 1480 0.719 100 1.315

Jaccard 250 0.770 2950 1.489

Log-likelihood 255 0.771 4760 1.447

Spearman 1740 0.764 6000 2.211

ﬁlters out all of the nearest neighbors that have not

rated considered item. The second step is to calculate

weighted average based on the similarities and ratings

of a ﬁnal set of users. The actual number of neighbors

in this implementation depends on how many users

among those selected at the beginning have rated an

item for which a rating is predicted. Figure 3 shows

Table 4: Best k-values for different similarity measures

received with the LensKit library on MovieLens 1M and

Book-Crossing datasets.

MovieLens 1M Book-Crossing

Similarity best k MAE best k MAE

Pearson 36 0,771 20 6.957

Cosine 54 0,763 56 1.590

how many users are actually taken into account (the

average of all cases in the test set) depending on the

neighborhood size given as a parameter. The analysis

was carried out on the MovieLens 1M dataset.

In the LensKit library, the k parameter speciﬁes

the actual number of users taken into account in the

rating prediction. After analysing the approaches

used in both libraries, we modiﬁed the implementa-

tion of the LensKit library so that the method of se-

lecting the nearest users would be done in the same

Things You Might Not Know about the k-Nearest Neighbors Algorithm

543

Figure 3: Dependency between an effective neighborhood size and a k value given as a parameter for the Mahout library on

the MovieLens 1M dataset.

way as in the Mahout library (see our source code

Figure 4 shows MAE value depending on the neigh-

borhood size on the MovieLens 1M dataset after

changing the implementation in the LensKit library.

The results obtained on both dataset for the Pear-

son Similarity and Cosine Similarity measures with

the LensKit library adapted to the method of select-

ing the neighborhood as in the Mahout library are pre-

sented in Table 5.

Table 5: Best k-values for different similarity measures re-

ceived with modiﬁed LensKit library on MovieLens 1M and

Book-Crossing datasets.

MovieLens 1M Book-Crossing

Similarity best k MAE best k MAE

Pearson 1000 0.765 5000 6.873

Cosine 250 0.766 6800 1.591

It should be noticed that k values increased drasti-

cally while MAE values remained almost the same

in comparison with the outcome from unchanged

LensKit library. However, all results still differ from

those obtained with the Mahout library. For further

experiments we use unchanged LensKit implementa-

tion.

https://github.com/marracz/praca-magisterska

5 TIME OF GENERATING

RECOMMENDATIONS FOR

KNN TYPE ALGORITHMS

In this section we focus on the time that the kNN algo-

rithm needs to generate a list of top-10 recommenda-

tions depending on a similarity measure and a library

that were used. We performed our experiments on a

computer with 16 GB of RAM and a processor In-

tel Core i5-7600K 3.80GHz with 4 1-thread cores and

x86 64 architecture. An installed operating system is

Linux 4.13.0-38-generic #43∼16.04.1-Ubuntu.

Experiments were run 20 times for each library

and similarity measure on each dataset. Based on the

results we computed average time of recommenda-

tions generation, its standard deviation (σ) and stan-

dard relative error (SRE). Because of big differences

in an execution time, some outcomes are reported in

seconds and some in minutes.

Tables 6 and 7 present results obtained with

the LensKit library on MovieLens 1M and Book-

Crossing datasets respectively. The time needed for

generating recommendations on the Book-Crossing

dataset is bigger than the one for the MovieLens. It

could be simply justiﬁed by the size of datasets.

Table 6: Average times (

t) of generating recommendations

for users from the MovieLens 1M dataset with the LensKit

library.

Similarity

t [s] σ [s] SRE [%]

Pearson 533.264 28.001 1.17

Cosine 523.266 20.993 0.90

KDIR 2019 - 11th International Conference on Knowledge Discovery and Information Retrieval

544

Figure 4: MAE depending on the k value computed for the MovieLens 1M dataset (modiﬁed LensKit).

Table 7: Average times (

t) of generating recommendations

for users from the Book-Crossing dataset with the LensKit

library.

Similarity

t [min.] σ [min.] SRE [%]

Pearson 50.359 2.303 1.02

Cosine 100.005 3.982 0.89

Tables 8 and 9 present results obtained with

the Mahout library on MovieLens 1M and Book-

Crossing datasets respectively.

Table 8: Average times (

t) of generating recommendations

for users from the MovieLens 1M dataset with the Mahout

library.

Similarity

t [min] σ [min] SRE [%]

Pearson 29.115 1.953 1.50

Cosine 52.105 5.249 2.25

Euclidean 21.571 1.270 1.32

Log-likelihood 50.321 2.654 1.18

Jaccard 27.891 1.044 0.84

Spearman 398.809 37.934 2.13

Table 9: Average times (

t) of generating recommendations

for users from the Book-Crossing dataset with the Mahout

library.

Similarity

t [s] σ [s] SRE

Pearson 244.964 34.732 2.59

Cosine 381.225 27.869 1.63

Euclidean 253.590 20.187 1.78

Log-likelihood 19450.016 1327.954 1.53

Jaccard 2581.383 166.905 1.45

Spearman 10580.837 730.008 1.54

Here, the situation is opposite as for the LensKit

library. The time of generating recommendations is

higher for the MovieLens 1M dataset. After all ex-

periments we reported in this paper it is not surpris-

ing. The Book-Crossing dataset is bigger than the

MovieLens but it is also very sparse. If we recall

how the Mahout library computes the neighborhood

for the kNN algorithm, we understand that the effec-

tive k value must be much smaller than the neighbor-

hood size parameter value.

Things You Might Not Know about the k-Nearest Neighbors Algorithm

545

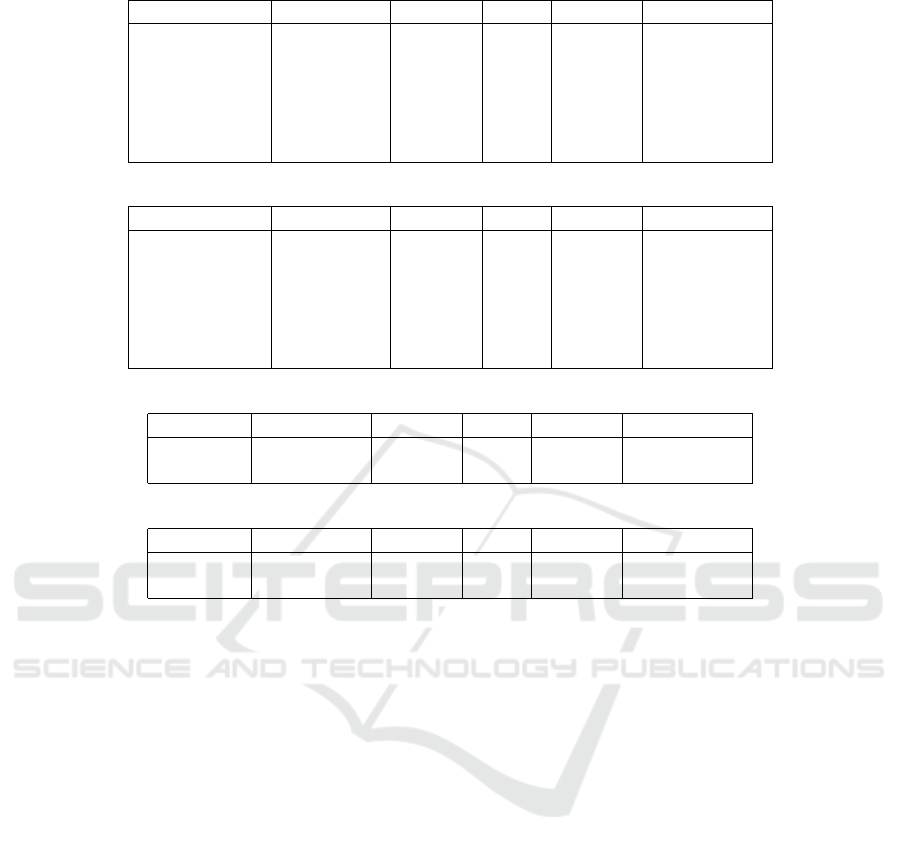
Table 10: Final results obtained with the Mahout library on the MovieLens 1M dataset.

Similarity Time [min.] Ranking MAE Ranking Total ranking

Euclidean 21.571 1 0.719 1 2

Pearson 29.115 3 0.760 2 5

Jaccard 27.891 2 0.770 5 7

Cosine 52.105 5 0.761 3 8

Log-likelihood 50.321 4 0.771 6 10

Spearman 398.809 6 0.764 4 10

Table 11: Final results obtained with the Mahout library on the Book-Crossing dataset.

Similarity Time [min.] Ranking MAE Ranking Total ranking

Euclidean 4.226 2 1.315 1 3

Cosine 6.354 3 1.454 3 6

Pearson 4.083 1 2.813 6 7

Jaccard 43.023 4 1.489 4 8

Log-likelihood 324.167 6 1.447 2 8

Spearman 176.347 5 2.211 5 10

Table 12: Final results obtained with LensKit library on MovieLens 1M dataset.

Similarity Time [min.] Ranking MAE Ranking Total ranking

Cosine 8.721 1 0.763 1 2

Pearson 8.888 2 0.771 2 4

Table 13: Final results obtained with LensKit library on Book-Crossing dataset.

Similarity Time [min.] Ranking MAE Ranking Total ranking

Cosine 100.005 2 1.590 1 3

Pearson 50.359 1 6.957 2 3

We can not clearly say which library is better con-

sidering the time that is needed for generating rec-

ommendations. The Mahout library performs faster

than the LensKit on the Book-Crossing dataset, while

for the MovieLens 1M dataset the opposite is true.

The reasons behind this behaviour are the same as

mentioned before: the size of datasets and their spar-

sity. We could conclude that the Mahout library is less

time consuming than the LensKit while run on sparse

dataset, even if this dataset is large.

6 OUTCOMES COMPARISON

Since the main aim of this paper is to compare simi-

larity measures and recommendation libraries, we had

to summarize obtained results. To do so, we prepared

rankings based on two comparison parameters, i.e. an

average time of generating recommendations and a

prediction error MAE. We report them in Tables 10-

13.

The euclidean similarity obtains the best results

with the Mahout library according to the average time

of generating recommendations and the prediction

error MAE. It outperforms other measures on both

datasets irrespectively of the dataset size or sparsity

(see Tables 10 and 11). The worst similarity mea-

sure regarding the considered datasets is the Spear-

man’s rank correlation coefﬁcient. The kNN algo-

rithm with that similarity performs really slow and

achieves big prediction errors, as shown in Tables 10

and 11. It is actually quite interesting, since similar

measure which is Pearson correlation coefﬁcient ob-

tained much better results for both criteria: an execu-

tion time and a prediction error.

It is hard to decide which similarity measure from

those available in the LensKit library performs the

best. According to Table 12, we could say that the

cosine similarity is better than the Pearson correlation

coefﬁcient on the MovieLens 1M dataset. However,

the differences in the average time of generating rec-

ommendation and the prediction error MAE are very

small. If we also consider results reported in Table

13, we should notice that the kNN algorithm with the

cosine similarity achieves good prediction accuracy,

but it performs two times slower than the same algo-

rithm that uses the Pearson correlation coefﬁcient as

a similarity measure.

To conclude, we could say that the LensKit li-

brary generates recommendations on the MovieLens

KDIR 2019 - 11th International Conference on Knowledge Discovery and Information Retrieval

546

1M dataset much faster than the Mahout library while

achieves similar prediction error values. However, the

Mahout library works pretty well on the sparse and

large Book-Crossing dataset.

7 CONCLUSIONS

This paper focuses on one of the most popular recom-

mendation algorithm, i.e. k Nearest Neighbors and

similarity measures that could be used with it. We

showed that evaluation measures for a ranking task,

i.e. precision, recall, F1-score or nDCG are not al-

ways a good choice for choosing the best neighbor-

hood size k. Better results could be obtained with

a simple prediction error like MAE. Simultaneously,

we identiﬁed differences in the kNN algorithm imple-

mentation between Mahout and LensKit libraries and

show that it inﬂuences the k value, which is much big-

ger for the Mahout library.

We compared different similarity measures ac-

cording to the average time of generating recommen-

dations and the prediction error MAE. The euclidean

similarity obtains the best results with the Mahout li-

brary according to considered criteria. The LensKit

library generates recommendations on the MovieLens

1M dataset much faster than the Mahout library while

achieves similar prediction error values. Neverthe-

less, the Mahout library is less time consuming than

the LensKit while run on sparse dataset, even if this

dataset is large.

REFERENCES

Aggarwal, C. C. (2016). Recommender Systems: The Text-

book. Springer Publishing Company, Incorporated,

1st edition.

Breese, J. S., Heckerman, D., and Kadie, C. (1998). Empir-

ical analysis of predictive algorithms for collaborative

ﬁltering. In Proc. of the 14th Conf. on Uncertainty

in Artiﬁcial Intelligence, UAI’98, pages 43–52, San

Francisco, CA, USA. Morgan Kaufmann Publishers

Inc.

Desrosiers, C. and Karypis, G. (2011). A Comprehen-

sive Survey of Neighborhood-based Recommendation

Methods, pages 107–144. Springer US, Boston, MA.

Dunning, T. (1993). Accurate methods for the statistics of

surprise and coincidence. COMPUTATIONAL LIN-

GUISTICS, 19(1):61–74.

Good, N., Schafer, J. B., Konstan, J. A., Borchers, A., Sar-

war, B., Herlocker, J., and Riedl, J. (1999). Combining

collaborative ﬁltering with personal agents for better

recommendations. In Proc. of the 16th National Conf.

on Artiﬁcial Intelligence and the 11th Conf. Innova-

tive Appl. of Artiﬁcial Intelligence, AAAI ’99/IAAI

’99, pages 439–446, Menlo Park, CA, USA. Ameri-

can Association for Artiﬁcial Intelligence.

Harper, F. M. and Konstan, J. A. (2015). The movielens

datasets: History and context. ACM Trans. Interact.

Intell. Syst., 5(4):19:1–19:19.

Herlocker, J., Konstan, J. A., and Riedl, J. (2002). An

empirical analysis of design choices in neighborhood-

based collaborative ﬁltering algorithms. Information

Retrieval, 5(4):287–310.

Herlocker, J. L., Konstan, J. A., Borchers, A., and Riedl,

J. (1999). An algorithmic framework for performing

collaborative ﬁltering. In Proc. of the 22Nd Annual

Int. ACM SIGIR Conf. on Research and Development

in Information Retrieval, SIGIR ’99, pages 230–237,

New York, NY, USA. ACM.

Jaccard, P. (1902). Lois de distribution ﬂorale dans la zone

alpine. Bulletin de la Soci

e vaudoise des sciences

naturelles, 38:69–130.

Jaccard, P. (1912). The distribution of ﬂora in the alpine

zone. New Phytologist, 11:37 – 50.

Jannach, D., Zanker, M., Felfernig, A., and Friedrich, G.

(2010). Recommender Systems: An Introduction.

Cambridge University Press, New York, NY, USA, 1st

edition.

Kim, J. K. and Cho, Y. H. (2003). Using web usage min-

ing and svd to improve e-commerce recommendation

quality. In Lee, J. and Barley, M., editors, Intelligent

Agents and Multi-Agent Systems, pages 86–97, Berlin,

Heidelberg. Springer Berlin Heidelberg.

Pearson, K. (1895). Note on regression and inheritance in

the case of two parents. Proc. of the Royal Society of

London, 58:240–242.

Singhal, A. (2001). Modern information retrieval: a brief

overview. Bulletin of the IEEE Computer Society

Technical Committee on Data Engineering, 24(4):35–

42.

Soper, H. E., Young, A. W., Cave, B. M., Lee, A., and

Pearson, K. (1917). On the distribution of the corre-

lation coefﬁcient in small samples. appendix ii to the

papers of ”student” and r. a. ﬁsher. a cooperative study.

Biometrika, 11(4):328–413.

Symeonidis, P., Ntempos, D., and Manolopoulos, Y. (2014).

Recommender Systems for Location-based Social Net-

works.

Ziegler, C.-N., McNee, S. M., Konstan, J. A., and Lausen,

G. (2005). Improving recommendation lists through

topic diversiﬁcation. In Proc. of the 14th Int. Conf. on

World Wide Web, WWW ’05, pages 22–32, New York,

NY, USA. ACM.

Things You Might Not Know about the k-Nearest Neighbors Algorithm

547