
A Discretized Enriched Technique to Enhance Machine Learning
Performance in Credit Scoring
Roberto Saia, Salvatore Carta, Diego Reforgiato Recupero, Gianni Fenu and Marco Saia
Department of Mathematics and Computer Science,
University of Cagliari, Via Ospedale 72 - 09124 Cagliari, Italy
Keywords:
Business Intelligence, Decision Support System, Credit Scoring, Machine Learning, Algorithms.
Abstract:
The automated credit scoring tools play a crucial role in many financial environments, since they are able to
perform a real-time evaluation of a user (e.g., a loan applicant) on the basis of several solvency criteria, without
the aid of human operators. Such an automation allows who work and offer services in the financial area to
take quick decisions with regard to different services, first and foremost those concerning the consumer credit,
whose requests have exponentially increased over the last years. In order to face some well-known problems
related to the state-of-the-art credit scoring approaches, this paper formalizes a novel data model that we
called Discretized Enriched Data (DED), which operates by transforming the original feature space in order
to improve the performance of the credit scoring machine learning algorithms. The idea behind the proposed
DED model revolves around two processes, the first one aimed to reduce the number of feature patterns
through a data discretization process, and the second one aimed to enrich the discretized data by adding
several meta-features. The data discretization faces the problem of heterogeneity, which characterizes such a
domain, whereas the data enrichment works on the related loss of information by adding meta-features that
improve the data characterization. Our model has been evaluated in the context of real-world datasets with
different sizes and levels of data unbalance, which are considered a benchmark in credit scoring literature.
The obtained results indicate that it is able to improve the performance of one of the most performing machine
learning algorithm largely used in this field, opening up new perspectives for the definition of more effective
credit scoring solutions.
1 INTRODUCTION
In the past decades, the credit scoring techniques have
assumed a great importance in many financial sec-
tors (Siddiqi, 2017), since they are able to take de-
cisions in real-time, avoiding the employment of hu-
mans in order to evaluate the available information
about people who request certain financial services,
such as, for instance, a loan.
In such a context, it should be noted how the major
financial losses of an operator that offers financial ser-
vices are those related to an incorrect evaluation of the
customers reliability (Bijak et al., 2015), For instance,
in the consumer credit context (Livshits, 2015), such
a reliability is expressed in terms of user solvency and
the losses are related to the loans that have not been
fully or partially repaid.
Many sector studies have reported that the con-
sumer credit has exponentially increased over the last
years, as shown in Figure 1, which reports a study
on the Euro area performed by Trading Economics
1
on the basis of the European Central Bank (ECB)
2
data. The Euro area has been used by way of exam-
ple, since a similar trend is also registered in other
world areas such as, for instance, Russia and USA.
Other aspects related to the role of the Credit Rating
Agencies (CRAs)
3
with regard to the globalization of
the financial markets have been investigated and dis-
cussed in (Doumpos et al., 2019).
For the aforementioned reasons, we are assisting
and supporting an important increase of the invest-
ments, in terms of money and number of researchers,
with the aim to develop increasingly effective credit
scoring techniques. Ideally, these technologies should
be able to correctly classify each user as reliable or
unreliable, on the basis of the available information
1
https://tradingeconomics.com/
2
https://www.ecb.europa.eu/
3
Also defined ratings services, they are companies that
assign credit ratings.
202
Saia, R., Carta, S., Recupero, D., Fenu, G. and Saia, M.
A Discretized Enriched Technique to Enhance Machine Learning Performance in Credit Scoring.
DOI: 10.5220/0008377702020213
In Proceedings of the 11th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2019), pages 202-213
ISBN: 978-989-758-382-7
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Apr. 2018 Jul. 2018 Oct. 2018 Jan. 2019 Apr. 2019
660
670
680
690
700
Millions of euros (×1000)
Figure 1: Euro Area Consumer Credit.
(e.g., age, current job, status of previous loans, etc.).
Basically, these techniques can be considered sta-
tistical approaches (Mester et al., 1997) focused on
the evaluation of the probability that a user will not re-
pay (or partially repay) a credit (Mester et al., 1997).
On the basis of this probability, typically calculated
in real-time, a financial operator can decide whether
to grant or not the requested financial service (Hassan
et al., 2018).
Similarly to other data domains such as, for in-
stance, those related to the Fraud Detection or the In-
trusion Detection tasks (Dal Pozzolo et al., 2014; Saia
et al., 2017; Saia, 2017), the information that is usu-
ally available to train a credit scoring model is charac-
terized by an unbalanced distribution of data (Rodda
and Erothi, 2016; Saia et al., 2018b).
Therefore, the data that is available to define the
evaluation model (from now on denoted as instances)
is composed by a huge number of reliable sam-
ples, with respect to the unreliable ones (Khemakhem
et al., 2018). Several studies in literature prove that
such a data unbalance reduces the effectiveness of
classification algorithms (Haixiang et al., 2017; Khe-
makhem et al., 2018).
1.1 Research Motivation
On the basis of our previous experience (Saia and
Carta, 2016c; Saia and Carta, 2016a; Saia and Carta,
2016b; Saia and Carta, 2017; Saia et al., 2018a), the
proposed Discretized Enriched Data (DED) model
has been designed by us in order to face some well-
known problems related to this data domain. The first
of them is given by the heterogeneity of the patterns
used to define a classification model, since they de-
pend on the available information about the users,
which is previously collected. Such information is
characterized by a number of features that could be
very different, even when they define the same class
of information.
Through our DED model we perform a twofold
process, the first one aimed to reduce the pattern by
adopting a discretization criterion, whereas the sec-
ond one aimed to enrich the discretized features by
adding a series of meta-features able to better char-
acterize the related class of information (i.e., reliable
or unreliable). In order to assess the real advantages
related to our approach, without the risk of results
being biased by over-fitting (Hawkins, 2004), differ-
ently from the majority of related works in literature,
we do not use a canonical cross-validation criterion.
This because a canonical cross-validation crite-
rion does not guarantee a complete separation be-
tween the data used to define the evaluation model and
the data used to evaluate its performance. For this rea-
son, we have adopted a criterion, largely used in other
domains, which focuses on the importance of assess-
ing the real performance of an evaluation/prediction
model (e.g. financial market forecasting (Henrique
et al., 2019)). Specifically, we assess the performance
of the DED model on never seen before data (conven-
tionally denoted as out-of-sample) and we define it on
different data (conventionally denoted as in-sample).
The canonical cross-validation criterion has been used
only in the context of these two sets of data.
The scientific contribution related to our work is
the following:
- formalization of the Discretized Enriched Data
(DED) model, which is aimed to improve the effec-
tiveness of the machine learning algorithms in the
credit scoring data domain;
- implementation of the DED model in the context
of a machine learning classifier we selected on the
basis of its effectiveness through a series of exper-
iments performed by using the in-sample part of
each credit scoring dataset;
- evaluation of the DED model performance, per-
formed by using the out-of-sample part of each
credit scoring dataset, comparing it with the perfor-
mance of the same machine learning algorithm that
uses the canonical data model.
The rest of the paper has been structured as fol-
lows: Section 2 provides information about the back-
ground and the related work of the credit scoring do-
main; Section 3 introduces the formal notation used in
this paper and defines the problem we address; Sec-
tion 4 provides the formalization and the implemen-
tation details of the proposed data model; Section 5
describes the experimental environment, the datasets,
the experimental strategy, and the used metrics, re-
porting and discussing the experimental results; Sec-
tion 6 makes some concluding remarks and directions
for future works.
A Discretized Enriched Technique to Enhance Machine Learning Performance in Credit Scoring
203

2 BACKGROUND AND RELATED
WORK
This section provides an overview of the concepts re-
lated to the credit scoring research field and the state-
of-the-art solutions, by also describing problems that
are still unsolved and by introducing the idea that
stands behind the DED model proposed in this paper.
2.1 Credit Risk Models
In accord with several studies in literature (Crook
et al., 2007), we start off by identifying the follow-
ing different types of credit risk models, with regard
to a default
4
event: the Probability of Default (PD)
model, which is aimed to evaluate the likelihood of a
default over a specified period; the Exposure At De-
fault (EAD) model, which is aimed to evaluate the
total value a financial operator is exposed to when a
loan defaults; the Loss Given Default (LGD) model,
which is aimed to evaluate the amount of money a fi-
nancial operator loses when a loan defaults.
In this paper we take into account the first of these
credit risk models (i.e., the Probability of Default),
expressing it in terms of binary classification of the
evaluated users, as reliable or unreliable.
2.2 Approaches and Strategies
The current literature offers a number of approaches
and strategies, designed to perform the credit scoring
task, such as:
- those based on statistical methods, where the au-
thors, for instance, exploit the Logistic Regression
(LR) (Sohn et al., 2016) method in order to de-
fine a fuzzy credit scoring model able to predict
the default possibility of a loan, or perform this op-
eration by using the Linear Discriminant Analysis
(LDA) (Khemais et al., 2016);
- those that rely on Machine Learning (ML) algo-
rithms (Barboza et al., 2017), such as the Support
Vector Machines (SVM) method employed in (Har-
ris, 2015), where the authors adopt a Clustered Sup-
port Vector Machine (CSVM) approach to perform
the credit scoring, or in (Zhang et al., 2018), where
instead the authors exploit an optimized Random
Forest (RF) approach to perform such a task;
- those that exploit Artificial Intelligence (AI) strate-
gies (Liu et al., 2019), such as the Artificial Neural
Network (ANN) (Bequ
´
e and Lessmann, 2017);
4
This term denotes the failure to meet the legal obliga-
tions/conditions related to a loan.
- those that rely on transformed data domains, such
as in (Saia and Carta, 2017; Saia et al., 2018a),
where the authors exploit, respectively, the Fourier
and Wavelet transforms;
- those where specific aspects, such as data
entropy (Saia and Carta, 2016a), linear-
dependence (Saia and Carta, 2016c; Saia and
Carta, 2016b), or word embeddings (Boratto et al.,
2016) have been taken into account to perform
credit scoring tasks (Zhao et al., 2019);
- those based on hybrid approaches (Ala’raj and Ab-
bod, 2016; Tripathi et al., 2018) where several dif-
ferent approaches and strategies have been com-
bined in order to define a model able to improve
the credit scoring performance.
The literature also provides many surveys where
the performance of the state-of-the-art solutions for
credit scoring have been compared, such as that
in (Lessmann et al., 2015b).
2.3 Open Problems
Regardless of the approach and strategy used to per-
form credit scoring tasks, there are several common
problems that have to be addressed. The most impor-
tant of them are:
- Datasets Availability: the literature puts an accent
on the limited availability of public datasets to use
in the validation process (Lessmann et al., 2015a).
This issue is mainly related to the fact that finan-
cial operators often refuse to share their data, or
to privacy reasons, e.g., there are many countries
where legal reasons, related to the protection of
privacy, prevent the creation of publicly available
datasets (Jappelli et al., 2000);
- Data Unbalance: the difference between the sam-
ples related to the reliable cases and the samples
related to the unreliable ones, is a common charac-
teristic between the available datasets (Brown and
Mues, 2012). A data configuration of this kind re-
duces the performance of evaluation models that are
trained with these unbalanced sets of data (Chawla
et al., 2004);
- Samples Unavailability: it is related to the well-
known cold start problem that affects many re-
search areas (Li et al., 2019). It happens when there
is no availability of samples related to a class of in-
formation (e.g., the unreliable one), making it im-
possible to train an evaluation model.
2.4 Evaluation Metrics
Several studies have also been performed in literature,
in order to identify the best performance evaluation
KDIR 2019 - 11th International Conference on Knowledge Discovery and Information Retrieval
204

1 2 3 4
5 6
7 8 9 10
0.0
20.0
40.0
60.0
80.0
100.0
5
19
41
71
Discretization range
Continuous values
Figure 2: Discretization Process.
criteria to adopt for a correct evaluation of credit scor-
ing models, such as that in (Chen et al., 2016). Some
of the most used metrics for assessing the effective-
ness of a credit scoring model are reported in the fol-
lowing:
- those based on the confusion matrix
5
, such as the
Accuracy, the Sensitivity, the Specificity, or the
Matthews Correlation Coefficient (MCC) (Powers,
2011);
- those based on the error analysis, such as the Mean
Square Error (MSE), the Root Mean Square Error
(RMSE), or the Mean Absolute Error (MAE) (Chai
and Draxler, 2014);
- those based on the the Receiver Operating Charac-
teristic (ROC) curve, such as the Area Under the
ROC Curve (AUC) (Huang and Ling, 2005).
Considering that some of these metrics do not
work well with data unbalance (Jeni et al., 2013),
such as, for instance, the majority of metrics based
on on the confusion matrix, many works in literature
addressing the problem of unbalanced datasets (e.g.,
as it happens in the credit scoring context taken into
account in this paper) adopt more that one metric to
correctly evaluate their results.
2.5 Data Transformation
Some basic concepts, related to data discretization
and enrichment processes, are briefly introduced in
this section, along with the reasons why we decided
to use them for defining the proposed DED model.
2.5.1 Discretization
Many algorithms must have knowledge of the type
and domain of the data where they operate and, in
addition, some of them (e.g., Decision Trees) require
categorical feature values (Garc
´
ıa et al., 2016), con-
straining us to perform a preprocessing of the contin-
uous feature values through a discretization method.
The process of data discretization is largely
adopted in literature as an effective data preprocess-
5
The matrix of size 2x2 that contains the number of True
Negatives (TN), False Negatives (FN), True Positives (TP),
and False Positives (FP).
ing technique (Liu et al., 2002). Its goal is to trans-
form the feature values from a quantitative to a quali-
tative form, by dividing each feature value into a dis-
crete number of non overlapped intervals. This means
that each numerical feature value (continuous or dis-
crete) is mapped into one of these intervals, improv-
ing the effectiveness of many machine learning al-
gorithms (Wu and Kumar, 2009) that deal with real-
world data usually characterized by continuous val-
ues.
However, regardless of the algorithms that need
a discretized data input, the discretization process
presents additional advantages, such as the data di-
mensionality reduction that leads towards a faster and
accurate learning (Garc
´
ıa et al., 2016) or the improve-
ment in terms of data understandability, given by the
discretization of the original continuous values (Liu
et al., 2002).
If, on one hand, the main disadvantage of a dis-
cretization process is given by the loss of information
that occurs during the transformation of continuous
values into discrete values, on the other hand, an op-
timal discretization of the original data represents a
NP-complete
6
process.
In the DED model proposed in this paper, the data
discretization process produces a twofold advantage:
the first one related to the aforementioned benefits for
the involved machine learning algorithms; the second
one related to the reduction of the possible feature
patterns, since all the continuous values have been
mapped to a limited range of discrete values.
By way of example, Figure 2 shows the discretiza-
tion of four feature values defined in a continue range
of values [0,100] into a discrete range {0,1,...,10}.
2.5.2 Enrichment
The literature indicates the data enrichment as a pro-
cess adopted in order to improve a data domain
through a series of additional information, such as
meta-features. For instance, the work presented
in (Giraud-Carrier et al., 2004) defines a set of meta-
features able to improve the prediction performance
of the learning algorithms taken into account.
The meta-features are usually defined by aggre-
gating some original features, according to a specific
metric (e.g., minimum value, maximum value, mean
value, standard deviation, etc.), which can be calcu-
lated in the space of a single dataset instance (row)
or in the context of the entire dataset (Castiello et al.,
2005).
6
The computational complexity theory defines NP-
complete a problem when its solution requires a restricted
class of brute force search algorithms
A Discretized Enriched Technique to Enhance Machine Learning Performance in Credit Scoring
205

It should be observed that the meta-features are
largely used in the field of Meta Learning (Vilalta and
Drissi, 2002), a branch of machine learning that ex-
ploits automatic learning algorithms on meta-data in
the context of machine learning processes.
For this paper purposes, we exploit them to bal-
ance the loss of information, which is a consequence
of the applied discretization process, in order to add
further information aimed to well characterize the in-
volved classes of information (i.e., reliable and un-
reliable). More formally, given a set of discretized
features {d
1
,d
2
,...,d
X
}, we add a series of meta-
features to them {m
1
,m
2
,...,m
Y
}, obtaining a new
set of features, as shown in Equation 1.
d
1,1
,d
1,2
,..., d
1,X
,m
1,X+1
,m
1,X+2
,. .., m
1,X+Y
(1)
3 NOTATION AND PROBLEM
DEFINITION
This section describes the formal notation adopted in
this paper and defines the addressed problem.
3.1 Formal Notation
Given a set I of already classified instances, com-
posed by a subset I
+
⊆ I of reliable cases and a sub-
set I
−
⊆ I of unreliable cases, and a set
ˆ
I of unclas-
sified instances, considering that an instance is com-
posed by a set of features F and that it belongs to only
one class in the set C, we define the formal notation
adopted in this paper as reported in Table 1.
Table 1: Formal Notation.
Notation Description Note
I = {i
1
,i
2
,...,i
X
} Set of classified instances
I
+
= {i
+
1
,i
+
2
,...,i
+
Y
} Subset of reliable instances I
+
⊆ I
I
−
= {i
−
1
,i
−
2
,...,i
−
W
} Subset of unreliable instances I
−
⊆ I
ˆ
I = {
ˆ
i
1
,
ˆ
i
2
,...,
ˆ
i
Z
} Set of unclassified instances
F = {f
1
, f
2
,..., f
N
} Set of instance features
C = {reliable,unreliable} Set of instance classifications
3.2 Problem Definition
We can formalize our objective as shown in Equa-
tion 2, where the function f (
ˆ
i,I) evaluates the classi-
fication of the
ˆ
i instance, performed by exploiting the
available information in the set I. It returns a binary
value β, where 0 denotes a misclassification and 1 de-
notes a correct classification. Therefore, our objec-
tive is the maximization of the σ value, which repre-
sents the sum of the β values returned by the function
f (
ˆ
i,I).
max
0≤σ≤|
ˆ
I|
σ =
|
ˆ
I|
∑
z=1
f (
ˆ
i
z
,I) (2)
4 APPROACH FORMALIZATION
The proposed DED model has been defined and im-
plemented in a credit scoring system by performing
the following four steps:
- Data Discretization: the values of all features in
the sets I and
ˆ
I are discretized in accord with a range
defined in the context of a series of experiments per-
formed by using the in-sample data;
- Data Enrichment: a series of meta-features are de-
fined and added to the discretized features of each
instance i ∈ I and
ˆ
i ∈
ˆ
I;
- Data Model: the DED model to use in the context
of a credit scoring machine learning algorithm is
defined on the basis of the previous data processes;
- Data Classification: the DED model is imple-
mented in a classification algorithm aimed to clas-
sify each instance
ˆ
i ∈
ˆ
I as reliable or unreliable.
4.1 Data Discretization
Each feature f ∈ F in the sets I and
ˆ
I has been pro-
cessed in order to move the original range of value of
each feature to a defined range of discrete integer val-
ues {0,1, . . . , ∆} ∈ Z, where the value of ∆ has been
determined in experimental way, as reported in Sec-
tion 5.4.5.
Denoting the data discretization process as f
∆
−→d,
we operate in order to move each feature f ∈ F from
its original value to one of the values in the discrete
range of integers {d
1
,d
2
,...,d
∆
}. Such a process re-
duces the number of possible patterns of values (con-
tinuous and discrete) given by the original feature
vector F, with respect to the ∆ value, as shown in
Equation 3.
{f
1
, f
2
, . .. , f
N
}
∆
−→ {d
1
,d
2
,. .., d
N
}, ∀ i ∈I
{f
1
, f
2
, . .. , f
N
}
∆
−→ {d
1
,d
2
,. .., d
N
}, ∀
ˆ
i ∈
ˆ
I
(3)
4.2 Data Enrichment
After performing the discretization process
previously described, the new feature vector
{d
1
,d
2
,...,d
∆
} of each instance in the sets I and
ˆ
I
has been enriched by adding some meta-features we
denoted µ. These meta-features have been calculated
in the context of each feature vector and they are:
Minimum (m), Maximum (M), Average (A), and Stan-
dard Deviation (S), then we have µ = {m,M, A, S}.
This new process mitigates the pattern reduction
KDIR 2019 - 11th International Conference on Knowledge Discovery and Information Retrieval
206

operated during the discretization by adding a series
of information able to improve the characterization
of the instances, and it is formalized in Equation 4.
µ =
m = min(d
1
,d
2
,. .., d
N
)
M = max(d
1
,d
2
,. .., d
N
)
A =
1
N
∑
N
n=1
(d
n
)
S =
q
1
N−1
∑
N
n=1
(d
n
−
¯
d)
2
(4)
4.3 Data Model
As a result of the data discretization and data enrich-
ment processes, we obtain our new DED data model
where the original values f ∈ F assumed by each
instance feature have been transformed into a new
value, in accord with an experimental defined value ∆,
and the number of features have been extended with a
series µ = {m,M,A,S} of new meta-features, as for-
malized in Equation 5. It should be noted that, for the
sake of simplicity, the equation refers to the set I only,
but the formalization is the same for the set
ˆ
I).
DED(I) =
d
1,1
d
1,2
... d
1,N
m
1,N+1
M
1,N+2
A
1,N+3
S
1,N+4
d
2,1
d
2,2
... d
2,N
m
2,N+1
M
2,N+2
A
2,N+3
S
2,N+4
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
d
X,1
d
X,2
... d
X,N
m
X,N+1
M
X,N+2
A
X,N+3
S
X,N+4
(5)
4.4 Data Classification
Finally, in the last step of our approach, we implement
the new DED model in the classification Algorithm 1,
in order to perform the classification of each unclas-
sified instance
ˆ
i ∈
ˆ
I.
At step 1, the procedure takes the following pa-
rameters as input: a classification algorithm alg, the
set of classified instances in the set I, and the unclas-
sified instances in the set
ˆ
I. The data transformation
related to our DED approach is performed for these
sets of data at steps 2 and 3, and the transformed data
of the set I is used in order to train the algorithm alg
model at step 4. The classification process is per-
formed at steps from 5 to 8 for each instance in the
set
ˆ
I and the classifications are stored in the out. At
the end of the process of classification, the results are
returned by the algorithm at step 9.
5 EXPERIMENTS
This section presents the experimental environment,
the adopted real-world datasets, the assessment met-
rics, the experimental strategy, and the obtained re-
sults.
Algorithm 1: Instance classification.
Require: alg=Classifier, I=Classified instances,
ˆ
I=Unclassified instances
Ensure: out=Classification of instances in
ˆ
I
1: procedure INSTANCECLASSIFICATION(alg, I,
ˆ
I)
2: I
00
← getDED(I)
3:
ˆ
I
00
← getDED(
ˆ
I)
4: model ←Classi f ierTraining(alg, I
00
)
5: for each
ˆ
i
00
∈
ˆ
I
00
do
6: c ←getClass(model,
ˆ
i
00
)
7: out.add(c)
8: end for
9: return out
10: end procedure
5.1 Environment
The code related to the performed experiments has
been written in Python language, using the scikit-
learn
7
library.
In addition, in order to grant the experiments re-
producibility, we have fixed the seed of the pseudo-
random number generator to 1 in the scikit-learn code
(i.e., the random state parameter).
5.2 Datasets
The German Credit (GC) and the Default of Credit
Card Clients (GC) are real-world datasets we selected
in order to validate the proposed DED model. They
represent two benchmarks in the credit score research
context and they both are characterized by different
size and data unbalance (as shown in Table 2), repro-
ducing different data configurations in the credit scor-
ing scenario. All of them are freely downloadable at
the UCI Repository of Machine Learning Databases
8
.
Premising that each instance (i.e., each dataset
row) in these datasets is numerically classified as reli-
able or unreliable, in the following we briefly provide
their description:
• the GC dataset is composed by 1,000 instances,
of which 700 classified as reliable (70.00%) and
300 classified as unreliable (30.00%), and each
instance is characterized by 20 features, as de-
tailed in Table 3.
• the DC dataset is composed by 30,000 instances,
of which 23,364 classified as reliable (77.88%)
and 6,636 classified as unreliable (22.12%), and
each instance is characterized by 23 features, as
detailed in Table 4;
7
http://scikit-learn.org
8
ftp://ftp.ics.uci.edu/pub/machine-learning-
databases/statlog/
A Discretized Enriched Technique to Enhance Machine Learning Performance in Credit Scoring
207

Table 2: Datasets composition.
Dataset Total Reliable Unreliable Number of
name instances instances instances features
GC 1,000 700 300 21
DC 30,000 23,364 6,636 23
Table 3: Features of GC Dataset.
Field Feature Field Feature
01 Status of checking account 11 Present residence since
02 Duration 12 Property
03 Credit history 13 Age
04 Purpose 14 Other installment plans
05 Credit amount 15 Housing
06 Savings account/bonds 16 Existing credits
07 Present employment since 17 Job
08 Installment rate 18 Maintained people
09 Personal status and sex 19 Telephone
10 Other debtors/guarantors 20 Foreign worker
Table 4: Features of DC Dataset.
Field Feature Field Feature
01 Credit amount 13 Bill statement in August 2005
02 Gender 14 Bill statement in July 2005
03 Education 15 Bill statement in June 2005
04 Marital status 16 Bill statement in May 2005
05 Age 17 Bill statement in April 2005
06 Repayments in September 2005 18 Amount paid in September 2005
07 Repayments in August 2005 19 Amount paid in August 2005
08 Repayments in July 2005 20 Amount paid in July 2005
09 Repayments in June 2005 21 Amount paid in June 2005
10 Repayments in May 2005 22 Amount paid in May 2005
11 Repayments in April 2005 23 Amount paid in April 2005
12 Bill statement in September 2005
5.3 Metrics
In order to assess the performance of the proposed
DED model, with regard to a canonical data model,
we have adopted two different metrics.
The first one is the Sensitivity, a metric based on
the confusion matrix that reports us the true positive
rate related to the performed classification, then the
capability of the evaluation model to correctly classify
the reliable instances.
The second one is the Matthews Correlation Co-
efficient, it is also based on the confusion matrix and
it is able to evaluate the effectiveness of the evalua-
tion model in terms of distinguishing the reliable in-
stances from the unreliable ones and, for this reason,
it is commonly used in order to evaluate the perfor-
mance of a binary evaluation model.
The third metric is based on the the Receiver Op-
erating Characteristic (ROC) curve. It is the Area
Under the Receiver Operating Characteristic curve
(AUC) and it represents a metric largely used for
its capability to evaluate the predictive capability of
an evaluation model, even when the involved data is
characterized by a high degree of data unbalance.
All the aforementioned metrics are formalized in
the following sections.
5.3.1 Sensitivity
According to the formal notation provided in Sec-
tion 3.1, the formalization of the Sensitivity metric
is shown in Equation 6, where
ˆ
I denotes the set of
unclassified instances, TP is the number of instances
correctly classified as reliable, and FN is the num-
ber of unreliable instances wrongly classified as reli-
able. This gives us the proportion of instances which
are correctly classified by an evaluation model (Bequ
´
e
and Lessmann, 2017).
Sensitivity(
ˆ
I) =
T P
(T P + FN)
(6)
5.3.2 Matthews Correlation Coefficient
The Matthews Correlation Coefficient (MCC) per-
forms a balanced evaluation and it also works well
with data imbalance (Luque et al., 2019; Boughorbel
et al., 2017). Its formalization is shown in Equation 7
and its result is a value in the range [−1,+1], with
+1 when all the classifications are correct and −1
when all the classifications are wrong, whereas 0 in-
dicates the performance related to a random predictor.
It should be observed how such a metric can be seen
as a discretization of the Pearson correlation (Benesty
et al., 2009) for binary variables.
MCC =
(T P·T N)−(F P·FN)
√
(T P+FP)·(TP+FN)·(T N+FP)·(T N+FN)
(7)
5.3.3 AUC
As reported in a large number of studies in litera-
ture (Abell
´
an and Castellano, 2017; Powers, 2011) ,
the Area Under the Receiver Operating Characteris-
tic curve (AUC) represents a reliable metric for the
evaluation of the performance related to a credit scor-
ing model. More formally, given the subsets of reli-
able and unreliable instances in the set I, respectively,
I
+
and I
−
, the possible comparisons κ of the scores
of each instance i are formalized in the Equation 8,
whereas the AUC is obtained by averaging over them,
as formalized in Equation 9. It returns a value in the
range [0,1], where 1 denotes the best performance.
κ(i
+
,i
−
) =
1, i f i
+
> i
−
0.5, i f i
+
= i
−
0, i f i
+
< i
−
(8)
AUC =
1
I
+
·I
−
|I
+
|
∑
1
|I
−
|
∑
1
κ(i
+
,i
−
) (9)
KDIR 2019 - 11th International Conference on Knowledge Discovery and Information Retrieval
208

5.4 Strategy
Here we report all the details of the experimental
strategy, from the choice of the best state-of-the-art
algorithm to the definition of the discretization range
∆.
5.4.1 Algorithm Selection
In order to evaluate the benefits of our DED model,
we will perform a series of experiments aimed to se-
lect the most performing state-of-the-art algorithm to
use as competitor. This means that we compare the
performance of this algorithm, before and after ap-
plying our data model.
For this task we have taken into account the
following five machine learning algorithms, since
they represent the most performing and widely used
ones in credit scoring literature: Gradient Boost-
ing (GBC) (Chopra and Bhilare, 2018); Adaptive
Boosting (ADA) (Xia et al., 2017); Random Forests
(RFA) (Malekipirbazari and Aksakalli, 2015); Multi-
layer Perceptron (MLP) (Luo et al., 2017); Decision
Tree (DTC) (Damrongsakmethee and Neagoe, 2019).
5.4.2 Evaluation Criteria
The proposed DED model has been evaluated by di-
viding each dataset in two parts: the first one (in-
sample), used to identify the most performing ap-
proach to use as a competitor and to define the ∆ pa-
rameter of our model, which will be applied to the
selected algorithm in order to assess its benefits, and
the second one (out-of-sample), which we use for this
operation (i.e., performance comparison).
This kind of strategy, analogously to other stud-
ies in the literature (Rapach and Wohar, 2006), allows
us to evaluate the results, by preventing the algorithm
selection and parameter definition process from intro-
ducing bias by over-fitting (Hawkins, 2004), a risk re-
lated to the use of a canonical k-fold cross-validation
process of data validation.
For this reason, each of the adopted datasets (i.e.,
GC and DC) has been divided into an in-sample part
(50%) and an out-of-sample part (50%) . In addition,
with the aim to further reduce the impact of the data
dependency, in the context of each of these subsets we
have adopted a k-fold cross-validation criterion (k=5).
5.4.3 Data Preprocessing
Before the experiments, we preprocessed the datasets
through a binarization method aimed to transform
each instance classification (when required) from its
original form to the binary form 0=reliable and 1=un-
reliable.
According to the literature (Ghodselahi, 2011;
Wang and Huang, 2009) that, in order to better ex-
pose the data structure to the machine learning algo-
rithms, allowing them to get better performance or
converge faster, suggests to convert the feature val-
ues to the same range of values, we decided to verify
the performance improvement related to the adoption
of two largely used preprocessing methods: normal-
ization and standardization.
The first method rescales each f feature value into
the range [0,1], whereas the second one (also known
as Z-score normalization) rescales the feature values
so that they assume the properties of a Gaussian dis-
tribution with µ = 0 and σ = 1, where µ denotes the
mean and σ the standard deviation from that mean,
according to Equation 10.
f
00
=
f −µ
σ
(10)
As shown in Table 5, which reports the mean per-
formance (i.e., related to the Accuracy, MCC, and
AUC metrics) measured in all datasets and all al-
gorithms after the application of the aforementioned
methods of data preprocessing, along to that mea-
sured without any data preprocessing. The best per-
formances are highlighted in bold and, furthermore,
in this case all the performed experiments involve
only the in-sample part of each dataset.
The results indicate that the data preprocessing
through the normalization and standardization meth-
ods does not lead toward significant improvement in
terms of overall mean performance, since 5 times out
of 10 we obtain a better performance without using
any data preprocessing (against 3 out of 10 and 2 out
of 10). For this reason we decided to not apply any
method of data preprocessing during the paper exper-
iments.
5.4.4 Competitor Selection
On the basis of the algorithms introduced in Sec-
tion 5.4.1, the evaluation criteria defined in Sec-
tion 5.4.2, and the data preprocessing performed
as described in Section 5.4.3, we selected Gradient
Boosting (GBC) as the competitor algorithm to use
in order to evaluate the effectiveness of the proposed
DED model.
It has been selected since the mean value of the
Gradient Boosting performance (i.e., in terms of Sen-
sitivity, MCC, and AUC) measured on all datasets is
better than that of the other algorithms taken into ac-
count, as shown in Table 6.
A Discretized Enriched Technique to Enhance Machine Learning Performance in Credit Scoring
209
0
50
100
150
200
0.50
0.55
0.60
(25)
∆ (GC Dataset)
Performance
0
50
100
150
200
0.61
0.62
(187)
∆ (DC Dataset)
Performance
Figure 3: Out-of-sample Discretization Range Definition.
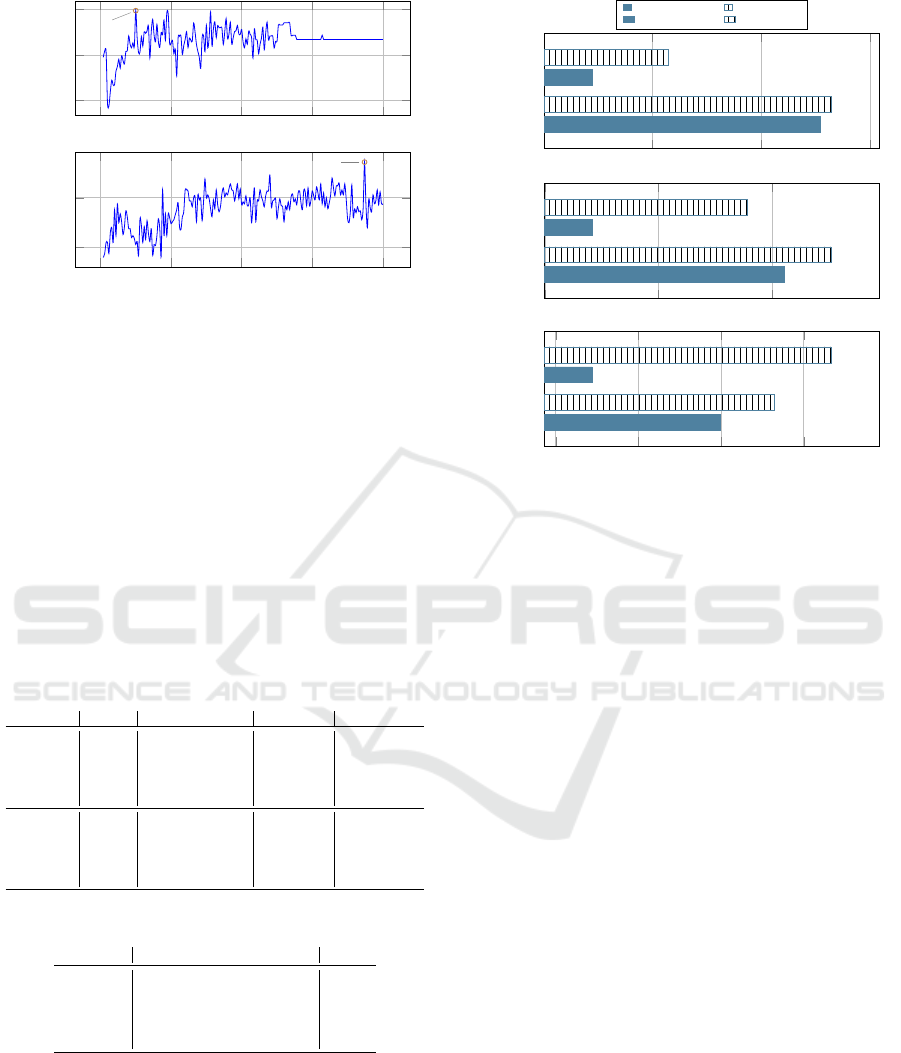
5.4.5 Discretization Range Definition
According to the previous steps, this new set of ex-
periments is aimed to define the optimal range of dis-
cretization ∆ by using the selected algorithm (i.e.,
Gradient Boosting) in the context of the in-sample
part of each dataset.
The obtained results are shown in Figure 3, where
Performance denotes the average value between Ac-
curacy, MCC, and AUC metrics, i.e., (Accuracy +
MCC + AUC)/3. They indicate 25 and 187 as the
optimal ∆ value for the GC and DC datasets, respec-
tively.
Table 5: Mean Performance After Features Preprocessing.
Algorithm Dataset Non-preprocessed Normalized Standardized
GBC GC 0.5614 0.5942 0.6007
ADA GC 0.5766 0.6246 0.5861
RFA GC 0.5540 0.5614 0.5579
MLP GC 0.6114 0.5649 0.5589
DTC GC 0.5796 0.5456 0.5521
GBC DC 0.6087 0.5442 0.6076
ADA DC 0.6031 0.5361 0.5980
RFA DC 0.5613 0.4909 0.5586
MLP DC 0.4613 0.6177 0.5985
DTC DC 0.4982 0.4572 0.5185
Table 6: Algorithms Performance.
Algorithm Sensitivity MCC AUC Mean
GBC 0,8325 0,7065 0,4463 0,6617
ADA 0,8204 0,6943 0,4283 0,6477
RFA 0,8216 0,6939 0,4344 0,6500
MLP 0,7501 0,6038 0,2317 0,5285
DTC 0,8222 0,6791 0,3605 0,6206
5.5 Results
This section presents and discusses the results of the
experiments, with the aim to assess the effectiveness
of the proposed model with regard to a canonical one.
0.80 0.82 0.84
GC
DC
0.7889
0.8308
0.8029
0.8330
Sensitivity
Datasets
Canonical model DED model
0.25
0.30
0.35
GC
DC
0.2708
0.3555
0.3393
0.3764
MCC
Datasets
0.62 0.63 0.64 0.65
GC
DC
0.6244
0.6399
0.6534
0.6464
AUC
Datasets
Figure 4: Out-of-sample Classification Performance.
5.5.1 Results Presentation
In this set of experiments, we apply the algorithm
and the ∆ value detected through the previous exper-
iments, described in Section 5.4, in order to evaluate
the capability of the proposed DED model with re-
gard to a canonical data model based on the original
feature space.
5.5.2 Results Analysis
The analysis of the experimental results leads toward
the following considerations:
- in terms of single metrics of evaluation, Figure 4
shows that our DED model outperforms the canoni-
cal one in terms of Sensitivity, MCC, and AUC met-
rics, in both datasets;
- the improvement measured in terms of Sensitivity is
not related to a degradation of the MCC and AUC
performance, meaning that there is not a direct cor-
relation between the increasing of the true positive
rate and the increasing of the false positive rate;
- considering that the used GC and DC datasets are
characterized by different size (respectively, 1,000
and 30,000 samples) and level of data unbalance
(respectively, 30.00% and 22.12% of unreliable
samples), our model has proved its effectiveness in
different credit scoring scenarios;
- it should be noted that the adopted in-sample/out-
of-sample validation strategy has further increased
the data unbalance in the GG dataset, since its out-
KDIR 2019 - 11th International Conference on Knowledge Discovery and Information Retrieval
210

GC DC
0.56
0.58
0.60
0.62
Datasets
Performance
Canonical model DED model
Figure 5: Overall Performance.
of-sample part contains a 27.20% of reliable sam-
ples (22.51% in the DC dataset);
- combining the in-sample/out-of-sample validation
strategy with the canonical k-fold cross-validation
criterion allowed us to verify the effectiveness of
the proposed model on never seen before data,
therefore without over-fitting;
- the DED model proposed in this paper has proved
its effectiveness in terms of instance characteriza-
tion, by exploiting a combined approach based on
data discretization/enrichment, outperforming the
best machine learning algorithm based on a canon-
ical data model, which we selected in the same data
domain (i.e., in-sample data) used to tune (i.e., the
∆ range of discretization) it;
- in conclusion, since the proposed data model is
able to improve the overall performance (i.e., mean
value of all metrics) of a machine learning algo-
rithm, as shown in Figure 5, it can be exploited in
many state-of-the-art solutions based on machine
learning algorithms, such as, for instance, those
based on hybrid or ensemble configurations.
6 CONCLUSIONS AND FUTURE
WORK
The growth in terms of importance and use of credit
scoring tools has led towards an increasing number
of research activities aimed to detect more and more
effective methods and strategies.
Similarly to other scenarios, characterized by a
data unbalance such as, for instance, the Fraud Detec-
tion or the Intrusion Detection ones, even in this sce-
nario a slight performance improvement of a classifi-
cation model produces enormous advantages, which
in our case are related to the reduction of the financial
losses.
The DED model proposed in this paper has proved
that the transformation of the original feature space,
made by applying a discretization and an enrichment
process, improves the performance of one of the most
performing machine learning algorithm (i.e., Gradi-
ent Boosting).
This result opens up new perspectives for the
definition of more effective credit scoring solutions,
considering that many state-of-the-art approaches are
based on machine learning algorithms (e.g., those that
perform credit scoring in the context of rating agen-
cies, financial institutions, etc.).
As future work we want to test the effectiveness
of the proposed data model in the context of credit
scoring solutions that implement more than a sin-
gle machine learning algorithm, such as, for exam-
ple, the homogeneous and heterogeneous ensemble
approaches.
ACKNOWLEDGEMENTS
This research is partially funded by Italian Ministry
of Education, University and Research - Program
Smart Cities and Communities and Social Innovation
project ILEARNTV (D.D. n.1937 del 05.06.2014,
CUP F74G14000200008 F19G14000910008). We
gratefully acknowledge the support of NVIDIA Cor-
poration with the donation of the Titan Xp GPU used
for this research.
REFERENCES
Abell
´
an, J. and Castellano, J. G. (2017). A compara-
tive study on base classifiers in ensemble methods
for credit scoring. Expert Systems with Applications,
73:1–10.
Ala’raj, M. and Abbod, M. F. (2016). A new hybrid ensem-
ble credit scoring model based on classifiers consen-
sus system approach. Expert Systems with Applica-
tions, 64:36–55.
Barboza, F., Kimura, H., and Altman, E. (2017). Machine
learning models and bankruptcy prediction. Expert
Systems with Applications, 83:405–417.
Benesty, J., Chen, J., Huang, Y., and Cohen, I. (2009).
Pearson correlation coefficient. In Noise reduction in
speech processing, pages 1–4. Springer.
Bequ
´
e, A. and Lessmann, S. (2017). Extreme learning ma-
chines for credit scoring: An empirical evaluation. Ex-
pert Systems with Applications, 86:42–53.
Bijak, K., Mues, C., So, M.-C., and Thomas, L. (2015).
Credit card market literature review: Affordability and
repayment.
Boratto, L., Carta, S., Fenu, G., and Saia, R. (2016). Us-
ing neural word embeddings to model user behavior
and detect user segments. Knowledge-based systems,
108:5–14.
Boughorbel, S., Jarray, F., and El-Anbari, M. (2017). Opti-
mal classifier for imbalanced data using matthews cor-
relation coefficient metric. PloS one, 12(6):e0177678.
A Discretized Enriched Technique to Enhance Machine Learning Performance in Credit Scoring
211

Brown, I. and Mues, C. (2012). An experimental compari-
son of classification algorithms for imbalanced credit
scoring data sets. Expert Systems with Applications,
39(3):3446–3453.
Castiello, C., Castellano, G., and Fanelli, A. M. (2005).
Meta-data: Characterization of input features for
meta-learning. In International Conference on Mod-
eling Decisions for Artificial Intelligence, pages 457–
468. Springer.
Chai, T. and Draxler, R. R. (2014). Root mean square er-
ror (rmse) or mean absolute error (mae)?–arguments
against avoiding rmse in the literature. Geoscientific
model development, 7(3):1247–1250.
Chawla, N. V., Japkowicz, N., and Kotcz, A. (2004). Special
issue on learning from imbalanced data sets. ACM
Sigkdd Explorations Newsletter, 6(1):1–6.
Chen, N., Ribeiro, B., and Chen, A. (2016). Financial credit
risk assessment: a recent review. Artificial Intelli-
gence Review, 45(1):1–23.
Chopra, A. and Bhilare, P. (2018). Application of ensemble
models in credit scoring models. Business Perspec-
tives and Research, 6(2):129–141.
Crook, J. N., Edelman, D. B., and Thomas, L. C. (2007).
Recent developments in consumer credit risk assess-
ment. European Journal of Operational Research,
183(3):1447–1465.
Dal Pozzolo, A., Caelen, O., Le Borgne, Y.-A., Wa-
terschoot, S., and Bontempi, G. (2014). Learned
lessons in credit card fraud detection from a practi-
tioner perspective. Expert systems with applications,
41(10):4915–4928.
Damrongsakmethee, T. and Neagoe, V.-E. (2019). Principal
component analysis and relieff cascaded with decision
tree for credit scoring. In Computer Science On-line
Conference, pages 85–95. Springer.
Doumpos, M., Lemonakis, C., Niklis, D., and Zopounidis,
C. (2019). Credit scoring and rating. In Analytical
Techniques in the Assessment of Credit Risk, pages
23–41. Springer.
Garc
´
ıa, S., Ram
´
ırez-Gallego, S., Luengo, J., Ben
´
ıtez, J. M.,
and Herrera, F. (2016). Big data preprocessing: meth-
ods and prospects. Big Data Analytics, 1(1):9.
Ghodselahi, A. (2011). A hybrid support vector machine
ensemble model for credit scoring. International
Journal of Computer Applications, 17(5):1–5.
Giraud-Carrier, C., Vilalta, R., and Brazdil, P. (2004). Intro-
duction to the special issue on meta-learning. Machine
learning, 54(3):187–193.
Haixiang, G., Yijing, L., Shang, J., Mingyun, G., Yuanyue,
H., and Bing, G. (2017). Learning from class-
imbalanced data: Review of methods and applica-
tions. Expert Systems with Applications, 73:220–239.
Harris, T. (2015). Credit scoring using the clustered sup-
port vector machine. Expert Systems with Applica-
tions, 42(2):741–750.
Hassan, M. K., Brodmann, J., Rayfield, B., and Huda, M.
(2018). Modeling credit risk in credit unions using
survival analysis. International Journal of Bank Mar-
keting, 36(3):482–495.
Hawkins, D. M. (2004). The problem of overfitting. Jour-
nal of chemical information and computer sciences,
44(1):1–12.
Henrique, B. M., Sobreiro, V. A., and Kimura, H. (2019).
Literature review: Machine learning techniques ap-
plied to financial market prediction. Expert Systems
with Applications.
Huang, J. and Ling, C. X. (2005). Using auc and accuracy
in evaluating learning algorithms. IEEE Transactions
on knowledge and Data Engineering, 17(3):299–310.
Jappelli, T., Pagano, M., et al. (2000). Information sharing
in credit markets: a survey. Technical report, CSEF
working paper.
Jeni, L. A., Cohn, J. F., and De La Torre, F. (2013). Fac-
ing imbalanced data–recommendations for the use of
performance metrics. In 2013 Humaine Association
Conference on Affective Computing and Intelligent In-
teraction, pages 245–251. IEEE.
Khemais, Z., Nesrine, D., Mohamed, M., et al. (2016).
Credit scoring and default risk prediction: A compar-
ative study between discriminant analysis & logistic
regression. International Journal of Economics and
Finance, 8(4):39.
Khemakhem, S., Ben Said, F., and Boujelbene, Y. (2018).
Credit risk assessment for unbalanced datasets based
on data mining, artificial neural network and support
vector machines. Journal of Modelling in Manage-
ment, 13(4):932–951.
Lessmann, S., Baesens, B., Seow, H., and Thomas, L. C.
(2015a). Benchmarking state-of-the-art classifica-
tion algorithms for credit scoring: An update of re-
search. European Journal of Operational Research,
247(1):124–136.
Lessmann, S., Baesens, B., Seow, H.-V., and Thomas,
L. C. (2015b). Benchmarking state-of-the-art classi-
fication algorithms for credit scoring: An update of
research. European Journal of Operational Research,
247(1):124–136.
Li, Q., Wu, Q., Zhu, C., Zhang, J., and Zhao, W. (2019).
Unsupervised user behavior representation for fraud
review detection with cold-start problem. In Pacific-
Asia Conference on Knowledge Discovery and Data
Mining, pages 222–236. Springer.
Liu, C., Huang, H., and Lu, S. (2019). Research on personal
credit scoring model based on artificial intelligence. In
International Conference on Application of Intelligent
Systems in Multi-modal Information Analytics, pages
466–473. Springer.
Liu, H., Hussain, F., Tan, C. L., and Dash, M. (2002). Dis-
cretization: An enabling technique. Data mining and
knowledge discovery, 6(4):393–423.
Livshits, I. (2015). Recent developments in consumer credit
and default literature. Journal of Economic Surveys,
29(4):594–613.
Luo, C., Wu, D., and Wu, D. (2017). A deep learn-
ing approach for credit scoring using credit default
swaps. Engineering Applications of Artificial Intel-
ligence, 65:465–470.
Luque, A., Carrasco, A., Mart
´
ın, A., and de las Heras, A.
(2019). The impact of class imbalance in classifica-
KDIR 2019 - 11th International Conference on Knowledge Discovery and Information Retrieval
212

tion performance metrics based on the binary confu-
sion matrix. Pattern Recognition, 91:216–231.
Malekipirbazari, M. and Aksakalli, V. (2015). Risk assess-
ment in social lending via random forests. Expert Sys-
tems with Applications, 42(10):4621–4631.
Mester, L. J. et al. (1997). What’s the point of credit scor-
ing? Business review, 3:3–16.
Powers, D. M. (2011). Evaluation: from precision, recall
and f-measure to roc, informedness, markedness and
correlation.
Rapach, D. E. and Wohar, M. E. (2006). In-sample vs.
out-of-sample tests of stock return predictability in the
context of data mining. Journal of Empirical Finance,
13(2):231–247.
Rodda, S. and Erothi, U. S. R. (2016). Class imbal-
ance problem in the network intrusion detection sys-
tems. In 2016 International Conference on Electrical,
Electronics, and Optimization Techniques (ICEEOT),
pages 2685–2688. IEEE.
Saia, R. (2017). A discrete wavelet transform approach to
fraud detection. In International Conference on Net-
work and System Security, pages 464–474. Springer.
Saia, R. and Carta, S. (2016a). An entropy based algorithm
for credit scoring. In International Conference on Re-
search and Practical Issues of Enterprise Information
Systems, pages 263–276. Springer.
Saia, R. and Carta, S. (2016b). Introducing a vector space
model to perform a proactive credit scoring. In In-
ternational Joint Conference on Knowledge Discov-
ery, Knowledge Engineering, and Knowledge Man-
agement, pages 125–148. Springer.
Saia, R. and Carta, S. (2016c). A linear-dependence-based
approach to design proactive credit scoring models. In
KDIR, pages 111–120.
Saia, R. and Carta, S. (2017). A fourier spectral pattern
analysis to design credit scoring models. In Proceed-
ings of the 1st International Conference on Internet of
Things and Machine Learning, page 18. ACM.
Saia, R., Carta, S., et al. (2017). A frequency-domain-
based pattern mining for credit card fraud detection.
In IoTBDS, pages 386–391.
Saia, R., Carta, S., and Fenu, G. (2018a). A wavelet-based
data analysis to credit scoring. In Proceedings of the
2nd International Conference on Digital Signal Pro-
cessing, pages 176–180. ACM.
Saia, R., Carta, S., and Recupero, D. R. (2018b). A
probabilistic-driven ensemble approach to perform
event classification in intrusion detection system. In
KDIR, pages 139–146. SciTePress.
Siddiqi, N. (2017). Intelligent credit scoring: Building and
implementing better credit risk scorecards. John Wi-
ley & Sons.
Sohn, S. Y., Kim, D. H., and Yoon, J. H. (2016). Technol-
ogy credit scoring model with fuzzy logistic regres-
sion. Applied Soft Computing, 43:150–158.
Tripathi, D., Edla, D. R., and Cheruku, R. (2018). Hy-
brid credit scoring model using neighborhood rough
set and multi-layer ensemble classification. Journal
of Intelligent & Fuzzy Systems, 34(3):1543–1549.
Vilalta, R. and Drissi, Y. (2002). A perspective view and
survey of meta-learning. Artificial intelligence review,
18(2):77–95.
Wang, C.-M. and Huang, Y.-F. (2009). Evolutionary-based
feature selection approaches with new criteria for data
mining: A case study of credit approval data. Expert
Systems with Applications, 36(3):5900–5908.
Wu, X. and Kumar, V. (2009). The top ten algorithms in
data mining. CRC press.
Xia, Y., Liu, C., Li, Y., and Liu, N. (2017). A boosted de-
cision tree approach using bayesian hyper-parameter
optimization for credit scoring. Expert Systems with
Applications, 78:225–241.
Zhang, X., Yang, Y., and Zhou, Z. (2018). A novel credit
scoring model based on optimized random forest. In
2018 IEEE 8th Annual Computing and Communica-
tion Workshop and Conference (CCWC), pages 60–
65. IEEE.
Zhao, Y., Shen, Y., and Huang, Y. (2019). Dmdp: A
dynamic multi-source default probability prediction
framework. Data Science and Engineering, 4(1):3–
13.
A Discretized Enriched Technique to Enhance Machine Learning Performance in Credit Scoring
213
