
A Sequential Heteroscedastic Probabilistic Neural Network for Online
Classification
Ali Mahmoudi
1 a
, Reza Askari Moghadam
1 b
and Kurosh Madani
2
1
Faculty of New Sciences and Technologies, University of Tehran, Tehran, Iran
2
LISSI Lab, S
´
enart-FB Institute of Technology, University Paris Est-Cr
´
eteil (UPEC), Lieusaint, France
Keywords:
Online Classification, Probabilistic Neural Network, Sequential Learning, Machine Learning.
Abstract:
In this paper, a novel online classification algorithm called sequential heteroscedastic probabilistic neural
network (SHPNN) is proposed. This algorithm is based on Probabilistic Neural Networks (PNNs). One of the
advantages of the proposed algorithm is that it can increase the number of its hidden node kernels adaptively
to match the complexity of the data. The performance of this network is analyzed for a number of standard
datasets. The results suggest that the accuracy of this algorithm is on par with other state of the art online
classification algorithms while being significantly faster in majority of cases.
1 INTRODUCTION
A longstanding goal in machine learning is mimick-
ing the human learning process. This becomes very
important in the area of cognitive robotics and human-
machine interaction, where a robot or an algorithm
has to learn in collaboration with a human tutor. It
is a well-established fact among researchers in the ar-
eas of machine learning and neuroscience that human
learning is a very complex process and we are far
from fully grasping the exact mechanism behind it.
However, some aspects of human learning are not ob-
scure to us. First, humans have a capacity to learn to
distinguish between concepts in real-time and update
their existing knowledge by encountering even one
new pattern. Secondly, human brain can adaptively
update its structure to cope with complexity and the
nature of data it is learning. This is at odds with the
majority of machine learning techniques developed in
the past few decades, which are batch-learning algo-
rithms with fixed structure that do not have the capac-
ity to learn in real-time (Hamid and Braun, 2017).
There has been several attempts to make on-
line supervised learning algorithms in the litera-
ture. Stochastic gradient descent back propagation
(SGBP), a variant of the popular BP algorithm can
be used for sequential learning applications (LeCun
et al., 2012). There are also several sequential learn-
a
https://orcid.org/0000-0002-7089-5167
b
https://orcid.org/0000-0001-8394-7256
ing algorithms that implement feedforward networks
with radial basis function (RBF) nodes (de Jes
´
us Ru-
bio, 2017; Giap et al., 2018). RAN (Platt, 1991),
MRAN (Yingwei et al., 1997), and GAP-RBF (Huang
et al., 2004) are also among these algorithms. An-
other algorithm that has a better accuracy and speed
compared to the ones mentioned before is online se-
quential extreme learning machine (OS-ELM), which
is an online variant of ELM that uses recursive least
square algorithm (Liang et al., 2006). There are var-
ious variations of OS-ELM algorithms suited for dif-
ferent sequential learning tasks, including the pro-
gressive learning technique that has the potential to
add new classes as new data arrives (Venkatesan and
Er, 2016). There is also an online supervised learn-
ing method for spiking neural networks (Wang et al.,
2014). Apart from SGBP, all of the other algorithms
can modify their structure during the training (in case
of OS-ELM a variant of it called SAO-ELM has this
ability (Li et al., 2010)).
The purpose of this work is to develop a new
supervised learning algorithm capable of learning
in real-time from a sequence of data that has the
ability to adaptively adjust its structure. The sug-
gested algorithm is based on the robust heteroscedas-
tic probabilistic neural network (RHPNN) proposed
by Yang and Chen (Yang and Chen, 1998). RH-
PNN uses expectation maximization (EM) algorithm
to construct maximum likelihood (ML) estimate of
a heteroscedastic probabilistic neural network. RH-
PNN also implements a powerful statistical method
Mahmoudi, A., Moghadam, R. and Madani, K.
A Sequential Heteroscedastic Probabilistic Neural Network for Online Classification.
DOI: 10.5220/0008495604490453
In Proceedings of the 11th International Joint Conference on Computational Intelligence (IJCCI 2019), pages 449-453
ISBN: 978-989-758-384-1
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
449

called Jack-knife to avoid numerical difficulties. RH-
PNN has been used in literature for different appli-
cations ranging from analog circuit fault detection
(Yang et al., 2000) and MEMS devices fault detec-
tion (Asgary et al., 2007) to cloud service selection
(Somu et al., 2018). In the proposed algorithm, the
Jack-knife is replaced by a simple threshold to mit-
igate numerical instabilities. Several changes to the
EM algorithm were also required by the sequential
nature of data in online learning. The performance
of this algorithm in standard benchmarks is also ana-
lyzed and compared with other state-of-the-art algo-
rithms in online supervised classification. The results
show that the proposed algorithm can achieve good
accuracy and speed in online classification tasks.
2 REVIEW OF RHPNN
Assuming that x ∈ R
d
is a d-dimensional pattern vec-
tor and its corresponding class is j ∈ {1, ...,K}, in
which K is the number of possible classes. A classi-
fier maps each pattern vector x to its class index g(x),
where g : R
d
→ {1,..., K}. If the conditional proba-
bility density function (PDF) of class j is f
j
and the a
priori probability of class j is α
j
, for 1 ≤ j ≤ K , the
Bayes classifier that minimizes the misclassification
error is given by:
g
Bayes
(x) = arg( max
1≤ j≤K
{α
j
f
j
(x)}) (1)
PNN is a four-layer feedforward neural network
that can realize or approximate the optimal classi-
fier in (1). In order to estimate the class conditional
PDFs and realizing the Bayes decision in (1), PNN
use mixtures of Gaussian kernel functions or Parzen
windows.
The first layer of a PNN is the input layer that ac-
cepts input patterns. The second layer consists of K
group of nodes. Each of these nodes is a Gaussian
basis function. For the i-th kernel in the j-th class the
Gaussian basis function is defined as:
p
i, j
(x) =
1
(2πσ
2
i, j
)
d/2
exp
−
x − c
i, j
2
2σ
2
i, j
!
(2)
Where σ
2
i, j
is a variance parameter and c
i, j
∈ R
d
is the center. Assuming the number of nodes in class
j is M
j
, then the total number of nodes in the second
layer is:
M =
K
∑
j=1
M
j
(3)
The third layer has K nodes, one for each class,
and using a mixture of Gaussian kernels it estimates a
class conditional PDF f
j
.
f
j
(x) =
M
j
∑
i=1
β
i, j
p
i, j
(x),1 ≤ j ≤ K (4)
Where β
i, j
is the positive mixing coefficient and
must satisfy:
M
j
∑
i=1
β
i, j
= 1,1 ≤ j ≤ K (5)
The fourth layer of PNN makes the decision
according to (1). We assume that every class is
equiprobable since the class a priori probability can-
not be estimated in advance purely from the training
set.
The RHPNN uses the EM algorithm to calculate
the ML estimate. Let the training patterns be sepa-
rated into K labelled subsets:
{x
n
}
N
n=1
= {{x
n, j
}
N
j
n=1
}
K
j=1
(6)
Where
K
∑
j=1
N
j
= N (7)
In (7), N is the total number of training patterns
and N
j
is the number of training patterns belonging
to class j. Under the assumption that every class is
equiprobable, the log posterior likelihood function of
the training set is:
logL
f
=
K
∑
j=1
N
j
∑
n=1
log f
j
(x
n, j
) (8)
Which after forming the appropriate Lagrangian
gives rise to the iterative formulas to compute the net-
work parameters. Assuming that β
m,i
|
(k)
, σ
2
m,i
(k)
, and
c
m,i
|
(k)
are the previous values of β
m,i
, σ
2
m,i
, and c
m,i
,
respectively. Assuming 1 ≤ m ≤ M
i
, 1 ≤ n ≤ N
i
, and
1 ≤ i ≤ K, the weights can be computed as follows.
w
(k)
m,i
(x
n,i
) =
β
m,i
|
(k)
p
(k)
m,i
(x
n,i
)
∑
M
i
l=1
β
l,i
(k)
p
(k)
l,i
(x
n,i
)
(9)
Where
p
(k)
l,i
(x
n,i
) =
1
(2πσ
2
l,i
(k)
)
d/2
exp
−
x
n,i
− c
l,i
(k)
2
2 σ
2
l,i
(k)
(10)
NCTA 2019 - 11th International Conference on Neural Computation Theory and Applications
450
After computing the weights, the parameters can
be updated.
c
m,i
|
(k+1)
=
∑
N
i
n=1
w
(k)
m,i
(x
n,i
)x
n,i
∑
N
i
n=1
w
(k)
m,i
(x
n,i
)
(11)
σ
2
m,i
(k+1)
=
∑
N
i
n=1
w
(k)
m,i
(x
n,i
)
x
n,i
− c
m,i
|
(k)
2
d
∑
N
i
n=1
w
(k)
m,i
(x
n,i
)
(12)
β
m,i
|
(k+1)
=
1
N
i
∑
N
i
n=1
w
(k)
m,i
(x
n,i
) (13)
In order to avoid numerical instabilities, the RH-
PNN implements the Jack-knife estimator on (11)-
(13). For the sake of conciseness the relations de-
scribing the Jack-knife estimator is not included in
this paper.
3 SEQUENTIAL
HETEROSCEDASTIC
PROBABILISTIC NEURAL
NETWORK
The first step to the proposed algorithm is to train an
initial batch of data with size of n
0
using the normal
RHPNN. Afterward, the arriving data is processed
one by one. Since the previous training data is dis-
carded in online learning algorithms, the algorithm
cannot use the normal EM. The modified version of
EM used in this work can only iterate once for each
data that arrives (true maximization of expectation re-
quires the presence of the whole training data up to
that point). It also modifies (9)-(13) so that their val-
ues can be obtained for the newly arriving data. In
order to do this, the previous values for these pa-
rameters, the value of Y
(k)
m,i
=
∑
N
i
n=1
w
m,i
(x
n,i
), and N
i
s
should be memorized by the algorithm. It should be
noted that unlike the previous section, in the sequen-
tial learning phase the superscript k does not repre-
sent the iteration step and is used to show that the k-th
training pattern is in the process of learning. Assum-
ing that the k + 1-th training pattern has arrived we
can write:
p
m,i
(x
k+1
) =
1
(2π σ
2
m,i
(k)
)
d/2
exp
−
x
k+1
− c
m,i
|
(k)
2
2 σ
2
m,i
(k)
(14)
w
(k)
m,i
(x
k+1
) =
β
m,i
|
(k)
p
m,i
(x
k+1
)
∑
M
i
l=1
β
l,i
(k)
p
l,i
(x
k+1
)
(15)
c
m,i
|
(k+1)
=
c
m,i
|
(k)
Y
(k)
m,i
+ w
m,i
(x
k+1
)x
k+1
Y
(k)
m,i
+ w
m,i
(x
k+1
)
(16)
σ
2
m,i
(k+1)
=
dσ
2
m,i
(k)
Y
(k)
m,i
+ w
m,i
(x
k+1
)
x
k+1
− c
m,i
|
(k)
2
d(Y
(k)
m,i
+ w
m,i
(x
k+1
))
(17)
β
m,i
|
(k+1)
=
1
N
i
Y
(k)
m,i
+ w
m,i
(x
k+1
)
(18)
Y
(k+1)
m,i
= Y
(k)
m,i
+ w
m,i
(x
k+1
) (19)
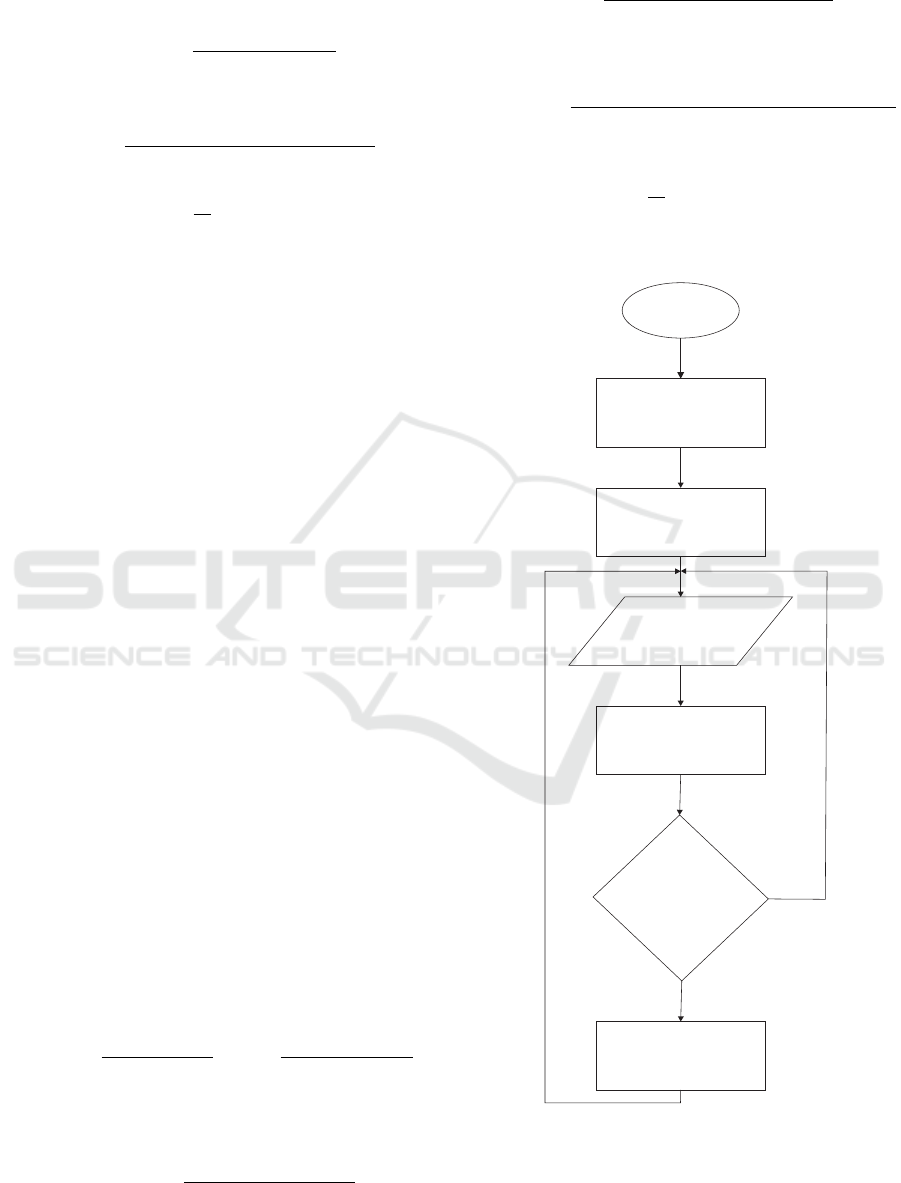
Start
Initialize the
kernel parameters
Learn the first
batch using RHPNN
Sequential
introduction
of data
Updating kernel
parameters using
(14)-(19)
Was the
pattern
classified
correctly?
Add a new kernel
at the location of
the pattern
Yes
No
Figure 1: Flow chart of the SHPNN algorithm.
It evident that by storing the previous sum of weights
in the memory, we have eliminated the need to have the
entire training sample in each training step. It is also
A Sequential Heteroscedastic Probabilistic Neural Network for Online Classification
451

Table 1: Specification of datasets used to evaluate SHPNN.
Dataset # Attributes # Classes # Training data # Testing data
iris 4 3 120 30
Image segmentation 19 7 2100 210
Satellite image 36 7 4435 2000
Table 2: Comparison between the performance of SHPNN and other prominent online supervised learning algorithms in
different datasets.
Dataset Algorithm Training time (s) Training accuracy Testing accuracy # Nodes
iris
SNN - 0.872 0.861 -
SHPNN 0.1829 0.9617 0.9267 13.5
Image segmentation
OS-ELM (RBF) 9.9981 0.9700 0.9488 180
SAO-ELM 9.1644 0.9725 0.9516 191
MRAN 7004.5 - 0.9330 53.1
SHPNN 4.4922 0.9426 0.9495 178.3
Satellite Image
OS-ELM (RBF) 319.14 0.9318 0.8901 400
SAO-ELM 211.034 0.9480 0.9139 413
MRAN 2469.4 - 0.8636 20.4
SHPNN 26.44 0.8867 0.8575 534.6
worth noting that since the Jack-knife cannot be used
without having the whole dataset available, it has been
replaced by a simple threshold for variance to avoid nu-
merical difficulties when facing sparse data.
If after updating the network parameters in the k+1-
th step the k+1-th pattern is not classified correctly, then
a new node centered at the pattern in question will be
added to the appropriate kernel group. The variance of
this kernel is set at a small value (about 0.01). In addi-
tion, the existing βs will be scaled so that with the addi-
tion of the new node their sum would stay at one. This
process is summerized in Fig. 1.
4 RESULTS
In order to evaluate the performance of the proposed al-
gorithm, three standard benchmarks were used. These
benchmarks are iris, image segmentation, and satellite
image datasets all from UCI machine learning reposi-
tory (Dua and Graff, 2017). The setup for these tests was
equipped with an Intel Core i7-8550U at 4 GHz with 8
GB of RAM. The specifications of these datasets are pre-
sented in TABLE 1.
The first dataset is Fisher’s Iris dataset that contains
the measured values of sepal and petal dimensions for
three types of Iris plant. The dataset contains 50 patterns
for each type.
The second dataset is image segmentation that con-
sists of a database of images that were drawn arbitrary
from 7 outdoor images and contains 2310 regions of 3x3
pixels. The aim here is to recognize which category
each of these regions belong. These categories consist
of brick facing, foliage, cement, sky, window, grass, and
path. From each of these regions 19 attributes were ex-
tracted.
The final dataset used for performance evaluation
of this algorithm is satellite image. It consists of a
databased derived from Landsat multispectral scanner.
Each frame of this scanner imagery comprises of four
digital images of a scene in four different spectral bands.
This dataset is a part of a scene with the size of 82x100
pixels and each pattern in the dataset is a region of 3x3
pixels. The goal here is to classify the central pixel in
a region into 7 categories of red soil, cotton crop, grey
soil, damp gray soil, soil with vegetation stubble, mix-
ture class, and very damp gray soil. It is worth noting
that there are no patterns belonging to the sixth class and
the dataset effectively has 6 classes.
In each dataset, the members of training and test sets
are constant, but the order of their introduction to the
algorithm is shuffled in each run.
For each test, the algorithm starts with three kernels
in each group for iris and five kernels in each group for
the other two datasets. In addition, 10 percent of the
training data is used as the initial batch. For each dataset,
the results are averaged over 10 runs and they are com-
pared with some of the prominent online supervised al-
gorithms in the literature. The results of the tests is pre-
sented in TABLE 2.
It is evident that the proposed algorithm can achieve
good accuracy when comparing with other prominent
online supervised learning algorithms. The training time
for each dataset is also among the best in the litera-
ture. However, the training times for other algorithms
are taken from the respective papers reporting their re-
sults and for a fair comparison, all of the algorithms
should be tested on the same setup.
It is worth noting that the closest algorithm in terms
NCTA 2019 - 11th International Conference on Neural Computation Theory and Applications
452

of both structure and performance to the SHPNN is
SAO-ELM. In the presented algorithm, the initial num-
ber of hidden layer nodes is 35 in the image segmen-
tation and satellite image datasets and this number rose
to 178.3 and 534.6 automatically. On the other hand,
the initial number of hidden nodes for SAO-ELM is 180
and 400 for these datasets respectively, which are opti-
mal node numbers for OS-ELM, and these numbers rose
to 191 and 413. In other words, it appears that the initial
number of nodes for SAO-ELM needs to be very close to
the optimal value, but the SHPNN is capable of finding
its optimal structure from a very rudimentary initial con-
figuration. This property makes SHPNN a well-suited
algorithm to simulate anthropomorphic learning process.
One of the important properties of the proposed al-
gorithm (which also applies to RHPNN) is the fact that
its hidden node kernels can be used to determine sub-
categories in data and can be used to get a sense of the
statistics of the classes. This property of SHPNN is in
line with the recent trend in machine learning commu-
nity to design interpretable algorithms.
5 CONCLUSIONS
In this paper, a novel algorithm for online supervised
classification is presented and its performance is com-
pared with other similar algorithms. The results show
that this algorithm has a great potential in terms of both
speed and accuracy. It is also worth noting that the al-
gorithm is still at the development phase and as future
work, more formula are developed to change the vari-
ances and centers adaptively, while the linking weights
can be adjusted too.
REFERENCES
Asgary, R., Mohammadi, K., and Zwolinski, M. (2007).
Using neural networks as a fault detection mecha-
nism in mems devices. Microelectronics Reliability,
47(1):142–149.
de Jes
´
us Rubio, J. (2017). A method with neural networks
for the classification of fruits and vegetables. Soft
Computing, 21(23):7207–7220.
Dua, D. and Graff, C. (2017). UCI machine learning repos-
itory.
Giap, C. N., Son, L. H., and Chiclana, F. (2018). Dynamic
structural neural network. Journal of Intelligent &
Fuzzy Systems, 34(4):2479–2490.
Hamid, O. H. and Braun, J. (2017). Reinforcement learn-
ing and attractor neural network models of associative
learning. In International Joint Conference on Com-
putational Intelligence, pages 327–349. Springer.
Huang, G.-B., Saratchandran, P., and Sundararajan, N.
(2004). An efficient sequential learning algorithm for
growing and pruning rbf (gap-rbf) networks. IEEE
Transactions on Systems, Man, and Cybernetics, Part
B (Cybernetics), 34(6):2284–2292.
LeCun, Y. A., Bottou, L., Orr, G. B., and M
¨
uller, K.-
R. (2012). Efficient backprop. In Neural networks:
Tricks of the trade, pages 9–48. Springer.
Li, G., Liu, M., and Dong, M. (2010). A new online learn-
ing algorithm for structure-adjustable extreme learn-
ing machine. Computers & Mathematics with Appli-
cations, 60(3):377–389.
Liang, N.-Y., Huang, G.-B., Saratchandran, P., and Sun-
dararajan, N. (2006). A fast and accurate online se-
quential learning algorithm for feedforward networks.
IEEE Transactions on neural networks, 17(6):1411–
1423.
Platt, J. (1991). A resource-allocating network for function
interpolation. MIT Press.
Somu, N., MR, G. R., Kalpana, V., Kirthivasan, K., and
VS, S. S. (2018). An improved robust heteroscedastic
probabilistic neural network based trust prediction ap-
proach for cloud service selection. Neural Networks,
108:339–354.
Venkatesan, R. and Er, M. J. (2016). A novel progressive
learning technique for multi-class classification. Neu-
rocomputing, 207:310–321.
Wang, J., Belatreche, A., Maguire, L., and Mcginnity, T. M.
(2014). An online supervised learning method for
spiking neural networks with adaptive structure. Neu-
rocomputing, 144:526–536.
Yang, Z. R. and Chen, S. (1998). Robust maximum like-
lihood training of heteroscedastic probabilistic neural
networks. Neural Networks, 11(4):739–747.
Yang, Z. R., Zwolinski, M., Chalk, C. D., and Williams,
A. C. (2000). Applying a robust heteroscedastic prob-
abilistic neural network to analog fault detection and
classification. IEEE Transactions on computer-aided
design of integrated circuits and systems, 19(1):142–
151.
Yingwei, L., Sundararajan, N., and Saratchandran, P.
(1997). A sequential learning scheme for function ap-
proximation using minimal radial basis function neu-
ral networks. Neural computation, 9(2):461–478.
A Sequential Heteroscedastic Probabilistic Neural Network for Online Classification
453
