Fuzzy Conﬁdence Intervals by the Likelihood Ratio with Bootstrapped

Distribution

edina Berkachy and Laurent Donz

Applied Statistics and Modelling, Department of Informatics, Faculty of Management, Economics and Social Sciences,

University of Fribourg, Boulevard de P

erolles 90, 1700 Fribourg, Switzerland

Keywords:

Bootstrap Technique, Likelihood Ratio, Fuzzy Conﬁdence Interval, Fuzzy Statistics, Fuzzy Hypotheses,

Fuzzy Data.

Abstract:

We propose a complete practical procedure to construct a fuzzy conﬁdence interval by the likelihood method

where the observations and the hypotheses are considered to be fuzzy. We use the bootstrap technique to

estimate the distribution of the likelihood ratio. For this step of the process, we mainly expose two algorithms:

the ﬁrst one consists on simply randomly drawing the bootstrap samples, and the second one is based on

drawing observations by preserving the location and dispersion measures of the primary data set. This is

achieved in accordance with a new metric written as d

SGD

. It is built on the basis of the known signed distance

measure. We also provide a simulation study to measure the performance of both bootstrap algorithms and

their inﬂuence on the constructed conﬁdence intervals. We illustrate our method via a numerical application

where we construct fuzzy conﬁdence intervals by the traditional and the defended methods. The aim is to

highlight important differences between them.

1 INTRODUCTION AND

MOTIVATION

A typical hypothesis testing procedure can be accom-

plished by, for example, constructing conﬁdence in-

tervals for a particular parameter. This method is

widely used in practice. However, once we consider

the data and/or the hypotheses to be fuzzy, the cor-

responding statistical methods have to be updated.

Some approaches already exist in the theory of fuzzy

sets. For instance, (Kruse and Meyer, 1987) pre-

sented a theoretical deﬁnition of fuzzy conﬁdence

intervals. Several researchers have afterwards pro-

posed reﬁned deﬁnitions of fuzzy conﬁdence inter-

vals. For instance, (Viertl and Yeganeh, 2016) pro-

posed a deﬁnition of the so-called conﬁdence regions.

Their main application was in the Bayesian context.

(Kahraman et al., 2016) described some approaches to

the construction of fuzzy conﬁdence intervals, as well

as the concept of hesitant fuzzy conﬁdence intervals.

(Couso and Sanchez, 2011) provided an approach that

considers the inner and outer approximations of con-

ﬁdence intervals in the context of fuzzy observations.

Unfortunately, these various approaches are limited

because they were all conceived to test a speciﬁc

parameter with a pre-deﬁned distribution. It would

therefore be advantageous to develop a uniﬁed gen-

eral approach to fuzzy conﬁdence intervals.

In classical statistics, the likelihood ratio method

is considered an alternative tool for the construction

of conﬁdence intervals. In the fuzzy environment, this

method using uncertain data has multiple advantages.

(Gil and Casals, 1988) used the likelihood ratio in a

hypothesis testing procedure where fuzziness is con-

tained in the data.

In (Berkachy and Donz

e, 2019a), we proposed a

practical procedure to construct conﬁdence intervals

by the likelihood ratio method which is seen in some

sense general. The procedure can be easily adapted to

speciﬁc cases. However, the distribution of the likeli-

hood ratio is a priori unknown and has to be estimated

or derived from strong assumptions. Under classical

assumptions, we note that this ratio is known to be

-distributed with degrees of freedom correspond-

ing to the number of constraints applied to parame-

ters. In this paper, we propose to use the bootstrap

technique extended to the fuzzy environment to esti-

mate the distribution of the likelihood ratio. A main

contribution is to provide two algorithms to constitute

the bootstrapped samples mainly using the location

and dispersion characteristics calculated based on a

new version of the signed distance measure written as

Berkachy, R. and Donzé, L.

Fuzzy Conﬁdence Intervals by the Likelihood Ratio with Bootstrapped Distribution.

DOI: 10.5220/0010023602310242

In Proceedings of the 12th International Joint Conference on Computational Intelligence (IJCCI 2020), pages 231-242

ISBN: 978-989-758-475-6

231

the d

SGD

metric and detailed in (Berkachy, 2020). We

highlight that the Expectation-Maximization (EM) al-

gorithm based on the fuzziness of data described by

(Denoeux, 2011) is used to calculate the maximum

likelihood estimators (MLEs).

The defended procedure is considered efﬁcient

and computationally light because we do not have to

consider every single value of the support set of the

involved fuzzy numbers, as in the traditional fuzzy

method. Indeed, four conveniently chosen values are

used in the construction process. The presented calcu-

lations are done using the R package FuzzySTs shown

in (Berkachy and Donz

e, 2020).

The remainder of the paper proceeds as follows.

In Section 2, we present the deﬁnition of the signed

distance measure, followed by the deﬁnition of the

SGD

metric in Section 3. Section 4 is devoted to the

construction of the traditional fuzzy conﬁdence inter-

vals. In Section 5, we discuss our concept of fuzzy

conﬁdence intervals constructed using the likelihood

method and detail the two bootstrap algorithms to ap-

proximate the distribution of the likelihood ratio. In

addition, a simulation study illustrates the proposed

algorithms. We end the paper with Section 6 by pre-

senting a numerical application where we estimate the

traditional and the defended fuzzy conﬁdence inter-

vals and compare them.

2 THE SIGNED DISTANCE

The signed distance was used by (Yao and Wu, 2000)

to rank fuzzy numbers. It has served in different

contexts, such as the evaluation of linguistic ques-

tionnaires described in, for example, (Berkachy and

Donz

e, 2016) or hypotheses testing (see (Berkachy

and Donz

e, 2019b)). This distance has intriguated

specialists because of its simplicity in terms of cal-

culation and computation, and its directionality. The

directionality of this distance means it can be nega-

tive or positive, indicating the direction between two

fuzzy numbers. For instance, (Dubois and Prade,

1987) presented it as an expected value of a particular

fuzzy number. It is deﬁned as follows:

Deﬁnition 2.1 (Signed distance of a real value). The

signed distance measured from the origin denoted by

(a, 0) for a ∈ R is a itself, that is d

(a, 0) = a.

Deﬁnition 2.2 (Signed distance between two real val-

ues). The signed distance between two values a and

b ∈ R is d(a, b) = a −b.

Now, let

X and

Y be two sets of the class of fuzzy

sets F(R). Their respective α-cuts are written as

and

such that their left and right α-cuts denoted

respectively by

and

are integrable for

all α ∈ [0; 1]. We deﬁne the signed distance between

the fuzzy numbers

X and

Y as:

Deﬁnition 2.3 (Signed distance between two fuzzy

sets). The signed distance d

SGD

between

X and

Y is

the mapping

SGD

: F(R) ×F(R) → R

X ×

Y 7→ d

SGD

(

Y ),

such that

SGD

(

Y ) =

(α) +

(α)

−

(α) −

(α)

dα. (1)

The signed distance of a particular fuzzy number

measured from the fuzzy origin

0 is deﬁned as:

Deﬁnition 2.4 (Signed distance of a fuzzy set). The

signed distance of the fuzzy set

X measured from the

fuzzy origin

0 is given by:

SGD

(

0) =

(α) +

(α)

dα. (2)

3 THE d

SGD

METRIC

Despite the simplicity and accessibility of the previ-

ously described distance d

SGD

, it has some important

drawbacks. First, it coincides with a central location

measure. In other words, the effects of extreme values

on a signed distance are strongly mitigated. There-

fore, neither the shape of the fuzzy numbers nor the

inner points between the extreme values affect this

distance. Second, as detailed in (Berkachy, 2020),

the signed distance cannot be deﬁned as a full met-

ric because it lacks topological characteristics, such

as separability and symmetry. For all these reasons,

we propose an L

metric denoted by d

SGD

, seen as a

generalisation of the signed distance d

SGD

. The metric

SGD

depends on a weight parameter called θ

. With

this new metric, we not only take into account the de-

viation in the shapes and its possible irregularities but

also the central location measure. (Berkachy, 2020)

proves that the measure d

SGD

has the necessary and

sufﬁcient conditions to constitute a metric of fuzzy

quantities.

We ﬁrst deﬁne the so-called deviations of the

shape of a particular fuzzy number written in terms

of the distance d

SGD

in the following way:

Deﬁnition 3.1. [(Berkachy, 2020)]. Let

X be a fuzzy

number with its α-level set

= [

] such that

FCTA 2020 - 12th International Conference on Fuzzy Computation Theory and Applications

232

∈ F(R). The left and right deviations of the shape of

X denoted by dev

X and dev

X can be given by:

dev

X(α) = d

SGD

(

0) −

, (3)

dev

X(α) =

−d

SGD

(

0), (4)

where d

SGD

(

0) is the signed distance of

X mea-

sured from the fuzzy origin

Now consider the following deﬁnition of the new met-

ric d

SGD

as expressed in (Berkachy, 2020).

Deﬁnition 3.2 (The d

SGD

distance). [(Berkachy,

2020)]. Suppose two fuzzy numbers

X and

Y of the

class of non-empty compact and bounded fuzzy num-

bers. Let θ

be the weight chosen for the modelling of

the shape of these fuzzy numbers such that 0 ≤θ

≤1.

Based on the signed distance between

X and

Y , the L

metric d

SGD

is the mapping

SGD

: F(R) ×F(R) → R

X ×

Y 7→ d

SGD

(

Y ),

such that

SGD

(

Y ) =





SGD

(

Y )



+ θ



max



dev

Y (α) −dev

X(α),

dev

X(α)−dev

Y (α)



dα



. (5)

It is useful to propose the concept of the nearest

trapezoidal symmetrical fuzzy number. The intention

is to show the direct relationship between the d

SGD

metric and the signed distance measure. In the follow-

ing context, the latter is considered as an optimum.

This concept is deﬁned by:

Deﬁnition 3.3 (Nearest trapezoidal fuzzy number).

[(Berkachy, 2020)]. The nearest symmetrical trape-

zoidal fuzzy number

S written by the quadruple

S =

−2ε, s

−ε, s

+ ε, s

+ 2ε] to a fuzzy number

with respect to the metric d

SGD

is given such that

= d

SGD





, (6)

ε =

SGD





−



2 −α



dα. (7)

The proof can be found in (Berkachy, 2020). Note

that this deﬁnition will be used in the upcoming sec-

tions to randomly generate samples with respect to the

characteristics s

and ε.

4 TRADITIONAL FUZZY

CONFIDENCE INTERVALS

FOR A PRE-DEFINED

PARAMETER

In an epistemic approach, the parameter θ for which

the conﬁdence interval is produced, is considered to

be vague. Therefore, getting a fuzzy-type interval is

a direct consequence of the fuzziness of the param-

eter. Fuzzy conﬁdence intervals can be deﬁned us-

ing, for example, the (Kruse and Meyer, 1987) ap-

proach, and many computation procedures can be de-

rived from this deﬁnition. This includes the known

approach based on considering a pre-deﬁned distribu-

tion. Hereafter, we recall the deﬁnition and the con-

struction procedure of a traditional fuzzy conﬁdence

interval.

Let us consider a random sample X

, . . . , X

of size

n. Suppose this sample to be fuzzy. We denote by

, . . . ,

its fuzzy perception. For a given parameter

θ, we are interested in testing the following hypothe-

ses:

: θ = θ

against H

: θ 6= θ

One could construct a fuzzy conﬁdence interval for

θ to accomplish this task at a particular signiﬁcance

level denoted by δ. Based on a vague sample, we de-

ﬁne a two-sided fuzzy conﬁdence interval

Π as de-

scribed in (Kruse and Meyer, 1987).

Deﬁnition 4.1 (Fuzzy conﬁdence interval). [(Kruse

and Meyer, 1987)]. We denote by [π

, π

] a symmetri-

cal conﬁdence interval for a particular parameter θ at

the signiﬁcance level δ. A fuzzy conﬁdence interval

is a convex and normal fuzzy set such that its left and

right α-cuts, respectively written by

= [

are given as follows:

= inf



a ∈ R : ∃x

∈ (

)

, ∀i = 1, . . . , n,

such that π

, . . . , x

) ≤ a



, (8)

= sup



a ∈ R : ∃x

∈ (

)

, ∀i = 1, . . . , n,

such that π

, . . . , x

) ≥ a



. (9)

This fuzzy conﬁdence interval is a 1 −δ conﬁdence

one if for a parameter θ, we have



≤ θ ≤



≥ 1 −δ, ∀α ∈ [0; 1]. (10)

In the same way, we could also write a one-sided

fuzzy conﬁdence interval as:

Remark 4.1. The α-level sets of a left one-sided fuzzy

conﬁdence interval at a conﬁdence level 1−δ denoted

are written as:

= [

, ∞],

Fuzzy Conﬁdence Intervals by the Likelihood Ratio with Bootstrapped Distribution

233

and the α-cuts of a right one-sided one are given by:

= [−∞,

By way of example, it is useful to describe the

two-sided fuzzy conﬁdence interval for the mean re-

lated to the normal distribution. It can be written as

follows:

Remark 4.2. Let X

, . . . , X

be a sample of size n

drawn from a normal distribution with a known vari-

ance and

, . . . ,

be the corresponding fuzzy ran-

dom variable.

X is the fuzzy sample mean such that its

left and right α-cuts are respectively written as (

and (

. The two-sided fuzzy conﬁdence interval for

the mean of this fuzzy sample is written by its α-cuts

in the following way:





(

−u

1−

√

, (

+ u

1−

√

,(11)

where σ is the standard deviation and u

1−

is the 1−

ordered quantile taken from the standard normal

distribution.

5 FUZZY CONFIDENCE

INTERVALS BY THE

LIKELIHOOD METHOD

Fuzzy conﬁdence intervals suit the statistical infer-

ence very well. Following Deﬁnition 4.1, construct-

ing a conﬁdence interval for a particular parameter de-

pends on a speciﬁc distribution. We therefore present

a generalisation of the previous construction and give

a practical tool to estimate a fuzzy conﬁdence inter-

val. In classical statistical theory, this task can be

done using the so-called ”likelihood ratio” method.

For fuzzy contexts, we proposed in (Berkachy and

Donz

e, 2019a) a new approach to constructing fuzzy

conﬁdence intervals based on the concept of the like-

lihood ratio, conveniently considering the fuzziness

contained in the variables. Note that the likelihood ra-

tio has been used several times in fuzzy environments

such as in (Gil and Casals, 1988) for hypotheses test-

ing.

Let us recall the deﬁnition of the likelihood func-

tion in classical theory.

Deﬁnition 5.1 (Likelihood function). Consider X

i = 1, . . . , n to be a sequence of random variables in-

dependent identically distributed (i.i.d). Let x

, i =

1, . . . , n be their corresponding realisations. We de-

note by f (x

;θ) the probability density function (pdf)

of the variable X

. Consider θ to be a vector of un-

known parameters in the parameter space Θ. We de-

ﬁne the likelihood function L(θ;x

) by:

L(θ;x

) = f (x

;θ). (12)

In this case, the expression f (x

;θ) is called the like-

lihood function because it is now on a function of the

vector of parameters θ rather than x

Now assume that the variable X

is fuzzy, and con-

sider its fuzzy perception. In other words, the fuzzy

random variable (FRV)

is such that its correspond-

ing fuzzy realisation ˜x

is associated with a measur-

able membership function written as µ

˜x

in the sense

of Borel, i.e. µ

˜x

: x → [0;1]. Following the probabil-

ity notions deﬁned by (Zadeh, 1968), we could then

expose the likelihood function described in the fuzzy

context as:

Deﬁnition 5.2 (Likelihood function of a fuzzy obser-

vation). Consider

θ to be a vector of fuzzy parameters

in the parameter space Θ. For a single fuzzy observa-

tion ˜x

, the likelihood function can be expressed by:

θ; ˜x

) = P( ˜x

;

θ) =

˜x

(x) f (x;

θ)dx. (13)

This probability can also be expressed using the α-

cuts of the involved fuzzy numbers.

Now we consider the fuzzy sample ˜x composed

of all the fuzzy realisations ˜x

of the fuzzy random

variable

. We can express the likelihood function

θ; ˜x) by:

θ; ˜x) = P( ˜x;

θ)

˜x

(x) f (x;

θ)dx ·. . . ·

˜x

(x) f (x;

θ)dx

∏

i=1

˜x

(x) f (x;

θ)dx.

(14)

We conclude that the log-likelihood function written

as l(

θ; ˜x) can be given as follows:

θ; ˜x) = logL(

θ; ˜x)

= log

˜x

(x) f (x;

θ)dx + . . .

+log

˜x

(x) f (x;

θ)dx. (15)

We call

θ a maximum likelihood estimator (MLE) of

the fuzzy parameter

θ. The likelihood ratio is given

by:

θ; ˜x)

such that L(

θ; ˜x) is the likelihood function related to

the fuzzy parameter

, and L(

θ; ˜x) is the likelihood

function depending on the estimator

θ with L(

θ; ˜x) 6=

FCTA 2020 - 12th International Conference on Fuzzy Computation Theory and Applications

234

0 and ﬁnite. It is important in this case to write the

logarithm of this ratio. This latter is nothing but the

difference between the log-likelihood functions eval-

uated at

θ and at

θ. Let us then write the statistic LR

given by:

LR = −2 log

θ; ˜x)

= 2



θ; ˜x) −l(

θ; ˜x)



, (16)

such that L(

θ; ˜x) 6= 0, L(

θ; ˜x) 6= 0 and are both ﬁnite.

Under classical statistical assumptions, the ratio LR

is known to be asymptotically χ

-distributed with a

particular number of degrees of freedom. Fuzzy sta-

tistical theories do not have any clear indication if this

asymptotical property can also be proved for the con-

sidered contexts. For this reason, in Section 5.2 we

propose a methodology to solve this problem using

bootstrap techniques.

Recall that our purpose in constructing a 100(1 −

δ)% conﬁdence interval is to ﬁnd every value of

θ for

which we reject or we do not reject the null hypothe-

sis. To construct the required 100(1 −δ)% fuzzy con-

ﬁdence interval, let η be the (1 −δ)-quantile of the

distribution of LR. The conﬁdence interval can then

be given by:



θ; ˜x) −l(

θ; ˜x)



≤ η. (17)

It can equivalently be given by

θ; ˜x) ≥ l(

θ; ˜x) −

. (18)

This latter can be explained as the interval composed

of all the possible values of

θ for which the log-

likelihood maximum varies by no more than

. We

add that depending on LR, the constructed fuzzy con-

ﬁdence interval

given by its left and right α-cuts

[(

)

;(

)

] has to insure the following equation



(

)

≤θ ≤(

)



≥1 −δ, ∀α ∈ [0;1] (19)

for every value of the parameter θ. Therefore, we

propose the construction of fuzzy conﬁdence intervals

using the following procedure.

5.1 Procedure

Our idea is to revisit the methodology of constructing

fuzzy conﬁdence intervals using the likelihood ratio.

In our case, the data set is considered to be impre-

cise. The log-likelihood becomes a function of fuzzy

information. Recall that the parameter is considered

to be fuzzy. It is then natural to see that the needed

MLE estimator has to be fuzzy nature-based. Con-

sequently, assume that the calculated crisp MLE es-

timator is modelled by a convenient fuzzy number.

Accordingly, the support set of this fuzzy number is

a set of crisp elements. Considering every element of

this set in the calculation process of the log-likelihood

function is computationally tedious. For this reason,

we propose choosing speciﬁc values leading to the

calculation of the so-called threshold points. The in-

tersection between these threshold points and the log-

likelihood curve will be particularly interesting for us

in the process of calculating the fuzzy conﬁdence in-

terval.

To develop this idea, let us ﬁrst expose the so-

called standardising function. It is deliberately pro-

posed to preserve the [0;1]-interval identity as a basic

property of α-level sets. It is given by:

Deﬁnition 5.3 (Standardising function). [(Berkachy,

2020)]. Let

θ be a fuzzy number with its member-

ship function µ

and θ ∈ supp (

θ). The standardising

function I

stand

is:

stand

: R → R

l(θ, ˜x) 7→ I

stand



l(θ, ˜x)



l(θ, ˜x)−I

−I

where I

and I

are arbitrary real values such

that I

≤ l(θ, ˜x) ≤ I

and I

6= I

. We have that

stand



l(θ, ˜x)



is bounded and 0 ≤ I

stand

(l(θ, ˜x)) ≤ 1.

The different steps of the calculation procedure

can now be given as follows:

1. Consider a fuzzy parameter

θ. We ﬁrst have to

calculate the log-likelihood function l(

θ; ˜x) de-

scribed in Equation 16.

2. Next, from the support and the core sets deﬁning

the fuzzy number modelling the MLE estimator

composed of an inﬁnity of values, we choose the

lower and upper bounds only. In this way, we re-

duce the number of considered elements to four,

and we denote them by p, q, r and s, such that

p ≤ q ≤ r ≤ s. Consider supp(

θ) and core(

θ) to

be the support and the core sets of

θ, respectively.

The four values p, q, r and s are given by:

p = min(supp(

θ)); q = min(core(

θ)); (20)

r = max(core(

θ)) and s = max(supp(

θ)). (21)

We know that the fuzzy parameter is bounded and

the sets supp(

θ) and core(

θ) are not empty. It is

then clear that the four values p, q, r and s always

exist. We mention that this choice of elements

is somehow evident speciﬁcally for the case of a

symmetrical probability function because the left

and right-hand sides of a log-likelihood function

are monotonic and continuous.

3. Next, we estimate η. We propose to use the boot-

strap technique developed in the next section.

Fuzzy Conﬁdence Intervals by the Likelihood Ratio with Bootstrapped Distribution

235

4. Once the parameter η is estimated, we calculate

the threshold values denoted by I

, I

and I

corresponding respectively to the chosen values

p, q, r and s. Thus, we affect θ by each of the

four values on the right-hand side of Equation 19.

They are then written in the following manner:

= l(p; ˜x) −

; I

= l(q; ˜x) −

; (22)

= l(r; ˜x) −

and I

= l(s; ˜x) −

.(23)

5. Next, we denote by I

min

and I

max

the minimum

and maximum thresholds given by:

min

= min(I

, I

), (24)

and I

max

= max(I

, I

). (25)

It is important to ﬁnd I

min

and I

max

and include

them in the calculation process in order to cover

the entirety of the interval of the possible values

verifying Equation 19.

6. We are now interested in ﬁnding the intersec-

tion between the log-likelihood function and the

threshold values I

, I

and I

. Let θ

, θ

and θ

, θ

be the intersection

abscisses. The letters ”L” and ”R” refer to the left

and right sides of a given entity. The abscisses can

be calculated by solving the following equations:

(θ

; ˜x) = I

and l

(θ

; ˜x) = I

, (26)

(θ

; ˜x) = I

and l

(θ

; ˜x) = I

, (27)

(θ

; ˜x) = I

and l

(θ

; ˜x) = I

, (28)

(θ

; ˜x) = I

and l

(θ

; ˜x) = I

. (29)

7. We then ﬁnd the minimum and maximum left in-

tersection abscisses written as

inf

= inf(θ

, θ

), (30)

and θ

sup

= sup(θ

, θ

). (31)

The minimum and maximum right intersection

abscisses are analogously given by:

inf

= inf(θ

, θ

), (32)

and θ

sup

= sup(θ

, θ

). (33)

Note that these left and right side intersection ab-

scisses are single and real values.

8. These intersection abscisses and the previously

calculated entities are consequently used to con-

struct the α-cuts of the fuzzy conﬁdence interval

using the likelihood ratio method

. We pro-

pose to write the left and right α-cuts (

)



(

)

;(

)



as follows:

(

)

θ ∈ R | θ

inf

≤ θ ≤ θ

sup

and

α = I

stand



l(θ, ˜x)



l(θ, ˜x)−I

min

max

−I

min

,(34)

(

)

θ ∈ R | θ

inf

≤ θ ≤ θ

sup

and

α = I

stand



l(θ, ˜x)



l(θ, ˜x)−I

min

max

−I

min

.(35)

We add that we are able to prove that the fuzzy conﬁ-

dence interval

previously described veriﬁes Deﬁ-

nition 4.1. In addition, it can be proved that regarding

the coverage rate, Equation 20 holds from a theoret-

ical point of view. The complete proofs of both as-

sumptions can be found in (Berkachy, 2020).

5.2 Bootstrap Technique for the

Approximation of the Likelihood

Ratio and Its Distribution

(Efron, 1979) formally proposed the bootstrap tech-

nique to empirically estimate a particular sampling

distribution using some observed data. Based on a

random primary sample drawn from an unknown

distribution, his method seeks to draw a large number

of samples and thus construct a so-called bootstrap

distribution of the statistic of interest. This technique

aims to ensure the estimation of such distributions

using random-based procedures. It has also been

thought in the fuzzy environment. For example, the

bootstrap technique was used in the hypotheses test-

ing procedure for the mean of fuzzy random variables

as discussed in (Gonzalez-Rodriguez et al., 2006).

(Montenegro et al., 2004) stated that a bootstrap

methodology is considered to be computationally

lighter than asymptotic designs, for example.

For our fuzzy context, our idea is to empirically

estimate the distribution of the likelihood ratio

LR shown in Equation 17—the difference of the

log-likelihood function evaluated at

θ compared to

the one evaluated at

θ. We propose the following

two approaches to construct the bootstrap imprecise

samples.

• The ﬁrst approach is based on simply generating

with replacement a number D of bootstrap sam-

ples. For each sample, we calculate the needed

deviance. The corresponding algorithm is as

follows:

FCTA 2020 - 12th International Conference on Fuzzy Computation Theory and Applications

236

Algorithm 1:

1. Consider a particular estimator

θ. Based on the

primary fuzzy sample, compute the value of the

deviance 2



θ; ˜x) −l(

θ; ˜x)



2. From the original data set, construct a bootstrap

data set by drawing randomly with replacement

a set of observations.

3. Calculate the bootstrapped deviance 2



θ; ˜x)−

θ; ˜x)



boot

4. Recursively repeat the Steps 2 and 3 a large

number D of times. The aim is to construct the

bootstrapped distribution composed of D val-

ues.

5. Find η, the (1 −δ)-quantile of the bootstrapped

distribution of the LR.

• The second approach is to generate D sam-

ples by preserving the location and dispersion

characteristics s

and ε, respectively, of the

nearest symmetrical trapezoidal fuzzy numbers.

These fuzzy numbers are calculated based on

the primary data set as seen in Proposition 3.3.

Algorithm 2 using the characteristics (s

, ε) is

given by:

Algorithm 2:

1. For each observation of the primary sample,

calculate the set of characteristics (s

, ε).

2. From the calculated set of characteristics (s

, ε)

related to the initial data set, randomly draw

with replacement and with equal probabilities a

set of characteristics (s

, ε). Based on this set,

construct a bootstrap sample.

3. For each bootstrap sample, calculate the de-

viance 2



θ; ˜x) −l(

θ; ˜x)



boot

4. Recursively repeat the Steps 2 and 3 a large

number D of times. The aim is to construct the

bootstrapped distribution composed of D val-

ues.

5. Find η, the (1 −δ)-quantile of the bootstrapped

distribution of LR.

For our approach, it is crucial to calculate a max-

imum likelihood estimator. The fuzzy EM algorithm

can be adopted as seen in (Denoeux, 2011). How-

ever, a drawback of this speciﬁc algorithm is that it

produces a crisp estimator instead of a fuzzy one. Be-

cause we lack of methods for obtaining a fuzzy maxi-

mum likelihood estimator in such contexts, we pro-

pose modelling the calculated EM crisp-based esti-

mator using a triangular fuzzy number. This crisp

element will serve as the core of the required fuzzy

number. Regarding its shape, we propose to use sym-

metrical triangles as a ﬁrst step in reducing as much

as possible the complexity that could be due to the

choice of shapes. The R package EM.Fuzzy described

in (Parchami, 2018) can be used to ﬁnd the crisp esti-

mators using the EM algorithm.

Finally, note that in practical settings the proposed

detailed procedure and calculations can be easily

computed using our R package FuzzySTs described

in (Berkachy and Donz

e, 2020) and developed for ap-

plication purposes.

5.3 Simulation Study

Next, we propose a simulation study illustrating the

use of the presented bootstrap algorithms in the pro-

cess of calculating fuzzy conﬁdence intervals. We

randomly generate data sets from different character-

istics and different sample sizes. Consider data sets

composed of N = 50, 100 and 500 observations and

taken from a normal distribution N(5, 1). To simplify

the situation, we model the observations of our data

sets by triangular symmetrical fuzzy numbers with a

support set of spread 2.

We calculate the fuzzy conﬁdence intervals us-

ing the likelihood ratio method for the theoretical

mean of the generated data sets at the conﬁdence level

1 −δ = 1 −0.05. Therefore, we have to estimate the

bootstrapped quantile η. This is done for each data

set using Algorithms 1 and 2 proposed in Section 5.2.

In our previous studies, we remarked that the num-

ber of iterations did not really inﬂuence the outcome

of the calculations. Therefore, we consider the case

of D = 1000 iterations for all our calculations. How-

ever, the fuzzy EM algorithm for calculating EM esti-

mators leads to crisp estimators instead of fuzzy ones.

For this reason, we assume the following two ways of

modelling the MLE estimator:

• the ﬁrst way is by using a triangular symmetrical

fuzzy number of spread 2;

• the second way is by using a triangular symmetri-

cal fuzzy number of spread 1.

One of our interests is to investigate the inﬂu-

ence of the intentionally chosen degree of fuzziness

of these estimators on the characteristics of the con-

structed fuzzy conﬁdence intervals. Note that we will

additionally use the fuzzy sample mean as a fuzzy es-

timor for the sake of comparison.

Table 1 shows the 95%-quantiles of the boot-

strapped distribution of the likelihood ratio LR for

the cases of 50, 100 and 500 sample sizes. From

Fuzzy Conﬁdence Intervals by the Likelihood Ratio with Bootstrapped Distribution

237

this table, we can brieﬂy remark that the quantiles

depending on the sample sizes and/or the algorithm

chosen are somehow close. Furthermore, it is clear

that greater fuzziness, that is modelling the MLE esti-

mator using a fuzzy number with spread 2, leads to a

greater quantile compared to the case where the mod-

elling fuzzy number is less fuzzy, that is, modelling

the MLE estimator by a fuzzy number with spread 1.

Table 1: The 95%-quantiles of the bootstrapped distribution

of LR - Case of a data set taken from a normal distribution

N(5, 1) modelled using triangular symmetrical fuzzy num-

bers at 1000 iterations.

Algorithm 1

Sample size N=50 N=100 N=500

Bootstrap quantile using 1.990 2.038 2.342

the sample mean

Bootstrap quantile using the 1.809 1.927 2.181

MLE estimator (Spread 2)

Bootstrap quantile using the 1.523 1.626 1.825

MLE estimator (Spread 1)

Algorithm 2

Sample size N=50 N=100 N=500

Bootstrap quantile using 1.802 1.845 2.118

the sample mean

Bootstrap quantile using the 1.854 1.971 2.201

MLE estimator (Spread 2)

Bootstrap quantile using the 1.563 1.671 1.864

MLE estimator (Spread 1)

Based on the boostrapped quantiles shown in Ta-

ble 1, we now calculate the fuzzy conﬁdence intervals

using the likelihood method following the instructions

given in Section 5.1. Note that for the construction of

conﬁdence intervals, we will develop the case with

N = 500 observations only. Table 2 gives the lower

and upper bounds of the support and the core sets of

the calculated fuzzy conﬁdence intervals.

Let us ﬁrst look at the inﬂuence of the choice of

the bootstrap algorithm on the constructed conﬁdence

intervals. From Table 2, it is clear that no notable dif-

ferences exist between the support and the core sets

obtained by both algorithms. We can conclude that

the choice of algorithms has no evident effect on the

outcome of the approach. Therefore, although the de-

sign of both algorithms is different relative to points

1 and 2, similar results are depicted. Obviously, the

small ﬂuctuations in the bootstrapped quantiles given

in Table 1 did not drastically inﬂuence the outcome of

our approach.

Contrarily, regarding the fuzziness chosen for

modelling the MLE estimator, we can clearly see a

difference in the support sets of the calculated fuzzy

conﬁdence intervals. In fact, less fuzziness in the

fuzzy number modelling the MLE estimator leads to

a smaller support set of the obtained conﬁdence in-

terval. By way of example for Algorithm 1, the fuzzy

conﬁdence interval for the MLE estimator with spread

1 has a smaller support set (i.e. [4.303; 5.685]) than

the fuzzy conﬁdence interval for the MLE estimator

with spread 2 (i.e. [3.804;6.184]). Consequently, be-

cause the degree of fuzziness of the estimator directly

affects the constructed fuzzy conﬁdence interval, it is

very important to carefully model this MLE estimator.

Next, we compare the constructed bootstrap fuzzy

conﬁdence intervals to the traditional fuzzy conﬁ-

dence interval

Π given by the trapezoidal fuzzy num-

ber

Π = (3.907, 4.907, 5.080, 6.080), as shown in

Section 4. We can see that the bootstrap fuzzy con-

ﬁdence interval using the MLE estimators results in

slightly larger core sets, while the characteristics of

the obtained support sets differ between the cases de-

pending on the degree of fuzziness of the MLE esti-

mator. In this context, we add that once we use the

fuzzy sample mean as an estimator in the calculation

process, we get a fuzzy conﬁdence interval for which

the support and the core sets are tighter than the ones

of the traditional fuzzy conﬁdence interval

Π.

Table 2: The fuzzy conﬁdence interval by the likelihood ra-

tio at the 95% signiﬁcance level - Case of 500 observations

taken from a normal distribution N(5, 1) modelled by trian-

gular symmetrical fuzzy numbers.

Algorithm 1

Support set Core set

Lower Upper Lower Upper

fci using the 3.991 5.996 4.940 5.047

sample mean

fci using the MLE 3.804 6.184 4.795 5.193

estimator (Spread 2)

fci using the MLE 4.303 5.685 4.797 5.191

estimator (Spread 1)

Algorithm 2

Lower Upper Lower Upper

fci using the 3.991 5.996 4.945 5.042

sample mean

fci using the MLE 3.803 6.184 4.795 5.193

estimator (Spread 2)

fci using the MLE 4.303 5.685 4.797 5.191

estimator (Spread 1)

Simulation Study on Coverage Rates. It is cru-

cial to investigate the coverage rates corresponding to

the fuzzy conﬁdence intervals calculated using the de-

fended likelihood method. We generated a large num-

ber of data sets composed of N = 100, 500 and 1000

observations. These data sets are considered to be un-

certain. Every observation is modelled by a triangu-

lar symmetrical fuzzy number such that its spread is

equal to 2. For these samples, we estimate fuzzy con-

ﬁdence intervals for the mean at the conﬁdence level

FCTA 2020 - 12th International Conference on Fuzzy Computation Theory and Applications

238

1 −δ = 1 −0.05. We are particularly interested in

calculating the coverage rates of the constructed con-

ﬁdence intervals.

For this study, we used both Algorithms 1 and 2

to estimate the bootstrapped distribution of the like-

lihood ratio LR. These calculations were performed

using the MLE estimators modelled by fuzzy num-

bers of spreads 1 and 2. For the sake of comparison,

we also considered the fuzzy sample mean, similar to

the previously described analysis. The fuzzy conﬁ-

dence intervals obtained using the likelihood method

are then constructed and their coverage rates calcu-

lated. As a ﬁnal step, we compare their coverage rates

with the rates of the traditional fuzzy ones given in

Equation 11.

It appears that the coverage rates of the boot-

strap fuzzy conﬁdence intervals calculated using Al-

gorithms 1 and 2 are overall very close in the various

setups. The difference is not noteworthy. Therefore,

we propose elaborating the rates of the intervals using

Algorithm 1 only.

Overall, the difference in the coverage rates of the

bootstrap fuzzy intervals compared to the ones of the

traditional fuzzy method is slight. This difference did

not exceed 1.4% in all the cases. Using similar setups

as in the previously described analysis, the results are

developed as follows.

Regarding the data sets composed of 500 obser-

vations, we found that the coverage rate of the fuzzy

conﬁdence interval achieved by the likelihood method

using the fuzzy sample mean is about 94.4% in the

core set and about 100% in the support set. It is ex-

actly the same as the rate for the traditional fuzzy con-

ﬁdence interval. Nevertheless, according to the fuzzy

conﬁdence intervals calculated using the spread 1 and

spread 2 fuzzy numbers modelling the MLE estima-

tors, the coverage rates are about 95.6% in the core

set for both cases and about 100% in the support set.

Remember that these rates are somehow acceptable

in this context since theoretically a 95% conﬁdence

level has to be guaranteed. From these numbers, it is

clear that the fuzziness contained in the MLE estima-

tor is supposed to be uncertain. Although affecting

its spread, the fuzziness did not actually inﬂuence the

coverage rate of the calculated fuzzy conﬁdence inter-

val.

As a general interpretation of the outcome of our

approach compared to the traditional fuzzy one, we

can say that the LR fuzzy conﬁdence interval us-

ing the MLE estimators modelled by fuzzy numbers

seemed to be slightly less restrictive than the tradi-

tional fuzzy one. Therefore, once the fuzzy sample

mean serves as an estimator, the support of the ob-

tained interval appears to be smaller. In this context,

it would be interesting to further investigate the be-

havior of the coverage rates in several setups and to

ﬁnd an appropriate theoretical method for calculating

fuzzy MLE estimators.

6 NUMERICAL APPLICATION

Let us now discuss the construction of such conﬁ-

dence intervals where we suppose our data and the

hypotheses to be fuzzy. We will consider the known

normal distribution in order to simplify understanding

the different steps.

Suppose a random sample composed of 10 ob-

servations X

, . . . , X

given in Table 3. This sample

is supposed to be taken from a normal distribution

with a mean µ and a known variance σ

= 1.29,

i.e. N(µ, σ

= 1.29). We consider this sample to

be uncertain and model its fuzzy perception using

triangular fuzzy numbers. The setups to estimate a

particular fuzzy conﬁdence interval for the mean µ at

the conﬁdence level 1 −δ = 1 −0.05 are given in the

following steps:

Table 3: The data set and the fuzziﬁed observations.

Index X

Triangular Fuzzy Number

1 4 (3, 4, 5)

2 1 (0, 1, 2)

3 3 (2, 3, 4)

4 2 (1, 2, 3)

5 3 (2, 3, 4)

6 2 (1, 2, 3)

7 5 (4, 5, 6)

8 2 (1, 2, 3)

9 3 (2, 3, 4)

10 3 (2, 3, 4)

X = 2.8

X = (1.8, 2.8, 3.8)

• Model the Data: Suppose the following mod-

elling schema:

– the value ”1” modelled by

= (0, 1, 2),

– the value ”2” modelled by

= (1, 2, 3),

– the value ”3” modelled by

= (2, 3, 4),

– the value ”4” modelled by

= (3, 4, 5),

– the value ”5” modelled by

= (4, 5, 6).

Based on this, we obtain the modelled sample

shown in Table 3.

Fuzzy Conﬁdence Intervals by the Likelihood Ratio with Bootstrapped Distribution

239

• Deﬁne the Required Test: We test a fuzzy null

hypothesis

against a fuzzy alternative one

for the mean µ at the signiﬁcance level δ = 0.05.

Let us consider the following fuzzy hypotheses

and

= (1.8, 2, 2.3) against

= (2.25, 2, 5).

• Calculate the Fuzzy Sample Mean: The

fuzzy sample average

X of the fuzzy percep-

tions of the n = 10 observations denoted by

X = (1.8, 2.8, 3.8) can be written by its α-cuts

(

= [(

;(

] = [1.8 + α; 3.8 −α].

6.1 Estimation of the Traditional Fuzzy

Conﬁdence Interval for the Mean

A traditional fuzzy conﬁdence interval for the mean

µ at the conﬁdence level 1 −δ = 1 −0.05 can be es-

timated as presented in Deﬁnition 4.1. We obtain the

lower and upper bounds of the conﬁdence interval at

the conﬁdence level 1 −0.05:



;



(

−u

1−

√

;(

+ u

1−

√



1.0965 + α; 4.5034 −α



where u

1−

= u

0.975

= 1.96 is the 0.975-quantile of

the normal distribution, σ = 1.135 is the standard de-

viation and n = 10 is the number of observations. The

obtained interval is shown in Figure 1.

0.0 0.2 0.4 0.6 0.8 1.0

Fuzzy confidence interval for the mean

0.0 0.2 0.4 0.6 0.8 1.0

0.0000 1.0965 2.0965 3.0000 3.5034 4.5034

Figure 1: Traditional fuzzy conﬁdence interval for the mean

Π - Section 6.

6.2 Estimation of the Fuzzy Conﬁdence

Interval for the Mean using the

Likelihood Method

We now re-calculate the fuzzy conﬁdence interval

for the mean but use the likelihood methodol-

ogy presented above. At the conﬁdence level

1 − δ = 1 − 0.05, the fuzzy conﬁdence interval

obtained using the likelihood method denoted by

can then be constructed in the following way:

1. Consider the probability density function f (x;

θ)

of the standard normal distribution such that σ =

1.135. For the fuzzy sample

, i = 1, . . . , 10, we

ﬁrst calculate the log-likelihood function written

as:

θ; ˜x) = log

(x) f (x;

θ)dx + . . .

+log

(x) f (x;

θ)dx

= log

(3 + x) f (x;

θ)dx

+ log

(5 −x) f (x;

θ)dx + . . .

+ log

(2 + x) f (x;

θ)dx

+ log

(4 −x) f (x;

θ)dx.

2. Once we assume the sample to be fuzzy, we can

consider the parameter to be fuzzy as well. How-

ever, we ﬁrst calculate a crisp maximum likeli-

hood estimator for the mean. The EM algorithm

for the fuzzy context gives the crisp MLE estima-

tor

θ = 3.6568. Let us now model this crisp esti-

mator using the following triangular symmetrical

fuzzy number (3.1568, 3.6568, 4.1568). We high-

light that its support set is nothing but the interval

[3.1568;4.1568], and its core set is reduced to the

element 3.6568.

3. Let us now consider Algorithm 1 to estimate the

distribution of the likelihood ratio LR by the boot-

strap technique. At the signiﬁcance level δ =

0.05, the bootstrapped (1 −δ)-quantile η is esti-

mated to be η = 1.4778. We then get

1.4778

0.7389. The threshold points I

, I

and I

described in Equations 23 and 24 have to be cal-

culated afterwards. They are given by:

= l(3.1568; ˜x) −0.7389 = −16.2258,

= l(3.6568; ˜x) −0.7389 = −18.3079,

= l(4.1568; ˜x) −0.7389 = −22.1101.

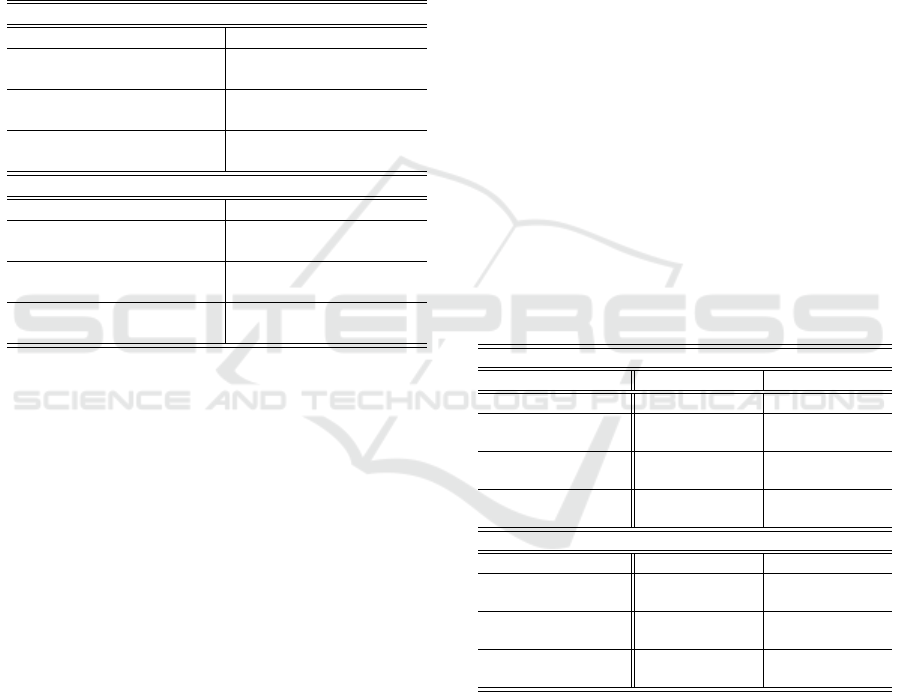
Note that the minimum and maximum

thresholds shown in Figure 2(a) are

min

= min(I

, I

) = −22.1101, and

max

= max(I

, I

) = −16.2258.

4. The intersection points θ

, θ

and θ

, θ

have to be found as proposed in

FCTA 2020 - 12th International Conference on Fuzzy Computation Theory and Applications

240

−22 −20 −18 −16

Fuzzy log Likelihood ratio approach

l(θ,x

)

min

max

●

1.3674 1.8276 2.2175

●

3.3838 3.7736 4.2332

●

2 3 4

(a) Fuzzy log-likelihood function for the mean and the inter-

section with the upper and lower bounds of the fuzzy parame-

ter

0.0 0.2 0.4 0.6 0.8 1.0

Fuzzy confidence interval by the likelihood ratio approach

0.0 0.2 0.4 0.6 0.8 1.0

1.3674 1.8276 2.2175 3.3838 3.7736 4.23320 1 3 5

(b) Fuzzy conﬁdence interval by likelihood ratio method

Figure 2: The construction process of the fuzzy conﬁdence interval by the likelihood ratio method - Section 6.

Equations 27, 28, 29 and 30. We get:

= 2.2175, θ

= 3.3838,

= θ

= 1.8276, θ

= θ

= 3.7736,

= 1.3674, θ

= 4.2332.

The minimum and maximum intersection ab-

scisses θ

inf

, θ

sup

, θ

inf

and θ

sup

are given by:

inf

= inf(θ

, θ

) = 1.3674,

inf

= inf(θ

, θ

) = 3.3838,

sup

= sup(θ

, θ

) = 2.2175,

sup

= sup(θ

, θ

) = 4.2332.

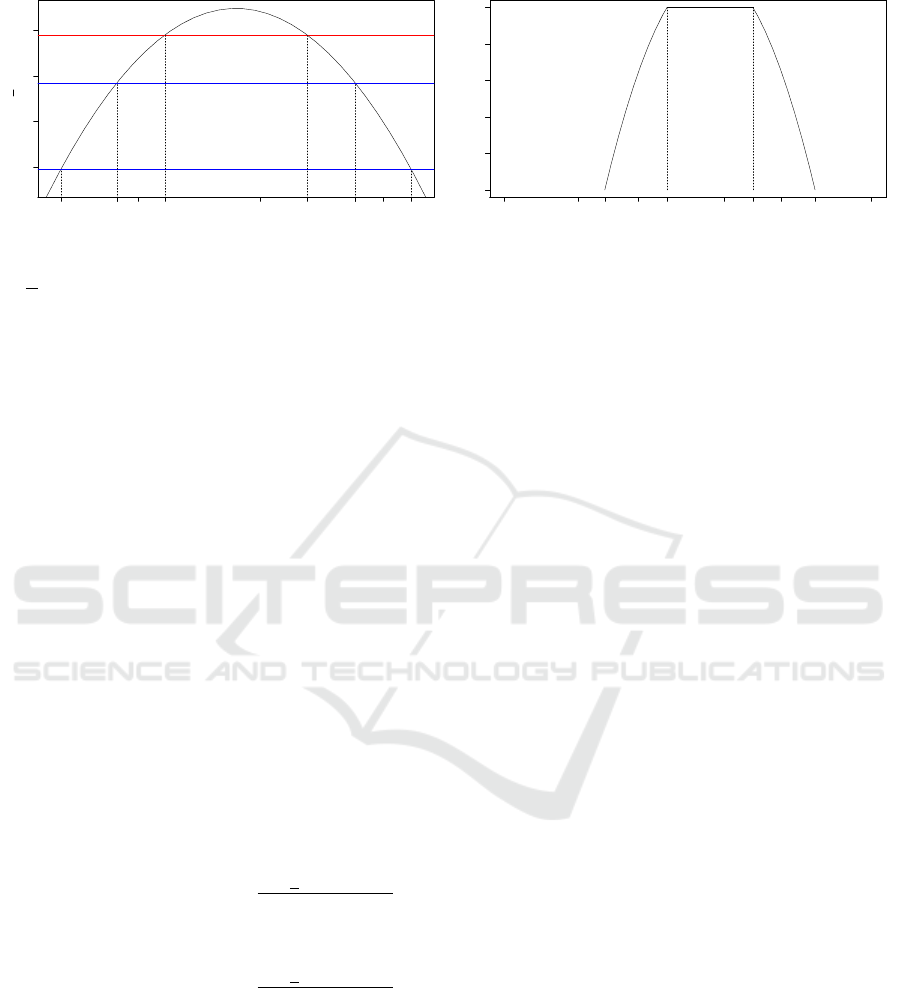
5. For the last step, we standardise the obtained func-

tion to the y-interval [0;1] and get the following

fuzzy conﬁdence interval

given by its left

and right α-cuts (

)



(

)

, (

)



shown in Equations 35 and 36:

(

)

θ ∈ R | 1.3674 ≤θ ≤ 2.2175

and α =

l(θ, ˜x)+ 22.1101

5.8843

(

)

θ ∈ R | 3.3838 ≤θ ≤ 4.2332

and α =

l(θ, ˜x)+ 22.1101

5.8843

This latter is shown in Figure 2(b).

6.3 Comparison and Interpretation

At this stage, it would be interesting to compare the

fuzzy conﬁdence interval obtained using the likeli-

hood approach

to the traditional fuzzy conﬁ-

dence interval

Π. If we superpose Figures 1 and 2(b),

we can clearly see that the likelihood-based interval

has a tighter support set than the traditional in-

terval

Π, i.e.

⊆

Π. In the considered speciﬁc se-

tups, we can say that our approach appears to be more

restrictive. In other words, with our approach we tend

to reject the hypothesis under study more often. We

highlight that this interpretation can be slightly op-

posite in the situation with a larger support set of

the fuzzy conﬁdence interval. This could be mainly

due to a greater amount of fuzziness contained in the

fuzzy number modelling the MLE estimator.

Furthermore, concerning the shape of the obtained

conﬁdence intervals, i.e. their membership functions,

it is clear that the shape of the traditional one strongly

depends on the modelling procedure of the studied

sample—in other words on the shape of the chosen

fuzzy numbers. Note that this statement is similar in

the case of the fuzzy sample mean. Contrarily, the

fuzzy conﬁdence interval obtained using the likeli-

hood method relies directly on the probability density

function connected to the considered data set. Finally,

we can clearly see that the shape of the LR interval is

more elaborated than the traditional one. This is con-

sidered an increase in the accuracy of such calculation

methodologies.

7 CONCLUSION

This study proposed a complete procedure to estimate

fuzzy conﬁdence intervals using the likelihood ratio

method. This required estimating the distribution of

the likelihood ratio. A contribution of this research is

the use of the bootstrap technique to accomplish this

task. Two algorithms are discussed—a simple one

and a more complex one based on preserving the loca-

tion and dispersion measures related to a new metric

called the d

SGD

metric.

Fuzzy Conﬁdence Intervals by the Likelihood Ratio with Bootstrapped Distribution

241

It is clear that such methodologies are computa-

tionally expensive. However, our procedure consti-

tutes an affordable tool to reduce this computational

complexity. Furthermore, our contribution is in some

sense general, as it can be applied to a variety of esti-

mators.

Finally, the main problem encountered is in the

fuzziness contained in the fuzzy number modelling

the maximum likelihood estimator. An investigation

of different use cases depending on several modelling

schemas for this estimator is welcome. Overall, a

method of calculating a fuzzy-nature maximum like-

lihood estimator needs to be developed in future re-

search.

REFERENCES

Berkachy, R. (2020). The signed distance measure in fuzzy

statistical analysis. Some theoretical, empirical and

programming advances. PhD thesis, University of Fri-

bourg, Switzerland.

Berkachy, R. and Donz

e, L. (2016). Individual and global

assessments with signed distance defuzziﬁcation, and

characteristics of the output distributions based on an

empirical analysis. In Proceedings of the 8th Inter-

national Joint Conference on Computational Intelli-

gence - Volume 1: FCTA,, pages 75 – 82.

Berkachy, R. and Donz

e, L. (2019a). Fuzzy conﬁdence in-

terval estimation by likelihood ratio. In Proceedings

of the 2019 Conference of the International Fuzzy Sys-

tems Association and the European Society for Fuzzy

Logic and Technology (EUSFLAT 2019).

Berkachy, R. and Donz

e, L. (2019b). Testing Hypotheses

by Fuzzy Methods: A Comparison with the Classical

Approach, pages 1 – 22. Springer International Pub-

lishing, Cham.

Berkachy, R. and Donz

e, L. (2020). FuzzySTs: Fuzzy

statistical tools, R package, url = https://CRAN.R-

project.org/package=FuzzySTs.

Chachi, J., Taheri, S. M., and Viertl, R. (2012). Testing

statistical hypotheses based on fuzzy conﬁdence inter-

vals. Austrian Journal of Statistics, 41(4):267 –286.

Couso, I. and Sanchez, L. (2011). Inner and outer fuzzy ap-

proximations of conﬁdence intervals. Fuzzy Sets and

Systems, 184(1):68 – 83. Preference Modelling and

Decision Analysis (Selected Papers from EUROFUSE

2009).

Denoeux, T. (2011). Maximum likelihood estimation from

fuzzy data using the em algorithm. Fuzzy Sets and

Systems, 183(1):72 – 91. Theme : Information pro-

cessing.

Dubois, D. and Prade, H. (1987). The mean value of a fuzzy

number. Fuzzy Sets and Systems, 24(3):279 – 300.

Fuzzy Numbers.

Efron, B. (1979). Bootstrap methods: Another look at the

jackknife. The Annals of Statistics, 7(1):1–26.

Gil, M. A. and Casals, M. R. (1988). An operative extension

of the likelihood ratio test from fuzzy data. Statistical

Papers, 29(1):191 – 203.

Gonzalez-Rodriguez, G., Montenegro, M., Colubi, A., and

Gil, M. A. (2006). Bootstrap techniques and fuzzy

random variables: Synergy in hypothesis testing with

fuzzy data. Fuzzy Sets and Systems, 157(19):2608 –

2613. Fuzzy Sets and Probability/Statistics Theories.

Kahraman, C., Otay, I., and

Oztays¸i, B. (2016). Fuzzy Ex-

tensions of Conﬁdence Intervals: Estimation for µ, σ

and p, pages 129 – 154. Springer International Pub-

lishing.

Kruse, R. and Meyer, K. D. (1987). Statistics with vague

data, volume 6. Springer Netherlands.

Montenegro, M., Colubi, A., Rosa Casals, M., and

Angeles Gil, M. (2004). Asymptotic and bootstrap

techniques for testing the expected value of a fuzzy

random variable. Metrika, 59(1):31–49.

Parchami, A. (2018). EM.Fuzzy: Em algorithm

for maximum likelihood estimation by non-precise

information, R package, url = https://CRAN.R-

project.org/package=EM.Fuzzy.

Viertl, R. and Yeganeh, S. M. (2016). Fuzzy Conﬁdence

Regions, pages 119 – 127. Springer International Pub-

lishing, Cham.

Yao, J.-S. and Wu, K. (2000). Ranking fuzzy numbers

based on decomposition principle and signed distance.

Fuzzy sets and Systems, 116(2):275 – 288.

Zadeh, L. (1968). Probability measures of fuzzy events.

Journal of Mathematical Analysis and Applications,

23(2):421–427.

FCTA 2020 - 12th International Conference on Fuzzy Computation Theory and Applications

242