Merging Partial Fuzzy Rule-bases

Martina Da

nkov

Institute for Research and Applications of Fuzzy Modeling, University of Ostrava,

30. dubna 22, 701 03 Ostrava 1, Czech Republic

Keywords:

Fuzzy Rules, Graded Properties, IF–THEN Rules, Extensionality, Functionality, Partiality, Fuzzy Relations.

Abstract:

We propose two basic ways of merging various partial fuzzy rule-bases containing knowledge related to the

same process or dependency in general. The knowledge that is not at the disposal is considered undeﬁned and

encoded using some dummy value. For simplicity, we use only one code for undeﬁned membership value,

and we handle the undeﬁned membership values using operations of variable-domain fuzzy set theory, i.e., the

theory that allows fuzzy sets to have undeﬁned membership values. Moreover, we study one of the essential

properties in fuzzy modeling–a graded property of functionality. We provide estimations for degrees of the

functionality of input models and merged models of partial fuzzy rule-bases.

1 INTRODUCTION

In this contribution, we focus on fuzzy models of IF–

THEN rules due to their natural ability to handle the

gradualness of expert knowledge. Models of vari-

ous fuzzy IF–THEN rules (Mamdani and Assilian,

1975; H

ajek, 1998) are closely related to the domain

of deﬁnition. For example, we often deal with many

rule bases in hierarchical systems such as in (Del-

gado et al., 2003; K

oczy et al., 2003; Magdalena,

2019; Nolasco et al., 2019), or in ensemble techniques

(Scherer, 2012;

epni

cka et al., 2016; Fletcher et al.,

2020), which can generally differ in the domains. It

means that each particular rule base (a set of fuzzy

IF–THEN rules) has its domain, and outside of it is

considered to be undeﬁned.

The problem of merging rule bases from differ-

ent domains (Lughofer, 2011; Casillas et al., 2013;

Latkowski and Mikołajczyk, 2004; Peters et al., 2004)

arose from the practical need to join rule-bases based

on various expert knowledge, given data, or fact base

etc. Roughly speaking, it consists in unifying the do-

mains into a common one and extending the member-

ship functions of particular fuzzy sets by ﬁlling in an

appropriately chosen membership degree such that an

output merged rule-base keeps non-conﬂicting knowl-

edge and preserves properties owned by both input

rule-bases.

Since in some cases, we want to carry information

about undeﬁned parts of input models; consequently,

none of the standard membership degrees would

be applicable for ﬁlling in. Here, variable-domain

fuzzy set theory (VFST) introduced in (B

ehounek and

nkov

a, 2020a) is applicable. It provides essential

tools for handling fuzzy sets with undeﬁned member-

ship values.

Note that there are also other approaches to handle

undeﬁned membership values, such as in (

epni

cka

et al., 2019; d’Allonnes and Lesot, 2017). An ad-

vantage of an inference system involving operations

of VFST is robustness in the sense of being able to

handle some exceptions automatically. Generally, ex-

ceptions have various sources, e.g., an integer divide

by zero or using too much memory. In our case, ex-

ceptions related to undeﬁned values are relevant.

In VFST, various ways of merging rule-bases

from two different domains are deﬁnable as an al-

ternative to the know approaches. In the following,

we will investigate which avoids artifacts and behaves

as expected. Moreover, we will present the notion

of functionality and study its properties w.r.t. merged

rule-bases.

The paper is organized as follows. In Sec-

tion 2, we recall notions of partial fuzzy sets and

relations, two essential extensions of residuated lat-

tice operations, and other necessary notions mostly

from (B

ehounek and Nov

ak, 2015; B

ehounek and

nkov

a, 2020a). Conjunctive and disjunctive mod-

els of partial fuzzy rule-bases are presented in Sec-

tion 3. Next, in Section 4, we introduce basic merg-

ing techniques that use partial fuzzy set operations.

All presented notions are together with illustrative ex-

nková, M.

Merging Partial Fuzzy Rule-bases.

DOI: 10.5220/0010058302430251

In Proceedings of the 12th International Joint Conference on Computational Intelligence (IJCCI 2020), pages 243-251

ISBN: 978-989-758-475-6

243

amples that should help a reader with understanding.

The study of the transmission of functionality prop-

erty by merged models is in Section 5. Finally, the

main results and features of the used formalism are

summarized in Section 6.

2 BASIC NOTATIONS

Consider a complete residuated lattice

L = hL,∨,∧,, ⇒,0, 1i, (1)

and a single dummy element ∗ /∈ L representing an er-

ror code related to undeﬁned truth degree. We extend

the operations of L to ∗ by the following truth tables:

• The Bochvar-style operations

β ∗

α α c β ∗

∗ ∗ ∗

(2)

where c ∈ {∧, ∨,,⇒}. Here, ∗ behaves as the

annihilator and it can be viewed as the representa-

tive of a fatal error.

• The Soboci

nski-style operations

β ∗

α α c β α

∗ β ∗

(3)

c ∈ {∧, ∨,} and

⇒

β ∗

α α ⇒ β α⇒0

∗ β ∗

(4)

These operations treat ∗ as the neutral element,

which means that they ignore ∗ as far as possi-

ble. The only suspicious operation is ⇒

, where

⇒ is monotone in the second argument and anti-

tone in the ﬁst one. These properties of ⇒ lead to

inputting 0 instead of ∗ to compute α ⇒ ∗ in (4).

Both names of classes of extensions are inspired by

{0,1, ∗}-valued connectives in (Ciucci and Dubois,

2013).

Additionally, we introduce two basic bivalent or-

derings of truth values:

• The following ordering treats ∗ as a bottom ele-

ment:

≤

∗

β ∗

α α ≤ β 0

∗ 1 1

(5)

• And dually, we treat ∗ as a top element:

≤

∗

β ∗

α α ≤ β 1

∗ 0 1

(6)

Let L

∗

= L ∪{∗} and α

∈ L

∗

for each i ∈ I (where

I is an arbitrary index set). Then we deﬁne:

• The Bochvar inﬁmum

i∈I







i∈I

if α

6= ∗ for each i ∈ I;

∗ otherwise.

• The Bochvar supremum

i∈I







i∈I

if α

6= ∗ for each i ∈ I;

∗ otherwise.

• The Soboci

nski inﬁmum

i∈I











i∈I

6=∗

if α

6= ∗ for some i ∈ I;

∗ otherwise.

• The Soboci

nski supremum

i∈I











i∈I

6=∗

if α

6= ∗ for some i ∈ I;

∗ otherwise.

2.1 Partial Fuzzy Sets and Relations

Ordinary fuzzy sets are identiﬁed with their L-valued

membership functions, while the partial fuzzy sets

introduced by (B

ehounek and Nov

ak, 2015) allow

membership functions to be undeﬁned. The member-

ship functions of partial fuzzy sets are total functions

from some universe of discourse to L ∪ {∗}. The ad-

ditional dummy value ∗ /∈ L allows us to capture the

domain of partial fuzzy set.

Deﬁnition 2.1. Let U be a universe of discourse,

⊆ U, ∗ /∈ L, L

∗

= L ∪ {∗} and µ

: X

→ L be a

membership function from X

to a suitable structure L

of membership degrees.

1. A partial fuzzy set is a pair A = (X

,µ

). This

fact is denoted by A

⊂

∼

, X

is called the crisp

domain of A and we often write Dom(A) instead

of X

2. A partial fuzzy set A = (X

,µ

) in a universe

U ⊇ X

is represented by a L

∗

-valued member-

ship function A on U, deﬁned for each x ∈ U as:

A(x) =

(

(x) if x ∈ X

;

∗ if x ∈ U \X

(7)

FCTA 2020 - 12th International Conference on Fuzzy Computation Theory and Applications

244

Fuzzy relations between two crisp sets A and B

are fuzzy sets on A × B, while the domain of a partial

fuzzy relation is intended to be a subset of A ×B. It is

deﬁned as follows:

Deﬁnition 2.2. Let A, B 6=

We say that a partial fuzzy set R = (X

,µ

) is a

partial fuzzy relation between A and B if X

⊆ A × B

and µ

: X

→ L.

If A = B, we speak of partial fuzzy relations on A.

Consider A, B ⊂ U. Due to Deﬁnition 2.1, L

∗

valued membership function of a partial fuzzy rela-

tion R between A and B is deﬁned for each (x,y) ∈

U ×U as:

R(x,y) =

(

(x) if x ∈ X

;

∗ if x ∈ (U ×U) \ X

(8)

Example 2.3. Let U = h0, 1i, X

= X

⊆ U, A =

,µ

), B = (X

,µ

) due to Figure 1. Then we

deﬁne partial fuzzy relations (A ×

B), (A ×

B),

(A o

B) and (A o

B) with the following represen-

tations on U:

(A ×

B)(x,y) =

A(x) 

B(y), x,y ∈ U, (9)

(A ×

B)(x,y) =

A(x) 

B(y), x,y ∈ U, (10)

(A o

B)(x,y) =

A(x) ⇒

B(y), x,y ∈ U, (11)

(A o

B)(x,y) =

A(x) ⇒

B(y), x,y ∈ U, (12)

depicted on Figures 2–5, respectively. Observe that

the domain of A ×

B is (X

×U) ∪ (U × X

Partial fuzzy relations A ×

B and A ×

B can be

viewed as two variants of Cartesian product of partial

fuzzy sets A and B.

0.3 0.35 0.4 0.45 0.5 0.55 0.6 0.65 0.7 0.75 0.8

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Figure 1: Fuzzy sets A (solid line) and B (dotted line) on

= X

= h0.3,0.8i.

2.2 Partial Fuzzy Relational Operations

We have the following two main options to deﬁne re-

lational operations based on a various treatments of

undeﬁned values:

• Bochvar intersection:

(R u

S)(x,y) =

R(x,y)∧

S(x,y)

0 0.2 0.4 0.6 0.8 1

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Figure 2: A ×

B from Example 2.3.

0 0.2 0.4 0.6 0.8 1

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Figure 3: A ×

B from Example 2.3.

0 0.2 0.4 0.6 0.8 1

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Figure 4: A o

B from Example 2.3.

0 0.2 0.4 0.6 0.8 1

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Figure 5: A o

B from Example 2.3.

• Soboci

nski intersection:

(R u

S)(x,y) =

R(x,y)∧

S(x,y)

• Bochvar strong-intersection:

(R ∩

S)(x,y) =

R(x,y)

S(x,y)

• Soboci

nski strong-intersection:

(R ∩

S)(x,y) =

R(x,y)

S(x,y)

Merging Partial Fuzzy Rule-bases

245

• Bochvar union:

(R t

S)(x,y) =

R(x,y)∨

S(x,y)

• Soboci

nski union:

(R t

S)(x,y) =

R(x,y)∨

S(x,y)

3 MODELS OF PARTIAL FUZZY

IF-THEN RULES

Let I be some index set. A collection R of rules

“IF x ∈ A

THEN y ∈ B

”,

where each A

,i ∈ I is modeled by a partial fuzzy

set, is called partial fuzzy rules or partial fuzzy rule-

base. Fuzzy rules have two main models; we call

them disjunctive and conjunctive models of IF-THEN

rules due to a type of connective used to join rules. We

can write formally

i∈I

× B

), (13)

i∈I

o B

), (14)

where A

⊂

∼

(A × B)(x,y) =

A(x)  B(y),

(A o B)(x,y) =

A(x) ⇒ B(y), for all x,y ∈ U,

and

are the usual union and intersection of fuzzy

sets based on lattice operations ∨ and ∧, respectively.

In case of partial fuzzy rules, disjunctive and con-

junctive models are deﬁned as

i∈I

), (15)

i∈I

), (16)

respectively. These models are partial fuzzy sets with

the same domain

i∈I

(Dom(A

) × Dom(B

)). In the

sequel, we will simply write D,C,D

instead

of D

, respectively, provided that R is

clear from the context.

Notice that the introduced models use Bochvar

and Soboci

nski extensions that are very similar to ex-

tended operations that form the so-called Dragonﬂy

algebra (

epni

cka et al., 2019). They differ only at

values 0 and 1 because in Dragonﬂy algebra ∗ is sup-

posed to represent some degree lying between these

two values.

Example 3.1. Let U = h0,1i, A

be partial

fuzzy sets with membership functions as on Figure 6

and

Dom(A

) = Dom(B

) = [0.2, 0.7] (17)

Dom(A

) = Dom(B

) = [0.4, 0.9] (18)

Then, the partial fuzzy relations D

and C

are

depicted on Figures 7 and 8, respectively.

0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Figure 6: Partial fuzzy sets A

(solid line) and B

(dotted line).

0 0.2 0.4 0.6 0.8 1

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Figure 7: D

model of partial fuzzy rules.

0 0.2 0.4 0.6 0.8 1

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Figure 8: C

model of partial fuzzy rules.

In the following examples, we will overview other

possible combinations of extensions of operations

than in (15) and (16).

Example 3.2. Consider the same setting as in the pre-

vious example and deﬁne the following partial fuzzy

FCTA 2020 - 12th International Conference on Fuzzy Computation Theory and Applications

246

relations:

i∈I

) (19)

i∈I

) (20)

In D

and C

, Soboci

nski and Bochvar extensions

of operations are reversed comparing with D

and

. Their domain is

i=1

(Dom(A

) ×U) ∪ (U ×Dom(B

)) (21)

is drawn on Figures 7 for partial fuzzy sets

from Figure 6. As seen from this ﬁgure, D

and

cannot represent a functional dependence in ap-

propriate way. Outside

i=1

(Dom(A

) × Dom(B

)),

Soboci

nski-operations add relational dependencies by

means of partial fuzzy sets A

,i = 1,2, which

changes signiﬁcantly meaning and understandabil-

ity. Consequently, we do not include them in mod-

els of partial fuzzy rules. Observe that use of only

Soboci

nski-extension of operations leads to the same

problem as described above.

0 0.2 0.4 0.6 0.8 1

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Figure 9: D

from Example.

0 0.2 0.4 0.6 0.8 1

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Figure 10: C

from Example.

Example 3.3. Consider the same setting as in Ex-

ample 3.1 and deﬁne the following partial fuzzy re-

lations:

i∈I

) (22)

i∈I

) (23)

In D

and C

, only Bochvar extensions of opera-

tions are used, which leads to the following domain

i=1

(Dom(A

) × Dom(B

)) (24)

Hence, these partial fuzzy relations can be viewed as

minimalist models of partial fuzzy rules, where infor-

mation outside of a common domain is refused. Such

information can be viewed as unreliable and therefore

it do not propagate into the models.

0 0.2 0.4 0.6 0.8 1

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

0.4

0.5

0.6

0.7

0.8

0.9

Figure 11: C

model of partial fuzzy rules.

0 0.2 0.4 0.6 0.8 1

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Figure 12: D

model of partial fuzzy rules.

Due to deﬁciencies explained in the above ex-

amples, we focus only on the models given by (15)

and (16).

We deﬁne a sup-T composition of partial fuzzy re-

lations using Bochvar and Soboci

nski operations as

follows:

• Soboci

nski–Bochvar sup-T composition

(R ◦

S)(x,y) =

z∈U



R(x,z)

S(z,y)



Notice that Dom(R ◦

S) = Dom(R) ◦ Dom(S) and

a sup-T composition of partial fuzzy relations is as

usual on the composition of the domains and other-

wise, it remains undeﬁned.

Merging Partial Fuzzy Rule-bases

247

4 MERGING MODELS OF

PARTIAL FUZZY RULE-BASES

In this section, we will deal with disjunctive and con-

junctive models of partial fuzzy rule-bases given by

(15) and (16), respectively. Recall that these mod-

els are partial fuzzy relations. Therefore, we can ap-

ply partial fuzzy operations for merging several par-

tial fuzzy rule-bases describing the same dependency

into the single one. This process is visualized on Fig-

ure 13. The used operation with its corresponding ex-

tension determines the merging uniquely.

Figure 13: Merging of two rule-bases describing the same

dependency.

Soboci

nski extensions of operations ignores un-

deﬁned inputs represented by ∗. Hence, using these

operations we unite various information from differ-

ent sources. We apply this fact and deﬁne a family of

unifying merging operations.

Deﬁnition 4.1. Let R ,S be partial fuzzy rule-bases

and R,S be their models, respectively. Moreover, let

M = R ∪S and o ∈ {u,t,∩,∪}.

Then, we say that a unifying merging of R and S

using operation o is M with a model

M =

R o

S. (25)

Analogously, we employ Bochvar extensions of

operations for incorporating information from various

sources, which is assumed to be unreliable outside a

domain of common knowledge.

Deﬁnition 4.2. Under the assumptions of Deﬁni-

tion 4.1, we say that a strict merging of R and S using

operation o is M with a model

M =

R o

S. (26)

An extension to n models is straightforward.

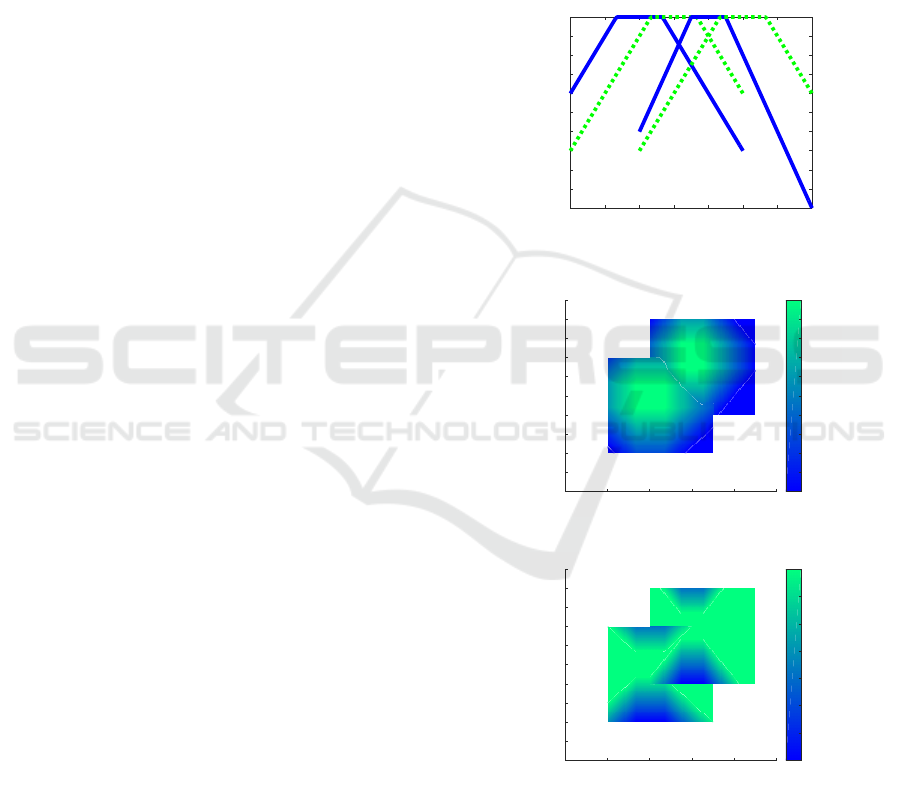
Example 4.3. Assume two models R = (X

,µ

) and

S = (X

,µ

) of some partial fuzzy rule-bases R and S ,

respectively. For a simplicity, assume R consists of

3 rules, where Dom(A

) = [0.3, 0.8] and Dom(B

) =

[0.3,0.9] for all i ∈ I = {1, 2,3}, and moreover, S

consists of 3 rules, where Dom(A

) = [0,0.6] and

Dom(B

) = [0.2,0.95] for all j ∈ J = {1,2,3,4}.

Their disjunctive models are depicted on Figures 14

and 15.

Figure 16 shows a model of unifying merging of

R and S using u, i.e., R u

S. Similarly, Figure 17

depicts R t

S. A model of strict merging of R and

S using u (t) is the same as R u

S (R t

S) on the

intersection of domains X

∩ X

, and otherwise it re-

mains undeﬁned. Hence, graphs of R u

S and R t

can be easily derived from Figure 16 and Figure 17,

respectively.

0 0.2 0.4 0.6 0.8 1

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Figure 14: R from Example 4.3.

0 0.2 0.4 0.6 0.8 1

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Figure 15: S from Example 4.3.

0 0.2 0.4 0.6 0.8 1

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Figure 16: R u

FCTA 2020 - 12th International Conference on Fuzzy Computation Theory and Applications

248

0 0.2 0.4 0.6 0.8 1

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Figure 17: R t

5 PRESERVATION OF GRADED

FUNCTIONALITY BY MERGED

MODELS

In this section, we will focus on a special kind of rule-

bases, i.e., the one that describes a functional depen-

dency. A functional dependency of a rule-base means

functionality property of the related model (fuzzy re-

lation). Provided that we work with partial fuzzy sets,

we have to introduce functionality into this frame-

work.

Deﬁnition 5.1. Let U 6=

0 be a universe of discourse,

X,Y ⊂ U, and R be a partial fuzzy relation between X

and Y . The functionality property of R w.r.t. ≈

,≈

is deﬁned as

Func

≈

,≈

(R) ≡

∈U

[(x ≈



R(x,y)

R(x

)) ⇒

y ≈

] (27)

We say that R is functional to degree d if d =

Func

≈

,≈

(R).

This deﬁnition stems from graded notion of func-

tionality for fuzzy sets by (Demirci, 2001; Da

nkov

2018). Func

≈

,≈

(R) is designed in agreement with

our intuitive expectations, i.e., its degree is computed

for all elements from the respective domains of partial

fuzzy relations ≈

,≈

, and R.

Provided that we deal with a partial fuzzy rule-

base R, it is necessary to construct partial fuzzy rela-

tions ≈

and ≈

from partial fuzzy sets {A

}

i∈I

and

}

i∈I

, respectively, using Valverde’s representation

theorem (Valverde, 1985) modiﬁed for partial fuzzy

sets.

Theorem 5.2. Let I be some index set, {A

}

i∈I

be a

family of partial fuzzy sets, and {c

}

i∈I

be a family of

elements such that c

∈ X

and A

) = 1 for each

i ∈ I, U be a common universe set such that X

⊆ U

for all i ∈ I. Moreover, let

x ≈ y =

i∈I

(x) ⇔

(y)). (28)

Then the following two statements are equivalent.

(1) A binary partial fuzzy relation ≈ on

i∈I

such that

(x) = x ≈ c

, for all x ∈ U. (29)

(2) For all i, j ∈ I

x∈U

(x) 

(x)) ≤

y∈U

(y) ⇔

(y)) (30)

where ≤ ∈ {≤

∗

,≤

∗

Proof. We provide only a sketch of the proof. (1) fol-

lows from (2) by replacing undeﬁned parts of {A

}

i∈I

by ﬁlling in the membership value 0. Then {A

}

i∈I

become total on U and we can apply Valverde’s rep-

resentation theorem for fuzzy sets. The resulting sim-

ilarity (reﬂexive, symmetric and transitive) relation ≈

is total on U. Let us deﬁne

Dom

∗

(A)(x) =

(

1 if x ∈ X

;

∗ if x ∈ U \ X

(31)

Then A

(x) = (x ≈ c

) = (x ≈

)

Dom

∗

)(x) for

all x ∈ U , where ∗ is either top or bottom element

w.r.t. ≤.

The reverse implication follows from the fact that

≈

is similarity relation for which (30) is valid. For

the partial fuzzy sets {A

}

i∈I

, the expressions on both

sides of (30) are computed over the same sets X

∩

⊆ U for all i, j ∈ I. Hence, (30) is valid for partial

fuzzy sets {A

}

i∈I

deﬁned by (28).

In the sequel, we will study translation of func-

tionality property of merged partial fuzzy rule-bases.

Let us consider two partial fuzzy rule-bases R and S

with partial fuzzy sets {A

}

i∈I

and {C

}

j∈J

, re-

spectively. Their models D

are given by

(15) and (16). Moreover, let us deﬁne

x ≈

y =

i∈I

(x) ⇔

(y)) (32)

x ≈

y =

i∈I

(x) ⇔

(y)) (33)

x ∼

y =

i∈J

(x) ⇔

(y)) (34)

x ∼

y =

i∈J

(x) ⇔

(y)) (35)

for all x,y ∈ U, k = 1,2, where U ⊇ X

i ∈ I, j ∈ J.

Let F be one of the models of R and G be one

of the models of S . Then, we can prove the follow-

ing boundaries for graded functionality in the case of

strict merging of R and S using u and also ∩:

Func

≈

,≈

(F) ∧

Func

∼

,∼

(G)

≤

∗

Func

(F u

G), (36)

Merging Partial Fuzzy Rule-bases

249

where w

(≈

) u

(∼

), k = 1,2.

Func

≈

,≈

(F) 

Func

∼

,∼

(G)

≤

∗

Func

(F ∩

G), (37)

where w

(≈

) ∩

(∼

), k = 1,2.

The union operator is not applicable in the case of

functionality property provided that the domains of

partial fuzzy sets in the models are arbitrary. Easily,

we can ﬁnd two functional fuzzy relations such that

their union is not functional. It can be proved for both

orderings ≤ ∈ {≤

∗

,≤

∗

} that if

i∈I

∩

j∈J

0 then

Func

≈

,≈

(F) ∧

Func

∼

,∼

(G)

≤ Func

(F t

G), (38)

is trivially valid, because (F t

G)(x,y) = ∗ for all

x,y ∈ U. However, a unifying merging via t operator

leads to a non-trivial estimation based on the same

requirement as above, i.e., if

i∈I

∩

j∈J

then

Func

≈

,≈

(F) ∧

Func

∼

,∼

(G)

≤ Func

(F t

G). (39)

Recall that the domain of Soboci

nski operations

∩

is the union of domains of the input partial

fuzzy sets. Therefore, if

i∈I

∩

j∈J

0 then

the following inequalities are trivially valid for both

orderings:

Func

≈

,≈

(F) ∧

Func

∼

,∼

(G)

≤ Func

(F u

G), (40)

where w

(≈

) u

(∼

), k = 1,2,

Func

≈

,≈

(F) 

Func

∼

,∼

(G)

≤ Func

(F ∩

G) (41)

where where w

(≈

) ∩

(∼

), k = 1,2, and ≤ ∈

{≤

∗

,≤

∗

As can be observed in Figure 16, if

i∈I

∩

j∈J

0 then it can happen that the output of

unifying merging is not functional anymore. Though

functionality comes with degrees, the functionality of

merged rule-basis can be of zero. There are several

ways to overcome this deﬁciency: we can specify

a particular rule base’s reliability and then incorpo-

rate it into the merging process; or erasing all knowl-

edge lowering the degree of functionality using, e.g.,

a newly designed merging operator.

Observe that in Deﬁnitions 4.1 and 4.2, we used

only partial fuzzy set operations. Consequently, it is

suitable for merging rule-bases describing the same

dependency between sets X and Y . Now, let us con-

sider that our rule-bases describe dependencies be-

tween sets X and Y in the case of R , and between

sets Y and Z in the case of S . Such rule-bases can be

joined as “serial” using sup-T composition of partial

fuzzy relations for which we can prove the following

estimation:

Func

≈

,≈

(F) 

Func

∼

,∼

(G)

≤ Func

(F ◦

G), (42)

where ≤ ∈ {≤

∗

,≤

∗

}, and w

(≈

) ◦

(∼

) for

k = 1,2. For simplicity of exposition, merging using

◦ was not included in formal deﬁnitions of merging

methods because it does not have strict either unify-

ing character. It can be viewed as a reasonable merg-

ing operator. Moreover, we have proposed only one

combination of Bochvar and Soboci

nski extensions

for sup-T composition. It is not in the scope of this pa-

per to investigate other ways of extensions. For prop-

erties of ◦

, we refer to (B

ehounek and Da

nkov

2020b), and also consult (

epni

cka and Cao, 2018)

for other extensions of ◦ to partial fuzzy relations.

6 CONCLUSIONS

We have proposed two basic ways of merging rule-

bases describing the same dependency. Moreover, we

have studied a graded property of functionality, which

is one of the essential properties in fuzzy modeling.

We extended the so-called Valverde’s representation

theorem for partial fuzzy sets to build a bridge be-

tween partial fuzzy rule-bases and functional partial

fuzzy relations. Using this theorem, we were able

to move from partial fuzzy rule-bases to functional

partial fuzzy relations and then to provide estimations

for degrees of the functionality of input models and

merged models. Proofs of these estimations are left

for a full paper.

ACKNOWLEDGEMENTS

This research was supported by Czech Science Foun-

dation through the grant 20-07851S.

REFERENCES

ehounek, L. and Da

nkov

a, M. (2020a). Variable-domain

fuzzy sets—part I: Representation. Fuzzy Sets and

Systems, 380:1–18.

ehounek, L. and Da

nkov

a, M. (2020b). Variable-domain

fuzzy sets—part II: Apparatus. Fuzzy Sets and Sys-

tems, 380:19 – 43.

FCTA 2020 - 12th International Conference on Fuzzy Computation Theory and Applications

250

ehounek, L. and Nov

ak, V. (2015). Towards fuzzy partial

logic. In Proceedings of the IEEE 45th International

Symposium on Multiple-Valued Logics (ISMVL 2015),

pages 139–144. IEEE.

Casillas, J., Cord

on, O., Triguero, F., and Magdalena, L.

(2013). Interpretability Issues in Fuzzy Modeling.

Studies in Fuzziness and Soft Computing. Springer

Berlin Heidelberg.

Ciucci, D. and Dubois, D. (2013). A map of dependen-

cies among three-valued logics. Information Sciences,

250:162–177.

d’Allonnes, A. R. and Lesot, M. (2017). If I don’t know,

should I infer? reasoning around ignorance in a many-

valued framework. In Joint 17th World Congress of

International Fuzzy Systems Association and 9th In-

ternational Conference on Soft Computing and Intel-

ligent Systems, IFSA-SCIS 2017, Otsu, Japan, June

27-30, 2017, pages 1–6. IEEE.

nkov

a, M. (2018). A graded notion of functionality.

Fuzzy Sets and Systems, 339(15 May 2018):134 – 151.

Delgado, M. R., Zuben, F. V., and Gomide, F. (2003).

Hierarchical Genetic Fuzzy Systems: Accuracy, In-

terpretability and Design Autonomy, pages 379–405.

Springer Berlin Heidelberg, Berlin, Heidelberg.

Demirci, M. (2001). Gradation of being fuzzy function.

Fuzzy Sets and Systems, 119(3):383 – 392.

Fletcher, S., Verma, B., and Zhang, M. (2020). A non-

specialized ensemble classiﬁer using multi-objective

optimization. Neurocomputing, 409:93 – 102.

ajek, P. (1998). Metamathematics of Fuzzy Logic, vol-

ume 4 of Trends in Logic. Kluwer, Dordercht.

oczy, L. T., Muresan, L., Cs

anyi, K., and Hirota, K.

(2003). Interpolation in hierarchical rule bases. In

Rutkowski, L. and Kacprzyk, J., editors, Neural Net-

works and Soft Computing, pages 48–53, Heidelberg.

Physica-Verlag HD.

Latkowski, R. and Mikołajczyk, M. (2004). Data decom-

position and decision rule joining for classiﬁcation of

data with missing values. In Peters, J. F., Skowron, A.,

Grzymała-Busse, J. W., Kostek, B.,

Swiniarski, R. W.,

and Szczuka, M. S., editors, Transactions on Rough

Sets I, pages 299–320, Berlin, Heidelberg. Springer

Berlin Heidelberg.

Lughofer, E. (2011). Evolving Fuzzy Systems - Methodolo-

gies, Advanced Concepts and Applications. Studies in

Fuzziness and Soft Computing. Springer Berlin Hei-

delberg.

Magdalena, L. (2019). Semantic interpretability in hierar-

chical fuzzy systems: Creating semantically decou-

plable hierarchies. Information Sciences, 496:109 –

123.

Mamdani, E. H. and Assilian, S. (1975). An experiment

in linguistic synthesis with a fuzzy logic controller.

International Journal of Man–Machine Studies, 7:1–

13.

Nolasco, D. H., Palmeira, E. S., and Costa, F. B. (2019).

A cascade-type hierarchical fuzzy system with ad-

ditional defuzziﬁcation of layers for the automatic

power quality diagnosis. Applied Soft Computing,

80:657 – 671.

Peters, J., Skowron, A., Grzymala-Busse, J., Kostek, B.,

Swiniarski, R., and Szczuka, M. (2004). Transactions

on Rough Sets I. Lecture Notes in Computer Science.

Springer.

Scherer, R. (2012). Multiple Fuzzy Classiﬁcation Systems.

Studies in Fuzziness and Soft Computing. Springer

Berlin Heidelberg.

epni

cka, M. and Cao, T. H. N. (2018). Compositions

of partial fuzzy relations. In Medina, J. et al., edi-

tors, IPMU 2018, volume 855 of Communications in

Computer and Information Science, pages 187–198,

Cham. Springer.

epni

cka, M., Burda, M., and

epni

ckov

a, L. (2016).

Fuzzy rule base ensemble generated from data by lin-

guistic associations mining. Fuzzy Sets and Systems,

285:140 – 161. Special Issue on Linguistic Descrip-

tion of Time Series.

Valverde, L. (1985). On the structure of F-indistinguisha-

bility operators. Fuzzy Sets and Systems, 17(3):313–

328.

epni

cka, M., Cao, N., B

ehounek, L., Burda, M., and

Doln

y, A. (2019). Missing values and dragonﬂy oper-

ations in fuzzy relational compositions. International

Journal of Approximate Reasoning, 113:149 – 170.

Merging Partial Fuzzy Rule-bases

251