Improving Word Association Measures in Repetitive Corpora with

Context Similarity Weighting

Aleksi Sahala and Krister Lindén

University of Helsinki, Finland

Keywords: Collocation Extraction, Distributional Semantics, Computational Assyriology.

Abstract: Although word association measures are useful for deciphering the semantic nuances of long extinct

languages, they are very sensitive to excessively formulaic narrative patterns and full or partial duplication

caused by different copies, edits, or fragments of historical texts. This problem is apparent in the corpora of

the ancient Mesopotamian languages such as Sumerian and Akkadian. When word associations are

measured, vocabulary from repetitive passages tends to dominate the top-ranks and conceal more interesting

and descriptive use of the language. We propose an algorithmic way to reduce the impact of repetitiveness

by weighting the co-occurrence probabilities by a factor based on their contextual similarity. We

demonstrate that the proposed approach does not only effectively reduce the impact of distortion in

repetitive corpora, but that it also slightly improves the performance of several PMI-based association

measures in word relatedness tasks in non-repetitive corpora. Additionally, we propose normalization for

PMI

, a commonly-used association measure, and show that the normalized variant can outperform the base

measure in both, repetitive and non-repetitive corpora.

1 INTRODUCTION

Collocation extraction is a central part of

distributional semantics, an area of linguistics that

studies meanings of words by observing their co-

occurrence patterns. The statistical significance of

word co-occurrences can be measured in several

different ways. A common idea is to first calculate a

chance for some co-occurrence to be independent

withing given constraints, and then to compare it

with the actual observed co-occurrence probability.

The more the observed probability exceeds chance,

the stronger the lexical association likely is.

A lot of work has been invested in developing

and improving the association measures, especially

to correct their bias toward low-frequency events.

However, largely unaddressed issue of word

association measures concerns their application to

corpora with vast amount of repetition or

duplication. This problem is apparent in some

historical corpora containing very formulaic and

repetitive language, as well as slightly diverging

versions or editions of same texts. Naturally, for a

history researcher it is essential to preserve all

existing versions of the documents, but for

computational semantic analysis, any full or partial

duplicates may give too much weight to certain co-

occurrences. In this particular study, we use the

ancient Akkadian language as an example, although

the issue is also relevant in the Sumerian corpora.

In this paper we propose a metric for measuring

contextual similarity within collocation windows,

which can be used to weight the co-occurrence

probabilities of association measures in order to

reduce the impact of repetition without removing

any content from the corpus. Our evaluation shows,

that the proposed method consistently improves the

results in a word relatedness task not only in corpora

with repetition, but that it is also slightly

advantageous in corpora without noticiable amount

of repetition.

We begin this paper with a summary of related

work and a short description of the Akkadian

language and its resources. Then we give a short

review on the different association measures and

propose some modifications, which are better

compatible with our context similarity weighting

(CSW). The last part of the paper will be dedicated

to evaluation and discussion.

Sahala, A. and Lindén, K.

Improving Word Association Measures in Repetitive Corpora with Context Similarity Weighting.

DOI: 10.5220/0010106800480058

In Proceedings of the 12th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2020) - Volume 1: KDIR, pages 48-58

ISBN: 978-989-758-474-9

2 RELATED WORK

Identification of duplicated or reused text has been

addressed in multiple publications, especially in the

context of file systems (Manber, 1993), web pages

(Broder et al., 1997), newspapers (Clough et al.,

2002; Smith et al., 2013), plagiarism detection

(Gipp, 2014; Citron & Gingsparg, 2015) and

historical corpora (Lee, 2007), but to our knowledge,

only one paper has addressed the effect of

duplication on distributional semantics. Schofield et

al. (2017) measured the effect of duplication on

topic-modeling methods, namely LSA (Deerwester

et al., 1990) and LDA (Blei et al., 2003). They

discovered that LDA is more resistant to duplication

if the model is trained with an increased number of

topics, and that both models tend to sequester

repeated text templates, unless there is not heavy

overlapping with topics of interest. Nonetheless,

they also suggested that using different

deduplication methods such as n-gram removal

should have positive impact on the models’

performance if the data contains lots of repetition.

Methods of duplicate detection have been widely

discussed. Some well-known approaches include

approximate fingerprinting (Manber, 1994), Greedy

String-Tiling (Wise, 1993) used in plagiarism

detection and biology, n-gram overlap (Clough et

al., 2002), and w-shingling (Broder et al., 1997), that

divides documents or their parts into sequences and

measure their resemblance by using Jaccard

similarity coefficient. Motivation for our work

comes from shingling and n-gram overlap methods.

3 AKKADIAN AND ITS

RESOURCES

Akkadian was an East-Semitic language documented

in hundreds of thousands of cuneiform clay tablets

and their fragments excavated from the modern day

Iraq and the surrounding regions. Although the

earliest attested written sources are dated back to the

Old Akkadian Period (2350–2150 BCE), the largest

mass of texts and inscriptions were written between

1900 BCE and 500 BCE by the Babylonians and the

Assyrians, which both spoke dialects of the

Akkadian language. The latest exemplars of

Akkadian are dated around 100 CE, after which the

cuneiform writing tradition disappeared and the

language was forgotten until its rediscovery in the

middle of the 19th century CE. (Kouwenberg, 2011)

The cultural-historical importance of Akkadian is

significant in many respects. First, it was one of the

earliest written languages alongside Sumerian,

Elamite and Ancient Egyptian. Second, it enjoyed a

prestigious status in the ancient Middle-East, and

was studied and used in certain contexts by the

Hittites, Elamites and the Persians. It was also used

as a lingua franca during the Middle-Babylonian

period (1590–1100 BCE), for example in Amarna

correspondence between Egyptian administration

and its representatives in Levant (Streck, 2011).

Third, the Akkadian corpus comprises a vast

diversity of texts representing many different genres:

astronomical texts, administrative and legal

documents and law codes, wisdom literature, epics

and myths, letters, mathematical texts, lexical and

grammatical texts, royal inscriptions, omens,

medical texts, as well as several others

(Huehnergard & Woods, 2008). Thus, the Akkadian

text material opens an interesting and concrete

window to the distant past for a wide range of topics.

Despite being a language that became extinct

two millennia ago and studied only by a handful of

people, Akkadian is fairly well resourced. Some

important digital resources of Akkadian texts are

Archives babyloniennes (ARCHIBAB), Cuneiform

Digital Library Initiative (CDLI), Sources of Early

Akkadian Literature (SEAL), SAAo (State-Archives

of Assyria Online) and Open Richly Annotated

Cuneiform Corpus (Oracc). Currently only Oracc

provides extensive annotation. About 1.5M tokens

of the corpus has been POS-tagged and lemmatized.

However, as the corpus covers a time-span of almost

2500 years, it is often not advisable to use it as a

whole for linguistic analysis. Instead it is more

fruitful to limit the scope to a certain time period or

dialect. This limits the size of useable data for

studying distributional semantics.

4 CHALLENGES OF AKKADIAN

DATA

4.1 Repetition and Repetitiveness

A challenge concerning the Akkadian text data is its

high degree of repetition and repetitiveness. In

literary texts, repetition is used as a stylistic feature

within single pieces (Groneberg, 1996). Well-known

examples can be found in the epic of Gilgameš, for

instance, in the description of Gilgameš’s travel

through the subterranean path of the sun (George,

2003), and the Babylonian creation myth Enūma

Improving Word Association Measures in Repetitive Corpora with Context Similarity Weighting

Eliš (Lambert, 2013), where a vizier repeats his

master’s 53 line long message word by word, which

is again almost a word to word repetition of an

earlier description of their enemies gathering an

army of monsters. Repetitiveness, on the other hand

is a genre-defining feature encountered in Assyrian

and Babylonian royal inscriptions, divinatory texts

and astrological reports (Maul, 2013). Assyrian

royal inscriptions, for example, were copied many

times over the years with yearly updates and

additions of new episodes of that year’s campaign.

The older passages were often shortened, and the

new ones were written closely following the earlier

descriptions to promote the stability and prosperity

of the Empire (Bach, 2020). Additionally, formulaic

epithets contribute to the repetitiveness of the royal

inscriptions (Cifola, 1995). Although the copies

often show only a slight divergence from each other,

Assyriologists consider them as different texts, and

they are added into corpora as such.

A part of the repetitiveness, or rather (semi-)

duplication, in some Akkadian corpora is also

caused by the fragmentary nature of texts. It is not

very common that a single fully preserved copy of a

text is ever found, especially of larger and

linguistically more diverse works. Instead, the

Assyriologists often work with small fragments of

texts, which they later collate into composite texts.

The fragments do not necessarily come from the

same place or time period, nor contain the same

wording, as copying texts was a central part of the

ancient scribal curriculum (Gesche, 2001). Thus,

parts of texts may exist in different versions. In

Oracc, however, the fragments are not a significant

issue, as it mostly consists of edited composites.

When collocation extraction is performed on

Akkadian corpora, the formulaic and report-like

patterns, extended texts, and to some extent,

fragments, tend to distort the association metrics. It

is not very rare that even half of the co-occurrences

of certain words (including those with rather high

co-occurrence frequency) come from identical or

almost identical passages.

One option to tackle this issue would be pre-

processing the whole corpus as a whole and remove

all the “almost duplicate” parts. The disadvantage of

this approach would be the need to argue in every

case why exactly this part was removed instead of

some other. Additionally, drawing a line between

too similar and acceptably similar would be

arbitrary. Thus, a better and less troublesome

approach is not to remove anything, but to reduce

the significance of the repeating passages in an

algorithmically consistent and reproducible way.

Naturally, it is a valid methodological question to

what extent the repetition should be reduced. It is

much easier to justify reducing the duplication

caused by the fragmentary nature of the corpus, than

it is to argue in favor of reducing the impact of the

formulaic way of expression. The first mentioned

has nothing to do with the language itself, but it is

rather a remnant of the scribal training curriculum,

evolution of compositions, and unfortunate historical

events where tablets or their parts have been

damaged or destroyed. The latter, on the other hand,

can be considered as a part of the language, at least

in its written form.

If we consider this question from the viewpoint

of gathering new insights to the Akkadian lexicon,

having a look on the freer use of the language by

reducing the impact of very obvious associations

may be justified. Assyriologists are already well

aware of the vocabulary and concepts of the long

formulaic litanies, but it is not necessarily obvious

that one can see larger patterns in more varied and

spread out use of words.

4.2 Lack of Data

As a low-resource language, applying machine

learning methods such as word2vec (Mikolov et al.,

2013) or fastText (Bojanowski et al., 2017) do not

necessarily provide outstanding results. Our

previous experiments have shown, that in order to

get useful results, machine learning approaches have

to be applied hundreds of times on the data, and the

conclusions must be drawn from the averages (Svärd

et al. 2018). Thus it is often more convenient to use

count-based approaches such as Pointwise Mutual

Information (PMI) (Church & Hanks, 1990), the

results of which can later be transformed into word

embeddings by using matrix factorization. In fact,

the matrix factorization approach has been shown to

be on par (Levy et al. 2015), or even to outperform

machine learning methods in low-resource settings,

especially in word similarity tasks (Jungmaier,

2020).

Although only a limited number of PMI variants

work well with matrix factorization (Levy et al.,

2014, 2015), the variety of useable measures is

much greater for collocation analysis. For this

reason, we will evaluate our method on several

different variants of PMI.

KDIR 2020 - 12th International Conference on Knowledge Discovery and Information Retrieval

5 MEASURING CONTEXT

SIMILARITY

Our method for measuring context similarity

involves stacking all the co-occurrence windows of

the bigram (a;b) into a two-dimensional array and

calculating the relative frequencies of all unique

words vertically in each window position. The

context similarity weight (CSW) is calculated as the

average of these relative frequencies.

To make each element of the array uniform, we

pad the windows to equal length. This keeps the

keywords aligned in case they occur near the

beginning or end of a line, sentence, paragraph or

whatever boundary is chosen to restrict the window

span. All padding symbols (#), the keyword (a), and

its potential collocate (b), are ignored from relative

frequency counts, because they are expected to

occur within the same window. Taking them into

account would impose a penalty for all co-

occurrences.

Formally, over all n co-occurrences of words a

and b, let V be a set and W a bag or multiset of

context words {x: x ∉ {a, b, #}} that occur at

position i in a window of size w, and let m be the

number of window positions where V ≠ {∅}. We

define the context similarity weight (a;b) with a

magnitude of k as

(a,b) =





|



max(|



|,1)









)

The context words x at position i are perfectly

dissimilar if |V

| = |W

| and perfectly similar if |V

| =

1. Thus the bounds for φ are (1/n)

in the case of

perfect similarity, and 1 in the case of perfect

dissimilarity. The weight can be adjusted by raising

it to the power of k. Our experiments show that k-

values of 2 and 3 have generally the best

performance in word relatedness task, and that k-

values higher than 3 are typically detrimental, unless

the amount of repetition is very low.

The context similarity weight is applied as a

multiplier to the co-occurrence frequency f(a,b),

which causes some co-occurrences to be statistically

removed from the counts. Thus, the context

similarity weighted joint distribution p(a,b) is

redefined for a corpus of N words as

(,)=

(

)∙



(,)



(2)

Applying CSW on the co-occurrence frequencies

changes the base definition of PMI and related

association measures: a perfect association is no

longer determined by two words co-occurring only

within a given window, but the context where the

words co-occur must also be completely unique. In

other words, their distribution is expected to convey

previously unseen information.

As the method operates oblivious to the adjacent

window positions, it does not systematically take

into account deletion or insertion. For this reason it

may be useful to remove certain stop words such as

articles and prepositions from the corpus altogether

to improve the alignment of the windows. The

blindness to adjacent positions is merely a safety

feature to prevent changes in word order to be

considered as exactly same expression. Naturally,

attention is also not paid to morphological detail if

the text has been lemmatized: for example in

English the same sentence in the present and the past

tense are considered to contain same information.

One advantage of CSW is that it does not alter

the bounds of the association measures, but rather

changes their definition. Modifying the observed co-

occurrence frequencies can be considered a re-

ordering operation: if the co-occurrence does not

include any new information, the words are not

removed from the corpus but just considered to exist

somewhere else than within the same window. If it

provides only some new information, the

significance of the co-occurrence is partially

reduced. For this reason, the marginal probabilities

and the corpus size are not modified.

Calculating the CSW is very fast, as much of it

can be done by set operations, which are usually

well optimized in programming languages. In terms

of space complexity, the method can get heavy if the

window size and the corpus are both large.

However, this can be reduced significantly by pre-

filtering stop words and using frequency thresholds.

6 PMI VARIANTS USED IN

EVALUATION

In this chapter we briefly discuss the properties of

common PMI variants we later use in the evaluation.

Our aim is to cover variants used in collocation

extraction and matrix factorization, as well as

measures featuring different frequency biases.

Pointwise mutual information (PMI) was

introduced in lexicography by Church and Hanks

(1990) by the name association ratio. They defined

it as a logarithmic ratio of the observed probability a

word co-occurrence within a given window size to

Improving Word Association Measures in Repetitive Corpora with Context Similarity Weighting

the expected chance of this co-occurrence under the

assumption of independence. The formula itself was

based on an earlier definition of mutual information

by Fano (1961), but Church and Hanks were the first

to apply it on collocation extraction.

PMI(;)=log



(,)



(



)

()

(3)

After the introduction of PMI, several researchers

have proposed various ways to enhance it. The

proposed variants generally differ from each other in

two respects: in terms of frequency bias and the way

scores are bounded and oriented.

Often acknowledged weaknesses of PMI are its

sensitivity to low-frequency words (Daille, 1994;

Bouma, 2009; Role & Nadif, 2011; Levy et al.,

2015), and its moving upper bound, which makes

the scores somewhat unintuitive (Bouma, 2009). In

the case of non-co-occurrence, independence and

perfect dependence, PMI takes scores of ∞<0<

log



(,). The issue of low-frequency bias and

the moving upper bound are interrelated. The perfect

dependence is achieved when the joint an marginal

distributions are equal to each other: p(a,b) = p(a) =

p(b), which translates to the denominator being the

numerator squared. This means, that a decrease in

word frequency increases the value of the upper

bound log



(,).

Normalized PMI. Bouma (2009) proposed a variant

called Normalized PMI (NPMI), which normalized

the score orientation to 101 by dividing the

score by its moving upper bound.

NPMI(;)=log





(

,

)



(



)



(



)

/log



(,)

)

In addition to providing a more intuitive score

orientation, NPMI nullified the effect of an extreme

score increase in the case of perfect dependence

However, the low-frequency bias reduction of NPMI

decreases in practical cases, where the score is not

close to the maximum.

PMI

. In terms of low-frequency bias correction, a

more robust association measure called PMI

was

proposed by Daille (1994). The core idea of this

measure was to introduce a factor k, to which power

the p(a,b) is raised to overcome the shrinking

denominator problem. The most balanced measure

in this family of measures is PMI

(Evert, 2005), as

it preserves the symmetry between the numerator

and denominator and keeps the scores consistent

regardless of word frequencies.

PMI



(;)=log





(

,

)





(



)



(



)

The orientation of PMI

scores is negative: ∞<

log





(

,

)

<0, which can be generalized for PMI

∞<(1)log





(

,

)

<(2)log





(

,

)

This is somewhat problematic, as the score that

defines the independence of the co-occurrence is not

fixed and the scores are only ranked based on their

difference to the perfect association. For this reason,

PMI

with k > 2 tends to give high scores for

frequently occurring words, regardless if the co-

occurrences are statistically dependent or not. This

feature makes PMI

good for finding very general

level associations, as demonstrated by Role & Nadif

(2011). PMI

is less biased toward high frequency

words, and it is not very common to see independent

co-occurrences in the top ranks if stop words have

been removed from the corpus.

Normalized (Positive) PMI

. From the viewpoint

of CSW and general readability, it is often more

intuitive if the measures feature a fixed threshold for

independence as PMI and NPMI do. We propose the

following general normalization for PMI

, which

first involves removal of the logarithm and then

aligning the threshold of independence with zero.

We can fix the upper bound at 1 by following the

example of Bouma (2009):

NPMI



(;)=



(

,

)





(



)



(



)

(,)



(,)



(,)



(6)

This yields two bounds: 0 for non-co-occurring and

independently co-occurring words, and 1 for perfect

dependences. The disadvantage of the measure is

that co-occurrences rarer than the assumption of

independence become unsortable. In fact, co-

occurrences may get negative scores as well, but as

they approach either the non-co-occurrence or

independence, they get closer to 0. For this reason, it

is advisable to use a max-operator as in the popular

positive variant of PMI known as PPMI. Thus we

define Normalized Positive PMI

NPPMI



(a;b)=max(NPMI



(

;

)

,0)

)

Generally the normalization is useful only for PMI

due to the aforementioned characteristics of PMI

capturing very high frequency associations, which

are not necessarily statistically dependent. For PMI

the normalization yields slightly better performance

in both, context similarity weighted and non-

weighted relatedness tasks, as will later be shown in

the chapter 8.4.

Some of the PMI variants introduce various

constants or discount factors based on word

frequencies to balance the frequency distribution.

KDIR 2020 - 12th International Conference on Knowledge Discovery and Information Retrieval

PMI

(Pantel & Lin, 2002) weights the PMI by

multiplying it with a discount factor δ defined as

(;)=



(,)





(

,

)



∙

min





(



)



(



)



min





(



)



(



)



(8)

The bounds of this variant can be shown to be the

same as for the PMI, except for the upper bound at

(f(a,b) / (f(a,b)+1))

· –log

p(a,b). The low-

frequency bias reduction provided by PMI

falls

between PMI

and PMI

Semi-Conditional Information weighted with

significance of association (SCI

sig

) (Washtell &

Markert, 2009) involves first weighing the

occurrence probability of the collocate b and

multiplying the score with an external factor to

reduce the impact of low-frequency bias.

SCI



(;)=



min

(



)

,

(



)

∙log





(

,

)



(



)



()

)

The bounds are not mentioned in the original

research paper, but they can be shown to exist at 0<



(,)

<1 if p(a) ≤ p(b) and 0<()<1 if

p(a)

≥ p(b) for non-co-occurring, independent and

perfectly dependent events. Alongside PMI

, SCI

sig

has the highest frequency bias of the measures

discussed in this chapter and is thus suitable for

finding very general level associations.

Context distribution smoothed PMI (PMI

)

(Levy et al., 2015) is a variant of PMI inspired by

negative sampling used in word2vec. This is

achieved by raising the p(b) to power of α, which is

normally set to 0.75 following Mikolov et al. (2013).

This measure is among the state-of-art PMI variants

for matrix factorization.

PMI



(;)=log



(,)



(



)

()



(10

)

As an empirical demonstration of frequency

distributions of different measures, we scored 1000

random words from ten randomly extracted 10M

token samples of the English Wikipedia corpus and

plotted the average frequency of each top-100

collocate (Figure 1).

PMI, NPMI and PMI

tend to have the highest bias

for low-frequency words, whereas NPPMI

and

PMI

are more balanced. PMI

falls in the middle

between balanced and high-frequency sensitive

measures: PMI

and SCI

sig

Figure 1: Rank-wise average frequency distributions.

7 OBSERVATIONS OF CSW ON

THE AKKADIAN CORPUS

Although the effect of CSW cannot be properly

evaluated with the Akkadian data due to the lack of

a gold standard, we can observe its effect on a very

general and subjective level. For these examples we

use a symmetric window of seven words and a

selection of first millennium BCE texts of various

genres comprising 900k tokens.

At first, we examine the top ten ranks of the

word nakru ‘enemy’ by using context similarity

weighted PMI

with k-values of 0 (no CSW), 1 and

3. The purpose of this test is to demonstrate how the

very top ranks are affected when CSW is used. For

the sake of simplicity we use the English translations

of the Akkadian words.

Table 1: Top-10 collocates of ‘enemy’ in Akkadian using

CSW with different k-values.

k = 0 k = 1 k = 3

1 dangerous attack attack

2 attack enemy to attack

3 enemy army enemy

4 army to attack army

5 weapon downfall downfall

6 *gall bladder *gall bladder *gall bladder

7 *bright to kill to kill

8 to overthrow to overthrow border (of land)

9 *frost weapon stranger, outsider

10 people *bright to bind

The first observation is, that the number of

collocates that seem intuitively strange (marked with

asterisks) tend to decrease in this particular case. A

closer examination of the corpus reveals that these

words mainly come from very repetitive or

formulaic contexts. Collocates ‘bright’ and ‘frost’

come from astrological reports, which predict an

attack by the enemy if certain ominous signs such as

Improving Word Association Measures in Repetitive Corpora with Context Similarity Weighting

bright Mars or frost are observed. Word ‘gall

bladder’ comes as well from omen texts. It is,

however, preserved because the ominous conditions

are more diversely described than the astrological

phenomena.

We can also see that two collocates, ‘dangerous’

and ‘people’, disappear from the top ranks when the

k-value is increased, and that the ranking of word

‘weapon’ decreases. This is due to their appearance

in almost identical contexts, as can be seen in the

concordance view in Figure 2. We can observe all

these words, nakru ‘enemy’ (here written as a

Sumerian logogram

LU2

KUR

), bahūlātu ‘people’,

akṣu ‘dangerous’ and

GIŠ

TUKUL ‘weapon’ in this

very context.

Figure 2: Concordance view of repetition in Neo-Assyrian

royal inscriptions.

Another interesting detail is revealed if we examine

the words associated with a very common word

šarru ‘king’. If the CSW is not used, the top-10

results are filled with words that have positive

connotations: šulmu ‘well-being’, dannu ‘strong

one’, karābu ‘to pray’ etc. However, when the k-

value is increased to 3, the positive words disappear

from the list and collocations with more negative

connotations appear to the top ranks. The first

ranked collocate is now ḫamma’u ‘rebel’ and also a

word bīšu ‘malicious’ appears to the eighth rank of

the list. Here, reducing the impact of repetitiveness

seems to switch the viewpoint from the Assyrians to

their enemies. The reason for this is not very

surprising: the Assyrian kings are practically always

accompanied with a long litany of praise, and

mentioned in very repetitive patterns in royal

inscriptions, whereas the enemy kings are just

mentioned here and there in more varying contexts.

To experiment numerically how CSW balances

the similarity distribution on different k-values, we

sampled 1000 random words from Oracc, scored

them by using PMI

and plotted the average context

similarity for each rank (Figure 3).

Figure 3: Rank-wise average context similarity.

The figure shows CSW’s effect on average context

similarity on the top-50 ranks. From the viewpoint

of the average context similarity over the whole

corpus (0.265), a k-value of 2 seems to give the most

balanced distribution.

8 EVALUATION

8.1 Test Settings and Parameters

Because there is no word relatedness gold standard

available for the Akkadian language, we

experimented on the effect of CSW by generating

repetitive versions the English Wikipedia corpus,

which we first tokenized and lemmatized using the

NLTK (Bird et al., 2009). To get some numerical

estimate of general repetitiveness in the Akkadian

texts, we sampled 1000 random words from Oracc

and measured the average context similarity between

them and their collocates in symmetric windows of

3, 5 and 7 words. On average, this value was 0.265,

which means that 26.5% of the context words of any

given bigram spanning over an average window of

5.0 are non-unique. For comparison, this figure for

the English Wikipedia corpus is only 0.029.

We generated test corpora featuring low,

moderate and high degree of repetition, corres-

ponding to average context similarities of <0.1,

<0.17 and <0.25 respectively. This process was done

by duplicating random segments of the corpus.

To ensure that the test setting was not either

favorable or unfavorable by chance, we first

extracted ten different random 2M and 10M word

samples from the Wikipedia corpus. For each

evaluation cycle, we generated ten different

repetitive versions for each corpus randomly. Thus,

for each sample corpus size, the CSW was evaluated

on 100 different corpora.

KDIR 2020 - 12th International Conference on Knowledge Discovery and Information Retrieval

We scored the WS353 (Agirre et al., 2009) and

the Mturk-771 (Halawi et al., 2012) word

relatedness test sets using eight different association

measures: PMI, NPMI, PMI

, PMI

, NPPMI

, SCI

sig

PMIα and PMI

with CSW k-values between 0 and 3

in symmetric windows of 3, 5 and 7 words, and

compared the rankings to the gold standard by using

Spearman ρ

-correlation. Our ρ-values represent the

average correlation over the 100 evaluations for each

test setting.

We discarded out-of-vocabulary (OOV) words

due to the small sizes of our test corpora. Thus, for

the 2M and 10M settings, the task was to rank

correctly about 30 and 80 words respectively for the

WS353, and 35 and 215 words for the Mturk-771

test set. This explains differences between ρ values

in different test settings, and also makes the results

incomparable between different window and corpus

sizes. We did not consider this a problem, because

the scope of the evaluation was only to observe, how

much CSW contributes to the performance

compared to results without it being used.

Due to the large number of association measures

included, we choose to discuss in detail only the

results for PMI

, as is had on average the best

performance on the unmodified corpora without

CSW. The best performance was measured as

follows: we scored all our 2M and 10M token base

corpora (20 in total) and ranked the measures by

their average performance from 1 to 8. PMI

had an

average rank of 1.83, and the other measures

NPPMI

3.50, PMI

4.0, NPMI 4.17, PMIα 5.0,

SCI

sig

5.33, PMI

5.83 and PMI 6.33. We will

discuss the other measures briefly in chapter 8.3.

8.2 Overall Performance

Using CSW generally improves association

measures, but the degree of improvement is tied

closely to window size and amount of repetition.

The overall tendency is that when the window size

and amount of repetition increases, the more CSW

contributes to the result. This is expected, as larger

windows offer a better sample of the surrounding

context.

Experiments with unmodified corpora show that

CSW provides a slight improvement to the measures

on larger windows even if the corpus does not have

noticeable repetition. The results for PMI

are

summarized in Table 2.

This observation supports our theoretical

definition of context similarity weighted association

measures mentioned in chapter 5: emphasizing

previously unseen contexts over something that has

Table 2: CSW on unmodified test corpora (WS353).

No CSW k = 1 k = 2 k = 3

2M-3

0.55

0.55 0.54 0.54

2M-5 0.61 0.61 0.62

0.62

2M-7 0.63 0.64 0.64

0.65

10M-3 0.40 0.40

0.40

10M-5 0.51 0.51 0.52

0.52

10M-7 0.54 0.55 0.55

0.56

already been observed provides more significant

information about the co-occurrence. This

hypothesis seems to hold even with small amount of

repetition (r < 0.03).

Experiments with repetitive corpora show more

noticeable improvement in performance. Table 3

shows the improvement in different repetitiveness

settings with different parameters. We set the best

results from the unmodified corpora (Table 2) as our

target scores.

Table 3: CSW on modified test corpora PMI

with

different k-values (WS353).

No CSW k = 1 k = 2 k = 3 Target

Low repetitiveness (< 0.1)

2M-3 0.48 0.51

0.51

0.51 0.55

2M-5 0.54 0.58 0.59

0.59

0.62

2M-7 0.55 0.59 0.61

0.61

0.65

10M-3 0.39 0.40 0.40

0.40

10M-5 0.48 0.50 0.52

0.52

10M-7 0.52 0.54 0.55

0.56

Moderate repetitiveness (< 0.17)

2M-3 0.44

0.48

0.48 0.46 0.55

2M-5 0.48 0.53 0.55

0.55

0.62

2M-7 0.49 0.55 0.57

0.58

0.65

10M-3 0.37 0.38

0.39

0.39 0.40

10M-5 0.46 0.50 0.51

0.52

10M-7 0.50 0.53 0.55

0.56

High repetitiveness (< 0.25)

2M-3 0.37

0.39

0.39 0.36 0.55

2M-5 0.36 0.42 0.45

0.46

0.62

2M-7 0.39 0.45 0.49

0.51

0.65

10M-3 0.34 0.36

0.37

0.37 0.40

10M-5 0.42 0.46 0.48

0.49

0.52

10M-7 0.45 0.50 0.53

0.54

0.56

Similarly to unmodified corpora, giving too much

emphasis on contexts captured by very small

windows may have negative impact on the results

compared to lower k-values. This issue could be

solved by using a secondary context window around

the actual collocation window.

The CSW is able to reach, or at least to get very

close to the target scores in the 10M setting. This

indicates that it effectively reduces or even nullifies

the impact of the repetition. In the 2M setting the

target scores are not reached, but the improvement is

Improving Word Association Measures in Repetitive Corpora with Context Similarity Weighting

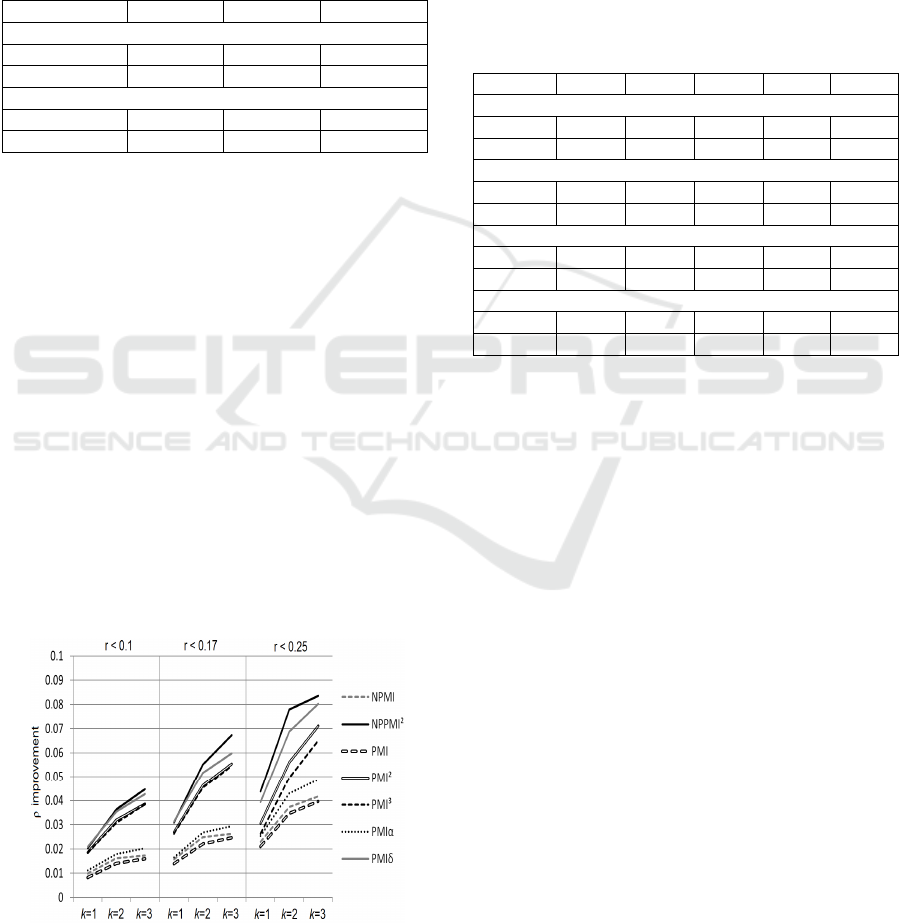
still noticeable in larger window sizes: in the 2M-7

setting the ρ improves 0.09 and 0.12 points in the r <

0.17 and r < 0.25 settings respectively.

Evaluation using the Mturk-771 test set yields

similar results. For reasons of space, the comparison

in Table 4 is limited to the average of low, medium

and high repetitiveness settings in windows of 5 and

7 scored with PMI

Table 4: ρ-improvement compared to CSW not being

used.

k = 1 k = 2 k = 3

10M corpora (0.03 < r < 0.25)

Mturk-771 +0.03 +0.04 +0.05

WS353 +0.03 +0.05 +0.06

2M corpora (0.03 < r < 0.25)

Mturk-771 +0.03 +0.05 +0.07

WS353 +0.05 +0.07 +0.08

8.3 Measure Specific Improvement

All measures except SCI

sig

show consistent

improvement in performance in all test settings. The

reason why CSW is detrimental to SCI

sig

lies likely

in the sig-factor, as PMI

does not show similar

performance decrease regardless of its very high

similarity to Semi-Conditional Information: these

measures are only distinguished from each other by

the amount of weight that is given to p(b).

Association measures with low-frequency bias

benefit less of the CSW. This is, because low-

frequency bias corrected measures, such as PMI

modify the weighted joint-distribution amplifying

the CSW’s effect. Figure 4 summarizes the average

improvement of different measures using window

sizes of 5 and 7 in the 10M token corpora. SCI

sig

excluded from the figure due to its negative

performance.

Figure 4: Measure-specific improvement (WS353).

Results gained from the 2M corpora and Mturk-771

test set follow similar distribution.

8.4 Performance of NPPMI

Normalizing the PMI

has positive impact on its

performance in all non-repetitive and repetitive test

settings. As seen in Figure 4, NPPMI

gains slightly

more advantage from CSW than PMI

does. Table 5

summarizes the difference in performance in the

10M token corpora using the WS353 test set and a

window size of 7.

Table 5: Performance difference of PMI

and NPPMI

k = 0 k = 1 k = 2 k = 3 Diff

10M (r < 0.03)

PMI

0.51 0.52 0.52 0.52 +0.01

NPPMI

0.54 0.55 0.55 0.55 +0.01

10M (r < 0.1)

PMI

0.48 0.50 0.51 0.52 +0.04

NPPMI

0.51 0.53 0.55 0.56 +0.05

10M (r < 0.17)

PMI

0.46 0.49 0.51 0.51 +0.05

NPPMI

0.49 0.52 0.55 0.56 +0.07

10M (r < 0.25)

PMI

0.41 0.44 0.47 0.48 +0.07

NPPMI

0.43 0.49 0.52 0.53 +0.10

The better performance of NPPMI

can be explained

as a result of subtracting information from

statistically less significant co-occurrences, which in

conjunction with CSW becomes even less

significant in repetitive contexts.

9 CONCLUSIONS AND FUTURE

PLANS

We introduced a context similarity based weighting

for word association measures, which was aimed to

improve the results in repetitive corpora. Evaluation

of the approach by using artificially repeated random

extracts of the Wikipedia corpus indicated that the

CSW can reduce the impact of repetitiveness and

duplication effectively when larger window sizes are

used. We also demonstrated, that CSW can slightly

improve the results in a word relatedness task even

in corpora which had no noticeable repetition. Thus

it seems, that in general reducing the impact of

previously seen context information about co-

occurrences can improve the performance of

association measures.

We also introduced a modification to PMI

which better takes into account the statistical

KDIR 2020 - 12th International Conference on Knowledge Discovery and Information Retrieval

relevance of co-occurrences, and showed a small,

yet consistent improvement over the original

definition of PMI

Although the results gained from CSW may

seem very corpus specific, it is likely that there are

other similar datasets that may benefit from it. Some

examples may be other historical corpora, discussion

forum data (consisting of quotes of previous

messages) and movie subtitle collections. In general,

the advantage of CSW is that it is more resistant to

duplicate or semi-duplicate entries in case the corpus

is poorly pre-processed.

We only discussed collocation analysis in this

paper, but an obvious path for future investigation

would be to apply CSW to word embeddings. Our

preliminary experiments indicate, that cleaning word

vector representations with CSW do improve the

results in word similarity tasks, but a more

comprehensive evaluation and tests will be required

before drawing further conclusions.

ACKNOWLEDGEMENTS

We acknowledge funding from the Academy of

Finland for the Centre of Excellence in Ancient Near

Eastern Empires and from the University of Helsinki

for the Deep Learning and Semantic Domains in

Akkadian Texts Project (PI Saana Svärd for both).

We also thank Johannes Bach, Mikko Luukko and

Saana Svärd for their valuable feedback, Niek

Veldhuis for providing us with the JSON Oracc data

and Heidi Jauhiainen for pre-processing it.

REFERENCES

Agirre, E., Alfonseca, E., Hall, K., Kravalova, J., Pasca,

M., Soroa, A., 2009. A Study on Similarity and

Relatedness Using Distributional and WordNet-based

Approaches. In NAACL-HTL 2009.

Bach, J., 2020 (forthcoming). Untersuchungen zur

transtextuellen Poetik assyrischer herrschaftlich-

narrativer Texte. SAAS 30.

Bird, S., Loper, E., Klein, E., 2009. Natural Language

Processing with Python. O’Reilly Media Inc.

Blei, D. M., Ng, A. Y, Jordan, M. I. 2003. Latent Dirichlet

Allocation. In The Journal of Machine Learning

Research 3, pp. 994–1022.

Bojanowski, R., Grave, E., Joulin, A., Milokolov, T.,

2017. Enriching Word Vectors with Subword

Information. In TACL 5, pp. 135–146.

Bouma, G., 2009. Normalized (Pointwise) Mutual

Information in Collocation Extraction. In GSCL, pp.

31–40.

Broder, A. Z., Glassman, S. C., Manasse, M. S., Zweig, G.

1997. Syntactic Clustering of the Web. Digital Systems

Research Center.

Church, K., Hanks, P., 1990. Word association norms,

mutual information and lexicography. Computational

Linguistics 16, pp. 22–29.

Cifola, B., 1995. Analysis of Variants on the Assyrian

Royal Titulary. Istituto Universitario Orientale.

Citron, D. T., Ginsparg, P., 2015. Patterns of Text Reuse

in a Scientific Corpus. In the National Academy of

Sciences in the USA.

Clough, P., Gaizauskas, R., Piao, S, S. L., Wilks, Y. 2002.

Meter: Measuring Text Reuse. In the 40

Annual

Meeting of the ACL, pp. 152–159.

Daille, B., 1994. Approche mixte pour l’extraction

automatique de terminologie: statistiques lexicales et

filtres linguistiques. PhD thesis, Université Paris 7.

Deerwester, S., Dumais, S. T., Furnas, G. W., Laudauer,

T. K., Harsman, R. 1990. Indexing by Latent Semantic

Analysis. In JASIST.

Evert, S., 2005. The Statistics of Word Cooccurrences:

Word Pairs and Collocations. PhD thesis. IMS

Stuttgart.

Fano, R., 1961. Transmission of Information: A Statistical

Theory of Communications. MIT Press.

Gesche, P. D., 2001. Schulunterricht in Babylonien im

ersten Jahrtausend v. Chr. AOAT 275. Ugarit Verlag.

George, A., 2003. The Babylonian Gilgamesh Epic:

Critical Edition and Cuneiform Texts. Oxford

University Press.

Gipp, B., 2014. Citation-Based Plagiarism Detection:

Detecting Disguised and Cross-Language Plagiarism

using Citation Pattern Analysis. Springer.

Groneberg, B. 1996. Towards a Deﬁnition of Literariness

as Applied to Akkadian Literature. In Mesopotamian

Poetic Language: Sumerian and Akkadian, Edited by

M. Vogelzang, H. Vanstiphout. Groningen, pp. 59–84.

Halawi, G., Dror, G., Gabrilovich, E., Koren, Y. 2012:

Large-scale learning of word relatedness with

constraints. In KDD 2012, pp. 1406–1414.

http://www2.mta.ac.il/~gideon/mturk771.html

Huehnergard, J., Woods, C. 2008. Akkadian and Eblaite.

In The Ancient Languages of Mesopotamia, Egypt and

Aksum. Edited by R. R. Woodard. Cambridge

University Press.

Jungmaier, J., Kassner, N., Roth, B., 2020. Dirichlet-

Smoothed Word Embeddings for Low-Resource

Settings. In 12

LREC 2020, pp. 3560–3565.

Kouwenberg, B., 2011. Akkadian in General. In Semitic

Languages. An International Handbook. Edited by S.

Weninger, G. Khan, M. P. Streck, J. C. E. Watson, pp.

330–339. De Gruyter Mouton.

Lambert, G. W., 2013. Babylonian Creation Myths.

Eisenbrauns.

Lee, J. 2007. A Computational Model of Text Reuse in

Ancient Literary Texts. In he 45

Annual Meeting of

the ACL, pp. 472–479.

Levy, O., Goldberg, Y. 2014. Neural Word Embedding as

Implicit Matrix Factorization. In Advances in Neural

Information Processing Systems, pp. 2177–2185.

Improving Word Association Measures in Repetitive Corpora with Context Similarity Weighting

Levy, O., Goldberg, Y., Dagan, I., 2015. Improving

Distributional Similarity with Lessons Learned from

Word Embeddings. In TACL 3, pp. 211–225.

Manber, U., 1994. Finding Similar Files in a Large File

System. In proc. of USENIX Technical Conference.

Maul, S., 2003. Die Wahrsagekunst im Alter Orient:

Zeichen des Himmels und der Erde. Beck.

Mikolov, T., Chen, K., Corrado, G., Dean, J., 2013.

Efficient Estimation of Word Representations in

Vector Space. https://arxiv.org/abs/1301.3781

Pantel, P., Lin, D., 2002. Discovering word senses from

text. In the 9

ACM SIGKDD, pp. 613–619. ACM.

Role, F., Nadif, M. 2011. Handling the Impact of Low

Frequency Events on Co-occurrence based Measures

of Word Similarity: A Case Study of Pointwise

Mutual Information. In KDIR 2011, pp. 226–231.

Schofield, A., Thompson, L., Mimno, D., 2007.

Quantifying the Effects of Text Duplication on

Semantic Models. In EMNLP 2017, pp. 2737–2747.

Smith, D. A, Cordell, R., Dillon, E. M., 2013. Infectious

Texts: Modeling Text Reuse in Nineteenth-Centrury

Newspapers. In IEEE BigData 2013.

Streck, P. M., 2011. Babylonian and Assyrian. In Semitic

Languages. An International Handbook. Edited by S.

Weninger, G. Khan, M. P. Streck, J. C. E. Watson, pp.

359–395. De Gruyter Mouton.

Svärd, S., Alstola, T., Sahala, A., Jauhiainen, H. &

Lindén, K. 2018. Semantic Domains in Akkadian

Text. In CyberResearch on the Ancient Near East and

Neighboring Regions: Case Studies on Archaeological

Data, Objects, Texts, and Digital Archiving. Juloux,

V. B., Gansell, A. R. & di Ludovico, A. (eds.). Leiden:

Brill.

Washtell J., Markert, K., 2009. A comparison of

windowless and window-based computational

association measures as predictors of syntagmatic

human associations. In EMNLP, pp. 628–637.

Wise, M. J. 1993. Running Karp-Rabin Matching and

Greedy String Tiling. Basser Department of Computer

Science Technical Report 463.

RESOURCES

ARCHIBAB, 2008. Archives babyloniennes.

http://www.archibab.fr/

CDLI, 2000. The Cuneiform Digital Library Initiative.

https://cdli.ucla.edu/

Oracc, 2014. The Open Richly Annotated Cuneiform

Corpus. http://oracc.org/

SAA(o), 1986. State Archives of Assyria (Online).

http://www.helsinki.fi/science/saa/

SEAL, 2008. Sources for Early Akkadian Literature.

https://www.seal.uni-leipzig.de/

The Wikipedia Corpus, (downloaded 2019-01-28).

https://www.english-corpora.org/wiki/

KDIR 2020 - 12th International Conference on Knowledge Discovery and Information Retrieval