The Max-Cut Decision Tree: Improving on the Accuracy and Running
Time of Decision Trees
Jonathan Bodine and Dorit S. Hochbaum
University of California, Berkeley, U.S.A.
Keywords:
Decision Tree, Principal Component Analysis, Maximum Cut, Classification.
Abstract:
Decision trees are a widely used method for classification, both alone and as the building blocks of multiple
different ensemble learning methods. The Max-Cut decision tree involves novel modifications to a standard,
baseline model of classification decision tree, precisely CART Gini. One modification involves an alternative
splitting metric, Maximum Cut, which is based on maximizing the distance between all pairs of observations
that belong to separate classes and separate sides of the threshold value. The other modification is to select the
decision feature from a linear combination of the input features constructed using Principal Component Anal-
ysis (PCA) locally at each node. Our experiments show that this node-based, localized PCA with the novel
splitting modification can dramatically improve classification, while also significantly decreasing computa-
tional time compared to the baseline decision tree. Moreover, our results are most significant when evaluated
on data sets with higher dimensions, or more classes. For the example data set CIFAR-100, the modifications
enabled a 49% improvement in accuracy, relative to CART Gini, while reducing CPU time by 94% for compa-
rable implementations. These introduced modifications will dramatically advance the capabilities of decision
trees for difficult classification tasks.
1 INTRODUCTION
Decision trees are a widely used method for classifi-
cation, both alone and as the building blocks of multi-
ple different ensemble learning methods. A standard
approach for the construction of decision trees uti-
lizes the Classification and Regression Trees (CART)
method (Breiman et al., 1984). This method con-
structs decision trees by selecting a threshold value
on some feature to separate, or split, the observations
into two branches, based on some evaluation method.
This process continues recursively until a preset stop-
ping criterion is reached. Throughout our analysis,
we define the stopping rule as either the node having
only one class present, or no split existing such that
both sides of the branch contain at least one observa-
tion.
One of the standard methods for evaluating the
different splits is Gini Impurity, which was provided
in the original CART methodology (Breiman et al.,
1984). Gini Impurity is defined in equation 1, where
p
c
is the fraction of observations that belong to class
c.
∑
c
p
c
(1 −p
c
) (1)
Define a threshold as a value in range of one of the
features’ values such that the observations are par-
titioned into two subsets, the samples whose values
for that feature are less than the threshold, and those
whose values are greater than the threshold. Then, a
threshold is selected such that the average Gini Im-
purity of the resulting two subsets, weighted by their
cardinality, is minimized. We will use this method-
ology as the baseline to compare our novel splitting
procedure against.
Our splitting procedure is motivated by a short-
coming of Gini Impurity. The partitions generated by
Gini Impurity depend only on a threshold value while
ignoring the fact that some partitions are to two sets
that are very dissimilar in terms of the distances be-
tween their feature vectors, whereas others are closer
in terms to this distance. The more dissimilar the
partition, the more meaningful it is. Given two op-
tions for a threshold that both partition the observa-
tions into the same ratios and same sizes, Gini Im-
purity would show no preference, regardless of the
distance between these classes. We believe that this
distance information is meaningful and preferable, as
it produces thresholds that separate the classes further
apart in space, resulting in decreased susceptibility to
overfitting.
Bodine, J. and Hochbaum, D.
The Max-Cut Decision Tree: Improving on the Accuracy and Running Time of Decision Trees.
DOI: 10.5220/0010107400590070
In Proceedings of the 12th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2020) - Volume 1: KDIR, pages 59-70
ISBN: 978-989-758-474-9
Copyright
c
 2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
59

Our splitting procedure takes inspiration from the
Max Cut problem, which in general is NP-complete
(Karp, 1972). Our use of Max Cut is in one dimen-
sion, based on distances with respect to a single fea-
ture, and restricted to a single threshold. It is there-
fore polynomial-time solvable. Indeed, in the ap-
pendix, we show a linear-time implementation given
the sorted observations. The Max Cut criterion is to
find θ maximizing equation 2, where x
i, j
represents
the value of feature j for observation i, y
i
represent
the class of observation i, and θ represent the thresh-
old value.
∑
{i|x
i, j
≤θ}
∑
{k|x
k, j
>θ}
1
y
i
6=y
k


x
i, j
−x
k, j


(2)
Given the fact that the observations can be sorted
based on any feature in O (n logn) and the linear-time
implementation of Max Cut, we have an O (n log n)
algorithm for solving this problem on any given fea-
ture of the feature vector, where n is the number of
observations. It is important to note that this is the
same asymptotic time complexity achieved when im-
plementing the Gini Impurity method.
Modifying how the features are represented can
have a significant impact on the performance of a de-
cision tree. If the feature vector x
i
is modified through
a change of basis, the splits of the decision tree can be
changed. This paper seeks to find a good basis to rep-
resent the feature vector. One common way to find a
natural basis to represent the feature vector in is Prin-
cipal Component Analysis (PCA), first proposed by
Karl Pearson F.R.S. (F.R.S., 1901). PCA iteratively
finds the direction that accounts for the most variance
in the data, given that it is orthogonal to all the di-
rections previously found. The use of PCA as a pre-
processing step when utilizing decision trees is not
new. However, we propose that it should instead be
used throughout the construction of the decision tree,
at every node. This is motivated by the idea that dis-
tributions could vary in different subspaces of the fea-
ture space. Therefore, a meaningful direction overall
might not be significant in specific sub-spaces. To ac-
count for this, we introduce the following two meth-
ods for finding locally meaningful directions Node
Features PCA and Node Means PCA (see section 2
for details).
To understand how these changes affect a deci-
sion tree’s performance, we performed extensive ex-
perimental analysis on 8 different decision tree algo-
rithms listed in Table 2, each of which uses differ-
ent combinations of the methods discussed in section
2. Moreover, we implemented all of the algorithms
in python to understand the relative performance be-
tween the algorithms without having different levels
of code optimization effecting the results. This does
mean our baseline code is not as fast as commercially
available versions; however, by choosing our own im-
plementation for the baseline we are able to minimize
the differences between the code for the different im-
plementations. This highlights differences in perfor-
mance caused by the changes to the algorithm and not
different implementation choices.
An analysis was conducted on over 20,000 syn-
thetic data sets (section 3.1) with training set sizes
ranging between 100 and 300,000 and testing sets
fixed at 100,000 observations. We first considered bi-
nary classification problems (section 3.1.2), followed
by multiclass classification problems (section 3.1.3).
On the synthetic data we validated that the modifica-
tion produced statistically significant improvements
to the baseline Gini Impurity CART model. Simi-
larly, these results were then validated on real-world
data sets (section 3.2). These modifications were
found to provide dramatic improvements in both ac-
curacy and computational time, and these advantages
further increased with the dimensionality of the data
or the number of classes (section 4). The signifi-
cance of these results is demonstrated here with the
CIFAR-100 dataset (Krizhevsky, 2009), which has
100 classes, 3,072 dimensions, and 60,000 total ob-
servations (of which 48,000 are used for training). In
this case, compared to the baseline CART Gini model,
our Max Cut Node Means PCA algorithm (see section
2) resulted in a 49.4% increase in accuracy relative to
the baseline while simultaneously reducing the CPU
time required by 94%.
2 DESCRIPTION OF
ALGORITHMS
We introduce two methods for finding locally mean-
ingful bases. The first method that we consider is
Node Features PCA. At every decision node, PCA is
performed on the original feature vectors using only
the observations that have reached that node in order
to find the local principal components. These local
principal components are then used as the input fea-
tures to find the optimal threshold, rather than using
the original features.
The second method, referred to as Node Means
PCA, is derived from the idea that it is not the di-
rections that best describe the data, but rather the dif-
ference between the classes, that are important. Like
Node Features PCA, this algorithm is used at every
decision node; the difference is in what points get
fed into the PCA algorithm. Specifically, the first
step is to think of the data set in a one-vs-rest con-
text, locally calculating the mean position of each of
KDIR 2020 - 12th International Conference on Knowledge Discovery and Information Retrieval
60

the possible ‘rest’ collections. For example, if there
are 3 local points (1,0,0), (0, 1, 0), and (0,0,1), each
belonging to classes A, B, and C respectively, then
(0,0.5,0.5), (0.5,0,0.5), and (0.5,0.5,0) would be
the resulting means, calculated by excluding the first,
second, and third points respectively. These newly
generated means vectors would be passed into the
PCA algorithm to find a new basis, and the original
features are then transformed into this new basis. It is
important to note that this transformation will neces-
sarily result in a dimensionality reduction in the case
where the number of classes locally present is less
than the dimension of the original feature vector. The
features in this new basis are then used as the input
features to find the optimal threshold, instead of us-
ing the original features.
A high level description of a generic decision tree
and how the specification of the split method and the
feature type of basis selected generates the algorithms
proposed, see Figure 1. The notation used in Fig 1 is
U for the set of all observations; X, y for the feature
vectors and classes respectively. Let the ”split” pa-
rameter function take the value of either Gini or Max-
Cut, which are functions that return the two subsets
implied by the optimal split of their respective objec-
tive functions. Let featureType be 1, 2, 3, or 4 for
Original, Global PCA, Local PCA, and Local Means
PCA respectively. Let PCA(X) and PCAMapping(X)
be functions that return the principal components of
X or the function that maps X to its principal compo-
nents respectively. Let C(y) be the set of class values
of vector y, {i|∃y
j
= i}, and let U
−i
= {u|u ∈U,y
u
6=
i}.
In our analysis, we consider a total of 8 different
algorithms, which we implemented in the Python pro-
gramming language (Van Rossum and Drake, 2009).
In order to improve the run time of these algorithms,
both the Gini Impurity and Max Cut optimal thresh-
old calculation for a given feature were implemented
as NumPy (Oliphant, 2006) vector operations to avoid
the use of slower Python for loops. Moreover, both
utilize efficient O (n log n) implementations. We re-
mark that both the Gini Impurity and Max Cut met-
ric were implemented so that in the event of a tie,
they favored more balanced splits, and the split was
chosen to be the mean value between the two closest
points that should be separated. Other than these sub-
routines, in order to make time-based comparisons as
consistent as possible, no difference existed between
the implementations of Gini Impurity and Max Cut
based trees. The scikit-learn (Pedregosa et al., 2011)
package was used to perform PCA.
As a result of Gini Impurity and Max Cut having
the same time complexity, the following results on
the time complexity of each algorithm hold regard-
less of the choice of evaluation criterion. The time
complexities for computing the optimal split at each
node are given in Table 1, where n is the number of
procedure decisionTree(U, (X ,y),split, f eatureType):
begin
if type = 2 do X ← PCA(X);
list ← {(U,X,y)};
while list 6=
/
0 do
pop (U,X,y) from list;
if type = 1,2 do X
0
← X;
else if type = 3 do X
0
← PCA(X);
else do X
0
← meansPCA(U, X ,y);
P
1
,P
2
← split(U,X
0
,y);
if |C(y(P
1
))| 6= 1 do list ← list ∪{(P
1
,X(P
1
),y(P
1
))};
if |C(y(P
2
))| 6= 1 do list ← list ∪{(P
2
,X(P
2
),y(P
2
))};
end
procedure meansPCA(U,X,y):
begin
means ← {};
for each i ∈C(y) do
means ← means ∪{
1
|U
−i
|
∑
u∈U
−i
x
u
};
T ← PCAMapping(means);
X
0
← T (X);
return X
0
;
end
Figure 1: High-Level description of decision tree fitting and means PCA algorithms.
The Max-Cut Decision Tree: Improving on the Accuracy and Running Time of Decision Trees
61

observations, d is the number of input features, and p
is the number of principal components considered.
Table 1: Time Complexity of Node Splitting.
Algorithm Time Complexity
Baseline O(dn log n)
Node Features PCA O(n
2
p)
Node Means PCA O(d
2
+ nlogn)
In order to be able to evaluate the relative per-
formance of the algorithms we ran them all with the
same implementation. Our baseline implementation
is obviously slower than that of open source pack-
ages (such as scikit-learn (Pedregosa et al., 2011)),
which have been optimized and are not implemented
in Python, yet it provides a cleaner basis for compar-
ison. The code that we used has not been made pub-
licly available as it does not represent the levels of
optimization needed for a production grade package.
Our code, however, is made available upon request.
Each of the algorithms is determined by:
1. Split criterion, which is Gini or Max Cut.
2. Which feature vector type to choose: Original,
Global PCA, Local PCA, or Local Means PCA.
Table 2 provides the nomenclature we use to refer to
each of these different combinations. Each of these
algorithms was put through the same rigorous exper-
imentation, using both synthetic and real-world data
sets.
3 A COMPARATIVE STUDY
3.1 Synthetic Data Sets
We first consider the performance of the 8 algorithms
on synthetic data sets, which provide key advantages
compared to real-world data sets. Foremost, synthetic
datasets allow for generating an arbitrary number of
independent datasets. This allowed us to draw sta-
tistically significant conclusions from the 20,000 plus
datasets we generated. Moreover, we were able to
generate an arbitrarily large number of training and
test examples with datasets ranging from 100,100
to 400,000 observations. This gave us greater in-
sights into the algorithms’ performances on larger
datasets than we could have achieved using only real-
world data. Lastly, we had fine-grained control of the
datasets’ different characteristics.
3.1.1 Experimental Design
To generate the synthetic data sets, we used the
datasets.make classification tool found within the
scikit-learn package (Pedregosa et al., 2011). This
was designed such that only the case where each class
would have one cluster was analyzed. These clusters
were then centered around the vertices of a hyper-
cube of a specified dimension (one of the character-
istics that we would modify). Random points would
then be generated from a normal distribution around
each cluster’s center, and these points would be as-
signed to that cluster’s corresponding class, except in
1% of cases where the class is randomly assigned.
The features were then randomly linearly combined
within each cluster to generate covariance. The op-
tion of having redundant or repeated features was not
used in our experiments. We use the option of adding
an arbitrary number of random features to the feature
vector as a second characteristic that we control. Fi-
nally, the features were randomly shifted and scaled.
Throughout our experiments, we observed how
the following four factors changed the accuracy, wall
clock time, and the number of leaves in the tree. The
factors that we controlled were:
1. The number of training examples. Note that since
we were able to generate arbitrarily many data
points per data set, we were able to have arbitrar-
ily large testing set. We chose to fix the size of the
testing set at 100,000 data points. For instance,
if the training set consisted of 10,000 points, we
would generate a data set of 110,000 data points
where 10,000 points would be randomly selected
for training and the remaining 100,000 would be
for testing.
2. The number of classes.
3. The number of informative dimensions, referred
to as the Dimension of Data in our results.
4. The number of meaningless dimensions, referred
to as the Noise Dimension in our results.
Table 2: Algorithms’ nomenclature.
Split Criteria
Feature Type Gini Max Cut
(0) Original Gini Features Max Cut Features
(1) Global PCA Gini Pre PCA Features Max Cut Pre PCA Features
(2) Local PCA Gini Node Features PCA Max Cut Node Features PCA
(3) Local Means PCA Gini Node Means PCA Max Cut Node Means PCA
KDIR 2020 - 12th International Conference on Knowledge Discovery and Information Retrieval
62

For each combination of parameter settings ex-
plored, we evaluated the models’ results on 30 in-
dependently generated datasets. For each of these
datasets, the models were presented with the same
training/testing examples, which were standardized
(zero mean and unit variance) using the scikit-learn
StandardScaler (Pedregosa et al., 2011) fit to the train-
ing examples. Standardization was used to make the
distances in each feature more comparable, which
will be important in the PCA analysis as well as find-
ing the Max Cut. Note that both the Gini Impurity
method and the orientation of the original feature vec-
tor are invariant under this transformation, indicating
that the baseline algorithm’s performance should also
be invariant.
Relying on multiple independent data sets, we can
calculate the significance of our results, for each data
generation setting, using a one-tailed Paired Sample
T-Test. For each algorithm, j, and data generation
setting we consider 14 alternative hypotheses {A
i
}
14
i=1
and corresponding null hypotheses {N
i
}
14
1=1
. Specifi-
cally, let {A
i
}
7
i=1
represent the alternative hypotheses
that algorithm j out performed, in a pairwise com-
parison, each of the other 7 algorithms. Conversely,
let {A
i
}
14
i=8
represent the alternative hypotheses that
algorithm j under performed, in a pairwise compar-
ison, each of the other 7 algorithms. We then used
the Holm-Bonferroni Method (Holm, 1979), to cor-
rect for multiple hypotheses testing, testing for signif-
icance at the 5% level. In the case where all {N
i
}
7
1=1
were rejected we labeled that data setting on the accu-
racy significance graph as ”Best”. In the case where
any of the of {N
i
}
14
1=8
were rejected we we labeled
that data setting on the accuracy significance graph as
”Not Best”. Else we labeled the region as ”Undecid-
able”.
All of these experiments were run on server nodes
that each contained two Intel Xeon E5-2670 v2 CPUs
for a total of 20 cores (no hyper-threading was used).
Each decision tree was constructed using a single core
and thread, such that up to 20 experiments were run-
ning simultaneously on a single node.
3.1.2 Binary Classification
The first set of experiments served to evaluate how the
accuracy and run time of each algorithm varied with
the size of the training set as well as the number of
informative dimensions. For this experiment, we set
the number of noise dimensions to zero. The results
of these experiments are summarized in Figure 2 and
Figure 3.
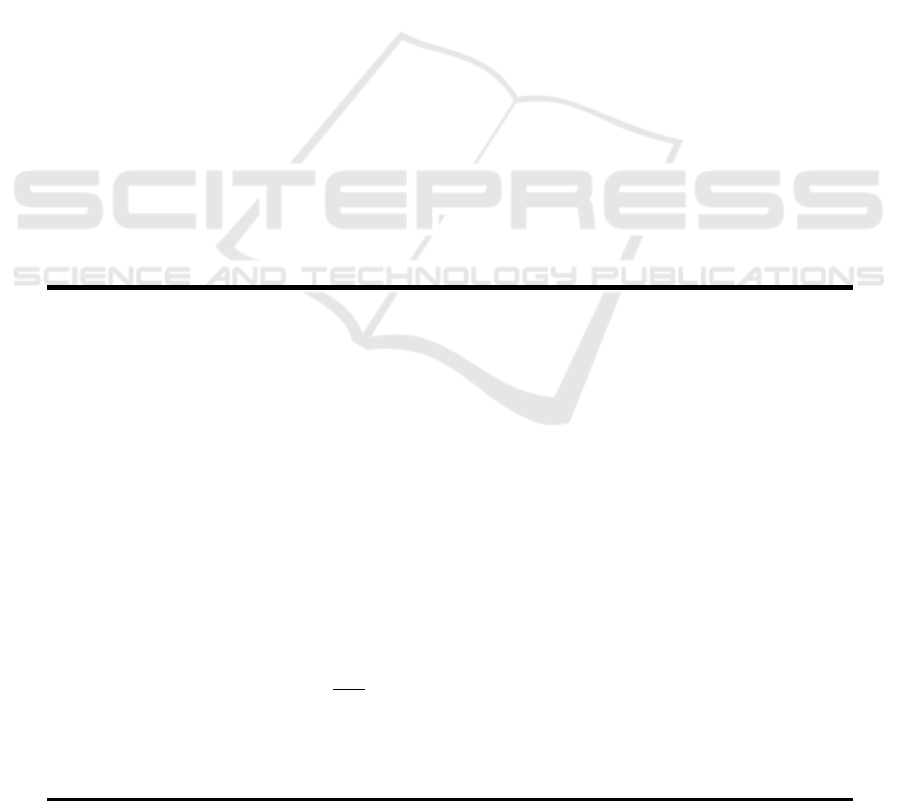
Examining Figure 2 and 3, it is apparent that Lo-
calized PCA dramatically improves the model accu-
racy compared to the baseline, as well as the model
with PCA applied in preprocessing. Figure 3 makes it
clear that with statistical significance the baseline al-
gorithm is not the best performing algorithm on aver-
age. On the the other hand Figure 3 indicates that the
most promising algorithms are Gini Node Features
PCA, Gini Node Means PCA, and Max Cut Node
Means PCA
We first consider Gini Node Means PCA vs. Max
Cut Node Means PCA. When looking at Figure 2 and
Figure 3, there are no significant trends that can be
seen when comparing the two, except that Max Cut
Node Means PCA seems to perform better more often
for smaller training sets. We then examine the accu-
racy ratio of Max Cut Node Means PCA / Gini Node
Means PCA for each of the 5,640 data sets in this ex-
periment. From this analysis, we found the mean ratio
to be 1.0003 and the sample standard deviation to be
0.0087, implying a 95% confidence interval for the
mean ratio of (1.00008, 1.00053). This implies that
Max Cut Node Means PCA had a slight advantage
over the Gini Node Means PCA when considering the
average ratio. Therefore, we decided to compare Gini
Node Features PCA vs. Max Cut Node Means PCA.
When considering Gini Node Features PCA vs.
Max Cut Node Means PCA the most prominent pat-
tern that emerges is that Gini Node Features PCA per-
forms better for large training sets (based on accu-
racy) and Max Cut Node Means PCA performs bet-
ter for smaller training sets. This pattern of Max
Cut Node Means PCA performing better for harder
datasets can be seen in Figure 4. It is important to note
that this out performance is almost entirely attributed
to the choice of feature vector type as the same pattern
emerges if Gini Node means PCA was used instead of
Max Cut Node Means PCA. In the cases where 1,000
training samples were used, Node Means PCA, after a
small dip for low dimensional data, increasingly out-
performs Node Features PCA as the dimensionality
increases. One reason for this is that Node Means
PCA uses averaging, thereby reducing noise. As a re-
sult of the dimensionality reduction Node Means PCA
searches fewer basis vectors than Node Features PCA.
In fact, in the binary case there are only two classes,
hence the Node Means PCA algorithm searches only
two basis vectors to select a threshold.
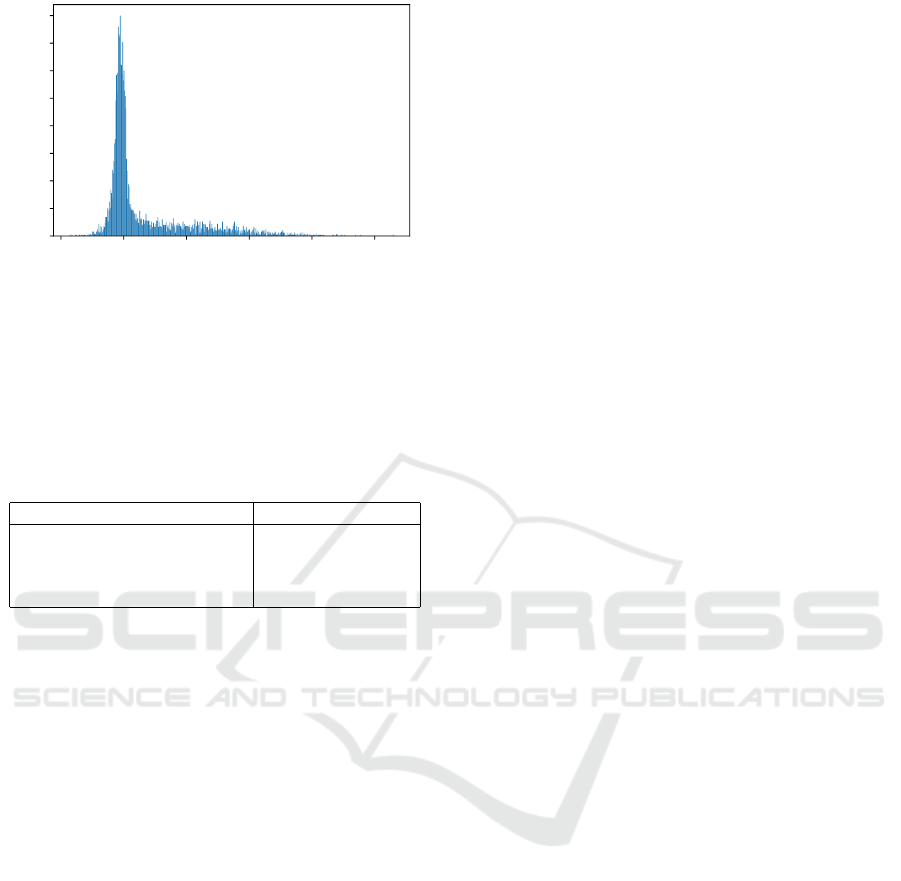
Figure 5 is the histogram all 5,640 ratios of Max
Cut Node Means PCA Accuracy divided by Gini
Node Features PCA Accuracy. It is evident from
the right skew in figure 5 that when Node Means
PCA provides better accuracy it does so considerably.
On the other hand when it provides less accuracy it
does so with only a minor loss. To further demon-
strate this point, we consider the mean and max ratios.
Conditioned on the ratio being greater than 1 (which
The Max-Cut Decision Tree: Improving on the Accuracy and Running Time of Decision Trees
63

0.0 0.2 0.4 0.6 0.8 1.0
Dimension of Data
0.0
0.2
0.4
0.6
0.8
1.0
Size of Training Data
10
2
10
3
10
4
10
5
Gini Features Gini Pre PCA Features Gini Node Features PCA Gini Node Means PCA
10 20 30 40 50
10
2
10
3
10
4
10
5
Max Cut Features
10 20 30 40 50
Max Cut Pre PCA Features
10 20 30 40 50
Max Cut Node Features PCA
10 20 30 40 50
Max Cut Node Means PCA
0.65
0.70
0.75
0.80
0.85
0.90
0.95
Mean Accuracy
Figure 2: Mean accuracy of binary classification on synthetic data, evaluated on test sets of 100,000.
0.0 0.2 0.4 0.6 0.8 1.0
Dimension of Data
0.0
0.2
0.4
0.6
0.8
1.0
Size of Training Data
10
2
10
3
10
4
10
5
Gini Features Gini Pre PCA Features Gini Node Features PCA Gini Node Means PCA
10 20 30 40 50
10
2
10
3
10
4
10
5
Max Cut Features
10 20 30 40 50
Max Cut Pre PCA Features
10 20 30 40 50
Max Cut Node Features PCA
10 20 30 40 50
Max Cut Node Means PCA
Not Best
Undecidable
Best
Mean Accuracy
Figure 3: Significance of Mean accuracy of binary classification on synthetic data, evaluated on test sets of 100,000.
10 20 30 40 50
Dimension of Data
−0.02
−0.01
0.00
0.01
0.02
0.03
0.04
0.05
0.06
Node Means PCA - Node Features PCA
Figure 4: Mean Max Cut Node Means PCA Accuracy mi-
nus Mean Gini Node Features PCA Accuracy with 95%
confidence interval using the 1,000 Training Sets.
happens 49.6% of the time), the mean is 1.075 and
the max is 1.430. When the ratio is conditioned to be
less than 1 (which happens 50.4% of the time), the
mean is 0.989 and the minimum is 0.915. This shows
that Node Means PCA has the potential of a signifi-
cant improvement in accuracy with only a minor risk
of accuracy loss.
When examining the experimental results of Node
Means PCA vs. Node Features PCA, we see that
Node Means PCA has significantly better proper-
ties in regard to computational cost. Max Cut Node
Means PCA took between 27% and 98% less time
compared to Gini Node Features PCA to fit; and be-
tween 21% and 98% less time compared to the base-
line model. The computational efficiency of Node
Means PCA is partially explained by the computa-
KDIR 2020 - 12th International Conference on Knowledge Discovery and Information Retrieval
64

0.9 1.0 1.1 1.2 1.3 1.4
Max Cut Node Means PCA Accuracy / Gini Node Features PCA Accuracy
0
25
50
75
100
125
150
175
200
Number of Data Sets
Figure 5: Histogram of Max Cut Node Means PCA Accu-
racy / Gini Node Features PCA Accuracy.
tional efficiency of the split as provided in table 1.
However, another factor is the size of the decision tree
for witch the number of leaves is a proxy. The mean
number of leaves across all data sets is provided in
Table 3.
Table 3: Mean Number of Leaves in Decision Tree.
Algorithm Mean # of Leaves
Baseline 1129
Gini Node Features PCA 418
Gini Node Means PCA 429
Max Cut Node Means PCA 448
Table 3 shows that the average number of leaves
is significantly less for Gini Node Features PCA, Gini
Node Means PCA, and Max Cut Node Means PCA
when compared to the Baseline model. This reduction
can help account for the significant observed com-
putational efficiency of the Node Means PCA vs the
Baseline. Therefore, taking into account the costs and
benefits related to computational time, accuracy, and
robustness to higher dimensional problems, the Node
Means PCA algorithm has the best performance, with
a slight preference towards the Max Cut metric over
Gini Impurity.
The second experiment that was performed con-
sidered the addition of noise features in order to see
if the Localized PCA algorithms would be negatively
affected. For this experiment, the training set sizes
were fixed to 10,000 and then for each combination of
meaningful dimensions in {5,10,15,...,50}and noise
dimensions in {0, 5, 10, ..., 50}, we generated and an-
alyzed 30 datasets. The major result of this exper-
iment was that localized PCA only under performs
in extreme cases. When the real dimension was five
and the noise dimension was greater than or equal to
15, our modifications had no improvement upon the
baseline, with the baseline actually outperforming our
algorithm. However, this represents the cases where
noise features accounted for 75% or more of the avail-
able features and the number of informative features
was small. Therefore, we do not regard this as a fun-
damental issue with our algorithm.
3.1.3 Multiclass Classification
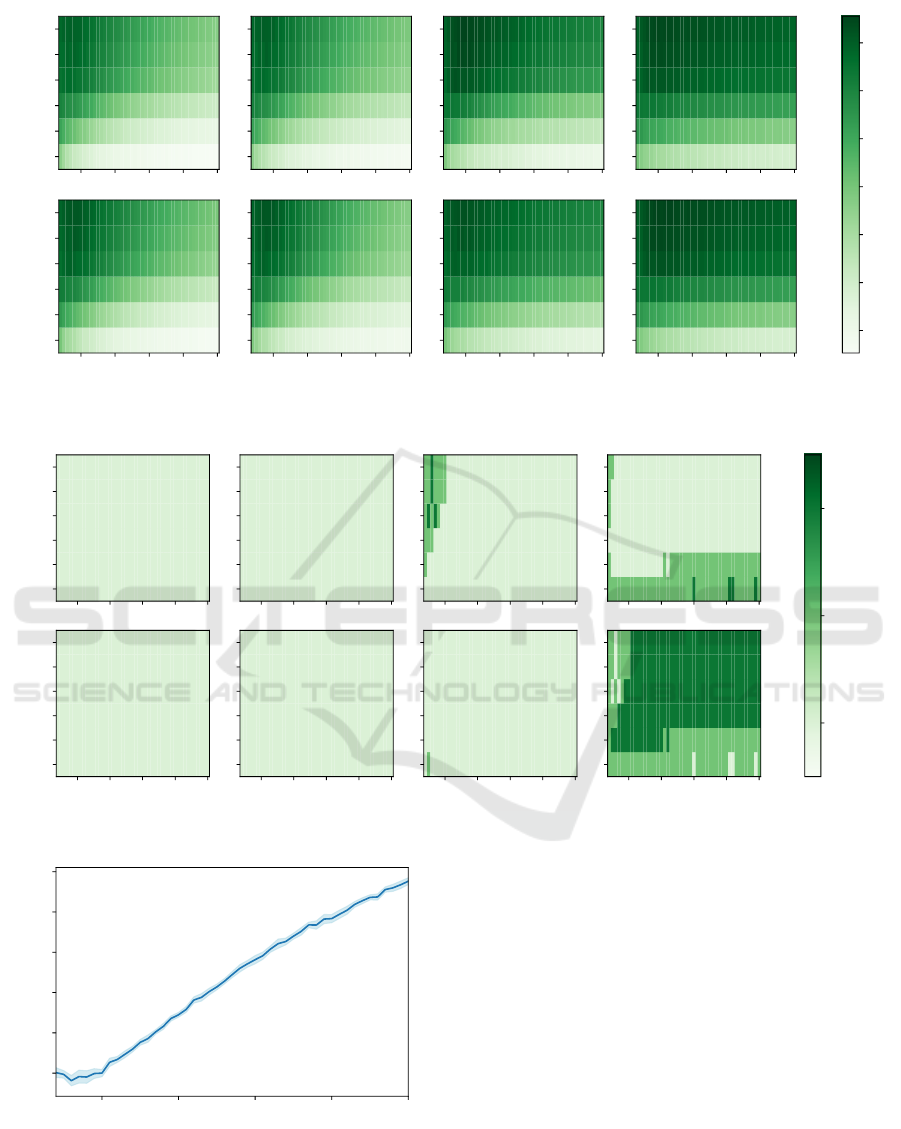
The next experiment investigates the impact of using
data with ten classes rather than just two. Referring
to the same steps as in section 3.1.2, one can see how
different training set sizes, informative dimensions,
and noise dimensions can affect the algorithm’s per-
formance. The main results derived from varying the
training data size and the underlying dimension of the
data can be seen in Figure 6 and Figure 7. An impor-
tant note is that these plots do not use a perfect loga-
rithmic scale for the y-axis. The values for each hor-
izontal bar are 10
2
, 10
3
, 10
4
, 10
5
, 2 ×10
5
, and 3 ×
10
5
(note that the last two are not 10
6
and 10
7
as one
might initially suspect).
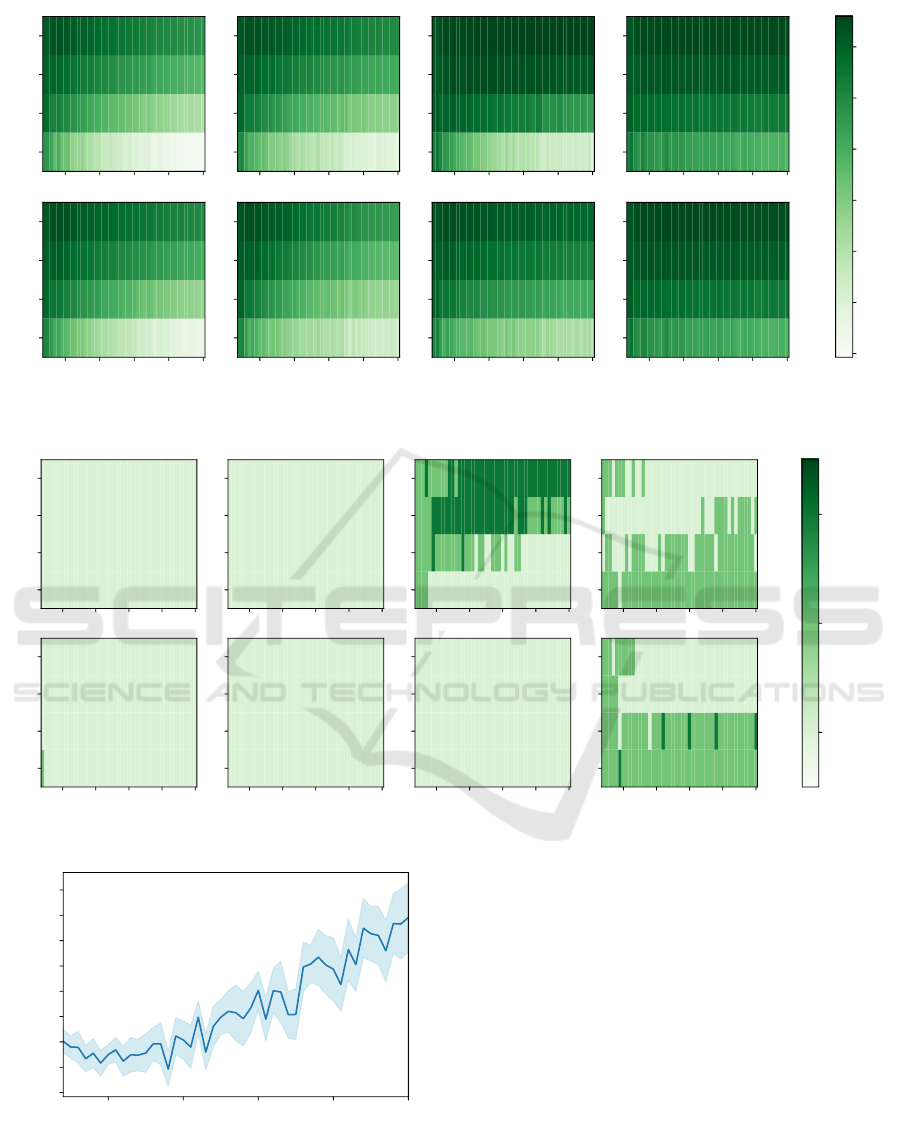
As seen in Figure 7, the baseline Gini Features al-
gorithm is ”Not Best” for all tested synthetic dataset
parameters. The prevalence of these ”Not Best”
markings indicates with statistical significance that
the baseline is not the best algorithm on average,
much like in the binary case (section 3.2). The ”Best”
markings actually indicate, from an accuracy stand-
point, that Max Cut Nodes Means PCA was the best
option in most cases. Moreover, Max Cut Nodes
Means PCA provides significant computational ad-
vantages for high dimensional data (taking up to 93%
less time). It can, however, take up to 22% longer
when looking at low dimensional problems, but we do
not view this as a fundamental issue. In general, lower
dimensional problems are computationally faster, so
the increased relative time does not translate to sig-
nificantly more realized computational time.
Upon close inspection of Figure 7, the markings
indicate that the Gini Node Features algorithm may
be the best option in terms of accuracy for larger train-
ing sets and fewer dimensions. This is the same pat-
tern that emerged in the binary case, and Figure 8 al-
lows for a closer comparison of these two algorithms,
focusing specifically on the 300,000 case. It demon-
strates that while Gini Node Features may outperform
in the fewer dimensional, larger training set case, Max
Cut Node Means PCA rapidly and dramatically out-
performs Gini Node Features as the number of dimen-
sions increases.
When the comparison is made between the Max
Cut Node Means PCA algorithm and the Gini Node
Means PCA algorithm, Figure 9 helps demonstrates
the marginal but statistically significant improvement
by utilizing the Max Cut metric. Specifically, the
95% confidence interval for the mean ratio between
the accuracy of the Max Cut Node Means PCA al-
The Max-Cut Decision Tree: Improving on the Accuracy and Running Time of Decision Trees
65

0.0 0.2 0.4 0.6 0.8 1.0
Dimension of Data
0.0
0.2
0.4
0.6
0.8
1.0
Size of Training Data
10
2
10
3
10
4
10
5
2 × 10
5
3 × 10
5
Gini Features Gini Pre PCA Features Gini Node Features PCA Gini Node Means PCA
10 20 30 40 50
10
2
10
3
10
4
10
5
2 × 10
5
3 × 10
5
Max Cut Features
10 20 30 40 50
Max Cut Pre PCA Features
10 20 30 40 50
Max Cut Node Features PCA
10 20 30 40 50
Max Cut Node Means PCA
0.2
0.3
0.4
0.5
0.6
0.7
0.8
Mean Accuracy
Figure 6: Mean accuracy of multiclass classification on synthetic data, evaluated on test sets of 100,000.
0.0 0.2 0.4 0.6 0.8 1.0
Dimension of Data
0.0
0.2
0.4
0.6
0.8
1.0
Size of Training Data
10
2
10
3
10
4
10
5
2 × 10
5
3 × 10
5
Gini Features Gini Pre PCA Features Gini Node Features PCA Gini Node Means PCA
10 20 30 40 50
10
2
10
3
10
4
10
5
2 × 10
5
3 × 10
5
Max Cut Features
10 20 30 40 50
Max Cut Pre PCA Features
10 20 30 40 50
Max Cut Node Features PCA
10 20 30 40 50
Max Cut Node Means PCA
Not Best
Undecidable
Best
Mean Accuracy
Figure 7: Significance of Mean accuracy of multiclass classification on synthetic data, evaluated on test sets of 100,000.
10 20 30 40 50
Dimension of Data
0.00
0.02
0.04
0.06
0.08
0.10
Node Means PCA - Node Features PCA
Figure 8: Mean Max Cut Node Means PCA Accuracy mi-
nus Mean Gini Node Features PCA Accuracy with 95%
confidence interval using the 300,000 Training Sets.
gorithm and the Gini Node Means PCA algorithm
is (1.0060,1.0071). Thus, we can conclude that the
use of Max Cut does appear to improve accuracy on
average.
When analyzing how the performance of the al-
gorithms were affected by the inclusion of noise fea-
tures, the same results as in the binary analysis are
seen. That is, for low dimensional data (informative
dimensions of 5 and 10) and high amounts of noise
(noise dimensions greater than or equal to 5 and 25
respectively), the baseline model has better perfor-
mance. However, these cases have very high percent-
ages of noise features (greater than 50%) and few di-
mensions. Since the improved accuracy of Max Cut
Node Means PCA still held for higher dimensions,
even when the percentage of noise features exceeded
50%, we believe that our Max Cut Node Means PCA
KDIR 2020 - 12th International Conference on Knowledge Discovery and Information Retrieval
66

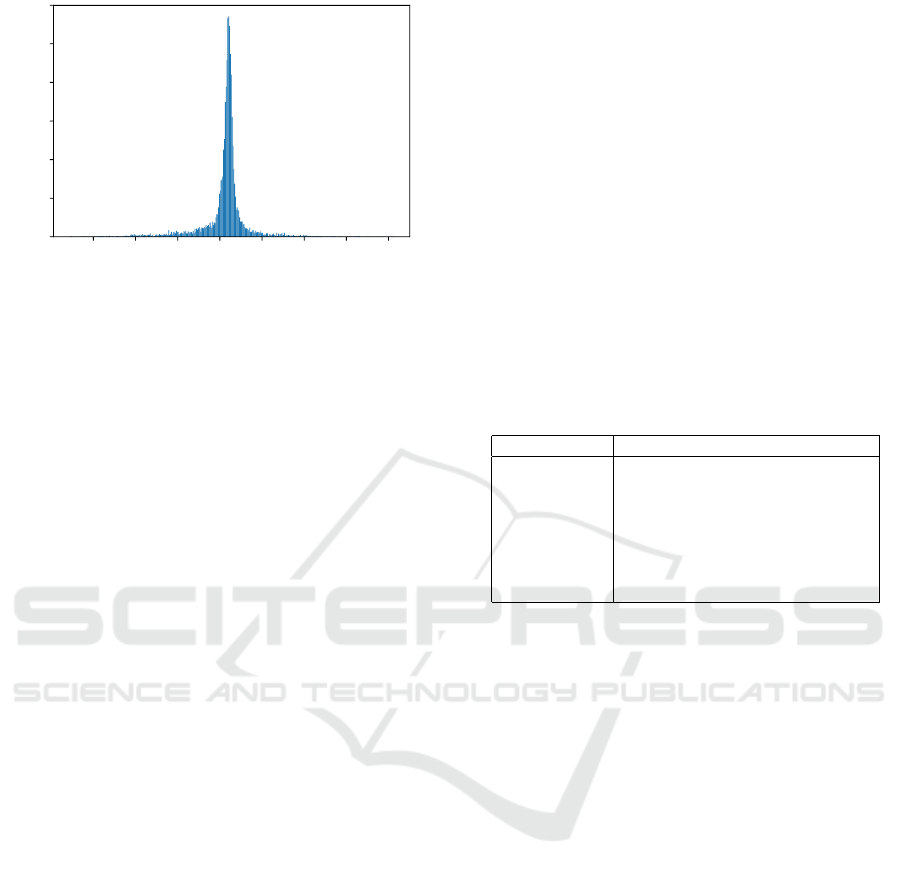
0.85 0.90 0.95 1.00 1.05 1.10 1.15 1.20
Max Cut Node Means PCA Accuracy / Gini Node Means PCA Accuracy
0
100
200
300
400
500
600
Number of Data Sets
Figure 9: Histogram of Max Cut Node Means PCA Accu-
racy / Gini Node Means PCA Accuracy.
algorithm is broadly applicable.
3.1.4 Synthetic Dataset Results Summary
After extensive testing, it is apparent that our local-
ized PCA algorithms provide dramatic improvements
over the baseline model in all but the most extreme
noise conditions. A thorough analysis of these lo-
calized PCA algorithms found that from an accuracy
standpoint, Node Means PCA should be preferred
for increasingly difficult classification tasks, partic-
ularly in cases where there are more classes, higher
dimensions, and/or fewer training examples. More-
over, when Node Means PCA was not the best op-
tion, it was typically only outperformed by a small
margin, and when it was the best option, it could end
up dramatically improving results. Empirically, Node
Means PCA results in significantly faster computa-
tion times compared to the baseline method and the
Node Features method. Thus, Node Means PCA pro-
vides dramatic improvements in both accuracy and
run time.
We further compared the Max Cut and Gini Impu-
rity metrics and found that when the Max Cut met-
ric was used in conjunction with the Node Means
PCA algorithm, on average, it can increase a decision
tree’s performance. Based on our experimentation on
more than 20,000 diverse datasets, we generally rec-
ommend that Max Cut Node Means PCA be consid-
ered as an alternative to the traditional baseline model.
We have thus shown that for synthetic datasets Max
Cut Node Means PCA yields a significant and dra-
matic improvement over the baseline model in both
accuracy and computational efficiency. We present
next the performance of our algorithm for real-world
datasets.
3.2 Real-world Data Sets
We proceeded to explore the effects of the eight dif-
ferent algorithms on real-world datasets, considering
a total of 5 different datasets. We used the Iris Data
Set and Wine Quality Data Set (Cortez et al., 2009),
both taken from the UCI Machine Learning Reposi-
tory (Dua and Graff, 2017). The Wine Quality Data
Set is separated into 2 sets, red and white wines, and
in our experimentation, we consider each of these
sets as a single combined dataset and as individual
sets. In the combined dataset, the wine’s classifica-
tion was included as another feature, one if red, zero
otherwise. We also used the MNIST dataset (LeCun
et al., 2010), as well as the CIFAR-10 and CIFAR-100
datasets (Krizhevsky, 2009). Table 4 provides a brief
overview of each of these datasets.
Table 4: Data Set Characteristics.
Data Set Samples Features Classes
Iris 150 4 3
Wine-Red 1,599 11 6
Wine-White 4,898 11 7
Wine-Both 6,497 12 7
MNIST 70,000 784 10
CIFAR-10 60,000 3,072 10
CIFAR-100 60,000 3,072 100
All of these experiments on real-world data were
run on server nodes that each contained two Intel
Xeon E5-2670 v2 CPUs, for a total of 20 cores (no
hyper-threading was used). Each decision tree was
constructed using a full server node utilizing paral-
lel processing due to the NumPy vector operations.
Rather than recording wall clock time as in the previ-
ous synthetic data set experiments, the total CPU time
was used for these experiments.
We considered each algorithm with modified fea-
tures as well as with standardized features in the ini-
tial input and reported the best result. To evaluate
the performance of each algorithm we used one of
two methods: either 10 ×10 cross-validation (as in
the case of Iris, Wine-Red, Wine-White, and Wine-
Both), or an 80%-20% train-test data split (as in the
case of MNIST, CIFAR-10, and CIFAR-100). The de-
cision to not use 10 ×10 cross-validation for MNIST,
CIFAR-10, and CIFAR-100 was a result of signifi-
cant computational requirements for computing these
trees. Moreover, due to the large size of the datasets,
the variance in accuracy should be lower than that
in smaller datasets, implying that the 10 ×10 cross-
validation would not be as beneficial. The results of
these experiments are reported in Table 5, with the
mean value provided for the Iris, Wine-Red, Wine-
White, and Wine-Both datasets.
The Max-Cut Decision Tree: Improving on the Accuracy and Running Time of Decision Trees
67

Table 5: Results of Real-World Data Set Experiments.
Iris Wine-Red
Accuracy
Relative
Time Scaled Accuracy
Relative
Time Scaled
Gini Features 0.945 1.000 False 0.626 01.000 False
Gini Pre PCA Features 0.941 1.000 True 0.636 03.229 True
Gini Node Features PCA 0.944 1.309 True 0.619 11.690 True
Gini Node Means PCA 0.950 0.894 False 0.638 06.707 True
Max Cut Features 0.947 1.032 True 0.629 00.799 True
Max Cut Pre PCA Features 0.950 0.915 False 0.632 03.308 True
Max Cut Node Features PCA 0.941 1.213 False 0.636 12.479 True
Max Cut Node Means PCA 0.960 0.798 False 0.631 05.539 True
Wine-White Wine-Both
Accuracy
Relative
Time Scaled Accuracy
Relative
Time Scaled
Gini Features 0.623 1.000 False 0.624 1.000 False
Gini Pre PCA Features 0.615 1.216 True 0.617 1.214 False
Gini Node Features PCA 0.615 8.301 True 0.608 9.122 True
Gini Node Means PCA 0.635 3.788 True 0.633 4.231 True
Max Cut Features 0.627 0.548 True 0.623 0.648 True
Max Cut Pre PCA Features 0.628 1.076 True 0.626 1.046 True
Max Cut Node Features PCA 0.634 8.740 True 0.633 9.755 True
Max Cut Node Means PCA 0.635 4.449 True 0.636 4.251 True
MNIST CIFAR-10
Accuracy
Relative
Time Scaled Accuracy
Relative
Time Scaled
Gini Features 0.869 1.000 False 0.262 1.000 False
Gini Pre PCA Features 0.823 1.558 True 0.246 1.162 False
Gini Node Features PCA 0.863 2.612 False 0.290 1.173 False
Gini Node Means PCA 0.922 0.186 False 0.342 0.085 False
Max Cut Features 0.847 0.744 False 0.243 1.313 False
Max Cut Pre PCA Features 0.866 1.091 False 0.271 1.503 False
Max Cut Node Features PCA 0.897 1.552 False 0.309 1.034 True
Max Cut Node Means PCA 0.924 0.093 False 0.349 0.075 False
CIFAR-100
Accuracy
Relative
Time Scaled
Gini Features 0.083 1.000 False
Gini Pre PCA Features 0.073 1.259 False
Gini Node Features PCA 0.090 1.010 True
Gini Node Means PCA 0.116 0.132 False
Max Cut Features 0.077 0.626 False
Max Cut Pre PCA Features 0.090 0.637 False
Max Cut Node Features PCA 0.109 0.491 False
Max Cut Node Means PCA 0.124 0.061 True
The results of the real-world analysis verify that
the improvements in accuracy are similar to those in
the synthetic datasets. In the case of the Node Means
PCA modification, we found that this was the best
option to use for all the problems analyzed. Defin-
ing performance as the percentage improvement in
accuracy relative to the baseline model (utilizing the
better-performing metric between Max Cut and Gini),
this modification had improvements of 1.6%, 1.9%,
1.9%, 1.9%, 6.3% 33.3%, and 49.4% for each of the
data sets. Moreover, Max Cut was the best choice
in 5 out of 7 problems. Defining performance as
the percentage improvement of the best Max Cut al-
gorithm compared to the best performing Gini algo-
rithm, Max Cut had improvements of 1.1% -0.3%,
0.0%, 0.5%, 0.2% 2.0%, and 6.9%. Finally, Max
Cut Node Means PCA was the best choice in 5 out
of 7 problems and was tied for the best in 1 problem.
Defining performance as the percentage improvement
of accuracy compared to the baseline model, Max
Cut Node Means PCA represented an improvement of
1.6%, 1.0%, 1.9%, 1.9%, 6.3%, 33.3%, and 49.4%.
From Table 5, it can be seen that Max Cut Node
Means PCA is invariably the fastest algorithm for
larger problems. Although Max Cut Node Means
PCA took more time for small datasets, we do not be-
KDIR 2020 - 12th International Conference on Knowledge Discovery and Information Retrieval
68

lieve this discounts its overall performance. Regard-
less of the algorithm chosen, the decision trees are fit
in a negligible amount of time for the smaller datasets
relative to the larger datasets. Moreover, Max Cut
Node Means PCA still provides the previously men-
tioned accuracy benefits. For the larger datasets, such
as CIFAR-100, the Max Cut Node Means PCA algo-
rithm reduced the required CPU time by 94% com-
pared to the baseline algorithm. Thus, Max Cut Node
Means PCA provides significant computational and
accuracy advantages.
4 CONCLUSIONS
In this paper, we propose two important modifications
to the CART methodology for constructing classifica-
tion decision trees. We first introduced a Max Cut
based metric for determining the optimal binary split
as an alternative to the Gini Impurity method (see ap-
pendix for an O(nlogn) implementation of Max Cut
along a single feature) . We then introduced the use of
localized PCA to determine locally viable directions
for considering splits and further modified the tradi-
tional PCA algorithm, Means PCA, to find suitable
directions for discriminating between classes. We
follow this study with a theoretical commentary on
how these modifications are reflected in the asymp-
totic bounds of node splitting and demonstrate that
Means PCA improves upon the traditional method.
Our extensive experimental analysis included
more than 20,000 synthetically generated data sets
with training sizes ranging from 100 and 300,000
and informative dimensions ranging between 4 and
50, We further considered both binary and multiclass
classification tasks. These experiments demonstrate
the significant improvements in increased accuracy
and decreased computational time provided by uti-
lizing localized Means PCA and Max Cut. Further-
more, we show that the accuracy improvements be-
come even more substantial as the dimension of the
data and/or the number of classes increases and that
the runtime improves with the dimension and size of
the datasets.
Analysis was also done on real-world datasets.
Our results indicate that the Max Cut Node Means
PCA algorithm remains advantageous even when us-
ing real-world data. For example, we show that in
the case of CIFAR-100 (100 classes, 3,072 dimen-
sions, and 48,000 training points out of 60,000 total)
our algorithm results in a 49.4% increase in accuracy
performance compared to the baseline CART model,
while simultaneously reducing the CPU time required
by 94%. This novel algorithm helps bring decision
trees into the world of big, high-dimensional data.
Our experiments demonstrate the significant improve-
ments that Max Cut Node Means PCA has on con-
structing classification decision trees for these types
of datasets. Further research on how these novel deci-
sion trees affect the performance of ensemble meth-
ods may lead to even greater advancements in the
area.
ACKNOWLEDGEMENTS
This research used the Savio computational cluster re-
source provided by the Berkeley Research Comput-
ing program at the University of California, Berke-
ley (supported by the UC Berkeley Chancellor, Vice
Chancellor for Research, and Chief Information Of-
ficer). This research was supported in part by NSF
award No. CMMI-1760102.
REFERENCES
Breiman, L., Friedman, J., Stone, C., and Olshen, R. (1984).
Classification and Regression Trees. The Wadsworth
and Brooks-Cole statistics-probability series. Taylor
& Francis.
Cortez, P., Cerdeira, A., Almeida, F., Matos, T., and Reis,
J. (2009). Modeling wine preferences by data min-
ing from physicochemical properties. Decis. Support
Syst., 47:547–553.
Dua, D. and Graff, C. (2017). UCI machine learning repos-
itory.
F.R.S., K. P. (1901). Liii. on lines and planes of closest fit to
systems of points in space. The London, Edinburgh,
and Dublin Philosophical Magazine and Journal of
Science, 2(11):559–572.
Holm, S. (1979). A simple sequentially rejective multi-
ple test procedure. Scandinavian Journal of Statistics,
6(2):65–70.
Karp, R. M. (1972). Reducibility among combinatorial
problems. In Miller, R. E., Thatcher, J. W., and
Bohlinger, J. D., editors, Complexity of Computer
Computations, pages 85–103. Plenum Press, New
York.
Krizhevsky, A. (2009). Learning multiple layers of features
from tiny images. Technical report.
LeCun, Y., Cortes, C., and Burges, C. (2010). Mnist hand-
written digit database. ATT Labs [Online]. Available:
http://yann.lecun.com/exdb/mnist, 2.
Oliphant, T. E. (2006). A guide to NumPy, volume 1. Trel-
gol Publishing USA.
Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V.,
Thirion, B., Grisel, O., Blondel, M., Prettenhofer,
P., Weiss, R., Dubourg, V., Vanderplas, J., Passos,
A., Cournapeau, D., Brucher, M., Perrot, M., and
Duchesnay, E. (2011). Scikit-learn: Machine learning
in Python. Journal of Machine Learning Research,
12:2825–2830.
Van Rossum, G. and Drake, F. L. (2009). Python 3 Refer-
ence Manual. CreateSpace, Scotts Valley, CA.
The Max-Cut Decision Tree: Improving on the Accuracy and Running Time of Decision Trees
69

APPENDIX
Implementation of Max Cut Metric in O(nlogn):
The first step is to sort the observations in ascend-
ing order such that x
i, j
< x
k, j
∀i < k, which is known
to be implemented in O(n log n) time. There are a total
of n possible splits to consider; let the value achieved
by the split between x
i, j
and x
k, j
be referred to as θ
i
.
We will now show that given θ
i−1
, θ
i
can be com-
puted in constant time. It is evident that the following
equality holds:
θ
i
= θ
i−1
−
∑
t<i
1
y
i
6=y
t


x
i, j
−x
t, j


+
∑
t>i
1
y
i
6=y
t


x
i, j
−x
t, j


= θ
i−1
−
∑
t<i
1
y
i
6=y
t
(x
i, j
−x
t, j
)
+
∑
t>i
1
y
i
6=y
t
(x
t, j
−x
i, j
)
= θ
i−1
+
∑
t<i
1
y
i
6=y
t
x
t, j
−1
y
i
6=y
t
x
i, j
+
∑
t>i
1
y
i
6=y
t
x
t, j
−1
y
i
6=y
t
x
i, j
Since 1
y
i
6=y
i
= 0 ∀i:
= θ
i−1
+
∑
t
1
y
i
6=y
t
x
t, j
−1
y
i
6=y
t
x
i, j
= θ
i−1
+

∑
t
1
y
i
6=y
t
x
t, j

−x
i, j

∑
t
1
y
i
6=y
t

Since
∑
t
1
y
i
6=y
t
x
t, j
and
∑
t
1
y
i
6=y
t
are only dependent
on the class of observation i, these can be calculated
once for each class c and recorded as S
c
and N
c
re-
spectively. Then,
θ
i
= θ
i−1
+ S
y
i
−x
i, j
N
y
i
Therefore, the complexity of the split per feature is
O(nlogn).
KDIR 2020 - 12th International Conference on Knowledge Discovery and Information Retrieval
70