GA-based U-Net Architecture Optimization Applied to Retina Blood

Vessel Segmentation

Vipul Popat

1 a

, Mahsa Mahdinejad

1,2 b

, Oscar S. Dalmau Cede

3 c

, Enrique Naredo

1,2 d

and Conor Ryan

1,2 e

University of Limerick, Limerick, Ireland

Lero –Science Foundation Ireland Research Centre for Software, Ireland

Centro de Investigaci

on en Matem

aticas (CIMAT), Mexico

Keywords:

Image Segmentation, U-Net, Deep Learning.

Abstract:

Blood vessel extraction in digital retinal images is an important step in medical image analysis for abnormal-

ity detection and also obtaining good retinopathy diabetic diagnosis; this is often referred to as the Retinal

Blood Vessel Segmentation task and current state-of-the-art approaches all use some form of neural networks.

Designing neural network architecture and selecting appropriate hyper-parameters for a speciﬁc task is chal-

lenging. In recent works, increasingly more complex models are starting to appear, but in this work, we present

a simple and small model with a very low number of parameters with good performance compared with the

state of the art algorithms. In particular, we choose a standard Genetic Algorithm (GA) for selecting the pa-

rameters of the model and we use an expert-designed U-net based model, which has become a very popular

tool in image segmentation problems. Experimental results show that GA is able to ﬁnd a much shorter archi-

tecture and acceptable accuracy compared to the U-net manually designed. This ﬁnding puts on the right track

to be able in the future to implement these models in portable applications.

1 INTRODUCTION

Diabetes is a serious and commonly occurring disease

that can lead to early death (Ogurtsova et al., 2017)

or vision loss (Ciulla et al., 2003). Damaging to and

accumulation of blood vessels in the eye can increase

the risk of the blindness of diabetes better known as

Diabetic Retinopathy (DR). Speciﬁcally, the occur-

rence of hard exudates close to the fovea is one of the

main threats to blindness, but timely diagnosis and

laser photo-coagulation can help to reduce the spread

of DR in the retina. However, DR is not recognizable

before the ﬁrst diagnosis of diabetes, early screening

of DR requires specialists to examine manually the

retinal images.

Nowadays, image processing and machine learn-

ing techniques are used to assist specialists in the

analysis of abnormalities in the retina and in the

https://orcid.org/0000-0002-0511-4563

https://orcid.org/0000-0003-4288-3991

https://orcid.org/0000-0002-1828-8458

https://orcid.org/0000-0001-9818-911X

https://orcid.org/0000-0002-7002-5815

retinopathy diabetic diagnosis. These techniques are

used to extract blood vessels from the retinal images

and this process is often referred to as the Retinal

Blood Vessel Segmentation task. To address this task,

all state of the art techniques use some form of Neural

Networks (NN).

The Convolutional NN (CNN) (LeCun et al.,

1995), is an updated version of the traditional NN and

became the preferred choice to address these types of

interesting problems. Even though CNNs have been

successfully applied to solve a wide range of image

processing tasks, its success came with an increase

in its complexity. Therefore, designing a CNN archi-

tecture and selecting its appropriate hyper-parameters

for a speciﬁc task is not trivial.

In this project, we design two sets of experi-

ments to design CNN architectures to address the

Retina Blood Vessel Segmentation task; i) manually

designed, and ii) automatically designed. For the ﬁrst

experiment, we use as a baseline an expert-designed

CNN (Xiancheng et al., 2018), and manually derive

other designs from it. For the automatic choice, we

select a standard Genetic Algorithm (GA) to automat-

ically select the parameters of a CNN architecture.

192

Popat, V., Mahdinejad, M., Cedeño, O., Naredo, E. and Ryan, C.

GA-based U-Net Architecture Optimization Applied to Retina Blood Vessel Segmentation.

DOI: 10.5220/0010112201920199

In Proceedings of the 12th International Joint Conference on Computational Intelligence (IJCCI 2020), pages 192-199

ISBN: 978-989-758-475-6

Furthermore, we explain in detail how to implement

GA to address this task.

Experimental results show that the architectures

proposed by the GA, not only reach competitive per-

formance results against the baseline and other state

of the art approaches but even are able to ﬁnd much

shorter CNN architectures. These results conﬁrm that

it is worth applying an optimizer such as GA to take

better the available computational resources. Further-

more, reducing the CNN architecture complexity mo-

tivates us to follow our research line and address other

related research questions to contribute to implement-

ing these models, in a not too distant future in portable

applications.

The structure of this paper is as follows: the back-

ground is presented in Section 2. Section 3 is dedi-

cated to the description and discussion of the experi-

mental setup, then Section 4 is the results, and ﬁnally,

Section 5, contains our conclusions and future work.

2 BACKGROUND

In this section, we explain the basic concepts related

to the Retina Blood Vessel Segmentation task in sub-

section 2.1, diabetic retina in subsection 2.2, the con-

cepts of CNNs focusing on a particular version named

as U-net in subsection 2.3, and ﬁnally we explain the

algorithm related to a standard GA in subsection 2.4.

2.1 Iris Segmentation

The ﬁrst step is to detect, from a given image the in-

ner and outer boundaries of an iris; i) pupillary, and

ii) limbic, correspondingly. This process helps in ex-

tracting features from the discriminative texture of the

iris while excluding the surrounding regions.

Even though in this project, we do not perform any

pre-processing, and instead we use an already pre-

processed image dataset, we give a brief description

of the process to address this task in order to give con-

text for our work.

There are several methods to address the iris seg-

mentation task, they can be classiﬁed into; Boundary-

based methods (Roy and Soni, 2016), pixel-based

methods (Parikh et al., 2014), active contour and cir-

cle ﬁtting-based methods (Chai et al., 2015), and

CNN-based methods (Liu et al., 2016).

2.2 Diabetic Retina

Once obtained the region of interest, the next step is

to analyze the retina looking for any vessel abnor-

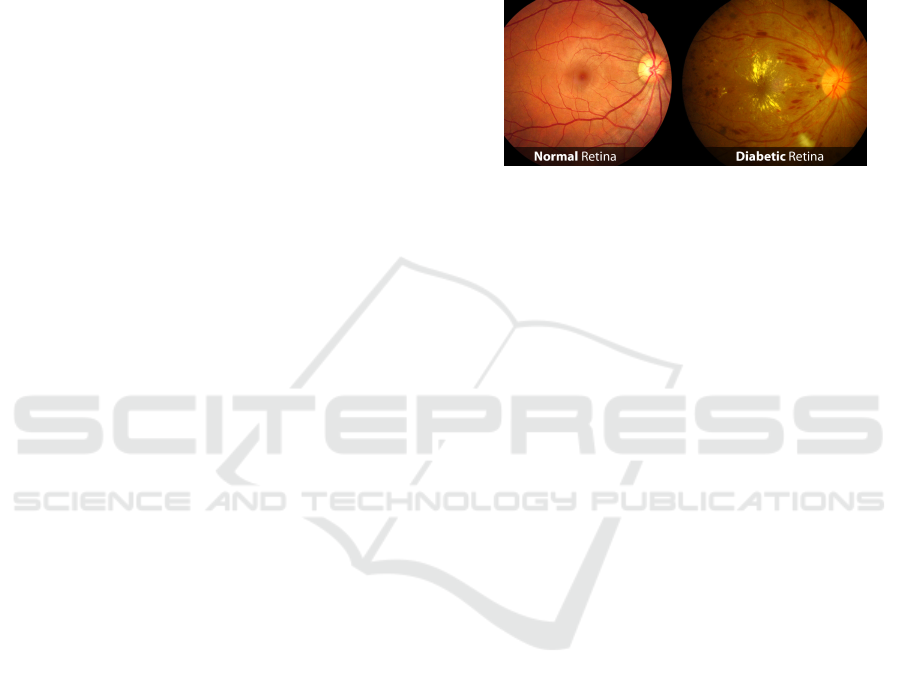
malities. A normal retina is depicted at the left hand

sub-ﬁgure in the Figure 1, taken from (Vision, 2020),

where we can observe the blood vessels without any

notorious damage. Whereas, at the right hand sub-

ﬁgure in the Figure 1, we can observe a typical retina

showing the characteristic abnormalities related to di-

abetic retinopathy, the earliest signs of this disease are

little spots usually red or white color, they can only be

detected by a trained eye from a specialist.

Figure 1: Images taken from the retina, on the left a normal

retina, and on the right a retina damaged by diabetes.

2.3 U-Net

Nowadays, the current state of the art approaches used

to address the blood vessel segmentation task are all

some form of NNs. Among the wide range of NNs

architectures proposed in the literature, U-net (Ron-

neberger et al., 2015a) is a modiﬁcation of a fully

CNN, which according to the authors is able to de-

liver good prediction based on even few data sets.

The U-net architecture is an encoder-decoder ar-

chitecture, the encoder takes the input features and

creates a smaller dimensional of them, while the de-

coder takes the features from the encoder, and gives

the best match to the actual input or planned output.

The U-net consists of two main parts; i) contract-

ing path and ii) expansive path, located at the left and

right side correspondingly. The contracting path per-

forms a down-sampling, whereas the expansive path

performs an up-sampling.

The major advantage of this architecture is its abil-

ity to take into account a wider context when making

a prediction from the actual image pixel by pixel and

speciﬁcally applied to the retinal blood vessel seg-

mentation.

Nevertheless, designing a U-net is not a trivial

task, for this reason, in this project we use a standard

GA to automatically design U-net architectures.

2.4 Genetic Algorithm

The GA is inspired by the theory of the evolution by

natural selection. GAs resemble the process of nat-

ural selection by selecting the ﬁttest individuals and

reproduction in order to produce offspring of the next

generation (Davis, 1991).

GA-based U-Net Architecture Optimization Applied to Retina Blood Vessel Segmentation

193

In order to use GA as an optimizer, we must de-

sign the encoding ﬁrst of a typical solution from a

given problem. Using similar jargon from the biolog-

ical evolution, we say that the individuals I represent

solutions for a given problem, and we can deﬁne I

composed in general by three elements; I = (P,G,S),

where P stands for the phenotype, G for the genotype,

and S for the score.

The observable properties of the individual I is

known as the phenotype P, i.e. U-net architecture.

Say, we have a set of ﬁve parameters to optimize;

]. Even though, this array of param-

eters are not the full solution, we will refer to it as to

the phenotype; then P = [p

Using P, we can build a solution and evaluate its

quality trough a function, which will we refer as to

the ﬁtness function, because it assigns a quality score

to P, named as ﬁtness score S.

In order to create new solutions, we need to re-

combine the information from a set Q of I, named as

population. To recombine easily the information from

the current solutions, we encode P, in a similar way,

as the DNA encode the information of a living organ-

ism. Nevertheless, there are several ways to encode

P, we use the more frequent and easy way of to im-

plement; a bitstring.

Then, the task is to encode P using an array

of bits, we name this encoding as the genotype G,

which encodes a solution with an array of genes

] same length as P. When using a bit-

string to encode a solution, then each g

is composed

by an array of bits [b

, ..., b

], where k is the max-

imum number of bits used to encode the choices of

a given parameter. If g

has four choices, then us-

ing just a pair of bits is enough to represent all of the

choices; g

= [b

], where g can take any of four

choices; g

=00, g

=01, g

=10, g

=11. Following this

example, we can build G to encode fully P.

GA choose with more probability individuals I

from the population Q, which have higher S to recom-

bine between them their G or just to mutate some po-

sition in G, creating in this way new solutions. The

process is repeated until some stop criterion is met as

shown in the Algorithm 12.

Through the evolutionary process, one expects to

see increasingly better solutions until ideally an opti-

mal or near optimal one appears.

3 EXPERIMENTAL SETUP

The goal of this work is to build deep learning models

to address the retinal blood vessel segmentation task.

We address this problem with two different experi-

Algorithm 1: Genetic Algorithm.

Input: G = [g

, g

, ..., g

] // Genotype

Output: P = [p

, p

, ..., p

] // Phenotype

1 I

← (G,P,S)

2 S = ∅

3 Q

t=0

← I

// Initial population

4 while t < m // m = max generations

5 do

6 Evaluate each phenotype P ∈ Q

t−1

7 S(I

) ← eval(P

) assign ﬁtness score

8 Select parents from Q

t−1

using S

9 Genetic operations on G

of selected parents

10 Q

← (G,P) offspring (new pop)

11 t ← t + 1

12 Return I

from Q

with the best S.

ments, namely the manual and automatic design of the

U-net architecture using a very well known dataset.

3.1 Dataset

In our experimental setup, we use the Digital Retinal

Images for Vessel Extraction (DRIVE, ), consisting

of 40 retinal images in total, 20 for training, and 20

for testing, obtained for a diabetic retinopathy screen-

ing program conducted in the Netherlands. Retinal

diseases can be detected by the size, shape, widening,

branching patterns, and angles of vessel bend.

3.2 Manual Design

The manual design of a U-net architecture is not

trivial, and expert knowledge about architecture is

required. The baseline for this set of experiments

named as Exp-1, is taken from (Ronneberger et al.,

2015b), taking the source code from (Unet-code, ) and

updating it to meet the requirements of the dependen-

cies new versions.

In general, the parameters used to run each U-net

architecture are as follows: Number of epochs: 150,

Kernel size: (3,3), Pooling type: ‘MaxPooling’, and

‘sgd’ as the optimizer. In experiments Exp-2 to Exp-

4, we manually changed the U-net architecture to get

fewer possible combinations of reduced depths, and

reduced number of the ﬁlters in order to decrease the

number of parameters required for training and test-

ing. Exps-1, 2, and 3 all have similar conﬁgurations

as shown in Table 1, those U-net architectures differ

only on the parameters related to the ﬁlters shown in

Table 2, but all of them use 16 ﬁlters. In Exp-2, in

order to get an idea of how the number of ﬁlters was

affecting the accuracy performance, we reduced the

number of ﬁlters to half from the baseline U-net ar-

chitecture used in Exp-1, as shown in the second row

of Table 2.

ECTA 2020 - 12th International Conference on Evolutionary Computation Theory and Applications

194

Table 1: U-Net parameters selected manually. Experiments 1,2, and 3, have similar conﬁguration and differ only on the

parameters related to the ﬁlters shown in Table 2.

D P

Exp-1,2,3 4 MaxPooling MaxPooling MaxPooling MaxPooling (3,3) (3,3) (3,3) (3,3) sgd

Exp-4 2 MaxPooling MaxPooling MaxPooling MaxPooling (3,3) (3,3) (3,3) (3,3) sgd

Table 2: U-Net ﬁlter parameters selected manually. The ﬁrst and last values are related to the input L

and output L

out

image

correspondingly, F

, F

, and F

are mirrors of F

, F

, and F

correspondingly. The symbol # stands for the ﬁlter position

not used.

out

Exp-1 3 32 64 64 128 128 256 256 256 512 256 128 256 128 64 128 64 64 3

Exp-2 3 16 32 32 64 64 128 128 128 256 128 64 128 64 32 64 32 32 3

Exp-3 3 16 16 16 32 32 64 64 64 128 64 32 64 32 16 32 16 16 3

Exp-4 3 32 64 64 128 # # # # # # 128 256 128 64 128 64 64 3

In Exp-3, fewer ﬁlters are changed by keeping

their number the same at level 1, but reducing them

to half in the levels below as shown in the third raw of

Table 2. In Exp-4, we entirely removed the ﬁnal two

layers in the U-net architecture and hence running the

experiment with 2 layers and just 10 ﬁlters; as shown

in the fourth raw of Table 2.

3.3 Automatic Design

We used a GA-based approach to automatically de-

sign U-net architectures using the parameters shown

in Table 3, where there are two values for the num-

ber of epochs used to optimize the hyper-parameters

of the U-nets. In the training process, we used just

20 epochs to pre-optimize each U-net evolved by GA

and at the end of the run, we choose the best U-net and

then we use 150 epochs to get a full hyper-parameter

optimization of the U-net and get a fair comparison

against the manual designed U-nets.

The genome is showed in Table 4, the list of pa-

rameters to optimize are: Depth (D), Filter Filter (F),

Pooling Type (T ), Kernel Type (K), and the Optimizer

(O).

The genotype G is composed by the following set

of genes: [D,F,T,K,O]. The size of the genotype is

ﬁxed to a total of 55 bits; 2 bits for D, 3 bits for F,

just one for T , 2 for K, and 2 for O.

The maximum level D is 4, then there are four

choices; D = 1, D = 2, D = 3, D = 4. Therefore, the

gen for D is composed by just 2 bits [b

] to encode

all choices; 00=1, 01=1,10=2, 11=3.

The parameter D is very important because it con-

trols the size of the U-net architecture, and the use

of the rest of the parameters too. For instance, with

D = 4, then the full range of parameters is consid-

ered to build the U-net. But, if D < 4 then some of

the parameters are not considered. Say D = 2, then

we have P

, K

, but F

to F

are not considered

as shown in Table 6, where the unused positions are

marked with the symbol #.

Similarly, the rest of the parameters are encoded

using enough bits according to the available choices

for each of them as shown in Table 4 and Table 3

shows the main parameters used to run the GA-based

experiments.

Table 5 summarizes the parameters selected by

GA, it can be noted how GA prefers shorter U-net

architectures with D = 2. In general, GA prefers

the pooling type; ‘AveragePooling’, and ‘adam’ as

the optimizer, whereas the choices when the U-net is

manually designed are ‘MaxPooling’ and ‘sgd’ cor-

respondingly. Another interesting observation is that

GA prefers bigger sizes of the kernels K with (9,9) as

the most used.

Table 3: List of the main parameters used to run GA.

Parameter Value

Runs 1 per exp

Total Generations 20

Population Size 10

Crossover Rate 0.7

Mutation Rate 0.1

Epochs 20 (Training)

Epochs 150 (Best)

Table 6 show the ﬁlters selected by the GA-based

experiments, where the ﬁrst observation is that the ﬁl-

ters F

to F

are not used because of D = 2. Exp-6

takes the lowest values for the ﬁlters F in the contract-

ing path, whereas Exp-8 takes the lowest values in the

expansive path. In general, Exp-5 uses the largest val-

ues of the ﬁlters. One interesting difference is that in

the GA-based experiments the ﬁlters are not acting as

‘mirrors’ from other ﬁlters as in the manually-based

experiments.

GA-based U-Net Architecture Optimization Applied to Retina Blood Vessel Segmentation

195

3.4 Evaluation

We evaluated the models from both sets of experi-

ments using several metrics: Accuracy (ACC), Sen-

sitivity, Speciﬁcity, Precision.

Sensitivity =

T P

T P + FN

(1)

Speci f icity =

T N

T N + FP

(2)

Accuracy =

T P + T N

T P + T N + FP + FN

(3)

Precision =

T P

T P + FP

(4)

where TP is the number of the true positive samples,

TN is the number of the true negative samples, FP is

the number of the false positive samples, FN is the

number of the false negative samples. Nevertheless,

ACC is used to guide the search when using GA, and

the Area Under the Curve (AUC) of Receiver Operat-

ing Characteristic (ROC) is used to get a comparison

with several state of the art methods. The AUC-ROC

curve is TP-FP plot that commonly used for classiﬁ-

cation problems and represents the degree or measure

of separability and shows how much a model is capa-

ble of distinguishing between classes. The higher the

AUC, the better the model is at predicting.

3.5 Tools

The source code used in this work is taken from

the (Unet-code, ), this code is originally coded in

Python 2 and in order to meet the requirements of the

current TensorFlow version and its dependencies, we

updated the version to work with Python 3.7.4. We

used the evolutionary tool; Distributed Evolutionary

Algorithms (DEAP, ) coded in Python (Fortin et al.,

2012).

4 RESULTS

In this section, we discuss the results from both sets

of experiments; manual and automatic design of U-

net architectures to address the retinal blood vessel

segmentation task. A summary of this experimental

results is shown in Table 7, and a comparison against

the state of the art method is shown in Table 8 using

the result AUC ROC performance from Exp-6.

The results in Table 7 are split into two sections:

Manual and GA-based. The GA-based results are ob-

tained from just one experimental run due to compu-

tational cost of training each individual. The results

from Sensitivity, Speciﬁcity, and Precision are given

as reference, but they were used neither to guide the

search nor to give a comparison against other meth-

ods.

For the set of experiments to manually design U-

net architectures, this performance is taken from just

one architecture and using the corresponding opti-

mizer using a certain number of epochs to tune-up the

U-net hyper-parameters. On the other hand, the GA-

based experiments use the same process to each U-net

to optimize its hyper-parameters, in this case, GA is

used to ﬁnd optimal architectures but is not used as

hyper-parameter optimizer. In the GA-based exper-

iments there are two optimizations happening at the

same time; i) hyper-parameter optimization using ei-

ther sgd or adam, and ii) U-net architecture optimiza-

tion using GA. The performance in training is given

by TrainAcc showed in the ﬁrst column of the Table 7,

which stands for the accuracy performance in train-

ing computed using the Equation 5, presented in the

subsection 3.4. The score obtained from the accuracy

measure is used as a ﬁtness score from the best U-net

architecture on the GA-based experiments. Exp-3 got

the best training performance from the manual design

experiments, whereas Exp-6 is the winner of the GA-

based experiments, and the latter is the best from both

sets of experiments. But the difference is not really

signiﬁcant. The accuracy performance using the test

set is given by TestAcc showed in the second column

of the Table 7. Exp-1 gets the best test performance

from the manual design experiments, and Exp-6 gets

better from the GA-based, Exp-1 in this case is the

winner, but again by a little margin. The following

results consider the overall best performance, Exp-1,

gets the overall best sensitivity performance and the

Figure 2 shows the U-net architecture from Exp-1 and

Exp-6. Exp-2 is the best on the speciﬁcity and on the

precision measure. Considering the AUC-ROC mea-

sure, Exp-1 and Exp-2 reach the same performance in

the manual design experiments, whereas Exp-6 and

Exp-7 got a tie getting the best performance from the

GA-based experiments. The performance obtained

from the U-net evolved by GA in Exp-6 can be ob-

served numerically from the Table 7. From the pre-

vious analysis, we can agree that the architectures

evolved by GA show competitive performance against

the U-nets designed manually.

Two interesting results from the experiments are

from the model size and time shown in the latter

columns in the Table 7. The ﬁrst three experiments

from the manual set show a bigger size than Exp-4,

where the architecture was reduced to half, and it is

reﬂected in the size and the size is reduced by one

order of magnitude. This ﬁnding was our motivation

ECTA 2020 - 12th International Conference on Evolutionary Computation Theory and Applications

196

Table 4: Genome composition showing the parameters and genes, making a genotype representation of a total of 55 bits

length.

Parameter Gens Choices Bit-string Bits Qty Size

Depth D { 1, 2, 3, 4 } [b

, b

] 2 1 2

Filter Size F

, ..., F

{ 8, 16, 32, 64, 128, 256, 384, 512 } [b

, b

], ... , [b

, b

] 3 13 39

Pooling Type T

, T

{ MaxPooling, AveragePooling } [b

], ... , [b

] 1 4 4

Kernel Type K

, K

{ (3,3), (5,5), (7,7), (9,9) } [b

, b

], ... , [b

, b

] 2 4 8

Optimizer O { sgd, adam, adamax, nadam } [b

, b

] 2 1 2

Table 5: U-Net parameters selected automatically (GA-based) for each experiment. Parameters related to the ﬁlters shown in

Table 6.

D P

Exp-5 2 AveragePooling AveragePooling AveragePooling AveragePooling (3,3) (5,5) (7,7) (9,9) adam

Exp-6 2 AveragePooling AveragePooling AveragePooling AveragePooling (9,9) (9,9) (9,9) (9,9) adam

Exp-7 2 MaxPooling MaxPooling AveragePooling MaxPooling (9,9) (9,9) (3,3) (3,3) adam

Exp-8 2 MaxPooling AveragePooling MaxPooling AveragePooling (9,9) (9,9) (5,5) (5,5) adam

Table 6: U-Net ﬁlter parameters selected automatically (GA-based). The ﬁrst and last values are related to the input L

and

output L

out

image correspondingly. The symbol # stands for the ﬁlter position not used.

out

Exp-5 3 32 64 256 512 # # # # # # 512 1024 512 64 128 32 32 3

Exp-6 3 16 32 8 16 # # # # # # 16 32 16 32 64 32 32 3

Exp-7 3 64 128 16 32 # # # # # # 32 64 32 64 128 64 64 3

Exp-8 3 16 32 16 32 # # # # # # 32 64 32 16 32 16 16 3

Table 7: Experimental results, bold numbers are the best results in each setup and underlined numbers are the best results

from both setups.

Experiment TrainAcc TestAcc Sensitivity Speciﬁcity Precision AUC ROC Model size TrainTime TestTime

Manual

Exp-1 0.9663 0.9549 0.7537 0.9843 0.8752 0.9776 4.2 MB 04:01:00 00:07:59

Exp-2 0.9664 0.9547 0.7486 0.9848 0.8780 0.9776 1.1 MB 02:02:00 00:05:59

Exp-3 0.9665 0.9547 0.7518 0.9843 0.8747 0.9774 5.0 MB 03:17:00 00:06:14

Exp-4 0.9653 0.9535 0.7480 0.9835 0.8688 0.9745 939.4 KB 02:02:00 00:06:01

GA-based

Exp-5 0.9526 0.9356 0.5967 0.9850 0.8532 0.9465 186 KB 01:00:00 00:05:45

Exp-6 0.9662 0.9534 0.7506 0.9829 0.8651 0.9751 557.3 KB 20:58:00 00:05:43

Exp-7 0.9668 0.9534 0.7501 0.9831 0.8662 0.9751 8.1 MB 21:02:00 00:06:06

Exp-8 0.9664 0.9525 0.7309 0.9849 0.8757 0.9742 557 KB 21:44:00 00:05:52

to use a GA to evolve U-net architectures. As can

be noted all U-net architectures evolved by GA from

Exp-5 to Exp-8 are always smaller than the architec-

ture of Exp-4. The U-net from Exp-5 got a reduc-

tion of more than 80% from the smaller manually de-

signed in Exp-4, and 95% reduction from Exp-1. This

reduction in size is reﬂected in the computational ef-

fort used as shown in the TrainTime column in Ta-

ble 7. Even though, the difference between the time

taken by Exp-2 or Exp-3 is not much against the time

taken by Exp-5; just half the time reduction on the

GA-based experiments, we need to recall that we are

using a set of U-nets during a certain number of gen-

erations when running GA. The last column of the

Table 7 the time taken for each U-net to deliver 20

images with a retinal blood vessel segmentation using

the test set is in average six minutes, considering just

one image the time taken is about 18 seconds.

Finally, in Table 8 shows the results from 9 previ-

ous related works using the result AUC-ROC perfor-

mance taken from (Unet-code, ), where the top results

are from (Xiancheng et al., 2018) and (Liskowski and

Krawiec, 2016). It can be noted that the prediction

performance from the GA-based Exp-6 is competitive

against those top results.

GA-based U-Net Architecture Optimization Applied to Retina Blood Vessel Segmentation

197

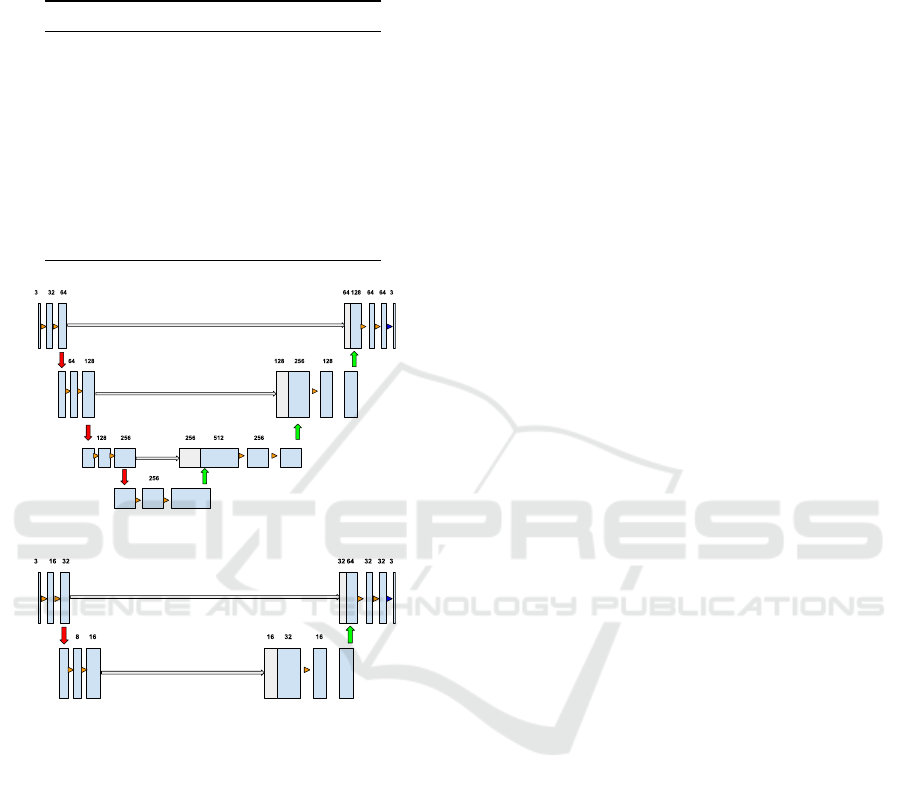
Table 8: Comparison of the AUC ROC performance from

the manually designed U-net from Exp-1 and the GA-based

from Exp-6 both marked with an asterisk (*) against differ-

ent state-of-the-art methods, showing on the top the best.

Method AUC ROC

(Ronneberger et al., 2015b) 0.9790

(Liskowski and Krawiec, 2016) 0.9790

Exp-1 (Manual) 0.9776*

Exp-6 (GA-based) 0.9751*

(Melin

cak et al., 2015) 0.9749

(Fraz et al., 2012) 0.9747

(Li et al., 2015) 0.9738

(Roychowdhury et al., 2014) 0.9670

(Osareh and Shadgar, 2009) 0.9650

(Soares et al., 2006) 0.9614

(Azzopardi et al., 2015) 0.9614

(a) Unet Exp-1

(b) Unet Exp-6

Figure 2: (a) U-net architecture manually designed from

experiment 1, (b) U-net architecture evolved through GA

from experiment 6.

5 CONCLUSIONS

In this research project, we address the retinal blood

vessel segmentation task using the benchmark from

the DRIVE images dataset. Current state of the art ap-

proaches all use some form of NNs which are increas-

ing its complexity, then manually designing them is

challenging. We implemented two sets of experi-

ments; manual and automatic design of U-net archi-

tectures. From the ﬁrst experiment, we designed man-

ually a U-net with competitive results and half the size

of the baseline architecture used from previous re-

lated work. On the other hand, we use standard GA to

evolve U-net architectures. Furthermore, we explain

in detail how to implement GA to address speciﬁcally

this task, but can easily be extended to address other

problem domains. The experimental results show that

GA is able to ﬁnd even smaller architectures from

our smaller manually designed U-net with a reduc-

tion in the size of more than 95% from the and getting

competitive accuracy performance against state of the

art methods. This ﬁnding puts on the right track to

be able in the future to implement these models in

portable applications. For future work, we are plan-

ning to increase the size of the population and num-

ber generations to see if GA is able to further improve

the performance on this problem. Furthermore, an ex-

tension of this work is to apply GA to evolve U-nets

considering different architecture types.

ACKNOWLEDGEMENTS

This work was conducted with the ﬁnancial sup-

port of the Science Foundation Ireland (SFI) Centre

for Research Training in Artiﬁcial Intelligence under

Grant No. 18/CRT/6223, by the research Grant No.

16/IA/4605, and by Lero, the Irish Software Engi-

neering Research Centre (www.lero.ie).

REFERENCES

Azzopardi, G., Strisciuglio, N., Vento, M., and Petkov, N.

(2015). Trainable cosﬁre ﬁlters for vessel delineation

with application to retinal images. Medical image

analysis, 19(1):46–57.

Chai, T., Goi, B., Tay, Y. H., Chin, W., and Lai, Y. (2015).

Local chan-vese segmentation for non-ideal visible

wavelength iris images. In 2015 Conference on Tech-

nologies and Applications of Artiﬁcial Intelligence

(TAAI), pages 506–511.

Ciulla, T. A., Amador, A. G., and Zinman, B. (2003). Dia-

betic retinopathy and diabetic macular edema: patho-

physiology, screening, and novel therapies. Diabetes

care, 26(9):2653–2664.

Davis, L. (1991). Handbook of genetic algorithms.

DEAP. Distributed evolutionary algorithms. https://deap.

readthedocs.io/en/master/. [Online; accessed 20-June-

2020].

DRIVE. Digital retinal images for vessel extraction. http:

//www.isi.uu.nl/Research/Databases/DRIVE/. Ac-

cessed: 2020-06-21.

Fortin, F.-A., Rainville, F.-M. D., Gardner, M.-A., Parizeau,

M., and Gagn

e, C. (2012). Deap: Evolutionary al-

gorithms made easy. Journal of Machine Learning

Research, 13(70):2171–2175.

Fraz, M. M., Remagnino, P., Hoppe, A., Uyyanonvara,

B., Rudnicka, A. R., Owen, C. G., and Barman,

ECTA 2020 - 12th International Conference on Evolutionary Computation Theory and Applications

198

S. A. (2012). An ensemble classiﬁcation-based

approach applied to retinal blood vessel segmenta-

tion. IEEE Transactions on Biomedical Engineering,

59(9):2538–2548.

LeCun, Y., Bengio, Y., et al. (1995). Convolutional net-

works for images, speech, and time series. The

handbook of brain theory and neural networks,

3361(10):1995.

Li, Q., Feng, B., Xie, L., Liang, P., Zhang, H., and Wang, T.

(2015). A cross-modality learning approach for vessel

segmentation in retinal images. IEEE transactions on

medical imaging, 35(1):109–118.

Liskowski, P. and Krawiec, K. (2016). Segmenting retinal

blood vessels with deep neural networks. IEEE trans-

actions on medical imaging, 35(11):2369–2380.

Liu, N., Li, H., Zhang, M., Jing Liu, Sun, Z., and Tan, T.

(2016). Accurate iris segmentation in non-cooperative

environments using fully convolutional networks. In

2016 International Conference on Biometrics (ICB),

pages 1–8.

Melin

cak, M., Prenta

c, P., and Lon

cari

c, S. (2015). Reti-

nal vessel segmentation using deep neural networks.

In 10th International Conference on Computer Vision

Theory and Applications (VISAPP 2015).

Ogurtsova, K., da Rocha Fernandes, J., Huang, Y., Lin-

nenkamp, U., Guariguata, L., Cho, N. H., Cavan, D.,

Shaw, J., and Makaroff, L. (2017). Idf diabetes at-

las: Global estimates for the prevalence of diabetes

for 2015 and 2040. Diabetes research and clinical

practice, 128:40–50.

Osareh, A. and Shadgar, B. (2009). Automatic blood vessel

segmentation in color images of retina.

Parikh, Y., Chaskar, U., and Khakole, H. (2014). Effec-

tive approach for iris localization in nonideal imaging

conditions. In Proceedings of the 2014 IEEE Students’

Technology Symposium, pages 239–246.

Ronneberger, O., Fischer, P., and Brox, T. (2015a). U-

net: Convolutional networks for biomedical image

segmentation. CoRR, abs/1505.04597.

Ronneberger, O., Fischer, P., and Brox, T. (2015b). U-

net: Convolutional networks for biomedical image

segmentation. In Navab, N., Hornegger, J., Wells,

W. M., and Frangi, A. F., editors, Medical Image Com-

puting and Computer-Assisted Intervention – MICCAI

2015, Lecture Notes in Computer Scienc, Munich,

Germany. Springer International Publishing.

Roy, D. A. and Soni, U. S. (2016). Iris segmentation us-

ing daughman’s method. In 2016 International Con-

ference on Electrical, Electronics, and Optimization

Techniques (ICEEOT), pages 2668–2676.

Roychowdhury, S., Koozekanani, D. D., and Parhi, K. K.

(2014). Blood vessel segmentation of fundus images

by major vessel extraction and subimage classiﬁca-

tion. IEEE journal of biomedical and health infor-

matics, 19(3):1118–1128.

Soares, J. V., Leandro, J. J., Cesar, R. M., Jelinek, H. F., and

Cree, M. J. (2006). Retinal vessel segmentation using

the 2-d gabor wavelet and supervised classiﬁcation.

IEEE Transactions on medical Imaging, 25(9):1214–

1222.

Unet-code. Retina blood vessel segmentation with a con-

volutional neural network. https://github.com/orobix/

retina-unet. Accessed: 2020-04-15.

Vision, S. (2020). Diagnosing and treating diabetic

retinopathy in dallas. https://salandvision.com/

eye-conditions/diabetic-retinopathy/. [Online; ac-

cessed 20-June-2020].

Xiancheng, W., Wei, L., Bingyi, M., He, J., Jiang, Z.,

Xu, W., Ji, Z., Hong, G., and Zhaomeng, S. (2018).

Retina blood vessel segmentation using a u-net based

convolutional neural network. In Procedia Computer

Science: International Conference on Data Science

(ICDS 2018), Beijing, China, pages 8–9.

GA-based U-Net Architecture Optimization Applied to Retina Blood Vessel Segmentation

199