Towards Strength-sensitive Social Profiling in Ego Networks

Asma Chader

, Hamid Haddadou

, Leila Hamdad

and Walid-Khaled Hidouci

Laboratoire de la Communication dans les Systèmes Informatiques (LCSI),

Ecole Nationale Supérieure d’Informatique (ESI), BP 68M, 16309, Oued-Smar Algiers, Algeria

Keywords: Social Profile, Social Profiling, Ego Networks, Tie Strength, Online Social Networks.

Abstract: In online social networks, the incomplete or noisy data are usual conditions raising increasingly the need for

more accurate methods; especially in user attribute profiling. This work explores the influence of social tie

strength in such settings, based on the intuition that the stronger the relationship is, the more likely its members

are to share the same attribute values. A Strength-sensitive community-based social profiling process, named

SCoBSP, is introduced under this research and the above hypothesis is tested on real world co-authorship

networks from the DBLP computer science bibliography. Experimental results demonstrate the ability of

SCoBSP to infer attributes accurately, achieving an improvement of 9.18 % in terms of F-measure over the

strength-agnostic process.

1 INTRODUCTION

Online Social Networks (OSNs) have gained

overwhelming popularity in recent years. From

generic (e.g., Facebook, Twitter), professional

(e.g.,LinkedIn, Xing) and academic networks (e.g.,

ReasearchGate, Academia) to photo and video sharing

(e.g., Instagram, YouTube), these platforms have

become an integral part of people’s daily life and

accumulated a great amount of data about human

society. Several models aiming to leverage generated

content were proposed for a myriad of applications.

Amongst them, focus has continuously been on social

profiling to enable more effective user engagement via

personalization (Piao and Breslin, 2018). One of the

main challenges facing such models is the incomplete

and noisy data. Indeed, many users, preserving their

privacy, disclose only few information publicly and,

on the other hand, passive use of OSNs becomes

increasingly prevalent (Piao and Breslin, 2018).

Addressing this, phenomena such as homophily and

social influence (Lee, 2015) were typically explored

in several studies. These latter speculate that people

tend to befriend others who share common interests

(homophily) and influence each other to become more

https://orcid.org/0000-0002-0037-5529

https://orcid.org/0000-0003-0824-0124

https://orcid.org/0000-0003-4515-5519

https://orcid.org/0000-0002-8290-1093

similar over time (social influence). Thus, different

profiling techniques exploit social relationships via

several properties such as community structure

(Tchuente et al., 2013), and link type (Li et al., 2014).

In our research team, we are working on different

approaches using topological properties of networks

in social profiling (Chader et al., 2017). In this paper,

we explore the influence of tie strength (along with

community structure) to enhance profile inference

from user’s ego network (consisting of his direct

relations, known as alters, and the existing

relationships among them).

The concept of tie strength was introduced by

Mark Granovetter in his landmark paper (Granovetter,

1973) and defined as “a (probably linear)

combination of the amount of time, the emotional

intensity, the intimacy (mutual confiding), and the

reciprocal services which characterize the tie”.

Therefrom, several research studies were conducted,

some discussed the quantitative measurement of tie

strength (Gupta et al., 2019) while others were

interested at applications that could benefit from its

computation, in network analysis such as community

detection (Fan et al., 2007) and link prediction (Sett et

al., 2016) or in decision support systems such as

210

Chader, A., Haddadou, H., Hamdad, L. and Hidouci, W.

Towards Strength-sensitive Social Proﬁling in Ego Networks.

DOI: 10.5220/0010113002100217

In Proceedings of the 12th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2020) - Volume 1: KDIR, pages 210-217

ISBN: 978-989-758-474-9

recommendation (Seo et al., 2017) and location

prediction (McGee et al., 2013). In particular, it has

been shown that the community structure in social

networks is deeply correlated with ties strength and

communities extracted under the binary

correspondence of the network are often less

representative of the real community structure (Fan et

al., 2007; Newman, 2004). The study of tie strength

speculates, moreover, that “the stronger the tie

connecting two individuals, the more similar they are”

(Granovetter, 1973). Obviously, in social profiling,

not all relationships are the same to the profiled user.

Some of them being more frequent or intense than

others are, presumably, more revealing of his interests.

Thus, close friends in generic social media or frequent

collaborations in co-authorships networks should not

be treated the same as acquaintances or occasional

collaborations.

Accordingly, we propose a strength-sensitive

community-based profiling approach (named

SCoBSP) , built upon an existing community-based

process (Tchuente et al., 2013) which assumed the

network to be binary, i.e. all friends are equally related

to ego user (who is to be profiled) as well as to each

other. In the light of above findings, such assumption

has two key problems. On the one hand, interests are

inferred from less relevant people (those having weak

ties) and, in the other hand, the community structure

on which the profiling process is completely based is

not correctly depicted. To handle this, our approach

leverages strength of both ego-friend and friend-friend

relationships. The former allows to identify most

relevant people from whom to infer worthwhile

interests, while the latter enables to depict the most

realistic community structure of the ego network.

The remainder of the paper is organized as

follows: The next section presents works most related

to ours. Section 3 describes our approach to social

profiling on weighted ego networks. Section 4

presents evaluation results on real world co-authorship

networks and Section 5 concludes the paper with some

future directions.

2 RELATED WORK

The scientific literature outlines many studies that

exploit relationship information and social graph

characteristics in user profiling ((Piao and Breslin,

2018), Bilal et al., 2019). We review in this section

those closely related to ours, i.e. research based on

user’s ego network. Most of work within this line

were conducted on Twitter and considered only user-

friend’s connections (Piao and Breslin, 2018). For

instance, (Bhattacharya et al., 2014) mine user’s

interests from the topical expertise of the users whom

he follows in twitter. Other studies consider

connections among friends too. (Li et al., 2014)

proposed a new co-profiling approach to jointly infer

users’ attributes and relationship type (being the

reason behind link formation) in ego networks. They

assume connections are discriminatively correlated

with user attributes (e.g., employer) through

relationship type (e.g., colleague). Similarly, (Ma et

al., 2017) attempts to learn profile via a social-aware

semi-supervised topic model that relies on latent

reasons behind social connections and refined the

profiling results by a novel label propagation strategy.

Exploring another aspect of social graphs, (Tchuente

et al., 2013) described a community-based process to

infer user’s attributes via user-groups affinities and

achieved very satisfactory performance compared to

individual based models. This process is later

extended in several ways, (On-At et al., 2014)

addressed the sparse network problem by adding

distance-2 neighbors (friends of a friend) using

snowball sampling technique, while (On-At et al.,

2017a,b) integrated temporal criteria and considered

evolution of both relationships and shared

information in the network.

As for studies exploring tie strength, (McGee et

al., 2013) developed a network-based model to infer

user's locations by leveraging the strength between

users on twitter. To the best of the author’s

knowledge, this is the only study that directly

investigates tie strength in attribute profiling.

However, their model is designed to predict a single

attribute (i.e. specific to location prediction).

Conversely, the community-based process proposed

in (Tchuente et al., 2013) is intended to be generic but

assumed the network to be binary. This motivates us

to investigate tie strength contribution over such

model to infer more relevant social profile.

3 PROPOSITION

In this section, we first introduce the ego network and

user profile models and then present our strength-

sensitive profiling process that leverages relationship

strength and community structure.

3.1 Notation

For a given user u (who is to be profiled), let G =

(V,E’,E,U) be the undirected ego network graph with

positive edge strengths, where V is the set of u’s direct

relations (alters) , E’ the set of ego-alter connections

Towards Strength-sensitive Social Proﬁling in Ego Networks

211

strengths, E’={Suv, v ∈ V} and E the set of alter-alter

ones, E= {Svv’, v,v’∈ V}. The set U, for its part,

describes alters’ profiles, U= {P(v), v

∈

V}. In this

study, we discuss profiles with respect to user’s

interests. Each profile is represented as a vector of

weighted interests (Eq.1):

,,,∈,∈ (1)

where I denotes the set of interests, V the set of alters

and w(i,v) the weight of the interest in v’s profile, it

indicates its importance with respect to the user.

We aim to predict u’s interests by leveraging

community structure and relationship strength (both

ego-alter, E’, and alter-alter, E, sets) to produce his

social profile, called Sp(u), for Social profile of u.

3.2 SCoBSP: Strength-sensitive

Community based Social Profile

This section presents our strength-sensitive process

while highlighting at each stage the main differences

with the existing CoBSP.

3.2.1 Community Detection

Community extraction is well-studied in literature

and various solutions were proposed to handle

different graph properties (e.g. weights, dynamics,

and overlap among others). In OSNs, users usually

belong to multiple groups at once and network

structure evolves continuously. Thus, to extract

communities in user’s ego network we use the

OSLOM algorithm (Lancichinetti et al., 2011) which

considers edges’ weights as well as dynamics and

overlapping communities. The community structure

is denoted by C = {c

, c

...}, for simplicity we refer

to c

as c if there is no confusion. Note that this first

stage involves exclusively alter-alter tie strength.

3.2.2 Community Profiling

In this phase, the profile of each community, I(c) is

constructed as a set of weighted interests. Each

interest i in I(c) is weighted according to two scores:

its semantic score (denoted Sm

) in the community c

and the structural score of c (denoted Str

Semantic Score. Like in the existing CoBSP and

following idea of the TF-IDF measure (Tchuente et

al., 2013), each interest i

∈

I(c) is assigned a score

according to its frequency in profiles of community c

members (Sif) and the relevance of interest i for the

community (Sicf), as in Eq. (2):







,







,







,



(2)

The Sif score, standing for Semantic Interest

Frequency, allows to identify interests characterizing

the community c through their frequency (and

weights) among c members. The more an interest is

shared (and important), the more it characterizes the

community. The Sif score is computed as follows:

Sif



i,c



∑

w i, P







|c|

wi,P











i,v





,ifi,w



i,v





∈P







0otherwise

(3)

where P(v

) is the profile of the node v

∈ c, w(i,v

)

represents the weight of the interest i in P(v

) and |c|

is the number of users in community c.

The Sicf score, for Semantic Inverse Community

Frequency (Eq. (4)), allows to find out the specificity

of each community regarding other ones. As it seems

easier for users to share very popular interests (e.g.,

the movie ‘Harry Potter’) than rare ones (e.g., an

astronomy documentary), we consider rare interests

among other communities as more relevant for c.





,









∈/∈









(4)

where |C| is the number of communities and {c ∈ C:i

∈ I(c)} is the set of communities having i as interest.

Structural Score. This score (denoted (Str

)) relies

only on network topology to characterize the

communities. In the CoBSP process, it is computed

as the degree centrality measure. Differently, we

consider the relationship strength between ego user u

and each community (treated as a whole) as its

structural score. Thus, it sums to how to formulate the

ego-community c strength from relationship strength

of all its members. To do so we propose two different

method where we take into account not only strength

but also number of ego-community links. This latter

results from an analogy we did with Centrality

measures for weighted networks (Opsahl et al., 2010)

where the presence of many ties is considered to

measure the involvement of communities. Note that

only ego-alter tie strength is implicated at this stage.

Proposition 1. In the first, we compute Str

as a

normalized combination between the size of the

community, denoted |c|, and the sum of strength,

denoted W(c), formally:









’



































 













,



 





(5)

KDIR 2020 - 12th International Conference on Knowledge Discovery and Information Retrieval

212

where |E’|, W

denote respectively the total number

of links and the total strength, S

∈ E’

is the tie

strength between ego and node v and γ is a damping

factor to relativize the importance between

community size and strength. Setting γ above 1

decreases the value of the degree in favor of a greater

concentration of node strength whereas a value of γ

between 0 and 1 allows to consider both number and

strength of links. If set to 0, the outcomes of the

measures are solely based on the number of ties and

conversely, if set to 1, the measure is based on ties

strength only and the number of ties is disregarded.

We describe in Sect.4 the parametric study enabling

to identify γ fittest values.

Proposition 2. In the second, we compute Str

as a

degree centrality. Unlike CoBSP, this centrality is

computed by taking ego-community relationships

(i.e. without considering the relationships between

communities). Thus, for each community we keep

only the links connecting its members to

ego user and then apply the degree centrality.

In our context, two aspects must be considered to

measure centrality. On the one hand, the degree

centrality at a group level (we deal with communities

instead of individuals); and on the other hand, the

strength of relationships. Based on a combination of

extensions proposed in literature, the group centrality

degree (Tchuente et al., 2013) and the weighted

degree centrality (Opsahl et al., 2010), we compute

the structural score of community c as follows:









’

||





















\













 











,

\

 





\

(6)

where |N(c)| denotes the number of people outside the

community that are connected to at least one c

member (the group extended degree centrality) and

S(c) denotes the group extended strength centrality

similarly computed. |E’|-|c|, S

T\c

denote respectively

the total number of links and strength excluding

community c members and γ is a damping factor to

relativize the importance between community size

and strength.

Interest Weight Calculation. At this stage, the

communities’ profiles are actually computed once

both semantic and structural score estimated. Each

interest i

∈

Ic

is assigned a score, w (i,c), computed

as in following Eq. (7):





,





















,



(7)

Note that this latter is different from the existing

CoBSP where w(i,c) is computed as a linear

combination, (X,Y, α) = α × X + (1-α) × Y, of

semantic and structural scores using the tuning

parameter α ∈0,1to set the importance between

them. The reason why this combination was used is

the approximate value of structural score they

computed (community centrality) which is not the

case in our study since we use real strengths.

3.2.3 Social Profile Derivation

The last stage consists in deriving the social profile

Sp(u) by computing the final weight of each interest

∈

Sp(u), called w(i,Sp(u)). Since communities are

treated separately in previous stages, an interest i may

appear in different community profiles and with

different weights; these latter should be combined

into one to represent the final weight of the interest.

To this end, authors in (Tchuente et al., 2013)

apply a linear function borrowed from IR field

(merging results of different search engines) where

each score given by a community to an attribute is

multiplied by a coefficient that relativizes its

contribution in the final score according to the

importance of the interest for each community. For

instance, if there are n communities in the ego

network, the highest score for the interest is

privileged and its score is multiplied by n, the second

score by n-1, …, the lowest score of the interest is not

privileged and multiplied by 1. Further details can

be found in (Tchuente et al., 2013).

In our approach, since the strength associated to

communities is already considered in structural score

calculation (Eq. (5) and (6)), we believe that

following their combination might affect negatively

the profiling results. In fact, in the interest calculation

stage (Eq. (7)) the semantic score of an interest i is

directly multiplied by the structural score of the

community c. Which means that a high structural

score implies systematically a highest final score for

interest i in c. Thus, privileging the highest scores

given to the interest will overvalue the weights of

communities, they will be considered twice.

To avoid such overvaluation, we propose to

compute the combined weight w(i,Sp(u)) of each

interest i in Sp(u) by simply summing its different

weights from all communities. Formally:

,







  ,













,









(8)

Towards Strength-sensitive Social Proﬁling in Ego Networks

213

where w(i,c

) is the weight of the interest i in the

community c

as in formula (7).

In summary, with the combination of the equation

presented at each stage, we distinguish in our

strength-sensitive process two different algorithms

depending on how structural score of communities is

computed. We call SCoBSP-Ego, the one that

considers the ego-community strengths as structural

score (Eq.5) and SCoBSP-Cent, the one that applies

the degree centrality (Eq.6).

In the next section we empirically demonstrate the

effectiveness of our approach performed on real

world co-authorship networks.

4 EXPERIMENT

4.1 Experimental Setup

Dataset. To construct a ground-truth dataset for

evaluation, we collected a set of 75 ego networks

from DBLP

as co-authorship networks; where ego

network is composed of his co-authors and the set of

the weighted relationships between them. The DBLP

database provides a comprehensive list of research

papers with several metadata (publication date,

venue, authors...) (Ley, 2009). Specifically, authors’

profiles (the set U in our ego model) are built by

analyzing keywords (considered as interests) from

their publications’ titles as done in (Tchuente et al.,

2013) whereas co-authorship relations (sets E’,E in

G

) are weighted by a measure of strength of their

collaboration according to two factor, the frequency

of co-authorship (higher strength to frequent

collaborations) and the total number of authored

articles (exclusivity of co-authorship relation). Note

that both ego-alter and alter-alter strengths are

computed this way. Thus, for each couple of nodes

(u,v) ∈

EorE’

, its strength denoted 



is calculated

as:







2











(9)

where 



is the number of co-authored papers, and





, 



represent the total number of author’s u and v

publications.

Evaluation Protocol. To evaluate the performance of

our strength-sensitive process, we consider the ego

users’ real profiles from ReasearchGate

as a ground

truth and determine which of CoBSP and SCoBSP

Computer science bibliography: https://dblp.uni-trier.de/

(his two versions: SCoBSP-Ego and SCoBSP-Cent)

provides the most relevant social profiles, i.e. the

closest to the users’ real profiles. The real profiles of

ego users are built from a different network in order

to avoid the bias of using identical data sources

(publication titles). This demarche allows, moreover,

to evaluate the proposed approach against realistic

author’s interests.

In this experiment, we retain authors having at

least 50 co-authors (to get consistent data for

community extraction) and that have more than six

interests in their ResearchGate profile. The

identification of these authors is conducted manually.

A set of 75 ego networks was collected. The studied

authors have an average of 95 co-authors (between 50

and 214) and an average of 19 interests in their

ResearchGate profiles.

To fairly compare SCoBSP and existing CoBSP

and ensure that no processing external to the profiling

process alters the results, the same community

extraction algorithm (OSLOM, see Sect.3.2.1) is

applied for both approaches.

Performances are evaluated in terms of precision,

recall and F-measure metrics as commonly done in

related work (Tchuente et al., 2013; Ma et al., 2017;

On-At et al., 2017a,b). In our context, the precision

represents the proportion of relevant found interests

and the total number of found interests and the recall

represents the proportion of relevant found interests

compared to the total number of real interests (user’s

real profile). The F-measure is the harmonic mean of

precision and recall. As the number of interests

computed in the social profile can be too large, we only

consider the top N interests, i.e. the most relevant ones.

4.2 Results and Discussions

In this section, we present the results of our

evaluations and parametric study. We perform a lot of

experiments with different values of N and α, γ

parameters (to infer their fittest values). We remind

that γ is used in SCoBSP when computing structural

score (Eqs. (5, 6)) to represent the proportion of the

number of ties compared to their strength; and α

(taking part in CoBSP) represents the proportion of

the structural score compared to the semantic one in

community profiling (sect. 3.2.2); results are

presented by the average of metrics for all users.

Results presented hereafter are computed at the top 20

returned interests. This value (N=20) is observed to

offer a good compromise between precision and

recall and to ensure significant values of these metrics

https://www.researchgate.net/

KDIR 2020 - 12th International Conference on Knowledge Discovery and Information Retrieval

214

(users have an average of 19 interests indicated in

their real profiles). In following, we first compare our

approach against the existing CoBSP and then

investigate SCoBSP specifically.

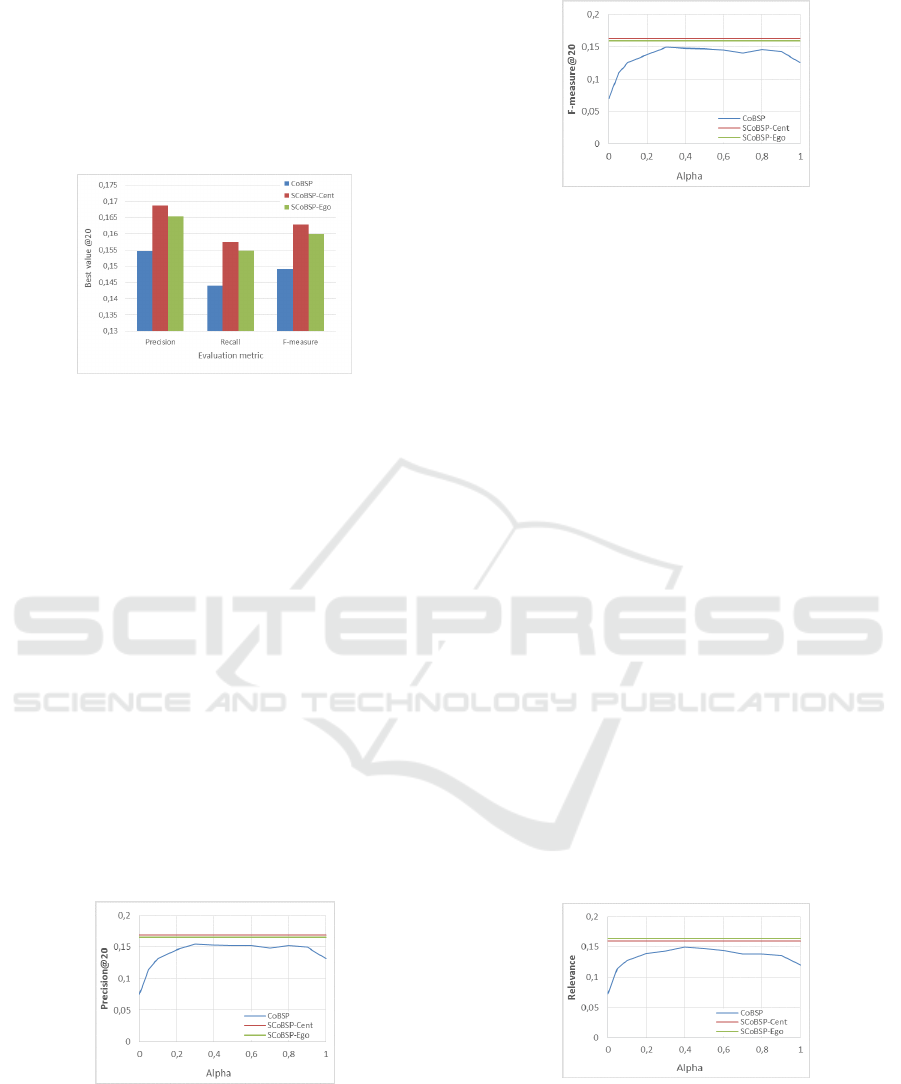
Figure 1 presents the overall performance

comparison in terms of best precision, recall and F-

measure considering the top 20 interests.

Figure 1: Comparison of best metric values @ top 20

interests with best parameters for each proccess.

For the CoBSP approach, the best values (0.154 and

0.149 in terms of mean precision and recall

respectively) are observed when α=0.3. In comparison,

for our strength-sensitive approach best performance is

achieved by SCoBSP-Cent with 0.168 precision and

0.154 recall when γ=0.7; with improvements of

respectively 9.05 and 9.31% over the CoBSP process

and of 2.06 and 1.72% compared to SCoBSP-Ego (for

which best results are obtained when γ=0.8). This

improvement shows the effectiveness of our

proposition and confirms our premise that relationship

strength plays an important role in social profiling.

Figures 2 and 3 show results by the average precision

and F-measure according to α values. Note that this

parameter is not involved in SCoBSP calculation

whose results will never vary whatever the values of

α; hence its straight line representation. For SCoBSP,

reported results are achieved when γ=0.7 and 0.8 for

SCoBSP-Cent and SCoBSP-Ego respectively.

Figure 2: Comparison of average precision according to α.

Figure 3: Comparison of average F-measure according to α.

In these figures, we can clearly see that the two

strength-sensitive algorithms outperform the CoBSP

one in terms of all metrics irrespectively to α values.

The best result can be observed when α=0.0 with

successively 9.16% and 9.4% precision and F-

measure gain rate compared to CoBSP for SCoBSP-

Cent (improvements of up to twice CoBSP results,

132% of F-measure for instance). Regarding the best

results of CoBSP process (when α takes values in

[0.3, 0.6]) we observe average improvements of

10.12% in precision (respectively 10.50% in F-

measure) by SCoBSP-Cent and of 7.94% in precision

(respectively 8.48% F-measure) by SCoBSP-Ego.

We have also studied SCoBSP performance

against CoBSP when setting the value of N to the

number of real interests of each user. In this case, the

precision and recall are reduced to one single

measure. This experiment suggests that the number of

interests to derive is already known to both

approaches; in which case, our strength-sensitive

process proved also its effectiveness. Figure 4 shows

obtained results where we observe improvements of

9.27 and 11.93% for SCoBSP_Cent and

SCoBSP_Ego respectively. Based on the above

results, we can globally see that the overall

performances of strength-sensitives approaches

(SCoBSP_Ego and SCoBSP_Cent) are quite

comparable, SCoBSP_Cent being slightly superior.

Figure 4: Comparison of performance when N=real number

of interests.

We analyze in a second time the variation of results

according to the values of γ parameter to deduce its

fittest value and assess the contribution of strength.

We recall that according to our hypothesis, both

Towards Strength-sensitive Social Proﬁling in Ego Networks

215

number of links and strengths are important to

characterize the involvement of communities in ego

networks. Thus, γ parameter values range between 0

and 1. Figure 5 and 6 depict results in terms of recall

and F-measure according to γ. This latter is not

involved in CoBSP calculations; represented as a

straight line (best result recorded, α=0.3) in following

graphs. Note that at this stage, we assess the relevance

of strength in ego-community connections; which

were completely ignored in CoBSP (neither their

number or strength were studied). The combination

adopted in our approach allows to evaluate both.

Indeed, if the tuning parameter is set to 0, the

outcomes are only based on links number which

enables to study separately its effect.

Figure 5: Comparison of average precision according to γ.

Figure 6: Comparison of average F-measure according to γ.

As follows from the figures, we can clearly see that

our approaches consistently outperform the baseline

regardless of γ values. These results demonstrate the

relevance of ego-community connections and the

valuable information they hold. For instance, best

results of SCoBSP-Cent are achieved when γ=0.7

with substantial improvement of 7.21% F-measure

upon worst observed results when γ=0.0 (which

disregards strength) and 4.33% over γ=1.0 results

(which disregards links’ number). Optimal

performances are achieved when γ is set relatively

high but always when both links number and strength

are considered; which supports our premise.

Moreover, the considerable improvements observed

for γ ranging between 0.6 and 0.8 demonstrate that

strength is relatively more important.

Comparing results when fixing γ to 0 (only links

number considered), we can see improvement over

CoBSP; which can also result from effect of alter-

alter connections. Thus, we leave a detailed study of

this latter to future work.

Finally, to verify our hypothesis that using the

same linear function as existing CoBSP to compute

the final score of interests negatively affects

performance, we evaluate results by applying this

formula. Figure 7 shows results in terms of F-measure

(both precision and recall showed such behaviour).

We can clearly see a very substantial loss of gain (red

curve in the plots); which supports our prior premise.

The overvaluation of communities’ strengths

degrades significantly the results.

Figure 7: Results using linear combination of CoBSP.

In essence, this empirical evaluation amply

demonstrates the potential of our strength-sensitive

process to accurately profile users in ego networks.

5 CONCLUSIONS

This paper investigates the influence of tie strength

considering the problem of social profiling, based on

the intuition that the stronger the relationship is, the

more likely its members are to share the same

interests. We propose a strength-sensitive community

based approach that achieved promising performance

over existing state of the art method on real word co-

authorship networks, with lifts of up to 9.18% in

terms of F-measure.

As our future work, our short-term perspective is

to investigate other models to tie strength integration

in social profiling as well as to evaluate separately the

contribution of alter-alter and ego-alter connections.

We would like further to evaluate our approach with

larger datasets from different social networks having

distinct characteristics (e.g., Facebook and Twitter).

As a long term perspective, it would be interesting to

incorporate other factors or social features into the

model to further enhance profiling accuracy.

KDIR 2020 - 12th International Conference on Knowledge Discovery and Information Retrieval

216

REFERENCES

Bhattacharya P, Zafar MB, Ganguly N, Ghosh S, Gummadi

KP (2014) Inferring user interests in the twitter social

network. In: Proceedings of the 8th ACM Conference

on Recommender systems, pp 357-360.

Bilal, M., Gani, A., Lali, M. I. U., Marjani, M., & Malik, N

(2019) Social profiling: A review, taxonomy, and

challenges. Cyberpsychology, Behavior, and Social

Networking, 22(7), 433-450.

Chader, A., Haddadou, H., & Hidouci, W. K. (2017). All

friends are not equal: weight-aware egocentric

network-based user profiling. In 2017 IEEE/ACS 14th

International Conference on Computer Systems and

Applications (AICCSA), IEEE, pp. 482-488.

Fan Y, Li M, Zhang P, Wu J, Di Z (2007). The effect of

weight on community structure of networks. Physica A:

Statistical Mechanics and its Applications 378(2):583-

590.

Granovetter, M. S. (1973). The Strength of Weak Ties.

American Journal of Sociology, 78(6):1360–1380.

Gupta, J. P., Kärkkäinen, H., Torro, O., & Mukkamala, R.

R. (2019). Revisiting Social Media Tie Strength in the

Era of Data Access Restrictions. In Proceedings of the

11th International Joint Conference on Knowledge

Discovery, Knowledge Engineering and Knowledge

Management (IC3K): Volume 3: KMIS, pp. 187-194.

Lancichinetti A, Radicchi F, Ramasco JJ, Fortunato S

(2011) Finding statistically significant communities in

networks. PloS one 6(4):e18961

Lee SY (2015) Homophily and social influence among

online casual game players. Telematics and Informatics

32(4):656-666

Ley M (2009) Dblp: some lessons learned. Proceedings of

the VLDB Endowment 2(2):1493-1500

Li R, Wang C, Chang KCC (2014) User profiling in an ego

network: co-profiling attributes and relationships. In:

Proceedings of the 23rd international conference on

World wide web, ACM, pp 819-830

Ma C, Zhu C, Fu Y, Zhu H, Liu G, Chen E (2017) Social

user profiling: A socialaware topic modeling

perspective. In: International Conference on Database

Systems for Advanced Applications, pp 610-622

McGee, J., Caverlee, J., & Cheng, Z. (2013, October).

Location prediction in social media based on tie

strength. In Proceedings of the 22nd ACM

international conference on Information & Knowledge

Management (pp. 459-468).

Newman ME (2004) Analysis of weighted networks.

Physical review E 70(5):056131

On-At S, Canut MF, Péninou A, Sèdes F (2014) Deriving

user’s profile from sparse egocentric networks: Using

snowball sampling and link prediction. In: Ninth

International Conference on Digital Information

Management (ICDIM 2014), IEEE, pp 80-85

On-At S, Péninou A, Canut MF & Sèdes, F. (2017a).

Toward a combinatorial analysis and parametric study

to build time-aware social profile. In Proceedings of the

9th International Conference on Management of Digital

EcoSystems, pp. 113-120.

On-at S, Quirin A, Péninou A, Baptiste-Jessel N, Canut MF,

Sèdes F (2017b) A parametric study to construct time-

aware social profiles. In: Trends in Social Network

Analysis, Springer, pp 21-50

Opsahl T, Agneessens F, Skvoretz J (2010) Node centrality

in weighted networks: Generalizing degree and shortest

paths. Social networks 32(3):245-251

Piao G, Breslin JG (2018) Inferring user interests in

microblogging social networks: a survey. User

Modeling and User-Adapted Interaction 28(3):277-329

Seo, Y. D., Kim, Y. G., Lee, E., & Baik, D. K. (2017).

Personalized recommender system based on friendship

strength in social network services. Expert Systems

with Applications, 69, 135-148.

Sett, N., Singh, S. R., & Nandi, S. (2016) Influence of edge

weight on node proximity based link prediction

methods: an empirical analysis. Neurocomputing, 172,

71-83.

Tchuente D, Canut MF, Jessel N, Péninou A, Sèdes F

(2013) A community-based algorithm for deriving

users’ profiles from egocentrics networks: experiment

on facebook and dblp. Social Network Analysis and

Mining 3(3):667-683.

Towards Strength-sensitive Social Proﬁling in Ego Networks

217