
Batch Contrastive Regularization for Deep Neural Network
Muhammad Tanveer
1
, Hung Khoon Tan
1a
, Hui Fuang Ng
1b
,
Maylor Karhang Leung
1c
and Joon Huang Chuah
2d
1
Faculty of Information and Communication Technology, Universiti Tunku Abdul Rahman, Malaysia
2
Faculty of Engineering, Universiti Malaya, Malaysia
Keywords: Batch Contrastive Loss, Batch Regularization, Center-level Contrastive Loss, Sample-level Contrastive Loss,
Neural Network.
Abstract: As neural network becomes deeper, it becomes more capable of generating more powerful representation for
a wide variety of tasks. However, deep neural network has a large number of parameters and easy to overfit
the training samples. In this paper, we present a new regularization technique, called batch contrastive
regularization. Regularization is performed by comparing samples collectively via contrastive loss which
encourages intra-class compactness and inter-class separability in an embedded Euclidean space. To facilitate
learning of embedding features for contrastive loss, a two-headed neural network architecture is used to
decouple regularization classification. During inference, the regularization head is discarded and the network
operates like any conventional classification network. We also introduce bag sampling to ensure sufficient
positive samples for the classes in each batch. The performance of the proposed architecture is evaluated on
CIFAR-10 and CIFAR-100 databases. Our experiments show that features regularized by contrastive loss has
strong generalization performance, yielding over 8% improvement on ResNet50 for CIFAR-100 when trained
from scratch.
1 INTRODUCTION
As neural networks (He et al., 2016; Zagoruyko et al.,
2016; Xie et al., 2017) become deeper over the years,
it has become more adept at tackling more complex
classification and detection tasks. However, deeper
networks have a large number of parameters which
makes it more prone to overfitting especially when
trained on a small training set. Different
regularization methods have been designed over the
recent years to improve generalization performance.
Widely used techniques include weight decay (Krogh
et al., 1992), data augmentation (Shorten et al., 2019),
and dropout (Srivastava et al., 2014). In general, these
techniques inject random noise into the network
(Srivastava et al., 2014) or data samples (Shorten et
al., 2019) when training the network. One common
feature of these techniques is that samples are treated
individually. Although training is carried out in
a
https://orcid.org/0000-0001-9964-7186
b
https://orcid.org/0000-0003-4394-2770
c
https://orcid.org/0000-0002-1023-7162
d
https://orcid.org/0000-0001-9058-3497
batches, most computations (e.g., forward
propagation, loss, regularization and propagation) are
done with little interaction between the samples
except for simple averaging at the end.
Recently, batch loss regularization techniques
(Wen et al., 2016; Huang et al., 2017; Zhao et al.,
2019) explores how to regularize a network
collectively by tapping into the relationship between
batch samples. Compared to the softmax loss (Figure
1(a)) which learns separable decision boundaries,
center loss (Wen et al., 2016) further encourages
intra-class compactness (Figure 1(b)) by penalizing
the distance between embedding features and their
corresponding centers. Exclusive regularization
(Zhao et al., 2019) additionally ensures that the
centers are far apart by penalizing the angles between
two neighbouring centers (Figure 1(c)). The
generated features are more representative and
discriminative.
368
Tanveer, M., Tan, H., Ng, H., Leung, M. and Chuah, J.
Batch Contrastive Regularization for Deep Neural Network.
DOI: 10.5220/0010135303680377
In Proceedings of the 12th International Joint Conference on Computational Intelligence (IJCCI 2020), pages 368-377
ISBN: 978-989-758-475-6
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
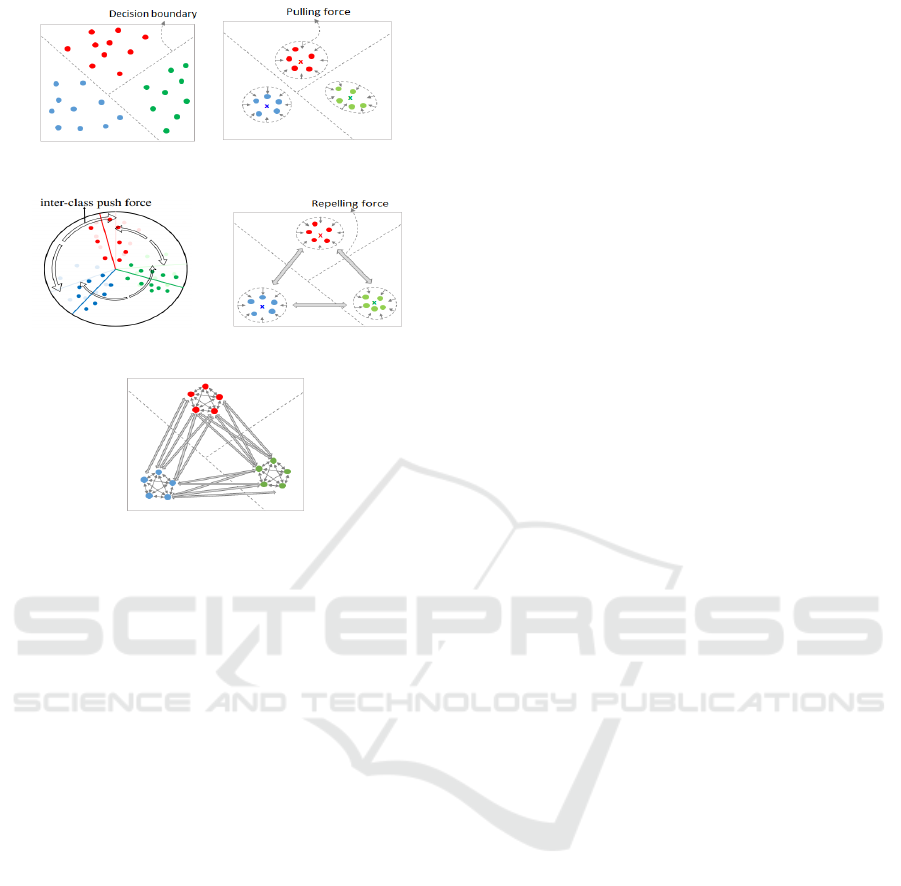
Figure 1: Embedding features trained under various loss
functions. (a) Softmax loss generates embedding features
that are separable (b) Center loss (Wen et al., 2016) ensures
intra-class compactness. (c) Exclusive regulation (Zhao et
al., 2019) ensures both intra-class compactness and inter-
class separability using angular loss (d) Our proposed
center contrastive loss uses the contrastive loss function in
an euclidean embedding space. (e) Our proposed sample
contrastive loss is similar to (d) except that the distance is
computed between sample-pairs.
Intra-class compactness and center separability
apparently exhibit promising regularizing effect.
Interestingly, some studies in perceptual learning
(Mitchell et al., 2014; Mundy et al. 2007) show that
the performance of human on categorization task can
be enhanced when the stimuli are presented side by
side so that the subject is given the opportunity for
comparison. In (Mundy et al., 2007), human subjects
were found to perform better at categorization tasks
when two stimuli such as face pairs or checkerboard
pattern pairs were presented simultaneously as
opposed to successively. Interestingly, the ability to
learn from comparison is potentially unique to
human, not found in animal, which shows that
learning from simultaneous samples represents a
higher order of learning.
In this paper, we novelly use contrastive loss to
realize batch loss regularization. Contrastive loss has
been widely adopted for distance metric learning.
More importantly, features generated from
contrastive loss has been shown to deliver superior
performance for a multitude of tasks compared to
softmax loss when the training set is small (Horiguchi
et al., 2019). Hence, we posit that the network
regularized by contrastive loss has good
generalization property. We explore two different
contrastive losses: (1) the center contrastive loss
shown in Figure 1(d) which uses embedding feature
centers as the reference point and (2) the sample
contrastive loss shown in Figure 1(e) which is based
on sample-pair distances.
Our contribution are as follows. First, we propose
a novel batch loss regularization method called batch
contrastive loss. We devise two variants of batch
contrastive loss to regularize the network. Second,
our work is the first to seriously explore batch loss
regularization for general classification. Previous
works on batch loss regularization are limited to
specific domain e.g., face recognition (Wen et al.,
2016; Zhao et al., 2019), or scene classification
(Huang et al., 2017). In our experiments, our
proposed method displays strong generalization
performance for the CIFAR-100 dataset. Third, we
use a two-headed network architecture in order to
decouple regularization from classification. During
inference, the regularization head is dropped and only
the classification head remains. Lastly, we introduce
bag sampling to guarantee that the classes in a batch
are not under-represented.
2 RELATED WORK
As neural network becomes deeper, the huge number
of parameters causes the network to become prone to
overfitting especially when trained on a small
targeted dataset, leading to poor generalization
performance. To solve this problem, a number of
powerful regularization techniques have been
developed to overcome the problem. Classical
methods include weight decay (Krogh et al., 1992),
elastic net (Zou et al., 2005) and early stopping
(Morgan et al., 1990). For modern neural networks,
dropout (Srivastava et al., 2014; Wan et al., 2013;
Tompson et al., 2015; DeVries et al., 2017; Ghiasi et
al., 2018) and data augmentation (Krizhevsky et al.,
2012; Zhong et al., 2020 ; Cubuk et al., 2019) have
gained wide adoption.
Dropout (Srivastava et al., 2014) stochastically
deactivates activations in the network during training.
This causes the model to be simpler and discourages
co-adaptation among feature detectors. Drop connect
(Wan et al., 2013) further generalizes dropout by
masking connections between neurons. Standard
dropout techniques (Srivastava et al., 2014; Wan et
(a) Softmax loss (b) Center Loss (Wen
et al., 2016)
(c) Exclusive Reg (Zhao (d) Center Contrastive Loss
et al., 2019)
(e) Sample Contrastive Loss
Batch Contrastive Regularization for Deep Neural Network
369

al., 2013) are effective for fully connected layers but
not suited for convolutional layers which exhibits
strong spatial correlation. Hence, spatial dropout
(Tompson et al., 2015) drops an entire channel from
the feature map while cutout (DeVries et al., 2017)
and drop block (Ghiasi et al., 2018) mask out local
and contiguous regions in the input layer and
convolutional layer, respectively. Some dropout
techniques are customized for particular architecture.
For example, drop path (Larsson et al., 2016) drops
sub-paths to prevent co-adaptation of parallel paths in
a fractal architecture while stochastic depth (Huang et
al., 2016) makes a residual network appear shallower
by dropping some residual branches. Shake-shake
(Gastaldi et al., 2017) uses a stochastic affine
combination of parallel residual paths for ResNeXt
(Xie et al., 2017). To generalize shake-shake
regularization to single residual path architectures
(He et al., 2016; Zagoruyko et al., 2016; Han et al.,
2017). ShakeDrop (Yamada et al., 2018) integrates
shake-shake (Gastaldi et al., 2017) with stochastic
depth (Huang et al., 2016) where the latter acts as a
stabilization mechanism which is missing in single
residual path networks. Recent dropout techniques
has devised selective dropping schemes. For
example, spectral dropout (Khan et al., 2019) drops
less significant spectral component. Similar to spatial
dropout, weighted channel dropout (Hou et al., 2019)
drops a whole channel in a more judicious manner
based on their strength of the activations.
Another popular regularization technique is data
augmentation (Shorten et al., 2019) where a variety
of geometric and photometric transformations are
applied on the image to increase the size and diversity
of the data set. Krizhevsky et al., (2012) apply
random cropping, horizontal reflection as well as
color jittering. Algorithms such as cutout (DeVries et
al., 2017) and random erasing (Zhong et al., 2020)
augments the data by cutting out random regions from
the input image. Sample pairing (Inoue et al., 2018)
synthesize new image by mixing two images.
Recently, more intelligent augmentation schemes
have been proposed. AutoAugment (Cubuk et al.,
2019) and Fast AutoAugment (Lim et al., 2019) learn
to augment by searching for data augmentation
policies while DevVries et al. (2017) performs
transformation in a learned feature space rather than
the input space.
Our proposed method belongs to an emerging
family of regularization techniques called batch loss
regularization which regularizes batch samples
collectively. In the work by Wen et al. (2016), class
centers are computed from the embedding features of
the batch sample. Then, the center loss penalizes the
Euclidean distance between batch samples and their
corresponding centers to emphasize intra-class
compactness. The model is jointly trained by center
loss and the softmax loss. Huang et al. (2017)
employs a similar formulation for aerial scene
classification. Zhao et al. (2019) proposes exclusive
regularization which further penalizes inter-class
angular distance to enhance inter-class separability.
In our current work, we explore using a different loss
function based on batch contrastive loss to achieve
both intra-class compactness and inter-class
separability.
3 BATCH CONTRASTIVE LOSS
In this section, we formulate our proposed batch
contrastive loss. The underlying idea is to regularize
the network by comparing batch data. Given a batch
data 𝑋
𝑥
,…,𝑥
and its corresponding
labels 𝑌
𝑦
,…,𝑦
, we use a ConvNet (c.f.
Section 3) to extract two outputs: (1) the embedding
features generated by the regularization head,
henceforth referred to as contrastive features 𝐸
𝑒
,…,𝑒
and (2) the probit outputs for each sample
𝑆
𝑠
,…,𝑠
by the classification head. The former
is used to regularize the network while the latter is the
classification output of the network. The
regularization head is only used during training and is
discarded during inference. In the following sub-
sections, we introduce two versions of batch
contrastive loss functions. The first regularizes batch
samples with reference to the class centers whereas
the second regularizes based on sample-pair
distances.
3.1 Center Contrastive Loss
Our first contrastive regularization term learns the
features and class centers that enforce intra-class
compactness and inter-class separability. Distances
are measured with respect to the class centers as
reference points. The loss function is given as
follows:
ℒ
𝐸,𝑌,𝐶
𝜆𝑒
𝑐
𝛽 max
0,𝑚 𝑐
𝑐
(1)
where the class centers 𝐶
𝑐
,…,𝑐
are updated in
each iteration based on the mean of the batch samples
for each class.
𝑐
𝑦
𝑖
is the actual class center for the
contrastive feature 𝑒
𝑖
. The loss function is based on
the classical contrastive loss function (Chopra et al.,
2005) which comprises two parts. The first part is the
positive loss which penalizes the distance between
NCTA 2020 - 12th International Conference on Neural Computation Theory and Applications
370

generated contrastive feature with their class centers.
This encourages intra-class compactness and is
similar in form to the center loss (Wen et al., 2016).
The second part is the negative loss which pushes
class centers apart by penalizing any two centers with
distance less than the margin m. This promotes inter-
class separability. The relative strength of the positive
and negative losses can be controlled by the
hyperparameters 𝜆 and 𝛽. A larger 𝜆 enhances the
intra-class compactness whereas a larger 𝛽 imposes
greater inter-class separability.
Since the distances are computed relative to the
class centers, we refer to Eq. (1) as the center
contrastive loss. The proposed center-level
contrastive regularization term is similar in form to
Zhao et al. (2019). However, Zhao et al. (2019) uses
an angular distance measure which disregards the
magnitude of the embedding vectors. In contrast, our
method employs the contrastive loss formulation
(Chopra et al., 2005) which is based on straight-line
distance in an Euclidean space. Contrastive loss has
been popularly used for the task of metric learning but
has never been used for batch loss regularization.
Furthermore, Horiguchi et al. (2019) shows that it is
more effective to use angular distance when
comparing embedding features extracted from a
softmax-based classifier. Since Zhao et al. (2019)
employs the same features for computing softmax
(classification) loss and exclusive (regularization)
loss, it has naturally adopted the angular-based
distance. Our network does not suffer from the same
restriction due to a two-headed network design which
decouples regularization from classification. In fact,
Horiguchi et al. (2019) shows that the Euclidean
distance is more effective for comparing features
extracted from a distance metric-learning based
learning classifier as implemented by the
regularization head in our approach. More discussion
on the network architecture can be found in Section
3.3.
3.2 Sample Contrastive Loss
The cluster contrastive regularization proposed in the
previous section is efficient, but it restricts each class
to a single class center which may not be desirable for
classes with high-intra-class variation. Furthermore,
the cluster centers are dynamically updated in each
iteration based on batch data and may not be
representative of the whole dataset. Hence, we
propose a second loss function which performs
regularization at the sample level. It is based on the
vanilla contrastive loss function. Recently, one-shot
learning (Koch et al., 2015) uses Siamese network to
learn using a single example of a new class. The
network was pre-trained for some verification task
using contrastive loss by comparing image pairs.
Figure 2: Proposed two-headed network architecture. The
body of the network generates the activation map. The
regularization head is used. The classification head is a
softmax classifier. For inference, the regularization head is
dropped.
Once optimized, the network is not only
discriminative for the original classes it was trained
on, but it generalizes well to learn entirely new
classes with unknown distribution. Motivated by this
observation, we adopt the contrastive loss as a
regularization term to tap into the generalization
capability of contrastive features. The sample
contrastive loss is given as follows:
ℒ
𝐸,𝑌
𝜆𝟏𝑦
𝑦
𝑒
𝑒
𝛽𝟏𝑦
𝑦
max
0,𝑚 𝑒
𝑒
(2)
𝟏
∙
is an indicator function that values to 1 when the
condition is true
and to 0 otherwise.
The first term
computes the distance for all positive pairs in the
batch. The second term computes the negative loss
which penalizes when the distance between any two
negative samples are less than m. Since the distances
are measured sample-wise, we refer to Eq. 2 as
sample contrastive loss.
Our work differs from the work Koch et al. (2015)
in two important aspects. The system by Koch et al.,
(2015) is designed to function as a comparator.
Hence, the constructed model is a bi-input model that
expects two input samples even during inference and
outputs the distance between them. In contrast, (i) we
use contrastive loss for a different purpose, i.e., to
regularize the training and (ii) our network remains as
a uni-input model and receives single sample as input
during inference. Hence, our method can be applied
to any classification tasks and not confined to a
comparative setup.
Compared to center contrastive loss (Eq. 1), the
sample contrastive loss (Eq. 2) incurs some
computational overhead due to an exhaustive
computation of pair-wise distances between sample
Batch Contrastive Regularization for Deep Neural Network
371

pairs in a batch, especially when a large batch size is
used. The time complexity involved is O(N
2
). In our
experiments, the training duration increases to 1.5
times of the original training time for a batch size of
16. However, this can be easily overcome by
combining hashing and hard sampling (Hermans et
al., 2017). An off-the-shelve nearest neighbour
search, e.g., LSH (Indyk et al., 1998) can be used to
find the hardest positive and hardest negative to
compute the loss for each sample. The hardest
positive and negative samples are then used to
compute the triplet loss. Hard sampling has been
shown to produce better performance and
convergence rate. The runtime can thus be reduced to
O(N). In our experiments, we simply compute the
distance for all sample pairs.
3.3 Model Architecture
Figure 2 shows an overview of our network
architecture. The proposed network is a two-headed
network. The body of the network can be
implemented by any current ConvNet architecture. Its
function is to generate the features for the two heads.
The regularization head converts the feature into a
low-dimensional contrastive features (256-D) for
regularizing the network via contrastive loss whereas
the classification head is a softmax classifier to
predict the label. The classification head uses softmax
activation. No activation is imposed for the
regularization head.
Although Zhao et al. (2019) has similar design as
ours, it uses the softmax-based feature (features
extracted from a softmax classifier) to compute the
angular loss. As mentioned, softmax-based features
are more appropriately evaluated using angular
distance. In contrast, our two-headed network design
allows us to use the softmax-based feature for
classification and contrastive-based feature (feature
learnt from distance metric learning) for
regularization. A previous study (Horiguchi et al.,
2019) has pit softmax-based feature against
contrastive-based feature. It shows that the softmax-
based features perform better on classification,
clustering and retrieval tasks when the size of the
training set is large, but the contrastive-based feature
becomes more competitive when the dataset is small.
This lend strong support for using contrastive loss to
regularize the network. For inference, the
regularization head is dropped leaving only the
classification head. Hence, our network remains as a
uni-input model and works just like any other
classification model during inference.
3.4 Bag Sampling
Special attention needs to be paid to sample selection.
When sampling batch data, each class in a batch
should be represented by at least 2 samples for
contrastive regularization to be effective. However,
this requirement will likely be violated when number
of classes is larger than the batch size. For example,
ImageNet has 1000 class whereas the typical bag size
is from 4 to 256. To remedy the issue, we perform bag
sampling. In this scheme, samples are organized into
groups of k samples called bags. When sampling
batch data for training, we sample in bags rather than
individual samples. The samples in the bags are non-
overlapping except for the last one to ensure
consistent batch size. Thus, one epoch in bag
sampling performs almost the same number of
forward propagations as one epoch in conventional
sampling.
3.5 Proposed Algorithm
To measure classification performance, we use the
cross entropy loss:
ℒ
𝑆,𝑌
1
𝑁
log𝑠
(3)
where
𝑠
is the probit of the correct class for
sample𝑥
. To train the network, we perform joint
supervision of cross entropy loss and batch
contrastive loss. The final loss is given as follows:
ℒ
ℒ
ℒ
(4)
where the contrastive loss
ℒ
can be either ℒ
or ℒ
. The training algorithm is summarized in
Algorithm 1.
Algorithm 1: Training algorithm with Batch
Contrastive Regularization.
Input: Training data
𝑋, 𝑌
Output: Trained network weights 𝑊
1. Repeat for n epochs
2. Organize samples into bags
3. Repeat for each batch data 𝑋
(bag
sampling):
4. 𝐸,𝑆 model(𝑋
)
5. Compute cluster centers 𝐶 from 𝐸
6. Compute contrastive loss ℒ
𝐸,𝑌,𝐶
(Eq.1) or ℒ
𝐸,𝑌
(Eq. 2)
7. Compute classification loss ℒ
𝑆,𝑌
(Eq. 3)
8. Compute combined loss ℒ (Eq. 4)
9. Backpropagate and update 𝑊
NCTA 2020 - 12th International Conference on Neural Computation Theory and Applications
372

4 IMPLEMENTATION DETAILS
Network Architecture. ResNet (He et al., 2016) is
employed as the backbone of our two-headed
network. We use two networks with different depth,
namely ResNet18 and ResNet50. The output of
global pooling layer serves as input to the
regularization and classification heads. Both the
regularization head and classification has only one
fully connected layer. The classification head uses
softmax activation whereas the regularization has no
activation.
Experimental Settings. All images are resized to
224x224. For data augmentation, we apply random
crop, random horizontal flip and color jittering during
training. We set the learning rate lr=0.1, =10
-4
and
the margin m=1.25. For , we set it to 0.550 for
CIFAR-10 and 5.0 for CIFAR-100. The network is
trained for 100 epochs using stochastic gradient
descent with momentum set to 0.9. A learning rate
schedule is used with decay = 0.1 and milestone =
[50, 75]. Unless specified otherwise, for our methods,
we use bag sampling with a bag size of 2 to sample
the training set. All models are trained from scratch.
In other words, we do not use any pre-training. The
above settings are used to train both the ResNet18 and
ResNet50 backbone network.
Benchmark Algorithms. We compare our
algorithms against the weight decay (Krogh et al.,
1992) which suppresses the parameters of the
network
𝑊 through the L2 norm thus enforcing a
simpler network.
ℒ
2
𝛾
‖
𝑤
𝑖
‖
2
2
∈
(5)
The weight decay can also be combined with
contrastive loss.
ℒ
ℒ
ℒ
ℒ
2
(6)
We also compare our algorithm with another more
recent regularization function. The center loss (Wen
et al., 2016) is similar to our center contrastive loss
(Eq 1) except that it only considers intra-class
compactness.
Center Loss
𝐸,𝑌,𝐶
𝑒
𝑐
(7)
Dataset. We evaluated on two datasets: CIFAR-
10 and CIFAR-100. CIFAR-10 has 10 distinct classes
whereas CIFAR-100 has 100 classes. Each image
contains only single object and has a size of 32 32
pixels. Both datasets contain 50,000 training images
and 10,000 test images. CIFAR-10 has around 5,000
images per class for training whereas CIFAR-100 has
only 500 images. In addition, some classes in CIFAR-
100 (e.g., maple, oak, palm, pine and willow) are
visually similar and hence difficult to classify.
Therefore, CIFAR-100 is a more challenging dataset
compared to CIFAR-10 and needs more fine-grained
classification.
5 EXPERIMENTS
Effectiveness of Batch Loss Regularization. First,
we evaluate the effectiveness of different batch loss
regularization techniques for regularizing networks.
We compare our method against another batch loss
regularization technique, namely center loss (Wen et
al., 2016). Table 1 shows the experimental result.
Table 1: Testing Accuracy of Batch Loss Regularization for
ResNet18 (No Pre-Training).
Method CIFAR-10 CIFAR-100
CE 92.20% 69.68%
CE + Center 93.00%
(
+0.80
)
67.12%
(
-2.56
)
CE + CL1 93.16% (+0.96) 73.78% (+4.10)
CE + CL2 93.18% (+0.98) 71.18%
(
+1.50
)
* CE: Cross entropy loss (no regularization), Center: Center Loss
(Wen et al., 2016), CL1: Center contrastive loss (proposed), CL2:
Sample contrastive loss (proposed).
* The numbers in the bracket indicates the improvement for the
various regularization methods compared to the baseline (no
regularization).
For CIFAR-10, center contrastive loss (CL1) and
sample contrastive loss (CL2) improve test accuracy
to 93.16% (+0.96) and 93.18% (+0.98), respectively
compared to the baseline test accuracy of 92.20%.
This shows that both contrastive losses successfully
regularize the network. The improvement is much
more pronounced for CIFAR-100. The sample
contrastive loss (CL2) improves the test accuracy
from 69.68% to 71.18% (+1.50). The improvement
for center contrastive loss (CL1) is bigger where the
test accuracy improves to 73.78% (+4.1). The impact
of regularization is more significant in CIFAR-100
since it has a less samples per class compared to
CIFAR-10.
The performance of center loss (Wen et al., 2016)
is noticeably not stable. Although delivering slight
improvement for CIFAR-10 (+0.80), it is somehow
surprising to see test accuracy drop from 69.86% to
67.12% (-2.56) after applying center loss
regularization for CIFAR-100. We offer several
possible explanations. First, to reduce computational
consideration, the centers are computed on batch
samples rather than the whole data set. Since a bag
Batch Contrastive Regularization for Deep Neural Network
373

size of 2 is used in the experiments, and there is a
relatively large number of classes (100 in CIFAR-
100), the cluster centers tend to fluctuate wildly from
batch to batch. As a result, center loss regularization
may have difficulty converging. A second plausible
explanation is intra-class variability where the visual
appearance of the samples for a class may be diverse
and the assumption of a single class center may not
be a good one for general classification tasks. This
also explains why center loss (Wen et al., 2016)
manage to deliver good regularization performance
for face recognition - there is only one single visual
category (face) and the within-class visual
appearance is not diverse. In contrast, general object
classification involves multiple classes and within-
class samples are more varied.
Compared to center loss, both versions of
contrastive loss improve test accuracy. This is
apparently attributed to the negative distances which
imposes inter-class separability. As mentioned,
CIFAR-100 contains a lot of visually similar classes,
e.g., maple, oak, palm, pine and willow. By imposing
inter-class separability into the loss function, the
network will be compelled to learn cluster centers are
well separated in the embedding space. This in turn
improves generalization performance.
Effect of Network Depth. Next, we evaluate the
effect of network depth towards regularization
performance. For this experiment, we use a deeper
network namely ResNet50 and repeat the
experiments in the previous section. Table 2 shows
the test accuracies obtained from the network.
Table 2: Testing Accuracy of Batch Loss Regularization for
ResNet50 (No Pre-Training).
Method
CIFAR-10 CIFAR-100
CE
89.62% 63.50%
CE + Center 77.89%
(
-11.73
)
67.81%
(
+4.31
)
CE + CL1 86.45% (-3.17) 71.51% (+8.01)
CE + CL2 91.85% (+2.23) 71.92% (+8.42)
* CE: Cross entropy loss (no regularization), Center: Center Loss
(Wen et al., 2016), CL1: Center contrastive loss (proposed), CL2:
Sample contrastive loss (proposed).
Compared to ResNet18 (Table 1), the test
accuracy (without regularization) for ResNet50 drops
from 92.20% to 89.62% for CIFAR-10 and from
69.68% to 63.50% for CIFAR-100. This shows that
overfitting is more severe for ResNet50. As a deeper
network, ResNet50 contains around 25 million
parameters, which is more than double than that of
ResNet18 which has only around 11 million. This
makes ResNet50 more difficult to train and prone to
overfitting.
For CIFAR-10, when center loss is applied, test
performance drops sharply to 77.89%. Again, we
attribute this to an unstable batch center and
unrepresentative cluster center. For CL1, the
performance also drops but not as much. This shows
that the negative loss has offset the effect of the
positive loss. Sample contrastive loss regularization
improves test accuracy to 91.85% (+2.23). Here, we
notice that the performance of CL2 consistently
deliver better performance compared to the baseline
in all our experiments for networks of different depth
and dataset of different sizes. A decentralized method
with no notion of a class center seems to provide more
stable regularization in our case.
For CIFAR-100, all three batch regularization
techniques improves test accuracy performance
significantly. With no regularization, test accuracy is
63.50%. Both CL1 and CL2 see an improvement of
more than 8%, registering a test accuracy of 71.51%
(+8.01) and 71.92% (+8.42), respectively. This is
extremely significant performance improvement.
Again, center loss produces the least improvement. In
summary, batch contrastive loss displays good
generalization performance on a deeper network and
smaller samples.
Effect of Bag Sampling. Next, we evaluate the
effect of bag sampling. We evaluated 3 different bag
sizes: 0, 2 and 4. The experiment is conducted for
CE+CL2 on CIFAR-10. A batch size of 16 is used.
Note that when the bag size is 0, this is equivalent to
disabling bag sampling. Table 3 shows the result of
the effect of different bag size.
Table 3: Effect of Bag Size in Bag Sampling (CE+CL2).
Bag Size ResNet18 ResNet50
0
92.76% 90.70%
2
93.18% 91.85%
4
91.19%
89.84%
* CE: Cross entropy loss, CL2: sample contrastive loss.
Clearly, bag sampling improves regularization
performance for our method. The optimal bag size is
2. The test accuracy decreases when bag size
increases to 4 for both ResNet18 and ResNet50.
When the bag size increases, there are more positive
pairs and less negative pairs. As shown previously,
the performance of the positive loss (center loss) is
not stable and consequently a bigger bag size has a
negative impact on the performance of the system.
Detailed Analysis. In this section, we investigate
if the classes indeed benefit from the proposed batch
contrastive regularization. To do this, we compare the
performance of individual classes before and after
applying sample contrastive regularization (CL2).
Figure 3 shows the changes to the test accuracy after
applying CL2 on ResNet50 for CIFAR-100. Classes
NCTA 2020 - 12th International Conference on Neural Computation Theory and Applications
374

Figure 3: Changes to test accuracy for all classes after applying sample contrastive loss (CL2) of ResNet50 on the CIFAR-
100 dataset. Positive value means test accuracy improves after applying CL2 and vice versa. A huge number of classes
benefits from contrastive loss regularization. (Not all class labels are displayed in x-axis due to space constraint.
with values above the line y = 0 successfully
improve their test accuracies and vice versa. Indeed,
majority of the classes (87 out of 100) are above the
line. Out of these, 20 classes improve their accuracies
by more than 20%. This shows contrastive loss indeed
successfully regularizes the network for a wide
variety of classes.
Next, we further analyze the result for class
separability. Table 4 shows a partial confusion table
for the 5 most improved classes. Note that there are
100 test samples per class.
Table 4: Partial Confusion Table for 5 Classes without
Regularization (CE) and with Regularization (CE+CL2).
Before applying contrastive loss, these classes are
typically confused with one or two other dominant
classes. Noticeably, most are confused with hamster
and lamp most likely due to their cluttered
background. After applying the contrastive loss, the
network no longer confuses these classes.
Comparison to Weight Decay. In this section,
we compare the performance of batch contrastive loss
with weight decay (Krogh et al., 1992), or
equivalently L2 regularization. L2 is a well-trusted
technique that reduces overfitting by controlling the
network complexity by controlling the network
parameters. We repeat our experiments using L2
regularization on CIFAR10. The proposed batch loss
regularization can be additionally imposed on top of
L2. We further run our experiment with a
combination of both L2 + CL2. Table 5 shows the
result for our experiments
Table 5: Comparison with L2 Regularization on CIFAR-10
(No Pre-Training).
Metho
d
Res
N
et18 Res
N
et50
CE 92.20% 89.62%
CE + CL2 93.18% (+0.98) 91.85% (+2.23)
CE + L2 94.95% (+2.75) 94.54% (+5.33)
CE + L2 + CL2 95.32% (+3.12) 94.63% (+5.70)
* CE: Cross Entropy (no regularization), L2: weight decay (Krogh
et al., 1992)
, CL2: sample contrastive loss (proposed).
In the experiment, weight decay displays good
regularization performance and even outperforms
sample contrastive loss when considered separately.
When the two regularization techniques are fused
together, weight decay and the proposed contrastive
loss compensate each and deliver better
improvement. This shows that controlling the
network complexity directly by suppressing the
network parameter values still remains the most direct
and effective way of regularizing the network.
However, L2 regularization can benefit from
additionally imposing the contrastive loss.
Actual
Class
Prediction result
Predicted Class
CE CE+CL2
Chair
Chair 23 87
Hamster 45 0
Lamp 16 1
Lawn Mover
Lawn Mover 40 88
Hamster 45 0
Telephone
Telephone 27 72
Hamster 26 0
Lamp 18 4
Cockroach
Cockroach 42 92
Hamster 29 0
Beetle 5 3
Dinosaur
Dinosaur 44 75
Hamster 18 0
Lamp 9 0
Batch Contrastive Regularization for Deep Neural Network
375
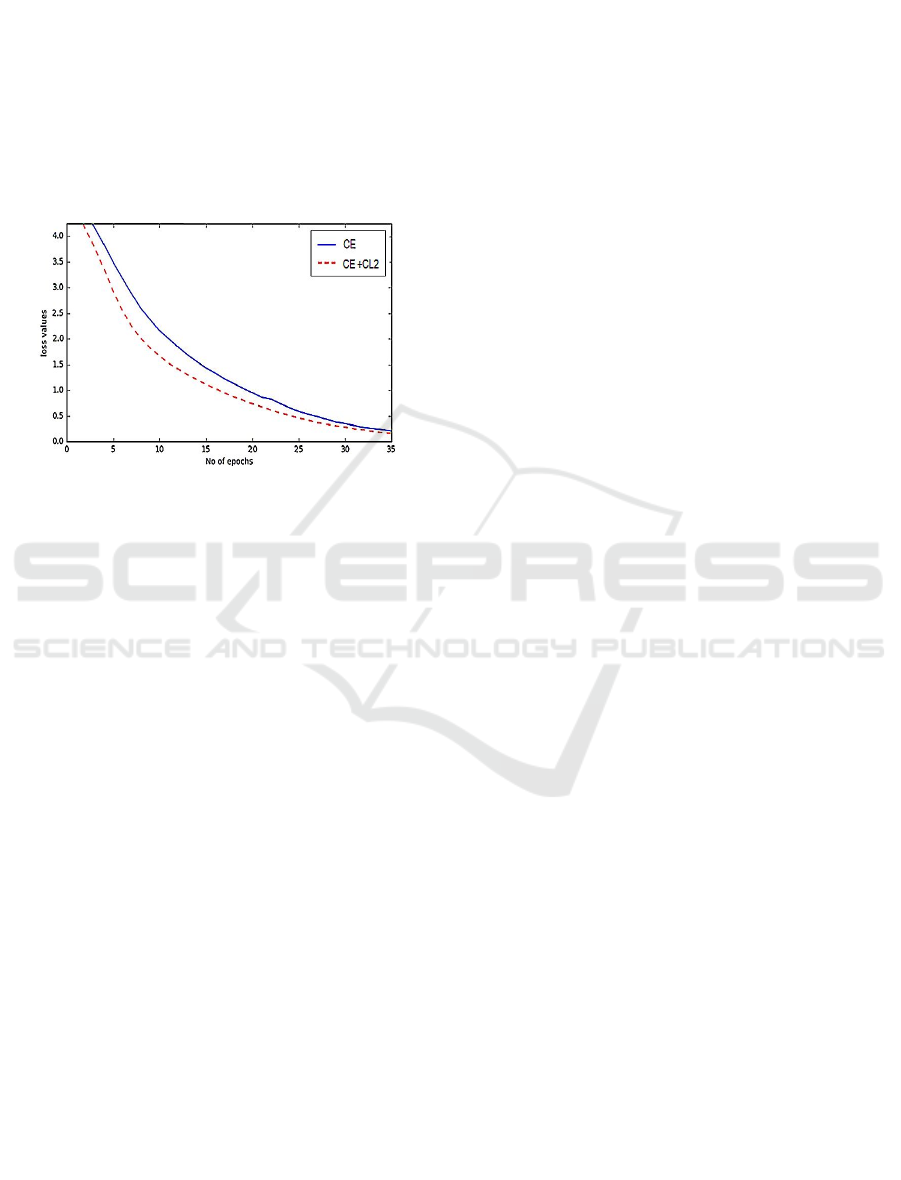
Convergence Rate. Lastly, we show the loss
function of the cross entropy (CE) loss and sample
cross entropy (CE+CL2) on ResNet50 network and
CIFAR-100 dataset to evaluate their convergence
rate. For CE + CL2, we only extract the CE
component to be plotted. Figure 4 shows the two
plots. Obviously, when the training is regulated by
sample contrastive loss, the cross entropy loss
converges faster compared to without regularization.
However, the network then converges to roughly the
same level after epoch 35. The same pattern is
observed for all other experiments.
Figure 4: The cross entropy loss for CE and CE+CL2 on
ResNet50 and CIFAR-100 dataset. For CE+CL2, only the
cross entropy loss component is used to plot the graph. With
CL2 regularization, the cross entropy converges faster.
6 CONCLUSION
Deep networks have shown impressive performance
on a number of computer vision tasks. However,
deeper networks are more susceptible to overfitting
especially when the number of samples per class are
small. In this work we introduced batch contrastive
loss to regularize the network by comparing samples
in a batch loss. Our experiments show that batch
contrastive loss has good generalization performance
especially on deeper network and dataset with smaller
number of samples per class. It also further reveals
potential issue with the positive loss for general
classification tasks which is a subject for future
investigation. In the future, we plan to perform more
evaluation to demonstrate that the technique
generalize well to other datasets as well as tasks (e.g.,
video action classification). We will also look into the
efficiency issues of contrastive loss.
ACKNOWLEDGMENT
This work was supported by a FRGS grant
(FRGS/1/2018/ICT02/UTAR/02/03) from the
Ministry of Higher Education (MOHE) of Malaysia.
REFERENCES
Chopra, S., Hadsell, R., & LeCun, Y. (2005, June).
Learning a similarity metric discriminatively, with
application to face verification. In 2005 IEEE
Computer Society Conference on Computer Vision and
Pattern Recognition (CVPR'05) (Vol. 1, pp. 539-546).
IEEE.
Cubuk, E. D., Zoph, B., Mane, D., Vasudevan, V., & Le, Q.
V. (2019). Autoaugment: Learning augmentation
strategies from data. In Proceedings of the IEEE
conference on computer vision and pattern
recognition (pp. 113-123).
DeVries, T., & Taylor, G. W. (2017). Dataset augmentation
in feature space. arXiv preprint arXiv:1702.05538.
DeVries, T., & Taylor, G. W. (2017). Improved
regularization of convolutional neural networks with
cutout. arXiv preprint arXiv:1708.04552.
Gastaldi, X. (2017). Shake-shake regularization of 3-branch
residual network. In 5th International Conference on
Learning Representations
Ghiasi, G., Lin, T. Y., & Le, Q. V. (2018). Dropblock: A
regularization method for convolutional networks.
In Advances in Neural Information Processing
Systems (pp. 10727-10737).
Han, D., Kim, J., & Kim, J. (2017). Deep pyramidal residual
networks. In Proceedings of the IEEE conference on
computer vision and pattern recognition (pp. 5927-
5935).
He, K., Zhang, X., Ren, S., & Sun, J. (2016). Deep residual
learning for image recognition. In Proceedings of the
IEEE conference on computer vision and pattern
recognition (pp. 770-778).
Hermans, A., Beyer, L., & Leibe, B. (2017). In defense of
the triplet loss for person re-identification. arXiv
preprint arXiv:1703.07737.
Horiguchi, S., Ikami, D., & Aizawa, K. (2019).
Significance of softmax-based features in comparison
to distance metric learning-based features. IEEE
transactions on pattern analysis and machine
intelligence, 42(5), 1279-1285.
Hou, S., & Wang, Z (2019, July). Weighted channel
dropout for regularization of deep convolutional neural
network. In Proceedings of the AAAI Conference on
Artificial Intelligence (Vol. 33, pp. 8425-8432).
Huang, G., Sun, Y., Liu, Z., Sedra, D., & Weinberger, K.
Q. (2016, October). Deep networks with stochastic
depth. In European conference on computer vision (pp.
646-661). Springer, Cham.
Huang, Y., Cao, X., Zhang, B., Zheng, J., & Kong, X.
(2017, April). Batch loss regularization in deep learning
method for aerial scene classification. In 2017
Integrated Communications, Navigation and
Surveillance Conference (ICNS) (pp. 3E2-1). IEEE.
Indyk, P., & Motwani, R. (1998, May). Approximate
nearest neighbors: towards removing the curse of
dimensionality. In Proceedings of the thirtieth annual
ACM symposium on Theory of computing (pp. 604-
613).
NCTA 2020 - 12th International Conference on Neural Computation Theory and Applications
376

Inoue, H. (2018). Data augmentation by pairing samples for
images classification. arXiv preprint
arXiv:1801.02929.
Khan, S. H., Hayat, M., & Porikli, F. (2019). Regularization
of deep neural networks with spectral dropout. Neural
Networks, 110, 82-90.
Koch, G., Zemel, R., & Salakhutdinov, R. (2015, July).
Siamese neural networks for one-shot image
recognition. In ICML deep learning workshop (Vol. 2).
Krizhevsky, A., Sutskever, I., & Hinton, G. E. (2012).
Imagenet classification with deep convolutional neural
networks. In Advances in neural information
processing systems (pp. 1097-1105).
Krogh, A., & Hertz, J. A. (1992). A simple weight decay
can improve generalization. In Advances in neural
information processing systems (pp. 950-957).
Larsson, G., Maire, M., & Shakhnarovich, G. (2016).
Fractalnet: Ultra-deep neural networks without
residuals. arXiv preprint arXiv:1605.07648.
Lim, S., Kim, I., Kim, T., Kim, C., & Kim, S. (2019). Fast
autoaugment. In Advances in Neural Information
Processing Systems (pp. 6665-6675).
Mitchell, C., & Hall, G. (2014). Can theories of animal
discrimination explain perceptual learning in
humans?. Psychological Bulletin, 140(1), 283.
Morgan, N., & Bourlard, H. (1990). Generalization and
parameter estimation in feedforward nets: Some
experiments. In Advances in neural information
processing systems (pp. 630-637).
Mundy, M. E., Honey, R. C., & Dwyer, D. M. (2007).
Simultaneous presentation of similar stimuli produces
perceptual learning in human picture
processing. Journal of Experimental Psychology:
Animal Behavior Processes, 33(2), 124.
Shorten, C., & Khoshgoftaar, T. M. (2019). A survey on
image data augmentation for deep learning. Journal of
Big Data, 6(1), 60.
Srivastava, N., Hinton, G., Krizhevsky, A., Sutskever, I., &
Salakhutdinov, R. (2014). Dropout: a simple way to
prevent neural networks from overfitting. The journal
of machine learning research, 15(1), 1929-1958.
Tompson, J., Goroshin, R., Jain, A., LeCun, Y., & Bregler,
C. (2015). Efficient object localization using
convolutional networks. In Proceedings of the IEEE
conference on computer vision and pattern
recognition (pp. 648-656).
Wan, L., Zeiler, M., Zhang, S., Le Cun, Y., & Fergus, R. (
2013, February). Regularization of neural networks
using dropconnect. In International conference on
machine learning (pp. 1058-1066).
Wen, Y., Zhang, K., Li, Z., & Qiao, Y. (2016, October). A
discriminative feature learning approach for deep face
recognition. In European conference on computer
vision (pp. 499-515). Springer, Cham.
Xie, S., Girshick, R., Dollár, P., Tu, Z., & He, K. (2017).
Aggregated residual transformations for deep neural
networks. In Proceedings of the IEEE conference on
computer vision and pattern recognition (pp. 1492-
1500).
Yamada, Y., Iwamura, M., & Kise, K. (2018). Shakedrop
regularization.
Zagoruyko, S., & Komodakis, N. (2016). Wide residual
networks. In Proceedings of the British Machine Vision
Conference.
Zhao, K., Xu, J., & Cheng, M. M. (2019). RegularFace:
Deep face recognition via exclusive regularization.
In Proceedings of the IEEE Conference on Computer
Vision and Pattern Recognition (pp. 1136-1144).
Zhong, Z., Zheng, L., Kang, G., Li, S., & Yang, Y. (2020).
Random Erasing Data Augmentation. In AAAI (pp.
13001-13008).
Zou, H., & Hastie, T. (2005). Regularization and variable
selection via the elastic net. Journal of the royal
statistical society: series B (statistical
methodology), 67(2), 301-320.
Batch Contrastive Regularization for Deep Neural Network
377
