
Devising Asymmetric Linguistic Hedges to Enhance the Accuracy of
NEFCLASS for Datasets with Highly Skewed Feature Values
Jamileh Yousefi
Shannon School of Business, Cape Breton University, Sydney, NS, Canada
Keywords:
Fuzzy, Discretization, NEURO-FUZZY, Classification, Skewness, NEFCLASS, EQUAL-WIDTH, MME,
Linguistic Hedge, Asymmetric Hedge.
Abstract:
This paper presents a model to address the skewness problem in the NEFCLASS classifier by devising several
novel asymmetric linguistic hedges within the classifier. NEFCLASS is a common example of the construction
of a NEURO-FUZZY system. The NEFCLASS performs increasingly poorly as data skewness increases. This
poses a challenge for the classification of biological data that commonly exhibits feature value skewness.
The objective of this paper is to device several novel asymmetric linguistic hedges to modify the shape of
membership functions, hence improving the accuracy of NEFCLASS. This study demonstrated that devising
an appropriate asymmetric linguistic hedge significantly improves the accuracy of NEFCLASS for skewed
data.
1 INTRODUCTION
NEURO-FUZZY systems are common machine learn-
ing approaches in healthcare because of their ability
to learn and formulate rules from training data and
represent the knowledge in an understandable way.
NEFCLASS is a popular NEURO-FUZZY classifier in
clinical research. The NEFCLASS classifier performs
poorly on skewed datasets (Yousefi and Hamilton-
Wright, 2016). This poses a challenge for the classi-
fication of biological data which commonly exhibits
positive skewness. Addressing skewness in medical
diagnosis systems is vital for finding rare events, such
as rare diseases (Gao et al., 2010).
This is an extension of our previous studies pub-
lished at the 9th and 11th International Joint Con-
ference on Computational Intelligence (Yousefi and
Hamilton-Wright, 2016; Yousefi et al., 2019). In the
previous paper, we performed a study to analyze the
relationship between skewness and the classification
accuracy of classifiers. The study showed that the
misclassification percentages of five examined classi-
fiers from different families, i.e., NEFCLASS, ANFIS,
BP-ANN, PD, and SVM, are significantly increased
as the level of skewness is increased in the datasets.
Also, the study indicated that the behaviour of NE-
FCLASS can dramatically change depending on the
underlying data distribution. Further analysis of the
NEFCLASS behaviour showed that the choice of dis-
cretization method affects the classification accuracy
of the NEFCLASS classifier and that this effect was
very strong in skewed datasets. The study demon-
strated that the fuzzy sets constructed by the EQUAL-
WIDTH discretization method, used in NEFCLASS, do
not reflect the data distribution. This fault resulted
in a classification accuracy that is lower for the NEF-
CLASS classifiers than for other techniques, especially
when the feature values of the training and testing
datasets exhibit significant skew. This motivated us
to use methods such as Maximum Marginal Entropy
(MME) and Class Attribute Interdependence Maxi-
mization (CAIM) which take into account the statis-
tical information of data. Our study proved that utiliz-
ing MME and CAIM discretization methods in NEF-
CLASS significantly improved the classification accu-
racy for highly skewed data (Yousefi and Hamilton-
Wright, 2016).
In this paper, we present a novel approach to
modify the shape of membership functions where
their shape resembles the skewness in the data. This
leads to minimizing the effect of bias within the data,
hence improving the accuracy of the NEFCLASS clas-
sifier for skewed datasets. NEURO-FUZZY systems
store their knowledge as linguistic values between in-
put neurons and rule layers. We hypothesized that
adding weights to the connections between features
with skewed distribution and rules increases the in-
fluence of those features on the decision making pro-
Yousefi, J.
Devising Asymmetric Linguistic Hedges to Enhance the Accuracy of NEFCLASS for Datasets with Highly Skewed Feature Values.
DOI: 10.5220/0010143103090320
In Proceedings of the 12th International Joint Conference on Computational Intelligence (IJCCI 2020), pages 309-320
ISBN: 978-989-758-475-6
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
309

cess. This motivated us to use asymmetric linguis-
tic hedges for increasing connection weights between
neurons, hence increasing the membership values of
the skewed features. We show that this novel hybrid
model based on the combination of an appropriate
discretization method and an appropriate asymmet-
ric hedge significantly improves the accuracy of NE-
FCLASS when dealing with positive skewed datasets
(Yousefi, 2018).
The model is trained on several synthetically gen-
erated datasets with different levels of feature values
skewness. Besides, we conducted a set of experiments
to evaluate the effectiveness of our approaches for
two real-world datasets, Electromyography and Wis-
consin Diagnostic Breast Cancer datasets, which are
known to have highly skewed feature values. We eval-
uated the performance of the classifiers using misclas-
sification percentages and the number of rules.
The next section of this paper contains a short re-
view of the NEFCLASS classifier, discretization meth-
ods, and linguistic hedges that will be used to mod-
ify the NEFCLASS classifier. Section 3 describes the
methodology of our study, and in section 4 the ex-
perimental results and statistical analysis are given.
Finally, conclusions are presented.
2 BACKGROUND
2.1 The NEFCLASS Classifier
NEFCLASS (Nauck et al., 1996; Nauck and Kruse,
1998; Klose et al., 1999) is a NEURO-FUZZY classi-
fier that generate fuzzy rules and tune the shape of
the membership functions to determine the correct
class label for a given input. NEFCLASS consists of
a three-layer fuzzy perceptron containing a heuristic
learning algorithm based on fuzzy error propagation.
A three-layer fuzzy perceptron has the same struc-
ture as a three-layer-feed-forward neural network, but
the weights between the input neurons and the hid-
den neurons are modelled as fuzzy sets, and the links
between hidden neurons and output neurons are un-
weighted. Fig. 1 shows a NEFCLASS model that clas-
sifies input data with two features into two output
classes by using three fuzzy sets and two fuzzy rules.
The fuzzy sets and the fuzzy rules are obtained from
the training data through a supervised learning algo-
rithm. Input features are supplied to the nodes at the
bottom of the figure. These are then fuzzified, using
a number of fuzzy sets. The sets used by a given rule
are indicated by linkages between input nodes and
rule nodes. If the same fuzzy set is used by multi-
ple rules, these links are shown passing through an
Figure 1: A NEFCLASS model with two inputs, two rules,
and two output classes. The figure extracted from (Yousefi
and Hamilton-Wright, 2016).
oval, such as the one marked “large” in Fig. 1. Rules
directly imply an output classification, so these are
shown by unweighted connections associating a rule
with a given class. Multiple rules may support the
same class, however that is not shown in this diagram.
In Fig. 2a, a set of initial fuzzy membership func-
tions describing regions of the input space are shown,
here for a two-dimensional problem in which the
fuzzy sets are based on the initial discretization pro-
duced by the EQUAL-WIDTH algorithm. As will be
demonstrated, NEFCLASS functions work best when
these regions describe regions specific to each in-
tended output class, as is shown here, and as is de-
scribed in the presentation of a similar figure in the
classic work describing this classifier (Nauck et al.,
1996, pp. 239).
As is described in the NEFCLASS overview pa-
per (Nauck and Kruse, 1998, pp. 184), a relationship
is constructed through training data to maximize the
association of the support of a single fuzzy set with a
single outcome class. This implies both that the num-
ber of fuzzy sets must match the number of outcome
classes exactly, and in addition, that there is an as-
sumption that overlapping classes will drive the fuzzy
sets to overlap as well.
Fig. 2a shows the input membership functions as
they exist before membership function tuning per-
formed by the original NEFCLASS algorithm, when
the input space is partitioned into EQUAL-WIDTH
fuzzy intervals.
Fig. 2b demonstrates that during the fuzzy set tun-
ing process, the membership function is shifted and
the support is reduced or enlarged, in order to better
match the coverage of the data points belonging to
the associated class, however as we will see later, this
process is strongly informed by the initial conditions
set up by the discretization to produce the initial fuzzy
FCTA 2020 - 12th International Conference on Fuzzy Computation Theory and Applications
310
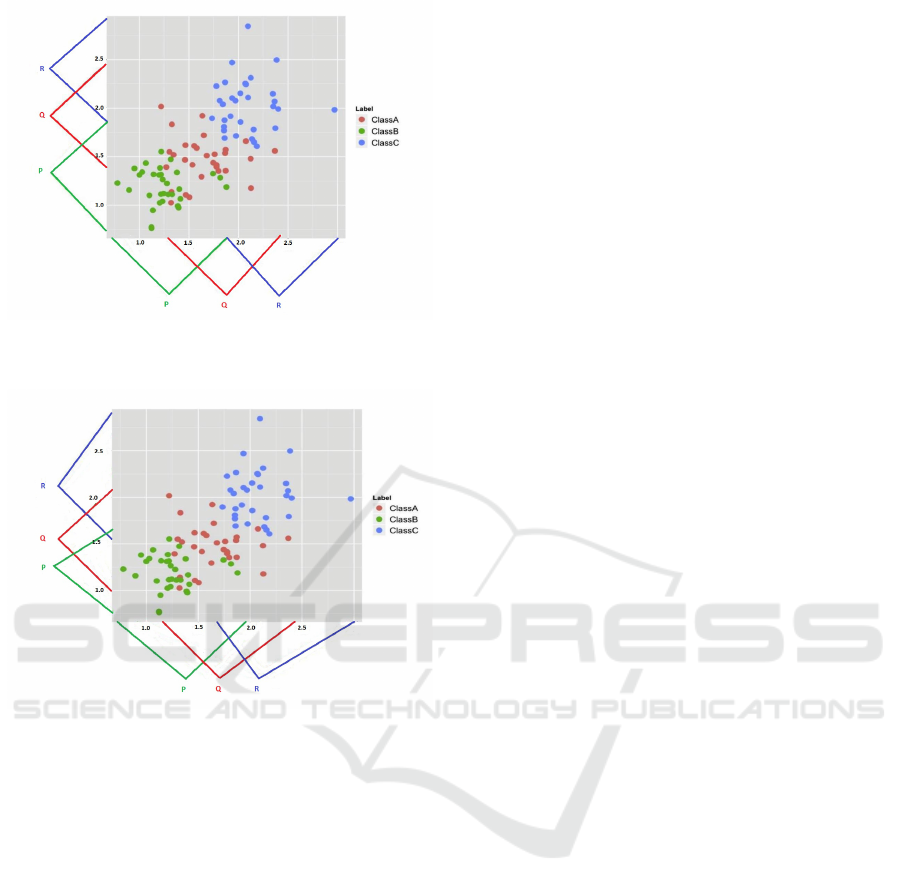
(a) Initial fuzzy set membership functions in NEFCLASS, pro-
duced using EQUAL-WIDTH discretization
(b) Results of tuning the above membership functions to bet-
ter represent class/membership function information
Figure 2: Fuzzy membership functions before and after
training data based tuning using the NEFCLASS algorithm.
The figure extracted from (Yousefi and Hamilton-Wright,
2016).
membership functions.
There are three different modes to be used for rule
selection in NEFCLASS. These modes are based on
the performance of a rule or on the coverage of the
training data. The three options for the rule selec-
tion mode presented here are Simple, Best and Best-
PerClass. The Simple rule selection chooses the first
generated rules until a predefined maximum number
of rules is achieved. The Best rule selection is an al-
gorithm that ranks the rules based on the number of
patterns associated with each rule and select the rules
from this list. The BestPerClass option is selection of
rules by creating an equal number of rules for each
class. This method uses the Best rule selection algo-
rithm to ranks the rules.
After the construction of the fuzzy rules, a fuzzy
set learning procedure is applied to the training data,
so that the membership functions are tuned to better
match the extent of the coverage of each individual
class in the training data space (Nauck et al., 1996,
pp. 239). Fuzzy membership functions will grow or
shrink, as a result, depending on the degree of ambi-
guity between sets and the dataset coverage.
2.2 Discretization
A discretization process divides a continuous numeri-
cal range into a number of covering intervals where
data falling into each discretized interval is treated
as being describable by the same nominal value in
a reduced complexity discrete event space. In fuzzy
work, such intervals are then typically used to define
the support of fuzzy sets, and the precise placement
in the interval is mapped to the degree of membership
in such a set.
In the following discussion, we describe the
EQUAL-WIDTH, MME, and CAIM discretization
methods. For example, imagine a dataset formed of
three overlapping distributions of 15 points each, as
shown with the three coloured arrangements of points
in Fig. 3. The points defining each class are shown
in a horizontal band, and the points are connected to-
gether to indicate that they are part of the same class
group. In parts 3a and 3b, the results of binning these
points with two different discretization techniques are
shown. The subfigures within Fig. 3 each show the
same data, with the green, red and blue rows of dots
(top, middle and bottom) within each figure describ-
ing the data for each class in the training data.
Fig. 3a demonstrates the partitioning using
EQUAL-WIDTH intervals. Note that the intervals
shown have different numbers of data points within
each (21, 19 and 5 in this case).
2.2.1 Marginal Maximum Entropy
Marginal Maximum Entropy based discretization
(MME) (Chau, 2001; Gokhale, 1999) divides the
dataset into a number of intervals for each feature,
where the number of points is made equal for all of
the intervals, under the assumption that the informa-
tion of each interval is expected to be equal. The in-
tervals generated by this method have an inverse rela-
tionship with the points’ density within them. Fig. 3b
shows the MME intervals for the example three-class
dataset. Note that the intervals in Fig. 3b do not
cover the same fraction of the range of values (i.e.,
the widths differ), being the most dense in regions
where there are more points. The same number of
points (15) occur in each interval. In both of these
discretization strategies, class identity is ignored, so
Devising Asymmetric Linguistic Hedges to Enhance the Accuracy of NEFCLASS for Datasets with Highly Skewed Feature Values
311
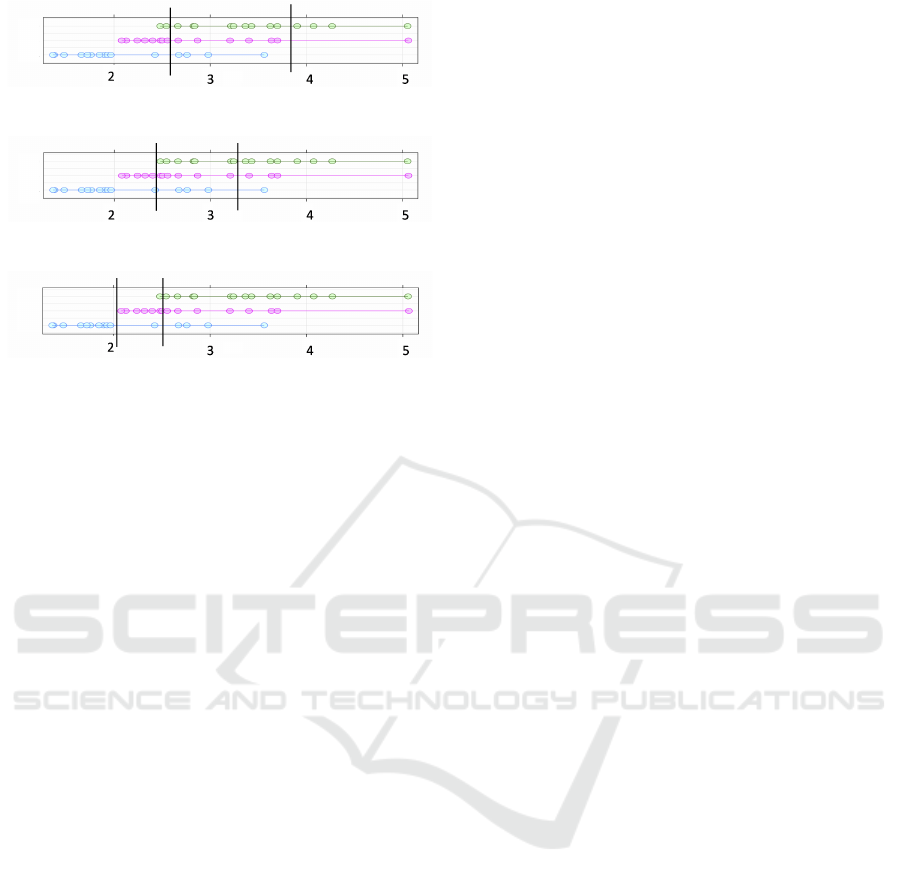
(a) EQUAL-WIDTH
(b) MME
(c) CAIM
Figure 3: Three discretization techniques result in different
intervals produced on the same three-class dataset. The fig-
ure extracted from (Yousefi and Hamilton-Wright, 2016).
there is likely no relationship between class label dis-
tribution and discretization boundary.
2.2.2 Class-Attribute Interdependence
Maximization
CAIM (class-attribute interdependence maximiza-
tion) discretizes the observed range of a feature into
a class-based number of intervals and maximizes
the inter-dependency between class and feature val-
ues (Kurgan and Cios, 2004). CAIM discretiza-
tion algorithm divides the data space into partitions,
which leads to preserve the distribution of the original
data (Kurgan and Cios, 2004), and obtain decisions
less biased to the training data.
Fig. 3c shows the three CAIM intervals for our
sample data set. Note how the placement of the dis-
cretization boundaries is closely related to the points
where the densest portion of the data for a particular
class begins or ends.
2.3 The Modified NEFCLASS Classifier
using Alternative Discretization
Methods
The fuzzy sets constructed by the EQUAL-WIDTH
discretization method do not reflect the data distri-
bution. Modification of NEFCLASS through alterna-
tive discretization methods takes into account an im-
portant difference between the discretization methods
and their effects on the classifier’s accuracy. In our
previous study (Yousefi and Hamilton-Wright, 2016),
we implemented a modified NEFCLASS classifier,
embedded with a choice of two alternative discretiza-
tion methods, MME and CAIM, here are called NEF-
MME and NEF-CAIM. We showed that NEF-MME
and NEF-CAIM achieved greater classification ac-
curacy when dealing with skewed distributed data.
Since the accuracy of NEF-MME and NEF-CAIM
were significantly higher than NEFCLASS, we used
only NEF-MME and NEF-CAIM in this study, and
NEFCLASS was discarded.
2.4 Linguistic Hedges
Membership function parameters can be defined and
tuned in a number of ways. For one, the shape of
membership functions can be slightly modified by
using linguistic hedges (Zadeh, 1965). Linguistic
hedges are fuzzy operators that increase or decrease
the membership degrees of the associated fuzzy sets.
A new membership function, for example, can be
obtained by applying a power or square root to the
existing membership function. In other words, lin-
guistic hedges modify the meaning of a membership
function. For example, the linguistic hedge “very”
changes the meaning of the linguistic variable “tall”
to “very tall”. This approach allows a composite
linguistic variable to be generated from the primary
terms (Huynh et al., 2002).
Using linguistic hedges allows for the descrip-
tion of more complex relationships among variables,
hence, leading to an improvement in the efficiently of
a fuzzy system. Using linguistic hedges helps to tune
the membership functions, which can lead to an in-
crease in the classification accuracy. Zadeh (Zadeh,
1965) categorized linguistic hedges into three differ-
ent operations: concentration, dilation, and contrast
intensification. The concentration and dilation hedges
that used in this work are defined as follow.
• Concentration Hedge
Applying a concentration hedge to a fuzzy set P
decreases the degree of the membership function
of x in the fuzzy set P while retaining the same
support. The hedge operation of Con(µ
P
(x)) is
defined as :
Con(µ
P
(x)) = µ
α
P
(x);α > 1. (1)
Based on the concentration definition, some
hedge operations, such as “more”, “much more”,
“very”, “extremely”, and “absolutely” can be de-
fined by specifying the values of α in the equa-
tion 1 as 1.25, 1.5, 2, 3, and 4, respectively.
• Dilation Hedge
Applying dilation hedge to a fuzzy set P increases
the degree of the membership function of x in the
FCTA 2020 - 12th International Conference on Fuzzy Computation Theory and Applications
312

Hedge Mathematical Expression Graphical Representation
VERY Con(µ
P
(x)) = µ
2
P
(x)
ABSOLUTELY Con(µ
P
(x)) = µ
4
P
(x)
FAIRLY Dil(µ
P
(x)) = µ
1
2
P
(x)
Figure 4: Examples of linguistic hedges.
fuzzy set P while retaining the same support. The
dilation hedge operation of Dil(µ
P
(x)) is defined
as:
Dil(µ
P
(x)) = µ
α
P
(x);0 < α < 1. (2)
Based on the dilation definition, some hedge
operations, such as “fairly”, “somewhat”, and
“slightly’’, can be defined by specifying the val-
ues of α in the equation 2 as
1
2
,
1
3
and
1
4
, respec-
tively.
Figure 4 shows three examples of concentration
and dilation hedges.
In this work, we build several asymmetric lin-
guistic hedges, based on the concentration and dila-
tion, and incorporate them into a neuro-fuzzy system
to address the skewness problem. In total six lin-
guistic terms, including VERY, EXTREMELY, ABSO-
LUTELY, FAIRLY, SOMEWHAT, and SLIGHTLY will
be used to build the asymmetric hedges. These hedges
are discussed in more detail in Section 3.
3 METHODOLOGY
In this section, we present the system design, the ex-
perimental setup, the classifiers’ configurations, the
evaluation measures, and the datasets that are used in
our experiments.
3.1 System Design
In this section we describe the modifications made
to the NEFCLASS design. NEFCLASS consists of the
following major components (the new design compo-
nents are denoted as (modified NEFCLASS) :
• Initialization
– Initialization of fuzzy sets using one of the
three options:
∗ EQUAL-WIDTH (This is the only choice pro-
vided by the original NEFCLASS)
∗ Marginal Maximum Entropy (MME)
(modified NEFCLASS)
∗ Class Attribute Interdependent maximization
(CAIM) (modified NEFCLASS)
– Initialization of fuzzy rules
• Rule learning
• Fuzzy sets learning
• Fuzzy sets tuning by linguistic hedges (modified
NEFCLASS)
The detailed of the above steps are discussed as
follows:
Step1: Initialization
• Initialization of fuzzy sets (modified NEF-
CLASS): our proposed modified NEFCLASS
begins by selecting one of three possible types
of discretization methods, namely, EQUAL-
WIDTH, MME, and CAIM methods.
• Initialization of fuzzy rules: after the initializa-
tion of the fuzzy sets, the initialization of fuzzy
rules takes place. The fuzzy rules’ antecedents
are completed by adding fuzzy sets for each
feature where triangular membership functions
are used.
Devising Asymmetric Linguistic Hedges to Enhance the Accuracy of NEFCLASS for Datasets with Highly Skewed Feature Values
313

Step 2: Rule Learning
After constructing the initial fuzzy sets and the
antecedents of fuzzy rules, the fuzzy rule learn-
ing procedure is applied to the training data. At
this phase, the activation of a rule unit and the ac-
tivation of the output unit are computed for each
pattern.
Step 3: Fuzzy Sets Learning
After the construction of the fuzzy rules, a fuzzy
sets learning procedure is applied to the train-
ing data such that the membership functions are
tuned to better match the extent of the coverage of
each individual class in the training data space, as
shown in Figure 2.1.
Step 4: Fuzzy Sets Tuning by Asymmetric Lin-
guistic Hedges (modified NEFCLASS)
At this phase, a linguistic hedge can be selected to
adjust the membership functions. The objective of
this step is to increase or decrease the membership
functions using linguistic hedges. The linguistic
hedge parameter takes the type of the hedge. The
parameter can be set to NONE or one of the 11
asymmetric linguistic hedges provided. The effect
of the various settings of the parameter is the main
focus of this work.
3.2 Improving Accuracy by
Asymmetric Linguistic Hedges
NEURO-FUZZY systems stores their knowledge as lin-
guistic values between neurons of input and rule lay-
ers (Bargiela and Pedrycz, 2001, p. 276). Adding
weights to the connections between features and their
associated rules increases the influence of those fea-
tures on the decision making process. This motivates
us to use asymmetric linguistic hedges for increasing
connection weights between neurons, hence increas-
ing the membership values of the skewed features.
We argue that asymmetric hedges can be used to ex-
press the information distribution and bias member-
ship functions toward bias within data. We hypothe-
size that if the shape of a membership function resem-
bles the skewness in the data, the information distri-
bution will be similar to data distribution; it will min-
imize the effect of bias within data, thus improving
the accuracy of the classifier. In particular, we ex-
amine the treatment of positively skewed data. How-
ever, this approach can be extended and modified for
treatment of negative skewness. Our design modifica-
tion aims to improve the accuracy of NEFCLASS, uses
asymmetric linguistic hedges to tune and optimize the
membership functions. Hence, the objective of this
paper is to answer the research question as follows:
Does devising asymmetric linguistic hedges im-
prove the accuracy of the NEFCLASS classifier for
skewed datasets?
• Null Hypothesis: There will be no significant de-
crease in the misclassification percentage of the
NEFCLASS classifier after applying the asymmet-
ric hedges.
• Alternative Hypothesis: Applying asymmetric
linguistic hedges to the membership functions sig-
nificantly reduces the misclassification percentage
of NEFCLASS for skewed data.
Our asymmetric hedges apply different hedges
to each side of a membership function. The effect
of asymmetric hedges results in the skewing of a
membership function in a positive or negative direc-
tion (Bargiela and Pedrycz, 2001). Table 1 displays
the name, the mathematical operation, and the type
of the 11 asymmetric hedges that are defined for our
experiments. The name assigned to each asymmetric
hedge has been chosen to reflect the type of operation
and the amount of change that are applied to each side
of the membership functions.
Five asymmetric hedges are defined to change
the right side of a membership function, while the
left side remains unchanged. For example, the BIG-
CONCAVERIGHT hedge applies ABSOLUTELY to the
right side of the membership function, which results
in a big decrease (concavity) on the right side, while
the left side remains unchanged. The other six hedges
apply a concentration operation on one side and a
dilation operation on the other side. For example,
BIG-CONVEXLEFT-CONCAVERIGHT hedge applies
SLIGHTLY to the left side, and ABSOLUTELY to the
right side of the triangular fuzzy set, which results in
a big increase of the membership function in the left
side (convexity), and a big decrease in the right side
(concavity).
In this work we will use the terms MF
(2)
, MF
(3)
,
MF
(4)
, MF
(
1
2
)
, MF
(
1
3
)
, and MF
(
1
4
)
to denote VERY,
EXTREMELY, ABSOLUTELY, FAIRLY, SOMEWHAT,
and SLIGHTLY, respectively. Note that in tables and
figures, linguistic hedges have been replaced with
these terms for the sake of clarity of the operations
and to save space.
3.3 Synthesized Datasets
Three synthesized datasets were used for experi-
ments. The synthesized datasets were produced
by randomly generating numbers following the F-
DISTRIBUTION with different degrees of freedom
FCTA 2020 - 12th International Conference on Fuzzy Computation Theory and Applications
314

Table 1: List of asymmetric hedges used in the modified NEFCLASS.
Asymmetric Hedge Operation Left Side Hedge Right Side Hedge
NONE * NONE NONE NONE
SMALL-CONCAVERIGHT NONE-MF
(2)
NONE VERY
BIG-CONCAVERIGHT NONE-MF
(4)
NONE ABSOLUTELY
SMALL-CONVEXRIGHT NONE-MF
(
1
2
)
NONE FAIRLY
MODERATE-CONVEXRIGHT NONE-MF
(
1
3
)
NONE SOMEWHAT
BIG-CONVEXRIGHT NONE-MF
(
1
4
)
NONE SLIGHTLY
SMALL-CONCAVELEFT-CONVEXRIGHT MF
(2)
-MF
(
1
2
)
VERY FAIRLY
SMALL-CONVEXLEFT-CONCAVERIGHT MF
(
1
2
)
-MF
(2)
FAIRLY VERY
BIG-CONVEXLEFT-CONCAVERIGHT MF
(
1
4
)
-MF
(4)
SLIGHTLY ABSOLUTELY
BIG-CONCAVELEFT-CONVEXRIGHT MF
(4)
-MF
(
1
4
)
ABSOLUTELY SLIGHTLY
MODERATE-CONVEXLEFT-CONCAVERIGHT MF
(
1
3
)
-MF
(3)
SOMEWHAT EXTREMELY
MODERATE-CONCAVELEFT-CONVEXRIGHT MF
(3)
-MF
(
1
3
)
EXTREMELY SOMEWHAT
* No hedge is applied. This is the default.
chosen to control skew. The F-DISTRIBUTION (Na-
trella, 2003) has been chosen as the synthesis
model because the degree of skew within an F-
DISTRIBUTION is controlled by the pairs of degrees
of freedom specified as a pair of distribution control
parameters. This allows for a spectrum of skewed
data distributions to be constructed. We designed
the datasets to present different levels of skewness
with increasing skew levels. Three pairs of degrees
of freedom parameters have been used to generate
datasets with different levels of skewness, including
low, medium, and high-skewed feature values. After
initial experiments datasets with degrees of freedom
(100, 100) was chosen to provide data close to a nor-
mal distribution, (100, 20) provides moderate skew,
and (35, 8) provides high skew.
A synthesized dataset consisting of 1000 ran-
domly generated examples consisting of four-feature
(W , X, Y , Z). F-DISTRIBUTION data for each of
three classes was created. The three classes (ClassA,
ClassB and ClassC) overlap, and are skewed in the
same direction. We have taken care to ensure that
all datasets used have a similar degree of overlap,
and same degree of variability. The size of datasets
were designed to explore the effect of skewness when
enough data is available to clearly ascertain dataset
properties. Ten-fold cross validation was used to di-
vide each dataset into training (2700) and testing (300
point) sets in which an equal number of each class is
represented. This method provides a better estimate
of median performance, as well as a measure of vari-
ability.
Table 2 shows the minimum and maximum values
of skewness for each feature based on 10 jackknife-
based datasets (i.e., dataset LOW-100,100, with the
degree of skewness between 0.582 and 0.907, is
low-skewed and dataset HIGH-35,8, with the de-
gree of skewness between 1.289 and 3.764, is highly
skewed). The high variability of the skewness values
shown in Table 2 is due to the fact that these values
are average, minimum, and maximum over three class
labels for each feature.
3.4 Real-world Datasets
To show the pertinence of this analysis to real-world
data problems, we ran all tests on two publicly avail-
able datasets: the Wisconsin Diagnostic Breast Can-
cer Dataset (WBDC) from UCI Machine Learning
Repository, and a clinically applicable world of quan-
titative electromyography (EMG). The characteristic
information of these datasets is presented in the fol-
lowing sections.
• Electromyography Dataset (EMG): QEMG is
the study of the electrical potentials observed
from contracting muscles as seen through the
framework of quantitative measurement. QEMG
is used in research and diagnostic study (Stashuk
and Brown, 2002). EMG datasets are known to
contain features with highly skewed value distri-
butions (Enoka and Fuglevand, 2001).
The EMG dataset used here contains seven fea-
tures of MUP templates (Amplitude, Duration,
Phases, Turns, AAR, SizeIndex, and MeanMU-
Voltage) observed on 791 examples representing
three classes (Myopathy, Neuropathy, Healthy),
collected through a number of contractions, and
used in previous work (Varga et al., 2014).
• Wisconsin Diagnostic Breast Cancer Dataset
(WDBC) : The Wisconsin Diagnostic Breast Can-
cer Dataset (WDBC) dataset contains 30 features
Devising Asymmetric Linguistic Hedges to Enhance the Accuracy of NEFCLASS for Datasets with Highly Skewed Feature Values
315

Table 2: Summary of skewness for the F-DISTRIBUTED and CIRCULAR-UNIFORM-DISTRIBUTED datasets.
Dataset
Minimum skewness Maximum skewness
W X Y Z W X Y Z
UNIFORM −0.020 −0.050 −0.048 −0.060 −0.006 0.074 0.017 0.093
LOW-100,100 0.582 0.432 0.443 0.679 0.799 0.618 0.536 0.907
MED-100,20 1.354 1.178 1.198 1.403 1.947 2.144 1.547 1.721
HIGH-35,8 1.289 2.038 2.506 2.746 2.247 3.081 3.534 3.764
and two classes (benign and malignant). The
WDBC dataset, observed from 569 examples,
contains a class distribution of 357 benign and 212
malignant. Features have been extracted from a
digitized image of a fine needle aspirate of a breast
mass. This dataset is characterized by high di-
mensionality, very precise values, and almost no
missing data. In examining the normality of the
features, we found that seven features were highly
positively skewed.
4 RESULTS AND DISCUSSIONS
This section presents the results and discussion. Sec-
tion 4.1 presents the results and discussions for exper-
iments using the synthesized data. Section 4.2 gives
the results for the real-world data.
4.1 Experiments using Synthesized Data
In Table 1, all of the full names of the hedges are
given. As these names are quite long, and the
strength of the operation is apparent from the value
of the power, the mathematical terms are used here
for brevity. Table 3 show the misclassification per-
centages (as median± IQR) obtained by NEF-MME
and NEF-CAIM classifiers using the 11 asymmet-
ric hedges, as well as without application of a hedge
(shown as NONE in the table). Comparisons between
classifiers were performed as follows: for each dis-
cretization method and each dataset, results obtained
without applying hedge (shown as NONE) were com-
pared with those obtained from the application of
each hedge. We conducted one-tailed M-W-W tests
at a 0.05 significance level.
• Comparison of Misclassification Percentages:
Table 4 reports the M-W-W test results. Note that
we reported results only for those hedges, listed in
Table 3, whose application led to a significant im-
provement in accuracy. The P-VALUES obtained
for non significant results were greater than or
equal to 0.23 (not shown in the table).
As shown in Table 4, in the case of medium and
high skewed data, the test yielded a main ef-
fect for applying four asymmetric hedges, such
that the misclassification percentages were signif-
icantly lower for hedges with a root of 3 or 4 on
the right side. These four hedges are shown as
grey shade in Table 3. In the case of HIGH-35,8, a
smaller interquartile range in the misclassification
percentage was achieved for these four hedges,
compared to NONE. Since there is no significant
improvement in the accuracy of the low-skewed
data, there is no apparent penalty when applying
the hedge; however, as skew increases the utility
of the hedge becomes significant.
Hedges with higher roots increase membership
functions more than those with lower roots.
Hence, hedges with root 3 or 4 cause a higher
degree of skewness in membership functions
than hedges with root 2. For example, the
changes in membership functions by “SOME-
WHAT” and “SLIGHTLY” are more pronounced
than the change by “FAIRLY”. In particular, the
hedges with roots of 3 or 4 on the right side,
i.e., NONE-MF
(
1
4
)
, NONE-MF
(
1
3
)
, MF
(3)
-MF
(
1
3
)
and MF
(4)
-MF
(
1
4
)
, cause a greater increase in
the membership value of inputs presented in the
right side of the triangular membership functions.
Hence, assigning a higher membership value puts
more emphasis on inputs presented on the right
side of the membership functions. which leads to
the inclusion of more information in the decision-
making process.
As shown in table 3, the results obtained using
the NONE-MF
(
1
4
)
and MF
(4)
-MF
(
1
4
)
hedges were
similar. Given the fact that these two hedges
have different operators on the left side, the sim-
ilarity in their obtained accuracy suggests that
applying MF
(
1
4
)
to the right side of the mem-
bership function could be the main reason for
the increase in accuracy. As shown in the ta-
ble, results obtained using the NONE-MF
(
1
3
)
and
MF
(3)
-MF
(
1
3
)
hedges provides further evidence
to support this suggestion. Furthermore, the re-
sults show that hedges with concentration opera-
tor in the right side, i.e., NONE-MF
(4)
, MF
(
1
3
)
-
MF
(3)
, and MF
(
1
4
)
-MF
(4)
did not improve accu-
racy, when data is positively skewed (see also Ta-
FCTA 2020 - 12th International Conference on Fuzzy Computation Theory and Applications
316
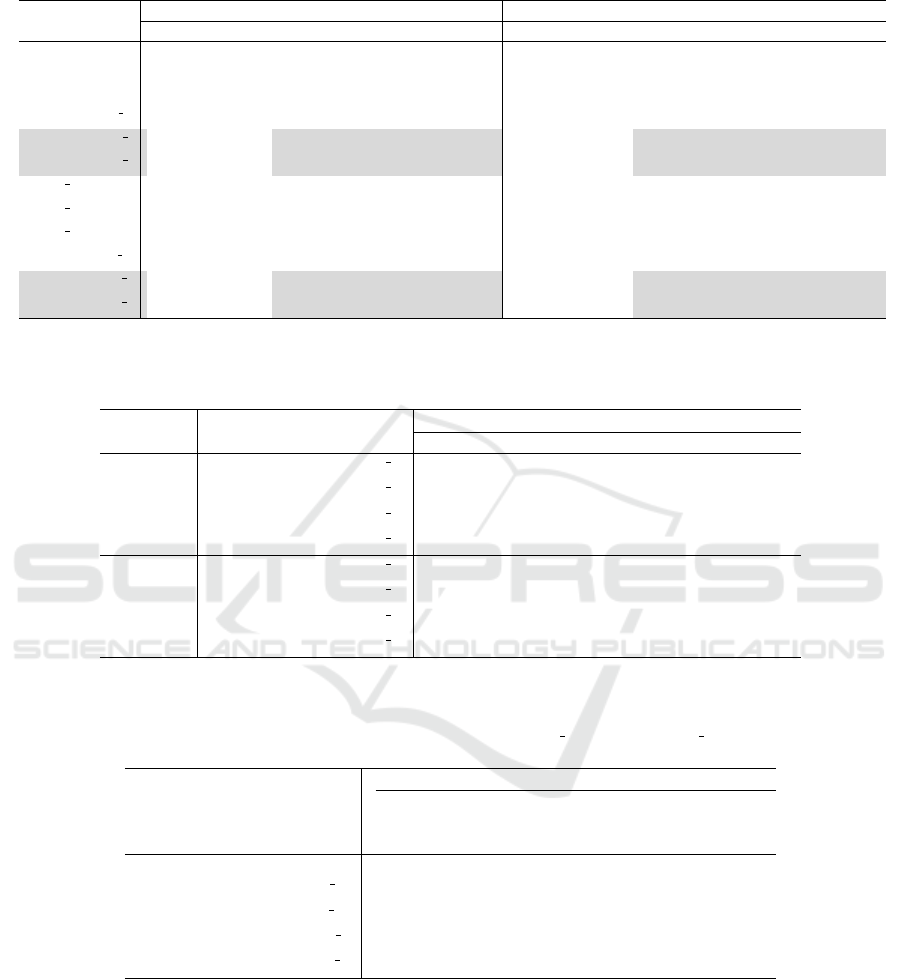
Table 3: Misclassification percentages (Median ± IQR) obtained from NEF-MME and NEF-CAIM with and without the
application of hedges.
NEF-MME NEF-CAIM
Hedge LOW-100,100 MED-100,20 HIGH-35,8 LOW-100,100 MED-100,20 HIGH-35,8
NONE 26.00 ± 1.75 34.16 ± 2.66 42.50 ± 4.25 24.33 ± 4.17 34.16 ± 2.60 41.67 ± 4.33
NONE-MF
(2)
32.30 ± 1.90 48.23 ± 2.90 52.83 ± 4.10 30.67 ± 2.08 48.43 ± 18.58 54.26 ± 12.08
NONE-MF
(4)
26.67 ± 0.66 37.80 ± 1.50 48.00 ± 7.20 26.00 ± 1.60 38.50 ± 0.92 46.00 ± 4.70
NONE-MF
(
1
2
)
28.65 ± 2.42 39.50 ± 5.83 51.16 ± 3.58 27.16 ± 3.66 40.00 ± 4.75 50.35 ± 9.25
NONE-MF
(
1
3
)
28.50 ± 1.16 27.66 ± 3.83 33.50 ± 2.68 28.67 ± 0.90 27.17± 2.60 34.50 ± 2.17
NONE-MF
(
1
4
)
28.33 ± 1.15 27.66 ± 3.80 33.50 ± 2.67 28.00 ± 1.25 27.00 ± 3.25 34.50 ± 2.17
MF
(
1
2
)
-MF
(2)
26.00 ± 1.75 34.16 ± 2.66 42.50 ± 4.25 24.13 ± 4.16 34.30 ± 2.58 41.67 ± 4.16
MF
(
1
3
)
-MF
(3)
37.83 ± 5.40 64.83 ± 1.58 59.50 ± 5.83 33.00 ± 10.50 64.15 ± 0.70 67.33 ± 24.33
MF
(
1
4
)
-MF
(4)
26.50 ± 1.00 33.83 ± 2.40 41.65 ± 3.90 25.00 ± 3.40 33.67 ± 2.75 41.67 ± 2.66
MF
(2)
-MF
(
1
2
)
26.00 ± 1.75 34.16 ± 2.70 42.50 ± 4.25 24.13 ± 4.16 34.30 ± 2.58 41.67 ± 4.16
MF
(3)
-MF
(
1
3
)
28.50 ± 1.16 27.66 ± 3.83 33.50 ± 2.68 28.67 ± 0.90 27.17± 2.60 34.50 ± 2.17
MF
(4)
-MF
(
1
4
)
28.33 ± 1.16 27.66 ± 3.83 33.68 ± 2.66 27.83 ± 2.50 27.17 ± 3.12 34.50 ± 2.17
Table 4: Results of the M-W-W test to compare the misclassification percentages obtained by NEF-MME and NEF-CAIM
between NONE and each hedge.
Classifier Hege1 vs. Hedge2 Dataset
LOW-100,100 MED-100,20 HIGH-35,8
NEF-MME
NONE vs. NONE-MF
(
1
4
)
0.98 *** ***
NONE vs. MF
(4)
-MF
(
1
4
)
0.98 *** ***
NONE vs. NONE-MF
(
1
3
)
0.98 *** ***
NONE vs. MF
(3)
-MF
(
1
3
)
0.98 *** ***
NEF-CAIM
NONE vs. NONE-MF
(
1
4
)
0.98 *** ***
NONE vs. MF
(4)
-MF
(
1
4
)
0.98 *** ***
NONE vs. NONE-MF
(
1
3
)
0.98 *** ***
NONE vs. MF
(3)
-MF
(
1
3
)
0.98 *** ***
*** significant at 95% confidence (p < .05)
Table 5: Results of the M-W-W test to compare the misclassification percentages between each pair of datasets for all baseline
classifiers and the NEFCLASS classifiers with employment of the NONE-MF
(
1
4
)
and MF
(4)
-MF
(
1
4
)
hedges.
Classifier Datasets
LOW-100,100 LOW-100,100 MED-100,20
vs. vs. vs.
MED-100,20 HIGH-35,8 HIGH-35,8
NEF-ORG *** *** .93
NEF-MME-NONE-MF
(
1
4
)
.57 *** ***
NEF-MME-MF
(4)
-MF
(
1
4
)
.57 *** ***
NEF-CAIM-NONE-MF
(
1
4
)
.84 *** ***
NEF-CAIM-MF
(4)
-MF
(
1
4
)
1.00 *** ***
*** significant at 95% confidence (p < .05)
ble 3). The reinforcing of a concentration operator
to a membership function results in the reduction
of magnitude to the grade of membership in which
it is relatively large for those with low member-
ship. This leads to the exclusion of those points
presented on the skewed side from the decision
making process.
In light of these findings, it can be concluded that
applying dilation hedges with the root of 3 or
4 to the right side of membership functions sig-
nificantly improved accuracy, when data is posi-
tively skewed. In contrast, applying concentration
hedges to the right side of the membership func-
tions did not have a positive effect on accuracy.
Therefore, a higher accuracy can be achieved by
Devising Asymmetric Linguistic Hedges to Enhance the Accuracy of NEFCLASS for Datasets with Highly Skewed Feature Values
317

means of an appropriate choice of a hedge. We
suggest that it is beneficial to consider choosing
an appropriate hedge based on the amount and di-
rection of skew.
• Comparison of Number of Rules: the test did
not identify a significant increase in the num-
ber of rules obtained by each hedge compared to
NONE. Hence, the reductions in the misclassi-
fication percentages by using the MF
(3)
-MF
(
1
3
)
,
MF
(4)
-MF
(
1
4
)
, NONE-MF
(
1
3
)
, and NONE-MF
(
1
4
)
hedges were not accompanied by any significant
increase in the number of rules.
We conclude that combining MME or CAIM
with an appropriate asymmetric hedge, such
as NONE-MF
(
1
4
)
, when the hedge was applied
to the side of the direction of the skew, led to a
significant improvement in accuracy over the original
NEFCLASS classifier.
4.2 Experiments using Real-world Data
In this section, we assess the performance of these
classifiers using real-world data. The EMG and
WDBC datasets were used for training and testing
the best performed modified classifiers, NEF-MME-
NONE-MF
(
1
4
)
and NEF-MME-MF
(4)
-MF
(
1
4
)
.
4.2.1 Experiments on the EMG Dataset
Table 6 depicts the misclassification percentages (as
median± IQR) and the number of rules (as median±
IQR). Table 7 gives the test results.
• Comparison of Misclassification Percentages:
As shown in Table 7, the test revealed that the mis-
classification percentages significantly decreased
by applying the combination of the MME dis-
cretization method and the NONE-MF
(
1
4
)
asym-
metric hedge.
• Comparison of Number of Rules: Additionally,
the test showed that the higher accuracy of NEF-
MME-NONE-MF
(
1
4
)
was achieved with a signif-
icantly lower number of rules compared to that of
NEF-ORG.
4.2.2 Experiments on the WDBC Dataset
Table 8 depicts the misclassification percentages (as
median± IQR) and the number of rules (as median±
IQR). Table 9 reports the results of the M-W-W test.
• Comparison of Misclassification Percentages:
as shown in Table 9, the test indicated a signifi-
cant decrease in the misclassification percentages
obtained by NEF-MME-NONE-MF
(
1
4
)
compared
to NEF-ORG.
• Comparison of Number of Rules: the test did
not identify a significant decrease in the num-
ber of rules obtained by applying an asymmetric
hedge.
We conclude that the accuracy of the NEFCLASS
classifiers, when trained by the EMG and WDBC
datasets, was significantly improved by the combina-
tion of MME discretization method with the NONE-
MF
(
1
4
)
hedge. Also, in the case of EMG data, the
higher accuracy of NEF-MME-NONE-MF
(
1
4
)
was
achieved with considerably lower number of rules.
However, it is notable that the application of the
MF
(4)
-MF
(
1
4
)
hedge did not show a significant pos-
itive effect on the accuracy. The presence of fea-
tures with negative and zero skewed distribution in the
EMG and WDBC datas might be the cause of a lower
accuracy for the NEF-MME-MF
(4)
-MF
(
1
4
)
classifier
of which applies a hedge to the both sides of a mem-
bership function. Therefore, we suggest choosing an
appropriate hedge based on the amount and direction
of skew in data.
5 CONCLUSIONS
Devising the asymmetric hedges with an appropriate
dilation hedge significantly improved the accuracy of
the NEFCLASS classifiers. Combining MME with
an appropriate asymmetric hedge, such as NONE-
MF
(
1
4
)
, when the hedge was applied to the side of
the direction of the skew, led to a significant improve-
ment in accuracy over the original NEFCLASS clas-
sifier. This study revealed that if the shape of the
membership function resembles the skewness in the
data, then it minimizes the effect of bias within the
data. Hence, this improves the accuracy of the classi-
fier. Therefore, we suggest using asymmetric hedges
to express the information distribution in the domain
of fuzzy logic. Higher classification accuracy can be
achieved using a proper choice of a hedge. We sug-
gest that it is fruitful to consider choosing an appro-
priate hedge based on the skew amount and direction.
This study demonstrates that applying asymmetric
hedges to the membership functions not only resulted
in improving classification accuracy but also led to
the building of a more robust classifier when trained
by skewed data. This improvement of accuracy was
achieved without increasing the number of rules.
Employment of asymmetric hedges is not limited
to the NEFCLASS neuro-fuzzy classifier; it can be ap-
plied to any application where fuzzy logic is used.
FCTA 2020 - 12th International Conference on Fuzzy Computation Theory and Applications
318
Table 6: Misclassification percentages (Median ± IQR) and number of rules (Median ± IQR) obtained from applying asym-
metric hedges using the EMG dataset.
Classifier Misclassification Percentage Number Of rules
NEF-ORG 54.18 ± 28.00 149.00 ± 4.00
NEF-MME-NONE-MF
(
1
4
)
33.00 ± 35.00 88.00 ± 7.00
NEF-MME-MF
(4)
-MF
(
1
4
)
52.00 ± 28.00 167.00 ± 14.00
Table 7: Results of one-tailed M-W-W to compare the results with and without using asymmetric hedges for the EMG dataset.
Classifier Misclassification Percentage Number Of rules
NEF-ORG vs. NEF-MME-NONE-MF
(
1
4
)
*** .01
NEF-ORG vs. NEF-MME-MF
(4)
-MF
(
1
4
)
.29 .95
*** significant at 95% confidence (p < .05)
Table 8: Misclassification percentages (Median ± IQR) and the number of rules (Median ± IQR) obtained from applying
asymmetric hedges using the WDBC dataset.
Classifier Misclassification Percentage Number Of rules
NEF-ORG 17.39 ±5.00 77.00 ± 89.00
NEF-MME-NONE-MF
(
1
4
)
12.50 ± 5.00 157.00 ± 7.00
NEF-MME-MF
(4)
-MF
(
1
4
)
17.80 ± 8.75 80.00 ± 10.00
Table 9: Results of one-tailed M-W-W to compare the results with and without using asymmetric hedges for the WDBC
dataset.
Classifier Misclassification Percentage Number Of rules
NEF-ORG vs. NEF-MME-NONE-MF
(
1
4
)
*** .98
NEF-ORG vs. NEF-MME-MF
(4)
-MF
(
1
4
)
.19 .40
*** significant at 95% confidence (p < .05)
This method can be applied in areas such as health-
care, security, and finance where datasets are skewed.
In this work, we examined positively skewed data.
However, this approach can be extended and modified
to address negative skewness.
ACKNOWLEDGEMENTS
The authors gratefully acknowledge the support of
NSERC, the National Sciences and Engineering Re-
search Council of Canada, for ongoing grant sup-
port. The authors would like to thank Dr. Andrew
Hamilton-Wright who initiated the idea, and for his
earlier funding and guidance on this research. The
authors are also grateful to Dr. Rozita Dara and Dr.
Charlie Obimbo for their valuable contributions to
this work.
REFERENCES
Bargiela, A. and Pedrycz, W. (2001). Granular Computing:
An Emerging Paradigm. Springer.
Chau, T. (2001). Marginal maximum entropy partition-
ing yields asymptotically consistent probability den-
sity functions. IEEE Transactions on Pattern Analysis
and Machine Intelligence, 23(4):414–417.
Enoka, R. and Fuglevand, A. (2001). Motor unit physiol-
ogy: some unresolved issues. Muscle & Nerve, 24:4–
17.
Gao, J., Hu, W., Li, W., Zhang, Z., and Wu, O. (2010).
Local outlier detection based on kernel regression.
In Proceedings of the 10th International Conference
on Pattern Recognition, pages 585–588, Washington,
DC, USA. EEE Computer Society.
Gokhale, D. V. (1999). On joint and conditional entropies.
Entropy, 1(2):21–24.
Huynh, V., Ho, T., and Nakamori, Y. (2002). A paramet-
ric representation of linguistic hedges in zadeh’s fuzzy
logic. International Journal of Approximate Reason-
ing, 30:203–223.
Klose, A., N
¨
urnberger, A., and Nauck, D. (1999). Im-
proved NEFCLASS pruning techniques applied to a
real world domain. In Proceedings Neuronale Netze
in der Anwendung, University of Magdeburg. NN’99.
Devising Asymmetric Linguistic Hedges to Enhance the Accuracy of NEFCLASS for Datasets with Highly Skewed Feature Values
319

Kurgan, L. A. and Cios, K. (2004). CAIM discretization al-
gorithm. IEEE Transactions on Knowledge and Data
Engineering, 16:145–153.
Natrella, M. (2003). NIST SEMATECH eHandbook of Sta-
tistical Methods. NIST.
Nauck, D., Klawonn, F., and Kruse, R. (1996). Neuro-Fuzzy
Systems. Wiley.
Nauck, D. and Kruse, R. (1998). NEFCLASS-X – a soft
computing tool to build readable fuzzy classifiers. BT
Technology Journal, 16(3):180–190.
Stashuk, D. W. and Brown, W. F. (2002). Quantitative elec-
tromyography. In Brown, W. F., Bolton, C. F., and
Aminoff, M. J., editors, Neuromuscular Function and
Disease, volume 1, pages 311–348. W.B. Saunders,
Philadelphia.
Varga, R., Matheson, S. M., and Hamilton-Wright, A.
(2014). Aggregate features in multi-sample classifi-
cation problems. IEEE Trans. Biomed. Health Inf.,
99:1.
Yousefi, J. (2018). Improved NEFCLASS for Datasets with
Skewed Feature Values. PhD thesis, University of
Guelph.
Yousefi, J. and Hamilton-Wright, A. (2016). Classifica-
tion confusion within nefclass caused by feature value
skewness in multi-dimensional datasets. In Proceed-
ings of the 9
th
International Joint Conference on Com-
putational Intelligence, Porto. IJCCI-2016.
Yousefi, J., Hamilton-Wright, A., and Obimbo, C. (2019).
A synergistic approach to enhance the accuracy-
interpretability trade-off of the neclass classifier for
skewed data distribution. In Proceedings of the 11
th
International Joint Conference on Computational In-
telligence, Viena. IJCCI-2019.
Zadeh, L. A. (1965). Fuzzy sets. Information and Control,
8:338–353.
FCTA 2020 - 12th International Conference on Fuzzy Computation Theory and Applications
320
