A Structured Approach to Modifying Successful Heuristics

Simon P. Martin

1 a

, Matthew J. Craven

2 b

and John R. Woodward

3 c

Brook, Isle of Wight, PO30 4EU, U.K.

Centre for Mathematical Sciences, University of Plymouth, Drake Circus, Plymouth PL4 8AA, U.K.

Computer Science, Queen Mary University of London, Mile End Road, London E1 4FZ, U.K.

Keywords:

Heuristic, Gadget, Approximation Algorithm, Optimisation Problem.

Abstract:

In some cases, heuristics may be transferred easily between different optimisation problems. This is the case

if these problems are equivalent or dual (e.g., maximum clique and maximum independent set) or have similar

objective functions. However, the link between problems can further be deﬁned by the constraints that deﬁne

them. This reﬁning can be achieved by organising constraints into families and translating between them

using gadgets. If two problems are in the same constraint family, the gadgets tell us how to map from one

problem to another and which constraints are modiﬁed. This helps better understand a problem through its

constraints and how best to use domain speciﬁc heuristics. In this position paper, we argue that this allows

us to understand how to map between heuristics developed for one problem to heuristics for another problem,

giving an example of how this might be achieved.

1 INTRODUCTION

Karp reductions show that if a problem can be re-

duced to a known NP-complete problem, then it

too must be NP-complete (Karp, 1972). Such NP-

complete problems are commonly solved with meta-

heuristics (Krawiec et al., 2018), of which there many

approaches (e.g., genetic algorithm, ant colony opti-

misation, particle swarm optimisation). The number

of such approaches is growing dramatically.

orensen, 2015) examined this plethora of meta-

heuristic approaches and identiﬁed the need for an

underlying theory, observing that ostensibly distinct

metaheuristics in fact share many key components.

The author recommended that the design of meta-

heuristics be performed with regard to problem struc-

ture. This problem structure thus informs the design

of components of metaheuristics, too. Seeds of such

an approach were originally suggested by the work of

(Cook, 1971), commonly referred to as Cook-Levin,

who show that any problem in NP can be written as

a collection of clauses in conjunctive normal form

(SAT).

(Karp, 1972) showed that, supplementary to

https://orcid.org/0000-0003-1399-860X

https://orcid.org/0000-0001-9522-6173

https://orcid.org/0000-0002-2093-8990

Cook-Levin, there is a structure to NP-complete prob-

lems in general, ﬁnding reductions between his fa-

mous 21 NP-complete problems. These transitive re-

ductions may be seen as fundamental relations be-

tween structures of each of the problems. Since

then, there have been thousands of NP-complete prob-

lems produced and, since they are all NP-complete,

there are fundamental reductions or relations between

the structures of these problems. Combined with

the work of Cook-Levin, this backs up the work

of (S

orensen, 2015), suggesting that there is a def-

inite structure between effective algorithms for NP-

complete problems. This also holds for NP-hard op-

timisation variants of these problems. Furthermore,

this suggests that some extension of reductions be-

tween problems may be produced between those algo-

rithms. This means that a fundamental view of meta-

heuristic frameworks is possible, reducing (or map-

ping) between metaheuristic components. Finally,

(Trevisan et al., 2000) showed that by writing prob-

lems as linear programs, it is possible to construct op-

timal gadgets (in polynomial time) via reducing be-

tween the constraints (or families of constraints) of

these linear programs.

220

Martin, S., Craven, M. and Woodward, J.

A Structured Approach to Modifying Successful Heuristics.

DOI: 10.5220/0010143702200225

In Proceedings of the 12th International Joint Conference on Computational Intelligence (IJCCI 2020), pages 220-225

ISBN: 978-989-758-475-6

1.1 Motivation

As there are many existing algorithms that are not

designed for a speciﬁc problem (e.g., NSGA-II,

SPEA2), and many existing NP-complete/hard prob-

lems, our approach aims to build a bridge between

existing theoretical work done on NP-complete prob-

lems and existing empirical work done by the meta-

heuristics community.

It could be argued that a well-designed meta-

heuristic is designed for a problem. For exam-

ple, the well-known Lin-Kernighan heuristic (Lin and

Kernighan, 1973) proves effective for the Travelling

Salesman Problem (TSP) since it explicitly treats the

topology of the problem. As another example, hill-

climbers are excellent at solving unimodal problems.

Our aim is to allow metaheuristics which are proved

to work well on one problem to be ported to other

problems via gadget transformations. Thus we wish

to make use of knowledge we already have about

mapping between problems and use this knowledge

to make new algorithms.

Further, we may interpret the following points

from (Cook, 1971):

1. A problem in NP is a problem that is only solv-

able by a polynomial-time algorithm that runs on

a Nondeterministic Turing Machine (NTM);

2. They show how to implement any algorithm on an

NTM as a Boolean formula;

3. Since any problem can encoded as an Boolean for-

mula, any algorithm can thus be encoded as an

Boolean formula.

In other words, we do not concentrate on the prob-

lems in NP - instead, we should be focusing on the

algorithms that solve them. We are motivated by this

approach of focusing on the algorithms and using the

mapping to exploit these algorithms.

We can exploit existing theory which effectively

provides a mapping (reﬁnement of problem con-

straints) between problems. We build on this by sug-

gesting that an algorithm that performs well on one

domain can then be applied to another domain via

such a mapping between problems. Thus we wish to

take a promising algorithm from one domain and en-

able it to be applied to a new domain (which hopefully

will also be well performing), hoping to avoid the is-

sue of the ever increasing number of metaheuristics,

as mentioned by (S

orensen, 2015). Building on Tre-

visan (Trevisan et al., 2000), we show how a heuristic

appropriate for a given problem can be modiﬁed to be

used on another different problem.

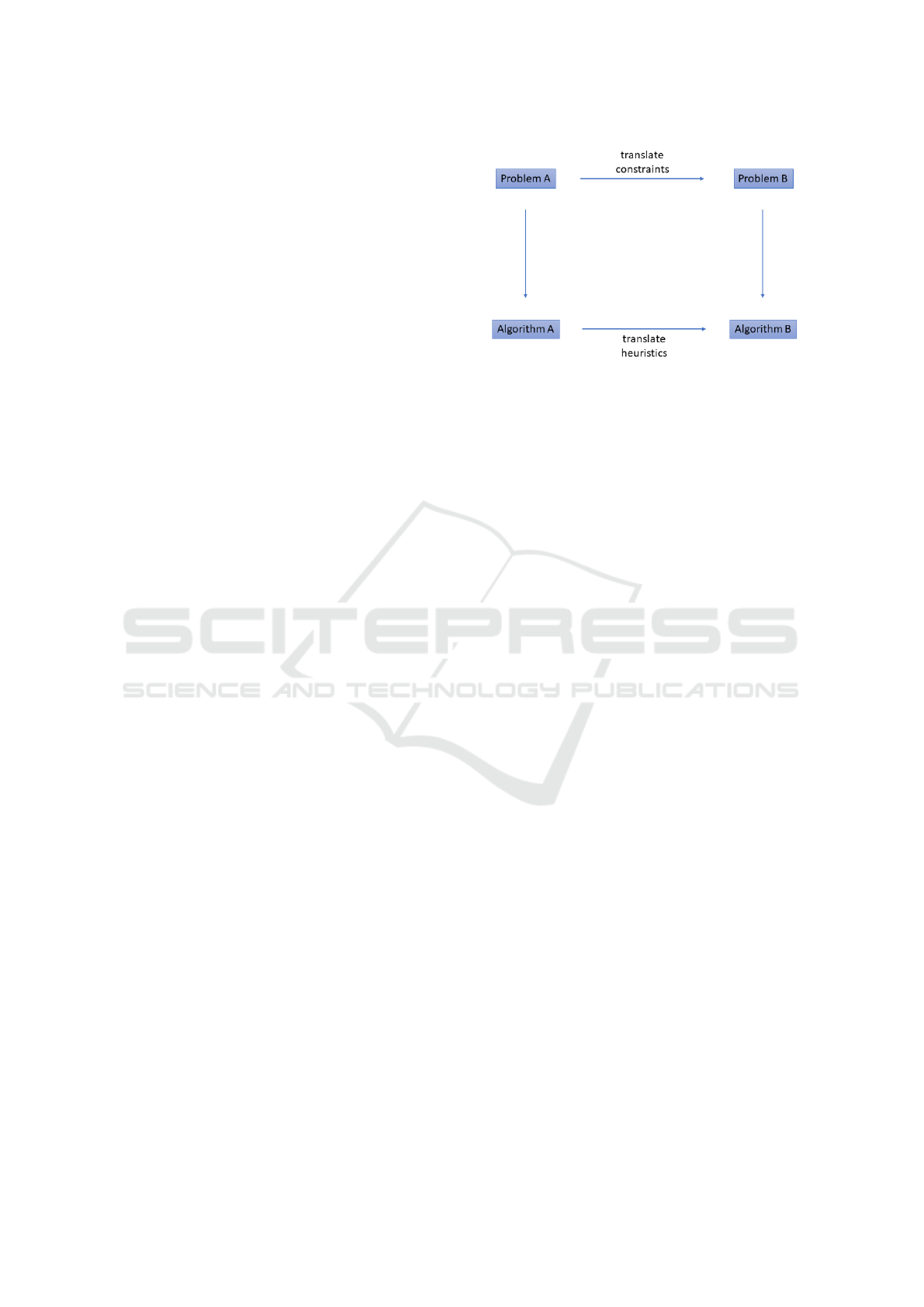
Figure 1: A diagrammatic explanation of our approach.

1.2 Contribution of the Paper

The contribution of this position paper is that the work

of the aforementioned authors may be built upon to

provide a method of producing mappings between

heuristics. A visual explanation of our work is repre-

sented by Figure 1. Algorithms A and B denote algo-

rithms that solve problems A and B respectively. The

arrow between problems A and B denotes the trans-

lation of integer programming (IP) constraints from

problem A to B via a gadget. That is, we translate

modify or reﬁne the constraints of problem A into

those for problem B. Through an analogous approach

to the gadget via judicious simulation of problem B

in Algorithm A, we create Algorithm B. Note that,

of course, this makes no guarantees of the efﬁcacy of

the new algorithm (Algorithm B) on problem B. The

vertical arrows denote that algorithm A is applied to

problem A and algorithm B is applied to problem B.

Our contribution is the concept and our further work

will be the implementation.

Note that, in this position paper, we use the words

’algorithm’ and ’heuristic’ interchangeably. Also im-

portant to note that we do not make any guarantees of

the efﬁciency of the new algorithm in this work; the

implementation of such algorithms, based upon the

ideas given in this work, is classiﬁed in the realms of

further work.

This remainder of the paper is structured as fol-

lows. In Section 2 we introduce the technical back-

ground to our approach, examining constraints and

their families, and then lead into gadgets. In Sec-

tion 3 we detail our approach to constructing maps

between algorithms by utilising existing gadgets de-

ﬁned between constraint families deﬁning problems.

We end the work in Section 4, giving a conclusion and

an overview of further work.

A Structured Approach to Modifying Successful Heuristics

221

2 BACKGROUND

In this section, we introduce the technical background

to the work. Firstly, constraints that deﬁne problems

and the families of constraints arising are examined,

after which gadgets are brieﬂy deﬁned. Subsequently,

an example of an existing gadget from Vertex Cover

to Hamiltonian Circuit (both NP-complete problems)

is given. Finally, these constraint families are parti-

tioned into two types, the idea being gadgets to map

between constraints in a particular type of constraint

family are practical.

2.1 Constraint Families and Gadgets

In this paper, we write deﬁnitions of NP problems as

IPs since it is straightforward to understand the con-

straints that deﬁne the problem. Constraint families

are essentially a common language which allow us to

show some problems are reﬁnements of other prob-

lems. Further, (Trevisan et al., 2000) goes on to de-

ﬁne constraint functions and constraint families, on

which gadgets act, in terms of IPs. We adopt the com-

mon notation of B = {0, 1}. A constraint function is,

by (Trevisan et al., 2000), simply a Boolean function

f : B

→ B. A constraint family is a set of constraint

functions, and a constraint is then an assignment of a

constraint function.

A gadget is an algorithm that transforms the con-

straints of one problem to another in polynomial time.

Thus gadgets may be seen as methods for deﬁning

one problem in terms of another, only possible be-

cause of inherent constraint-wise similarities between

those problems. Further, a gadget is, by (Trevisan

et al., 2000, p. 2074), “a ﬁnite combinatorial struc-

ture which translates a given constraint of one opti-

mization problem into a set of constraints of a second

optimization problem.” Thus, gadgets not only pre-

serve (NP-)complexity, but structure also.

Historically, creating gadgets was, at the very least

difﬁcult and somewhat contrived, until the work of

(Trevisan et al., 2000), using a linear programming

(LP) implementation to ﬁnd optimal gadgets in poly-

nomial time. There is an extensive literature on gad-

gets (e.g., the works (Cai et al., 2012; Garey and

Johnson, 1978; Papadimitriou and Yannakakis, 1988;

Sipser, 2012; Skiena, 2008)). There is also a small

amount of work on using gadgets to assist algorithms;

e.g., the work of (Letchford and Vu, 2019) on using

gadgets to generate cutting planes for algorithms on

the Stable Set and Clique Partitioning problems.

2.2 An Example of an Existing Gadget:

Vertex Cover to Hamiltonian

Circuit

Reductions involve the modiﬁcation of the constraints

of one problem to encompass the constraints of an-

other problem. We know that the Minimum Vertex

Cover problem (i.e., ﬁnding the minimum set of ver-

tices that touch every edge of a graph) is NP-complete

via the famous reduction of its decision variant Vertex

Cover from 3SAT (Skiena, 2008, pp. 333). We also

recall that there is a reduction from Vertex Cover to

Hamiltonian Circuit by manipulation of their respec-

tive IPs. Assume G = (V, E, k) is an undirected graph,

where V is the set of vertices in the graph, E ⊆ V ×V

is the set of edges in the graph and k is the size of the

vertex cover.

For each vertex v ∈ V we have a variable x

. We

interpret the variable as chosen to be included in a

vertex cover if x

= 1, and otherwise x

= 0. The de-

cision version of this problem is to return 1 if there is

a vertex cover of size k, or 0 otherwise. The optimisa-

tion version of the problem is to minimise the number

of vertices in the cover. As an IP, this is written as:

min

∑

v∈V

(minimize total cost)

subject to

+ x

≥ 1 for all e = {u, v} ∈ E (1)

∈ {0, 1} for all v ∈ V. (2)

The Hamiltonian Circuit problem is to decide

whether, given a graph G(V, E, k), there is a circuit

of size k of vertices, each with degree 2, where each

vertex is visited only once. Here, k is the required cy-

cle size. Constraint (1) refers to covering every edge

in the graph, whereas constraint (2) states that every

vertex is either in or not in the cover.

Let x

i j

∈ {0, 1} be a variable representing an edge,

with value 1 if the edge is part of the route connecting

and v

, and 0 otherwise. Let c

i j

be the distance (un-

der some appropriate metric) between vertices i and

j. The following gives the well-known Miller-Tucker-

Zemlin formulation of the TSP (Miller et al., 1960):

min

∑

i=1

∑

j6=i, j=1

i j

(minimise total distance)

subject to the following constraints:

i j

∈ {0, 1} i, j = 1, . . . , n (3)

∈ Z i = 2, . . . , n (4)

ECTA 2020 - 12th International Conference on Evolutionary Computation Theory and Applications

222

∑

i=1,i6= j

i j

= 1 j = 1, . . . , n (5)

∑

j=1, j6=i

i j

= 1 i = 1, . . . , n (6)

− u

+ nx

i j

≤ n − 1 1 < i 6= j ≤ n. (7)

0 ≤ u

≤ n − 1 1 < i ≤ n (8)

Constraint (7) is the subtour constraint, designed

to ensure that a tour does not break into at least two

subtours (the vertices clearly cannot cross but edges,

of course, may). Note that there are other formula-

tions of the TSP that are possible (Langevin et al.,

1990; Cheung, 2005; Sawik, 2016).

The well-known gadget of (Skiena, 2008) maps

Vertex Cover to Hamiltonian Circuit. The gadget con-

verts the instance of Vertex Cover into one of Hamil-

tonian Circuit. The process involves turning the undi-

rected graph of the source problem into the digraph

of the target problem. The edge gadget turns an undi-

rected edge into a directed edge. The digraph of the

target problem is then a chain of successive edge gad-

gets governed by the vertices originally connected to-

gether in the vertex cover. In terms of constraints,

the edge gadget converts constraint (1) in the Vertex

Cover IP, and maps it to constraints (5) and (6) of the

Hamiltonian Circuit IP formulation.

We consider Vertex Cover and Hamiltonian Cir-

cuit to be part of the constraint family that we call

allocation, where an algorithm allocates a vertex if it

lies on the vertex cover or route.

2.3 Constraint Families: Allocation and

Partition

The work of (Trevisan et al., 2000) discussed con-

straint families with respect to deﬁning approxima-

tion algorithms. They used polynomial time reduc-

tions to deﬁne constraint families and showed how

they could be used to help ﬁnd new approximation

algorithms. In this work, we study reductions using

gadgets to show how they reﬁne or redeﬁne the con-

straints of one problem to encompass the constraints

of another. In this way, they do not just preserve

complexity from one problem to another, but prob-

lem structure (i.e., IP constraints) also. It is in this

way gadgets can show how one problem is related to

another in the context of constraint families.

Graphs are used to express combinatorial optimi-

sation problems. The vertices simply represent “ob-

jects”, but the edges have a more complex role to play;

edges have different interpretations depending on the

problem. Let us compare three examples.

1. in Vertex Cover, an edge from one vertex to an-

other vertex (assuming one vertex is in the cover

set) tells us that the other vertex is covered;

2. in Graph Colouring, the edge tells us that each

vertex (connected by the edge) must be a differ-

ent colour; and

3. in Hamiltonian Circuit the edge tells us that this

edge is part of the route.

The constraints tell us how to interpret and deal

with the edges for each type of problem. In other

words, vertices typically have a simple interpretation,

i.e., “objects” in the problem, while edges are inter-

preted as the “relationship between objects”, and give

meaning to the different problems (i.e., expressed by

the constraints). The meaning of a graph in terms of

the problem being expressed originates from the inter-

pretation of the edges, and not the vertices, and this is

why focusing on the constraints is fundamentally im-

portant.

We have called the constraint family containing

3SAT, Vertex Cover and Hamiltonian Circuit alloca-

tion because the constraints cause the algorithm to al-

locate vertices with a certain property to a result set.

The allocation constraint family essentially means us-

ing an edge to represent relations between elements of

the source problem.

However, when this is not the case, this leads us

to another constraint family we call partition. This

involves using an edge to represent that two objects

have no relation. In other words, we must parti-

tion a result set rather than allocate elements to one.

The constraint family then represents those prob-

lems which involve partitioning or colouring sets, or

the search for independent objects or subgraphs with

given properties. Two examples of problems in this

constraint family are 3-Colour, where we partition the

vertices into three sets (each set corresponding to a

different colour), and Subset Sum, where we partition

into two sets (where one of the sets has a given tar-

get sum). Again, we can deﬁne this constraint family

as we know there are reductions between problems

in the constraint family (Garey and Johnson, 1979).

In this way, the types of algorithms effective on prob-

lems from each type of constraint family may be anal-

ogously partitioned, and mapping between algorithms

of a given type is possible because the key operations

of the algorithm on each problem are essentially the

same. The next section gives our proposed approach.

A Structured Approach to Modifying Successful Heuristics

223

3 OUR PROPOSED APPROACH

3.1 Introduction

The ﬁeld of metaheuristics has suffered in the past few

years by an overwhelming number of unexplained al-

gorithms. We believe to progress the ﬁeld we need

fewer, but better understood, algorithms. We propose

a method of taking an algorithm designed with in-

sights into one problem, and then making that algo-

rithm applicable to a different problem type by us-

ing gadgets to map between the constraint classes of

problems. This mapping is effectively a mapping be-

tween an existing algorithm and a new algorithm (see

Figure 1).

3.2 Steps in Approach

The proposed approach involves the following steps.

1. Identify a successful heuristic on a speciﬁc do-

main (e.g., Lin-Kernighan on the TSP). We call

this heuristic the source algorithm and the prob-

lem the source problem;

2. Either identify an existing gadget from the ex-

isting research literature, or design a new gad-

get which maps between the constraints of source

problem and the target problem (e.g., a gadget

mapping from TSP to Minimum Vertex Cover);

3. Then apply the existing source algorithm to the

problem which has been translated from the target

problem to the source problem.

This mapping process, in effect, gives us a new al-

gorithm acting on a different problem to which it was

intended by exploiting the mapping provided by the

gadget. The gadget directly maps between the con-

straints of problems and indirectly maps between al-

gorithms.

3.3 An Example of the Approach

We discuss a practical example of how this transfor-

mation might be achieved. We take a Vertex Cover

problem such as one of the benchmark problems

found at (Xu, 2014). We can then create an algo-

rithm based on the gadget described in Section 2.2,

and show how the Vertex Cover instance is trans-

formed into a tour and solved accordingly. As such,

this problem could be solved using a well-known TSP

solver such as the Lin-Kernighan algorithm (Lin and

Kernighan, 1973).

The gadget in Section 2.2 is an example of a poly-

nomial time algorithm which maps one problem to

another problem. It does not directly transform one

algorithm into another. Rather, it shows how the con-

straints of one problem may be reﬁned to the con-

straints of another. To do this we need to make a

number of observations. A Vertex Cover graph has

predeﬁned edges and as such will have leaves that do

not lead to other edges. It might also have highly in-

terconnected subgraphs, which means there will be

internal loops.

This means the gadget described shows how a so-

lution to a Vertex Cover problem can also be a solu-

tion to Hamiltonian Circuit problem at the same time.

If we look at constraint (1) of the Vertex Cover IP

and constraints (5) and (6) of the Hamiltonian Cir-

cuit IP, we can see how the two Hamiltonian Circuit

constraints are reﬁnements of the Vertex Cover con-

straint. That is, an edge in a Vertex Cover can have

at most two vertices in a cover set. As a brief exam-

ple, take an edge from vertex i to vertex j in a Vertex

Cover graph. This can be represented as a route from

i to j if only one vertex of the edge is in the cover. If

both vertices are in the cover we route from i to j and

then j to i.

From this observation we can suggest a method

for solving Vertex Cover using an algorithm which is

designed to solve Hamiltonian circuits. This might

be efﬁcacious as Hamiltonian Circuit and TSP prob-

lems have received a lot of attention by researchers

and there are many algorithms that ﬁnd good solutions

to these types of problems. This is because construc-

tive heuristics tell us something about the solution and

the process by which we arrive at a solution. Let us

deﬁne a {0, 1}-adjacency matrix where the value 0 in-

dicates the absence of an edge from i to j, while the

value 1 indicates the presence of an edge. We can

modify a well-known algorithm for solving the ver-

tex cover problem. Let C =

0 be the cover set and let

E be the set of all edges in the graph G. Then while

E 6=

0 pick an arbitrary edge (u, v) and put both ver-

tices in the cover. Then remove all edges incident to

those two vertices. Repeat until the set E is empty.

We can modify this algorithm to produce a Hamilto-

nian Circuit by noticing that the edges (u, v) in the

Vertex Cover algorithm can be seen as edges that are

visited in both directions in any circuit, i.e., (i, j) and

( j, i). The edges incident to these edges are of the

type where they are visited only once in a Hamilto-

nian circuit. The next section concludes the paper.

4 CONCLUSION

This position paper has presented an approach for

modiﬁcation of a given heuristic acting on one prob-

ECTA 2020 - 12th International Conference on Evolutionary Computation Theory and Applications

224

lem to be applicable on another problem, where the

two problems are connected by a gadget. An exist-

ing gadget between Vertex Cover and Hamiltonian

Circuit was detailed, after which constraint families

were covered. These constraint families are vital to

the “translatability” between IP formulations of prob-

lems. Subsequently, our proposed approach was in-

troduced, using speciﬁcally the detailed gadget to re-

ﬁne the constraints from Vertex Cover to Hamiltonian

Circuit. This then applies naturally to the optimisa-

tion versions of these two problems: Minimum Ver-

tex Cover and the TSP. This clearly suggests further

avenues of research with respect to implementation of

the approach, experimentation and future generalisa-

tions.

What we are proposing here is a way to transfer

between algorithms in order to bring about meaning-

ful comparisons. Constraint classes and their respec-

tive gadgets allow us to translate from one problem to

another and preserve underlying problem structure. It

is this preserved problem structure we wish the new

algorithm to be able to exploit. By representing prob-

lems as IPs, we can see which constraints need to be

modiﬁed when transforming between problems. They

also show us how to modify algorithms for solving

one problem into algorithms to solve another. This

observation is fundamental to our argument. The ap-

proach is useful since we can use it to modify exist-

ing algorithms intended for one domain, and therefore

design “new” heuristics which are applied to a differ-

ent domain (see Figure 1 for a graphical interpreta-

tion). This approach goes some way to addressing

the concerns of (S

orensen, 2015). Our outlook, then,

is a framework in which we can take algorithms de-

signed for one problem, and meaningfully compare

them with algorithms designed for another problem.

ACKNOWLEDGEMENTS

The authors should like to thank Queen Mary Uni-

versity of London and the University of Plymouth for

their generous hospitality when writing this paper. Fi-

nally, the authors thank the anonymous referees for

their suggestions which helped improve the work.

REFERENCES

Cai, J.-Y., Kowalczyk, M., and Williams, T. (2012). Gad-

gets and anti-gadgets leading to a complexity di-

chotomy. In Proceedings of the 3rd Innovations in

Theoretical Computer Science Conference, ITCS ’12,

pages 452–467, New York, NY, USA. ACM.

Cheung, K. K. (2005). On Lov

asz–Schrijver lift-

and-project procedures on the Dantzig–Fulkerson–

Johnson relaxation of the tsp. SIAM Journal on Opti-

mization, 16(2):380–399.

Cook, S. A. (1971). The complexity of theorem-proving

procedures. In Proceedings of the Third Annual ACM

Symposium on Theory of Computing, pages 151–158.

ACM.

Garey, M. R. and Johnson, D. S. (1978). “Strong” np-

completeness results: Motivation, examples, and im-

plications. J. ACM, 25(3):499–508.

Garey, M. R. and Johnson, D. S. (1979). Computers and in-

tractability: a guide to the theory of NP-completeness.

W. H. Freeman & Co., New York, NY, USA.

Karp, R. M. (1972). Reducibility among combinatorial

problems. Complexity of Computer Computations,

pages 85–103.

Krawiec, K., Simons, C., Swan, J., and Woodward, J.

(2018). Metaheuristic design patterns: new perspec-

tives for larger-scale search architectures. In Hand-

book of Research on Emergent Applications of Opti-

mization Algorithms, pages 1–36. IGI Global.

Langevin, A., Soumis, F., and Desrosiers, J. (1990). Classi-

ﬁcation of travelling salesman problem formulations.

Operations Research Letters, 9(2):127–132.

Letchford, A. N. and Vu, A. N. (2019). Facets from gadgets.

Mathematical Programming, pages 1–18.

Lin, S. and Kernighan, B. W. (1973). An effective heuristic

algorithm for the traveling-salesman problem. Opera-

tions research, 21(2):498–516.

Miller, C. E., Tucker, A. W., and Zemlin, R. A. (1960). In-

teger programming formulation of traveling salesman

problems. J. ACM, 7(4):326–329.

Papadimitriou, C. and Yannakakis, M. (1988). Optimiza-

tion, approximation, and complexity classes. In Pro-

ceedings of the Twentieth Annual ACM Symposium

on Theory of Computing, STOC ’88, pages 229–234,

New York, NY, USA. ACM.

Sawik, T. (2016). A note on the miller-tucker-zemlin model

for the asymmetric traveling salesman problem. Bul-

letin of the Polish Academy of Sciences. Technical Sci-

ences, 64(3).

Sipser, M. (2012). Introduction to the Theory of Computa-

tion. Cengage Learning.

Skiena, S. S. (2008). The algorithm design manual.

Springer.

orensen, K. (2015). Metaheuristics — the metaphor ex-

posed. International Transactions in Operational Re-

search, 22(1):3–18.

Trevisan, L., Sorkin, G. B., Sudan, M., and Williamson,

D. P. (2000). Gadgets, approximation, and linear pro-

gramming. SIAM Journal on Computing, 29(6):2074–

2097.

Xu, K. (2014). Benchmarks with hidden opti-

mum solutions for graph problems. available

at http://sites.nlsde.buaa.edu.cn/

∼

kexu/benchmarks/

graph-benchmarks.htm.

A Structured Approach to Modifying Successful Heuristics

225