Using Dynamic Vector Diagrams to Study Mechanical Motion Models at

Agrarian University with GeoGebra

Leonid O. Flehantov

1 a

, Yuliia I. Ovsiienko

1 b

, Anatolii V. Antonets

1 c

and Vladimir N. Soloviev

2 d

Poltava State Agrarian Academy, 1/3 Skovorody Str., Poltava, 36000, Ukraine

Kryvyi Rih State Pedagogical University, 54 Gagarin Ave., Kryvyi Rih, 50086, Ukraine

Keywords:

ICT in Learning and Instruction, Teaching the Basics of Mathematical Modeling, Learning of Mechanical

Motion, Visualization Technique in Learning and Instruction, Dynamic Vector Diagrams, GeoGebra.

Abstract:

This article is devoted to study of effectiveness of one of the visualization options we use when teaching

the students of an agricultural university the basics of math modeling. The main goal of this research is to

test the hypothesis that visibility and visualization improve the educational achievements of students if for

visualization we use the dynamic vector diagrams of characteristics of mechanical movement (in particular,

these are velocity and acceleration or the acting force). There are discussion of the methodology and examples

of the use of dynamic vector diagrams when teaching the basics of mathematical modeling. We described how

our students are computing and plotting graphs and dynamic vector diagrams when they doing their practical

learning exercises in math modeling and how they using them to analyze the mechanical motion of a body.

Primarily we research and discuss the effectiveness of using dynamic vector diagrams. Other visualization

options such as using plots of the dynamic characteristics of mechanical movement by Excel and GeoGebra

was discussed earlier in (Flehantov and Ovsiienko, 2019). In this article we described our experience of using

of dynamic vector diagrams in teaching the basics of math modeling at agrarian university and compared the

research results were obtained with previous ones. Also we compare the educational achievements of students

in the basics of math modeling were obtained by them using Excel and by GeoGebra software which allow to

plot and study the dynamic vector diagrams much easy.

1 INTRODUCTION

Recently there are a lot of changes in education tech-

nologies: in fact we are living at a new time. Now it is

clear that some of researches in the ﬁeld of education

that were made earlier are obsolete. The one of the

main things today is the transition from verbal chan-

nel of communication in learning to visual. Although

the scientists have not yet had time fully to study and

investigate this process but the young people already

have mastered all these.

The approach to teaching the basics of mathemat-

ical modeling (BMM) that this study focuses on is

based on visualization (Ivanova et al., 2020) and it can

be described by the saying: “I hear and forget. I see

https://orcid.org/0000-0002-4689-1457

https://orcid.org/0000-0002-4873-9061

https://orcid.org/0000-0002-2332-6711

https://orcid.org/0000-0002-4945-202X

and remember. I do and understand” (Xunzi, 2020).

This article devoted to results of our research on

the impact of visualization to teaching BMM with

the use of popular mathematical computer program –

the GeoGebra dynamic geometry system (GeoGebra,

2021; Kramarenko et al., 2020a). At ﬁrst, we points

out some researches that were the starting point for

the hypothesis and objectives of this work.

The methodological principles of using ICT in the

teaching of mathematical disciplines at universities

we used were elaborated in (Bobyliev and Vihrova,

2021; Klochko and Bondarenko, 2013; Kramarenko

et al., 2020b; Rakov, 2005; Tarasenkova et al., 2019;

Tryus, 2005). Some important issues of the use of

ICT in the educational process at the universities were

shown in (Abdula et al., 2020; Bakum and Morozova,

2015; Polhun et al., 2021; Spivakovsky et al., 2019;

Hrybiuk et al., 2014).

Note in passing that to using of Excel spreadsheets

in the teaching of BMM which is also mentioned in

336

Flehantov, L., Ovsiienko, Y., Antonets, A. and Soloviev, V.

Using Dynamic Vector Diagrams to Study Mechanical Motion Models at Agrarian University with GeoGebra.

DOI: 10.5220/0010924200003364

In Proceedings of the 1st Symposium on Advances in Educational Technology (AET 2020) - Volume 1, pages 336-353

ISBN: 978-989-758-558-6

this article were devoted to a number of scientiﬁc pub-

lications about an array of the some aspects of this

direction. For review of the early studies may be of

utility the works by Illia O. Teplytskyi (Teplytskyi and

Semerikov, 2002; Teplytskyi, 2010; Semerikov et al.,

2018).

We can’t be said the same about the GeoGebra dy-

namic geometry system. There are many articles de-

voted to this software but most of them describe of

only the capabilities and show some examples how

to use it in teaching. As examples we can point out

for publication by Osypova and Tatochenko (Osy-

pova and Tatochenko, 2021) on improving the learn-

ing environment for future mathematics teachers with

the use application of the dynamic mathematics sys-

tem GeoGebra AR. In the article by Drushlyak et al.

(Drushlyak et al., 2020) the methodology of forma-

tion of modeling skills based on a constructive ap-

proach was shown the on the example of GeoGebra.

It shows the basic techniques for using GeoGebra in

teaching and studying mathematics, with an empha-

sis on examples from geometry. Noteworthy alone is

the article by Kyslova et al. (Kyslova et al., 2014) de-

voted to the problems of teaching higher mathematics

for students of engineering specialties and to the cre-

ation of dynamic models in GeoGebra.

Caligaris et al. (Caligaris et al., 2015a,b) were

concluded that using GeoGebra applets is an effective

teaching methodology for teaching Calculus. Arbain

and Shukor (Arbain and Shukor, 2015) noted that the

students have more positive perception towards learn-

ing and have better learning achievement using Ge-

oGebra. The article by Vald

es y Medina and Medina

Vald

es (Vald

es y Medina and Medina Vald

es, 2015)

is show in practice how the GeoGebra software can

be used to exemplify the different mathematical con-

cepts.

In addition let’s we say that a lot of examples the

using of GeoGebra software for teaching mathematics

and science daily replenished on the GeoGebra web-

site (GeoGebra, 2021; Hall and Lingefjard, 2016). It

is also known that MS Excel has built-in functions for

visualizing changes in calculated values just like Ge-

oGebra has the built-in SpreadSheet component that

allows you to partially perform the tasks the same of

Excel. However, the using of these tools needs the re-

sults of the previous teaching of information technol-

ogy which are not provided for curriculum of agrarian

universities.

The problems of teaching the basics of mathemat-

ical modeling are closely related to the issues of ap-

plied orientation of mathematical (fundamental, natu-

ral sciences) disciplines. In this regard we note the re-

searches (Blomhøj and Kjeldsen, 2006; Blomhøj and

Jensen, 2007; Burghes, 1980; Finlay and King, 1986;

Flores et al., 2016; Geiger et al., 2010; Kaiser et al.,

2011; Kapur, 1982; Klymchuk et al., 2008; Lofgren,

2016; Oke, 1980; Schukajlow et al., 2018; Soloviev

et al., 2019; Temur, 2012; Verschaffel and De Corte,

1997; Vos, 2011). There are some applied issues of

mathematical modeling in agroengineering are con-

sidered in the textbook (Flehantov, 2006).

In general, despite a signiﬁcant number of stud-

ies and publications, the problems of teaching the ba-

sics of mathematical modeling using ICTs still remain

outside the attention of the integrated approach of re-

searchers.

Our interest for the main topic of this research

based on its practical importance for the train-

ing of modern agricultural production engineers,

since “teaching the basics of mathematical modeling

(BMM) is an important component in the training of

modern agricultural production engineers. Its prac-

tical value is due to the fact that training on the basis

of mathematical modeling can be an effective strategy

in modern realities” (Flehantov and Ovsiienko, 2019).

This research is a logical extension of article (Flehan-

tov and Ovsiienko, 2019) where we also were tested

the hypothesis that visualization of the dynamic char-

acteristics of mechanical processes using GeoGebra

improves the student’s learning outcomes for BMM

(in this article for visualize the dynamic characteris-

tics of mechanical motion were used graphs of trajec-

tories of moved bodies in Excel and GeoGebra).

After the experiment with the simultaneous use of

Excel and GeoGebra we were conducted in the fall of

2018 we observed a reversal of negative dynamics in

the results of training of BMM the students of engi-

neering and technical specialties of the Poltava State

Agrarian Academy, Poltava, Ukraine (PSAA) (2014 –

75.8; 2015 – 75.6; 2016 – 72.6; 2017 – 70.1). Ac-

cording to the results of the fall semester of 2018 the

average score in this discipline was 74.8 (Flehantov

and Ovsiienko, 2019). At the same time in the ex-

perimental groups E (Excel users) and G (GeoGebra

users) we obtained almost the same average values of

student performance, equal to 73.4 and 73.7, in fact at

the level of 2016 (taking into account the permissible

statistical error). Whereas in the EG group (simul-

taneous use of Excel and GeoGebra) the mean value

was 77.4. You can try to explain this result by the fact

that already in 2017 we recognized the negative trend

of lowering student performance as a problem and

showed some enthusiasm in solving it. The results

of the EG group obtained on the basis of the assump-

tion of the leading role of visualization in teaching the

basics of mathematical modeling with the simultane-

ous use of Excel and GeoGebra showed a statistically

Using Dynamic Vector Diagrams to Study Mechanical Motion Models at Agrarian University with GeoGebra

337

signiﬁcant difference from the results of the E and

G. The average score in the EG group exceeded even

quite high learning outcomes of 2014 and 2015. Thus

it can be already considered now as a fact that the vi-

sualization of modeling results creates additional con-

ditions for improving students’ knowledge taking into

account the speciﬁcs of their professional training.

The main goal of this article is to test with new

idea the hypothesis that visibility and visualization

improve the educational achievements of students of

an agricultural university when studying the basics of

mathematical modeling. This research is devoted to

the study of the effectiveness of one of the visual-

ization options, which we use when teaching the ba-

sics of mathematical modeling to students of an agri-

cultural university. As a way of visualization in this

research were used the dynamic vector diagrams of

the characteristics of mechanical movement. Our stu-

dents build these diagrams when they perform practi-

cal educational tasks in mathematical modeling, and

use them to analyze the mechanical motion of a body

thrown at an angle to the horizon, as shown in this ar-

ticle. Further in this article we describe the experience

of using dynamic vector diagrams in teaching the ba-

sics of mathematical modeling, compare the obtained

research results with previous ones and also compare

the educational achievements of students in the ba-

sics of mathematical modeling which were obtained

by them using Excel and GeoGebra.

2 EXPERIMENT DESCRIPTION

2.1 General Design

This article based on the results of the peda-

gogical experiment that was performed by authors

in September-November 2019 and in September-

November 2020. The experiment was enrolled by

167 students of the Faculty of Engineering and Tech-

nology. The provided sample size makes it possible

with ANOVA method to establish signiﬁcant differ-

ences between group means at the level of 1 point: at

a signiﬁcance level of 0.05, number of groups 3 and a

power of 80% the required sample size for groups is

at least 50 units.

At the beginning of the experiment the students

was attended were categorized into three groups

called E, G and EG; for this we used the technique

described in (Flehantov and Volchkova, 2010) which

allow us to initially form groups homogeneous by

the criterion of academic performance (Flehantov and

Volchkova, 2012). The group E used Excel spread-

sheets during the training of BMM. The group G used

the GeoGebra. The group EG used simultaneously

Excel and GeoGebra. Throughout the entire study

period, these groups were not permanent: students re-

maining in their academic group could arbitrarily mi-

grate from one experimental group to another. The

ﬁnal composition of the groups was ﬁxed at the end

of the experiment. All groups underwent BMM train-

ing in a single program using the methodology of a

differentiated approach to training presented in (Fle-

hantov and Ovsiienko, 2019). The training time in all

groups was the same. Each of group was offered com-

plete the same learning task has a direct connection

with the topics important in the training of engineers

of agrarian production. Learning outcomes of the stu-

dents of groups E, G and EG were evaluated on the

results of solving a set of typical tasks for individual

independent work.

The main learning task for all students was: mod-

eling the movement of spherical body was thrown at

an angle to the horizon, with taking into account air

resistance, gravitational interaction, electrostatic in-

teraction, magnetic interaction, etc.

We have applied a differentiated approach in

learning by doing considered the gradual construction

of end-to-end mathematical models (MM) of several

levels of complexity their computer implementation

and study through numerical calculus. The purpose of

these works is to familiarize students with the practice

of creating MM, the construction of computational

circuits and their computer implementation, forming

the skills of conducting a computer experiment and

interpreting its results.

The typical task for the students’ practice was:

create MM of free motion of the body in the grav-

ity ﬁeld and ﬁnd its solution. Further we build a cal-

culation algorithm and in the environment of the se-

lected software implement the calculation and com-

puting scheme for MM, conduct a computing exper-

iment and draw conclusions from it. The basic of

such MM is the classical model of the motion of a

body thrown at an angle to the horizon well known

from the school physics course. It’s generalized in the

ﬁrst year of engineering faculties of agricultural uni-

versities in the study of the discipline “Physics”, also

used in “Higher Mathematics” to illustrate the physi-

cal meaning of the solutions of differential equations

and in the second year in “Theoretical Mechanics”.

Several previously published articles have considered

some options for solving this training exercise using

Excel (Teplytskyi, 2010; Horda and Flehantov, 2015)

and MathCAD (Flehantov and Antonets, 2017). A

similar technique was also used by authors for im-

plementation a differentiated approach in teaching of

BMM (Flehantov and Ovsiienko, 2016). The algo-

AET 2020 - Symposium on Advances in Educational Technology

338

rithm for solving this learning problem has several

stages are described in detail in the article (Flehantov

and Ovsiienko, 2019).

The students’ ﬁnal learning outcomes were eval-

uated after completing the full course of discipline.

We also retained the methodology for assessing stu-

dent academic achievements: the learning outcomes

of students were assessed on a 100-point scale (Fle-

hantov and Ovsiienko, 2019) on the basis of the per-

formance results of an individual independent learn-

ing problems.

2.2 Mathematical Model Creation

It’s assumed that the students should use the compe-

tencies they acquired were learning “Higher Math-

ematics”, “Physics”, “Theoretical Mechanics”, “Ap-

plied Mathematics”, etc when constructing and ana-

lyzing math models.

The algorithm of actions by students when they

performing the learning exercises is detailed in (Fle-

hantov and Ovsiienko, 2019). The students creates

three mathematical models (MM) in different levels

of complexity named MM I, MM II and MM III using

the mechanical meaning of the derivative and analyz-

ing the vector equations of the resultant forces acting

on the body in three different cases. The MM I model

describes the motion of a body thrown at an angle to

the horizon without air resistance. The MM II model

describes the motion of a spherical body thrown at an

angle to the horizon with air resistance but no rota-

tion. The MM III model additionally takes into ac-

count the Magnus effect – the Magnus force arising

from the rotation of the body during the translational-

rotational motion of the body in dense medium. An

approximate line of reasoning follows next.

Based on the mechanical meaning of the deriva-

tive all models will include these two ordinary differ-

ential equations of the ﬁrst order:

= v

. (1)

If a body thrown at an angle to the horizon is

affected only by gravity force F





then

= 0 and F

= −mg. Therefore, two more equa-

tions will be added to MM I:

= 0,

= −g. (2)

The MM I is described by four differential equa-

tions (1) and (2). This elementary model describes

the motion of a body thrown at an angle to the hori-

zon in the ﬁeld of gravity force without air resistance.

It corresponds to the ﬁrst (lowest) level of difﬁculty in

BMM training.

The MM II is the second level of complex-

ity. In this case the equivalent force acting on the

body is F

= F

+ F

, where F

= −k

– force

of air resistance, v =

+ v

– velocity of the

body, k

– factor of medium resistance. From here:

= −k

v, F

= −g − k

v. Thus in addition to

(1) MM II will also include the following two equa-

tions:

= −

+ v

= −g −

+ v

(3)

MM III corresponds to the third (highest) level

of complexity in our training program. In this case

there will be an equivalent force F

= F

+ F

where F

= −k

(ω × v), k

– coefﬁcient related to

the Magnus effect. From here: F

= −k

v ± k

= −g − k

v ∓ k

v (the upper sign ”+” is on if

body rotate clockwise, the lower sign “–” is on if body

rotate counterclockwise). Therefore in addition to (1)

MM III will include next two equations:



−



+ v

= −g +



−

∓



+ v

(4)

In mathematical models we built the following no-

tation used:

x = x(t), y = y(t) – coordinates of center of the

body at the point of time t, s;

= v

(t), v

= v

(t) – the body’s velocity projec-

tions on axis of reference at time t, m/s;

g – gravity acceleration, m/s

; m – mass of the

body (m 6= 0), kg;

ρS – factor of medium resistance, kg/m;

ρS – factor of Magnus force, kg/m;

– drag coefﬁcient, depends on body shape and

characteristics of medium (for sphere in air C

0.47), no the unit of measurement;

– coefﬁcient characterizing the Magnus effect

depends on the shape of the body, the quality of

its surface and the properties of medium (for sphere

0.1 ≤ C

≤ 0.6), no the unit of measurement;

ρ – ambient density (for air = 1, 213), kg/m

;

S – normal cross-sectional area of the body rela-

tive to direction of motion, m

; in general S = S(t),

for a spherical body S = πr

, where r – radius of the

sphere, m.

Using Dynamic Vector Diagrams to Study Mechanical Motion Models at Agrarian University with GeoGebra

339

2.3 Performing the Learning Exercises

by Excel (Group E)

This part of our research we presented here in a con-

cise statement. A detailed description of the relevant

methodology and other explanations are presented in

the article (Flehantov and Ovsiienko, 2016).

The calculation scheme of the computer imple-

mentation of MM I (1), (2) in the MS Excel envi-

ronment is obtained directly from its analytical so-

lution (Klochko and Bondarenko, 2013; Kalitkin and

Koryakin, 2013):

= v

− gt

= x

+ v

= y

+ v

−

,i = 0, n

(5)

The following notation used here:

, y

– initial coordinates the center of the body,

– initial velocity of the body, m/s;

– initial angle to the horizon which the body is

thrown, radians;

= v

cosα

, v

= v

sinα

– projections the

initial velocity of the body v

;

= i · ∆t,t

∈ [0, t

],i = 0, n – the time points of

observation; i – numbers of body observation posi-

tions (ﬁxation points); n – numbers of ﬁxation points;

∆t = t

/n – time between the time points of observa-

tion, s; t

– simulation time, s;

= x(t

), y

= y(t

) – coordinates the center of the

body in the time point t

;

= v

), v

= v

) – projections velocity of

the body in the time point t

; v

+ v

– veloc-

ity of the body in the time point t

Models MM II (1), (3) and MM III (1), (4), unlike

MM I, do not allow an analytical solution. Therefore

the computational schemes of the models are based

on numerical methods.

The computational scheme for MM II according

to the Euler method for the ﬁst order ODE systems is

(Kalitkin and Koryakin, 2013):

x i+1

= v

−

∆t,

y i+1

= v

−



g +



∆t,

i+1

= x

+ v

∆t,y

i+1

= y

+ v

∆t.

(6)

For MM III the calculation scheme is the same but

the ﬁrst two equations in (6) need to replace by fol-

lowing ones:

x i+1

= v

−



− rot



∆t,

y i+1

= v

−



g +

+ rot



∆t.

(7)

The initial data for calculations by formulas (5),

(6), (7) are the values of parameters g, x

, y

, v

, α

r, m, ρ , C

, C

, t

, n and rot. The rot param-

eter can take three ﬁxed values: (–1) – means coun-

terclockwise rotation, (+1) – clockwise rotation, 0 –

no rotation. Model MM III with rot = −1 further we

denote as MM III–, and with rot = +1 – as MM III+.

With rot = 0 the model MM III is equally matched to

model MM II.

Numerical calculations by formulas (5), (6), (7)

are performed by standard MS Excel tools. As a result

the next tables of values are obtained: i, t

, x

, y

, v

, α

, E

, where α

= arctg

– the angle of

the trajectory of the body to the horizon; E

–

kinetic energy of translational motion of the body;

= mgy

– the potential energy of the body.

Figure 1 demonstrates of the data input interface

of the models MM I, MM II and MM III in MS Ex-

cel. Figure 2 displays a part of table of calculations

according to MM III for values of input parameters

presented in ﬁgure 1.

Figure 1: Interface for input of initial data for math models

MM I – MM III in MS Excel.

Figure 3 and ﬁgure 4 depicts the plots of trajec-

tories and velocities of the bodies calculated for all

the models under consideration. Visual comparison

and analysis of such graphs allows students to formu-

late meaningful conclusions about the characteristics

of those movements in various conditions.

In this way, the students using Excel analyze the

obtained numerical results and graphs by changing

the input parameters of the models. Thus, they can

to study the motion of body thrown at an angle to the

AET 2020 - Symposium on Advances in Educational Technology

340

Figure 2: Fragment of the table of calculations for MM I in

MS Excel.

horizon in various conditions to answer by itself to

control questions and to prepare to exam.

2.4 Performing the Learning Exercises

by GeoGebra (Group G)

The description and implementation of the mathe-

matical model of the mechanical motion of bodies

in GeoGebra has its own characteristics, which we

were mentioned in the work (Flehantov and Ovsi-

ienko, 2019).

The main feature of GeoGebra is an algebraic-

geometric approach to the description of mathemat-

ical objects. To solve MM I, MM II and MM III by

GeoGebra is much easier than by Excel. In GeoGe-

bra is not necessary to build and describe in detail

(step by step) complex calculation schemes for solv-

ing systems of differential equations of models. All

you need is write down the models following the Ge-

oGebra syntax and use the built-in NSolveODE com-

mand for numerical solutions of ﬁrst order differential

equations (wiki.geogebra.org, 2020).

The MM I represents in GeoGebra by formulas (1)

and (2) as follow (all commands are entered through

the command line of the program). From now on the

GeoGebra’s notation used:

x1’(t,x1,y1,vx1,vy1) = vx1

y1’(t,x1,y1,vx1,vy1) = vy1

vx1’(t,x1,y1,vx1,vy1) = 0

vy1’(t,x1,y1,vx1,vy1) = -g

Next input command used to solve the system of

differential equations above by GeoGebra is:

NSolveODE({x1’,y1’,vx1’,vy1’},

0,{x0,y0,vx0,vy0},TM)

The NSolveODE command implements the 4th

order numerical Runge-Kutta method in GeoGebra

command line (GeoGebra, 2021; Hall and Linge-

fjard, 2016; wiki.geogebra.org, 2020). It gener-

ates the numerical solution the Cauchy problem

per segment t ∈ [0, t

] with initial conditions

{x0, y0, vx0, vy0} and other input parameters

of model – tabulates four functions x

= x

(t),

= y

(t), v

= v

(t), v

= v

(t) (according

to the number of unknown functions in the model).

The resulting solutions are assigned with identiﬁers

called numericalIntegral with sequential number-

ing (according to the order of unknown functions in

the system of differential equations), namely:

numericalIntegral1 = x1(t)

numericalIntegral2 = y1(t)

numericalIntegral3 = vx1(t)

numericalIntegral4 = vy1(t)

The same way, the MM II by formulas (1) and (3)

is represented as:

x2’(t,x2,y2,vx2,vy2)=vx2

y2’(t,x2,y2,vx2,vy2)=vy2

vx2’(t,x2,y2,vx2,vy2)=-k_2*vx2

*sqrt(vx2ˆ2 + vy2ˆ2)/m

vy2’(t,x2,y2,vx2,vy2)=-g - k_2*vy2

*sqrt(vx2ˆ2 + vy2ˆ2)/m

We ﬁnd the solution of the MM II by the com-

mand:

NSolveODE({x2’,y2’,vx2’,vy2’},0,

{x0,y0,vx0,vy0},TM)}

This command also gives us four functions – MM

II solution:

numericalIntegral5 = x2(t)

numericalIntegral6 = y2(t)

numericalIntegral7 = vx2(t)

numericalIntegral8 = vy2(t)

Same as previous the MM III by formulas (1) and

(4) is represented next way:

x3’(t,x3,y3,vx3,vy3)=vx3

y3’(t,x3,y3,vx3,vy3)=vy3

vx3’(t,x3,y3,vx3,vy3)=-k_2*vx3*

sqrt(vx3ˆ2+vy3ˆ2)/m+rot*k_3*vy3*

sqrt(vx3ˆ2+vy3ˆ2)/m

vy3’(t,x3,y3,vx3,vy3)=-g-k_2*vy3*

sqrt(vx3ˆ2+vy3ˆ2)/m-rot*k_3*vx3*

sqrt(vx3ˆ2+vy3ˆ2)/m

And the MM III solution we will ﬁnd by the com-

mand:

NSolveODE({x3’,y3’,vx3’,vy3’},0,

{x0,y0,vx0,vy0},TM)}

This way we have got the MM III solution:

numericalIntegral9 = x3(t)

numericalIntegral10 = y3(t)

numericalIntegral11 = vx3(t)

numericalIntegral12 = vy3(t)

Now then we have saw that due to the unifor-

mity of actions the solutions of all three models are

obtained by GeoGebra much faster than with Excel.

Using Dynamic Vector Diagrams to Study Mechanical Motion Models at Agrarian University with GeoGebra

341

Figure 3: Plots of trajectories of bodies for MM I – MM III in MS Excel.

Figure 4: Graphs of velocities of bodies for MM I – MM III in MS Excel.

Also, if the students have this solutions, than they can

fast and easy visualizing dynamic characteristics of

the math models by GeoGebra as it shown in ﬁgure 5.

The trajectories of bodies visualized in GeoGebra

according to the models MM I, MM II and MM III

using the values of functions x1(t), y1(t), x2(t),

y2(t), x3(t), y3(t) as coordinates for three moving

points A=(x1, y1), B=(x2, y2) and C=(x3, y3)

respectively. Figure 5 shows the trajectories of spher-

ical bodies thrown at an angle to the horizon (for three

different values of initial angles) for models: MM I –

red line; MM II – green line; MM III – blue line.

These colors we will use for convenience in all ﬁg-

ures next. The current values of the basic parameters

of the models are shown in the ﬁgure on the interac-

tive controls. The arrows shown in ﬁgure 5 are vectors

AET 2020 - Symposium on Advances in Educational Technology

342

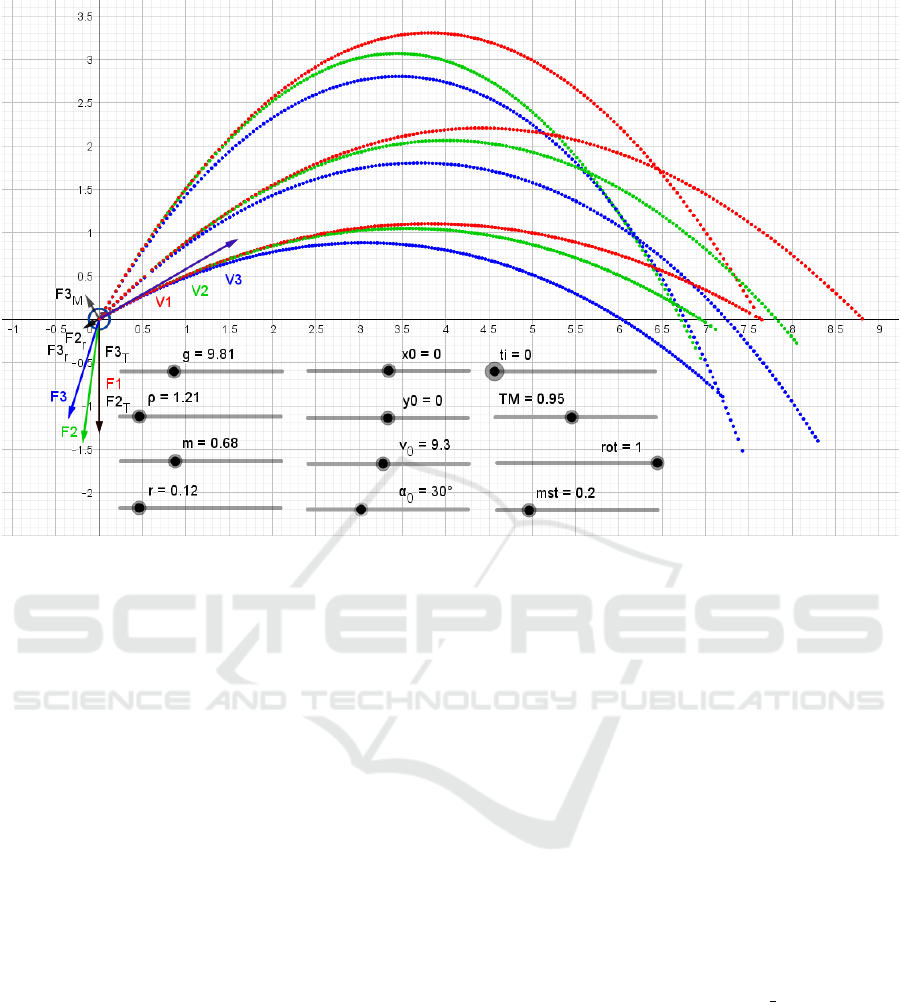
Figure 5: Graphs of trajectories of bodies for MM I – MM III in GeoGebra for different values of initial angles α

: 30

◦

, 45

◦

and 60

◦

of velocities and vectors of forces acting on the bodies

as they moves.

As we see, the GeoGebra software has better

graphics than Excel and provides additional visual-

ization capabilities. In particular, using the animation

feature, the students can observe with GeoGebra dy-

namic graphing of functions – a computer simulation

the process of mechanical movement of the body. By

using dynamic zooming in the GeoGebra window the

students can to view graph details on a larger scale.

Figure 6 and ﬁgure 7 shows some fragments trajecto-

ries of bodies for opposite directions of body rotation

which controlled in MM III by parameter rot. The

plots in these ﬁgures are presented for compare one

to others as an example.

Vectors of velocities of the bodies in

ﬁgure 6 and ﬁgure 7 describes in GeoGe-

bra as follow: V1=Vector(A, A3), where

A3=(x(A1), y(A2)), A1=(x(A)+mst*y(Point(

numericalIntegral3, c)), y(A)) or A1=(x(A)

+ mst*vx1,y(A)), A2=(x(A),y(A)+mst*y(Point

(numericalIntegral4,c))) or A2=(x(A),y(A)

+mst*vy1); V2=Vector(B,B3), where

B3=(x(B1),y(B2)), B1=(x(B)+mst*y(Point

(numericalIntegral7, c)), y(B)) or B1=

(x(B)+mst*vx2,y(B)), B2=(x(B),y(B)+mst

*y(Point(numericalIntegral8,c))) or B2=

(x(B),y(B)+mst*vy2); V3=Vector(C,C3), where

C3=(x(C1),y(C2)), C1=(x(C)+mst*y(Point

(numericalIntegral11, c)), y(C)) or C1=

(x(C)+mst*vx3,y(C)), C2=(x(C),y(C)+mst*y

(Point(numericalIntegral12,c))) or C2=

(x(C),y(C)+mst*vy3);

mst – scale factor for displaying vectors used

for convenience because in normal scale they can

be disproportionate in size – some much larger than

others (in ﬁgure 5, ﬁgure 6 and ﬁgure 7 value of

mst = 0.1).

Vectors of forces acting on the bodies and their

resultants for three different models are represented

in ﬁgure 6 and ﬁgure 7 (in order of construction).

Indices 1, 2 and 3 are referring to models MM I, MM

II and MM III respectively:

F1=Vector(A,F1_1), where F1 1=(x(A),y(A)

-mst*m*g);

F2=Vector(B,F2_3), where F2_3=F2_1 + F2_2-B,

F2_1=(x(B),y(B)-mst*m*g),

F2_2=(x(B) + mst*F2x_r, y(B) + mst*F2y_r),

F2x_r= -k_2*vx2*sqrt(vx2ˆ2 + vy2ˆ2),

F2y_r= -k_2*vy2*sqrt(vx2ˆ2 + vy2ˆ2);

F2_T= Vector(B,F2_1); F2_r= Vector(B,F2_2);

F3= Vector(C, F3_5), where F3_5=F3_3+F3_4-C,

F3_3= F3_1 + F3_2-C,

F3_4= (x(C) + mst*F3x_M, y(C) + mst*F3y_M),

Using Dynamic Vector Diagrams to Study Mechanical Motion Models at Agrarian University with GeoGebra

343

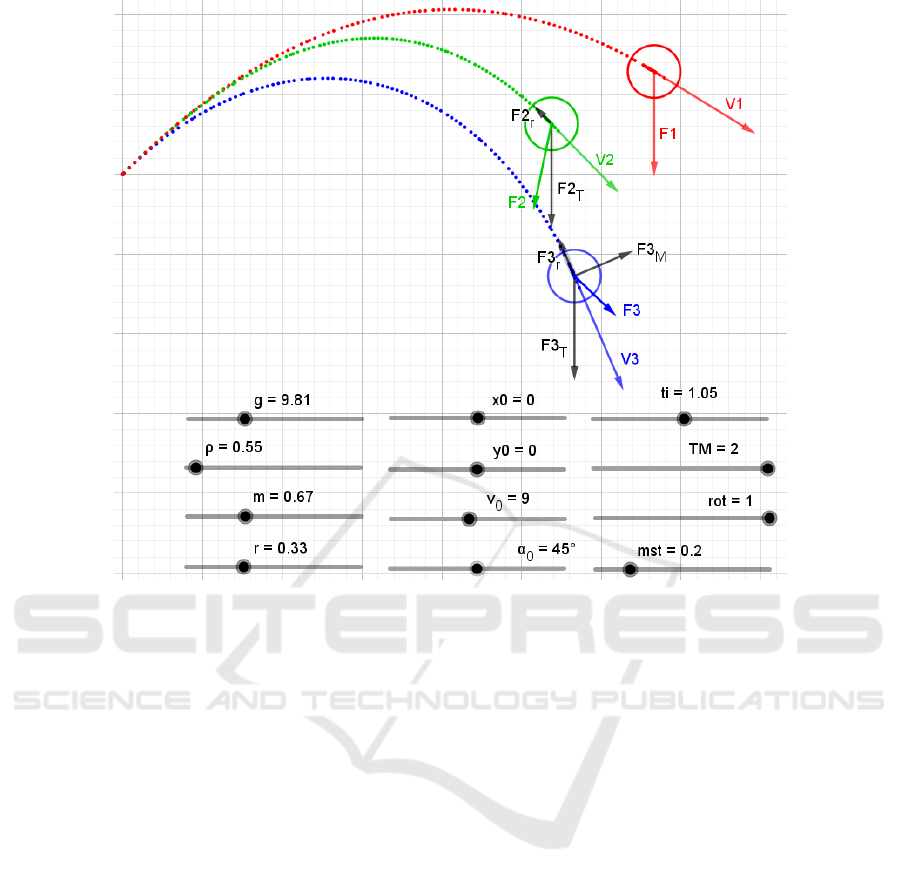
Figure 6: Fragments of trajectories of bodies plotted in GeoGebra for MM I – MM III with rot=+1.

F3_1= (x(C), y(C) - mst*m*g),

F3_2= (x(C) + mst*F3x_r, y(C) + mst*F3y_r),

F3x_r=-k_2*vx3*sqrt(vx3ˆ2 + vy3ˆ2),

F3y_r=-k_2*vy3*sqrt(vx3ˆ2 + vy3ˆ2),

F3x_M=rot*(-k_3)*vy3*sqrt(vx3ˆ2 + vy3ˆ2),

F3y_M=rot*k_3*vx3*sqrt(vx3ˆ2 + vy3ˆ2).

Vectors of the gravity force F3

, the force of air

resistance F3

and the Magnus force F3

for model

M III are represented as follows:

F3_T=Vector(C,F3_1),

F3_r=Vector(C,F3_2),

F3_M=Vector(C,F3_4).

Thus, the students implements the mathematical

models MM I, MM II, MM III in the GeoGebra en-

vironment with the help of this simple mathematical

apparatus based on the method of coordinates and el-

ementary vector algebra.

Figure 8, ﬁgure 9 and ﬁgure 10 shows the dy-

namic vector diagrams which our students are plot-

ting in GeoGebra and studying by computer simu-

lation. On them in dynamics are displayed the vec-

tor diagrams of the velocities of bodies and their

projections in different phases of motion according

to the models MM I, MM II, MM III. These dia-

grams are dynamic and interactive because they au-

tomatically changes if you use the sliders shown in

the ﬁgure to set new values for the model inputs.

At moment represented results at time ti = 1.04 s

for the following values of the initial parameters:

g=9.81, ro=1.213, m=0.68, r=0.12\verb, x0=0,

y0=0, v0=9.3, alpha0=45, rot=1, mst=0.1.

The using of dynamic vector diagrams for visu-

alizing dynamic characteristics to study and analyze

mechanical movement when teaching students the ba-

sics of mathematical modeling is the main difference

between this studies from the previous ones. The

computer simulation and the studying dynamic vec-

tor diagrams of velocities of bodies allows for stu-

dents interactively observe changes that occur with

vectors of velocities depending on changes of values

of various model parameters and study and compare

the dynamic characteristics of motion of the bodies in

different phases of its movement.

The students simultaneously study and analyze the

corresponding plots of velocities of the bodies and

their projections on the coordinate axes similar to

those shown in ﬁgure 11 and ﬁgure 12. In contrast to

vector diagrams these plots better shows how changes

the absolute value of velocity of the body. The anal-

ysis allow to us to ﬁnd the direction of movement of

body at different times. At the same time dynamic

vector diagrams of velocities give us a clear visual

AET 2020 - Symposium on Advances in Educational Technology

344

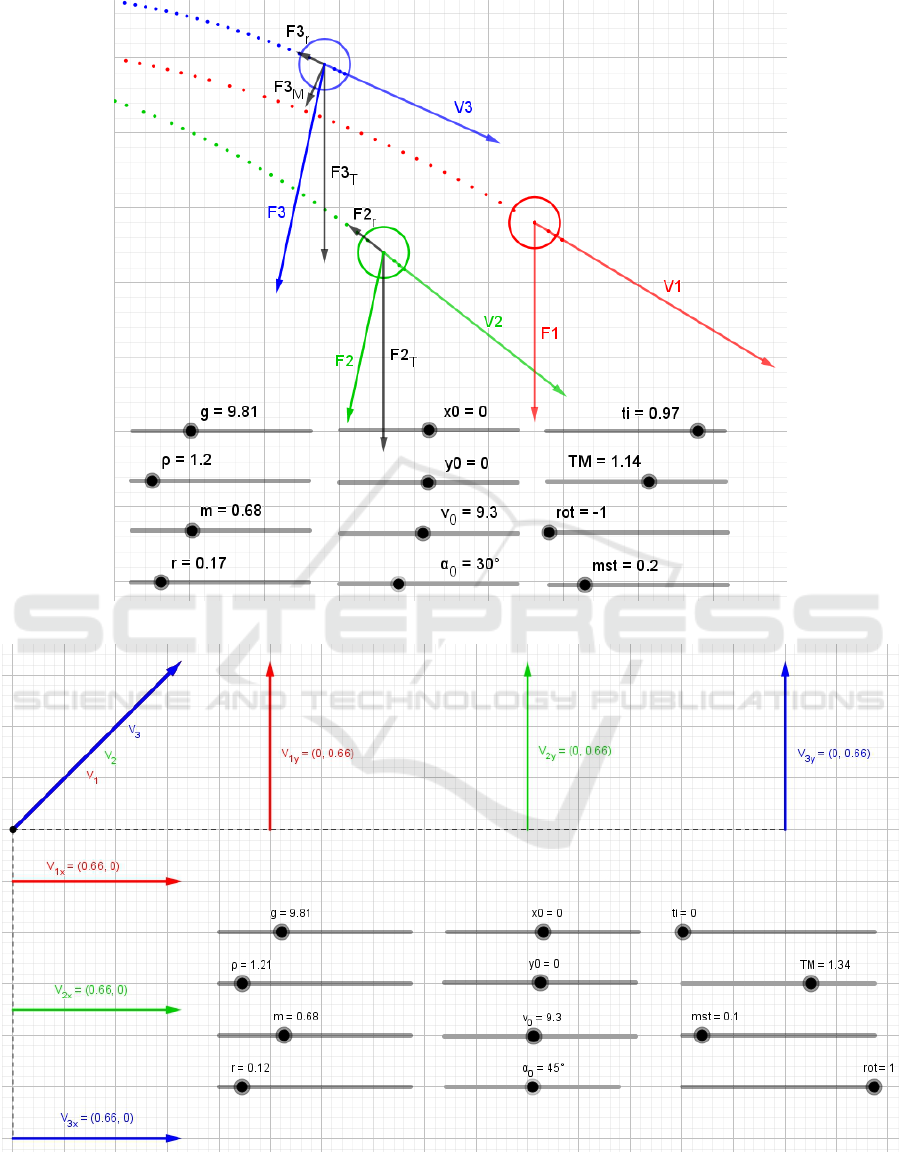
Figure 7: Fragments of trajectories of bodies plotted in GeoGebra for MM I – MM III with rot=-1.

Figure 8: The dynamic vector diagram of velocities of bodies plotted in GeoGebra for MM I – MM III+ (clockwise rotation)

at start of movement: ti=0, rot = +1.

Using Dynamic Vector Diagrams to Study Mechanical Motion Models at Agrarian University with GeoGebra

345

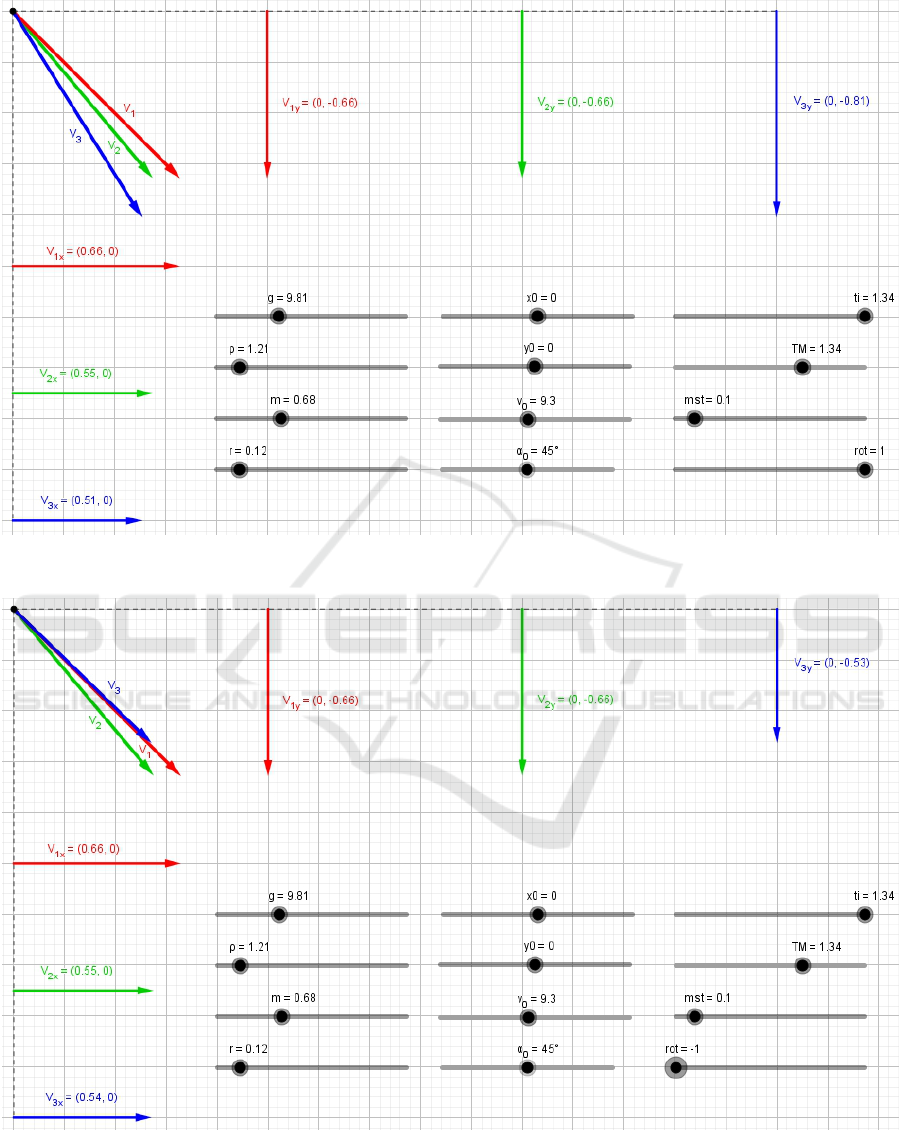
Figure 9: The dynamic vector diagram of velocities of bodies plotted in GeoGebra for MM I – MM III+ (clockwise rotation)

at the end of motion: ti=1.34, rot=+1.

Figure 10: The dynamic vector diagram of velocities of bodies plotted in GeoGebra for MM I – MM III- (counterclockwise

rotation) at the end of motion: ti=1.34, rot=-1.

representation not only of the absolute value of the

body’s velocity and its projections (this can be judged

by the length of the corresponding vectors) but also of

the direction of motion of the body (this can be seen

AET 2020 - Symposium on Advances in Educational Technology

346

directly in the direction of the vector of body veloc-

ity).

Figure 11 allow us to compare the plots of the hor-

izontal projections of velocity of the body vx1(t),

vx2(t), vx3(t) for the three different models MM I,

MM II and MM III for two cases: when rot=+1

(clockwise rotation) and rot=-1 (counterclockwise

rotation). Studying these plots provides for the stu-

dents a lot of useful information about the features of

body movement thrown at an angle to the horizon un-

der different conditions. In particular, these plots are

shows clearly that when rotated clockwise the body at

the beginning of the movement accelerates in the hor-

izontal direction and then slows down. On the con-

trary, for rot=-1 the body slows down at ﬁrst, but

somewhat accelerates at the end of the movement.

The GeoGebra allows us to build similar plots and

diagrams for all functions that are the solution of the

models. Performing their interactive comparisons at

various values of the parameters of the models we

can quickly conduct a mini-study to establish the all

necessary facts or identify the patterns. For example,

the Fig. 12 shows the plots of the functions y1(t),

y2(t), y3(t) for the MM I, MM II, MM III when

rot=1 and rot=-1. Changing the time of simulation

TM we can quickly set the time point when the body

touches the surface of the earth (determine the ﬂight

time). As you see, for identical input parameters of

the model, the body rotating clockwise will fall to the

surface of the earth in 1.14 s and the body rotating

counterclockwise will be ﬂying 1.46 s. This technique

ensures the effective formation of research competen-

cies of the students.

Similarly, our students study and analyze the

forces acting on the body during movement and their

resultants, as well as their projections. Performing

computer simulations in Excel and GeoGebra based

on the created mathematical models they observe and

analyze, for example, how these vector quantities

change at different points in time, what are the ten-

dencies of these changes, what they mean and what

they indicate. The corresponding illustrations using

GeoGebra will be given below. This approach con-

tributes to formation of the analytical abilities and de-

velopment of skills of graphic analysis of students.

2.5 Performing the Learning Exercises

with Excel and GeoGebra (Group

EG)

The experimental group EG performed the same

learning exercises using simultaneously Excel and

GeoGebra in accordance with methodology described

above.

The participants of this group used Excel (if feel

it necessary or expedient, in particular, for numeri-

cal calculations or for presenting the results in tabular

form) or the GeoGebra software for visual representa-

tion and analysis the dynamic characteristics in form

of plots and dynamic vector diagrams. As example

of these works you may see the vector diagrams of

the forces acting on the body plotting according to

the models M I, MM II and MM III in ﬁgure 13 and

ﬁgure 14.

3 RESULTS

The table 1 shows the results of ﬁnal learning out-

comes of students of the Faculty of Engineering and

Technology of the agricultural university at the end of

the experiment described in this article: training the

basics of mathematical modeling using visualization

of the dynamic characteristics of mechanical move-

ment in the form of dynamic vector diagrams. The

ﬁnal learning outcomes of the students of groups E,

G and EG were evaluated on the results of solving

a set of typical learning problems or individual inde-

pendent works. These results are presented here on a

100-point scale (Flehantov and Ovsiienko, 2019).

The primary statistical data processing results of

the experiment (table 2) are showed that the average

scores in all groups (mean) are different. The means

for groups E and G close to each other (73.36 and

73.85) but both lower than the mean of group EG

(78.25). The mean values in groups E and G almost

coincide with similar indicators in the same groups

of the previous years: MeanE=73.36 (2019) vs. 73.4

(2018); MeanG=73.85 (2019) vs. 73.7 (2018). At

the same time the mean value in group EG-2019

exceed the corresponding ﬁgure in group EG-2018:

MeanEG=78.25 (2019) vs. 77.4 (2018). The result of

Shapiro-Wilk test shows the trust of hypothesis about

normal data distribution in all groups.

Analysis of variance (ANOVA) showed a sta-

tistically signiﬁcant difference in average values of

learning outcomes (Score/Point/Bal) in all groups

(F = 4.678693; p = 0.010613) (table 3). The post-

hoc comparison for means of groups E vs. G, E vs.

EG, G vs. EG shows that the difference between the

means of groups E and G is within the statistical er-

ror (table 4). The pair-wise post-hoc comparisons

results indicate the statistical signiﬁcance of the dif-

ference between the mean for group EG and the mean

groups E and G.

Using Dynamic Vector Diagrams to Study Mechanical Motion Models at Agrarian University with GeoGebra

347

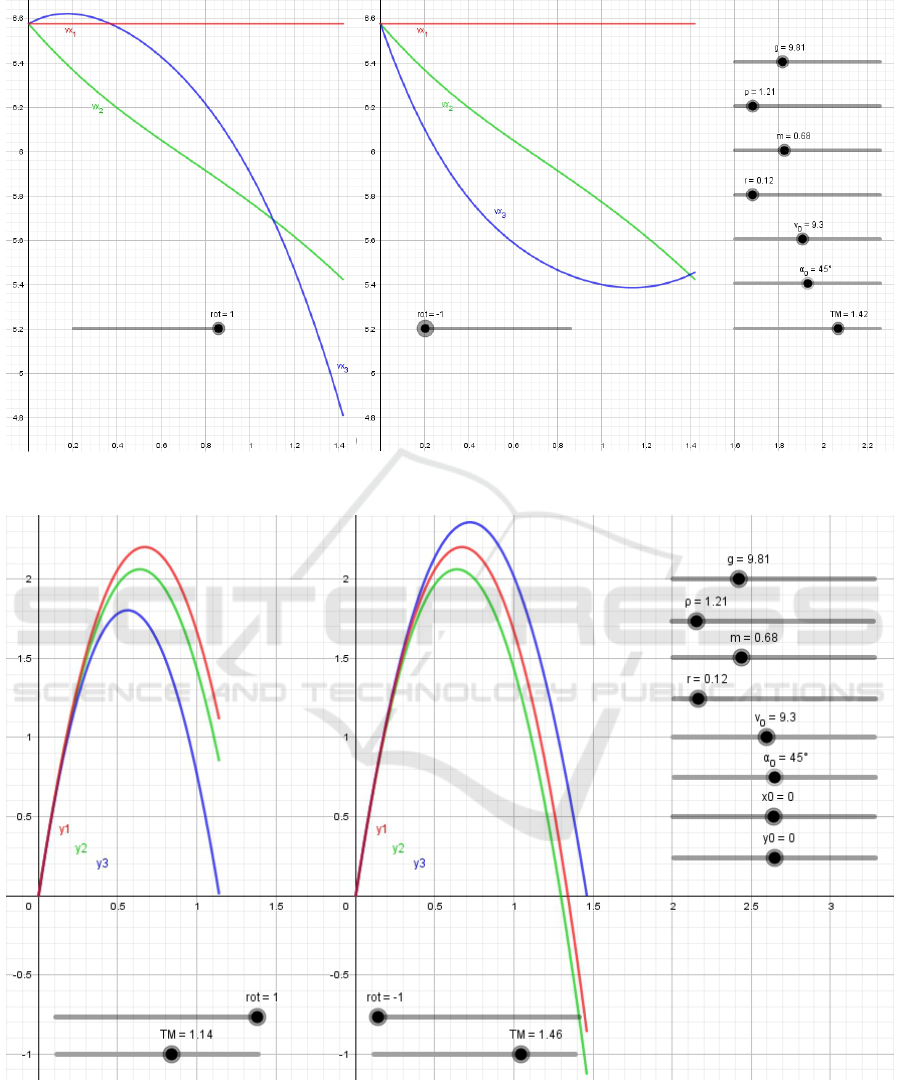
Figure 11: The visual study in GeoGebra: how changes the projection v

for math models MM I, MM II, MM III+ (rot = +1,

clockwise rotation) and MM III- (rot=-1, counterclockwise rotation).

Figure 12: The visual study in GeoGebra: how long is the spherical body ﬂight in air according to different math models if

the body rotate clockwise and counterclockwise? (rot=+1 and rot=-1).

4 DISCUSSION

In this article we made compare the earlier results we

obtained when our students at ﬁrst used Excel spread-

sheets as the tool for solving learning exercises and

then the GeoGebra dynamic geometry system was

added. At the same time during the training sessions

AET 2020 - Symposium on Advances in Educational Technology

348

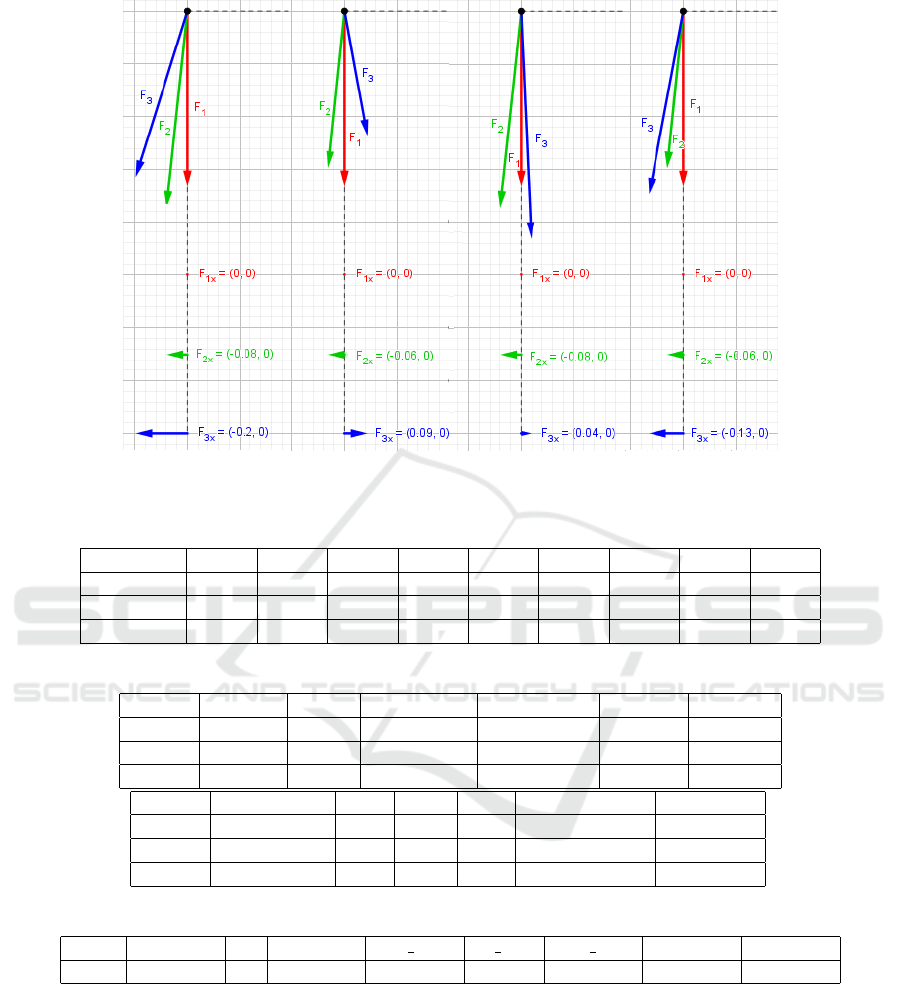
Figure 13: The dynamic vector diagram of X-component F

of the resultant of the forces acting on the body in the four cases

of ﬂight: ti = 0, rot = 1; ti = TM, rot = 1; ti = 0, rot = -1; ti = TM, rot = -1.

Table 1: Final learning outcomes of students after the experiment.

Score 50-55 55-60 60-65 65-70 70-75 75-80 80-85 85-90 90-95

Group E 1 2 6 9 14 10 7 4 -

Group G - 3 6 10 13 15 8 3 1

Group EG - 1 3 5 10 15 9 7 5

Table 2: Primary statistical data processing results.

Group Valid N Mean Conf.-95% Conf.+95% Median Mode

E 53 73.36 71.16 75.55 74 Multiple

G 59 73.85 71.74 75.95 74 76

EG 55 78.25 75.94 80.57 77 76

Group Freq. Mode Min Max SD Shapiro-Wilk test

E 5 55 90 7.96 W=0.98823 p=0.87840

G 5 56 91 8.08 W=0.98749 p=0.80486

EG 6 60 95 8.56 W=0.98158 p=0.55809

Table 3: ANOVA results.

SS df MS SS Err df Err MS Err F p

Point 1249.818 2 624.9091 10588.73 164 64.56544 4.678693 0.010613

we consistently and systematically studied how vari-

ous methods and techniques of visualizing the results

of modeling affect the results of educational achieve-

ments of students who study at the agrarian univer-

sity (the speciﬁcs of teaching this group of students

to mathematical disciplines were discussed by us ear-

lier).

Based on the above we conclude that visualization

of the dynamic characteristics of mechanical move-

ment in the form of dynamic vector diagrams using

the GeoGebra software allow to improve the educa-

tional achievements of students of the agrarian univer-

sity when studying the basics of mathematical model-

ing.

There are several possible reasons for this result.

At ﬁrst, since implementation of mathematical mod-

els in MS Excel, in fact, is a stepwise reproduction

of the sequence of the mathematical operations by

means of spreadsheets, than their use contributes to

a better understanding of the students of the technical

Using Dynamic Vector Diagrams to Study Mechanical Motion Models at Agrarian University with GeoGebra

349

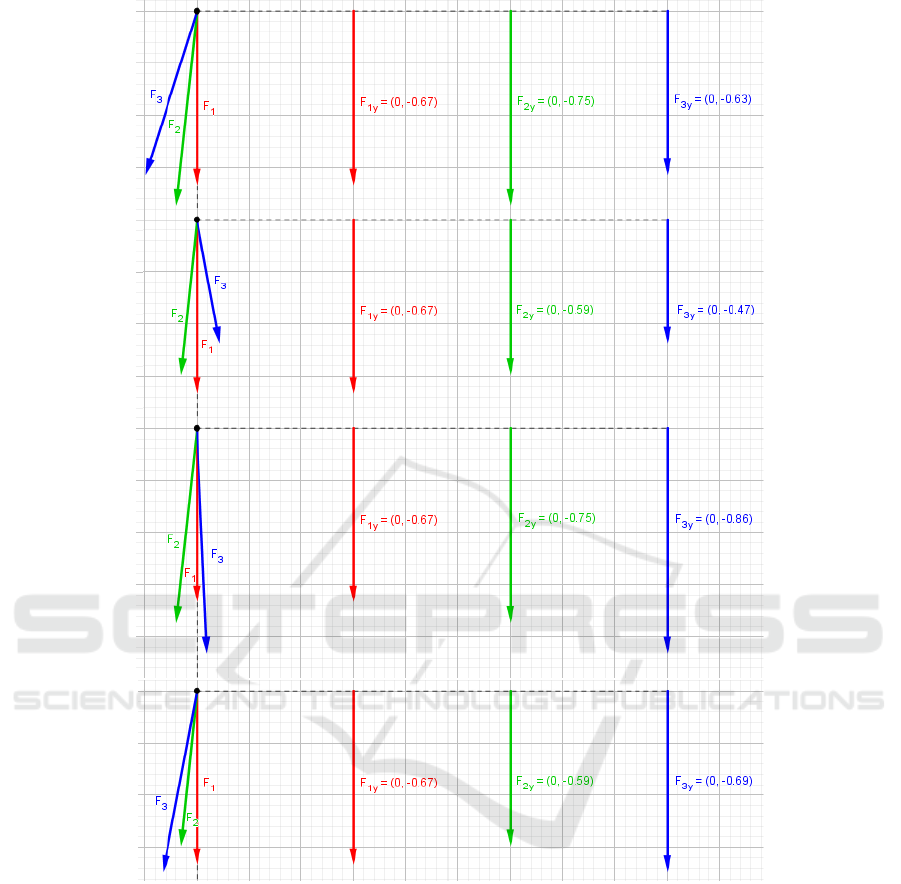
Figure 14: The dynamic vector diagram of Y-component F

of the resultant of the forces acting on the body in four cases

(from top to right): ti = 0, rot = 1; ti = TM, rot = 1; ti = 0, rot = -1; ti = TM, rot = -1.

component of mathematical modeling, provides them

with the opportunity to diagnose calculations by it-

self, and also creates additional didactic beneﬁts for

the teacher, such as being able to identify and discuss

with students all the intermediate effects and simu-

lation outcomes that may remain invisible (hidden)

when using professional computer math systems such

as Mathcad (Flehantov and Antonets, 2017), Mathe-

matica, MATLAB or Maple, etc.

In addition, visualization of the trajectory of me-

chanical motion of bodies in the form of Excel charts

provides the formation of intuitive ideas about how

the characteristics of movement of bodies changes de-

pending on the initial conditions and other parame-

ters. This allows to students to acquire the skills of

consciously adjusting input parameters to achieve the

desired simulation result. However the standard Excel

features do not allow them to visualize the changes in

the instantaneous velocities and the direction of mo-

tion of bodies along their trajectories. Therefore us-

ing of Excel in training does not create sufﬁcient con-

ditions for the formation of skills to analyze the dy-

namic characteristics of movement based on numeri-

cal data.

AET 2020 - Symposium on Advances in Educational Technology

350

Table 4: Pair-wise post-hoc comparisons results.

Pair-wise post-hoc comparisons of means E vs. G E vs. EG G vs. EG

LSD-test p>0.9468 p<0.0262 p<0.0120

Duncan-test p>0.9475 p<0.0135 p<0.0151

Tukey HSD for unequal N test p>0.9977 p<0.0061 0.0048

On the other hand the GeoGebra allows to the stu-

dents to form their intuitive spatial perceptions faster

by visual analyzing dynamic motion characteristics.

In our view this is made possible primarily by the dy-

namic visualization of vector characteristics of mo-

tion. We observed that after completing the proposed

learning exercises with the help of GeoGebra the stu-

dents more easy formulated the meaningful answers

to questions of qualitative evaluation. Studying the

dynamic plots such as ﬁgure 11 in an interactive mode

allows them quickly and accurately answer the ques-

tions such as: “How does the change the direction of

rotation will affect the linear velocity of the body?”,

“At what points in time the velocity of the body will

in airless space be equal to the speed of the body in

air?” and so on. However, the students who were

working in Excel environment were better at answer-

ing questions about the quantitative characteristics of

the models.

That’s why as in our previous study (Flehantov

and Ovsiienko, 2019, 2016) we are of the opinion that

using only GeoGebra to study the basics of modeling

creates the inconvenience to evaluate the simulation

results in a numerical dimension. Therefore it does

not provide a sufﬁcient level of skills to numerically

evaluate the characteristics of the phenomenon or the

simulated process. At the same time the wide using of

GeoGebra during BMM training contributes to the ef-

fectively formation of intuitive spatial representations

that are very important for engineering professionals.

Because, as in the previous study, there is no signif-

icant difference between ﬁnal learning outcomes in

groups E and G, this could mean that simultaneous

use of Excel and GeoGebra compensates for these

shortcomings and therefore provides the best educa-

tional achievements. At the same time, the using of

dynamic vector diagrams in GeoGebra environment

to learning the basics of mathematical modeling fur-

ther up these results.

5 CONCLUSION

The analysis of the data we collected shows that

the students who simultaneously used GeoGebra and

Excel at the highest level of learning difﬁculty in

dynamic vector diagram visualization mode demon-

strated a better understanding of mathematical model-

ing problems and improved their ability to use math-

ematical modeling to solve problems. At the same

time, we found no statistically signiﬁcant difference

in learning outcomes between groups of students who

used only Excel or only GeoGebra separately during

BMM training. In addition, we noticed that students

who used Excel for computer modeling responded

better to quantitative questions of exam. The students

who performed their learning exercises exclusively in

the GeoGebra environment were much better at deal-

ing with quality questions.

Results of this study we get conclusion that the si-

multaneous use of Excel and GeoGebra with vizual-

isation mode by dynamic vector diagrams demon-

strated improved the academic achievement of stu-

dents with BMM. This is indicated by the statisti-

cally signiﬁcant difference between the average re-

sults of students’ academic achievement, shown in ta-

ble 2 conﬁrmed with the results of table 3 and table

So, this research show that the proper use of ap-

propriate software to visualize the dynamic charac-

teristics of mathematical models in the context of the

teaching BMM at an agrarian university is an effec-

tive way to improve student performance. We were

concluded that the hypothesis that visualization of the

characteristics of mechanical movement by the dy-

namic vector diagrams can to improve the educational

achievements of students is true. However the as-

sumption that visualizing the results of modeling us-

ing GeoGebra in conjunction with a differentiated ap-

proach to learning creates additional conditions for

improving students’ knowledge, taking into account

the speciﬁcs of their vocational training requires fur-

ther veriﬁcation.

REFERENCES

Abdula, A., Baluta, H., Kozachenko, N., and Kassim, D.

(2020). Peculiarities of using of the Moodle test tools

in philosophy teaching. CEUR Workshop Proceed-

ings, 2643:306–320.

Arbain, N. and Shukor, N. A. (2015). The effects of geoge-

bra on students achievement. Procedia - Social and

Behavioral Sciences, 172:208–214.

Bakum, Z. and Morozova, K. (2015). Didactical conditions

Using Dynamic Vector Diagrams to Study Mechanical Motion Models at Agrarian University with GeoGebra

351

of development of informative-communication com-

petence of future engineers during master preparation.

Metallurgical and Mining Industry, 7(2):164–167.

Blomhøj, M. and Jensen, T. (2007). What’s all the fuss

about competencies?: Experiences with using a com-

petence perspective on mathematics education to de-

velop the teaching of mathematical modelling. New

ICMI Study Series, 10:45–56.

Blomhøj, M. and Kjeldsen, T. (2006). Teaching mathe-

matical modelling through project work - experiences

from an in-service course for upper secondary teach-

ers. ZDM - International Journal on Mathematics Ed-

ucation, 38(2):163–177.

Bobyliev, D. Y. and Vihrova, E. V. (2021). Problems and

prospects of distance learning in teaching fundamental

subjects to future mathematics teachers. Journal of

Physics: Conference Series, 1840(1):012002.

Burghes, D. (1980). Mathematical modelling: A positive

direction for the teaching of applications of mathe-

matics at school. Educational Studies in Mathematics,

11(1):113–131.

Caligaris, M., Rodr

ıguez, G., and Laugero, L. (2015a).

Learning styles and visualization in numerical anal-

ysis. Procedia - Social and Behavioral Sciences,

174:3696–3701.

Caligaris, M. G., Schivo, M. E., and Romiti, M. R. (2015b).

Calculus & geogebra, an interesting partnership. Pro-

cedia - Social and Behavioral Sciences, 174:1183–

1188.

Drushlyak, M. G., Semenikhina, O. V., Proshkin, V. V.,

Kharchenko, S. Y., and Lukashova, T. D. (2020).

Methodology of formation of modeling skills based

on a constructive approach (on the example of GeoGe-

bra). CEUR Workshop Proceedings, 2879:458–472.

Finlay, P. and King, M. (1986). Teaching management

students to love mathematical modelling. Teaching

Mathematics and its Applications, 5(1):31–37.

Flehantov, L. and Antonets, A. (2017). Computer simu-

lation the mechanical movement body by means of

MathCAD. Information technologies in education,

30(1):97–109.

Flehantov, L. and Ovsiienko, Y. (2019). The simultaneous

use of Excel and GeoGebra to training the basics of

mathematical modeling. CEUR Workshop Proceed-

ings, 2393:864–879.

Flehantov, L. O. (2006). Mathematical models of mass ser-

vice in the practice of agricultural engineers. Inter-

graphica, Poltava.

Flehantov, L. O. and Ovsiienko, Y. I. (2016). Differentiated

approach in teaching the basics of mathematical mod-

eling with ms excel for students of agricultural univer-

sities. Information Technologies and Learning Tools,

54(4):165–182. https://journal.iitta.gov.ua/index.php/

itlt/article/view/1407.

Flehantov, L. O. and Volchkova, M. I. (2010). Method-

ology and algorithm of stafﬁng of student academic

groups. In Methods of Improving Basic Education in

Schools and Universities, Proceedings of the 15th In-

ternational Scientiﬁc and Methodological Conference,

Sevastopol.

Flehantov, L. O. and Volchkova, M. I. (2012). Method

of manning student academic groups. Utility model

patent. Registered in the State Patent Register of

Ukraine for Inventions No. 69586 10.05.2012.

Flores, E., Montoya, M., and Mena, J. (2016). Challenge-

based gamiﬁcation and its impact in teaching math-

ematical modeling. In ACM International Confer-

ence Proceeding Series, volume 02-04-November-

2016, pages 771–776.

Geiger, V., Faragher, R., and Goos, M. (2010). CAS-

enabled technologies as ’Agents Provocateurs’ in

teaching and learning mathematical modelling in sec-

ondary school Classrooms. Mathematics Education

Research Journal, 22(2):48–68.

GeoGebra (2021). Geogebra — Free Math Apps - Used

By Over 100 Million Students & Teachers Worldwide.

https://www.geogebra.org.

Hall, J. and Lingefjard, T. (2016). Mathematical Modeling:

Applications with GeoGebra. John Wiley & Sons,

Hoboken.

Horda, I. M. and Flehantov, L. O. (2015). Computer mod-

elling of process of the mechanical motion of body

with the help of ms excel means. Information Tech-

nologies and Learning Tools, 47(3):99–109. https:

//journal.iitta.gov.ua/index.php/itlt/article/view/1245.

Hrybiuk, O., Demianenko, V., Zhaldak, M., Za-

porozhchenko, Y., Koval, T., Kravtsov, H., Lavren-

tieva, H., Lapinskyi, V., Lytvynova, S., Pirko, M.,

Popel, M., Skrypka, K., Spivakovskyi, O., Sukhikh,

A., Tataurov, V. P., and Shyshkina, M. (2014). Sys-

tema psykholoho-pedahohichnykh vymoh do zasobiv

informatsiino-komunikatsiinykh tekhnolohii navchal-

noho pryznachennia (System of psychological and

pedagogical requirements to ICT learning tools).

Atika, Kyiv.

Ivanova, H., Lavrentieva, O., Eivas, L., Zenkovych, I., and

Uchitel, A. (2020). The students’ brainwork intensiﬁ-

cation via the computer visualization of study materi-

als. CEUR Workshop Proceedings, 2643:185–209.

Kaiser, G., Blum, W., Ferri, R., and Stillman, G. (2011).

Trends in teaching and learning of mathematical mod-

elling – preface. International Perspectives on the

Teaching and Learning of Mathematical Modelling,

1:1–5.

Kalitkin, N. N. and Koryakin, P. V. (2013). Numerical

methods, volume 2. Mathematical Methods Physics of

University textbook. Series: Applied Mathematics and

Computer Science. Academy, Moscow.

Kapur, J. (1982). The art of teaching the art of mathemati-

cal modelling. International Journal of Mathematical

Education in Science and Technology, 13(2):185–192.

Klochko, V. I. and Bondarenko, Z. V. (2013). Higher math-

ematics. Ordinary differential equations (with com-

puter support). Vinnytsia.

Klymchuk, S., Zverkova, T., Gruenwald, N., and Sauerbier,

G. (2008). Increasing engineering students’ awareness

to environment through innovative teaching of mathe-

matical modelling. Teaching Mathematics and its Ap-

plications, 27(3):123–130.

AET 2020 - Symposium on Advances in Educational Technology

352

Kramarenko, T., Pylypenko, O., and Muzyka, I. (2020a).

Application of GeoGebra in Stereometry teaching.

CEUR Workshop Proceedings, 2643:705–718.

Kramarenko, T., Pylypenko, O., and Zaselskiy, V. (2020b).

Prospects of using the augmented reality application

in STEM-based Mathematics teaching. CEUR Work-

shop Proceedings, 2547:130–144.

Kyslova, M. A., Semerikov, S. O., and Slovak, K. I. (2014).

Development of mobile learning environment as a

problem of the theory and methods of use of infor-

mation and communication technologies in educa-

tion. Information Technologies and Learning Tools,

42(4):1–19. https://journal.iitta.gov.ua/index.php/itlt/

article/view/1104.

Lofgren, E. (2016). Unlocking the black box: Teaching

mathematical modeling with popular culture. FEMS

Microbiology Letters, 363(20).

Oke, K. (1980). Teaching and assessment of mathematical

modeling in an M.Sc. course in mathematical educa-

tion. International Journal of Mathematical Educa-

tion in Science and Technology, 11(3):361–369.

Osypova, N. V. and Tatochenko, V. I. (2021). Improving the

learning environment for future mathematics teachers

with the use application of the dynamic mathematics

system GeoGebra AR. CEUR Workshop Proceedings,

2898:178–196.

Polhun, K., Kramarenko, T., Maloivan, M., and Tomilina,

A. (2021). Shift from blended learning to distance one

during the lockdown period using Moodle: test con-

trol of students’ academic achievement and analysis

of its results. Journal of Physics: Conference Series,

1840(1):012053.

Rakov, S. A. (2005). Mathematical education: a compe-

tence approach using ICT. Kharkiv.

Schukajlow, S., Kaiser, G., and Stillman, G. (2018). Empiri-

cal research on teaching and learning of mathematical

modelling: A survey on the current state-of-the-art.

ZDM - Mathematics Education, 50(1-2):5–18.

Semerikov, S., Teplytskyi, I., Yechkalo, Y., and Kiv, A.

(2018). Computer simulation of neural networks us-

ing spreadsheets: The dawn of the age of Camelot.

CEUR Workshop Proceedings, 2257:122–147.

Soloviev, V., Moiseienko, N., and Tarasova, O. (2019).

Modeling of cognitive process using complexity

theory methods. CEUR Workshop Proceedings,

2393:905–918.

Spivakovsky, A., Petukhova, L., Kotkova, V., and Yurchuk,

Y. (2019). Historical approach to modern learn-

ing environment. CEUR Workshop Proceedings,

2393:1011–1024.

Tarasenkova, N., Akulenko, I., Hnezdilova, K., and

Lovyanova, I. (2019). Challenges and prospective di-

rections of enhancing teaching mathematics theorems

in school. Universal Journal of Educational Research,

7(12):2584–2596.

Temur,

O. (2012). Analysis of prospective classroom teach-

ers’ teaching of mathematical modeling and problem

solving. Eurasia Journal of Mathematics, Science and

Technology Education, 8(2):83–93.

Teplytskyi, I. O. (2010). Elementy kompiuternoho modeli-

uvannia (Elements of computer simulation). KSPU,

Kryvyi Rih, 2nd edition.

Teplytskyi, I. O. and Semerikov, S. O. (2002). Kompi-

uterne modeliuvannia mekhanichnykh rukhiv u sere-

dovyshchi elektronnykh tablyts (Computer modeling

of mechanical movements in an spreadsheets environ-

ment). Fizyka ta astronomiia v shkoli, (5):41–46.

Tryus, Y. V. (2005). Computer-Oriented Methodical System

for Teaching Mathematics. Cherkasy.

Vald

es y Medina, E. G. and Medina Vald

es, L. (2015). Dy-

namic models as change enablers in educational math-

ematics. Procedia - Social and Behavioral Sciences,

176:923–926.

Verschaffel, L. and De Corte, E. (1997). Teaching realistic

mathematical modeling in the elementary school: A

teaching experiment with ﬁfth graders. Journal for

Research in Mathematics Education, 28(5):577–601.

Vos, P. (2011). What is ‘authentic’ in the teaching and

learning of mathematical modelling? International

Perspectives on the Teaching and Learning of Mathe-

matical Modelling, 1:713–722.

wiki.geogebra.org (2020). NSolveODE

Command - GeoGebra Manual.

https://wiki.geogebra.org/en/NSolveODE

Command.

Xunzi (2020). English language & usage.

https://english.stackexchange.com/questions/226886/.

Using Dynamic Vector Diagrams to Study Mechanical Motion Models at Agrarian University with GeoGebra

353