
Digital Technologies in Specialized Mathematics Education: Application
of GeoGebra in Stereometry Teaching
Tetiana H. Kramarenko
1 a
, Olha S. Pylypenko
1,2 b
and Olga Yu. Serdiuk
3 c
1
Kryvyi Rih State Pedagogical University, 54 Gagarin Ave., Kryvyi Rih, 50086, Ukraine
2
State University of Economics and Technology, 37A Vatutin Str., Kryvyi Rih, 50096, Ukraine
3
Kryvyi Rih National University, 11 Vitaly Matusevich Str., Kryvyi Rih, 50027, Ukraine
Keywords:
GeoGebra 3D Graphing Calculator, Geometry, STEM Competencies, Stereometry Teaching, Methodology of
Teaching Mathematics, Cloud Technologies in Education.
Abstract:
The purpose of the paper is to improve methodology of teaching Mathematics via the use of digital technolo-
gies. The task of the paper is to identify the issues that require a theoretical and experimental solution. The
objective of the paper is the educational process in the higher education institution, the subject of the paper is
modern ICT. The result of the study is the learning tools of pedagogically considered and adequate bending
of conventional and modern learning environment implemented into the educational process. The possibilities
of using cloud technologies and Dynamic Mathematics system GeoGebra in the educational process through
Stereometry specialized training have been revealed. The use of GeoGebra Dynamic Mathematics in Stereom-
etry teaching will favourably influence the formation of students’ STEM competencies. In order to encourage
Mathematics and Computer Science teachers to implement effectively the elements of STEM education, it is
suggested that cloud-based learning tools such as GeoGebra be used in the teaching process.
1 INTRODUCTION
Velikova and Petkova (Velikova and Petkova, 2019)
point out that every society needs STEM profession-
als, talented people who design new technologies,
materials, constructions and processes. One of STEM
training related fields is an integrated problem-based
Mathematics training.
The results of the research study regarding the
development of teachers’ STEM competencies have
shown that most of them are not aware of the pe-
culiarities of students’ STEM competencies forma-
tion. And some contradictions between the necessity
to form the students’ STEM competencies and insuf-
ficient attention to the training of future teachers of
Mathematics occur.
One of the most effective tools for STEM-based
Mathematics teaching is the system of dynamic math-
ematics, e.g. GRAN 2D tool and cloud-based Ge-
oGebra. Lavicza et al. (Lavicza et al., 2020) claim
that GeoGebra was designed to integrate arithmetic,
a
https://orcid.org/0000-0003-2125-2242
b
https://orcid.org/0000-0003-0493-8429
c
https://orcid.org/0000-0003-0505-0800
algebra, geometry, calculus, statistics. In recent times
it is supposed to support STEM subjects as a single,
integrated system available on most technology plat-
forms. Moreover, teachers and students are offered
free access to it all over the world. GeoGebra was
originally created to integrate Algebra and Geometry
into a single environment. GeoGebra enables to use
such new technologies as Augmented (Striuk et al.,
2018) and Virtual Reality (Lavrentieva et al., 2020),
3D Printing (Hevko et al., 2020) and MID (Modlo
et al., 2019) in the learning Mathematics.
The use of GeoGebra Dynamic Mathematics in
Stereometry teaching will enhance the formation of
students’ STEM competencies. It can also be help-
ful in the formation of key mathematical and digi-
tal competences (Astafieva et al., 2020; Moiseienko
et al., 2020), self-study competences, as well as in the
development of spatial thinking.
In order to encourage Mathematics and Computer
Science teachers to implement the elements of STEM
education, it is suggested the cloud-based learning
tools, such as GeoGebra, be used in the learning pro-
cess.
The 3D Graphics application (3D feature graphs,
surface, and 3D geometry) can be used while develop-
576
Kramarenko, T., Pylypenko, O. and Serdiuk, O.
Digital Technologies in Specialized Mathematics Education: Application of GeoGebra in Stereometry Teaching.
DOI: 10.5220/0010926300003364
In Proceedings of the 1st Symposium on Advances in Educational Technology (AET 2020) - Volume 1, pages 576-589
ISBN: 978-989-758-558-6
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

ing the visuals with AR. The application is now avail-
able not only for users of gadgets in the iOS operating
system, but also for Android version 4.0 and higher.
This program includes some examples of 3D mathe-
matical objects that can be placed, such as on a desk-
top, floor, or any other flat surface. The fixed models
will be managed. They can be resized. Such visual-
ization will allow you to see more mathematics in the
surrounding world.
More detailed information about the application
3D Graphics can be found in our article (Kramarenko
et al., 2019b), teaching aids visualization during lec-
tures and practical classes, in particular in Mathemat-
ics, allows students to understand the learning mate-
rial better, to increase the applied orientation of learn-
ing and the communication competence both learners
and teachers.
Gartner attributes Artificial Intelligence Edu-
cation Applications, Conversational User Inter-
faces, Blockchain in Education, Immersive Tech-
nology Applications in Education, Design Thinking,
Competency-Based Education Platforms and Adap-
tive Learning Platforms to the main tendencies of us-
ing ICT in education (Panetta, 2019).
Since augmented reality technology already has
an important place in innovative development, it can
also have significant potential for implementation in
Mathematics learning. That is why this technology
needs more detailed study. Because augmented real-
ity is intrinsically linked to 3D construction, its usage
in conjunction with Dynamic Mathematics systems
like GeoGebra, can significantly increase the level
of visualization in Mathematics and enhance students
learning. In addition, Augmented Reality can be-
come a tool for enhancing STEM-based learning for
students majoring in Mathematics and Computer Sci-
ence.
2 LITERATURE REVIEW
According to the recommendation of the European
Commission (EC, 2018), competence is defined as a
combination of knowledge, skills and attitudes. In the
updated list of key competences of a personality eight
major ones are emphasized (EC, 2018). We are keen
to foster the development of students’ STEM compe-
tencies: mathematical competence and competence in
science, technology and engineering.
Rakov et al. (Rakov et al., 2009) explores the
possibilities of mastering mathematical competencies
in the learning by future teachers through the re-
search approach using the system of dynamic math-
ematics DG. The scientist distinguishes procedural,
logical, technological, research and methodological
competencies of Mathematics teacher. In particular,
methodological competence implies the ability to as-
sess the appropriateness of using mathematical meth-
ods to solve individual and social issues.
Consider in detail the opportunities which GeoGe-
bra gives to a teacher. Hohenwarter et al. (Hohen-
warter et al., 2008) emphasize a significantly impor-
tant role of free open-source software for teaching
mathematics world-wide. Open-source software do
not only offer opportunities for teachers and students
to use them both at home and in the classroom with-
out any restrictions, but they also provide the tools
for developing support and user communities reach-
ing across borders. Such collaboration as well con-
tributes to the equal access to technological resources
and democratization of learning and teaching mathe-
matics.
GeoGebra is available in multiple languages. Us-
ing GeoGebra a teacher can create interactive mate-
rials to solve the main tasks of teaching Geometry –
the development of spatial imagination, practical un-
derstanding and logical thinking.
GeoGebra can be used both in standalone and on-
line modes on mobile Internet devices (MID) which
offer new opportunities to improve learning and
teaching either inside or outside of classrooms. Fur-
ther advantage of GeoGebra is the Resources tab con-
taining a number of teaching materials: textbooks, ar-
ticles, instructions, and illustrations. Also, a regis-
tered users can share their own educational materials
on the official website via GeoGebraTube (this is a
kind of file-sharing site). Its essential feature is that
the created dynamic constructions can be accessed
online via the use of View Sheet tool. Any user is
allowed to comment on GeoGebraTube content.
A user is provided with a possibility to create their
own GeoGebraBook, a folder where selected materi-
als can be added and subfolders can be created. A
user can publish a game, a collection of visuals, lesson
workbook that may include text messages, GeoGe-
bra models, web pages, questions, videos, images and
manuals public to anyone. GeoGebraTube content
can be shared via social networks Facebook, Twitter,
emailed and uploaded to Google Drive. Cloud-based
tools affect favourably teacher-student interactions in
an informal learning environment.
Dikovi
´
c (Dikovi
´
c, 2009) statistically confirms the
fact that the use of GeoGebra applications in learning
calculus had a positive effect on the development of
students’ reasoning and visualization skills.
The issues of using GeoGebra are highlighted
in (Drushlyak et al., 2020; Semenikhina, 2017; Se-
menikhina and Drushliak, 2014). Application of Ge-
Digital Technologies in Specialized Mathematics Education: Application of GeoGebra in Stereometry Teaching
577

oGebra 5.0 to the solution of solid geometry problems
has been analyzed in (Semenikhina and Drushliak,
2014). Examples of solid geometry problems with
detailed solution and learning clues have been pre-
sented. Among them there are problems on auxiliary
section, polyhedron net, locus problems, space trans-
formations etc. Semenikhina (Semenikhina, 2017)
discusses the relevance of the study of the dynamic
Mathematics software for future teachers of Mathe-
matics in Ukraine.
The purpose of study by Zetriuslita et al. (Zetrius-
lita et al., 2021) was to identify improvements in Self
Efficacy and selfregulated through GeoGebra Based
Teaching seen from the level of students’ initial math-
ematical abilities. The research method used was a
mixed-method with a sequential explanatory strategy,
while the research design was an untreated control
group design with pretest and posttest. the experi-
mental group obtained direct learning using GeoGe-
bra software while the control group obtained conven-
tional learning. The population in this study were uni-
versity students of mathematics education department
at the Islamic University of Riau who took the field
and space analytic geometry course. The research in-
struments used were self-efficacy questionnaire and
self-regulated questionnaire for getting quantitative
data and interview guidelines for getting qualitative
data. It was concluded that GeoGebra based teach-
ing was effective in improving students’ self-efficacy
and self-regulated. Judging from the level of students’
initial mathematical abilities, there was an increase
in self-efficacy and self-regulated through GeoGebra
based teaching from both high, medium and low lev-
els.
Modelling implies simplifying thus providing the
model with its own characteristics, independent from
the original reality. Consequently, geometry, in its
interpretation and processing, acts like a new reality
both abstract in its logic and concrete in its represen-
tation modes.
Richard and Blossier (Richard and Blossier, 2012)
begin with classical theories of modelling representa-
tion processes in order to apply them to 3D dynamic
geometry software, GeoGebra3D, computing devel-
opment seeking to bring geometric models closer to
the reality of a school setting. The authors intro-
duce three key notions, developed from Mathematics
teaching, in order to support the exploration of two
interaction situations between mathematics and their
teaching. Finally, they finish on a few general consid-
erations for the teaching of mathematics.
A number of works of scientists and software de-
velopers are devoted to the research of integration is-
sues of the augmented reality technology into the ed-
ucational process. In particular, (Brzezinski, 2019;
Striuk et al., 2018), focus on the general trends and
special issues of the augmented reality application in
education.
In teaching Stereometry, the assignment work-
sheets on the construction of sections through the
trace method, internal projection and combination
method by Sidoruk (Sidoruk, 2018) should be taken
into consideration. Each of the assignments is pro-
vided with the possibility of step-by-step procedure
of the construction building. Thus, students are given
an opportunity to develop both mathematical compe-
tence and the ability to learn independently. Some as-
signments include constructions created on a 3D can-
vas.
Fariha and Lestari (Fariha and Lestari, 2019) de-
scribe in detail how to realize the Dandelin Sphere
more realistically, using GeoGebra Classic 5, which
supports the creation of 3D images.
At a profound methodological level, a number
of assignments on combinations of geometrical solid
shapes was created by Rykovskyi (Rykovskyi, 2018).
These models are designed as constructions of plane
geometric shapes through the use of parallel projec-
tion properties. They are intended to be used to vi-
sualize the properties of geometrical shapes. How-
ever, students might face a challenge with reproduc-
ing models as the algorithm of the construction and
details of the construction are not available for them.
The models are designed as constructions of plane
geometric shapes with the use of the properties of par-
allel projection. In particular, a book / collection of
visuals covering the topic “Prism” is recommended.
There is a number of visuals that represents combi-
nations of stereometric shapes: sphere and pyramid,
sphere and prism, sphere and cylinder etc. Consider
the visual “There is a cone inscribed in the sphere.
And there is the right triangular pyramid inscribed
into the cone. A pyramid is inscribed in the sphere”.
Even the name itself suggests that integrity is inher-
ent to visuals. It can be used in the process of teach-
ing Stereometry in school or teaching Methodology
of Mathematics on various topics. While using vi-
sual aids, users are advised to study the properties of
shapes inscribed into the sphere, to look into the re-
lationship between the sphere radius, radius of cone
base, the height of the cone and element of the cone.
These visuals are equipped with the Checkbox
tool which allows a user to do the revision and answer
to the questions: Which cone is called inscribed into
the sphere? What element of the cone is the center
of the sphere? Which pyramid is called inscribed in
the cone? Which pyramid is called inscribed into the
sphere? How to find the axial section of the cone?
AET 2020 - Symposium on Advances in Educational Technology
578

Which circle of the sphere is called a great circle?
Which properties of the diameter of the sphere per-
pendicular to its great circle?
Mobile applications such as Geometry, Graphing
Calculator, 3D Graphing Calculator have been rela-
tively recently launched and now they are available
on the official GeoGebra website. These applica-
tions are still undergoing improvements. However,
the methodology of their use, and especially in teach-
ing Stereometry, is not yet well developed. Therefore,
this paper aims at elucidating the features of creating
visuals with GeoGebra and their use in teaching how
to solve Stereometric problems.
3 RESULTS
3.1 GeoGebraBook “Models for
Stereometric Problems” as Training
Manual on the Methodology of
Teaching Mathematics
The methodical materials of the paper authors related
to the use of the GRAN software are presented in the
manual “Innovative information and communication
technologies of teaching Mathematics”. The issue of
GeoGebra use has been considered in an updated ver-
sion of the manual (Kramarenko et al., 2019a). On
the GeoGebra site, users can find the materials which
contain relevant visuals at GeoGebraBook “Models
for stereometric tasks” (Kramarenko, 2019). One can
find here problem situations to be solved by students
independently, self-assessment tests.
The study of the effectiveness of the use of Ge-
oGebra mobile applications in the process of teaching
Stereometry was conducted by us within the prepara-
tion of future teachers of Mathematics during Mathe-
matics teaching methodology classes, advanced train-
ing courses at Kryvyi Rih State Pedagogical Univer-
sity, in teaching students of Kryvyi Rih State Col-
lege of Economics and Technologies, and students
of classes with mathematical specialization of Kryvyi
Rih schools.
Particular interest in using GeoGebra was shown
during the advanced training courses by Kryvyi Rih
teachers of Mathematics who have been working at
school for a considerable time. The study was also
conducted on the effectiveness of the use of GeoGe-
bra applications by students in order to enhance stu-
dents’ motivation during extra-curricular vocational
activities at the university. And it was studied as well
during the course of Sereometry lessons conducted by
masters majoring in Mathematics education complet-
ing professional practice in secondary education insti-
tutions.
When using applications, it is useful for a student
to be able to reproduce the construction in the browser
window, open other temporarily hidden drawing ele-
ments in case of necessity, and receive text notifica-
tions. However, a considerable number of construc-
tions should be created later or simultaneously with
the viewing via the mobile application.
Consider the peculiarities of the implementation
of specific constructions and provide recommenda-
tions concerning their use.
One of the main issues that school students and
students of higher education establishments face is
the recognition of a 2D drawing representing the im-
age of a 3D shapes. In order to develop the spatial
imagination of students at schools and universities it
is necessary to provide them with the assignments on
constructing sections of polyhedron by planes.
3.2 Construction of Sections of
Polyhedron With Plane via the
Applications GeoGebra Geometry
and 3D Graphics
Consider examples of problems for constructing a
section of a polyhedron with a plane passing through
three given points that are not on the same line;
through a straight line and a point that does not belong
to it etc. It is necessary to construct a linear angle of a
dihedral angle and measure them; the angle between
the straight line and the plane.
Look into what four approaches to constructing a
section of a polyhedron in a plane which should be
distinguished by a teacher in order to be able to pro-
vide their students with the most appropriate one for
their educational trajectory (Kramarenko et al., 2020).
If a student has not fully mastered GeoGebra
tools, it is advisable to provide them with a sheet of
paper guiding the algorithm to follow in order to build
a construction. Moreover, a student should be sup-
plied with information regarding the icons that cor-
respond to the tools in question. It is appropriate to
place QR codes on printable worksheets for demon-
strations.
1. The construction on a 2D canvas is rather cum-
bersome and requires logically justified steps for
the construction. At first, it is necessary to fol-
low step-by-step construction procedures to build
several drawings, created via “the trace method”
on a 2D canvas. To intensify the material dissem-
ination, students may be at once provided with a
constructed polyhedron. However, in the course
Digital Technologies in Specialized Mathematics Education: Application of GeoGebra in Stereometry Teaching
579

of the study, there were cases when the students
constructed the polyhedron wrongly. That is, after
its construction on the plane, they were not able
to change it dynamically. For example, to build a
prism image on a 2D canvas made of an n-sided
polygonal base (n > 3), it is necessary to follow
the following steps. Firstly one should build an n-
sided polygon via the use of the appropriate tool.
Then it is preferable to build a vector along one of
the edges of the prism. Further, one should apply
a parallel translation of the n-sided polygon to the
constructed vector. The given vertexes are con-
nected. Such a construction is represented taking
into account the properties of the parallel projec-
tion.
2. Next it is necessary to compare the previous draw-
ing with the one presented according to the same
problem situation but on the 3D canvas. In this
case, all straight lines for the construction of the
section can be presented step by step. The advan-
tages of such a construction include the possibil-
ity to change the constructed polyhedron dynam-
ically and the location of points which the secant
plane passes through. Via the GeoGebra 3D Ge-
ometry (GeoGebra Team German, 2018) app, one
can simulate external actions aimed at geometri-
cal solid shapes which are necessary for a stu-
dent to be able to apply internal thinking regarding
them and as a result develop spatial thinking. In
our opinion, this approach is the most appropriate
for the development of students’ spatial imagina-
tion, logical thinking. In figure 1 the construction
of the section of the prisms with a secant plane
which passes through the point on the lateral edge
and a straight line drawn in the plane of the base
is presented.
3. The third option for constructing a section on the
3D canvas. Firstly, a polyhedron, and a secant
plane should be built, and then the tool “Inter-
section of two surfaces” should be applied. A
student, by “turning” the polyhedron, will have
an opportunity for the better perception and un-
derstanding of the construction. The approach
in question is appropriate when augmented real-
ity tools are used enabling to align the drawings
with the image of a real object (Kramarenko et al.,
2019b). It is advisable to encourage students to
find examples of such sections among the sur-
rounding objects, in architecture etc.
4. The use of both 2D and 3D canvases simultane-
ously. Such a combination is advisable if there is
some kind of difficulty in constructing a polygon
that is for a base of the pyramid or specifying the
position of the vertex of the pyramid, etc. For in-
stance, if a trapezoid, in particular, a rectangular
or equilateral one, is for a base of the pyramid or
prism (figure 2).
It is worth pointing out that such constructions can
only be built in the classic version of GeoGebra, and
the construction preview may also be available via
MID after uploading the file to the GeoGebra cloud
repository.
3.3 The Peculiarities of the Definition
and Angle Construction between
Planes and Linear Angle of the
Dihedral Angle
Via the assistant of GeoGebra (3D canvas) it is pos-
sible to build the base of the pyramid (OXY) on the
canvas, and in the process the constructions can be
synchronously displayed on the 3D canvas (figure 3).
Attention should be drawn to the convenience and
ease of the construction with the help of the linear an-
gle of the dihedral angle at the base. According to
the definition, to determine the linear angle of the di-
hedral angle at the base a plane perpendicular to the
edge of the dihedral angle should be drawn. Then
the angle between the rays formed as a result of the
intersection of this plane with the edges of the dihe-
dral angle will determine its linear angle (Bevz et al.,
2011).
It should be stated that the measure of the angle
between the planes varies from 0
◦
to 90
◦
. While the
measure of the dihedral angle can vary from 0
◦
to
360
◦
(Rykovskyi, 2018). Here is an example of the
problem from the textbook with major in Mathemat-
ics (No. 836, (Bevz et al., 2011)).
At the base of the pyramid there is an isosceles
triangle with angle β at the vertex and radius R of the
circle described. The plane of each face of the pyra-
mid forms an angle α with the plane of the base. Find
the area of the side surface.
It is recommended to use 2D and 3D canvases si-
multaneously to represent the drawing corresponding
to the set problem (Kramarenko, 2019).
The reason why mistakes are often made is that
only one case is under consideration. Whereas the
concept of “angle between the plane of the lateral face
and the plane of the base” is substituted by “dihedral
angle at the base”. If the problem situation said that
“dihedral angles at the base were congruent”, then we
would consider the pyramid the vertex of which is
projected into the center of the circle inscribed into
the triangle of the base (Pyramid of Type 1).
Since it concerns only congruent angles between
planes, the problem will have two solutions. It is also
AET 2020 - Symposium on Advances in Educational Technology
580

Figure 1: Construction of a section of the prisms with a plane.
Figure 2: Construction of a prism, using both 2D and 3D canvas simultaneously.
necessary to take under consideration the case when
one of the dihedral angles at the edge of the base is
obtuse (Pyramid of Type 2). In this case, the vertex
of the pyramid is projected into the center of the in-
scribed circle lying outside (figure 3).
Using the problem mentioned above and similar
ones we have conducted a research on the basis of
the two 11th grade classes specialized in Mathemat-
ics, and in particular with the teachers of Mathemat-
ics Svitlana Shakhmatova and Ruslan Kaluhin (Kra-
marenko et al., 2019a). 16 students of the experimen-
tal group (EG students) and 18 students of the con-
trol group (CG) have participated in the research. The
similar research has also been conducted at the ad-
vanced training courses among the teachers of Math-
ematics in Kryvyi Rih State Pedagogical University
Digital Technologies in Specialized Mathematics Education: Application of GeoGebra in Stereometry Teaching
581

Figure 3: Image of the pyramid and linear angles.
(group 1 – 22 teachers, group 2 – 26 teachers). Some
teachers among the participants of the courses did not
teach students in high school that is why they do not
deal with solving these very problems in their teach-
ing.
The suggested questionnaire consisted of several
questions and corresponded mainly to the Pyramid of
Type 2. The participants were supposed to deal with
the questions during the problem solving. Alongside
the questionnaire we present the results of the survey.
1. On reading the problem situation, have you distin-
guished two types of the Pyramid?
A positive answer: EG – 1 student (6%), CG – no
students (0%), group 1 – 5 teachers (23%), group 2 –
6 teachers (23%).
2. The participants received a clue about the way it
is possible to construct the Pyramid with the ob-
tuse dihedral angle at the base (Pyramid of type
2). The question was the following: Is it possible
to construct the vertex of the pyramid projection
on the plane base and in fact the Pyramid itself?
A positive answer: EG – 6 students (28%), CG –
5 students (28%), group 1 – 12 teachers (55%), group
2 – 13 teachers (50%).
3. First, a dynamic model, constructed with GeoGe-
bra, was demonstrated to the participants. The al-
gorithm of the Pyramid construction via the use
of the tool GeoGebra Construction Steps was dis-
played. The task was to construct the Pyramid
of Type 2 and create a problem solving algorithm
individually. Next, a paper Pyramid model was
demonstrated to the participants. The algorithm
of the construction was discussed. The task was
to construct the Pyramid of Type 2 and create a
problem solving algorithm.
A positive answer: EG – 12 students (75%), CG –
8 students (44%), group 1 – 19 teachers (86%), group
2 – 17 teachers (65%). Fisher’s angular transforma-
tion (Stevens, 1953) was used for the research results
processing. For this purpose, the task performance
proportions in the groups during the first and second
stages were compared.
ϕ (EG, CG) = 0,61 < 1,64; ϕ (group1, group2) =
0,31 < 1,64: the received results do not differ consid-
erably both in the groups of students and teachers.
After stage 3, the proportions of successful task
performance in groups were compared one more time.
ϕ (EG, CG) = 1,85 > 1,64; ϕ (group1, group2) = 1,73
> 1,64: the results differ significantly this time.
It has been defined that the use of dynamic models
created with GeoGebra was more effective in compar-
ison with the static paper ones.
On discussing the use of dynamic models created
with GeoGebra, participants pointed out the follow-
ing advantages: variability; dynamic visuals which
enhance the development of spatial imagination; mul-
tiple reproducibility of the construction, which will
contribute to the development of algorithmic think-
ing.
AET 2020 - Symposium on Advances in Educational Technology
582

3.4 Tasks on Combinations of
Polyhedron and Solids of Revolution
Consider the way it is possible to inscribe a sphere
into the right rectangular pyramid via the use of 3D
Geometry. In order to construct the base of the pyra-
mid, it is necessary to use the Right Polygon tool, by
pointing two points on the 3D canvas – adjacent ver-
texes of the base, and indicating that the right polygon
has 4 vertexes. Then one should construct the diago-
nals of the square (the Segment tool) and define the
center (Intersection point). Then through the center
of the square, which is also the center of the circle
inscribed in the square, one draws a straight line per-
pendicular to the plane of the square. On this straight
line, one chooses an arbitrary point (Point on the ob-
ject) and constructs a polyhedron (Pyramid). The per-
pendicular to the plane of the square straight line is
the geometric location of points, equidistant from the
sides of the base of the right pyramid.
To determine the position of the center inscribed
sphere in the pyramid, one constructs a geometric lo-
cation of points that are equidistant from the edges of
the dihedral angle at the base of the pyramid. Since
there is no construction of the bisector plane in the
GeoGebra tools, it is necessary to construct a linear
angle of the dihedral angle at the base and then bi-
sector of the very angle. The plane passing through
the vertex of the pyramid perpendicular to the edge of
the base is built (Plane through the point perpendicu-
lar to the straight line; Intersection point). Instead of
a plane, it is possible to draw a straight line from the
vertex of the pyramid perpendicular to the edge of the
base (straight, perpendicular to straight). Next, one
should find the intersection point of the constructed
plane / perpendicular with the edge of the base (Inter-
section point of the straight line and the plane / Inter-
section point of two straight lines). Then one builds
the bisector of the obtained linear angle.
The point of its intersection with the perpendicu-
lar to the base of the pyramid, drawn from the top of
the pyramid, will determine the center of the inscribed
sphere (Point of intersection). Finally, one constructs
the inscribed sphere (Sphere outside the center and ra-
dius), specifying in sequence the center of the sphere
and the point of intersection of the diagonals of the
square (Kramarenko et al., 2020).
For better understanding and mastering of the
algorithm the construction of the sphere inscribed
around the pyramid the students setting of the can-
vas are adjusted to be able to show the step-by-step
procedure of the construction.
With AR, the students can understand the basic
concepts of 3D geometrical shapes, their relationships
and ways to construct the 3D shapes and the objects
in 3D space. Importantly, AR can provide a dynamic
visualization of 3D structures of geometrical shapes.
This feature helps the students to understand a com-
prehensive background of 3D geometrical shapes and
improve the abilities of geometrical structures. More-
over, the hand gesture based interactions furnish an
intuitive and convenient way for the students to di-
rectly control and interact with geometrical shapes in
3D space.
GeoGebra Augmented Reality application allows
you to transfer the constructed figure into the space of
the room (figure 4). Having built a figure, we press
the “AR” button. Next, you need to use the camera
to select the environment in which we plan to move
the object. For example, on the table. By tapping on
the screen, the figure will be transferred to the real
world (Kramarenko and Pylypenko, 2021b) where it
can be explored. The phone camera will serve our
eyes. Immersing the phone in a virtual figure we will
see it from the inside, we can bypass it, also the ap-
plication allows you to resize, color (Kramarenko and
Pylypenko, 2021a).
With the experiences of interacting with the 3D
shapes using their own hand gestures, the students
can improve their own awareness of the relationships
of the 3D shapes and easily remember or retain the
knowledge about the 3D shapes.
3.5 Stereometric Problems of Applied
Content
Geometry is an abstract science, often taught without
proper implementation of its applied orientation. This
leads to the fact that a significant part of students do
not feel the need to study this subject, because they
do not see the possibility of using the acquired geo-
metric knowledge, in particular in stereometry, in the
future. And so there is a need to connect stereometric
problems with life. We propose to consider two prob-
lems of applied direction, for the solution of which
we consider it expedient to involve the GeoGebra 3D
application. We offered these tasks to students of the
State University of Economics and Technologies.
Problem 1. What percentage of wood goes to
waste when made of wooden logs, 5 m long and 20
cm and 15 cm in diameter, beams with a rectangular
cross-section of the maximum cross-sectional area?
Problem 2. Calculate the volume of the largest
beam with a base in the shape of a rectangle, which
can be carved from a log of cylindrical shape. The
length of the log is 5 m and the thickness is 20 cm.
What percentage of wood will go to waste?
Using these tasks, we conducted research on the
Digital Technologies in Specialized Mathematics Education: Application of GeoGebra in Stereometry Teaching
583

Figure 4: GeoGebra AR demos.
basis of two parallel groups majoring in “Finance and
Credit”. 18 students of the experimental group (EG)
and 17 students of the control group (CG) took part in
the study. In the experimental group, the task was to
solve problems based on a dynamic figure, the control
group solved the same problems, but with the help of
static.
The proposed questionnaire consisted of several
questions that students answered while solving prob-
lems.
1. What figures will we work with? Positive answer:
CG – 6 students (35%), EG – 7 students (39%).
2. How are the figures relative to each other? Posi-
tive answer: CG – 7 students (41%), EG – 7 stu-
dents (39%).
3. What shape should be the cross section of the
beam to maximize its size? The volume of the
beam will be the largest if the cross section of the
beam is square. It is not necessary to compose a
function and study it to the extreme, it is enough
to use the formula to calculate the area of a quadri-
lateral inscribed in a circle. Positive answer: CG –
4 students (24%), EG – 3 students (17%).
In the second stage, the CG group was shown a
figure for the problem on paper, the EG group was
shown a figure in GeoGebra (figure 5) and consid-
ered in dynamics.
4. After that, the groups were asked the last question
about the cross-section again, the statistics of pos-
itive answers improved: CG – 6 students (35%),
EG – 9 students (50%).
5. What is meant by waste from the manufacture of
logs? The positive answer that this is the differ-
ence between the volume of the truncated cone
and the volume of the parallelepiped was given
by: CG – 9 students (53%), EG – 12 students
67%.
The dynamic image in GeoGebra helped the EG
AET 2020 - Symposium on Advances in Educational Technology
584

Figure 5: A parallelepiped inscribed in a truncated cone.
group to improve the statistics of responses, after the
demonstration of the figure on paper this effect could
not be achieved. The results of the survey showed that
the highest efficiency is achieved when demonstrating
dynamic models.
Optimization tasks using Geogebra were proposed
by us in the textbook (Kramarenko and Pylypenko,
2021b). We supplemented the sets of tasks using Ge-
ogebra with visual aids for specialized teaching of
mathematics, realization of interdisciplinary connec-
tions of the beginnings of mathematical analysis and
stereometry. In this case, you can use the expressions
to calculate the volume of the body to track the change
in this value and find the optimal size of the beam. It
is also advisable to use the “Function Inspector” tool
in GeoGebra to find the extreme values of the function
and visualize the abstractions.
It is convenient to write the formulas on the canvas
at once, and then open them step by step during the
discussion. To make such a blank in the application
GeoGebra 3D, you must first build a truncated cone
(by crossing the cone plane), then through the center
of a smaller circle and a point on it build a line. Draw
a perpendicular line to the obtained line, choosing the
center of a smaller circle as a point. Mark the points
of intersection of the lines with the circle and through
the obtained 4 points build a square (using the Poly-
gon tool), connecting the points in series. From the
vertices of the square we lower the perpendiculars to
the lower base of the cone (larger circle) and mark the
points of intersection of the perpendiculars with the
plane of the base of the cone, through the obtained 4
points we build a square, connecting the points in se-
ries. Using the Prism tool, build a prism by selecting
a polygon of the base (square) and the vertex at one
of the points of the smaller circle.
During the in-depth study of mathematics at the
Kryvyi Rih Pokrovsky Lyceum, we offered students
the problem of stereometry for optimization accord-
ing to the textbook (Skanavi, 1990). After calculating
the optimal dimensions of the prism / pyramid, the
polygon scan was drawn and glued. Models in dy-
namics created by means of system of dynamic math-
ematics were offered for demonstrations. Here are ex-
amples of mathematical problems that students had to
reformulate as problems of applied content.
1. (15.194) What are the dimensions of the base ra-
dius and the height of the open cylindrical tank, so
that at a given volume V for its manufacture was
spent the least amount of sheet metal?
2. (15.195) The side face of a regular quadrangu-
lar pyramid has a constant given area and is in-
clined to the plane of the base at an angle α. At
what value of α is the volume of the pyramid the
largest?
Digital Technologies in Specialized Mathematics Education: Application of GeoGebra in Stereometry Teaching
585

3. (15.196) In a regular quadrangular pyramid with
the edge of the base a and the height H, a regular
quadrangular prism is inscribed so that its lower
base is located at the base of the pyramid, and the
vertices of the upper base are placed on the side
edges. Find the edge of the base and the height of
the prism that has the largest side surface.
4. (15.197) The side edge of a right triangular pyra-
mid has a constant given length and forms an an-
gle α with the plane of the base. At what value of
α will the volume of the pyramid be the largest?
5. (15.198) In a regular triangular pyramid, the side
face has a constant given constant area and forms
an angle α with the plane of the base. At what
value of α is the distance from the center of the
base of the pyramid to its side face the largest?
6. (15.199) A pyramid is inscribed in a cone with
a given constant volume, which is based on an
isosceles triangle with an angle at the vertex equal
to α. At what value of α is the volume of the pyra-
mid the largest?
7. (15.200) The generating cone has a constant
length and forms an angle α with the height of the
cone. A regular hexagonal prism with equal edges
is inscribed in the cone (the base of the prism is
located in the plane of the base of the cone). At
what value of α is the side surface of the prism the
largest?
Solving problems of applied content will provide
an opportunity to motivate, intensify the educational
and cognitive activities of students and promote the
practical application of acquired knowledge.
3.6 Project Work in GeoGebra 3D
One of the effective means of developing students’
cognitive activity is the project method. After all,
the project method includes a set of research, search,
problem, creative approaches, promotes the creative
development of students, prepares them to solve prob-
lem situations in everyday life. Therefore, it is advis-
able to offer students to perform mini-projects while
studying the section of stereometry.
The task of the project will be to build a
playground in the GeoGebra 3D application, using
the maximum number of studied geometric shapes:
prisms, pyramids, spheres, cones, cylinders, etc. (fig-
ure 6). Performance appraisal is a mandatory element
of the organization of project work. The effectiveness
of the project lies in the ratio of planned expectations
with the final results. Created designs can be designed
in the yard with an augmented reality application.
There are three stages of self-regulated, namely
the Planning Phase, at this stage students set steps
for learning, namely (1) Analyzing learning tasks,
(2) Determining learning objectives, and (3) Planning
learning strategies. In the analyzing stage, students
implement a plan that is constantly monitored to en-
sure it leads to learning goals. In the determining
stage, students determine how well the learning strat-
egy is chosen and how to achieve these learning goals
(Tomaschko et al., 2018).
Students were also asked to develop a project
“Artist’s Room”, in which students will model a room
from improvised means, and before that it is advis-
able to offer to make a layout in GeoGebra. In this
way, students will already know where to start, what
sizes of objects to take, what colors will impress, what
shapes are needed to create a room, they will learn
to break an object into simple geometric bodies and
shapes.
Project work interests students in the subject, in-
creases mental activity and creative thinking, helps
to mobilize knowledge in practice and quickly adapt
to unusual situations. During the construction of a
playground or an artist’s room, students use inno-
vative abilities, invention, STEM competencies are
formed, such as critical thinking, creativity, organiza-
tional skills, teamwork, emotional intelligence, ability
to interact effectively, cognitive flexibility.
4 CONCLUSIONS AND
PROSPECTS FOR FURTHER
RESEARCH
1. Investigating the possibilities of using GeoGebra
in the learning calculus and geometry, found out
that engaging students to research using GeoGe-
bra helps to expand the range of educational tasks,
including STEM problems. This allow to achieve
the high level of learning motivation and individ-
ualize the learning process.
2. Implementation of applied aspect in teaching
mathematics using GeoGebra 3D Calculator with
AR will help to solve one of the main problems of
STEM education –individualization. We can ex-
plore AR objects because this application brings
3D math to the real world. Systematic using of
GeoGebra 3D Calculator with AR can help to de-
velop students’ research skills, enhance their so-
cialization opportunities through the acquisition
of ICT, which should lead to the systematic de-
velopment of universal STEM competencies.
AET 2020 - Symposium on Advances in Educational Technology
586
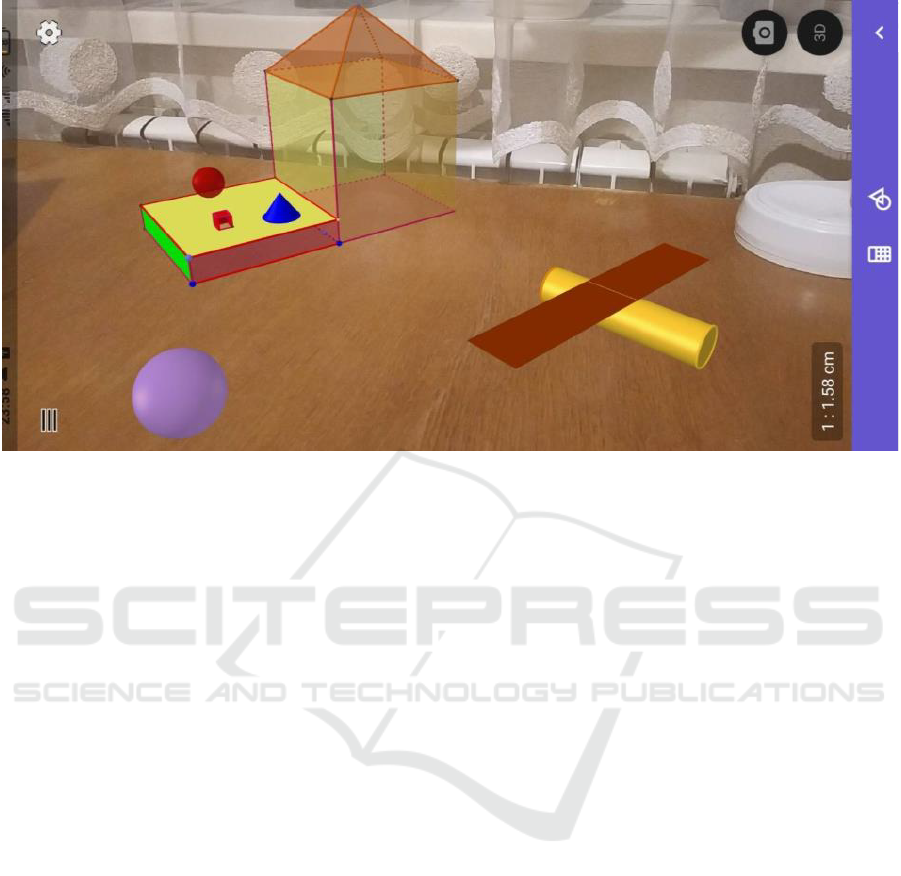
Figure 6: Sample implementation of the project “Playground”.
3. The use of dynamic geometry software GeoGe-
bra as a modeling tool makes it possible for scien-
tific experimental logic to engage students in dis-
covering new mathematical facts. Teachers who
are concerned by the issues of instrumented learn-
ing help to create activities which imply that the
main students’ motivation is in the understanding
of mathematical concepts.
4. In the process of Stereometry teaching, it neces-
sary to divide the students into subgroups accord-
ing to the type of spatial thinking. This will con-
tribute to the implementation of the individual ap-
proach to the development of the spatial imagina-
tion, taking into account individual peculiarities,
gradually complicating the task, supplementing
the teaching material with visual aids, focusing on
the practical application of knowledge. Actions
with the models created with GeoGebra serve as
an intermediate link between external actions with
geometrical solid shapes and internal mental pro-
cesses. Thinking must precede the external ones
to engage and develop a person’s imagination.
5. In order to increase the efficiency of the percep-
tion and assimilation of stereometric material, to
overcome the difficulties in transcoding the sym-
bols of a spatial body and to create an adequate
spatial image, it is necessary to supplement the
theoretical material with multimedia demonstra-
tion models created by the means of ICT, to en-
courage students and to engage them in the pro-
cess of creating such models for classes indepen-
dently. After all, the acquisition of mathematical
competence depends not on memory, but on the
activity in which the person is involved, on the
system of mental operations that they perform in
the process of knowledge acquisition.
6. In general, the result of the research study is the
improvement of teaching methods of Mathemat-
ics via the use of cloud technologies, the imple-
mentation in the educational process of method-
ological materials of pedagogically balanced and
appropriate blending of traditional and innovative
learning tools, which contribute to the intensifica-
tion of teachers’ readiness for the use of STEM
training in teaching.
In the future, it is necessary to explore the condi-
tions for the effective use of other GeoGebra mobile
applications in STEM learning.
REFERENCES
Astafieva, M., Zhyltsov, O., Proshkin, V., and Lytvyn, O.
(2020). E-learning as a mean of forming students’
mathematical competence in a research-oriented ed-
ucational process. CEUR Workshop Proceedings,
2643:674–689.
Bevz, H., Bevz, V., Vladimirova, N., and Vladimirov, V.
(2011). Geometry 11 grade. Geneza, Kyiv.
Brzezinski, T. (2019). GeoGebra 3D with AR (iOS): Explo-
rations & Lesson Ideas. https://www.geogebra.org/m/
rmfptnzu.
Dikovi
´
c, L. (2009). Applications GeoGebra into teaching
some topics of mathematics at the college level. Com-
Digital Technologies in Specialized Mathematics Education: Application of GeoGebra in Stereometry Teaching
587

puter Science and Information Systems, 6(2):191–
203.
Drushlyak, M. G., Semenikhina, O. V., Proshkin, V. V.,
Kharchenko, S. Y., and Lukashova, T. D. (2020).
Methodology of formation of modeling skills based
on a constructive approach (on the example of GeoGe-
bra). CEUR Workshop Proceedings, 2879:458–472.
EC (2018). Council Recommendation of 22 May
2018 on key competences for lifelong learn-
ing. https://eur-lex.europa.eu/legal-content/EN/TXT/
PDF/?uri=CELEX:32018H0604(01)&from=EN.
Fariha, N. F. and Lestari, H. P. (2019). Construction of
dandelin sphere on definition of conics using geoge-
bra classic 5. Journal of Physics: Conference Series,
1320:012085.
GeoGebra Team German (2018). Learn geogebra 3d calcu-
lator. https://www.geogebra.org/m/aWhYSpvy.
Hevko, I., Potapchuk, O., Sitkar, T., Lutsyk, I., and Ko-
liasa, P. (2020). Formation of practical skills mod-
eling and printing of three-dimensional objects in the
process of professional training of IT specialists. E3S
Web of Conferences, 166:10016.
Hohenwarter, M., Hohenwarter, J., Kreis, Y., and Lavicza,
Z. (2008). Teaching and Learning Calculus with Free
Dynamic Mathematics Software GeoGebra. In ICME
11 – 11th International Congress on Mathematical
Education. Nuevo Leon, Monterrey.
Kramarenko, T. and Pylypenko, O. (2021a). GeoGebra AR
Demo: A sphere described around a right quadrangu-
lar pyramid. Video. https://youtu.be/JSkdu1lgWlg.
Kramarenko, T. and Pylypenko, O. (2021b). GeoGebra AR
Demo: The sphere is inscribed in a pyramid. Video.
https://youtu.be/oohbLc19Llo.
Kramarenko, T., Pylypenko, O., and Muzyka, I. (2020).
Application of GeoGebra in Stereometry teaching.
CEUR Workshop Proceedings, 2643:705–718.
Kramarenko, T. H. (2019). Selected questions of Ele-
mentary Mathematics from GeoGebra. https://www.
geogebra.org/m/gqpk8yfu.
Kramarenko, T. H., Korolskyi, V. V., Semerikov, S. O.,
and Shokaliuk, S. V. (2019a). Innovative informa-
tion and communication technologies of Mathematics
teaching. Kryvyi Rih Pedagogical University, Kryvyi
Rih, 2 edition.
Kramarenko, T. H., Pylypenko, O. S., and Zaselskiy, V. I.
(2019b). Prospects of using the augmented reality ap-
plication in STEM based mathematics teaching. Edu-
cational Dimension, 53(1):199–218.
Lavicza, Z., Prodromou, T., Fenyvesi, K., Hohenwarter,
M., Juhos, I., Koren, B., and Diego-Mantecon, J.
(2020). Integrating STEM related technologies into
mathematics education at a large scale. International
Journal for Technology in Mathematics Education,
27(1):3–12.
Lavrentieva, O., Arkhypov, I., Kuchma, O., and Uchitel,
A. (2020). Use of simulators together with virtual and
augmented reality in the system of welders’ vocational
training: Past, present, and future. CEUR Workshop
Proceedings, 2547:201–216.
Modlo, Y., Semerikov, S., Nechypurenko, P., Bondarevskyi,
S., Bondarevska, O., and Tolmachev, S. (2019). The
use of mobile Internet devices in the formation of ICT
component of bachelors in electromechanics compe-
tency in modeling of technical objects. CEUR Work-
shop Proceedings, 2433:413–428.
Moiseienko, M., Moiseienko, N., Kohut, I., and Kiv, A.
(2020). Digital competence of pedagogical univer-
sity student: Definition, structure and didactical con-
ditions of formation. CEUR Workshop Proceedings,
2643:60–70.
Panetta, K. (2019). 5 Trends Appear on the Gart-
ner Hype Cycle for Emerging Technologies.
https://www.gartner.com/smarterwithgartner/5-
trends-appear-on-the-gartner-hypecycle-for-
emerging-technologies-2019/.
Rakov, S., Gorokh, V., and Osenkov, K. (2009). Math-
ematics, computer mathematical systems, creativity.
In Braman, J., Vincenti, G., and Trajkovski, G., ed-
itors, Handbook of Research on Computational Arts
and Creative Informatics, pages 253–279. IGI Global,
Hershey.
Richard, P. and Blossier, M. (2012). Instrumented
modelling and preliminary conceptions in threed-
imensional dynamic geometry with GeoGebra-3D.
In Bastiaens, T. and Marks, G., editors, Pro-
ceedings of E-Learn: World Conference on E-
Learning in Corporate, Government, Healthcare,
and Higher Education 2012, pages 322–330. As-
sociation for the Advancement of Computing in
Education (AACE), Montr
´
eal, Quebec, Canada.
https://www.learntechlib.org/p/41611.
Rykovskyi, M. Y. (2018). Mykhailo Yosypovych
Rykovskyi. https://www.geogebra.org/u/mirinf.
Semenikhina, O. V. (2017). Methodological approaches
to the formation of professional readiness of math-
ematics teacher for the use of mathematical knowl-
edge computer visualization tools. Pedahohichni
nauky: teoriya, istoriya, innovatsiyni tekhnolohiyi,
2(66):129–138.
Semenikhina, O. V. and Drushliak, M. H. (2014). GeoGebra
5.0 tools and their use in solving solid geometry prob-
lems. Information Technologies and Learning Tools,
44(6):124–133.
Sidoruk, V. A. (2018). Construction of polyhedra sections.
https://www.geogebra.org/m/Jd4va4rs.
Skanavi, M. I., editor (1990). Collection of problems in
mathematics for applicants to universities. Minsk.
Stevens, W. L. (1953). Tables of the angular transformation.
Biometrika, 40(1/2):70–73.
Striuk, A., Rassovytska, M., and Shokaliuk, S. (2018). Us-
ing Blippar augmented reality browser in the practical
training of mechanical engineers. CEUR Workshop
Proceedings, 2104:412–419.
Tomaschko, M., Kocadere, S., and Hohenwarter, M. (2018).
Opportunities for participation, productivity, and per-
sonalization through GeoGebra mathematics apps. In
Khan, A. and Umair, S., editors, Handbook of Re-
search on Mobile Devices and Smart Gadgets in K-12
Education, pages 45–56. IGI Global, Hershey.
AET 2020 - Symposium on Advances in Educational Technology
588

Velikova, E. and Petkova, M. (2019). Analysing students’
creativity in integrating GeoGebra applets in solv-
ing geometrical problems. Baltic Journal of Modern
Computing, 7(3):419–429.
Zetriuslita, Z., Nofriyandi, N., and Istikomah, E. (2021).
The Increasing Self-Efficacy and Self-Regulated
through GeoGebra Based Teaching reviewed from Ini-
tial Mathematical Ability (IMA) Level. International
Journal of Instruction, 14(1):587–598.
Digital Technologies in Specialized Mathematics Education: Application of GeoGebra in Stereometry Teaching
589
