The Development of Creative Thinking as an Important Task of
Educational Process
Arnold E. Kiv
1,2 a
, Kateryna V. Kolesnykova
2 b
, Tatyana I. Koycheva
2 c
,
Alina O. Vinkovska
2
and Ivan I. Donchev
2 d
1
Ben-Gurion University of the Negev, P.O.B. 653, Beer Sheva, 8410501, Israel
2
South Ukrainian National Pedagogical University named after K. D. Ushinsky, 26 Staroportofrankivska Str., Odessa,
65020, Ukraine
Keywords:
Creative Thinking, Lateral Thinking, Testing, Educational Process.
Abstract:
Current trends in improving the educational system involve the parallel acquisition of multifaceted knowledge,
the maximum expansion of horizons and the preparation of students for the optimal choice of profession.
Scientists and methodologists from many countries work in this direction. The solution of these problems is
inextricably linked with the task of developing general intelligence and creative thinking. In this work the role
of lateral thinking in the creative process is discussed. Lateral thinking is an important component of creative
thinking. The article discusses the essence of lateral thinking and possible ways to test it. Here we discuss
also the features of the probability distribution function for various psychological parameters characterizing
the personality. It was noticed that the more universal the psychological parameter, the closer its probability
distribution to the ideal normal distribution. It is shown that the probability distribution of the lateral thinking
parameter is similar to the normal distribution of Eysenck’s parameter for general intelligence. The latter
indicates that lateral thinking is a fairly universal personality trait.
1 INTRODUCTION
Educational process is aimed not so much at the trans-
fer of knowledge, but at the development of thinking
(Dickens and Flynn, 2001) and, in particular, creative
thinking (Chen et al., 2019; Vlasenko et al., 2020).
In the new programs created in connection with the
modernization of the education system, this is the cen-
tral task. This means that the teacher, along with the
knowledge of modern approaches to improving the
education system, in particular the STEM methodol-
ogy (Kramarenko et al., 2020; Lovianova et al., 2019;
Ponomareva, 2021; Semerikov et al., 2021), should be
quite familiar with the psychology of thinking and the
nature of creative thinking.
The problem of personality testing has a long his-
tory. Since ancient times, the assessment and predic-
tion of human capabilities has been of fundamental
and practical interest. And in our time, the creation
a
https://orcid.org/0000-0002-0991-2343
b
https://orcid.org/0000-0002-4818-5580
c
https://orcid.org/0000-0002-5518-4260
d
https://orcid.org/0000-0002-3373-6562
of psychological tests is an important task, which is
a subject of numerous studies and discussions. The
skill of a teacher to assess the abilities and creative
potential of students determines the level of the edu-
cational process.
There are different approaches to testing the in-
telligence and specific abilities of personality (Jes-
son, 2012; Kaufman, 2009; Katsko and Moiseienko,
2018). They are widely discussed, criticized, and at
the same time are often used to solve practical issues.
For example, one of the popular is Eysenck’s IQ test
(Eysenck et al., 1985; Cahan, 2018) for assessing the
general intelligence. Many studies have been carried
out using these tests in various countries, and these
results are reflected in a lot of publications (Cahan,
2018; Ju
ˇ
skevi
ˇ
c and Kopelevi
ˇ
c, 1994). For this test the
distribution of the probability of detecting a particular
level of intelligence IQ follows a normal law.
The law of normal distribution means that the pa-
rameter values tend to concentrate around the value of
the mathematical expectation. The degree of spread
of a random variable relative to the mathematical ex-
pectation is determined by the variance. Any empiri-
cal distribution curve is characterized by two parame-
528
Kiv, A., Kolesnykova, K., Koycheva, T., Vinkovska, A. and Donchev, I.
The Development of Creative Thinking as an Important Task of Educational Process.
DOI: 10.5220/0010933600003364
In Proceedings of the 1st Symposium on Advances in Educational Technology (AET 2020) - Volume 2, pages 528-534
ISBN: 978-989-758-558-6
Copyright
c
 2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

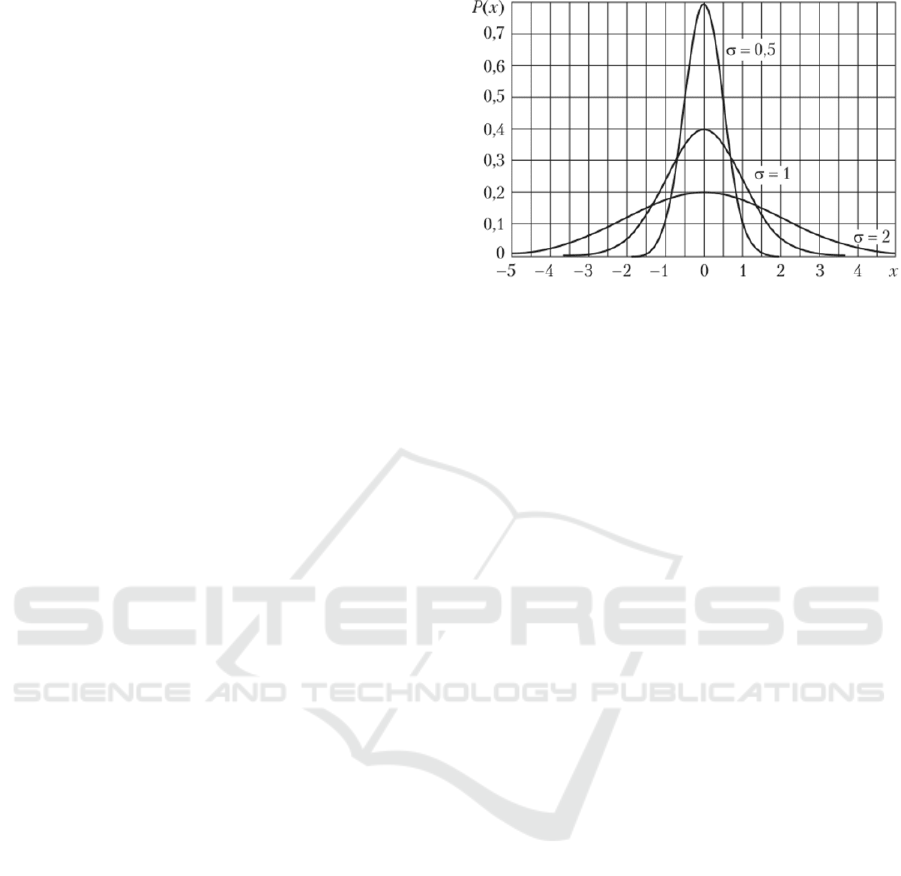
ters: the coefficient, which determines the symmetry
of the curve with respect to the mathematical expec-
tation (A
s
), and the coefficient of kurtosis (E
x
), which
sets the “sharpness” of the distribution peak. In the
case of a normal probability distribution law (Gaus-
sian curve) (Dickens and Flynn, 2001) A
s
= 0 and
E
x
= 0. Psychological parameters characterizing per-
sonality are described by different laws of probability
distribution.
The psychological characteristics of a person can
be classified according to the degree of their univer-
sality. For example, general intelligence is certainly
a fairly universal characteristic of a person. All peo-
ple have a certain level of intelligence. (We do not
consider options of pathological psychological char-
acteristics.)
At the same time, general intelligence is formed
on the basis of different individual abilities. The for-
mation of general intelligence depends on memory
(various types of memory), the peculiarities of think-
ing, in particular, creative thinking and other person-
ality abilities. It is obvious that the normal law of
probability distribution, which is fulfilled for the IQ
parameter, is not necessarily the case for other (less
universal) psychological characteristics of a person.
Therefore, we can judge the degree of universality
of the psychological characteristics of a personality
based on the proximity of the distribution function of
its probability to the normal law.
Let’s look at some different examples. What is the
probability distribution for those with musical mem-
ory? It should be noted that the perception of music
and musical memory characterize the emotional and
psychological sphere of the personality, to a large ex-
tent determining its psychological portrait.
Outstanding scientists saw in music the high-
est manifestation of human intellectual achievements.
Gottfried Wilhelm Leibniz wrote in the letter to Chris-
tian Goldbach: “music is a secret arithmetic exercise
of the soul, which calculates without knowing it” (Pa-
tel and Read, 1996). Helmholtz’s research (Cahan,
2018) touched upon various scientific and practical
issues related to the problems of perception, creativ-
ity, diagnostics of abilities, methods of musical edu-
cation, which gave a powerful impetus to the develop-
ment of almost all areas of musical psychology. At the
same time, if to compare the distribution of the proba-
bility of manifestation of high general intelligence of
IQ with the function of the probability of manifesta-
tion of musical memory, we can see significant differ-
ences (figure 1). They consist in the fact that in the
latter case the coefficient of kurtosis EX differs from
zero and the variance σ
2
is much less.
Let us turn to such a person’s condition as depres-
Figure 1: Illustration of the difference between the distri-
bution curves for the parameters: IQ (σ =1), parameter of
musical memory (σ = 0.5) (Stough et al., 1994), parameter
of depression (σ = 2) (Mozhaleva, 2015).
sion. This condition is experienced by a significant
proportion of the world’s population. The probability
distribution for carriers of this state differs from the
normal law already in opposite signs: the distribution
peak is sharply lowered, and the variance is sharply
increased (figure 1).
In our work, we set out to investigate lateral think-
ing as an important component of creative thinking.
Lateral thinking as a thought process was discovered
by De Bono (De Bono, 2015). The essence of such a
thought process is that we are distracted from the ob-
ject in question and switch to another object, which at
first glance has nothing to do with the first. However,
after such a transition, completely new possibilities of
considering the first object open up. Albert Einstein
said that life is like a bicycle: “as soon as you stop
pedaling, you fall” (Einstein, 2016). This is a good
example of lateral thinking.
Somebody think that a creative process is better
described as a process of logical thinking, trial and
error, feedback, and reflection. We do not reject such
opportunities. However, there are many people whose
experiments and articles show that training and devel-
oping lateral thinking leads to an improvement in the
emergence of creative solutions in standard or stress-
ful situations (Mellenbergh, 1989). There are guide-
lines for developing lateral thinking. But in order to
track the development of lateral thinking, there is a
need to measure it.
It is known that all scientific research tends to use
models. Lateral thinking is manifested in this. The
scientific result depends on a well-chosen model. The
famous models are used in the natural sciences, in par-
ticular, in physics: models of atom, atomic nucleus,
crystal etc.
In cosmology, models of the Universe are being
widely studied and discussed.
The Development of Creative Thinking as an Important Task of Educational Process
529

Our work is aimed at drawing attention to the
problem of the development and use of lateral think-
ing. A task set to compile a questionnaire to test
lateral thinking. An experiment was carried out
with groups of students and engineering workers.
The probability distribution functions for the studied
groups are obtained and analyzed.
2 TESTING LATERAL THINKING
Among the tests designed to assess the parameters of
thinking, very little are used to determine the level of
lateral thinking. This is due to the fact that some psy-
chologists underestimate the role of lateral thinking
in the creative process. However, understanding the
essence of lateral thinking and its development in stu-
dents is necessary to increase the creative potential of
the individual. A possible approach for assessing the
level of lateral thinking is proposed below.
2.1 Test Questions Formulation
Principle
In the case of lateral thinking, unobvious special “as-
sociations” take place. These are associations that are
not caused by the external similarity of objects. In
this case, objects and phenomena are compared on
the basis of the subjective view of a person having his
vision. A typical example is the creation by physi-
cists of a model for the fission of an atomic nucleus.
Frenkel and Weizsaeker “saw” in the atomic nucleus a
drop that drains from a drainpipe during rain (Frenkel,
1996). The picture of the separation of a drop from a
pipe led to the thought of a drip mechanism of nu-
clear fission. The drop model of the atomic nucleus is
described in all textbooks on nuclear physics (Hawk-
ing, 2018). The question of interest is of the extent
to which lateral thinking is present in human thinking
at various levels. In drawing up a questionnaire for
assessing lateral thinking, we chose triads of words in
which two words are far from each other in content,
and two words are close. It is proposed to determine
two words that at first glance are in no way linked as-
sociatively and try to find in these words something
common. The questionnaire is attached in figure 2. It
has been checked in accordance with the requirements
to tests (section 2.3).
2.2 Description of Experimental Results
For the study, 3 groups of subjects were selected, of
which two groups were students (140 and 70 people)
aged 19–22 and a group of engineers and technicians
(56 people) aged 30–45 years. A questionnaire was
used to assess the level of lateral thinking (figure 2).
The content of the questionnaire and the principle of
assessing the correctness of the answer are described
above.
No suggested choices for matching word pairs
were provided. It was suggested to make an appro-
priate choice of two words and in each case provide
a short justification for the choice made, similar to
those on the right side of the figure 2. The choices
made and their rationale may not be the same as those
suggested in figure 2.
The ratio of the number of (n) triads in which the
corresponding pairs of words were correctly selected
to the total number (N) of triads (in figure 1) was used
as a parameter characterizing the level of lateral think-
ing (LT = n/N).
Using the obtained data, in all cases the parameter
distribution characteristics were calculated: average
values of the measured value (x), mathematical ex-
pectations (µ), standard deviations (σ), third moment
of inertia (µ
3
) and fourth moment of inertia (µ
4
). The
results are shown in table 1.
Table 1: Characteristics of parameter LT distribution for
studied groups.
Number of group x σ µ
3
µ
4
1 0.43 0.65 0.05 0.48
2 0.37 0.68 0.10 0.44
3 0.32 0.54 0.02 0.42
Using the data in table 1, we calculate the values
for the coefficients of skewness (A
s
) and kurtosis (E
s
):
A
s
= µ
3
/ σ
3
and E
x
= (µ
4
/ σ
4
) – 3. The results are
presented in table 2.
Table 2: Values A
s
and E
x
for studied groups.
Number of group A
s
E
x
3 0.7 -0.53
1 0.18 -0.18
2 0.32 -0.98
Figure 3 shows the experimental distribution of
the parameter LT for the first group.
2.3 Checking the Applied Test
2.3.1 Validity of the Test
Validity is checked as the correspondence of the mea-
sured parameter to the psychological characteristic
that is being studied. In our case, we are talking about
the assessment of lateral thinking. Therefore, during
the testing process a survey was conducted to find out
AET 2020 - Symposium on Advances in Educational Technology
530

Figure 2: Questionnaire for testing lateral thinking. The words of the recommended choice are underlined.
what unity of the chosen word pairs a person implied.
In order for the correct result to be counted, it was
necessary for the test taker to explain his choice in the
spirit of the comment in figure 2. It was not necessary
that this explanation coincided with the comment in
figure 2. The main requirement was that the origi-
nal vision manifested the subject in the interpretation
of the unity of the objects being compared. Situa-
tions arose when the subject chose objects that had
obvious commonality, but at the same time a “lat-
The Development of Creative Thinking as an Important Task of Educational Process
531

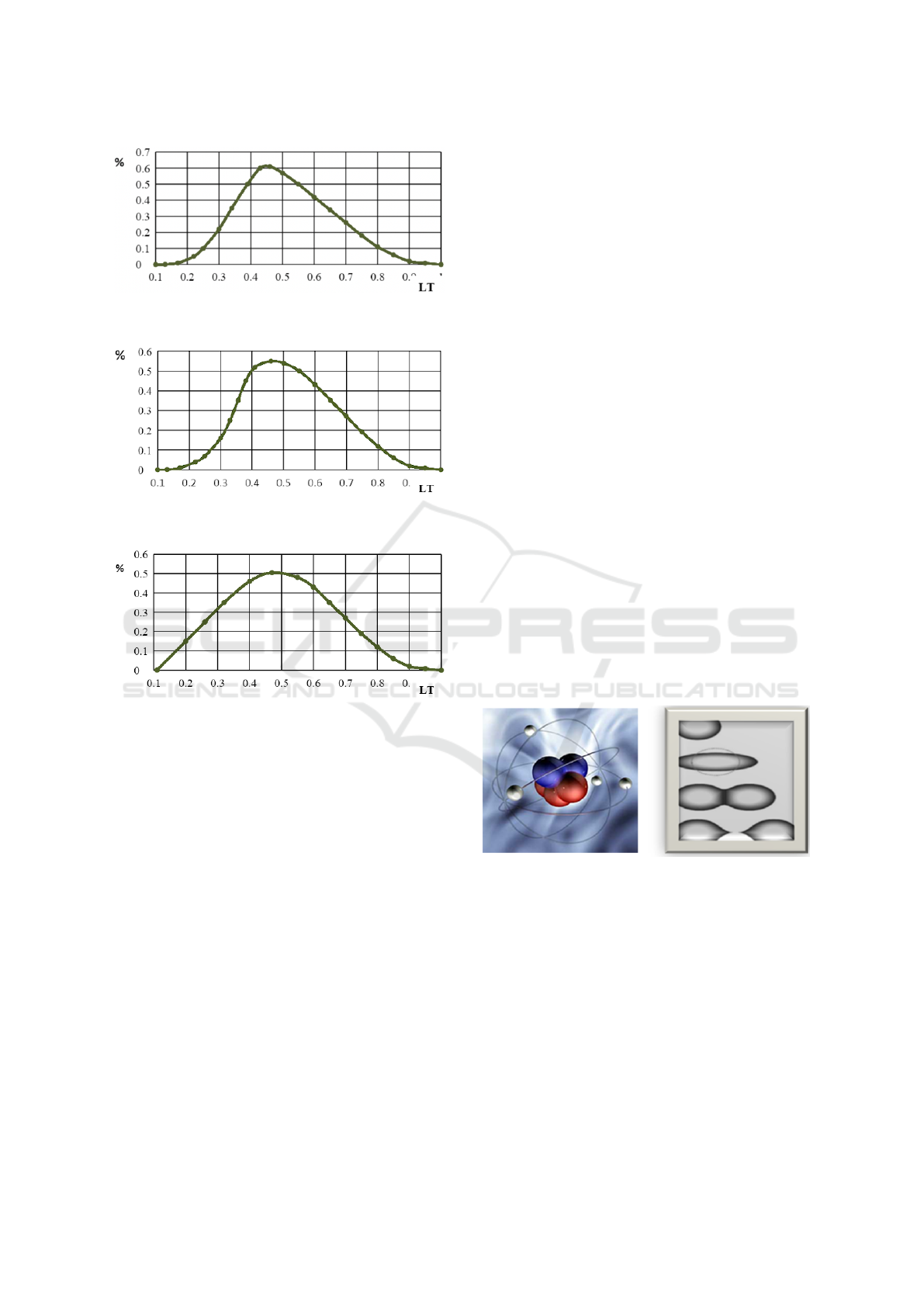
Figure 3: Experimental distribution of the parameter LT for
the first group.
Figure 4: Experimental distribution of the parameter LT for
the second group.
Figure 5: Experimental distribution of the parameter LT for
the third group.
eral” vision was manifested and the unity of objects
was noted that could not be noticed by another per-
son. Thus, for each subject in all three groups, the
parameter LT = n/25 was determined.
2.3.2 Test Reliability
Reliability of the test involves obtaining close re-
sults in repeated measurements as well as for subjects
whose parameters differ little. To check the test re-
liability, we conducted testing of studied groups at
different times with an interval of two-three months.
We obtained similar test result as a result of multiple
measurements of the parameters of the same group.
Discrepancies in the parameters of the various groups
also persisted.
2.3.3 Representativeness of Test
Representativeness suggests that test results obtained
for a specific group of people represent the large part
of population. To check the compliance of the test
with this characteristic, we have taken two groups
with twice as different the number of subjects (70
and 140). In both groups, the contingent is selected
with close characteristics (educational level, profes-
sional qualifications, etc.). We obtained that in these
groups the experimental results for the studied param-
eter (LT) differ slightly (table 1).
2.4 An Example When Studying
Vacancies in Crystals
When studying the real structure of crystals, the con-
cept of a vacancy (an empty place from which an atom
left) and an interstitial atom (an atom that left its place
with the emergence of a vacancy) are introduced. If an
atom leaves close to its vacancy, a so-called Frenkel
pair is formed. However, an intermediate variant is
possible, when the atom does not move far enough
from the vacancy, and the vacancy pulls it back in.
When this process is repeated, a so-called “blinking
vacancy” appears. Such a vacancy either appears or
is “healed” by the returned atom. The concept of a
“blinking vacancy” appeared relatively recently (Par-
itckaia et al., 2018). Physicists came up with the idea
of a blinking vacancy by observing raindrops falling
on the calm surface of a river. Raindrops leave a mark
on the water, which disappears with a blink. This is
a typical example of lateral thinking, just like in the
case of nuclear fission above (Hawking, 2018) (fig-
ure 6).
Figure 6: Illustration for the droplet model of the fission of
an atomic nucleus. Left – an image of an atomic nucleus,
on the right – an image of fission of a liquid drop.
3 DISCUSSION OF RESULTS
The problem of thinking, which is one of the central
problems of psychology, is given little attention in ad-
dressing issues of improving the system of education,
new methodological approaches, and developing new
curricula. Despite the ambiguous attitude of psychol-
ogists and teachers to existing models and ideas about
the mechanisms of thinking, it is useful to take into
AET 2020 - Symposium on Advances in Educational Technology
532

account the use of accumulated experience and ideas
in the educational process. The concepts of produc-
tive thinking introduced by Wertheimer (Wertheimer,
2020), the concepts of lateral thinking introduced by
De Bono (De Bono, 2015) and other well-known
models of thinking (Young, 2008), must be taken into
account in the learning process, when solving spe-
cific methodological problems. The teacher’s atten-
tion should be focused not only on effectively com-
municating knowledge, but on choosing a teaching
method that develops thinking. Therefore, it is im-
portant to be able to assess the student’s ability to a
certain type of thinking.
In this work, we investigated the possibilities of
objective assessment of lateral thinking. Testing this
type of thinking requires special care, since it is not
about solving specific tasks. It is required to trace
the course of a person’s thinking and to distinguish
the degree of originality of various approaches to the
assessment of the meaning of concepts.
In many cases of life, a person is faced with the
need to apply lateral thinking, in scientific research,
in the perception of humour and simply in everyday
life. When compiling a questionnaire for assessing
the level of lateral thinking, we tried to give the sub-
ject the opportunity to find a wide range of associa-
tions.
The proposed test has been verified in terms of va-
lidity, reliability and representativeness. During the
experiment, however, an additional approach was ap-
plied to assess the significance of this test. It is known
that the probability distribution of detecting a certain
value of the measured parameter during testing is typ-
ical for a particular test. In the case of measuring the
IQ parameter, this probability distribution obeys the
normal law. The IQ parameter is a fairly universal
characteristic of a person. This parameter character-
izes any person (except for pathological cases). It can
be assumed that the closer the probability distribution
of a given parameter is to the normal law, the more
universal psychological characteristic is this parame-
ter.
In the case of testing lateral thinking, an insignifi-
cant deviation of the measured empirical distribution
of the probability of the LT parameter from the nor-
mal law was revealed, which indicates a fairly high
universality of this personality characteristic.
4 CONCLUSION
The possibility of assessing the level of lateral think-
ing using the proposed verbal test is shown. The com-
piled questionnaire is a set of triads, in which each
triad includes three words, of which two words are
outwardly in no way connected in meaning. The task
is to select these two words that have no outwardly
any semantic connection and find something in com-
mon in these words. It is also required to briefly ex-
plain what exactly was found in common in the se-
lected words. An experiment was conducted with the
proposed test, in which two groups of students (140
and 70 people) and a group of engineering and tech-
nical workers (56 people) took part. As a result of
processing the results, the values of the asymmetry
and kurtosis coefficients were obtained, which char-
acterize the deviations of the obtained empirical dis-
tributions of the probabilities of detecting the parame-
ters of LT from the normal law. These deviations were
found to be small.
It is known that when testing general intelligence
using the Eysenck test, the probability distribution for
IQ parameter obeys the normal law. Since the IQ pa-
rameter is a fairly universal characteristic of the per-
sonality, it is suggested that rather general personality
traits are manifested also in lateral thinking.
REFERENCES
Cahan, D. (2018). Helmholtz: A Life in Science. University
of Chicago Press, Chicago.
Chen, Y., Spagna, A., Wu, T., Kim, T. H., Wu, Q., Chen, C.,
Wu, Y., and Fan, J. (2019). Testing a cognitive con-
trol model of human intelligence. Scientific Reports,
9(1):2898.
De Bono, E. (2015). Lateral thinking: creativity step by
step. Harper Colophon, New York.
Dickens, W. T. and Flynn, J. R. (2001). Heritability esti-
mates versus large environmental effects: the IQ para-
dox resolved psychological review. Psychological re-
view, 108(2):346–369.
Einstein, A. (2016). Albert Einstein. In Rat-
cliffe, S., editor, Oxford Essential Quotations.
Oxford University Press, 4 edition. https:
//www.oxfordreference.com/view/10.1093/acref/
9780191826719.001.0001/q-oro-ed4-00003988.
Eysenck, S. B. G., Eysenck, H. J., and Barrett, P. (1985). A
revised version of the psychoticism scale. Personality
and Individual Differences, 6(1):21–29.
Frenkel, V. Y. (1996). Yakov Ilich Frenkel: His work, life
and letters. Birkh
¨
auser Basel.
Hawking, S. (2018). Brief Answers to the Big Questions.
Bantam, New York.
Jesson, J. (2012). Developing Creativity in the Primary
School. Open University Press, Berkshire.
Ju
ˇ
skevi
ˇ
c, A. P. and Kopelevi
ˇ
c, J. K. (1994). Christian
Goldbach 1690–1764, volume 8 of Vita Mathematic.
Birkh
¨
auser Basel.
Katsko, O. O. and Moiseienko, N. V. (2018). Devel-
opment computer games on the Unity game engine
The Development of Creative Thinking as an Important Task of Educational Process
533

for research of elements of the cognitive thinking in
the playing process. CEUR Workshop Proceedings,
2292:151–155.
Kaufman, A. S. (2009). IQ Testing 101. Springer Publish-
ing, New York.
Kramarenko, T. H., Pylypenko, O., and Muzyka, I. O.
(2020). Application of GeoGebra in Stereometry
teaching. CEUR Workshop Proceedings, 2643:705–
718.
Lovianova, I. V., Bobyliev, D. Y., and Uchitel, A. D. (2019).
Cloud calculations within the optional course Op-
timization Problems for 10th-11th graders. CEUR
Workshop Proceedings, 2433:459–471.
Mellenbergh, G. J. (1989). Item bias and item response the-
ory. International Journal of Educational Research,
13(2):127–143.
Mozhaleva, N. (2015). Musical abilities, their nature
and development during the instrumental music per-
formance teacher training. Educational Dimension,
44:98–104.
Paritckaia, L. N., Kaganovskii, I. S., Gusak, A. M., Beke,
D., Naumovetc, A. G., Glikman, E. E., Shvindlerman,
L. S., Zyman, Z. Z., Solunskii, V. I., Geguzina, S. I.,
Perskii, E. E., Emetc, A. K., Levitin, V. V., Levina,
M. L., Rivlin, A. A., Krichevskii, O., Ter-Ovanesian,
E., Mostovoi, V. M., Chernov, A. A., Bokshtein, B. S.,
Kaganov, M. I., and Vorobeva, I. V. (2018). Yakov
Evseevich Geguzin: to the 100th anniversary of his
birth. Folio, Kharkiv.
Patel, J. K. and Read, C. B. (1996). Handbook of the Nor-
mal Distribution, volume 150 of STATISTICS: text-
books and monographs. Marcel Dekker, New York,
Basel, Hong Kong, 2nd edition.
Ponomareva, N. S. (2021). Role and place of informatics in
the training of future teachers of mathematics. Jour-
nal of Physics: Conference Series, 1840(1):012035.
https://doi.org/10.1088/1742-6596/1840/1/012035.
Semerikov, S. O., Mintii, M. M., and Mintii, I. S. (2021).
Review of the course “Development of Virtual and
Augmented Reality Software” for STEM teachers:
implementation results and improvement potentials.
CEUR Workshop Proceedings, 2898:159–177.
Stough, C., Kerkin, B., Bates, T., and Mangan, G. (1994).
Music and spatial IQ. Personality and Individual Dif-
ferences, 17(5):695.
Vlasenko, K., Achkan, V., Chumak, O., Lovianova, I., and
Armash, T. (2020). Problem-based approach to de-
velop creative thinking in students majoring in mathe-
matics at teacher training universities. Universal Jour-
nal of Educational Research, 8(7):2853–2863.
Wertheimer, M. (2020). Productive thinking (1945). In
Sarris, V., editor, Max Wertheimer Productive Think-
ing, pages 25–257. Springer International Publishing,
Cham.
Young, I. (2008). Mental Models: Aligning Design Strategy
with Human Behavior. Rosenfeld Media, New York.
AET 2020 - Symposium on Advances in Educational Technology
534