
Expanding Polygenic Risk Scores to Include Automatic Genotype
Encodings and Gene-gene Interactions
Trang T. Le
a
, Hoyt Gong
b
, Patryk Orzechowski
c
, Elisabetta Manduchi
d
and Jason H. Moore
e
Department of Biostatistics, Epidemiology and Informatics, Institute for Biomedical Informatics,
University of Pennsylvania, Philadelphia, PA 19104, U.S.A.
Keywords:
Precision Medicine, Machine Learning, Risk Scores, Genetics.
Abstract:
Polygenic Risk Scores (PRS) are aggregation of genetic risk factors of specific diseases and have been suc-
cessfully used to identify groups of individuals who are more susceptible to those diseases. While several
studies have focused on identifying the correct genetic variants to include in PRS, most existing statistical
models focus on the marginal effect of the variants on the phenotypic outcome but do not account for the
effect of gene-gene interactions. Here, we propose a novel calculation of the risk score that expands beyond
marginal effect of individual variants on the outcome. The Multilocus Risk Score (MRS) method effectively
selects alternative genotype encodings and captures epistatic gene-gene interactions by utilizing an efficient
implementation of the model-based Multifactor Dimensionality Reduction technique. On a diverse collection
of simulated datasets, MRS outperforms the standard PRS in the majority of the cases, especially when at
least two-way interactions between the variants are present. Our findings suggest that models incorporating
epistatic interactions are necessary and will yield more accurate and effective risk profiling.
1 INTRODUCTION
As the field of traditional genomics rapidly expands
its sequencing technologies and translational abili-
ties, novel applications of genomic data are start-
ing to arise in addressing disease burden. Comple-
menting the rapid growth in our understanding of hu-
man genetic variation was the emergence of genome-
wide association studies (GWAS) in the early 2000s
to identify gene variants associated with common hu-
man diseases. Non-candidate-driven in design, these
observational studies carry out chip array genotyp-
ing across population subsamples to subsequently as-
say for phenotype signal association via statistical ap-
proaches in silico. Measuring averaged allelic effects
across all genomics backgrounds and environmen-
tal exposures, GWAS have primarily sought to dis-
cern genetic association with phenotypes of interest
by studying single nucleotide polymorphisms (SNPs)
and other DNA variants across the human genome
a
https://orcid.org/0000-0003-3737-6565
b
https://orcid.org/0000-0001-9339-4763
c
https://orcid.org/0000-0003-3578-9809
d
https://orcid.org/0000-0002-4110-3714
e
https://orcid.org/0000-0002-5015-1099
(Bush and Moore, 2012; Hirschhorn and Daly, 2005;
Wang et al., 2005).
In tandem with the movement towards precision
medicine, the post-GWAS era strives to bring relevant
population-derived gene variants into individual level
metrics actionable in health delivery settings. While
GWAS indeed capture gene variants associated with a
phenotype of interest on a population level, translat-
ing such results to personalized individual metrics of
risk requires aggregating contributions of many gene
variants in the form of polygenic risk scores (PRS).
PRS provide an ability to explain inherited risk for
disease in an individual by representing a weighted
sum aggregate of risk alleles based on measured loci
effect contributions derived from GWAS (Chatterjee
et al., 2016; Torkamani et al., 2018). In quantifying
the effect of particular combinations of genetic SNP
variants towards risk prediction, PRS offers a prob-
abilisitic susceptibility value of an individual to dis-
ease. Such genetic risk estimation scores are central
to clinical decision-making, serving to reinforce indi-
vidual health management in heritable disease detec-
tion and early prevention of various adult-onset con-
ditions. The utility of PRS scores have been demon-
strated in previous studies towards disease risk strat-
ification across leading heritable causes of death in
Le, T., Gong, H., Orzechowski, P., Manduchi, E. and Moore, J.
Expanding Polygenic Risk Scores to Include Automatic Genotype Encodings and Gene-gene Interactions.
DOI: 10.5220/0008869700790084
In Proceedings of the 13th Inter national Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2020) - Volume 3: BIOINFORMATICS, pages 79-84
ISBN: 978-989-758-398-8; ISSN: 2184-4305
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
79

the developed world (Purcell et al., 2009; Khera et
al.,2019, 2018; Maas et al., 2016; Seibert et al.,
2018).
Because common PRS method assumes a sim-
plified genetic architecture consisting of indepen-
dent weights, understanding interactive relationships
among genes and SNPs that associate with disease
outcome remain a challenge. Existing standard multi-
variate categorical data analysis approaches fall short
in handling such enormous possible genetic inter-
action combinations with both linear and nonlinear
effects. In this context, more robust and efficient
methods towards a polygeneic risk calculation are
necessary in capturing the overlap between context-
dependent effects of both rare and common alleles on
human genetic disorder. Herein, we use the termi-
nology gene-gene (GxG) interactions to indicate any
genetic interaction including ones among SNPs that
may fall outside of coding regions.
With respect to better understanding the epista-
sis across an individual’s genome, various statistical
models have been designed with the intent of captur-
ing high dimensional GxG interactions. The Multi-
factor Dimensionality Reduction (MDR) method is
one such nonparametric framework that addresses
these challenges and has been extensively applied to
detect nonlinear complex GxG interactions associated
with individual disease (Ritchie et al., 2001; Moore
and Andrews, 2014). By isolating a specific pool
of genetic factors from all polymorphism and cross-
valiating prediction scores averaged across identified
high risk multi-locus genotypes, the original MDR
approach is able to categorize multilocus genotypes
into two groups of risk based on a threshold value.
While created with the primary intention towards
GxG interaction detection by reducing dimensional-
ity interactively in inferring genotype encodings, the
MDR model has additionally demonstrated applica-
bility as a risk score calculation model in constructing
PRS scores (Dai et al., 2013).
Modifications built on top of the MDR framework
have been proposed in order to better capture multiple
significant epistasis models and potential missed in-
teractions owning to limitations of the original model
in the higher dimensions. Model-Based Multifactor
Dimensionality Reduction (MB-MDR) was formu-
lated as a flexible GxG detection framework for both
dichotomous and continuous traits (Mahachie John et
al., 2011; Cattaert et al., 2010). Rather than a direct
comparison against a threshold level in the original
MDR method, MB-MDR merges multilocus geno-
types exhibiting significant High or Low risk levels
through association testing and adds an additional ‘No
evidence of risk’ categorization. In comparison to the
standard MDR framework which reveals at most one
optimal epistasis model, the MB-MDR method flexi-
bly weighs multiple models by producing a model list
ranked with respect to their statistical parameters.
In the present work, we aim to reformulate the
PRS leveraging the MB-MDR approach to better cap-
ture alternative encodings and epistatic interactions
of individual disease risk in a novel Multilocus Risk
Score (MRS). Through the following sections, we
briefly review the features of the MDR and MB-MDR
software, describe how our new MRS method evalu-
ates polygenic risk, and compare MRS profiling per-
formance to the standard PRS method on evidence-
based simulated dataset collections. In observing
prediction accuracy results, we demonstrate the im-
proved performance of our multi-model weighted
epistasis framework with inferred genotype encod-
ings over existing PRS methods, showing great po-
tential for more accurate identification of high risk in-
dividuals for a specific complex disease.
2 METHODS
2.1 Multifactor Dimensionality
Reduction (MDR) and Model-based
MDR (MB-MDR)
MDR is a nonparametric method that detects multi-
ple genetic loci associated with a clinical outcome
by reducing the dimension of a genotype dataset
through pooling multilocus genotypes into high-risk
and low-risk groups (Ritchie et al., 2001). MDR has
been applied to a number of real-world datasets and
sufficiently identified important variant interactions
that associated with various diseases (Motsinger and
Ritchie, 2006). Extended from the original MDR al-
gorithm, MB-MDR was first introduced in 2009 (Cat-
taert et al., 2010), and its current implementation ef-
ficiently and effectively detects multiple sets of sig-
nificant gene-gene interactions in relation to a trait of
interest while efficiently controlling type I error rates
via a cross-validation strategy. By merging multi-
locus genotypes exhibiting significant high or low risk
based on association testing rather than comparing to
an arbitrary threshold as in MDR, MB-MDR provides
a flexible framework to detect and measure epistasis.
Specifically, in addition to the test statistic and P
values associated with each genotype combination,
another important output of MB-MDR is the HLO
matrices. Briefly, in the case of a binary trait, for each
genotype combination, an HLO matrix is a 3 x 3 ma-
trix with each cell containing H (high), L (low) or O
BIOINFORMATICS 2020 - 11th International Conference on Bioinformatics Models, Methods and Algorithms
80

(no evidence), indicating risk of an individual whose
genotype pairs fall into that cell (Lishout et al. , 2013).
For an example binary outcome problem, a SNP pair
SNP
1
and SNP
2
will have an HLO matrix that looks
like
SNP
1
= 0 SNP
1
= 1 SNP
1
= 2
SNP
2
= 0 O O O
SNP
2
= 1 O H L
SNP
2
= 2 O L H
We discuss in the following subsection how these val-
ues were utilized in the formulation of the Multilocus
Risk Score (MRS).
2.2 From Polygenic Risk Scores (PRS)
to Multilocus Risk Scores (MRS)
In this subsection, we quickly review the standard
PRS formula then present our modification to this
popular risk score calculation. For both methods, we
consider a dataset of n individuals with genomes of m
possible SNPs.
In PRS, for each SNP j of an individual i, the PRS
score is calculated via a summation across k selected
SNPs as
PRS(i) =
k
∑
j=1
β
j
× SNP
i j
(1)
where β
j
is the weighted risk contribution of the j
th
SNP derived from the association test parameters and
SNP
i j
represents the number of minor alleles (0, 1,
or 2) at the j
th
locus of individual i. Various ap-
proaches towards predicting risk of the same disease
exist across PRS studies based on the above equation;
models may vary according to the specific statistical
model used to produce the weights β
j
for individual
genetic variations, the number of genetic variants con-
sidered k, and the ability of the PRS to generalize to
the entire population (Sugrue and Desikan, 2019).
In the MRS framework, we let k
d
denote the num-
ber of significant combinations for a specific model
dimension d (e.g. d = 2 results in pairs of SNPs). In
this study, no significance threshold is imposed at the
SNP combination level and, thus, k
d
reaches its max-
imum value of C
d
m
(m choose d). For each subject
i (i = 1, 2, ··· , n), the d-way multilocus risk score is
calculated as
MRS
d
(i) =
k
d
∑
j=1
γ
j
× HLO
j
(X
i j
) (2)
where γ
j
is the test statistic of the j
th
genotype com-
bination output from MB-MDR, X
i j
is the j
th
geno-
type combinations of subject i and HLO
j
represents
the j
th
recoded HLO matrix (1 = High, -1 = Low,
0 = No evidence). As an example, consider a pair
X
∗ j
= (SNP
j
1
, SNP
j
2
) with γ
j
= 8.3 and correspond-
ing HLO matrix of all O’s except an L in the first cell.
Then, the contribution of this pair to a subject’s risk
would be 0 for all subjects except those with genotype
0 at both SNPs. For the latter, the contribution would
be -8.3.
In this study, we consider 1-way and 2-way in-
teractions. We denote by MRS the combined risk
score MRS1 + MRS2. The significance level of each
combination of SNPs on a given dataset is obtained
by applying on that dataset the MB-MDR software
(Lishout et al., 2013; Cattaert et al., 2010) v.4.4.1.
We will compare the performance of the standard PRS
method to the combined risk MRS and also its com-
ponents, MRS1 and MRS2, separately.
2.3 Mutual Information and
Information Gain
For a given simulated data set, we apply entropy-
based methods to measure how much information
about the phenotype is due to either marginal effects
or the synergistic effects of the variants after sub-
tracting the marginal effects. A dataset’s amount of
main effect ME can be measured as the total of mu-
tual information between each SNP
j
and the pheno-
typic class Y based on Shannon’s entropy H (Shan-
non, 1948):
ME =
∑
j
I(SNP
j
;Y ) =
∑
j
(H(Y ) − H(Y |SNP
j
)).
(3)
We measure the 2-way interaction information
(i.e. degree of synergistic effects of genotypes on
the phenotype) of each dataset by summing the pair-
wise information gain between all pairs of genetic at-
tributes. Specifically, if we let X
j
denote the j
th
geno-
type combination (SNP
j
1
, SNP
j
2
), the total 2-way in-
teraction gain (i.e. synergistic effects SE) is calculated
as
SE =
∑
j
IG(X
j
;Y ) =
∑
j
(I(SNP
j
1
, SNP
j
2
;Y )−
I(SNP
j
1
;Y ) − I(SNP
j
2
;Y )), (4)
where IG measures how much of the phenotypic
class Y can be explained by the 2-way epistatic inter-
action within the genotype combination X
j
. We refer
the reader to Ref. (Moore and Hu, 2014) for more
details on the calculation of the entropy-based terms.
To prevent potential bias, we compute these val-
ues from the training set. However, because the train-
ing and holdout sets were randomly split, the amount
Expanding Polygenic Risk Scores to Include Automatic Genotype Encodings and Gene-gene Interactions
81
of main or interaction effect in both datasets are ex-
pected to be similar.
2.4 Simulated Data
The primary objective of this data simulation pro-
cess was to provide a comprehensive set of repro-
ducible and diverse datasets for the current study.
Each dataset was generated in the following man-
ner. For an individual, each genotype was randomly
assigned with 1/2 probability of being heterozygous
(Aa, coded as 1), 1/4 probability of being homozy-
gous major (AA, coded as 0) and 1/4 probability of be-
ing homozygous minor (aa, coded as 2). The binary
endpoint for the data was determined using a recently
proposed evolutionary-based method for dataset gen-
eration called Heuristic Identification of Biological
Architectures for simulating Complex Hierarchical
Interactions (Moore et al., 2017). This method uses
genetic programming to build different mathemati-
cal and logical models resulting in a binary endpoint,
such that the objective function called fitness is max-
imized. In this study, to arrive at a diverse collec-
tion of datasets, we aim to maximize the difference in
predictive performance of all pairs of ten pre-selected
classifiers. Details on data simulation are provided
in the README of the study’s analysis repository
https://github.com/lelaboratoire/rethink-prs/.
The final collection has 450 datasets containing
1000 samples and 10 SNPs with various amount of
epistatic effect on the binary phenotypic outcome. For
each simulated dataset, after randomly splitting the
entire data in two smaller sets (80% training and 20%
holdout), we built the MRS model on training data to
obtain the γ coefficients and the HLO matrices, and
then we calculated risk score for each sample in the
holdout set. We assess the performance of the MRS
by comparing the area under the Receiving Operator
Characteristic curve (auROC) with that of the stan-
dard PRS method on the holdout set.
2.5 Manuscript Drafting
This manuscript is collaboratively written using
Manubot, a software for writing scholarly documents
via GitHub (Himmelstein et al., 2019). With contin-
uous integration, Manubot automatically updates the
manuscript when its authors approve the changes. As
a result, the latest version of this manuscript is always
available for review at https://lelaboratoire.github.io/
rethink-prs-ms/.
40%
60%
80%
100%
PRS MRS
auROC
−30% 0% 30% 60%
auROC
MRS
− auROC
PRS
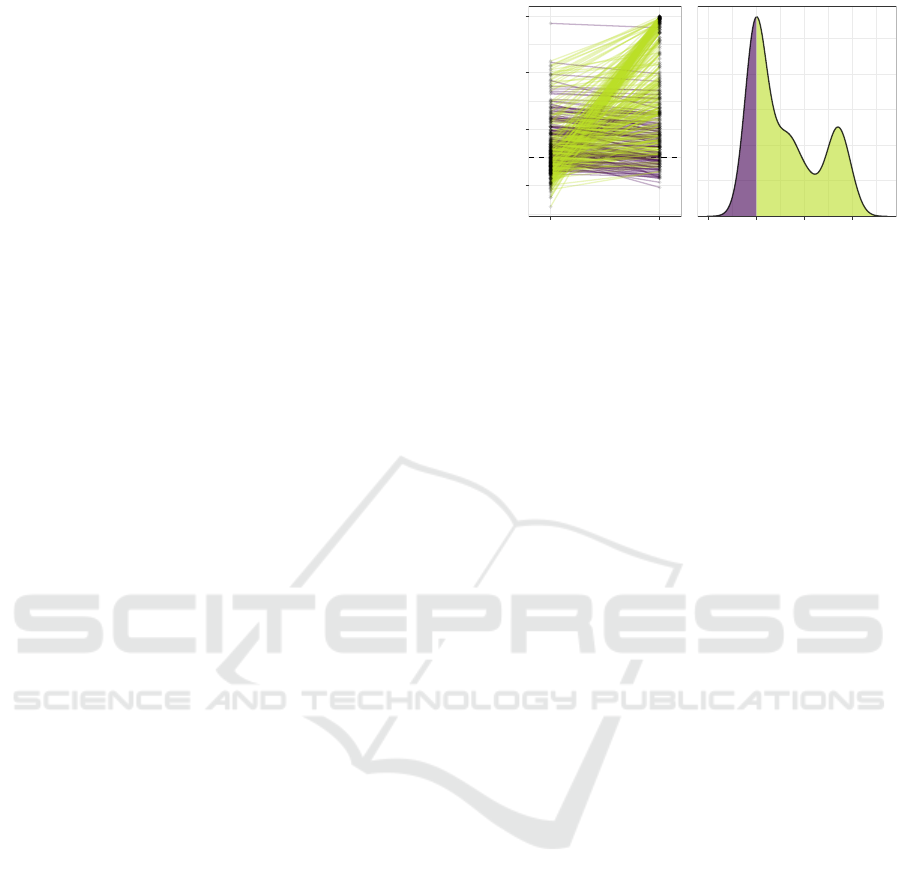
Figure 1: MRS produces improved auROC in the majority
(335 green lines) of the 450 simulated datasets (each line
represents a dataset). In many datasets, the standard PRS
method performs poorly (auROC < 60%) while the new
method yields auROC over 90%. This improvement in per-
formance can be seen at the second peak (≈ 50% auROC
increase) in the density of the difference between the au-
ROCs from the two methods (right).
2.6 Availability
Detailed simulation and analysis code needed to re-
produce the results in this study is available at https:
//github.com/lelaboratoire/rethink-prs/.
3 RESULTS
3.1 MRS Outperforms Standard PRS in
the Majority of Simulated Datasets
In 335 out of 450 simulated datasets, MRS produces
higher auROC compared to PRS (green lines, Fig. 1).
In 363 datasets where the standard PRS method per-
forms poorly (auROC < 60%), MRS performs par-
ticularly well (auROC > 90%) in 102 datasets. This
auROC increase of approximately 50% can be seen
at the second peak in the density of the difference
between the auROCs from the two methods (Fig. 1
right). When MRS yields smaller auROC, the dif-
ference is small (3.3% ± 2.8%, purple lines/areas).
Across all 450 datasets, the improvement of MRS
over PRS is significant (P < 10
−15
) according to a
Wilcoxon signed rank test. To assess whether this im-
provement in performance correlates with the amount
of interaction effect contained in each dataset, in the
following section, we untangled the two components
of MRS and test for the correlation between the dif-
ference in auROC and two entropy-based measures
for main and interaction effect of each dataset.
BIOINFORMATICS 2020 - 11th International Conference on Bioinformatics Models, Methods and Algorithms
82

Amount of main effect
Amount of interaction effect
MRS1 − PRS
MRS2 − PRS
MRS − PRS
1.0 1.5 2.0 0.5 1.0
0.00
0.25
0.50
−0.25
0.00
0.25
0.50
0.00
0.25
0.50
0.75
∆ auROC
Figure 2: Combining 1-way (MRS1) and 2-way (MRS2)
risk scores, MRS shows increasing outperformance to stan-
dard PRS as datasets contain more main and interaction ef-
fect.
3.2 Assess MRS’s Improvement in
Performance
We recall that MRS is combined from the 1-way
and 2-way interaction risk scores: MRS = MRS1 +
MRS2. Individually, MRS1 and MRS2 both signifi-
cantly outperformed the standard PRS method (both
P values < 10
−15
) according to a Wilcoxon signed
rank test. As the amount of main effect increases
(Fig. 2 left column), MRS1 increasingly performs
better than PRS, which is likely because encodings
are inferred (top left). Meanwhile, MRS2’s accuracy
remain mostly similar to that of PRS (middle left).
On the other hand, when the amount of interaction ef-
fect increases (Fig. 2 right column), MRS1 performs
mostly on par to PRS while MRS2 increasingly per-
forms better than PRS. Combining the gain from both
MRS1 and MRS2, MRS’s performance progressively
increases compared to the standard PRS.
All computation of MRS1 and MRS2 on 450 sim-
ulated datasets finished in less than 20 minutes on a
desktop with an Intel Xeon W-2104 CPU and 32GB
of RAM.
4 DISCUSSION
We introduce the Multilocus Risk Score (MRS)
method to improve the performance of the standard
PRS in disease risk stratification of patient popula-
tions. While PRS holds much promise for develop-
ment of new precision medicine approaches by iden-
tifying high risk individuals, one of its current lim-
itations is the model simplicity (Torkamani et al.,
2018). As a first step towards addressing this issue
and increasing comprehensiveness of risk profiling
models, in this study, we developed a new applied
MRS method from the MB-MDR framework that en-
ables automatic genotype encodings and takes into
account multiple models for detecting GxG interac-
tions. Utilizing the efficient implementation of MB-
MDR, MRS automatically infers the genotype encod-
ings and simultaneously computes the risk of variant
combinations. Through comparing method perfor-
mance on a diverse collection of simulated data, we
demonstrate the robust risk profiling ability of MRS
and suggest the importance of flexible, precise meth-
ods in better capturing epistasis behind individual pa-
tient risk.
We showed that the MRS method outperformed
standard PRS in many of the simulated datasets, high-
lighting the importance of genotype encodings and
consideration of epistasis. We further examined the
association between this improvement and the amount
of two-way epistatic effect induced in the binary phe-
notypic outcome. Appropriate phenotype encodings
are important for improving the accuracy when there
is a large amount of main effect of the variants on
the phenotypic outcome. Meanwhile, inclusion of
epistatic terms significantly increases the accuracy
from PRS, especially when two-way interactions are
present in the data. Although we only considered up
to two-way GxG interactions, it is straightforward to
incorporate higher order interactions (e.g. three-way,
four-way) into MRS. However, preliminary analyses
on the simulated datasets for such higher order inter-
actions did not show significant improvement from
the current MRS (results not shown). We also recom-
mend estimating the computational expense prior to
implementing high order interactions, especially for
larger datasets encountered in practice.
We acknowledge three main limitations of the cur-
rent study. First, MRS has not been applied to real-
world data. Although we compensated the lack of real
data with a diverse set of simulated datasets, a future
study analyzing real-world data will prove beneficial
to quantify the new MRS model’s utility in practice.
Second, accounting for epistasis, in principle, is more
computationally expensive compared to investigating
solely main effect. Therefore, even with fast and ef-
ficient software, pre-selecting the variants (e.g. based
on specific pathways or prior knowledge) will prove
beneficial for accurate MRS computing when analyz-
Expanding Polygenic Risk Scores to Include Automatic Genotype Encodings and Gene-gene Interactions
83

ing datasets containing a larger number of variants.
Nevertheless, we hope the promising preliminary re-
sults from this study will open the door to future ap-
proaches that encompass both main and interaction
effects while improving scalability.
Finally, we caution that a risk score model should
be evaluated based on not only sensitivity and speci-
ficity but also with respect to potential clinical effi-
cacy, and any genetic risk should be interpreted in
aggregate with other risk factors. Future works fo-
cusing on gene-environment interactions with time-
dependent risk factors will be crucial in order to com-
municate risk properly for preventive interventions.
In conclusion, MRS enhances the predictive ca-
pacity of current risk profiling model for complex dis-
eases with polygenic architectures. While there is
much work left to do in improving the clinical util-
ity of general risk profiling framework, we highlight
that more comprehensive models that infer proper
genotype encodings and account for epistatic effects
greatly improve the prediction accuracy and affords
new opportunities for more effective clinical preven-
tion.
ACKNOWLEDGEMENTS
We thank Dr. Kristel Van Steen and Aldo Camargo
for their helpful responses to our inquires about the
MB-MDR software.
REFERENCES
Bush,W.S. and Moore,J.H. (2012) Chapter 11: Genome-
Wide Association Studies. PLoS Comput Biol, 8,
e1002822.
Cattaert,T. et al. (2010) Model-Based Multifactor Dimen-
sionality Reduction for detecting epistasis in case-
control data in the presence of noise. Annals of Human
Genetics, 75, 78–89.
Chatterjee,N. et al. (2016) Developing and evaluating poly-
genic risk prediction models for stratified disease pre-
vention. Nat Rev Genet, 17, 392–406.
Dai,H. et al. (2013) Risk score modeling of multiple gene
to gene interactions using aggregated-multifactor di-
mensionality reduction. BioData Mining, 6.
Himmelstein,D.S. et al. (2019) Open collaborative writing
with Manubot. PLoS Comput Biol, 15, e1007128.
Hirschhorn,J.N. and Daly,M.J. (2005) Genome-wide as-
sociation studies for common diseases and complex
traits. Nat Rev Genet, 6, 95–108.
Khera,A.V. et al. (2018) Genome-wide polygenic scores for
common diseases identify individuals with risk equiv-
alent to monogenic mutations. Nat Genet, 50, 1219–
1224.
Khera,A.V. et al. (2019) Polygenic Prediction of Weight and
Obesity Trajectories from Birth to Adulthood. Cell,
177, 587–596.e9.
Lishout,F.V. et al. (2013) An efficient algorithm to perform
multiple testing in epistasis screening. BMC Bioinfor-
matics, 14.
Maas,P. et al. (2016) Breast Cancer Risk From Modifi-
able and Nonmodifiable Risk Factors Among White
Women in the United States. JAMA Oncol, 2, 1295.
Mahachie John,J.M. et al. (2011) Model-Based Multifactor
Dimensionality Reduction to detect epistasis for quan-
titative traits in the presence of error-free and noisy
data. Eur J Hum Genet, 19, 696–703.
Moore,J.H. and Andrews,P.C. (2014) Epistasis Analy-
sis Using Multifactor Dimensionality Reduction. In,
Methods in Molecular Biology. Springer New York,
pp. 301–314.
Moore,J.H. and Hu,T. (2014) Epistasis Analysis Using In-
formation Theory. In, Methods in Molecular Biology.
Springer New York, pp. 257–268.
Moore,J.H. et al. (2017) A heuristic method for simulating
open-data of arbitrary complexity that can be used to
compare and evaluate machine learning methods. Bio-
computing 2018. World Scientific. 259–267.
Ritchie,M.D. et al. (2001) Multifactor-Dimensionality
Reduction Reveals High-Order Interactions among
Estrogen-Metabolism Genes in Sporadic Breast Can-
cer. The American Journal of Human Genetics, 69,
138–147.
Seibert,T.M. et al. (2018) Polygenic hazard score to guide
screening for aggressive prostate cancer: development
and validation in large scale cohorts. BMJ, j5757.
Shannon,C.E. (1948) A Mathematical Theory of Commu-
nication. Bell System Technical Journal, 27, 379–423.
Sugrue,L.P. and Desikan,R.S. (2019) What Are Polygenic
Scores and Why Are They Important? JAMA, 321,
1820.
Torkamani,A. et al. (2018) The personal and clinical utility
of polygenic risk scores. Nat Rev Genet, 19, 581–590.
Wang,W.Y.S. et al. (2005) Genome-wide association stud-
ies: theoretical and practical concerns. Nat Rev Genet,
6, 109–118.
Purcell,S.M. et al. (2009) Common polygenic variation
contributes to risk of schizophrenia and bipolar dis-
order. Nature, 460, 748–752.
Motsinger,A.A. and Ritchie,M.D. (2006) Multifactor di-
mensionality reduction: An analysis strategy for mod-
elling and detecting gene - gene interactions in hu-
man genetics and pharmacogenomics studies. Hum
Genomics, 2.
BIOINFORMATICS 2020 - 11th International Conference on Bioinformatics Models, Methods and Algorithms
84
