
A Hybrid Approach for Segmenting and Fitting Solid Primitives to 3D
Point Clouds
Markus Friedrich
1
, Steffen Illium
1
, Pierre-Alain Fayolle
2
and Claudia Linnhoff-Popien
1
1
Institute for Computer Science, LMU Munich, Oettingenstraße 67, Munich, Germany
2
The University of Aizu, Ikki machi, Aizu-Wakamatsu, Japan
Keywords:
3D Computer Vision, Deep Learning, Evolutionary Computing, Fitting, RANSAC, Segmentation.
Abstract:
The segmentation and fitting of solid primitives to 3D point clouds is a complex task. Existing systems are
restricted either in the number of input points or the supported primitive types. This paper proposes a hybrid
pipeline that is able to reconstruct spheres, bounded cylinders and rectangular cuboids on large point sets. It
uses a combination of deep learning and classical RANSAC for primitive fitting, a DBSCAN-based clustering
scheme for increased stability and a specialized Genetic Algorithm for robust cuboid extraction. In a detailed
evaluation, its performance metrics are discussed and resulting solid primitive sets are visualized. The paper
concludes with a discussion of the approach’s limitations.
1 INTRODUCTION
The reconstruction of geometric primitives from 3D
point clouds is important in quality assurance and re-
verse engineering of mechanical structures and plays
a key-role for a lot of computer aided design mod-
elling tasks. Building a robust primitive reconstruc-
tion pipeline is complex: It needs to account for noise
in the input point cloud, find all potential primitives
and estimate their parameters as precisely as possible.
We propose a hybrid pipeline for the robust seg-
mentation and fitting of solid primitives that combines
the strengths of multiple approaches with a new tech-
nique for rectangular cuboid (or simply cuboid) gen-
eration based on Evolutionary Computing. A deep
neural network is adapted and trained to label points
from a point cloud with associated primitive types
(cylinder, sphere, plane). Then, the point cloud is
clustered based on point coordinate, surface normal
and primitive type label. A classic approach (efficient
RANSAC (Schnabel et al., 2007)) for primitive fitting
is applied to each cluster. Since the primitive fitting
step does not generate closed solids, we introduce an
additional step that estimates the height of cylinders
and generates cuboids based on fitted planes using a
Genetic Algorithm (GA).
The paper makes the following contributions:
• A modified deep neural network for primitive type
detection together with a fast training data set gen-
erator and a partitioning scheme for better scala-
bility with respect to input point cloud size.
• An improved primitive fitting method that uses
density-based clustering to stabilize the stochastic
fitting process and to decrease parameter sensitiv-
ity.
• A cuboid generation scheme based on a GA that
assembles fitted planes to form cuboids.
• A full pipeline for the segmentation and fitting
of solid primitives that combines state-of-the-art
techniques with the aforementioned, newly devel-
oped components.
The rest of the paper is structured as follows: We re-
view related works in Section 2. Section 3 describes
the tools that we use, followed by our proposed seg-
mentation and fitting pipeline in Section 4. The eval-
uation (Section 5) discusses experimental results and
limitations. A conclusion together with future work is
given in Section 6.
2 RELATED WORK
Segmentation, primitive detection and primitive fit-
ting are well studied problems in computer graphics,
computer aided design and related engineering disci-
plines. Several solutions have been proposed over the
years. In the following, we list some of the most rele-
38
Friedrich, M., Illium, S., Fayolle, P. and Linnhoff-Popien, C.
A Hybrid Approach for Segmenting and Fitting Solid Primitives to 3D Point Clouds.
DOI: 10.5220/0008870600380048
In Proceedings of the 15th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2020) - Volume 1: GRAPP, pages
38-48
ISBN: 978-989-758-402-2; ISSN: 2184-4321
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

vant works. The reader is also referred to the surveys
on mesh segmentation (Shamir, 2008) and primitive
detection (Kaiser et al., 2019) for a broader overview
of existing works.
2.1 Geometric Approaches
Segmentation, primitive detection and fitting are
some of the necessary steps in reverse engineering of
3D data, which is the process of recovering a com-
puter model of a 3D shape from acquired data. See,
for example, (V
´
arady et al., 1998; Marshall et al.,
2001; Benk
˝
o et al., 2001) and the references therein.
More recently, these problems of segmentation
and primitive detection have gained interest in the
computer graphics community. Some of the works
are only concerned with the segmentation of the input
point cloud (or triangle mesh) and assigning a prim-
itive type (e.g. cylinder, plane, torus) to each clus-
ter as, for example, in (Cohen-Steiner et al., 2004;
Lavou
´
e et al., 2005).
For other applications, it is also necessary to re-
cover the parameters (e.g. the radius and center of a
sphere) defining the primitives (Vanco and Brunnett,
2004; Attene et al., 2006; Schnabel et al., 2007; Li
et al., 2011; Le and Duan, 2017) in addition to the
segmentation and assignment of a primitive type to
each point.
A popular family of approaches relies on
RANSAC (Fischler and Bolles, 1981) and its vari-
ants. The efficient RANSAC method (Schnabel et al.,
2007) is a very fast RANSAC-based approach for
detecting primitives of different types in a 3D point
cloud, and recovering the corresponding parameters.
This approach is improved in (Li et al., 2011) by en-
forcing additional constraints during the fitting pro-
cess (e.g. parallelism of the cylinders’ main axes).
There are two differences between these approaches
and ours: First, we apply RANSAC to a pre-clustered
(by primitive type) point cloud, which allows us to
limit the primitives to try and make the process more
robust and less parameter sensitive. Second, unlike
RANSAC that fits unbounded primitives (planes, un-
bounded cylinders, . . . ), we generate bounded prim-
itives, in particular planes that are combined into
cuboids.
In some application domains, additional con-
straints are imposed on the primitives in considera-
tion. For example, in the reconstruction of buildings
from 3D point clouds, only planes need to be detected
and fitted, see e.g. (Monszpart et al., 2015; Oesau
et al., 2016). These planes are then combined to form
cuboids (Xiao and Furukawa, 2014; Li et al., 2016)
or more complex polyhedral shapes (Nan and Wonka,
2017). Contrary to these approaches, our method is
not limited to cuboids. Additionally, we have no lim-
itations, such as, all planes are required to be orthog-
onal to the main axes.
2.2 Machine Learning Approaches
With the increase of available 3D data sets, learn-
ing based approaches have gained interest as possible
techniques for primitive detection and fitting.
Earlier works, such as (Kalogerakis et al., 2010;
Kim et al., 2013), are based on traditional machine
learning techniques for learning segmentation and la-
belling (Kalogerakis et al., 2010) or template shapes
corresponding to each part (Kim et al., 2013).
Most of the recent approaches are based on deep
learning, however. Segmentation of point clouds us-
ing deep learning is proposed in the PointNet (Qi
et al., 2017a) and PointNet++ (Qi et al., 2017b) pa-
pers.
In (Li et al., 2019), Li et al. propose an end-to-end
learning framework for segmenting, detecting and fit-
ting primitives (plane, sphere, cylinder and cone) in
3D point clouds. It is interesting to note that this
approach relies on the point coordinates only, while
most methods (including the more classic and geo-
metric approaches) usually assume as well the pres-
ence of the surface normal at each point in the in-
put point cloud. Other approaches, such as (Zou
et al., 2017; Tulsiani et al., 2017), try to approxi-
mate the input 3D shape by predicting a collection
of cuboids. The approach described in (Paschalidou
et al., 2019) extends the previous works by replac-
ing cuboid primitives with superquadric primitives.
Generalizing these primitives leads to the learning of
shape templates (Genova et al., 2019). Compared to
these approaches, our method is not limited to a single
primitive type (e.g. cuboids). Additionally, there is no
restriction on the size of the input point cloud, which
these deep learning-based methods usually have.
3 BACKGROUND
In this section, we give a brief description of the tools
that are used in our approach described in Section 4.
3.1 Farthest Point Sampling
Farthest Point Sampling (FPS) is used as in (Qi et al.,
2017a) to down-sample a point cloud to k points while
still covering a certain surface area uniformly. It is
based on the idea of iteratively selecting the next sam-
ple as the farthest away point from the set of points
A Hybrid Approach for Segmenting and Fitting Solid Primitives to 3D Point Clouds
39

selected so far. We use a greedy implementation with
a O (n
2
) computational complexity (n is the number
of points in the point cloud to be down-sampled) that
meets our requirements in terms of point cloud size
and running time.
3.2 DBSCAN
Density Based Spatial Clustering of Applications
with Noise (DBSCAN) is a popular clustering method
introduced in (Ester et al., 1996). It works by start-
ing from high density samples and expanding clusters
from these samples. This expansion is done by con-
sidering the samples in the neighborhood. Neighbors
are determined based on a given metric. We use DB-
SCAN for clustering neighbor points assigned to the
same primitive type (Section 4.2). In (Czerniawski
et al., 2018), DBSCAN is also used for point cloud
clustering but without an additional per-point primi-
tive type label like in this work.
3.3 PointNet++
PointNet (Qi et al., 2017a) and its successor
PointNet++ (Qi et al., 2017b) are deep neural net-
works specialized in the processing of point clouds
(semantic segmentation, classification). PointNet++
offers better generalization capabilities and robust-
ness than PointNet by learning the context of local
features. We use a variant of PointNet++ for assign-
ing a label (primitive type) to each point in the input
point cloud (Section 4.2).
3.4 RANSAC
RANSAC (Fischler and Bolles, 1981) is a method for
estimating the parameters of a model (e.g. the param-
eters defining a plane) from a noisy data set. It works
by selecting a few points and directly determining the
parameters of the corresponding primitive. Then, all
points that are located on or near the fitted primitive’s
surface are collected. The process is repeated until the
probability that the fitted primitive best describes the
point cloud is above some threshold.
A RANSAC-based approach is used in our
pipeline for fitting the primitives’ parameters given
computed clusters of points (see Section 4.3). We
use the efficient RANSAC approach (Schnabel et al.,
2007).
3.5 Genetic Algorithms
Genetic Algorithms (GA) are biology-inspired,
stochastic metaheuristics for solving optimization
problems. The optimization process of the GA starts
with a randomly initialized population of individuals
sampled from the problem’s search space. At each it-
eration, these individuals are ranked according to their
fitness score, obtained by evaluating a fitness func-
tion. The best creatures are selected to be the next
generation’s parents. The parents are then recom-
bined by crossover and mutated to create offspring.
The new population is filled with the offspring to-
gether with selected surviving individuals from the
current population. This procedure is repeated until
a certain termination criteria is met. We use a GA for
combining fitted planes to cuboids (Section 4.4).
3.6 Signed Distance Functions
In this work, we represent primitives using the signed
distance function to their boundary. For a solid S,
its boundary surface ∂S is implicitly defined by the
zero level-set of its corresponding distance function
d
S
: {x ∈ R
3
: d
S
(x) = 0}. The surface normal at
point x ∈ R
3
is given by the gradient of the distance
function ∇d
S
(x), which has unit norm |∇d
S
(x)| = 1.
In this work, we consider the following primitives:
cuboids, spheres and cylinders.
4 CONCEPT
4.1 Pipeline
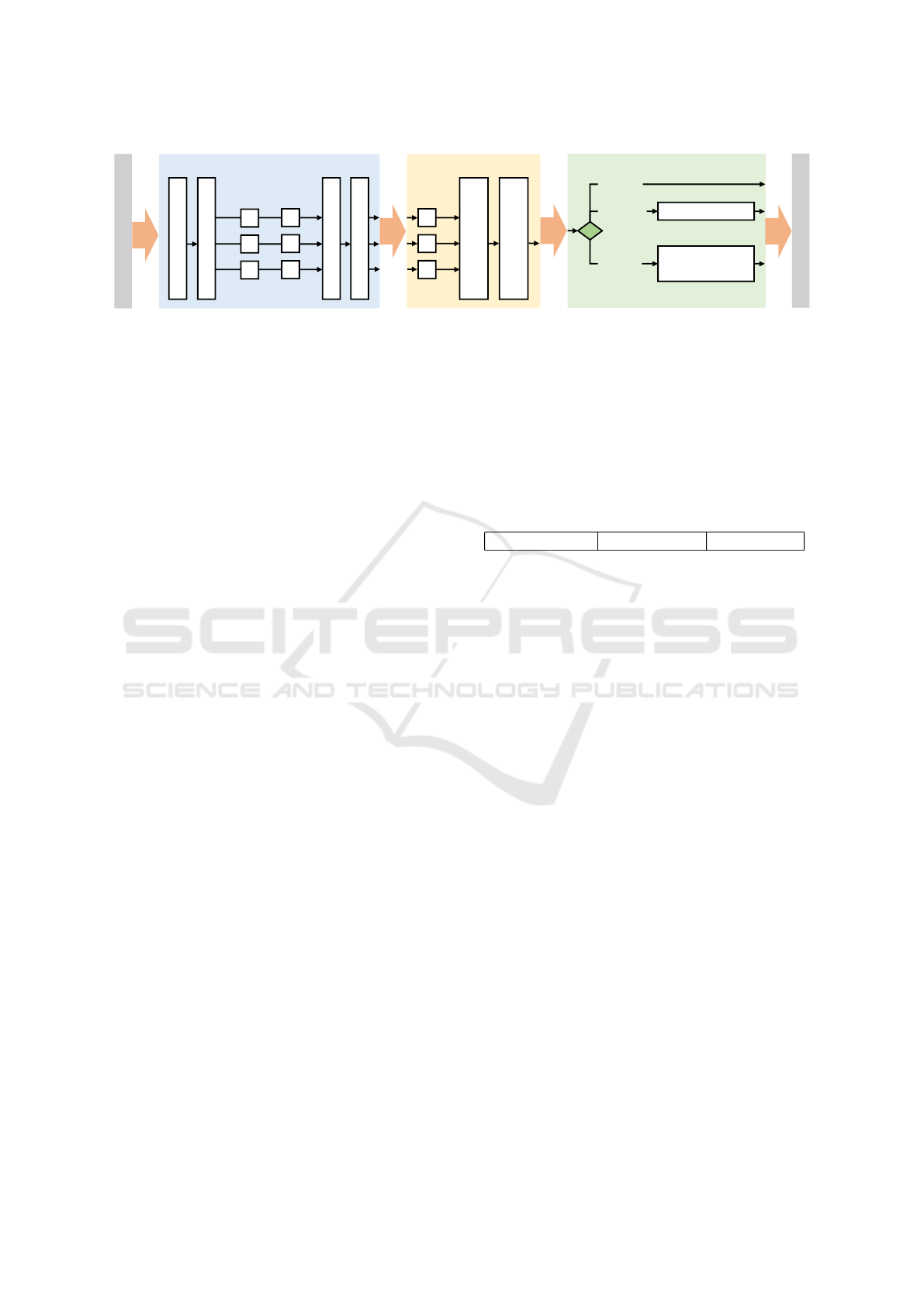
Our approach is summarized by the pipeline in Fig. 1.
It contains three major parts: The first part primitive
type detection predicts a primitive type label (plane,
sphere, cylinder) for each point in the input point
cloud O and clusters points using DBSCAN resulting
in homogeneous clusters of points associated to prim-
itives of the same type. The clustering leads to more
stable results in the next part, the primitive fitting,
which uses the efficient RANSAC algorithm (Schn-
abel et al., 2007) to extract primitive parameters for
primitives in each cluster. Resulting cylinders are not
closed (i.e. their height is not determined) and planes
need to be combined to form solids (cuboids). This
is done in the last step, the solid primitive generation
step.
GRAPP 2020 - 15th International Conference on Computer Graphics Theory and Applications
40
solid primitive generation
primitive type detection primitive fitting
pointcloud
solid primitive
generation GA
detection
RANSAC
spatial partitioning
FPS
pre-processing
merge
solid primitives
height estimation
merge & duplicate removal
clustering
sphere
cylinder
cuboid
per-primitive FPS
Figure 1: The pipeline for the segmentation and fitting of solid primitives.
4.2 Primitive Type Detection
Pre-processing. To remove outliers from the input
point cloud, we use a simple density-based unsuper-
vised outlier detection method (Breunig et al., 2000).
Additionally, we normalize the point coordinates so
that they fit into a unit cube. This assumption is used
in the primitive type detection step.
Spatial Partitioning. The input point cloud is parti-
tioned in n × n × n boxes of equal dimensions using
the point cloud’s axis-aligned bounding box (AABB)
as the initial volume to partition (we used n = 2 in
the evaluation). This is done for two reasons: Firstly,
for better generalization, the model for primitive type
label prediction is trained on model partitions. Thus,
point cloud partitions are closer to what the network
has learned, which results in better predictions. Sec-
ondly, the network architecture requires a fixed maxi-
mum number of points per input point cloud (we use
2048 points). The partitioning circumvents this re-
striction for the complete input point cloud since pre-
diction is done per-partition. See Fig. 6a for results of
this step.
Sampling and Detection. Since for performance rea-
sons (both in training and prediction), the maximum
input point cloud size for the PointNet++-based detec-
tion step is set to 2048, FPS with k = 2048 is applied
to each point cloud partition. Then, primitive type la-
bel prediction is conducted on each partition, result-
ing in a label (the primitive type) for each point. For
better prediction results, we extended PointNet++ to
use not only point coordinates but also point normals
for training and prediction. See Fig. 6b for results.
Merge. All point cloud partitions are merged together
resulting in a single set of labeled points.
Clustering. The point set is now clustered using DB-
SCAN. For performance reasons, the Euclidean dis-
tance is used as the distance metric for DBSCAN.
This requires a 1-hot-encoding of the primitive type
label (e.g. a cylinder’s encoding is (1,0, 0), a sphere’s
(0, 1, 0), . . . ) per point, together with its normalized
point coordinates and normal vector. Table 1 shows
the attributes of a single point as represented during
clustering. The collection of all such points is passed
to DBSCAN for clustering. The clustering process
consists of two stages: In the first stage, the input
point cloud is clustered using o
p
and o
n
. Then, in the
second stage, resulting clusters are clustered again us-
ing o
p
and o
t
. This 2-level hierarchical approach de-
livered the best clustering results in our experiments.
Table 1: Attributes of a single point o: Coordinates, normal
vector and 1-hot-encoded primitive type vector.
o
p
= (p
x
, p
y
, p
z
) o
n
= (n
x
, n
y
, n
z
) o
t
= (t
0
,t
1
,t
2
)
The approach leads to clusters containing points
with the same primitive type label. Using the point’s
normal and position additionally decreases the num-
ber of primitive types per cluster. For most of our test
models this results in a 1 : 1 ratio between primitive
types and clusters. Fig. 6c illustrates examples of re-
sults obtained by the clustering step.
4.3 Primitive Fitting
RANSAC. The RANSAC primitive fitting method is
applied to each cluster separately. The input is the
sampled (using FPS) cluster point cloud. The list
of primitive types for RANSAC to consider is ex-
tracted from the cluster’s predicted primitive type la-
bels available for each point. Based on our experi-
ments, this results usually in a single primitive type
- in rare cases, however, this number could be higher.
The number of primitives to detect is reduced, as well,
by the clustering, e.g. for most planes only a single
primitive needs to be fitted per cluster. Both, the re-
duced number of primitive types to consider and the
smaller amount of primitives to detect, have positive
influence on the robustness and parameter sensitivity
of the RANSAC approach.
Merge and Duplicate Removal. To make the output
of RANSAC more robust, we run it multiple times on
each cluster (3 times in our experiments), collect the
fitted primitives from all the runs and merge the prim-
itives that are close. This process works as follows:
Starting from the fitted primitives obtained from all
A Hybrid Approach for Segmenting and Fitting Solid Primitives to 3D Point Clouds
41

the runs of RANSAC, we first form clusters of close
primitives. Then, within each cluster, we merge those
primitives. Two primitives are considered to be close
if their parameters are within a certain threshold. For
example, we consider two spheres to be close if the
distance between their centers is within some thresh-
old, and similarly for their radii. Other primitives may
also involve comparing the angles between two direc-
tions and verify that they are within some threshold.
Merging close primitives is simply done by taking the
average of their defining parameters. For example,
for three close spheres, we would create a new sphere
with a radius, respectively center, equal to the average
of the three spheres radii, respectively centers.
Per-Primitive Sampling. We apply FPS (usually
with k = 100) to the point set associated to each fitted
primitive. This is done in order to reduce the com-
putational effort for evaluating the objective function
(Equation 1) in the GA executed in the solid primitive
generation step.
4.4 Solid Primitive Generation
4.4.1 Spheres and Cylinders
Spheres are already bounded primitives, they don’t
need to be processed any further. For cylinders, the
height must be estimated. A simple approach is used:
Each point of the point cloud corresponding to a
cylinder is projected on its main axis. The distance
between the points that are farthest away is used as
the cylinder’s height. The downside of this method is
potentially wrong alignment to other connected prim-
itives in case of missing scan points near the neigh-
boring objects.
4.4.2 Cuboids
Cuboids are more difficult to reconstruct. Please note
that we use the term cuboid as an abbreviation for
a convex polyhedron with six rectangular and pair-
wise perpendicular faces (rectangular cuboid). Since
the plane primitive’s parameters are already estimated
by RANSAC, it is possible to formulate the cuboid
construction problem as a combinatorial optimization
problem over all fitted planes: Given a set of n
P
planes P = {p
0
, . . . , p
n
P
−1
}, we would like to com-
pute a cuboid set C = {c
0
, . . . , c
n
C
−1
} containing n
c
cuboids that best represents the input point cloud O
according to an objective function F(C, O) to be max-
imized. Here O contains only those points from the
input point cloud that correspond to planes. To guar-
antee that plane sets form valid cuboids, we formulate
two constraints: 1) A cuboid must consist of exactly 6
planes, 2) A cuboid must contain planes that are pair-
wise parallel. Note that a plane from P can belong to
multiple cuboids.
To solve this combinatorial optimization problem,
a specialized GA, depicted in Fig. 2, is used. The
details about the GA are provided below.
Variation
Population
Parents
Offspring
Crossover
Mutation
Best Individual
Selection
Initialization
Selection
Ranking
Result
Termination Check
Optimization
Ghost Plane
Generation
Figure 2: The proposed GA for solving the combinatorial
cuboid generation problem with core GA parts in purple.
Ghost Plane Generation. So-called ghost planes
P
g
are planes added to the initial set of fitted planes
P
f
= P∪P
g
. Ghost planes are necessary in cases, such
as, where one side of a cuboid is fully covered by a
non-planar primitive (e.g. a cylinder, as depicted in
Fig. 3) Without these ghost planes, the constraint that
a plane set (cuboid) needs to have 6 planes could be
violated in the general case. Ghost planes are gener-
ated for each existing plane in P by computing the 2D
convex hull of the (projected) points associated to a
particular plane. Then, the minimum-area rectangle
that fully contains the convex hull is computed using
the Rotating Caliper Algorithm (Shamos, 1978). One
plane is generated for each side of the rectangle. Each
generated plane is perpendicular to the original plane
and fully contains the rectangle side (see Fig. 3 for
a visual explanation). Since the generation process
results in a large number of (often) similar planes,
an additional filter mechanism is applied that merges
similar planes.
Population. Each individual of the GA’s population
is a cuboid set, where each cuboid is a set of exactly 6
planes. A user-defined maximum number of cuboids
n
C max
restricts the size of each individual.
Initialization. The population is initialized with a
set of individuals, where each individual is a cuboid
set. The cuboid set size is randomly chosen from
{1, . . . , n
C max
}. Cuboids are generated as follows: At
first, a random plane is chosen from P
f
. Then, a plane
parallel to that plane is selected randomly. This is fol-
lowed by a selection of a plane that is perpendicular to
the two already selected ones. Now, a plane parallel to
GRAPP 2020 - 15th International Conference on Computer Graphics Theory and Applications
42

Figure 3: Ghost plane generation. Top left: The left side of
the cuboid is completely covered by the cylinder. Thus, a
plane is missing to form the complete cuboid. Ghost planes
are generated for each existing plane (the cuboid’s front
plane serves as an example). Top right: 2D convex hull,
bottom left: Minimum-area rectangle, bottom right: The 4
generated ghost planes for the cuboid’s front plane (orange).
the third plane is selected. Finally, a plane perpendic-
ular to all already selected planes is selected together
with its parallel companion. This results in a cuboid
fulfilling all constraints mentioned above. If a certain
selection does not lead to a valid cuboid, the process
is repeated.
Ranking. The fitness function F(C, O) determines
how well a set of cuboids C (an individual in the GA)
fits the point cloud O and reads:
F(C, O) = α · G(C, O) + β · A(C, O) − γ ·
|C|
n
C max
, (1)
where α, β and γ are weights and the last term is a
cuboid set size penalty term (|C| is the cardinality of
C). The geometry term G(C, O) counts the number
of points in the point cloud O whose distance to the
closest cuboid is below a certain ε
p
:
G(C, O) =
1
|O|
∑
o∈O
(
1, if min
c∈C
|d
c
(o
p
)| < ε
p
0, otherwise
,
(2)
where d
c
(·) is the signed distance function of the
cuboid c and |O| the number of points in O. Please
note that the points in O are re-projected to their corre-
sponding plane in order to account for potential noise.
The geometry term computes a score based on the
number of points in O that are close enough to the sur-
face of the closest cuboid in the cuboid set. However,
using only this metric is not enough: Even if all points
are close enough to a surface (and G(C, O) reaches its
maximum), cuboids might exist in the set that do not
contribute to the score since none of their surfaces is
the closest surface to any point. To avoid having these
additional cuboids in the set, we use two mechanisms:
First, a term to penalize large cuboid sets is used (the
third term in (1)). Second, we propose an additional
term A(C, O) that accounts for the surface area of the
cuboids that is actually covered by points of O:
A(C, O) =
∑
c∈C
|∂O
c
|
∑
c∈C
|∂c|
, (3)
where |∂O
c
| is the area covered by points from O as-
sociated to the surface of cuboid c and |∂c| is the sur-
face area of cuboid c.
For the area |∂O
c
|, an approximation is computed
using an approach based on rasterization and applied
to each of the six planes of a cuboid c. At first, the
plane-based cuboid representation is converted to a
face-and-vertex-based representation using the Dou-
ble Description Method (Fukuda and Prodon, 1995),
resulting in 6 quads each representing a side of the
cuboid. This is needed to get a bounded area per
cuboid side. For each quad, the subset of points from
O located on or near the quad is projected onto the
quad’s 2D plane. Then, the quad is rasterized using
a raster size dependent on the density of associated
points. For each raster cell, it is checked if it contains
a point. Cells that contain a point are accumulated and
multiplied by the raster cell area to get an approxima-
tion of the surface area covered by the point subset.
See Fig. 4 for a visual description of the method for a
single quad. In order to improve performance, scores
Figure 4: The rasterization of a single cuboid side with the
covered area estimation in green.
are cached and re-used, Our tests have shown that the
cache has a hit rate of around 50%.
Selection and Variation. Two individuals are se-
lected from the population as parents using a tourna-
ment selection. The crossover operator is applied to
both parents with probability p
c
. It exchanges ran-
domly selected cuboid sequences (subsets with con-
tiguous indices). The mutation operator is then ap-
plied to both parents with a probability of p
m
. Muta-
tion comes in 4 different variants:
• New: Creates a whole new cuboid set.
• Replace: Replaces a randomly selected cuboid
with a newly created cuboid.
• Modify: Selects a cuboid randomly and finds a
new parallel plane for a randomly selected one.
• Add: Adds a randomly created cuboid to the
cuboid set.
The variant to use is chosen randomly. The selec-
tion and variation process is repeated until enough
A Hybrid Approach for Segmenting and Fitting Solid Primitives to 3D Point Clouds
43

offspring for the new population is generated. In ad-
dition, a certain number of the best individuals is also
added to the new population.
Optimization. From all cuboid sets in the popula-
tion, the ones with the highest relative area coefficient
(
|∂O
c
|
|∂c|
) are collected in a new cuboid set, which is then
added to the population. This elitist selection guaran-
tees that a cuboid set exists with the best relative area
scores where other cuboid sets in the population offer
enough diversity to develop new best cuboid sets.
Termination Check and Best Individual Selection.
The GA is terminated if a certain number of iterations
has been reached or the best score has not changed
over a pre-defined number of consecutive iterations.
After termination, the best individual of the current
population is selected as the resulting cuboid set.
5 EVALUATION
5.1 Training of the Neural Network for
Primitive Type Detection
5.1.1 Data Generation
We developed a program for generating data sets
(point clouds with primitive type labels per point)
used for training our primitive type detection neu-
ral network. It is in parts similar to the one de-
scribed in (Friedrich et al., 2019): A triangle mesh
(we used models from the ModelNet data set (Zhirong
Wu et al., 2015)) is sampled. Then, a k-Means clus-
tering is applied to the sampled point cloud. For each
cluster, a primitive of random type (box, cylinder,
sphere) is fitted into the cluster as follows. The prim-
itive’s orientation is estimated using Principal Com-
ponent Analysis (PCA) applied to the cluster point
cloud. The primitive’s dimension is determined by
the cluster point cloud’s AABB dimensions, its posi-
tion is the center of mass of the cluster point cloud.
Each point belonging to a box is labeled as plane as
well as all points belonging to the cap planes of cylin-
ders.
This mechanism is efficient enough to generate
thousands of point clouds with primitive type labels
within hours. See Fig. 5 for an example.
5.1.2 Training
After data generation, our variant of PointNet++ is
trained on point clouds of about 100, 000 points each.
In addition to the point’s coordinates, we make use
of its estimated surface normal. To speed-up training,
Figure 5: A sample point cloud generated by our tool from
different views.
we extract points, which belong to the same primitive
from the initial point cloud in several subsets of 2048
points each. This procedure allows to handle larger
point cloud sizes while keeping inference and train-
ing times low. Additionally, we allow PointNet++ to
generalize further among the available points. Early
stopping prevents the model network from overfitting
to the training set. The prediction process is explained
in Section 4.2, primitive type detection.
5.2 Results of the Full Pipeline
We use 5 point clouds {PC1, . . . , PC5} with
{96.4k, 111.2k, 30.0k, 50.0k, 30.0k} points. The first
three columns in Fig. 6 show the results of the inter-
mediate steps in the primitive type detection module,
whereas the last column shows the set of solid prim-
itives obtained at the end of the full pipeline. Please
note that the goal here is not to reconstruct a com-
plete solid model but instead to generate a set of sim-
ple solid primitives, describing the point cloud and
from which the model can be reconstructed, e.g. by
CSG operations. We measured wall-clock times for
the data sets shown in Fig. 6 on an Intel Core i7-
7600U @ 2.9GHz with 16GB RAM.
Results for the primitive type detection step are
shown in Fig. 7. Within this step, the per-point prim-
itive type prediction (Detection in Fig. 7) is the most
expensive in terms of computation times.
For the primitive fitting step (see Fig. 8), the
RANSAC iterations (we used 3 iterations) are
the dominant factor contributing to the durations,
whereas the merge process is < 10ms for all data sets
and thus negligible. Please note that with clustering,
we are able to detect all relevant primitives for each
model.
The results of the solid primitive generation step
(wall-clock time and number of iterations) are de-
picted in Fig. 9. We used an unoptimized, single-
core implementation of the GA, which could eas-
ily be parallelized for better performance. We ran
the GA with a population size of 150 individuals,
a maximum cuboid set size of 75 (n
C max
), weights
(α = 1, β = 0.1, γ = 0.1) and a mutation and crossover
probability (p
m
, p
c
) of 0.4 for a maximum of 100 it-
GRAPP 2020 - 15th International Conference on Computer Graphics Theory and Applications
44

PC1PC2PC3PC4PC5
(a) Spatial Partitioning.
(b) Detection (red: cylinders,
grey: spheres, orange: planes).
(c) Clustering.
(d) Final set of solid primitives.
Figure 6: Results of the different pipeline steps.
erations. Additionally, in case of 25 consecutive iter-
ations without score improvement, the GA terminates
as well. For data sets PC1 and PC2, the maximum
number of iterations has been reached (see Fig. 9).
However, in both cases, the GA converged to a result
containing all necessary cuboids, as can be observed
in Fig. 6d. Since the GA is a non-deterministic al-
gorithm, each run could result in potentially different
cuboid sets, all having the same fitness function value.
Thus, for example, in the case of PC5, cuboids made
of different plane combinations could be obtained as
a possible result.
5.3 Comparison to Other Approaches
In Fig. 10 we compare the number of detected sur-
face primitives with and without clustering (as done
in primitive type detection). It shows that the primi-
tive fitting step improves over plain RANSAC by in-
creasing robustness (the variance of the number of
A Hybrid Approach for Segmenting and Fitting Solid Primitives to 3D Point Clouds
45

Figure 7: Timings for primitive type detection.
Figure 8: Timings for primitive fitting.
Figure 9: Timings and number of iterations for solid primi-
tive generation.
Figure 10: Number of primitives with and without cluster-
ing. Variance is indicated by the black lines.
(a)
(b)
Figure 11: (a) Detection on a real-world scan severely cor-
rupted by noise. Some planar parts are erroneously assigned
to a different type. (b) Perfect planes detection on the man-
ually cleaned point cloud.
primitives over multiple runs is decreased) and de-
creasing the number of redundant, as well as poorly
fitted primitives for all models with the exception of
PC5. For PC5, only planes need to be fitted, which is
a comparatively simple task that does not benefit from
additional clustering. Additionally, the solid primitive
generation step allows to generate solid primitives un-
like RANSAC.
Compared to existing deep learning-based tech-
niques, the proposed approach can handle larger point
clouds, does not rely on very specific training data
sets for particular model categories and does support
both, cuboids and capped quadric-based primitives
((Zou et al., 2017) and (Tulsiani et al., 2017) support
only cuboids, (Paschalidou et al., 2019) supports only
superquadrics and (Li et al., 2019) supports planes,
uncapped cylinders, uncapped cones and spheres).
5.4 Limitations
Here, we discuss issues found in the proposed ap-
proach that are left for future work.
Tolerance to Noise. The primitive type detection step
may fail on data corrupted by severe noise as shown in
Fig. 11a. For this example, a manual cleaning of the
data helps in detecting the correct types (Fig. 11b).
Please note that this manual pre-processing step was
not necessary for the evaluated data sets shown in
Fig. 6. We plan to improve our training data gener-
ator such that it implements a better scan simulation
instead of a simple mesh surface sampling with addi-
tional noise in order to increase robustness.
Redundant Primitives. Sometimes, our approach
can produce redundant cuboids, e.g. a cuboid that is
completely contained in another cuboid. This can be
controlled by tuning γ in (1).
Additionally, depending on the type of application
where the set of solid primitives produced by our ap-
proach is used, these problems may not be an issue at
all. One such example is when the set of solid primi-
tives is used as the input to a CSG tree reconstruction
GRAPP 2020 - 15th International Conference on Computer Graphics Theory and Applications
46

method such as (Fayolle and Pasko, 2016; Wu et al.,
2018; Du et al., 2018).
Missing Details. In some rare cases, fine geometric
details are not reconstructed correctly with the pro-
posed approach. This can be mitigated by increasing
the point cloud density as well as the GA’s maximum
number of iterations. In addition, the objective func-
tion weights (Equation 1) can be tweaked for a spe-
cific data set. A reduction of parameter sensitivity is
planned for future work.
Unconnected Cylinders. Since the height of a cylin-
der is estimated using the associated point cloud, it
can happen that the cylinder is not connected to other
parts and small gaps appear between primitives. This
can be mitigated by adding cylinders to the GA to find
their optimal capping planes.
6 CONCLUSION
In this paper, a hybrid primitive segmentation and fit-
ting pipeline is proposed. Our approach is capable of
handling large point clouds in reasonable time. As fu-
ture work, we plan to tackle the limitations discussed
in Section 5.4. In addition, we plan to add extra shape
types, such as arbitrary convex polytopes.
REFERENCES
Attene, M., Falcidieno, B., and Spagnuolo, M. (2006). Hi-
erarchical mesh segmentation based on fitting primi-
tives. The Visual Computer, 22(3):181–193.
Benk
˝
o, P., Martin, R. R., and V
´
arady, T. (2001). Algorithms
for reverse engineering boundary representation mod-
els. Computer-Aided Design, 33(11):839–851.
Breunig, M. M., Kriegel, H.-P., Ng, R. T., and Sander, J.
(2000). Lof: Identifying density-based local outliers.
SIGMOD Rec., 29(2):93–104.
Cohen-Steiner, D., Alliez, P., and Desbrun, M. (2004). Vari-
ational shape approximation. ACM Trans. Graphics,
3(23):905–914.
Czerniawski, T., Sankaran, B., Nahangi, M., Haas, C., and
Leite, F. (2018). 6D DBSCAN-based segmentation of
building point clouds for planar object classification.
Automation in Construction, 88(December 2017):44–
58.
Du, T., Inala, J. P., Pu, Y., Spielberg, A., Schulz, A., Rus,
D., Solar-Lezama, A., and Matusik, W. (2018). In-
versecsg: Automatic conversion of 3d models to csg
trees. ACM Trans. Graph., 37(6):213:1–213:16.
Ester, M., Kriegel, H.-P., Sander, J., and Xu, X. (1996).
A density-based algorithm for discovering clusters a
density-based algorithm for discovering clusters in
large spatial databases with noise. In Proceedings of
the Second International Conference on Knowledge
Discovery and Data Mining, KDD’96, pages 226–
231. AAAI Press.
Fayolle, P.-A. and Pasko, A. (2016). An evolutionary ap-
proach to the extraction of object construction trees
from 3d point clouds. Computer-Aided Design, 74:1–
17.
Fischler, M. A. and Bolles, R. C. (1981). Random sample
consensus: a paradigm for model fitting with appli-
cations to image analysis and automated cartography.
Communications of the ACM, 24(6):381–395.
Friedrich, M., Cuevas, F. G., Sedlmeier, A., and Ebert, A.
(2019). Evolutionary generation of primitive-based
mesh abstractions. In Proceedings of WSCG 2019.
Fukuda, K. and Prodon, A. (1995). Double description
method revisited. In Combinatorics and Computer
Science.
Genova, K., Cole, F., Vlasic, D., Sarna, A., Freeman, W. T.,
and Funkhouser, T. (2019). Learning shape templates
with structured implicit functions. arXiv preprint
arXiv:1904.06447.
Kaiser, A., Zepeda, J. A. Y., and Boubekeur, T. (2019). A
survey of simple geometric primitives detection meth-
ods for captured 3d data. Computer Graphics Forum,
38(1):167–196.
Kalogerakis, E., Hertzmann, A., and Singh, K. (2010).
Learning 3d mesh segmentation and labeling. ACM
Trans. Graph., 29(4):102:1–102:12.
Kim, V. G., Li, W., Mitra, N. J., Chaudhuri, S., DiVerdi,
S., and Funkhouser, T. (2013). Learning part-based
templates from large collections of 3d shapes. ACM
Trans. Graph., 32(4):70:1–70:12.
Lavou
´
e, G., Dupont, F., and Baskurt, A. (2005). A new
CAD mesh segmentation method, based on curvature
tensor analysis. Computer-Aided Design, 37(10):975–
987.
Le, T. and Duan, Y. (2017). A primitive-based 3d segmenta-
tion algorithm for mechanical cad models. Computer
Aided Geometric Design, 52:231–246.
Li, L., Sung, M., Dubrovina, A., Yi, L., and Guibas, L. J.
(2019). Supervised fitting of geometric primitives to
3d point clouds. In Proceedings of the IEEE Con-
ference on Computer Vision and Pattern Recognition,
pages 2652–2660.
Li, M., Wonka, P., and Nan, L. (2016). Manhattan-world
urban reconstruction from point clouds. In ECCV.
Li, Y., Wu, X., Chrysathou, Y., Sharf, A., Cohen-Or, D.,
and Mitra, N. J. (2011). Globfit: Consistently fitting
primitives by discovering global relations. ACM trans-
actions on graphics (TOG), 30(4):52.
Marshall, D., Lukacs, G., and Martin, R. (2001). Ro-
bust segmentation of primitives from range data in
the presence of geometric degeneracy. IEEE Trans-
actions on Pattern Analysis and Machine Intelligence,
23(3):304–314.
Monszpart, A., Mellado, N., Brostow, G. J., and Mitra, N. J.
(2015). RAPter: Rebuilding man-made scenes with
regular arrangements of planes. ACM Trans. Graph.,
34(4):103:1–103:12.
Nan, L. and Wonka, P. (2017). Polyfit: Polygonal surface
reconstruction from point clouds. In Proceedings of
A Hybrid Approach for Segmenting and Fitting Solid Primitives to 3D Point Clouds
47

the IEEE International Conference on Computer Vi-
sion, pages 2353–2361.
Oesau, S., Lafarge, F., and Alliez, P. (2016). Planar shape
detection and regularization in tandem. Computer
Graphics Forum, 35(1):203–215.
Paschalidou, D., Ulusoy, A. O., and Geiger, A. (2019). Su-
perquadrics revisited: Learning 3d shape parsing be-
yond cuboids. In Proceedings of the IEEE Conference
on Computer Vision and Pattern Recognition, pages
10344–10353.
Qi, C. R., Su, H., Mo, K., and Guibas, L. J. (2017a). Point-
net: Deep learning on point sets for 3d classification
and segmentation. In Proceedings of the IEEE Con-
ference on Computer Vision and Pattern Recognition,
pages 652–660.
Qi, C. R., Yi, L., Su, H., and Guibas, L. J. (2017b). Point-
net++: Deep hierarchical feature learning on point sets
in a metric space. In Advances in neural information
processing systems, pages 5099–5108.
Schnabel, R., Wahl, R., and Klein, R. (2007). Efficient
ransac for point-cloud shape detection. Computer
graphics forum, 26(2):214–226.
Shamir, A. (2008). A survey on Mesh Segmentation Tech-
niques. Computer Graphics Forum, 27(6):1539–1556.
Shamos, M. I. (1978). Computational Geometry. PhD the-
sis, Yale, New Haven, CT, USA. AAI7819047.
Tulsiani, S., Su, H., Guibas, L. J., Efros, A. A., and Malik,
J. (2017). Learning shape abstractions by assembling
volumetric primitives. In Proceedings of the IEEE
Conference on Computer Vision and Pattern Recog-
nition, pages 2635–2643.
Vanco, M. and Brunnett, G. (2004). Direct segmentation of
algebraic models for reverse engineering. Computing,
72(1):207–220.
V
´
arady, T., Benko, P., and Kos, G. (1998). Reverse en-
gineering regular objects: simple segmentation and
surface fitting procedures. Int. J. of Shape Modeling,
3(4):127–141.
Wu, Q., Xu, K., and Wang, J. (2018). Constructing 3d csg
models from 3d raw point clouds. Computer Graphics
Forum, 37(5):221–232.
Xiao, J. and Furukawa, Y. (2014). Reconstructing the
world’s museums. International Journal of Computer
Vision, 110(3):243–258.
Zhirong Wu, Song, S., Khosla, A., Fisher Yu, Lin-
guang Zhang, Xiaoou Tang, and Xiao, J. (2015).
3d shapenets: A deep representation for volumetric
shapes. In 2015 IEEE Conference on Computer Vision
and Pattern Recognition (CVPR), pages 1912–1920.
Zou, C., Yumer, E., Yang, J., Ceylan, D., and Hoiem, D.
(2017). 3d-prnn: Generating shape primitives with
recurrent neural networks. In Proceedings of the IEEE
International Conference on Computer Vision, pages
900–909.
GRAPP 2020 - 15th International Conference on Computer Graphics Theory and Applications
48
