
A CNN-based Feature Space for Semi-supervised Incremental Learning
in Assisted Living Applications
Tobias Scheck, Ana Perez Grassi and Gangolf Hirtz
Faculty of Electrical Engineering and Information Technology, Chemnitz University of Technology, Germany
Keywords:
Ambient Assisted Living, Convolutional Neural Networks, Semi-supervised, Incremental Learning.
Abstract:
A Convolutional Neural Network (CNN) is sometimes confronted with objects of changing appearance ( new
instances) that exceed its generalization capability. This requires the CNN to incorporate new knowledge, i.e.,
to learn incrementally. In this paper, we are concerned with this problem in the context of assisted living. We
propose using the feature space that results from the training dataset to automatically label problematic images
that could not be properly recognized by the CNN. The idea is to exploit the extra information in the feature
space for a semi-supervised labeling and to employ problematic images to improve the CNN’s classification
model. Among other benefits, the resulting semi-supervised incremental learning process allows improving
the classification accuracy of new instances by 40% as illustrated by extensive experiments.
1 INTRODUCTION
Convolutional Neural Networks (CNNs) are used for
all kinds of object recognition/classification based on
images. The basic idea is that CNNs learn how to
distinguish objects of interest from labeled images.
Although the ultimate goal of object classification is
to identify any possible object of any possible cate-
gory or class, for real-world applications, it is usu-
ally not feasible to generate a sufficient number of la-
beled images. Popular datasets such as MS COCO
and ILSVRC (Lin et al., 2014; Russakovsky et al.,
2015) contain 80 and 1000 classes respectively and,
hence, are not sufficient to describe all possible ob-
jects (Han et al., 2018).
On the other hand, most applications are not con-
cerned with detecting all kinds of objects, but only a
small subset of them related to their tasks/objectives.
For example, applications in the automotive domain
are typically focused on recognizing vehicles, traf-
fic signs, pedestrians, cyclists, etc., while other ob-
jects like those carried by pedestrians are not relevant.
Similarly, assisted living applications are concerned
with daily-life objects like mugs, chairs, tables, etc.,
while recognizing cars or traffic signs is out of scope.
This restriction to few object classes allows opti-
mizing CNNs for a specific task. However, a real-life
environment still undergoes continuous change. As
a result, CNNs need to incorporate new knowledge,
i.e., implement lifelong/incremental learning (K
¨
ading
et al., 2017; Parisi et al., 2019), which is a challeng-
ing endeavor bearing the risk of catastrophic forget-
ting (Goodfellow et al., 2013), i.e., losing the ability
to recognize known objects.
Contributions. In this work, we are concerned with
the above problem in assisted living applications. The
user in this context makes repeated use of the same
objects, i.e., the same mug, the same chair, etc., which
are thus easy to recognize with a CNN. On the other
hand, daily-life objects are often replaced by new
ones that, although belonging to the same class, can
have a very different appearance, i.e., new instances.
This sometimes exceeds the CNN’s capability of gen-
eralizing, which stops detecting these images reliably.
We propose a technique that combines semi-
supervised labeling and incremental learning to ap-
proach a personalized assisted living system, capa-
ble of adapting to new instances introduced by the
user at any point in time. To this end, an acquisi-
tion function selects and stores problematic images
that could not be classified with a satisfactory level of
confidence. We then make use of the feature space
generated from the training dataset to label these im-
ages without human intervention. Since the feature
space contains more information than the CNN’s clas-
sification model, it allows reliably classifying new in-
stances with only a small amount of label noise. Fi-
nally, the labeled problematic images are incorporated
into the CNN’s classification model by fine-tuning.
Structure of the Paper. This paper is organized as
Scheck, T., Grassi, A. and Hirtz, G.
A CNN-based Feature Space for Semi-supervised Incremental Learning in Assisted Living Applications.
DOI: 10.5220/0008871302170224
In Proceedings of the 15th Inter national Joint Conference on Computer Vision, Imaging and Computer Graphics Theor y and Applications (VISIGRAPP 2020) - Volume 5: VISAPP, pages
217-224
ISBN: 978-989-758-402-2; ISSN: 2184-4321
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
217

follows. Section 2 introduces the state of the art,
whereas the proposed approach is described in Sec. 3.
Section 4 then evaluates the proposed approach and
Sec. 5 concludes the paper.
2 RELATED WORK
There is an increasing interest in techniques such as
lifelong/incremental learning and semi-supervised la-
beling, which aim to alleviate CNNs’ dependency
on huge amounts of labeled data. While incremen-
tal learning focuses on the capability to successively
learn from small amounts of data, semi-supervised la-
beling looks for methods to replace the usually expen-
sive and time-consuming labeling of datasets.
An overview of incremental learning techniques
is presented by Parisi et al. (Parisi et al., 2019). One
challenge of incremental learning is to avoid catas-
trophic forgetting (McCloskey and Cohen, 1989).
That refers to the problem of new learning interfering
with old learning when the network is trained gradu-
ally. An evaluation of catastrophic forgetting on mod-
ern neural networks was presented by Goodfellow et
al. in (Goodfellow et al., 2013). Further, new metrics
and benchmarks for measuring catastrophic forgetting
are introduced by Kemker et al. (Kemker et al., 2018).
Although retraining from scratch can prevent
catastrophic forgetting from happening, this is very
inefficient. Approaches to mitigate catastrophic for-
getting are typically based on rehearsal, architecture
and/or regularization strategies. Rehearsal methods
interleave old data with new data to fine-tune the net-
work (Rebuffi et al., 2017). In (Hayes et al., 2018),
Hayes et al. study full rehearsal (i.e., involving all
old data) in deep neural networks. In this work, we
also use a mix of old and new data, however, similar
to (K
¨
ading et al., 2017) we only use a small percent-
age of old data, i.e., partial rehearsal. Architecture
methods use different aspects of the network’s struc-
ture to reduce catastrophic forgetting (Rusu et al.,
2016; Lomonaco and Maltoni, 2017). Further, regu-
larization strategies (Li and Hoiem, 2018; Kirkpatrick
et al., 2017) focus on the loss function, which is
modified to retain old data, while incorporating new
one. These alleviate catastrophic forgetting by limit-
ing how much neural weights can change. Basic reg-
ularization techniques include weight sparsification,
dropout and early stopping. Further works combine
regularization with architecture methods (Maltoni and
Lomonaco, 2019), as well as with rehearsal methods
(Rebuffi et al., 2017). In this paper, we opt to combine
partial rehearsal with early stopping, since this better
suits our application an provides good results.
In (K
¨
ading et al., 2017), K
¨
ading et al. conclude
that incremental learning can be directly achieved by
continuous fine-tuning. Our paper is in line with this
work, however, in contrast to (K
¨
ading et al., 2017),
the new data added during each incremental learning
step may belong to different classes reflecting the na-
ture of assisted living applications.
The concept of active learning (Gal et al., 2017)
also allows counteracting CNNs’ dependency on la-
beled data. Active learning implies first training a
model with a relatively small amount of data and only
letting an oracle — often a human expert — label fur-
ther data to retrain the model, if they are selected by
an acquisition function. This process is then repeated
with the training set increasing in size over time. As
already mentioned, we propose replacing the oracle
by a semi-supervised process, which labels the se-
lected data using the feature space generated from the
training dataset.
With respect to semi-supervised labeling, Lee
(Dong-Hyun Lee, 2013) proposed assigning pseudo-
labels to unlabeled data selecting the class with the
highest predicted probability. In (Enguehard et al.,
2019), Enguehard et al. present a semi-supervised
method based on embedded clustering, whereas Ras-
mus et al. propose combining a Ladder network with
supervised learning in (Rasmus et al., 2015).
3 SYSTEM DESCRIPTION
As shown in Fig. 1, our system can be divided in
three processes: classification, semi-supervised label-
ing and incremental learning. The classification pro-
cess is based on a trained CNN and performs the main
task of the system. It takes an image and assigns it a
class according to a computed confidence value. Dur-
ing this process an acquisition function selects those
images with unsatisfactory classification results (i.e.,
with confidence value lower than a given threshold)
and forwards them, together with their feature vec-
tors, to the semi-supervised labeling process.
The semi-supervised labeling process then tags
these images according to a pre-stored feature space.
This feature space is generated from the training data
and then successively updated during the incremental
learning process. The resulting labels together with
their images are incorporated into the CNN’s classi-
fication model by fine-tuning during the incremental
learning process. Finally, the new labeled images are
further added to the training dataset, their feature vec-
tors are added to the feature space and the classifica-
tion model is updated.
Note that copies of the classification model, the
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
218

training dataset and its corresponding feature space
need to be stored for the semi-supervised labeling
and the incremental learning processes. However, this
data is only required offline and does not affect per-
formance, albeit increasing memory demand. In the
following sections we describe each process in detail.
3.1 Classification Process
The classification process is responsible for identi-
fying objects displayed on the input images. This
process is the only one that runs online and is vis-
ible to the user. The classification is performed by
a pre-trained CNN. In this work, we use the well-
established ResNet50 (He et al., 2016), which not
only acts as a classification network, but also as fea-
ture extractor. ResNet50 can be described as a fea-
ture extractor followed by a fully connected Softmax
layer, where the first one generates feature vectors and
the second one classifies them.
Let C = {c
n
}with 1 ≤n ≤N be the set of N object
classes considered by the system. The training dataset
used to generate the first model M
0
is denoted by T
0
=
{(x
i
,l
i
) | l
i
∈ C , 1 ≤ i ≤ |T
0
|}, where x
i
is an image
and l
i
its corresponding label.
Once the first model M
0
is generated, T
0
is passed
through the network in order to obtain its feature
space. ResNet50 generates for each image x
i
a feature
vector f
i
:= f (x
i
) of 2048 elements (He et al., 2016).
The set of all feature vectors from T
0
together with
their corresponding labels l
i
is denoted F
0
= {(f
i
,l
i
)}
and constitutes our first feature space. Finally, T
0
and
F
0
are stored to be used during the semi-supervised
labeling and incremental learning processes.
During the classification process, ResNet50 gen-
erates a feature vector f
j
for each input image x
j
.
This vector is then passed to the final fully con-
nected Softmax layer, which returns a vector p
j
=
[p
1
j
,··· , p
N
j
], where p
n
j
denotes the probability of x
j
to belong to class c
n
. Finally, x
j
is classified ac-
cording to the greatest probability ˆp
j
∈ p
j
, where
ˆp
j
:= max{p
1
j
,··· , p
N
j
}. This means that x
j
is as-
signed to the class c
n
, for which ˆp
j
= p
n
j
holds.
The value of ˆp
j
, called confidence value, gives an
idea of how sure the classification model is about the
class assigned to the image x
j
. Therefore, when an
image x
j
is classified with a confidence value below a
certain threshold t, we conclude that the model is not
sufficiently sure about the nature of the imaged object
and its classification is considered invalid.
Images that are classified with a low confidence
value constitute a valuable source of knowledge for
the system. These contain information about objects
of interest, which is not considered in the current
classification model M
q
, with q ∈ N
0
. In order to
learn from these images later, an acquisition function
f
a
( ˆp
j
,t) is defined based on the confidence value and
a given threshold:
f
a
( ˆp
j
,t)
(
(x
j
,f
j
) selected if ˆp
j
< t,
(x
j
,f
j
) discarded else.
(1)
The selected images x
j
together with their feature
vectors f
j
are then passed to the labeling process.
3.2 Labeling Process
The images selected by f
a
( ˆp
j
,t) contain objects
whose class could not be satisfactorily identified.
That is, either objects belong to a new class not in-
cluded in C , or they belong to a known class, but are
not properly represented by the images in the current
training dataset T
q
. In this paper we focus on the lat-
ter, since this is the most common case in the applica-
tion of interest.
As mentioned before, ResNet50 is constituted by
a feature extractor followed by a Softmax layer (He
et al., 2016). During training, both, the feature ex-
tractor and the Softmax layer adapt their weights it-
eratively according to a training dataset and a loss
function. At the end of training, all weights inside
the feature extractor and the Softmax layer are fixed,
determining how to compute the features and how to
assign them a class. This means that the information
about how to separate classes inside a feature space
F
q
is summarized in the weights of the Softmax layer.
The Softmax layer does not memorize the com-
plete feature space, on the contrary, it learns a rep-
resentation of it, which should be sufficiently precise
to distinguish between classes and, at the same time,
general enough not to overfit. This results in an ef-
ficient classification method, but it also implies loss
of information. In particular, this loss of informa-
tion affects those images, that are underrepresented in
the training dataset. In many cases, although the fea-
ture space representation learned by the Softmax layer
does not describe these images correctly, the complete
feature space still does. As a consequence, the feature
space is suitable for labeling problematic images in a
semi-supervised fashion, as mentioned above.
As discussed later in Section 4.1, for images that
are well represented in the training dataset, the classi-
fication results achieved by using the complete fea-
ture space do not significantly differ from those of
the Softmax layer. That is, the representation of the
feature space by the Softmax layer is as good as the
complete feature space itself. However, if we consider
problematic images selected by f
a
( ˆp
j
,t), the classifi-
cation accuracy improves drastically when using the
A CNN-based Feature Space for Semi-supervised Incremental Learning in Assisted Living Applications
219

Semi-Supervised Labeling
𝑙
𝑗
Classification ProcessIncremental Learning
Softmax layer
f
𝑗
ො𝑝
𝑗
> 𝑇
f
𝑗
p
𝑗
no
𝑐
𝑛
yes
f
𝑗
save
delete
(x
𝑗
, f
𝑗
)
𝑥
𝑗
Incremental
Dataset
x
𝑗
Training
Dataset
Selecting and
Balancing
Transfer Learning
Updating
Feature Space and
Training Dataset
S
F
T
(f
𝑗
, 𝑙′
𝑗
)
(x
𝑗
, f
𝑗
)
Trained ResNet50
(Feature Extractor)
Figure 1: Proposed semi-supervised incremental learning system for assisted living application.
complete feature space. On the other hand, classify-
ing on the feature space is computationally expensive
and unsuitable for online applications. As a result,
ResNet50 should still be used for online classifica-
tions, while the feature space is used offline and only
for images where the Softmax layer has failed.
As mentioned above, images selected by f
a
( ˆp
j
,t)
are not properly represented in the current training set
T
q
. Hence, the idea is to use these images for a later
training. To this end, a semi-supervised labeling pro-
cess generates a label l
0
j
— also called pseudo-label
(Dong-Hyun Lee, 2013) — for each such image x
j
based on the whole feature space.
In order to calculate distances inside the feature
space, each feature is normalized using L2 and de-
noted by f
0
j
. For each class c
n
∈ C , M anchor points
a
n
m
, with 1 ≤ n ≤ N and 1 ≤m ≤M, are generated by
k-means clustering on the normalized feature space
F
0
q
. The probability of f
0
j
to belong to class c
n
is cal-
culated using soft voting:
p
0n
j
=
∑
M
m=1
e
−γkf
0
j
−a
n
m
k
2
2
∑
N
z=1
∑
M
m=1
e
−γkf
0
j
−a
z
m
k
2
2
, (2)
where γ is the parameter controlling the softness of
the label assignment, i.e., how much influence each
anchor point has according to its distance from f
0
j
(Cui
et al., 2016). Finally, the class c
n
with the highest con-
fidence value is assigned to the label l
0
j
= c
n
⇔ ˆp
0
j
=
p
0n
j
= max(p
01
j
,··· , p
0N
j
), where ˆp
0
j
denotes the confi-
dence values obtained by classifying in the complete
feature space, as opposed to the confident value ˆp
j
ob-
tained from the Softmax layer. The labeling process
forms a set S containing each selected image x
j
, its
assigned label l
0
j
and its feature vector f
0
j
:
S = {(x
j
,l
0
j
,f
0
j
),∀x
j
| ˆp
j
< t}. (3)
Once the set S reaches a given size |S|, it is passed to
the incremental learning process.
3.3 Incremental Learning Process
As stated above, images that could not be decided dur-
ing the classification process are separated by the ac-
quisition function f
a
( ˆp
j
,t) and labeled by the semi-
supervised labeling process leading to S as per (3).
When S becomes sufficiently large, it is incorporated
into the classification model by our incremental learn-
ing process.
Since not all N classes may be represented with a
similar number of examples in S or some classes may
not be represented at all, fine-tuning can potentially
lead to overfitting and catastrophic forgetting (Good-
fellow et al., 2013; K
¨
ading et al., 2017). To avoid this,
S is balanced with images from T
q
. In particular, ran-
dom images of each class from T
q
are appended to
S until reaching a minimum number of Q images per
class. This results in a balanced set S
0
used to fine-
tune the Softmax layer. This is performed offline us-
ing a copy of the current classification model M
q
.
This process allows evolving from M
q
to M
q+1
,
which already considers problematic images in S. By
incorporating images and labels from S into the train-
ing dataset T
q
, this latter evolves to T
q+1
and its size
grows from |T
q
| to |T
q
|+ |S |. The feature space is
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
220

also updated from F
q
to F
q+1
by adding the features
vectors f
0
j
∈ S. Finally, S is emptied and the current
M
q
is replaced by the new one M
q+1
.
4 EXPERIMENTS AND RESULTS
As already mentioned, the results reported in this
work are based on Resnet50 (He et al., 2016), which
has been pre-trainned with ImageNet (Deng et al.,
2009). To test and validate our system, a dataset with
four different classes (N = 4): mug, bottle, bowl and
chair was generated. To this end, we have extracted
all RoIs (Region of Interest) from the Open Images
Dataset (Krasin et al., 2017) that are labeled with
one of the mentioned classes and have an area of at
least 16,384 pixels. As a result, we obtain a dataset
of 19,207 images. This set is then separated in two
disjoint sets: the training dataset T
0
and a validation
dataset V , where |T
0
| = 15,366, |V | = 3841.
The training dataset T
0
is used to fine-tune the
Softmax layer. The training is performed using a
batch size of 128, the Stochastic Gradient Descent op-
timizer, a learning rate of 0.0005, a momentum of 0.9,
a maximum of 100 epochs and early-stopping. After
training the resulting model M
0
is used to generate
the feature space F
0
.
Then the model M
0
is tested on all images x
j
∈V .
The acquisition function f
a
( ˆp
j
,t) — see again (1) —
is used to divide V in two disjoint subsets: V
k
=
{(x
j
,l
j
) ∈ V | ˆp
j
≥ t} and V
u
= {(x
j
,l
j
) ∈ V | ˆp
j
<
t}. A threshold value of t = 0.9 for classification con-
fidence leads to |V
k
| = 3054 and |V
u
| = 787.
The classification of the images in V
k
is consid-
ered correct ( ˆp
j
≥ 0.9) and we conclude that the sys-
tem cannot learn more from them. On the other hand,
V
u
is formed by the images x
j
that could not be classi-
fied with sufficient confidence. Clearly, these images
contain information that the current model does not
know and, hence, can be used to improve the system.
4.1 Classifying and Labeling on the
Feature Space
In this section, we evaluate the efficiency of the fea-
ture space to classify images and specially to label
problematic images. First, we use V
k
to validate the
feature space as a classifier by comparing its perfor-
mance with that of the Softmax layer. This experi-
ment is based on the feature space F
0
(obtained from
the original training dataset T
0
), where we consider
k = 10, M = 10 and λ = 1.5 in (2), and the cor-
responding model M
0
. As shown in Fig. 2a, M
0
achieves an accuracy of 0.9, whereas F
0
reaches a
slightly better accuracy of 0.94 as per Fig. 2b. This
similar performance results from the fact that M
0
is
already efficient at describing the images in V
k
and,
hence, using F
0
does not considerably improve the
classification accuracy.
To evaluate the feature space as a semi-supervised
labeler, we now use V
u
. V
u
contains problematic im-
ages selected by the acquisition function for t = 0.9.
This time, the Softmax layer yields a low accuracy of
only 0.54 as shown in Fig. 2c. On the contrary, a clas-
sification using the complete feature space increases
the accuracy to 0.85 as shown in Fig. 2d.
bottle
bowl
chair
mug
Predicted label
bottle
bowl
chair
mug
True label
763 7 26 24
18 285 19 147
13 4 858 11
9 8 12 850
(a)
bottle
bowl
chair
mug
Predicted label
bottle
bowl
chair
mug
True label
781 13 20 6
4 424 15 26
8 10 867 1
5 52 4 818
(b)
bottle
bowl
chair
mug
Predicted label
bottle
bowl
chair
mug
True label
94 21 29 36
16 200 12 144
14 20 58 22
13 28 4 76
(c)
bottle
bowl
chair
mug
Predicted label
bottle
bowl
chair
mug
True label
140 9 24 7
6 346 6 14
6 6 98 4
3 26 3 89
(d)
Figure 2: Confusion matrices: (a) and (b) Softmax layer
and feature space classification on V
k
, (c) and (d) Softmax
layer and feature space classification on V
u
.
This result confirms our hypothesis from Sec.3.2
and validates using the complete feature space for
labeling problematic images. As in any semi-
supervised method, there is some label noise, which is
about 15% in our experiments. In the next section, we
evaluate the incremental learning process with respect
to robustness against label noise.
4.2 Incremental Learning
To evaluate the incremental learning process, we split
the set of problematic images V
u
by randomly select-
ing pictures into two disjoint sets: V
learn
and V
test
,
with |V
learn
| = 472 (i.e., around
3
5
of the images in
V
u
) and |V
test
| = 315 (i.e., |V
test
| = |V
u
|−|V
learn
|).
V
learn
is employed to investigate different S as de-
fined in (3) with 0 < |S|≤|V
learn
|, while V
test
and V
k
A CNN-based Feature Space for Semi-supervised Incremental Learning in Assisted Living Applications
221

are used to evaluate results. Testing on V
test
allows
us to evaluate how much the system improves after
learning from S , i.e., how good it starts recognizing
problematic images. On the other hand, testing on V
k
helps evaluating how much the systems worsens af-
ter learning from S , i.e., whether it stops recognizing
some known images.
To avoid catastrophic forgetting, the Softmax
layer must be fine-tuned with a well-balanced image
set. To this end, similar to (K
¨
ading et al., 2017), we fix
the number of images for each class to be equal to Q.
That is, we enforced |S
n
|= Q for each class c
n
, where
S
n
= {x
j
|l
0
j
= c
n
}, S
n
⊂S and Q > max
∀n
(|S
n
|) hold.
The Q −|S
n
| additional images necessary to balance
each class in S are randomly selected from T
q
. This
is also valid for classes that may not be represented in
S (S
n
=
/
0), where all Q images are extracted from T
q
.
Finding an Optimum Size for S. To investigate
how the size of S affects the classification accuracy,
we generate a sequence of sets by randomly select-
ing b images from V
learn
. The generated b|V
lean
|/bc
sets are then successively used to fine-tune the Soft-
max layer. The resulting classification models from
M
0
(before starting with incremental learning) to
M
b|V
lean
|/bc
(after fine-tuning with all images in V
learn
)
are tested on V
test
and V
k
.
We vary b from 5 to 95 in steps of 15, which re-
sults in |S| = {5,20,35,50,65,80,95}. Since we ran-
domly select images from V
learn
to form S and from
T
q
to balance S , every run of this experiment leads to
slightly different results. Hence, to reduce random-
ization effects, Fig. 3a and Fig. 3b show the average
result over three independent runs of the experiment.
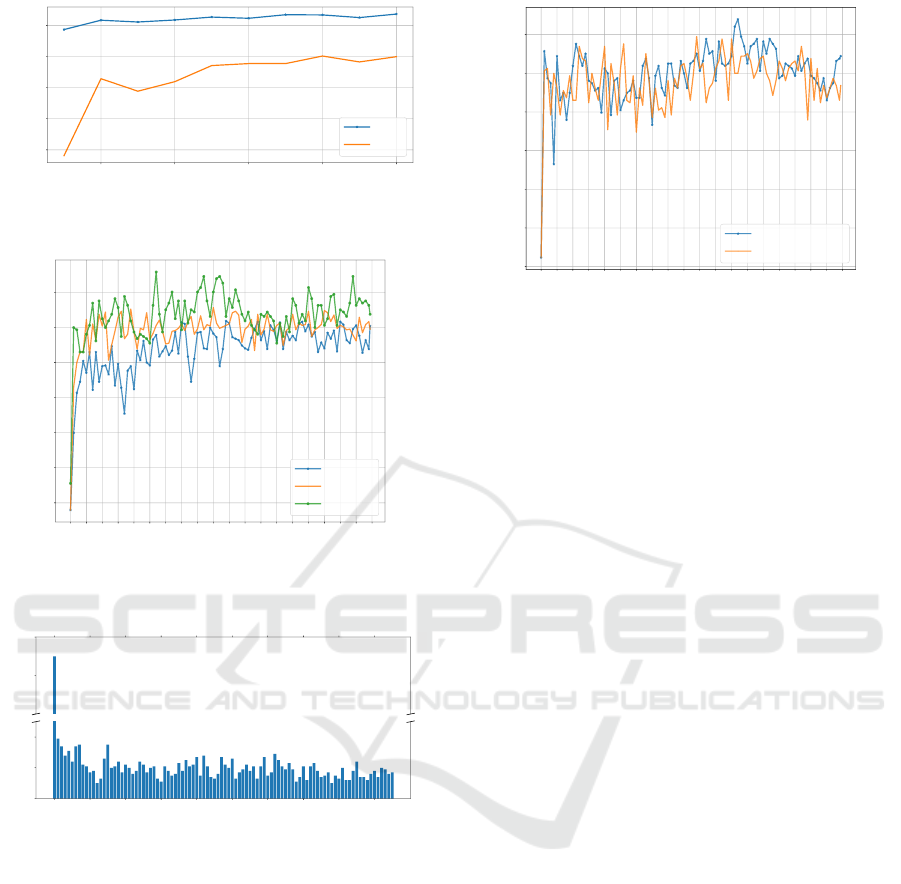
Figure 3a shows that the network is able to learn
already from |S | = 5 onward considering Q = 100.
A small |S | allows us to update of the classification
model faster, since less problematic images need to be
collected for an update. In addition, since the updated
classification model is expected to perform better, less
images will be considered as problematic next time,
which reduces the number of iterations. For these rea-
sons, we select |S | = 5 for the next experiments. For
|S| < 5, results start worsening, since S does not pro-
vide enough new information anymore.
Note that, for a fixed Q, the larger the size of S the
lower the percentage of known images in the balanced
S. As we can see in Fig. 3b, for |S | ≥ 65, the classifi-
cation accuracy decreases as Q = 100 is to small and
we start overfitting for the images in S . However, at
the end of the learning process, when all images of
V
learn
have been incorporated, the difference in accu-
racy is lower than 2% for all values of |S|.
Finding an Optimum Q. In the previous experiment,
we have fixed Q to 100 in order to study different val-
0
25
50
75
100
125
150
175
200
225
250
275
300
325
350
375
400
425
450
475
Number of added images
0.60
0.65
0.70
0.75
0.80
0.85
Accuracy
|S| = 5
|S| = 20
|S| = 35
|S| = 50
|S| = 65
|S| = 80
|S| = 95
(a) Test on V
test
0
25
50
75
100
125
150
175
200
225
250
275
300
325
350
375
400
425
450
475
Number of added images
0.90
0.91
0.92
0.93
0.94
0.95
0.96
Accuracy
|S| = 5
|S| = 20
|S| = 35
|S| = 50
|S| = 65
|S| = 80
|S| = 95
(b) Test on V
k
Figure 3: Incremental learning process for |S | =
{5,20, 35, 50,65,80, 95} and Q = 100.
ues of |S |. However, the optimum Q depends on the
value of |S|. Figure 4 shows the influence of different
values of Q on the classification accuracy for |S | = 5.
Each point of this plot represents the average accu-
racy reached by M
1
(i.e., after the first incremental
learning step) for 3 independent runs of the experi-
ment when varying Q from 10 bis 100. The accuracy
for M
0
on V
test
and V
k
(see Fig. 3a and 3b) is of 0.574
and 0.902 respectively. Consequently, as shown in
Fig. 4, M
1
starts outperforming M
0
from Q ≥ 20 on-
ward.
Finally Fig. 5 shows the average classification ac-
curacy on V
test
for 3 independent experiments along
the whole learning process considering |S | = 5 and
Q = {20,50,100}. The accuracy achieved at the end
of the incremental learning process is almost the same
for all three values of Q, where Q = 100 shows the
best results for |S | = 5. Same conclusions are ob-
tained by testing on V
k
.
Analyzing Classification Confidence. As mentioned
above, after each incremental learning step, the num-
ber of images classified with confidence values that
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
222
20 40 60 80 100
Q
0.5
0.6
0.7
0.8
0.9
Accuracy
V
k
V
test
Figure 4: Accuracy of M
1
for |S| = 5 and 10 ≤ Q ≤ 100.
0
25
50
75
100
125
150
175
200
225
250
275
300
325
350
375
400
425
450
475
Number of added images
0.55
0.60
0.65
0.70
0.75
0.80
0.85
Accuracy
Q = 20
Q = 50
Q = 100
Figure 5: Incremental learning process with |S|= 5 for Q =
{20,50, 100} tested on V
test
.
310
320
0
10
20
30
40
50
60
70
80
90
q
0
20
40
|P|
Figure 6: |P |number of images in V
test
classified with ˆp
j
<
0.9 for each model M
q
where 0 ≤q ≤ d|V
test
|/|S|e.
are below 0.9 decreases. This latter results in reduc-
ing the number of incremental learning iterations. To
visualize this effect, Fig. 6 shows the number of im-
ages |P | in V
test
that are classified with a confidence
ˆp
j
< 0.9 after every update of the classification model
(with |S|= 5 and Q = 100), i.e., P = {x
j
∈V
test
| ˆp
j
<
0.9}. Again, we repeat this experiment 3 times and
average results. It is remarkable that the number of
problematic images already falls from 315 to 39 af-
ter the first update. In other words, selecting larger S
delays any update of the model ending up collecting
images with redundant information.
Evaluation of Label Noise. As discussed in Sec. 4.1,
the proposed semi-supervised labeling has an error
rate of approximately 15% leading to wrong labels.
0
25
50
75
100
125
150
175
200
225
250
275
300
325
350
375
400
425
450
475
Number of added images
0.55
0.60
0.65
0.70
0.75
0.80
0.85
Accuracy
15 % Label noise
0 % Label noise
Figure 7: Incremental learning process for |S |= 5, Q = 100
with and without label noise tested on V
test
.
Figure 7 illustrates how this label noise impacts in-
cremental learning by plotting the classification re-
sults on V
test
with and without label noise. We again
repeated this experiment 3 times with |S| = 5 and
Q = 100 concluding that this amount of label noise
has a negligible impact on accuracy along the incre-
mental learning process. Same results are obtained by
testing on V
k
.
5 CONCLUSIONS AND FUTURE
WORK
In this paper, we proposed an approach for a CNN-
based semi-supervised incremental learning that effi-
ciently handles new instances. Our approach lever-
ages the feature space generated from the training
dataset of the CNN to automatically label problem-
atic images. Even though there is some label noise
(around 15%), we show that classification results con-
siderably improve when updating the CNN’s classifi-
cation model with the information contained in these
images. To avoid catastrophic forgetting we proposed
a combination of partial rehearsal and early stopping.
Our results indicate an improvement of around
40% more correctly detected new instances with re-
spect to the case of no incremental learning. More-
over, there is also an improvement of 4% in the classi-
fication accuracy of known images. That is, by learn-
ing from problematic images, the CNN is also able
to correct false classification results, that were not
detected by the acquisition function because of their
high confidence values. Finally, as future work, we
plan to extend our system to the case where new ob-
ject classes need to be learned.
A CNN-based Feature Space for Semi-supervised Incremental Learning in Assisted Living Applications
223

ACKNOWLEDGEMENTS
This work is funded by the European Regional Devel-
opment Fund (ERDF) under the grant number 100-
241-945.
REFERENCES
Cui, Y., Zhou, F., Lin, Y., and Belongie, S. (2016).
Fine-Grained Categorization and Dataset Bootstrap-
ping Using Deep Metric Learning with Humans in the
Loop. In 2016 IEEE Conference on Computer Vision
and Pattern Recognition (CVPR), pages 1153–1162,
Las Vegas, NV, USA. IEEE.
Deng, J., Dong, W., Socher, R., Li, L.-J., Kai Li, and Li
Fei-Fei (2009). ImageNet: A large-scale hierarchical
image database. In 2009 IEEE Conference on Com-
puter Vision and Pattern Recognition, pages 248–255,
Miami, FL.
Dong-Hyun Lee (2013). Pseudo-Label : The Simple and
Efficient Semi-Supervised Learning Method for Deep
Neural Networks. In ICML 2013 Workshop: Chal-
lenges in Representation Learning (WREPL), Atlanta,
Georgia, USA.
Enguehard, J., O’Halloran, P., and Gholipour, A. (2019).
Semi-Supervised Learning With Deep Embedded
Clustering for Image Classification and Segmentation.
IEEE Access, 7:11093–11104.
Gal, Y., Islam, R., and Ghahramani, Z. (2017). Deep
Bayesian Active Learning with Image Data. In
ICML’17 Proceedings of the 34th International Con-
ference on Machine Learning, Sydney, Australia.
Goodfellow, I. J., Mirza, M., Xiao, D., Courville, A.,
and Bengio, Y. (2013). An Empirical Investigation
of Catastrophic Forgetting in Gradient-Based Neu-
ral Networks. arXiv:1312.6211 [cs, stat]. arXiv:
1312.6211.
Han, J., Zhang, D., Cheng, G., Liu, N., and Xu, D. (2018).
Advanced Deep-Learning Techniques for Salient and
Category-Specific Object Detection: A Survey. IEEE
Signal Processing Magazine, 35(1):84–100.
Hayes, T. L., Cahill, N. D., and Kanan, C. (2018). Memory
Efficient Experience Replay for Streaming Learning.
arXiv:1809.05922 [cs, stat]. arXiv: 1809.05922.
He, K., Zhang, X., Ren, S., and Sun, J. (2016). Deep Resid-
ual Learning for Image Recognition. In 2016 IEEE
Conference on Computer Vision and Pattern Recogni-
tion (CVPR), pages 770–778, Las Vegas, NV, USA.
K
¨
ading, C., Rodner, E., Freytag, A., and Denzler, J. (2017).
Fine-Tuning Deep Neural Networks in Continuous
Learning Scenarios. In Chen, C.-S., Lu, J., and Ma,
K.-K., editors, Computer Vision – ACCV 2016 Work-
shops, volume 10118, pages 588–605. Springer Inter-
national Publishing, Cham.
Kemker, R., McClure, M., Abitino, A., Hayes, T., and
Kanan, C. (2018). Measuring Catastrophic Forgetting
in Neural Networks. New Orleans, Louisiana, USA.
Kirkpatrick, J., Pascanu, R., Rabinowitz, N., Veness, J.,
Desjardins, G., Rusu, A. A., Milan, K., Quan, J.,
Ramalho, T., Grabska-Barwinska, A., Hassabis, D.,
Clopath, C., Kumaran, D., and Hadsell, R. (2017).
Overcoming catastrophic forgetting in neural net-
works. Proceedings of the National Academy of Sci-
ences, 114(13):3521–3526.
Krasin, I., Duerig, T., Alldrin, N., Ferrari, V., Abu-
El-Haija, S., Kuznetsova, A., Rom, H., Uijlings,
J., Popov, S., Veit, A., Belongie, S., Gomes, V.,
Gupta, A., Sun, C., Chechik, G., Cai, D., Feng, Z.,
Narayanan, D., and Murphy, K. (2017). Openimages:
A public dataset for large-scale multi-label and multi-
class image classification. Dataset available from
https://github.com/openimages.
Li, Z. and Hoiem, D. (2018). Learning without Forgetting.
IEEE Transactions on Pattern Analysis and Machine
Intelligence, 40(12):2935–2947.
Lin, T.-Y., Maire, M., Belongie, S., Hays, J., Perona, P., Ra-
manan, D., Doll
´
ar, P., and Zitnick, C. L. (2014). Mi-
crosoft COCO: Common Objects in Context. In Fleet,
D., Pajdla, T., Schiele, B., and Tuytelaars, T., editors,
Computer Vision – ECCV 2014, volume 8693, pages
740–755. Springer International Publishing, Cham.
Lomonaco, V. and Maltoni, D. (2017). CORe50: a
New Dataset and Benchmark for Continuous Object
Recognition. In Proceedings of the 1st Annual Con-
ference on Robot Learning, California, USA.
Maltoni, D. and Lomonaco, V. (2019). Continuous learn-
ing in single-incremental-task scenarios. Neural Net-
works, 116:56–73.
McCloskey, M. and Cohen, N. J. (1989). Catastrophic In-
terference in Connectionist Networks: The Sequen-
tial Learning Problem. In Psychology of Learning and
Motivation, volume 24, pages 109–165. Elsevier.
Parisi, G. I., Kemker, R., Part, J. L., Kanan, C., and
Wermter, S. (2019). Continual lifelong learning with
neural networks: A review. Neural Networks, 113:54–
71.
Rasmus, A., Valpola, H., Honkala, M., Berglund, M., and
Raiko, T. (2015). Semi-Supervised Learning with
Ladder Networks. In NIPS’15 Proceedings of the 28th
International Conference on Neural Information Pro-
cessing Systems, volume 2, pages 3546–3554, Mon-
treal, Canada. MIT Press.
Rebuffi, S.-A., Kolesnikov, A., Sperl, G., and Lampert,
C. H. (2017). iCaRL: Incremental Classifier and Rep-
resentation Learning. In The IEEE Conference on
Computer Vision and Pattern Recognition (CVPR),
Honolulu, Hawaii.
Russakovsky, O., Deng, J., Su, H., Krause, J., Satheesh, S.,
Ma, S., Huang, Z., Karpathy, A., Khosla, A., Bern-
stein, M., Berg, A. C., and Fei-Fei, L. (2015). Ima-
geNet Large Scale Visual Recognition Challenge. In-
ternational Journal of Computer Vision, 115(3):211–
252.
Rusu, A. A., Rabinowitz, N. C., Desjardins, G., Soyer, H.,
Kirkpatrick, J., Kavukcuoglu, K., Pascanu, R., and
Hadsell, R. (2016). Progressive Neural Networks.
arXiv:1606.04671 [cs]. arXiv: 1606.04671.
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
224
