
A Novel Method for the Inverse QSAR/QSPR based on Artificial Neural
Networks and Mixed Integer Linear Programming with Guaranteed
Admissibility
Naveed Ahmed Azam
1 a
, Rachaya Chiewvanichakorn
1
, Fan Zhang
1
, Aleksandar Shurbevski
1 b
,
Hiroshi Nagamochi
1
and Tatsuya Akutsu
2 c
1
Department of Applied Mathematics and Physics, Kyoto University, Kyoto, Japan
2
Bioinformatics Center, Institute for Chemical Research, Kyoto University, Uji-city, Japan
Keywords:
QSAR/QSPR, Artificial Neural Networks, Mixed Integer Programming, Feature Vectors, Chemical Graphs.
Abstract:
Inverse QSAR/QSPR is a well-known approach for computer-aided drug design. In this study, we propose
a novel method for inverse QSAR/QSPR using artificial neural network (ANNs) and mixed integer linear
programming. In this method, we introduce a feature function f that converts each chemical compound G
into a vector f (G) of several descriptors of G. Next, given a set of chemical compounds along with their
chemical properties, we construct a prediction function ψ with an ANN so that ψ( f (G)) takes a value nearly
equal to a given chemical property for many chemical compounds G in the set. Then, given a target value y
∗
of the chemical property, we conversely infer a chemical structure G
∗
having the desired property y
∗
in the
following way. We formulate the problem of finding a vector x
∗
such that (i) ψ(x
∗
) = y
∗
and (ii) there exists a
chemical compound G
∗
such that f (G
∗
) = x
∗
(if one exists over all vectors x
∗
in (i)) as a mixed integer linear
programming problem (MILP). In an existing method for the inverse QSAR/QSPR, the second condition (ii)
was not guaranteed. For acyclic chemical compounds and some chemical properties such as heat of formation,
boiling point, and retention time, we conducted computational experiments.
1 INTRODUCTION
Drug design is one of the major goals of bioin-
formatics and chemo-informatics. Many computa-
tional methods have been proposed for computer-
aided drug design. Forward QSAR/QSPR (quanti-
tative structure-activity and structure-property rela-
tionships) is the problem of computing a numeri-
cal relationship between a chemical structure and a
biological activity from a given set of known data
and using this relationship to predict the activity of
unknown structures, whereas inverse QSAR/QSPR,
given such a relationship, attempts to find a chem-
ical compound that has a desired activity. There-
fore, inverse QSAR/QSPR (quantitative structure-
activity and structure-property relationships) is one of
the major approaches for the purpose (Miyao et al.,
2016; Skvortsova et al., 1993). In this approach, de-
sired chemical activities and/or properties are speci-
a
https://orcid.org/0000-0002-7941-3419
b
https://orcid.org/0000-0001-9224-6929
c
https://orcid.org/0000-0001-9763-797X
fied along with some constraints and then chemical
compounds satisfying these conditions are inferred,
where chemical compounds are usually represented
as chemical graphs. In many cases, it is also for-
mulated as an optimization problem to find a chem-
ical graph maximizing (or minimizing) an objective
function under various constraints, where objective
functions reflect certain chemical activities or prop-
erties. Objective functions are often derived from a
set of training data consisting of known molecules
and their activities/properties using statistical learn-
ing methods.
Recently, novel approaches have been proposed
for inverse QSAR/QSPR using Artificial Neural Net-
work (ANN) and deep learning technologies. For ex-
ample, recurrent neural networks (Segler et al., 2017;
Yang et al., 2017), variational autoencoders (G
´
omez-
Bombarelli et al., 2018), and grammar variational au-
toencoders (Kusner et al., 2017) have been applied. In
these approaches, neural networks are trained using
known compound/activity data and then novel chem-
ical graphs are obtained by solving a kind of inverse
problems on neural networks, that is, by looking for
Azam, N., Chiewvanichakorn, R., Zhang, F., Shurbevski, A., Nagamochi, H. and Akutsu, T.
A Novel Method for the Inverse QSAR/QSPR based on Artificial Neural Networks and Mixed Integer Linear Programming with Guaranteed Admissibility.
DOI: 10.5220/0008876801010108
In Proceedings of the 13th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2020) - Volume 3: BIOINFORMATICS, pages 101-108
ISBN: 978-989-758-398-8; ISSN: 2184-4305
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
101
input values for a trained neural network that will pro-
duce a desired output value. Usually, these inverse
problems are solved using various statistical meth-
ods. However, the solutions found by statistical meth-
ods are generally not optimal. In order to cope with
this issue, novel mixed integer linear programming
(MILP)-based methods have been proposed (Akutsu
and Nagamochi, 2019) for ANNs with rectified lin-
ear unit (ReLU) functions and sigmoid functions. In
their methods, activation functions on neurons are ef-
ficiently encoded as piece-wise linear functions so
as to represent ReLU functions exactly and sigmoid
functions approximately.
Chiewvanichakorn et al. (2020) recently com-
bined these previous approaches; efficient enumera-
tion of tree-like graphs (Fujiwara et al., 2008), and
MILP-based formulation of the inverse problem on
ANNs (Akutsu and Nagamochi, 2019). This com-
bined framework for QSAR/QSPR mainly consists
of two phases. The first phase solves (I) PREDIC-
TION PROBLEM, where each chemical compound G
is transformed into a feature vector f (G) and an ANN
N is trained from existing chemical compounds and
their values a(G) on a chemical property π to obtain
a prediction function ψ
N
so that a(G) is predicted as
ψ
N
( f (G)). The second phase solves (II) INVERSE
PROBLEM, where (II-a) given a target value y
∗
of the
chemical property π, a feature vector x
∗
is inferred
from the trained ANN N so that ψ
N
(x
∗
) is close to
y
∗
and (II-b) then a set of chemical structures G
∗
such
that f (G
∗
) = x
∗
is enumerated.
We call an inferred feature vector admissible if
it admits a chemical structure whose feature vec-
tor is equal to the inferred feature vector. How-
ever the above-mentioned previous method (Chiew-
vanichakorn et al., 2020) has no guarantee that ev-
ery inferred vector in (II-a) is admissible. In their
experiment, the probability that an inferred vector is
admissible was ranging from 20% to 50% on aver-
age. In this paper, we improve the method so that (i)
every feature vector x
∗
inferred from a trained ANN
N in (II-a) becomes admissible; and (ii) no chemi-
cal structure exists for a given target value when no
feature vector is inferred from the ANN N . Since
the new idea can be applied to any inference prob-
lem of a trained ANN, we describe the method in a
more general setting (see Section 2.1). We conducted
some preliminary computational experiments to in-
fer acyclic chemical compounds on several chemical
properties.
2 PRELIMINARY
Let R and Z denote the sets of reals and non-negative
integers, respectively. For two integers a and b, let
[a,b] denote the set of integers i with a ≤ i ≤ b.
2.1 Inference of Structures based on
ANNs and MILPs
This section reviews the previous method for the in-
verse QSAR/QSPR (Chiewvanichakorn et al., 2020),
and then shows how to improve the theoretical frame-
work of the method so as to increase the chance of
finding a larger number of solutions to the inverse
QSAR/QSPR. We here describe their and our meth-
ods in a general setting where the object to be inferred
with an ANN is not necessarily chemical compounds.
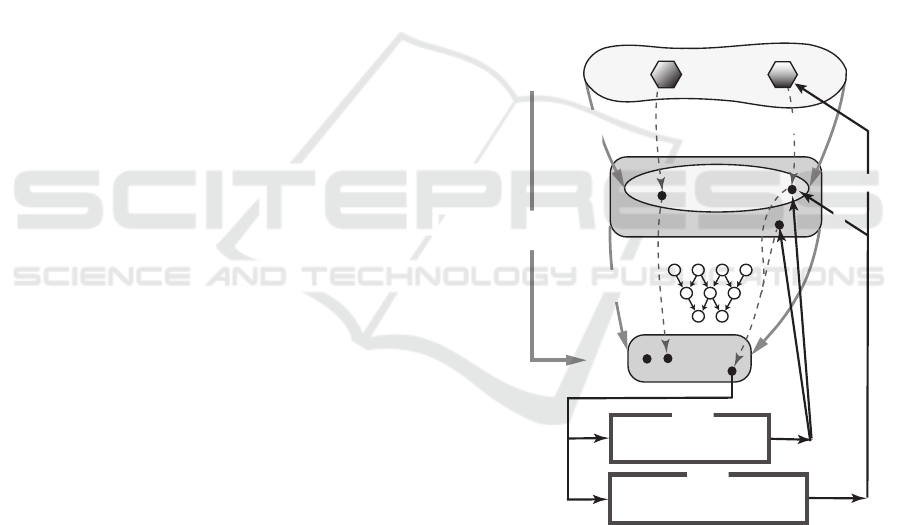
Fig. 1 illustrates the general setting.
S
R
k
R
l
x:=f(S)
x*
a(S)
y
(x)
ANN N=(A,B,w)
M(x,y,z;C
1
,C
2
)
M(x,y,z,s;C
1
,C
3
)
MILP
MILP
conversion
to feature vector
f : feature
function
y
N
: prediction
function
: a set of
structures
a: propety
function
admissible
inadmissible
S S*
s*
necessary condition only
necessary & sufficent condition
y*: target
vector
y*
f(S*)
input
input
output
output
N
x*
x*
Figure 1: An illustration of a property function a, a fea-
ture function f , a prediction function ψ
N
and MILPs
M (x,y,z, s;C
1
,C
2
) and M (x,y,z, s;C
1
,C
3
).
We start to formulate a prediction problem and its
inverse problem. Let S be a set of structures, and
a : S → R
`
be a property function for an integer ` ≥ 1
We assume that the function a is not explicitly given
and we are given the value a(S) only for structures S
in some subset S
0
of S.
(I) PREDICTION PROBLEM: Given a structure S ∈ S
(especially when S 6∈ S
0
), predict the value a(S) based
on the information {(S,a(S)) | S ∈ S
0
};
BIOINFORMATICS 2020 - 11th International Conference on Bioinformatics Models, Methods and Algorithms
102

(II) INVERSE PROBLEM: Given a vector y ∈ R
`
, gen-
erate a structure S ∈ S such that a(S) = y.
For Problem (I), we use artificial neural networks
(ANN) in a standard way. We first define a feature
space R
k
for an integer k ≥ 1 and a feature function
f : S → R
k
that converts each structure S ∈ S into a
vector f (S) ∈ R
k
, called the feature vector of S We
next construct an ANN N = (A,B,w), which consists
of an architecture A, a set B of activation functions and
a vector w ∈ R
h
that consists of arc weights and node
bias for some integer h ≥ 1. An ANN N = (A,B,w)
defines a prediction function ψ
N
: R
k
→ R
`
. For
some subset S
00
of S
0
, we try to choose an ANN
N = (A,B,w) so that the prediction ψ
N
( f (S)) of
each structure S ∈ S
00
is close to the value a(S) There
have been developed many learning algorithms that
choose such an ANN.
For Problem (II), Akutsu and Nagamochi (Akutsu
and Nagamochi, 2019) proposed a formulation based
on MILP assuming that an ANN N and its prediction
function ψ
N
are given. Let N = (A,B, w) be an ANN
such that all activation functions in B are continuous
piece-wise linear functions, n
A
denote the number of
nodes in the architecture A in N , and n
B
denote the
total number of break-points over all activation func-
tions in B. (We approximate activation functions that
are not piece-wise linear with piece-wise linear func-
tions, where the approximation may cause some nu-
merical errors in computing the predicted values with
ψ. See (Akutsu and Nagamochi, 2019) for details.)
Then it is known (Akutsu and Nagamochi, 2019)
that there is an MILP M (x, y, z; C
1
) without an objec-
tive function that consists of variable vectors x ∈ R
k
,
y ∈ R
`
and z ∈ R
p
and a set C
1
of integer restrictions
and linear equalities on these variables such that
- p = O(n
A
+ n
B
) and |C
1
| = O(n
A
+ n
B
);
- ψ
N
(x) = y if and only if there is a vector z ∈
R
p
such that (x, y, z) is feasible to the system
M (x,y,z;C
1
).
When a target value y
∗
∈ R
`
is specified for the
variable vector y ∈ R
`
, we can find a vector x
∗
∈ R
k
such that ψ
N
(x
∗
) = y
∗
by solving MILP M (x, y, z; C
1
)
with y = y
∗
. However, in general, there may be no
structure S
∗
∈ S such that f (S
∗
) = x
∗
, since no in-
formation on the structure of S is included in the
formulation of MILP M (x,y,z;C
1
). We call a vec-
tor x ∈ R
k
admissible if it admits a structure S
∗
∈ S
such that f (S
∗
) = x
∗
. To increase the chance to
have an admissible vector x ∈ R
k
, we impose a set
C
2
of linear constraints on x ∈ R
k
that are “neces-
sary conditions” for a vector x ∈ R
k
to be admissible.
Let M (x,y,z;C
1
,C
2
) denote the MILP obtained from
M (x,y,z;C
1
) by adding the set C
2
of linear constraints
on x ∈ R
k
. The previous method (Chiewvanichakorn
et al., 2020) for the inverse QSAR/QSPR followed
this idea. However there was no guarantee that every
inferred vector x
∗
by this method is admissible
In this paper, we impose to MILP M (x, y, z; C
1
)
a new set C
3
of constraints so that, for a given tar-
get value y
∗
, (i) every feature vector x
∗
inferred from
the new system becomes admissible; and (ii) no struc-
ture exists in S when the new system has no feasible
solution. For this, we introduce a new variable vec-
tor s ∈ R
h
for some integer h, and prepare a set C
3
of linear constraints on x ∈ R
k
and s ∈ R
h
to obtain
an MILP M (x, s; C
3
) that consists of variable vectors
x ∈ R
k
and s ∈ R
h
and a set C
3
of integer restrictions
and linear inequalities such that
- x ∈ R
k
is admissible if and only if there is a vec-
tor s ∈ R
h
such that (x,s) is feasible to MILP
M (x,s;C
3
); and
- s ∈ R
h
forms a structure S ∈ S if and only if there
is a vector x ∈ R
k
such that (x, s) is feasible to
MILP M (x,s;C
3
).
That is, the constraint set C
3
is “necessary and suffi-
cient condition” for a vector x ∈ R
k
to be admissible.
Now we combine the two systems M (x, y, z; C
1
) and
M (x,s;C
3
) to obtain an MILP M (x, y, z,s;C
1
,C
3
) that
consists of variable vectors x ∈ R
k
, y ∈ R
`
, z ∈ R
p
and
s ∈ R
h
and a set C
1
of constraints on x, y and z and a
set C
3
of constraints on x and s. Hence given a target
vector y
∗
∈ R
`
, we solve MILP M (x, y, z,s;C
1
,C
3
) to
find a feasible vector (x
∗
,y
∗
,z
∗
,s
∗
), where the vector
x
∗
∈ R
k
satisfies ψ
N
(x
∗
) = y
∗
, and the vector s
∗
∈ R
h
forms a structure S
∗
∈ S such that f (S
∗
) = x
∗
. Based
on the new idea, we design a method for the inverse
QSAR/QSPR in Section 3. Our M (x, s; C
3
) in the
method is presented in Section 4.
2.2 Modeling of Chemical Compounds
Graphs. Let H = (V,E) be a graph with a set V of
vertices and a set E of edges. For a vertex v ∈ V , the
set of neighbors of v in H is denoted by N
H
(v), and
the degree deg
H
(v) of v is defined to be |N
H
(v)|. The
length of a path is defined to be the number of edges
in the path. The distance dist
H
(u,v) between two ver-
tices u,v ∈ V is defined to be the minimum length of
a path connecting u and v in H. The diameter dia(H)
of H is defined to be the maximum distance between
two vertices in H. The sum-distance smdt(H) of H
is defined to be the sum of distances over all vertex
pairs.
Chemical Graphs. We represent the graph struc-
ture of a chemical compound as a graph with labels
A Novel Method for the Inverse QSAR/QSPR based on Artificial Neural Networks and Mixed Integer Linear Programming with Guaranteed
Admissibility
103

on vertices and multiplicity on edges in a hydrogen-
suppressed model. Let Λ be a set of labels each of
which represents a chemical element such as C (car-
bon), O (oxygen), N (nitrogen), S (sulfur) and so on,
where we assume that Λ does not contain H (hydro-
gen). Let mass(a) and val(a) denote the mass and
valence of a chemical element a ∈ Λ, respectively.
A chemical graph in a hydrogen-suppressed
model is defined to be a tuple G = (H,α,β) of a graph
H = (V,E), a function α : V → Λ (called an atom-
function) and a function β : E → {1,2,3} (called a
bond-function) such that
(i) H is connected; and
(ii)
∑
uv∈E
β(uv) ≤ val(α(u)) for each vertex u ∈ V.
Figure 2 illustrates an example of a chemical graph
G = (H,α,β), where the structure of the vector f (G)
is explained in Section 2.3.
We introduce a total order < over the elements
in Λ according to their mass values; i.e., we write
a < b for chemical elements a,b ∈ Λ with mass(a) <
mass(b). Choose a set Γ
<
of tuples γ = (a, b,k) ∈ Λ×
Λ × [1,3] such that a < b. For a tuple γ = (a,b, k) ∈
Λ × Λ × [1,3], let γ denote the tuple (b, a,k). Set
Γ
>
= {γ | γ ∈ Γ
<
}, Γ
=
= {(a,a,k) | a ∈ Λ, k ∈ [1,3]}
and Γ = Γ
<
∪ Γ
=
. A pair of two atoms a and b joined
with a bond of multiplicity k is denoted by a tuple
γ = (a, b,k) ∈ Γ.
C
N
O
C
C
C
f(G)=(n(H)=6, n
1
(H)=3, n
2
(H)=3,
n
3
(H)=1, n
4
(H)=0, n
5
(H)=0, n
6
(H)=0,
dia(H)=0.667, smdt(H)=0.1435,
n
C
(G)=4, n
O
(G)=1, n
N
(G)=1, ms(G)=13,
b
2
(G)=1, b
3
(G)=0, n
(C,C,1)
(G)=2,
n
(C,C,2)
(G)=1, n
(C,O,1)
(G)=1, n
(C,N,1)
(G)=1 )
Figure 2: An example of a chemical graph G = (H =
(V, E),α,β) and its feature vector f (G).
2.3 Descriptors in Feature Vectors
In our method, we use only graph-theoretical descrip-
tors for defining a feature vector, which facilitates
our designing an algorithm for constructing graphs.
Given a chemical graph G = (H = (V,E),α,β), we
define a feature vector f (G) that consists of the fol-
lowing eight kinds of descriptors: n(H): the number
of vertices; n
d
(H) (d ∈ [1,6]): the number of vertices
of degree d in H; dia(H): the diameter of H divided
by |V |; smdt(H): the sum of distances of H divided
by |V |
3
; n
a
(G) (a ∈ Λ): the number of vertices with
label a ∈ Λ; ms(G): the average mass of atoms in
G; b
i
(G) (i = 2, 3): the number of double and triple
bonds; n
γ
(G) (γ = (a,b, k) ∈ Γ): the number of label
pairs {a,b} with multiplicity k; Figure 2 illustrates an
example of a feature vector f (G).
3 A METHOD FOR INFERRING
CHEMICAL GRAPHS
Analogously with the previous method (Chiew-
vanichakorn et al., 2020), our new method for the
inverse QSAR/QSPR also solves two problems: (I)
PREDICTION PROBLEM and (II) INVERSE PROBLEM
introduced in Section 2.1. For a specified chemical
property such as boiling point, we denote by a(G) the
value of the specified chemical property for a given
chemical compound G, which is represented by a
chemical graph G = (H,α,β). We solve Problem (I)
for the inverse QSAR/QSPR as follows.
Phase 1.
1. Prepare a data set D = {(G
i
,a(G
i
)) | i =
1,2,.. ., p} for a specified chemical property,
where G
i
is a chemical graph. Set reals a, a ∈ R
such that a ≤ min{a(G
i
) | i = 1,2,.. ., p} and a ≥
max{a(G
i
) | i = 1,2,... , p}.
2. Set a graph class G to be a set of chemical graphs
such that G ⊇ {G
i
| i = 1,2, ..., p}. Introduce a
function f : G → R
K
for a positive integer K, as
we have observed in Section 2.3. We call f (G)
the feature vector of G ∈ G, and call each entry of
a vector f (G) a descriptor of G.
3. Select an architecture A and a set B of activation
functions to construct an ANN N that, given a
vector in R
K
, returns a real in the range [a,a].
Using the data set D as training data, choose a
vector w of arc weights and node biases of N
to construct a prediction function ψ
N
with N =
(A,B,w) so that ψ
N
( f (G)) takes a value nearly
equal to a(G) for many chemical graphs in D.
In this paper, we solve Problem (II) for the in-
verse QSAR/QSPR by treating the following infer-
ence problems.
(II-a) Inference of Vectors
Input: A real y
∗
∈ [a, a].
Output: Vectors x
∗
∈ R
K
and s
∗
∈ R
h
such that
ψ
N
(x
∗
) = y
∗
and s
∗
forms a chemical graph G
∗
∈ G
with f (G
∗
) = x
∗
.
(II-b) Inference of Graphs
Input: A vector x
∗
∈ R
K
.
Output: All graphs G
∗
∈ G such that f (G
∗
) = x
∗
.
In the previous method (Chiewvanichakorn et al.,
2020), they tried to find a vector x
∗
∈ R
K
such that
ψ
N
(x
∗
) = y
∗
in (II-a), which may not be admissible.
In this paper, we include into (II-a) another vector s
that represents a chemical graph so that an inferred
vector x
∗
becomes admissible. To treat Problem (II-
a), we assume that an ANN N with a piecewise-linear
BIOINFORMATICS 2020 - 11th International Conference on Bioinformatics Models, Methods and Algorithms
104

activation function (such as a ReLU) is given. As ob-
served in Section 2.1, there is an MILP M (x, y, z; C
1
)
that consists of variable vectors x ∈ R
K
, y ∈ R and
z ∈ R
p
for some integer p and a set C
1
of constraints
on these variables such that ψ
N
(x
∗
) = y
∗
if and only if
there is a vector (x
∗
,y
∗
,z
∗
) feasible to M (x,y,z;C
1
).
We here show how to construct an MILP M (x, s; C
3
)
that consists of variable vectors x ∈ R
K
and s ∈ R
h
and
a constraint set C
3
such that x
∗
∈ R
K
is admissible and
s
∗
∈ R
h
forms a chemical graph G
∗
∈ G if and only if
(x
∗
,s
∗
) is feasible to MILP M (x,s; C
3
). A more pre-
cise description of MILP M (x, s; C
3
) will be given in
Section 4. Given a value y
∗
∈ R, we can find an ad-
missible vector x
∗
∈ R
K
such that ψ
N
(x
∗
) = y
∗
(if one
exists) by solving the MILP M (x,y, z,s; C
1
,C
3
).
We design an algorithm to Problem (II-b) based
on the branch-and-bound method (see (Fujiwara et al.,
2008) for enumerating acyclic chemical compounds).
Phase 2.
4. Formulate Problem (II-a) as an MILP
M (x,y,z,s;C
1
,C
3
) based on N . Find a set
F
∗
of admissible vectors x
∗
∈ R
K
such that
(1 − ε)y
∗
≤ ψ
N
(x
∗
) ≤ (1 + ε)y
∗
for a tolerance ε
set to be a small positive real. A vector s
∗
∈ R
h
obtained together with x
∗
forms a chemical graph
G
∗
∈ G such that f (G
∗
) = x
∗
.
5. To solve Problem (II-b), enumerate all graphs
G
∗
∈ G such that f (G
∗
) = x
∗
for each admissible
vector x
∗
∈ F
∗
.
In our experiment in Section 5, we further im-
pose another set C
4
of constraints on the descriptors
in vector x not to change the feasibility of MILP
M (x,y,z,s;C
1
,C
3
) but to try to reduce the search
space required when we solve the MILP with some
solver. Also we fix the numbers of vertices and ver-
tices of degree 1 and the diameter to specified integers
n
∗
, n
∗
1
and dia
∗
, respectively in Section 5.
In Step 5 of the previous method (Chiew-
vanichakorn et al., 2020), some vector x
∗
∈ F
∗
may
not be admissible; i.e., there may not exist a graph
G
∗
∈ G such that f (G
∗
) = x
∗
. As discussed in Sec-
tion 2.1, we formulate an MILP in Phase 2 so that
every vector x
∗
∈ F
∗
obtained in Step 4 is admissible.
4 MILPs FOR REPRESENTING
ACYCLIC CHEMICAL GRAPHS
In this section, we propose a formulation of the MILP
M (x,s;C
3
) introduced in Section 2.1. For space lim-
itation, we show a sketch of the MILP. In our MILP,
we construct a tree H with n vertices and diameter
dia
∗
by selecting n − 1 pairs of vertices in an n × n
adjacency matrix (or a complete graph K
n
with n ver-
tices). For this, we introduce the following variables
and constraints:
- e(i, j) ∈ {0,1}, 1 ≤ i, j ≤ n (e(i, j) = 1 implies that
v
i
is the parent of v
j
in a tree H rooted at v
1
);
e( j, i) = 0, 1 ≤ i ≤ j ≤ n,
e(i,i + 1) = 1, i ∈ [1, dia
∗
],
e(dia
∗
+ 1, i) = 0, i ∈ [dia
∗
+ 2, n],
∑
1≤i< j
e(i, j) = 1, j ∈ [2, n].
For a tree H, we select functions α and β to define a
chemical graph G = (H,α,β) with the following vari-
ables and constraints:
-
e
α(i) ∈ {[a] | a ∈ Λ}, i ∈ [1,n] (
e
α(i) = [a] implies
α(v
i
) = a in G);
- δ
α
(i,a) ∈ {0,1}, i ∈ [1, n], a ∈ Λ (δ
α
(i,a) = 1
implies α(v
i
) = a in G);
-
e
β(i, j) ∈ [0,3], 1 ≤ i < j ≤ n (
e
β(i, j) = k implies
β(v
i
v
j
) = k for k ≥ 1 and v
i
v
j
6∈ E for k = 0);
∑
a∈Λ
δ
α
(i,a) = 1, i ∈ [1, n],
∑
a∈Λ
[a] · δ
α
(i,a) =
e
α(i), i ∈ [1, n],
e(i, j) ≤
e
β(i, j) ≤ 3e(i, j), 1 ≤ i < j ≤ n,
∑
h<i
e
β(h,i) +
∑
i< j
e
β(i, j) ≤
∑
a∈Λ
val(a) · δ
α
(i,a),
i ∈ [1, n].
Among the descriptors in our feature vector, we
show how the number n
γ
(G) of tuple γ ∈ Γ is rep-
resented in our MILP. We omit to show the linear
constraints for the other descriptors. Let Γ
fbn
de-
note the set of forbidden tuples; i.e., Γ
fbn
= (Λ × Λ ×
{1,2,3})\ (Γ
<
∪ Γ
=
∪ Γ
>
). We introduce the follow-
ing variables and constraints for descriptor n
γ
(G):
- δ
β
0
(i,k) ∈ {0,1}, i = 2,3,.. .,n, k ∈ [1,3] (for a
function β
0
: [2, n] → [1,3], δ
β
0
(i,k) = 1 implies that
v
h
is the parent of v
i
and β(v
h
v
i
) = k in G);
- δ
τ
(i,γ) ∈ {0,1}, i ∈ [2, n],γ ∈ Γ
<
∪ Γ
=
∪ Γ
>
(for
a function τ : {2,3,. ..,n} → {γ | γ ∈ Γ
<
∪ Γ
=
∪Γ
>
}, δ
τ
(i,γ) = 1 implies that v
h
is the parent of
v
i
and (α(v
h
),α(v
i
),β(v
h
v
i
)) = γ ∈ Γ
<
∪ Γ
=
∪ Γ
>
in G);
- n(γ) ∈ [0,n − 1], γ ∈ Γ
<
∪ Γ
=
(n(γ) represents
n
γ
(G));
∑
k∈[1,3]
δ
β
0
(i,k) ≤ 1, i ∈ [2, n],
∑
k∈[1,3]
kδ
β
0
(i,k) =
∑
h<i
e
β(h,i), i ∈ [2, n],
A Novel Method for the Inverse QSAR/QSPR based on Artificial Neural Networks and Mixed Integer Linear Programming with Guaranteed
Admissibility
105

δ
τ
( j, (a,b,k)) ≥ δ
α
(i,a) + δ
α
( j, b)
+ δ
β
0
( j, k)+ e(i, j ) − 3,
1 ≤ i < j ≤ n,(a,b,k) ∈ Γ
<
∪ Γ
=
∪ Γ
>
,
δ
α
(i,a) + δ
α
( j, b) + δ
β
0
( j, k)+ e(i, j ) ≤ 3,
1 ≤ i < j ≤ n,(a,b,k) ∈ Γ
fbn
,
∑
γ∈Γ
<
∪Γ
=
∪Γ
>
δ
τ
(i,γ) = 1, i ∈ [2, n],
∑
i∈[2,n]
(δ
τ
(i,γ) + δ
τ
(i,γ)) = n(γ), γ ∈ Γ
<
,
∑
i∈[2,n]
δ
τ
(i,γ) = n(γ), γ ∈ Γ
=
.
To reduce the number of graph-isomorphic so-
lutions in this MILP, we require the indexing
v
1
,v
2
,... ,v
n
of vertices in a tree H to be a depth-first
search ordering from v
1
. This can be attained with the
following variables and constraints:
- dist(i, j) ∈ [0,n], 1 ≤ i < j ≤ n (dist(i, j) represents
dist
H
(v
i
,v
j
));
- dist
lca
(i, j), 1 ≤ i < j ≤ n (dist
lca
(i, j) represents
dist
H
(w, v
1
) for the least common ancestor w
of v
i
and v
j
);
dist
lca
( j, i) ≥ dist(1, j) − n(1 − e ( j,h)),
1 ≤ j < i < h ≤ n.
5 EXPERIMENTAL RESULTS
We implemented our method for inferring acyclic
chemical graphs and executed on a PC with Intel Core
i5 1.6 GHz CPU and 8GB of RAM running under
the Mac OS operating system version 10.14.4. We
select five chemical properties: heat of atomization
(HA), heat of formation (HF), boiling point (BP), oc-
tanol/water partition coefficient (KOW) and retention
time (RT).
Results on Phase 1. In Step 1, we used a data set D
of acyclic chemical graphs in (Roy and Saha, 2003)
(resp., (Jalali-Heravi and Fatemi, 2001)) for HA, HF,
BP and KOW (resp., RT). Table 1 shows the size and
range of data sets that we prepared for each chemical
property, where we denote the following:
π: one of the chemical properties HA, HF, BP, KOW
and RT;
|D|: the size of data set D for a chemical property π;
[n,n]: the minimum and maximum number of
vertices in H over data set D.
The set Γ of all tuples γ and the number
K = |Λ| + |Γ| + 12 of descriptors in f (G) in
D are Γ = {(C, O,1),(C,S, 1),(C,C,1), (C,C,2)} and
K = 19 for HA, HF, BP and KOW and Γ =
{(C,O,1), (C,O,2),(C,C,1),(C,C,2)} and K = 18 for
RT. Some of the above parameters may be denoted
with a suffix π such as a
π
to indicate the underlying
property π ∈ {HA, HF, BP, KOW, RT}.
Table 1: The results on Steps 1 to 3 in Phase 1.
π |D| Λ [n,n] L-time R
2
HA 128 C,O,S [2,11] 11.240 0.999
HF 88 C,O,S [2,16] 1.437 0.985
BP 131 C,O,S [2,16] 7.335 0.974
KOW 62 C,O,S [2,16] 0.534 0.969
RT 39 C,O [11,16] 9.529 0.890
In Step 2, we set a graph class G to be the set of
all acyclic chemical graphs over the sets Λ and Γ in
Table 1.
In Step 3, we used scikit-learn version 0.21.3
with Python 3.7.4 to construct ANNs N where the
tool and activation function are set to be MLPRe-
gressor and ReLU, respectively. We tested several
different architectures of ANNs for each chemical
property. To evaluate the performance of the resulting
prediction function ψ
N
with cross-validation, we
partition a given data set D into five subsets D
i
,
i = 1, 2,3,4,5 randomly, where D \ D
i
is used for a
training set and D
i
is used for a test set in five trials
i = 1,2,3, 4,5. Table 1 shows the results on Step 3,
where
L-time: the average time (sec) to construct ANNs
for each trial;
R
2
: the average of coefficient of determination
over the five test sets.
For each chemical property π, we selected the
ANN N that attained the best test R
2
score among
the five ANNs to formulate an MILP M (x,y,z;C
1
) in
the second phase.
Results on Phase 2. We implemented Steps 4 and 5
in Phase 2 as follows.
Step 4. In this step, we solve the MILP
M (x,y,z,s;C
1
,C
3
) formulated based on the ANN N
obtained in Phase 1. In our computational experi-
ment, we further impose a set C
4
of several other
necessary conditions on the descriptors of our fea-
ture vector x ∈ R
K
so as to reduce the search space
for solving this MILP with a solver. Thus we solve
an MILP M (x,y,z,s; C
1
,C
3
,C
4
). We here omit de-
scribing the additional constraints in C
4
. To solve an
MILP in Step 4, we use CPLEX (ILOG CPLEX ver-
sion 12.8).
In Step 4, we conducted the following two options
in our experiments.
BIOINFORMATICS 2020 - 11th International Conference on Bioinformatics Models, Methods and Algorithms
106

(a) Choose some target y
∗
∈ [a,a] for each chemical
property in {HA, HF, BP, KOW, RT}; and
(b) For two combinations (π
1
,π
2
) ∈ {(HA, KOW), (BP,
HF)}, choose a pair of target values y
∗
π
i
∈ [a
π
i
,a
π
i
],
i = 1,2. When the same feature function f is used for
two chemical properties π
1
,π
2
∈ {HA, HF, BP, KOW,
RT}, we can combine the corresponding MILP
π
1
and
MILP
π
2
to find a vector x
∗
for a pair of target values
y
∗
π
i
∈ [a
π
i
,a
π
i
], i = 1,2. In our experiment, we choose
a target value y
∗
and fix or bound some descriptors in
our feature vector as follows:
- Choose two target values y
∗
π
∈ [a,a] for each
chemical property π and one pair of target val-
ues y
∗
π
i
∈ [a
π
i
,a
π
i
], i = 1,2 for each pair (π
1
,π
2
) ∈
{(HA, KOW), (BP, HF)};
- Choose some two values n
∗
∈ [n,n] to fix the num-
ber n(H) of vertices;
- Fix the number n
1
(H) of vertices of degree 1
to each n
∗
1
∈ {4,5,6} if n
∗
= 10,11,12, 13; n
∗
1
∈
{5,6,7} if n
∗
= 14, 15; and n
∗
1
∈ {6, 7,8} if n
∗
=
16;
- Choose some three values dia
∗
to fix the diameter
dia(H) so that dia
∗
∈ {4,5, 6} if n
∗
= 10; dia
∗
∈
{4,6,7} if n
∗
= 11; dia
∗
∈ {5,7, 8} if n
∗
= 12; and
dia
∗
∈ {6, 7,8} if n
∗
= 13, 14,15,16; and
- Bound the number n
(C,C,2)
(G) of double bonds
between two carbon atoms by choosing each of
the two ranges r ∈ {[0,1/2],(1/2, 1]} so that
n
(C,C,2)
(G)/(|V | − 1) ∈ r.
This scheme results in 3 × 3 × 2 = 18 MILPs
with different combinations of specifications for each
pair (y
∗
π
,n
∗
) (resp., each tuple (y
∗
π
1
,y
∗
π
2
,n
∗
)) of spec-
ified y
∗
π
, π ∈ {HA, HF, BP, KOW, RT} and n (resp.,
(y
∗
π
1
,y
∗
π
2
), (π
1
,π
2
) ∈ {(HA, KOW), (BP, HF)} and n).
Each of these MILPs is either feasible or infeasible
and we find one feasible vector x
∗
to each feasible
MILP. We set ε = 0.02 in Step 4.
Tables 2 to 4 show the results on Step 4, where we
denote the following:
y
∗
π
: a target value in [a, a] for a property π;
n
∗
: a specified number of vertices in [n,n];
|F
∗
|: the size of set F
∗
of vectors x
∗
generated from
feasible instances of these 18 MILPs in Step 4;
IP-time: the time (sec.) to solve the 18 MILP
instances to find a set F
∗
of vectors x
∗
.
We observe that MILPs with some restrictions
were infeasible. For example, |F
∗
| = 5 for (y
∗
Ha
=
2700,n
∗
= 10) in Table 2 means that six instances out
of the 18 MILPs were infeasible.
Step 5. In this step, we modified the algorithm
proposed in (Fujiwara et al., 2008) to enumerate all
acyclic graphs. For each x
∗
∈ F
∗
, we enumerate all
graphs G
∗
∈ G such that f (G
∗
) = x
∗
.
Tables 2 to 4 show the results on Step 5, where we
denote the following:
#G
∗
(): the number of acyclic chemical graphs G
∗
such that f (G
∗
) = x
∗
, where the number of
chemical graphs already registered in the
database PubChem among the generated
chemical graphs is indicated in parentheses;
G-time: the time (sec.) to generate all chemical
graphs G
∗
such that f (G
∗
) ∈ F
∗
.
Table 2: Results on Steps 4 and 5 with ε = 0.02.
π y
∗
n
∗
|F
∗
| IP-time #G
∗
G-time
HA 2700 10 7 0.503 50 (10) 0.0045
HA 2700 11 6 0.799 293 (4) 0.0067
HA 2900 10 7 0.362 8 (8) 0.0042
HA 2900 11 6 0.614 208 (29) 0.0043
HF 70 11 5 0.503 57 (45) 0.0033
HF 70 12 2 0.501 4 (4) 0.0016
HF 90 12 7 1.293 374 (0) 0.0147
HF 90 13 9 1.679 663 (1) 0.0126
BP 190 11 10 2.021 339 (6) 0.0334
BP 190 12 13 3.807 496 (0) 0.1423
BP 220 12 13 4.261 245 (0) 0.1240
BP 220 13 17 5.884 1675 (0) 0.3110
KOW 5 11 6 1.883 94 (4) 0.0047
KOW 5 12 7 4.196 356 (2) 0.0095
KOW 7 14 2 7.058 11 (0) 0.0041
KOW 7 15 9 16.174 975 (0) 0.0216
RT 1600 14 17 15.815 880 (0) 0.5046
RT 1600 15 17 13.933 6152 (0) 1.3607
RT 1900 15 16 14.829 6616 (2) 0.4782
RT 1900 16 18 24.100 19299 (0) 1.6018
Table 3: Results on Steps 4 and 5 for (HA, KOW) with y
∗
Ha
=
2700 and y
∗
Kow
= 5.
n
∗
|F
∗
| IP-time #G
∗
G-time
10 5 0.817 19 (6) 0.0027
11 3 1.298 25 (0) 0.0020
Table 4: Results on Step 4 and 5 for (HF, BP) with y
∗
Hf
= 90
and y
∗
Bp
= 220.
n
∗
|F
∗
| IP-time #G
∗
G-time
12 7 2.194 1056 (0) 0.0130
13 3 3.345 18 (1) 0.0090
From these tables, we observe that, for all chem-
ical properties we tested, each set of the 18 instances
for finding an acyclic chemical graph with specified
sizes n
∗
≤ 16, n
∗
1
(< n
∗
) and dia
∗
(< n
∗
) from a target
y
∗
was solved within 2 seconds based on our novel
MILP formulation; and that, for each inferred feature
A Novel Method for the Inverse QSAR/QSPR based on Artificial Neural Networks and Mixed Integer Linear Programming with Guaranteed
Admissibility
107

vector x
∗
, enumeration of all acyclic chemical graphs
G
∗
inferred from x
∗
was completed in 2 milli sec-
onds to 2 seconds. Note that our MILP outputs a fea-
ture vector for which we enumerated all structurally
unique chemical graphs as defined in Section 2.2, and
hence we were able to generate some chemical graphs
which are not registered in the PubChem database. In
these results, each inferred vector is admissible (i.e.,
has one or more corresponding chemical structures),
whereas only around 20% to 50% of the feature vec-
tors were admissible under a tolerance ε = 0.02 in
the previous method (Chiewvanichakorn et al., 2020).
Note that, for any small tolerance ε > 0, our new
method will infer an admissible vector, if one exists.
6 CONCLUDING REMARKS
In this paper, we proposed an improved method over
the previous method (Chiewvanichakorn et al., 2020)
for the inverse QSAR/QSPR by extending the MILP
so that, for a given target y
∗
, either (i) any feasible
solution to the MILP provides an admissible vector
x
∗
∈ R
K
and a chemical graph G = (H,α,β) such
that ψ
N
(x
∗
) = y
∗
and n
∗
= n(H), and n
∗
1
= n
1
(H)
and dia
∗
= dia(H) or (ii) the infeasibility of the MILP
tells us that there exists no such chemical graph G.
Although this paper presented such an MILP for the
class G of acyclic chemical graphs, it is not difficult
to modify the MILP to treat any class of chemical
graphs. Note that our MILP formulation provides a
vector s that forms a chemical graph, which means
that we can find an inferred chemical graph in Step 4
without designing an algorithm for Step 5 separately.
REFERENCES
Akutsu, T. and Nagamochi, H. (2019). A mixed integer lin-
ear programming formulation to artificial neural net-
works. In Proceedings of the 2nd International Con-
ference on Information Science and Systems, pages
215–220.
Chiewvanichakorn, R., Wang, C., Zhang, Z., Shurbevski,
A., Nagamochi, H., and Akutsu, T. (2020). A method
for the inverse QSAR/QSPR based on artificial neu-
ral networks and mixed integer linear programming.
ICBBB2020 (to appear).
Fujiwara, H., Wang, J., Zhao, L., Nagamochi, H., and
Akutsu, T. (2008). Enumerating treelike chemical
graphs with given path frequency. Journal of Chemi-
cal Information and Modeling, 48(7):1345–1357.
G
´
omez-Bombarelli, R., Wei, J. N., Duvenaud, D.,
Hern
´
andez-Lobato, J. M., S
´
anchez-Lengeling, B.,
Sheberla, D., Aguilera-Iparraguirre, J., Hirzel, T. D.,
Adams, R. P., and Aspuru-Guzik, A. (2018). Auto-
matic chemical design using a data-driven continuous
representation of molecules. ACS Central Science,
4(2):268–276.
IBM ILOG CPLEX Optimization Studio 12.8. https://www.
ibm.com/support/knowledgecenter/SSSA5P
12.8.0/
ilog.odms.studio.help/pdf/usrcplex.pdf.
Jalali-Heravi, M. and Fatemi, M. H. (2001). Artificial neu-
ral network modeling of Kovats retention indices for
noncyclic and monocyclic terpenes. Journal of Chro-
matography A, 915(1-2):177–183.
Kusner, M. J., Paige, B., and Hern
´
andez-Lobato, J. M.
(2017). Grammar variational autoencoder. In Pro-
ceedings of the 34th International Conference on Ma-
chine Learning-Volume 70, pages 1945–1954.
Miyao, T., Kaneko, H., and Funatsu, K. (2016). Inverse
QSPR/QSAR analysis for chemical structure genera-
tion (from y to x). Journal of Chemical Information
and Modeling, 56(2):286–299.
Roy, K. and Saha, A. (2003). Comparative QSPR stud-
ies with molecular connectivity, molecular negentropy
and TAU indices. Journal of Molecular Modeling,
9(4):259–270.
Segler, M. H., Kogej, T., Tyrchan, C., and Waller, M. P.
(2017). Generating focused molecule libraries for
drug discovery with recurrent neural networks. ACS
Central Science, 4(1):120–131.
Skvortsova, M. I., Baskin, I. I., Slovokhotova, O. L., Pa-
lyulin, V. A., and Zefirov, N. S. (1993). Inverse prob-
lem in QSPR/QSAR studies for the case of topological
indices characterizing molecular shape (Kier indices).
Journal of Chemical Information and Computer Sci-
ences, 33(4):630–634.
Yang, X., Zhang, J., Yoshizoe, K., Terayama, K., and
Tsuda, K. (2017). ChemTS: an efficient python li-
brary for de novo molecular generation. Science and
Technology of Advanced Materials, 18(1):972–976.
BIOINFORMATICS 2020 - 11th International Conference on Bioinformatics Models, Methods and Algorithms
108
