
A Grid-based Simulation Model for the Evolution of Influenza A
Viruses
Hsin-Ting Chung
1
and Yuh-Jyh Hu
1,2
1
Institute of Biomedical Engineering, National Chiao Tung University, 1001 University Rd., Hsinchu, Taiwan
2
College of Computer Science, National Chiao Tung University, 1001 University Rd., Hsinchu, Taiwan
Keywords: Influenza A Viruses, Evolution, Mutation, Simulation.
Abstract: We propose a simulation approach for analyzing and predicting the evolution of influenza A viruses (IAVs).
The simulation is conducted in a sequence-based space to constrain the evolutionary trends within a grid of
clusters of protein sequences. The simulated trajectories enable the investigation into point mutations on a
protein strain of IAVs in evolution, which cannot be accomplished easily by analyses of phylogenetic trees.
We tested the simulation model on three IAV internal proteins, NP, PB1 and PB2. The produced evolutionary
pathways were consistent with previous studies of the reassortment history of the 2009 human pandemic. In
addition, the chronological analysis of host-associated signature mutations on NP, PB1 and PB2 also agreed
with the previous findings.
1 INTRODUCTION
Influenza viruses belong to the viral family
Orthomyxoviridae, which includes seven genera:
influenza A, influenza B, influenza C, influenza D,
Thogotovirus, Isavirus and Quaranjavirus. The
accumulation of point mutations during genome
replication, and the reassortment of viral gene
segments during mixed infections, promote the
evolution of influenza viruses (Naffakh et al., 2008).
Influenza A viruses (IAVs) have the capacity to
evade host immune systems because of a wide variety
of potential combinations of the 18 HA and 11 NA
subtypes. Precursors to future pandemics could be
viruses carrying the HA subtypes Н1, Н2, Н3, Н5,
Н6, Н7, Н9, Н10, and NA subtypes N1, N2, N3, N8
that have been known to cause outbreaks or sporadic
human infections. Because of their vast genetic
diversity and unique host range, IAV have caused
recurrent annual epidemics and several major
worldwide pandemics in human history. The
emergence and spread of novel IAV remain of major
global concern; therefore, increased understanding of
the evolutionary trajectories is essential to maintain
the efficacy of antiviral drugs and influenza vaccines
(Timofeeva et al., 2017).
Most phenotypic evolution within species as well
as most morphological, physiological, and
behavioural differences between species can be
explained by adaptation due to natural selection
(Gerrish, 2001). To respond to a change in
environments, the task of adaption for a species is to
move the population from its current state toward the
new phenotypical optimum state.
Phylogenetic trees have been widely used to show
the evolutionary relationships between different or
distant species with a common anscestor. Successful
applications of phylogenetic trees to the study of IAV
evolution include identification of epistatic
interactions (Neverov et al., 2015) and development
of predictive fitness models for HA (Łuksza & Lässig,
2014). Unlike previous works, this paper presents a
new approach for analyzing IAV evolution by
addressing the evolutionary dynamics of IAV in
terms of the gradual accumulation of point mutations
in sequences toward the new phenotypical optimum
state.
2 MATERIALS AND METHODS
We model the simulation of IAV evolution in a
sequence-based space (Gillespie, 1984; Orr, 2002),
and constrain the simulated evolutionary trends in a
grid of clusters of protein sequences. Figure 1 shows
a sample simulated evolutionary trajectory on a grid
for a viral protein. The Y-axis indicates the specific
host species, and the X-axis represents the timescale.
Chung, H. and Hu, Y.
A Grid-based Simulation Model for the Evolution of Influenza A Viruses.
DOI: 10.5220/0008878401090116
In Proceedings of the 13th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2020) - Volume 3: BIOINFORMATICS, pages 109-116
ISBN: 978-989-758-398-8; ISSN: 2184-4305
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
109
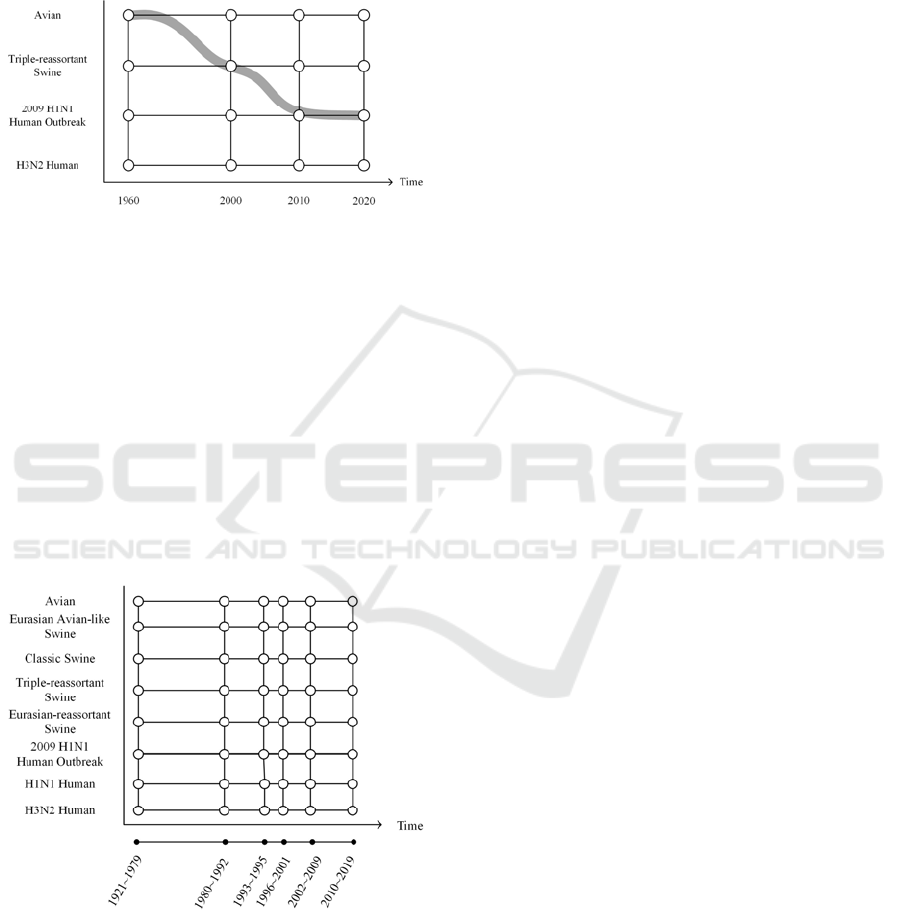
This evolutionary trajectory in Figure 1 shows that
the wild type protein started first as a segment in an
avian virus strain. It then went through the
reassortment events caused by cross-species
mutations, and finally evolved into a segment in the
2009 S-OIV human pandemic virus.
Figure 1: A sample evolutionary trajectory.
2.1 Construction of Evolutionary Grids
A simulated evolutionary trajectory is produced by a
stochastic process that is controlled within the grid. A
node in a grid, as shown in Figure 1, represents a
cluster of proteins that have high similarities
according to some metric, such as sequence
similarity, temporal, or geographical distributions, etc.
Different designs of evolutionary grids, such as the
number of nodes, the members in a node, and the time
interval between nodes, exert different influences
over the stochastic simulation process, which
warrants its flexibility.
Figure 2: A sample design of an evolutionary grid.
To construct an evolutionary grid, we first
determine the types of viruses to study and the
intervals on the time line to set up the framework of a
grid. Figure 2 shows a grid designed for the study of
viruses of various host species, e.g. classic swine. The
time line is divided into six intervals, e.g. 1921~1979.
After the framework of a grid is determined, to
complete the construction is to create the protein
clusters for the nodes on the grid. These clusters
together with the grid framework control the
stochastic simulation.
We first constructed a phylogenetic tree for the
IAV sequences downloaded from NCBI and GISAID
EpiFlu. Based on the phylogenetic analyses (Smith et
al., 2009) of human, swine and avian sample sets, we
assigned these sampled sequences (287 human, 115
swine and 411 avian) as the seeds to the appropriate
clusters according to their isolation years and
subtypes. For example, A PB1 protein
36_H1N1_Swine_swine_ohio_23_1935 in this case
was assigned to the node located at X-coordinate=
“1921~1979” and Y-coordinate= “classic swine” as
shown in Figure 2. Based on the locations of these
seeds in the phylogenic tree, we identified from the
phylogenic tree the lowest common ancestor (LCA)
per host species and subtype. For each LCA in
ascending order of its distance to the root, we
iteratively assigned the remaining sequences under
the LCA to the corresponding cluster on the grid. The
coordinate on the Y-axis was determined by the
LCA’s host species or subtype, and the isolation year
determined the coordinate on the X-axis. We
illustrate the process of host species assignment in
Figure 3 with an example of 10 seed sequences and 7
others. We start with Avian LCA, which is the closest
to the root. All sequences under the LCA except the
seeds are assigned to Avian, including the left-most
sequence in the tree. We next assign the remaining
sequences under Human LCA to H3N2 Human.
Finally, we process those non-seed sequences under
Swine LCA. Note the left-most sequence in the tree
is then reassigned to Swine from Avian. The final
host species assignments are presented at the bottom
of the tree, as shown in Figure 3, and their coordinates
on the timescale X-axis are determined by the
isolation years. We postprocess the clusters by
removing sequences with amino acid similarity
exceeding a certain threshold (set to 0.99) using CD-
HIT (Li & Godzik, 2006).
2.2 Grid-based Stochastic Simulation
We conduct a stochastic process in the sequence-
based space to simulate a point mutation that is
constrained by an evolutionary grid. By performing a
series of stochastic processes to simulate the
accumulation of point mutations, we can generate a
simulated evolutionary trajectory for a wild type IAV
protein.
BIOINFORMATICS 2020 - 11th International Conference on Bioinformatics Models, Methods and Algorithms
110

Figure 3: A sample process of host species assignment. The
seed sequences are denoted by a symbol within the vertical
bars, e.g. the 2
nd
×(Classic Swine) to the left. The others
are the remaining sequences to be assigned to a host species.
2.2.1 Point Mutation and Adaptive Walks
The adaptive walk and mutation landscape models
(Gillespie, 1991; Orr, 2003, 2006) assume that a
current wild-type sequence represents a local
optimum. After an environment change, the fitness of
this wild-type sequence drops, and its adaption is
required. A wild type IAV sequence of L amino acids
has 19L one-point mutants. To complete a beneficial
point mutation in adaption, one favorable mutant
sequence is stochastically selected based on the
fitness, and substituted for the current wild type.
The fitness is assigned to each one-point mutant
in two steps. First, for a given wild-type sequence, we
form a neighborhood of k nearest neighbors according
to sequence similarity. The details of constructing a
neighborhood is described in the next section. We
compute the average sequence similarity between the
k-nearest neighbors and each of the 19L one-point
mutants. Second, we generate and sort 19L+1 random
fitnesses based on a specified probability distribution
(e.g. normal, Gamma or exponential). The i
th
value is
reserved for the current wild type, where i can be set
to 10, 50 or 150 as in (Orr, 2002), and the remaining
sorted 19L values are assigned to the 19L one-point
mutants individually in descending order of sequence
similarity computed earlier. The 1
st
to the (i-1)
th
one-
point mutants in the sorted list are considered the
beneficial mutants as they have higher fitness than the
current wild type. Figure 4 illustrates the process of
fitness assignment.
After the assignment of the fitnesses is complete,
we calculate the mutation probability P
t
that the
current wild type (i.e. the i
th
sequence) mutates to the
t
th
one-point mutant (t = 1 ~ i-1) in the sorted list. We
define the probability P
t
as follows.
Figure 4: Fitness assignment.
⋯
(1)
1
(2)
1
,where 1…1 (3)
where F
r
is the fitness of the r
th
one-point mutant
sequence, S
m
is the selection coefficient of the m
th
one-point mutant sequence, and
v
is the probability
of fixation for the m
th
one-point mutant sequence, as
defined in Orr (Orr, 2002) and Gillespie (Gillespie,
1983). We select one of the beneficial mutants
randomly as the next wild-type sequence based on the
probability distribution of P
t
to implement a
stochastic point mutation. The fitness of the next wild
type (i.e. j
th
mutant as in Fig. 4) becomes the stopping
threshold for the next point mutation in an adaptive
walk. To check if one-point mutation should continue,
we generate a new set of 19L+1 random fitnesses. If
the current threshold is higher than all the fitnesses, it
indicates a convergence and we stop point mutation;
otherwise, we repeat the same point mutation process
as above. When a new wild type is fitter than all its
one-point mutants, an adaptive walk is complete, and
the fixation of the fittest wild-type sequence
represents a local optimum. This status remains until
the environment changes again. It will then trigger a
new adaptive walk, and the evolution continues. All
these adaptive walks connected together form a
simulated evolutionary trajectory of the initial wild
type.
Unlike previous works that focused on mutational
landscapes, adaption patterns and fitness distributions
(Gillespie, 1991; Orr, 2002; Orr, 2006), our study of
adaption considers sequence similarity, which
enables us to describe the accumulation of point
mutations along a simulated evolutionary trajectory.
Figure 5 shows the process of an adaptive walk.
A Grid-based Simulation Model for the Evolution of Influenza A Viruses
111
Figure 5: Process of an adaptive walk.
2.2.2 K-nearest-neighbor Neighborhood
As mentioned in the previous section, we sort the 19L
one-point mutants according to their sequence
similarities to a neighbourhood of k-nearest neighbors.
Because the ranking of the mutants is crucial to the
result of point mutation, the members in the
neighborhood consequently play an important role in
the control of adaptive walks.
Figure 6: Construction of neighbourhood for retrospective
simulation. The triangle denotes the initial wild type
isolated in 1978. The shaded area represents a forward k-
nearest-neighbor neighborhood.
We classify the simulated evolutionary
trajectories into two types: retrospective and
prospective. A retrospective trajectory describes the
events of point mutation that may have occurred to a
given wild type. By contrast, a prospective trajectory
predicts the events of point mutation that may occur
in the near future to some current wild type. The k-
nearest-neighbor neighborhood is therefore
constructed differently for retrospective and
prospective simulations.
For retrospective simulation, we construct a
neighborhood from the sequences available on the
evolutionary grid. Given a wild-type sequence, we
first identify its closest mapping sequence on the grid.
For this closest sequence, to form a neighborhood we
locate its k-nearest neighbors on the grid that were
isolated in the same year or later to warrant the
adaptive walk will move forward in time. We call
these neighbors “forward neighbors.”
Figure 7: Construction of neighbourhood for prospective
simulation. The triangle denotes the wild type of interest
isolated in 2010. The irregular shaded area to the left
represents a backward k-nearest-neighbor neighborhood.
The middle rectangular shaded area indicates a pool from
which to create a pseudoneighborhood. The irregular
shaded area to the right shows a k-nearest-neighbor
pseudoneighborhood.
Unlike retrospective simulation, it is not
appropriate to construct a neighborhood directly from
the sequences available on the grid because they were
isolated in the past, and they may mislead the
adaptive walk backward in time. To resolve the
problem with unavailability of forward neighbors, we
create pseudoneighbors. For a current wild type of
interest, we select a sequence available on the grid as
an initial wild type, and run retrospective simulation
multiple times until the simulated evolution reaches
the given wild type of interest or some similar
sequence. If the retrospective evolution cannot reach
the given wild type or even a similar sequence, we
start with a different initial wild type and repeat the
retrospective simulation. We collect the amino acid
mutation frequencies from the retrospective
trajectories, and estimate the first-order and second-
order transition probabilities of amino acids, P(AA
i
’ |
AA
i
) and P(AA
i
’ | AA
i-1
AA
i
), where AA is an old
BIOINFORMATICS 2020 - 11th International Conference on Bioinformatics Models, Methods and Algorithms
112

amino acid, AA’ is the new amino acid after point
mutation, and i is the position of the amino acid in the
sequence.
In contrast to the k-nearest-neighbor
neighborhood identified in retrospective simulation,
to create a pseudoneighborhood for a wild type of
interest, we first identify its k-nearest sequences that
are available on the grid and were isolated in the same
year or earlier than this wild type. We call these
neighbors “backward neighbors.” From each
backward neighbor sequence, we generate multiple
pseudosequences based on the first-order and second-
order transition probabilities, and collect them into a
pool. Subsequently, we select from the pool the k-
nearest pseudosequences to the wild type to construct
the pseudoneighborhood. Figures 6 and 7 illustrate
the construction of neighborhoods for retrospective
and prospective simulation, respectively.
3 RESULTS AND DISCUSSION
We tested the proposed simulation model on three
internal proteins, PB1, PB2, and NP, of IAVs. For
each protein, we selected four different strains and
tested them in retrospective and prospective
simulations, respectively. Table 1 lists the protein
strains in the study.
Table 1: List of protein strains for simulation tests.
Internal
Protein
(Host)
Strain Name
(retrospective simulation)
Strain Name
(prospective simulation)
PB1
(Human)
A/nt/60/1968
A/England/878/1969
A/Memphis/101/1972
A/England/1972
A/Waikato/16/2000
A/New South Wales/36/2000
A/Queensland/6/2000
A/Western Australia/12/2000
PB2
(Avian)
A/pintail duck/ALB/219/1977
A/mallard/Alberta/46/1977
A/duck/Alberta/35/1976
A/mallard/Wisconsin/524/1979
A/duck/NJ/7717-70/1995
A/mallard/Minnesota/282/2000
A/common teal/Netherlands/10/2000
A/shorebird/Delaware Bay/280/1999
NP
(Swine)
A/swine/Italy/2/1979
A/swine/Wisconsin/1/1967
A/swine/Tennessee/19/1976
A/swine/Illinois/1/1975
A/swine/Wisconsin/125/97
A/swine/Wisconsin/464/98
A/Swine/Iowa/533/99
A/swine/North Carolina/47834/2000
For both retrospective and prospective
simulations, we set the isolation year of the strain as
the start year, and 2018 as the end year. The
simulation model was evaluated from two
perspectives on the evolutionary trajectories. One was
the interspecies-transition pathway on a timescale;
the other was the mutation on IAV genomic
signatures. Unlike conventional phylogenetic tree
analyses, a simulated evolutionary trajectory of an
IAV is able to show when an interspecies transition
may have occurred or will occur, and what the
mutations on the amino acids are.
3.1 Analysis of Interspecies Transitions
We conducted the analysis differently according to
the type of evolutionary trajectories, retrospective or
prospective.
(a)
(b)
(c)
Figure 8: Retrospective evolutionary pathways. (a) NP, (b)
PB1 and (c) PB2.
Each retrospective simulation started with the
isolation year of the selected protein strain, and was
aborted when it reached the year 2018. For each
protein strain, we repeated the same simulation 10
times, and visualized the stochastic evolutionary
pathways in Figure 8. We divided the timescale into
intervals. The height of a rectangular bar in different
colors represents the probability of a host species (and
subtype) for a protein mutant within an interval. For
example, in Figure 8(a) during 2011-2018 the
probabilities of the host species, swine
(TripleReassortantSwine) and human
(2009HumanOutbreak), for an NP protein mutant are
0.05 and 0.95, respectively. We estimated the
probabilities from the ten simulated evolutionary
pathways. For each NP mutant during 2011-2018 on
the 10 evolutionary pathways, we first identified q (q
set to 40 in this study) real NP protein sequences
isolated during 2011-2018 from NCBI and GISAID
EpiFlu that are most similar to this mutant. We
subsequently derived the host species probabilities
A Grid-based Simulation Model for the Evolution of Influenza A Viruses
113
for an NP mutant from the proportions of these top-q
real sequences according to their host species and
subtypes.
(a)
(b)
(c)
Figure 9: Prospective evolutionary pathways. (a) NP, (b)
PB1 and (c) PB2.
We noted a marked rise in the probability of
TripleReassortantSwine during 1991-2000 for NP
proteins (28%), as shown in Figure 8(a). In addition,
the probability of 2009HumanOutbreak increased to
28% during 2001-2010, and reached 95% in the final
interval. Our simulation results of interspecies
transitions were consistent with the previous study
that the reassortment events may have occurred
during 1990-2001 and led to the human pandemic in
2009 (Smith et al., 2009). By contrast, Figure 8(b)
and (c) show that the probabilities of
TripleReassortantSwine during 1991-2000 were
infinitesimal for PB1 (< 1%) and PB2 (2%). Not until
the final two intervals, 2001-2010 and 2011-2018, did
the probabilities of TripleReassortantSwine and
2009HumanOutbreak become noticeable. These
discrepancies may be attributable to the genetic
variabilities in internal proteins that our simulation
failed to address due to the small number of protein
strains in our current study.
To evaluate the predictive performance of
prospective simulations, we selected protein strains
isolated during 1995-2000. For each strain, we first
conducted 10 retrospective simulations to estimate
the transition probabilities of amino acids from the
evolutionary trajectories. For each strain we
simulated 10 prospective pathways starting from its
isolation year to 2018 based on the estimated
transition probabilities. Note that the construction of
the prospective pathways for a protein strain did not
depend on any other real strains available but isolated
later than the strain in test. Therefore, these
prospective pathways were considered the
predictions about this protein strain, and their validity
could be verified by previous studies of IAVs. For
example, a simulated prospective pathway of
A/Waikato/16/2000 provides a prediction of its
potential interspecies transitions after 2000. We
summarize the results in Figure 9.
Similar to the results of the retrospective
simulations in Figure 8(a), Figure 9(a) shows the
highest probability of TripleReassortantSwine for NP
proteins during 1991-2000 and 2001-2010 in the
prospective simulations. The probability of
2009HumanOutbreak started to increase during
2001-2010, and became more evident during 2011-
2018, which was in accordance with the temporal
reconstruction of the reassortment history of the 2009
human pandemic (Smith et al., 2009). We also
observed from Figure 9(b) that the first reassortment
of swine lineages with PB1 proteins occurred during
2001-2010. The predicted interval agreed well with
the previous finding that a new triple reassortant
swine virus was first detected in 1998 (Brown et al.,
1998). In comparison with Figure 8(c), Figure 9(c)
shows similar probability distributions of the host
species during 1991-2000. While the interspecies
transition to 2009HumanOutbreak did not occur until
2011-2018, and the probability was small (1%), as
shown in Figure 9(c), the predicted interval was close
to when the outbreak occurred.
3.2 Analysis of Mutation on Genomic
Signatures
The establishment of an influenza virus in a new host
is rare because it requires the efficient and effective
transmission, replication, and adaptation of the virus.
Nevertheless, pandemics caused by widely
circulating viruses with the potential to transmit to
humans remain a threat (Naffakh et al., 2008). Unlike
BIOINFORMATICS 2020 - 11th International Conference on Bioinformatics Models, Methods and Algorithms
114

the analysis of molecular mechanisms, using in vitro
systems and reverse genetics of influenza viruses, the
analysis of a continuously increasing amount of
available viral sequence data enables a cost-effective
approach for the identification of genomic signatures
as host-range determinants (Hu et al., 2014).
Genomic signatures can change because of point
mutations and interspecies reassortment. The
simulation model could provide a deeper insight into
the transitions of these signatures, and increase our
understanding of the adaption trends.
Table 2: Results of genomic signature mutations based on
retrospective evolutionary trajectory analysis. (a) NP, (b)
PB1 and (c) PB2.
(a)
NP
Swine
Human
Interval
position
AA
mutation
1961
|
1970
1971
|
1980
1981
|
1990
1991
|
2000
2001
|
2010
2011
|
2018
313
F→V 0 0 0 0 17 70
F→Y 0 0 0 0 0 1
109 I→V 0 0 0 0 0 100
217 I→V 0 0 0 23 68 219
353 V→I 0 0 0 63 24 10
(b)
PB1
Swine
Human
Interval
position
AA
mutation
1961
|
1970
1971
|
1980
1981
|
1990
1991
|
2000
2001
|
2010
2011
|
2018
327 R→K 1 25 8 108 331 4
(c)
PB2
Avian
Human
Interval
position
AA
mutation
1961
|
1970
1971
|
1980
1981
|
1990
1991
|
2000
2001
|
2010
2011
|
2018
271 T→A 0 0 0 72 61 2
588 A→T 0 0 0 87 74 2
684 A→S 0 0 0 0 29 16
453 P→S 0 0 0 0 32 36
292
I→V 0 2 16 61 55 59
I→T 0 0 0 0 0 3
475 L→M 0 0 14 54 1 31
559 T→I 0 0 0 0 26 7
590 G→S 0 0 0 0 53 1
We examined the retrospective and prospective
evolutionary trajectories for the mutations on the
host-associated signatures that have been identified in
previous studies (Miotto et al., 2010; Hu et al., 2014;
Pan et al., 2009). Seventeen and one amino acid
signatures have been identified on NP and PB1
proteins, respectively, to separate swine influenza
viruses from human influenza viruses. Twenty amino
acid signatures have been found on PB2 proteins to
distinguish avian influenza viruses from human
influenza viruses.
Table 3: Results of genomic signature mutations based on
prospective evolutionary trajectory analysis. (a) NP, (b)
PB1 and (c) PB2.
(a)
NP
Swine
Human
Interval
position
AA
mutation
1991
|
2000
2001
|
2010
2011
2018
109 I→V 0 10 2
217 I→V 0 3 3
353
V→I 10 29 9
V→S 0 0 4
344 S→L 0 0 1
(b)
PB1
Swine
Human
Interval
position
AA
mutation
1991
|
2000
2001
|
2010
2011
|
2018
327 R→K 2 76 74
(c)
PB2
Avian
Human
Interval
position
AA
mutation
1991
|
2000
2001
|
2010
2011
|
2018
271 T→A 0 2 9
292
I→V 99 132 48
I→T 6 10 3
475 L→M 83 72 29
368 R→K 0 1 0
613 V→T 7 24 30
199 A→S 0 1 2
674 A→T 0 0 2
702 K→R 5 50 31
44 A→S 0 1 3
661 A→T 0 2 1
We checked each host-associated signature on
NP, PB1 and PB2 along the simulated evolutionary
trajectories, retrospective and prospective,
respectively. From all the simulated trajectories, we
recorded the frequency of signature mutations within
each time interval. We identified from the
retrospective trajectories 4 NP signatures, 8 PB2
signatures, and the one PB1 signature. In addition, we
also identified 4 NP signatures, 10 PB2 signatures,
and the same PB1 signature from the prospective
trajectories. They all showed at least one mutation at
some time on the evolutionary trajectories, and
different frequencies of mutations in different
intervals. We summarize the results in Tables 2 and
3. For example, Table 2(a) shows that on all the
simulated retrospective trajectories of NP, 17
occurrences of amino acid mutation from F to V were
identified during 2001-2010.
By comparing Table 2 with Table 3, we observed
that most of the signature mutations identified from
the prospective trajectories were coincident with
those identified from the retrospective trajectories.
Three out of four NP signatures found from the
prospective trajectories were also identified from the
A Grid-based Simulation Model for the Evolution of Influenza A Viruses
115

retrospective trajectories. The only PB1 signature
mutation, PB1-R327K, separating swine viruses from
human viruses was found from both the retrospective
and prospective trajectories. Three PB2 signatures
were also identified from both the retrospective and
prospective trajectories. These findings suggest that
the predicted evolutionary trajectories produced by
prospective simulations are rather consistent with the
retrospective evolutionary trajectories. Furthermore,
it is noteworthy that there was a marked rise in the
frequency of mutations on the signatures during
1990-2000 and 2001-2010, as shown in Tables 2 and
3, which was consistent with the time when the triple
reassortment events occurred.
4 CONCLUSIONS
We proposed a grid-based simulation model to
analyze and predict the evolutionary trends of IAVs.
Unlike previous approaches based on phylogenetic
trees or complex dynamics models, the proposed
simulation model only involves a series of adaptive
walks controlled by stochastic point mutations
constrained within an evolutionary grid. The
experiments of both interspecies transitions and
genomic signature mutations have demonstrated
promising results. It warrants further investigation
into the applicability of the simulation model for
predicting the evolutionary trends of IAVs.
ACKNOWLEDGEMENTS
The research was partially supported by Ministry of
Science and Technology of Taiwan (MOST 108-
2221-E-009-086).
REFERENCES
Brown, I. H., Harris, P. A., McCauley, J. W., Alexander,
D.J., 1998. Multiple genetic reassortment of avian and
human influenza A viruses in European pigs, resulting
in the emergence of an H1N2 virus of novel genotype.
J. Gen. Virol. 79, pp. 2947–2955.
Gerrish, P., 2001. The rhythm of microbial adaptation.
Nature, vol. 413, pp. 299–302.
Gillespie, J. H., 1983. A simple stochastic gene substitution
process. Theor. Popul. Biol. 23:202–215.
Gillespie, J. H., 1991. The causes of molecular evolution.
Oxford Univ. Press, Oxford, U.K.
Hu, Y., Tu, P., Lin, C., Guo, S., 2014. Identification and
Chronological Analysis of Genomic Signatures in
Influenza A Viruses. Plos ONE, 9(1), e84638.
Lässig, M., Łuksza, M., 2014. Adaptive Revolution: Can
we read the future from a tree. eLife Sci., 3, e05060.
Li, W., Godzik, A., 2006. Cd-hit: a fast program for
clustering and comparing large sets of protein or
nucleotide sequences. Bioinformatics, vol. 22(13), pp.
1658–1659.
Łuksza, M., Lässig, M., 2014. A Predictive Fitness Model
for Influenza. Nature, 507, pp. 57–61.
Miotto, O., Heiny, A. T., Albrecht, R., Garcı´a-Sastre, A.,
Tan, T.W., et al., 2010. Complete-Proteome Mapping
of Human Influenza A Adaptive Mutations:
Implications for Human Transmissibility of Zoonotic
Strains. PLoS ONE 5(2): e9025.
Naffakh, N., Tomoiu, A., Rameix-Welti, M-A, van der
Werf, S., 2008. Host Restriction of Avian Influenza
Viruses at the Level of the Ribonucleoproteins. Annu.
Rev. Microbiol 62: 403-424.
Neverov, A. D., Kryazhimskiy, S., Plotkin, J. B., Bazykin,
G. A., 2015. Coordinated Evolution of Influenza A
Surface Proteins. PLoS Genetics, 11(8), e1005404.
Orr, H. A., 2002. The distribution of fitness effects among
beneficial mutations. Genetics, vol. 163, pp. 1519–
1526.
Orr, H. A., 2002. The population genetics of adaptation: the
adaption of DNA sequences. Evolution, 56(7), pp.
1317–1330.
Orr, H. A., 2006. The population genetics of adaptation on
correlated fitness landscapes: the block model.
Evolution, 60(6), pp. 1113–1124.
Pan, C., Cheung, B., Tan, S., Li, C., Li, L., et al., 2010.
Genomic Signature and Mutation Trend Analysis of
Pandemic (H1N1) 2009 Influenza A Virus. PLoS ONE
5(3): e9549.
Perelson, A. S., Macken., C. A., 1995. Protein evolution on
partially correlated landscapes. Proc. Natl. Acad. Sci.
USA 92, pp. 9657–9661.
Smith, G. J. D. et al., 2009. Origins and evolutionary
genomics of the 2009 swine-origin H1N1 influenza A
epidemic. Nature, Vol. 459, pp. 1122–1126.
Timofeeva, T. A., Asatryan, M. N., Altstein, A. D.,
Narodisky, B. S., Gintsburg, A. L., Kaverin, N. V.,
2017. Predicting the Evolutionary Variability of the
Influenza A Virus. ACTA NATURAE, Vol. 9, No.
3(34), pp. 48–54.
BIOINFORMATICS 2020 - 11th International Conference on Bioinformatics Models, Methods and Algorithms
116
