The Effect of Maxblur-pooling in Neural Networks on Shift-invariance

Issue in Various Biological Signal Classiﬁcation Tasks

Xianyin Hu, Shangyin Zou, Yuki Ban and Shin’ichi Warisawa

Development of Human and Engineered Environmental Studies, The Graduate School of Frontier Sciences,

The University of Tokyo, Kashiwa, Chiba, Japan

Keywords:

Temporal Shift-invariance, Maxblur-pooling, Neural Network, Bio-signal Processing, Atrial Fibrillation (AF)

Detection, Emotion Recognition.

Abstract:

Modern neural networks are widely employed in bio-signal processing due to their effectiveness. However, re-

cent research showed that neural networks for image recognition is not shift-invariant as it was assumed, while

it is an important property in bio-signal processing. Fortunately, a simple methodology was proposed referred

to as Maxblur-pooling to improve the shift-invariance of neural networks for image recognition. However, the

corresponding issue in the domain of bio-signal processing remains untouched. To verify the shift-invariance

of neural networks when applied to bio-signal processing, we performed two experiments across different

tasks and types of bio-signals. One is Atrial Fibrillation (AF) detection from R-R interval and the other is

emotion recognition from multi-channel EEG. We were able to show that the lack of shift-invariance also hap-

pens in temporal bio-signal classiﬁcation. In the AF detection task, we succeed to validate the effectiveness of

Maxblur-pooling, which demonstrating improvements in both accuracy (2%-13%) and consistency (8%-15%)

compared to the baseline. While for the emotion recognition task, we did not observe any improvements using

Maxblur-pooling. Our research provided empirical knowledge for developing real-time diagnose systems that

is stable to temporal shifts.

1 INTRODUCTION

Deep learning approaches have achieved great suc-

cess in the ﬁeld of image recognition and natural lan-

guage processing. In recent years, deep neural net-

works are also widely employed in biosignal process-

ing served as feature extractors and pattern classiﬁers.

For example, the most commonly investigated bio-

signal is electrocardiogram (ECG). Work by Acharya

et al. (Acharya et al., 2017) used an 11-layer deep

CNN to automatically detect arrhythmias. Another

popular ﬁeld of bio-signal classiﬁcation using neural

networks is Electroencephalogram (EEG). Tripathi et

al. applied deep neural networks and convolutional

neural networks to emotion recognition and gained

rather high accuracy (Tripathi et al., 2017).

In most of the automatic diagnosis systems mod-

eled as bio-signal classiﬁcation task, there are usually

two steps, the ﬁrst step is feature extraction and the

second step is pattern classiﬁcation. In the ﬁrst step,

temporal shift-invariance, also referred to as time in-

variance or translation invariance (Mitra and Kaiser,

1993), is required. Temporal shift-invariance sim-

ply means that if you shift the input signal along

the time axis by an arbitrary amount, as long as the

ground truth does not change, all the features ex-

tracted should also stay the same. The ideal extracted

features should be only related to the ﬁnal target while

remaining irrelevant to time. That is, the contempo-

raneous features extracted from a given series of the

input raw signals should not depend on when the in-

put occurs.

Someone may get confused with the state-

ment:temporal shift-invariance is expected in biosig-

nal processing. They may consider the change in-

stead of the invariance should be expected since there

exists so many analysis performed on moving win-

dows to track the temporal evolution. In fact, mod-

els that do biosignal classiﬁcation tasks are exactly

time-invariant systems. It can be easily understand

by comparing between time-variant system and time-

invariant system. In a time-variant system, for the

same input that happens at differnt time, the out-

put is different. In a time-invariant system, for the

same input that happens at differnt time, the output

is the same. The temporal evolution to be tracked

is not the evolution of the time itself, but the evolu-

tion of the parameters and behaviors in the input sig-

nals along the time. According to the deﬁnition of

time-invariant system (Oppenheim, 1997), if a classi-

ﬁer depends only indirectly on the time-domain (via

the input function, for example), then that is a sys-

Hu, X., Zou, S., Ban, Y. and Warisawa, S.

The Effect of Maxblur-pooling in Neural Networks on Shift-invariance Issue in Various Biological Signal Classiﬁcation Tasks.

DOI: 10.5220/0008879900490059

In Proceedings of the 13th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2020) - Volume 4: BIOSIGNALS, pages 49-59

ISBN: 978-989-758-398-8; ISSN: 2184-4305

Figure 1: The temporal shift-invariance is lacked in modern neural networks for AF detection task and Maxblur-

pooling technique improved shift-invariance. The horizontal axis is the shift offset applied to the input RRI segment and

the vertical axis is the probability of making the correct estimation. We observed a drastic change of the conﬁdence in the

output of the baseline model using Max-pooling while the output of the model using Maxblur-pooling is more stable. This

ﬁgure generated from the outputs of 151-th RRI segment to 251-th RRI segment in the recording of No.07162. (Referring to

the expression S(x

, k) in Figure.3, here i = 151 and k = 1, 2, 3, . . . , 99).

tem that would be considered time-invariant. In our

cases, biosignal classiﬁers depend only indirectly on

the time-domain via the biosignals (time-dependent

function). Thus, the biosignal classiﬁers satisﬁed the

deﬁnition and should be modeled as time-invariance

systems.

Temporal shift-invariance is always addressed in

the traditional analysis method in biosignal process-

ing. For example, the discrete wavelet transform

(DWT) is a commonly used time-frequency anal-

ysis and signal-coding tool to extract suitable fea-

tures from raw biosignals (Addison et al., 2009),

but it is also well-known for its drawbacks of lack-

ing temporal shift-invariance. To solve the prob-

lem, a set of methods was proposed to overcome the

problem to maintain temporal shift-invariance, such

as the stationary wavelet transform (SWT) (Addison

et al., 2009), adaptive wavelet transform (Xiong et al.,

2000), etc.

Maintaining a high temporal shift-invariance is es-

pecially important and a challenging issue in devel-

oping real-time disease diagnosis systems. Real-time

analysis of patient data during medical procedures can

provide vital diagnostic feedback that signiﬁcantly

improves chances of success. The term ”real-time”

means the system should response immediately to the

input. In other words, the real-time system is required

to output a stream with a sampling rate that is same

with or near to the sampling rate of its input signal. If

the system has low temporal shift-invariance, the out-

put will suffer drastic change even when the input is

shifted by a very small offset, which is not desirable.

Although the temporal shift-invariance has been

addressed in traditional analysis methods of biosig-

nals, researchers utilized modern neural network tech-

nology have neglected this important property. The

reason is that these researchers take it for granted

that the neural network approach is temporal shift-

invariant and does not verify that.

In fact, in the ﬁrst place, the basic structures that

make up modern neural networks are designed un-

der the motivation of maintaining shift-invariance.

Proceeding researches believed that neural networks

can acquire shift-invariance from both the architec-

ture and the parameter.

For the way of acquiring from the architecture,

layers with shared weights and layers of downsam-

pling are proposed. For example, in convolutional

neural networks (CNN), the weights of the ﬁlters in

convolution layers are shared across all patches of the

image - so the weights learned can be invariant to po-

sition. And max-pooling layer, by taking the max

value of the pixel in the patch, approximate transla-

tion invariance can be gained since subsequent layers

of the CNN don’t care about the speciﬁc position in

the patch that the max value was in. Similarly, in re-

current neural networks (RNN), weights are shared

across time to gain temporal shift-invariance.

For the way of acquiring from parameter, a com-

monly used approach is to do data augmentation by

adding shifted data into the training set, then expect

the weights of the neural networks to learn shift-

invariance from the large amount of data.

It has been recently proved in the task of im-

age recognition that the neural network is not shift-

invariant as we expected (Azulay and Weiss, 2019).

However, in the ﬁeld of biosignal processing, the cor-

responding issue remained untouched. Therefore, it

is necessary to verify whether the neural networks ap-

plied in bio-signal processing also lack temporal shift-

invariance.

A novel methodology named Maxblur-pooling

BIOSIGNALS 2020 - 13th International Conference on Bio-inspired Systems and Signal Processing

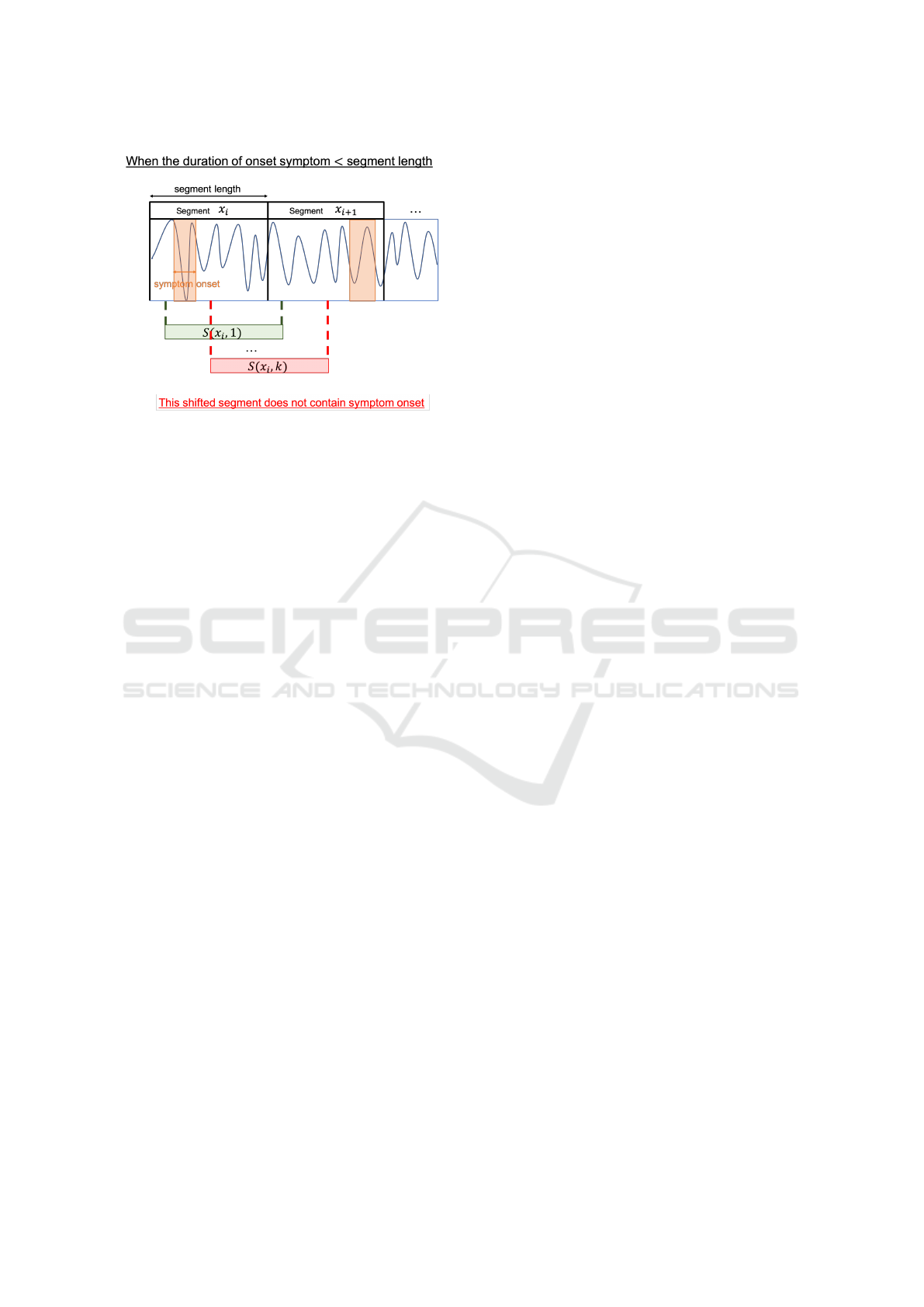
Figure 2: Testbeds selection criteria. A situation when the

duration of onset symptom is less than segment length and

we will not select the task to be our testbed. We denoted

S(x

, s) as given the input segment x

a temporal shift s. Al-

though the shifted segment S(x

, 1) contains the symptom,

the shﬁted segment S(x

, s) doesn’t.

was proposed by Zhang to overcome the drawback

of lacking shift-invariance in modern neural networks

(Zhang, 2019). This method has been validated in

the task of image recognition and image generation

across several challenging datasets such as ImageNet.

Zhang held that shift-invariance is lost because of the

down-sampling in the pooling layer. However, shift-

invariance can be simply ﬁxed if features are extracted

densely. This motivated them to break the Max-

pooling layer in modern neural networks into two op-

erations: (1) evaluating the max operator densely and

(2) naive subsampling. They proposed to add low-

pass (Gaussian) ﬁlters between them as a means of

anti-aliasing. This viewpoint enables low-pass ﬁl-

tering to augment, rather than replace Max-pooling

layers. As a result, they proved the anti-aliasing

and Max-pooling can be combined in a novel way

and shifts in the input leave the output relatively

unaffected (shift-invariance). Although this method

gained success in the task of image recognition, there

is no guarantee that this method could generalize well

to the neural networks that process biosignals for the

following two reasons. Firstly, the Gaussian low-

pass ﬁlter of Maxblur-pooling is widely used in im-

age processing served as a smoothing ﬁlter, while

in the bio-signal processing, most of the researches

use Savitzky-Golay ﬁlter (Savitzky and Golay, 1964)

to smooth the bio-signals. The Savitzky-Golay ﬁl-

ter is widely used for its main advantage to preserve

features of the signal such as maxima, minima, and

width, which are usually ﬂattened by the Gaussian

ﬁlter. Secondly, concerning the frequency domain

analysis, the low-pass ﬁlter of Maxblur-pooling has a

side-effect that cut off some high-frequency compo-

nents. In image processing, high-frequency com-

ponents are usually conceived noise or are not nec-

essary for the recognition and should be ﬁltered.

While in biosignals processing, although it’s case by

case, a large range of frequency components should

be taken into account. We concerned the Maxblur-

pooling employing the low-pass Gaussian ﬁlter may

lose important features of signals such as maxima and

high-frequency components for bio-signal processing

tasks, so we can’t say it certain that it will also im-

prove when applied to bio-signals.

Thus, the effectiveness of Maxblur-pooling and its

generalizability to biosignal processing is under dis-

cussion and needed validation.

In this work, we performed experiments on two

datasets using different biosignal, one is atrial ﬁbril-

lation (AF) detection from R-R interval and the other

is effective estimation from EEG. The contributions

can be summarized as follows:

• We showed the problem that neural networks

lack shift-invariance also happens when tackling

with biosignals. As demonstrated in Fig. 1, out-

puts of the baseline neural network using max-

pooling suffer drastic changes according to tem-

poral shifts.

• We showed that Maxblur-pooling improved accu-

racy (2%-13%), as well as consistency (8%-15%)

in the task of AF detection, compared to the base-

line using max-pooling.

• We did not observe improvements between the

Maxblur-pooling and the baseline in the task of

affective estimation, indicating that this method

performed poorly to process the EEG signal. The

reason was discussed that the blurring behavior

of Maxblur-pooling lost too much information on

the high-frequency components which is neces-

sary for the effective estimation to estimate human

emotion.

• Our work provided empirical knowledge for de-

veloping and designing neural networks for real-

time diagnose systems that is stable and robust to

temporal shifts.

2 TESTBEDS & EVALUATION

In this section, we described the two testbeds selected

to perform the validation and the selection criteria.

Then we described the metrics to evaluate the effec-

tiveness of the Maxblur-pooling method.

The Effect of Maxblur-pooling in Neural Networks on Shift-invariance Issue in Various Biological Signal Classiﬁcation Tasks

2.1 Testbeds Selection Criteria

Our criteria to select proper testbeds was as follows:

1) The task is to do biological signal classiﬁcation.

2) The duration of the true onset symptoms must be

longer than the segment length of the input signal in

the dataset.

In Fig. 2 we demonstrated an example of how a

testbed does not satisfy our criteria. When the du-

ration of symptom onsets is less than the segment

length, it will happen that a shifted segment doesn’t

contain symptoms. So in such a task, we will never

know the ground truth of each shifted segment.

The tasks in which different output labels were

annotated between sessions satisfy the criteria. For

example, in emotion recognition, participants were

asked to watch videos that evoke various emotions.

The time of watching a video served as a session. In

this case, the duration of a session, also known as the

duration of onset symptoms, is always longer than the

segment length. For the tasks that can have differ-

ent labels inside one session, investigation of the task

itself is needed to determine whether it satisﬁes the

criteria. Here we take the sleep apnea detection as

an example that does not reach the criteria. In the

task of sleep apnea detection (Penzel et al., 2000),

the ground truth indicating the presence or absence of

apnea was annotated by human experts by every one

minute. Apnea is deﬁned to happen when complete

pauses in breathing appear lasting at least 10 seconds

during sleep. However, the duration of onset symp-

tom (10 seconds) is much shorter than the segment

length which is one minute. So there is no guarantee

that the shifted ECG segment also contains the onset

symptom that makes it an apneic segment. Following

the above criteria, we selected two databases that can

be used for the veriﬁcation of shift-invariance.

2.2 Testbeds

Atrial Fibrillation (AF) Detection. We used MIT-

BIH atrial ﬁbrillation database (Moody, 1983) for the

task of atrial ﬁbrillation (AF) detection. This database

includes 25 long-term ECG recordings of human sub-

jects with normal heart rhythm and atrial ﬁbrillation.

The R peaks were annotated manually by human ex-

perts, so we can calculate R-R intervals from the an-

notated ﬁles directly without pre-processing. We used

100 R-R interval segments as input. Since the dura-

tion of atrial ﬁbrillation usually lasts for hours or even

days, and the segment length is about less than two

minutes for 100 R-R intervals, the test-bed satisﬁes

the selection criteria.

Emotion Recognition. We adopted the public

SEED IV Emotion Dataset (Zheng et al., 2018) for

the task of emotion recognition. The SEED IV

dataset contains 62 channels of EEG and eye move-

ment data of four different emotions—happy, sad,

fear, and neutral. In this work, we used the EEG part

of the dataset. The EEG data is of 200Hz sampling

rate, obtained from a total of 15 subjects during ex-

perimental sessions conducted in 3 separate days. For

each emotion stimulation, the subjects were asked to

watch a two-minute video. Therefore EEG data of

a label is about two minutes as the length of videos.

Each span of EEG data was cut into 1-second seg-

ments as the input. As also mentioned in the above

subsection, the duration of emotion equals the dura-

tion of the session which is two minutes, longer than

the segment length of one second, so the test-bed also

satisﬁed the selecting criteria.

The two tasks selected uses different types of bio-

signal, so we can verify if the lack of shift-invariance

is a universal problem across bio-signal types and if

the Maxblur-pooling method generalizes well to var-

ious tasks. In each task, we tested ﬁve different blur

sizes ranged from 3 to 7 with the baseline using the

Max-pooling layer. In the ﬁrst experiment on AF de-

tection, we also tested three different pooling factors,

denoted as p and p ∈ 1, 2, 3, p was also conceived to

be the number of pooling layers in the neural network.

Therefore, we tested three p-layer CNNs to ﬁnd out

how the effect of Maxblur-pooling was inﬂuenced by

the pooling factor p.

2.3 Evaluation Metrics

The classiﬁcation accuracy on the overall dataset (in-

cluding overlapped and non-overlapped segments) in-

tegrated the evaluation of how well the model per-

formed to make a correct estimation as well as how

much stable the model is. But the overall accuracy

failed to make a trade-off between the two aspects.

Zhang (Zhang, 2019) stated that the Maxblur-pooling

could improve the shift-invariance of a neural network

but may sacriﬁce accuracy. As a fact, he surprisingly

found that both accuracy and shift-invariance are im-

proved on the task of image classiﬁcation and image

generation. For the purpose of the validation, we also

have to evaluate the two aspects separately. We de-

ﬁned the accuracy and consistency as follows to eval-

uate the preciseness and shift-invariance of a model.

The accuracy is calculated based on the test dataset in

which all the segments are not overlapped with each

other. The consistency is deﬁned based on shifted seg-

ments with an overlap less than L −1 between two ad-

jacent segments that have the same label (L equals to

the segment length).

BIOSIGNALS 2020 - 13th International Conference on Bio-inspired Systems and Signal Processing

The average value of both metrics are calculated

with 5-fold cross-validation. Higher accuracy indi-

cates a more accurate diagnose and higher consis-

tency indicates more shift-invariance.

Accuracy. Classiﬁcation accuracy is deﬁned

as the proportion of correct predictions to the

total number of predictions, denoting the pre-

dictions as a vector p = (p

, p

, ..., p

)

( f (x

), f (x

), ..., f (x

))

and the ground truth

as y = (y

, y

, ..., y

)

. Accuracy can be deﬁned

using the following equations:

(

1, if p

= y

0, otherwise

(1)

Accuracy =

∑

i=1

(2)

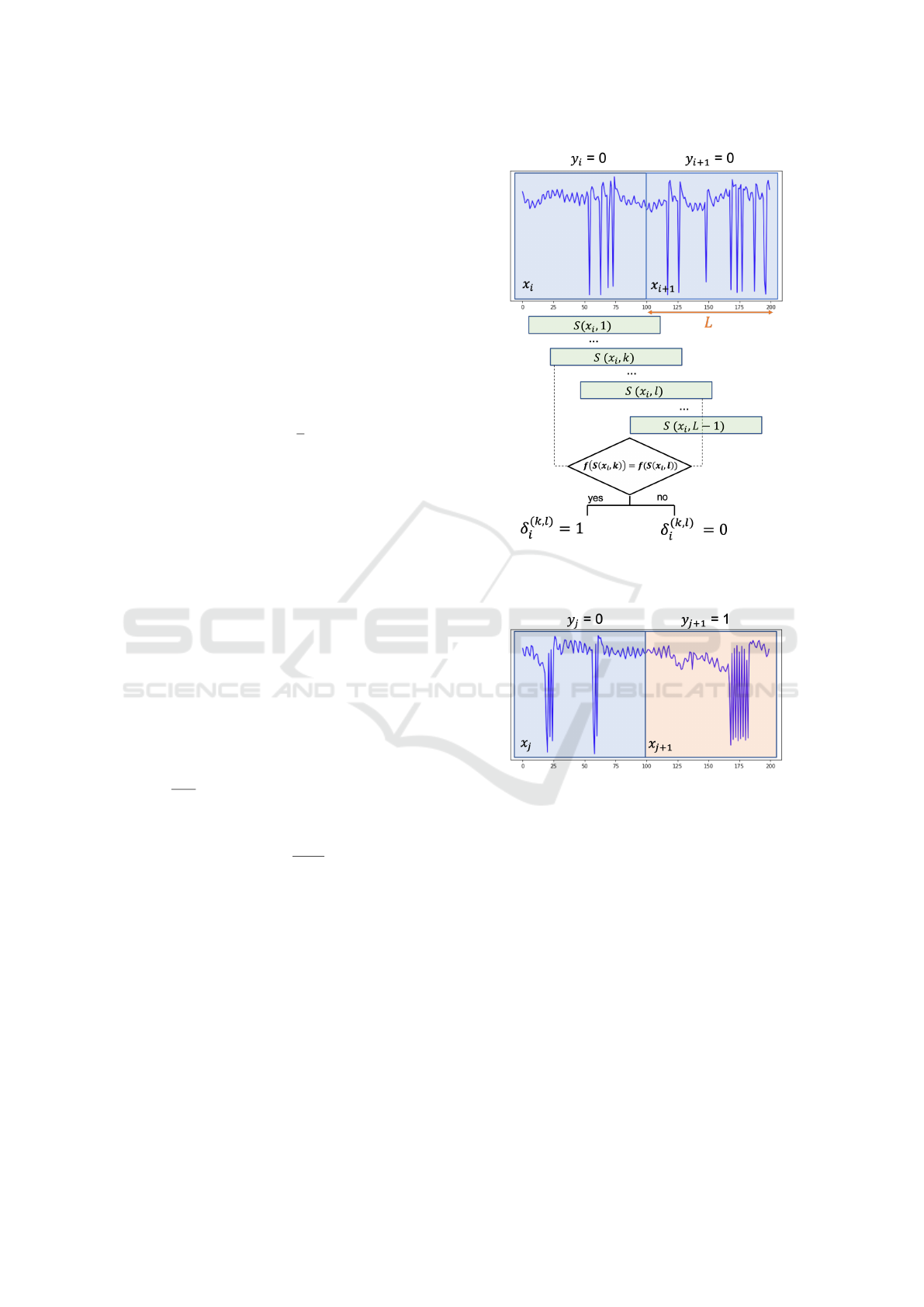
Consistency. The consistency checks how often the

network outputs the same label given the same input

bio-signal segment with two different temporal shifts.

For a piece of input segment, we denoted the segment

length as L, then there will be L − 1 shifts applied to-

tally. As demonstrated in Fig. 3(a), only the segments

that have the same label with its consecutively adja-

cent segment next in time will be used to calculate

consistency. For those segments that did not have the

same label with the next adjacent segment, shifts will

not be applied (Fig. 3(b)). We denoted S as the tempo-

ral shift function, and S(x, k) means temporally shift

the input x by an offset equals to k. The consistency

can be deﬁned as follows:

(k,l)

(

1, if f (S(x

, k)) = f (S((x

, l))

0, otherwise

(3)

(

L−1

∑

k,l∈{1,...,L−1},k<l

(k,l)

, y

= y

i+1

0, y

6= y

i+1

(4)

Consistency =

n − 1

n−1

∑

i=1

(5)

3 VALIDATION ON ATRIAL

FIBRILLATION (AF)

DETECTION

3.1 Tested models

For the model structure, we adopted the basic convo-

lutional neural network (CNN) as is shown in Fig. 4.

The unit block of the CNN consisted of a convolution

layer, a batch normalization layer, a ReLU activation

(a) For the segment that had the same label with

its next adjacent segment, shifts will be applied and

consistency is calculated.

(b) For the segment that didn’t have the same label

with its next adjacent segment, shifts will not be ap-

plied.

Figure 3: Calculation of the consistency.

layer, and a pooling layer. The unit block will repeat

for p times, which equals to the pooling factor, and we

tested six variations of the pooling layers including

one baseline and Maxblur-pooling with ﬁve blur sizes

for comparison.

The input of the model is a 100 R-R intervals

sequence. Thanks to the contributors of the dataset

(Moody, 1983), we can calculate the R-R intervals

from the manually annotated heart rhythm without

pre-processing. The output of the model is a binary

value (0 or 1) indicating the presence or absence of

atrial ﬁbrillation. We tested ﬁve different blur sizes

of Maxblur-pooling ranged from 3 to 7 together with

the baseline using Max-pooling. We also tested three

The Effect of Maxblur-pooling in Neural Networks on Shift-invariance Issue in Various Biological Signal Classiﬁcation Tasks

Figure 4: The structure of Convolution Neural Network

(CNN).

different pooling factors to ﬁnd out how the effect of

Maxblur-pooling was inﬂuenced by the pooling fac-

tor.

3.2 Results and Discussion

We were able to reveal that the lack of temporal shift-

invariance also exists in modern neural networks in

the task of AF detection. As the example showed in

Fig. 1, we observed that outputs of the baseline model

using Max-pooling suffered from drastic changes as

the input shifted. By using the Maxblur-pooling, this

vibration of output had been signiﬁcantly reduced.

The comparison results of CNN structures across

pooling factors were summarized in Table.1. To

demonstrate it more intuitively as shown in Fig. 5, the

upper right of the ﬁgure indicates better performance

on both metrics. We observed that all the models

using Maxblur-pooling with different blur sizes im-

proved consistency with various degrees compared to

the baseline of Max-pooling, but improvement in ac-

curacy was only observed with the blur size of 7 con-

sidering all the pooling factors.

For CNN with one layer, Maxblur-pooling with

blur size equaling to 7 obtained best results, which

improved accuracy by 1.72% and consistency by

7.94% compared to Max-pooling.

For CNN with two layers, Maxblur-pooling with

blur size equaling to 7 obtained best results, improv-

ing accuracy by 6.02% and consistency by 17.92%

compared to Max-pooling.

For CNN with three layers, Maxblur-pooling with

blur size equaling to 5 obtained best results, improv-

ing accuracy by 12.79% and consistency by 15.36%

compared to Max-pooling.

In the task of AF detection, we have observed that

Maxblur-pooling did improve accuracy and consis-

tency compared to Max-pooling. Although the best

performing ﬁlter varied by the pooling factor p, we

did not ﬁnd there is a relationship between them. Em-

Figure 5: Performance of models for AF detection. In

each ﬁgure, the upper right indicates better performance on

both metrics. Points are plotted with different shapes cor-

responding to the variants of the networks using Maxblur-

pooling. The number of edges equals to the blur size (trian-

gle means Maxblur-pooling with blur size of 3). Specially,

star mark represents Maxblur-pooling with blur size of 7

and the alphabet M represents the baseline of Max-pooling.

pirically, we recommend using the blur size of 7 be-

cause it both improved accuracy and consistency in

all the three CNNs with different pooling factor.

Next, we discussed the relationship between the

improvement of Maxblur-pooling and how many

times the Maxblur-pooling was applied. As showed

in Fig. 6, when the pooling factor increased, improve-

ments in accuracy and consistency also increased.

Speciﬁcally, improvements of consistency in three-

layer CNN was signiﬁcantly greater than that in one

BIOSIGNALS 2020 - 13th International Conference on Bio-inspired Systems and Signal Processing

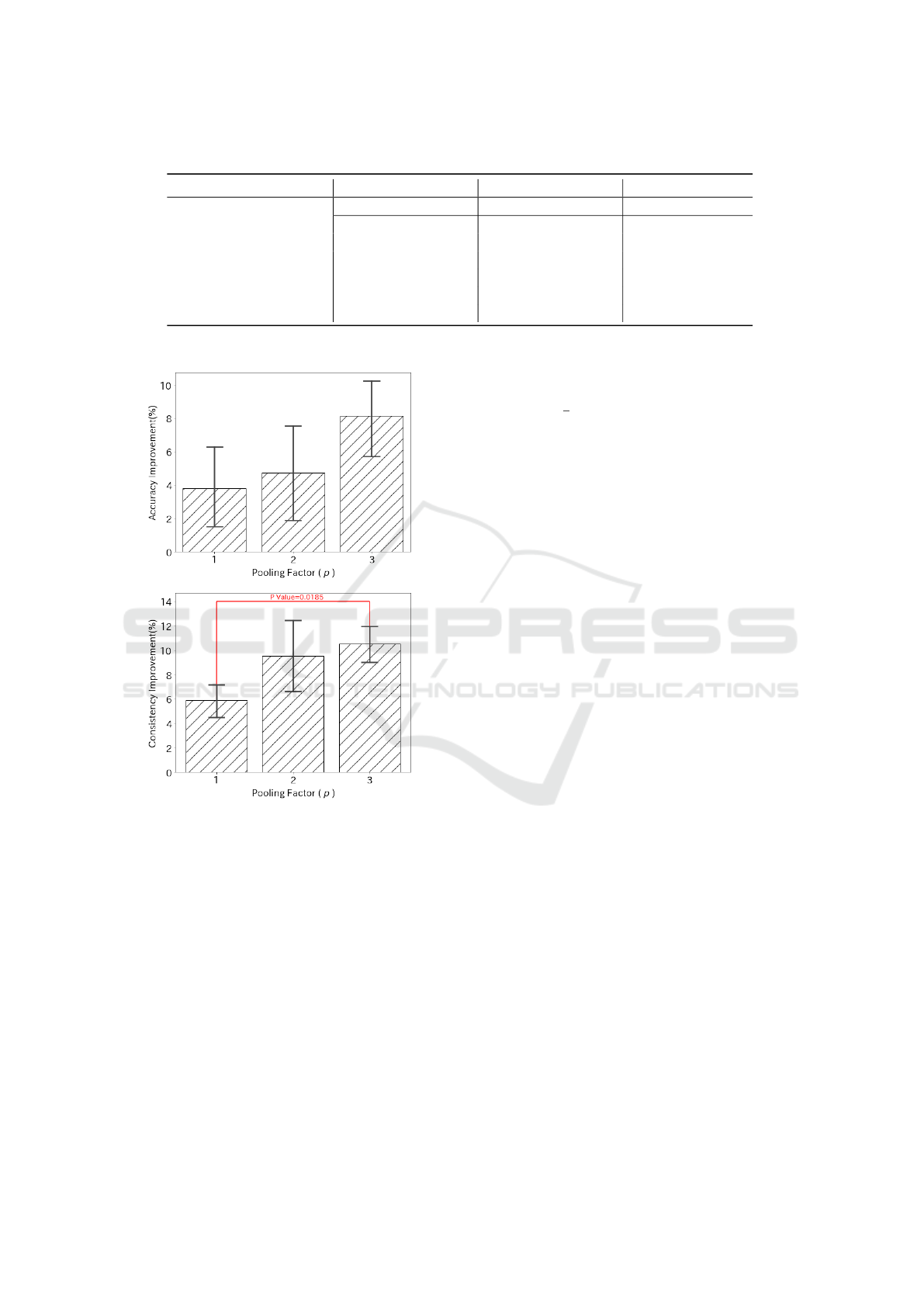
Table 1: Comparison between CNNs using different pooling layers for AF detection (accuracy and consistency are in %).

Task Pooling Layer 1-layer CNN 2-layer CNN 3-layer CNN

Detection

accuracy consistency accuracy consistency accuracy consistey

Max 86.11 80.44 80.54 72.76 77.70 77.32

Maxblur-3 86.54 84.91 80.75 77.80 87.78 85.39

Maxblur-4 86.66 84.05 80.29 80.66 87.43 86.88

Maxblur-5 85.05 82.41 84.88 83.32 87.64 89.20

Maxblur-6 85.61 86.42 78.14 76.47 83.60 84.65

Maxblur-7 87.59 86.83 85.39 85.80 83.83 86.60

Figure 6: Improvements of Maxblur-pooling with differ-

ent pooling factors compared to the baseline. We com-

pared how much improvement was made by using Maxblur-

pooling from the baseline of Max-pooling between different

pooling factors. Tukey’s multiple comparison test was em-

ployed to check the signiﬁcant difference (P value<0.05).

layer CNN, but a signiﬁcant difference in improve-

ments of accuracy was not observed. Although the

number of pooling layers needed parameter-tuning

and is depended on the task and data. If shift-

invariance is especially desired, we suggest employ-

ing Maxblur-pooling in a deeper network with more

pooling layers.

4 EMOTION RECOGNITION ON

SEED IV EEG DATASET

4.1 Data Description

In the previous section, we discovered and discussed

that the problem of shift-variance exists in AF de-

tection 1-dimensional RRI data, and tested whether

the Maxblur-pooling layer will solve the problem by

replacing the traditional Max-pooling layer. We be-

lieved that the shift-variance problem should also ex-

ist in the recognition of 2-dimensional physiological

signals. Among many kinds of physiological signals,

we found Electroencephalography (EEG) signals are

one suitable type of 2-dimensional signal. This is be-

cause EEG signals are usually measured by multiple

channels; hence, there are the time dimension and the

channel dimension in EEG data. EEG signals also

have different characteristics than RRI data, for exam-

ple, EEG signals contain a wide frequency range from

1 Hz to at least 100 Hz. Previous studies on neural sci-

ence have discovered that different frequency ranges

of EEG show respective properties of brain activities

(Henry, 2006). Therefore, recognition tasks on EEG

require the model to capture information of a wide

range of frequencies.

Furthermore, the application of CNN in various

kinds of recognition from EEG signals has been a

widely investigated topic so that it will be meaningful

to verify the effectiveness of the Maxblur-pooling

layers. The deep learning models of CNN have been

applied to the detection of seizure from single EEG

signals (Acharya et al., 2018), emotion recognition

(Zheng and Lu, 2015; Mei and Xu, 2017) and

limb motion recognition (Zhang et al., 2018) from

multi-channel EEG, combined with feature extraction

methods or other deep learning model architecture

like Recurrent Neural Network (RNN) and long short-

term memory (LSTM) units. In Zhang’s research, the

Maxblur-pooling layers were originally proposed to

The Effect of Maxblur-pooling in Neural Networks on Shift-invariance Issue in Various Biological Signal Classiﬁcation Tasks

Figure 7: The architecture of the CNN model used for the

emotion recognition task. Two types of blur ﬁlters are also

illustrated. The horizontal axis represents the time series,

and the vertical represents channels. Here blur ﬁlters of size

5 are taken as examples. (a) is the 2-axis blur ﬁlter that has a

blurring effect on both temporal and channel axes, while (b)

is of 1 axis that only has a blurring effect on the temporal

axis.

solve the shift-variance problem of 2D images,

and the 2D blur ﬁlters were proved to be effective

against shift-variance of image recognition (Zhang,

2019). Therefore we anticipate that the Maxblur-

pooling layers in 2-dimensional CNN will also

improve the shift-invariance of the CNN models on

2-dimensional EEG data.

To verify this hypothesis, we adopted the pub-

lic SEED IV Emotion Dataset (Zheng et al., 2018)

for the task of discrete emotion recognition using the

CNN model.

4.2 Validation Procedure

Overall, we performed 5-fold cross-validation on

each participant, which means that the recognition

is participant-dependent. In the validation process

on EEG data, we used 1-second segments of EEG

raw data as the input to the CNN networks, which

was proved feasible by previous research (Yanagi-

moto and Sugimoto, 2016). Hence the input shape

of the network is (62, 200), where 62 is the number

of channels, and 200 is the total time frames of 1-

second segments. The reason that we did not use

any frequency-domain feature extraction method as

in most previous researches (Zheng et al., 2018) is

that we needed to keep the input data in the time do-

main in order to verify the temporal shifting effect of

Maxblur-pooling layers.

As for the model architecture, we adopted a CNN

model structure of 2 convolution layers, which was a

simple modiﬁed version based on previous researches

of emotion recognition using CNN from EEG (Mei

and Xu, 2017; Moon et al., 2018). The general ar-

chitecture is illustrated in Fig. 7, where the numbers

of ﬁlters of the two convolutional layers are 16 and

32, and the kernel size is (3, 3).The baseline model

structure is the same with normal Max-pooling layers

replacing the Maxblur-pooling layers.

Unlike image classiﬁcation tasks, where the two

axes of a 2D image represent the same meaning, the

time axis and channel axis of EEG data include dif-

ferent information. We intend to ﬁnd out whether

Maxblur-pooling layers will make improvements by

blurring along both time and channel axis, or only

along the time axis. Therefore we tested Maxblur-

pooling layers with two kinds of blur ﬁlters, as are

shown in Fig. 7 as ﬁlter (a) and (b). One has a blurring

effect on both time and channel axes, and the other

only blurs along the time axis, which is similar to 1D

blur ﬁlter. blur ﬁlter sizes of 3, 4, 5, 6, and 7, respec-

tively of the two types of blur ﬁlters were tested.

4.3 Results and Discussion

The validation procedure was still in process, and the

following results are based on data of 5 participants

among all 15 in the SEED IV dataset. The results of

mean accuracy and consistency are listed in Table.2.

For the comparison between two types of 2D blur ﬁl-

ters, it was clear that 2-axis blurring outperformed 1-

axis blurring. The average accuracy and consistency

of 2-axis blurring of size from 3 to 7 were higher by

2.14% and 3.22% respectively than 1-axis blurring.

This shows that the blur ﬁlter on the channel axis im-

proved the recognition performance.

However, the best performance was gained by the

baseline model utilized Max-pooling layers, reached

an accuracy of 79.98% and consistency of 89.73%,

outperformed all the models with Maxblur-pooling

layers. On the contrary to our hypothesis, the appli-

cation of Maxblur-pooling in this task caused recog-

nition accuracy to drop about 6.28%, and consis-

tency dropped about 2.53% on average. These results

showed that the Maxblur-pooling layers performed

badly when processing EEG signals compared to

RRI, both accuracy-wise and consistency-wise. One

possible reason for this outcome we speculate is that

the ﬁlters in the Maxblur-pooling layers may have ex-

cluded some information contained in EEG signals

BIOSIGNALS 2020 - 13th International Conference on Bio-inspired Systems and Signal Processing

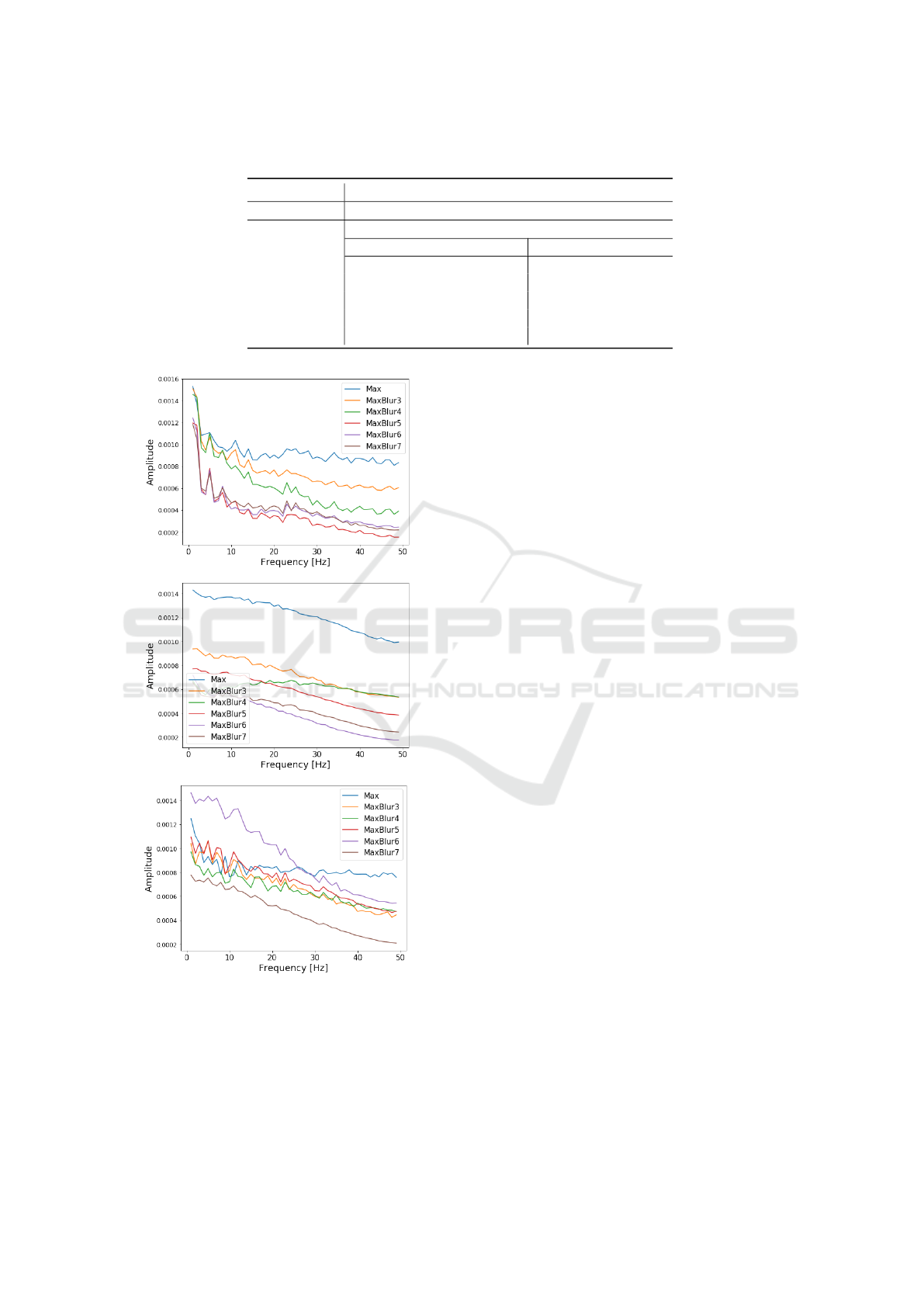
Table 2: Mean accuracy(%) and consistency(%) of two blur ﬁlters of the task of emotion recognition using EEG.

Pooling Layer

Max accuracy 79.98 consistency 89.73

2-axis blurring 1-axis blurring

accuracy consistency accuracy consistency

Maxblur-3 76.33 88.61 75.86 85.19

Maxblur-4 76.15 88.59 73.09 85.94

Maxblur-5 74.94 88.31 72.31 84.31

Maxblur-6 74.58 88.66 71.04 86.78

Maxblur-7 74.05 89.69 68.67 85.92

Figure 8: The FFT distribution of pooling layers’ output

feature. Three typical patterns are chosen.

that is important to emotions. This is because that,

as mentioned earlier, EEG signals cover a wide range

of frequencies, especially the gamma band (30-100

Hz) of which is crucial to emotion recognition, ac-

cording to previous research (Li and Lu, 2009). How-

ever, since the blur ﬁlters also served as low-pass ﬁl-

ters, the reason for the low accuracy was considered

to be the fact that the Maxblur-pooling layers ﬁltered

out the relatively high frequency components which

contained important information for emotion estimat-

ing, while Max-pooling layers maintained those in-

formation. Therefore applying Maxblur-pooling lay-

ers caused the accuracy to drop compared to Max-

pooling.

To verify the theory, we pulled out the output

matrices of the ﬁrst pooling layer in the CNN net-

works from individual test samples, and conducted

FFT along the temporal axis to compare the frequency

distribution between normal Max-pooling layers and

Maxblur-pooling layers. Although the FFT distribu-

tion of the Maxblur-pooling features cannot fully rep-

resent the actual frequencies of EEG signals, we can

interpret the amplitude values as the amount of energy

and information. The outcomes of some typical pat-

terns are illustrated in Fig. 8. We noticed that among

the most of FFT distribution of test samples, the am-

plitude values of Max-pooling are the highest in the

30-50 Hz frequency range, while values of Maxblur-

pooling of larger sizes tend to be lower. This gives

us the indication that the Maxblur-pooling layers ﬁl-

tered out more information contained in high frequen-

cies of EEG signals compared to Max-pooling layers.

As a result, the accuracy with Maxblur-pooling layers

dropped, and in the meantime, the consistency was

not improved.

5 GENERAL DISCUSSION

In the validation on AF detection task, we discussed

that the improvements of consistency in CNN with

more layers were signiﬁcantly more than that in CNN

with fewer layers, but a signiﬁcant difference in im-

provements of accuracy was not observed, suggest-

ing that deeper neural networks could be employed to

gain consistency.

The Effect of Maxblur-pooling in Neural Networks on Shift-invariance Issue in Various Biological Signal Classiﬁcation Tasks

Table 3: Compare between CNNs using different pooling layers for AF detection with data augmentation (accuracy and

consistency are in %).

Task Pooling Layer 1-layer CNN 2-layer CNN 3-layer CNN

Detection

accuracy consistency accuracy consistency accuracy consistey

Max 90.89 98.34 94.15 97.53 91.53 97.20

Maxblur-3 91.91 97.40 92.49 95.33 94.37 95.00

Maxblur-4 92.42 97.01 93.62 93.91 94.28 95.94

Maxblur-5 89.15 95.57 94.69 95.13 94.42 95.66

Maxblur-6 91.74 97.25 93.07 96.84 94.57 95.60

Maxblur-7 90.28 97.39 94.03 96.84 92.28 96.49

Figure 9: Results for AF detection using data augmentation.

We did not observe improvements.

In the validation on emotion recognition task,

Maxblur-pooling lost its advantage when applied to

EEG signals. We discussed the reason was to be

that the Maxblur-pooling layers ﬁltered out the impor-

tant high-frequency components while normal Max-

pooling layers didn’t. Therefore applying Maxblur-

pooling layers caused the accuracy and consistency to

drop, indicating that this method is not suitable for

such tasks.

Before the method of Maxblur-pooling was pro-

posed, researchers usually use data augmentation to

gain shift-invariance. We compared the Maxblur-

pooling and baselines in the task of AF detection

with data augmentation to verify if Maxblur-pooling

can make improvements as well when the data was

augmented. As the result shown in Fig. 9, Using

Maxblur-pooling made no improvements in accuracy

and consistency from the baseline when applied with

data augmentation (Refer to Table.3 for details). We

considered the reason was that there left little room to

be improved within the task of AF detection. The per-

formance of the baseline model using Max-pooling

with data augmentation already reached an accuracy

of 94% and consistency of 98%. In other tasks that

could not gain high accuracy with data augmentation,

it’s worth trying Maxblur-pooling. Maxblur-pooling

could also exert its effect when data augmentation is

not possible in some online learning systems.

6 CONCLUSION

The objective of this work is to verify if the problem

of lacking shift-invariance also happens in neural net-

works that applied to bio-signals processing, and to

validate the effect of Maxblur-pooling methodology

in this ﬁeld.

We succeeded to validate the lacking of shift-

invariance that also happens in modern neural net-

works applied in bio-signal processing. Besides, we

veriﬁed that the Maxblur-pooling method improved

accuracy and consistency in the task of AF detection

using RRI signal, but failed in the task of emotion

recognition using the EEG signal. In the tasks that are

BIOSIGNALS 2020 - 13th International Conference on Bio-inspired Systems and Signal Processing

similar to AF detection with RRI sequence as the in-

put signal, the results obtained indicate that Maxblur-

pooling, with a blur size of 7, should be used instead

of max-pooling. Moreover, if shift-invariance is espe-

cially desired, deeper networks with more Maxblur-

pooling is better. On the other hand, in the tasks

where high-frequency components are important, we

recommend to use the normal max-pooling layer. Fu-

ture work is to customize the Maxblur-pooling in a

way that is friendly to process bio-signals such as us-

ing the Avitzky-Golay ﬁlter instead of the Gaussian

ﬁlter.

REFERENCES

Acharya, U. R., Fujita, H., Lih, O. S., Hagiwara, Y., Tan,

J. H., and Adam, M. (2017). Automated detection

of arrhythmias using different intervals of tachycar-

dia ecg segments with convolutional neural network.

Information sciences, 405:81–90.

Acharya, U. R., Oh, S. L., Hagiwara, Y., Tan, J. H., and

Adeli, H. (2018). Deep convolutional neural network

for the automated detection and diagnosis of seizure

using eeg signals. Computers in biology and medicine,

100:270–278.

Addison, P. S., Walker, J., and Guido, R. C. (2009). Time–

frequency analysis of biosignals. IEEE engineering in

medicine and biology magazine, 28(5):14–29.

Azulay, A. and Weiss, Y. (2019). Why do deep convolu-

tional networks generalize so poorly to small image

transformations?

Henry, J. C. (2006). Electroencephalography: basic princi-

ples, clinical applications, and related ﬁelds. Neurol-

ogy, 67(11):2092–2092.

Li, M. and Lu, B.-L. (2009). Emotion classiﬁcation based

on gamma-band eeg. In 2009 Annual International

Conference of the IEEE Engineering in medicine and

biology society, pages 1223–1226. IEEE.

Mei, H. and Xu, X. (2017). Eeg-based emotion classiﬁca-

tion using convolutional neural network. In 2017 In-

ternational Conference on Security, Pattern Analysis,

and Cybernetics (SPAC), pages 130–135. IEEE.

Mitra, S. K. and Kaiser, J. F. (1993). Handbook for digital

signal processing. John Wiley & Sons, Inc.

Moody, G. (1983). A new method for detecting atrial ﬁb-

rillation using rr intervals. Computers in Cardiology,

pages 227–230.

Moon, S.-E., Jang, S., and Lee, J.-S. (2018). Convolu-

tional neural network approach for eeg-based emotion

recognition using brain connectivity and its spatial in-

formation. In 2018 IEEE International Conference on

Acoustics, Speech and Signal Processing (ICASSP),

pages 2556–2560. IEEE.

Oppenheim, A. V. (1997). Alan s. willsky with s. hamid

nawab, signals & systems.

Penzel, T., Moody, G. B., Mark, R. G., Goldberger, A. L.,

and Peter, J. H. (2000). The apnea-ecg database.

In Computers in Cardiology 2000. Vol. 27 (Cat.

00CH37163), pages 255–258. IEEE.

Savitzky, A. and Golay, M. J. (1964). Smoothing and dif-

ferentiation of data by simpliﬁed least squares proce-

dures. Analytical chemistry, 36(8):1627–1639.

Tripathi, S., Acharya, S., Sharma, R. D., Mittal, S., and

Bhattacharya, S. (2017). Using deep and convolu-

tional neural networks for accurate emotion classiﬁ-

cation on deap dataset. In Twenty-Ninth IAAI Confer-

ence.

Xiong, H., Zhang, T., and Moon, Y. (2000). A translation-

and scale-invariant adaptive wavelet transform. IEEE

Transactions on Image Processing, 9(12):2100–2108.

Yanagimoto, M. and Sugimoto, C. (2016). Convolutional

neural networks using supervised pre-training for eeg-

based emotion recognition. In Proceedings of the 8th

International Workshop on Biosignal Interpretation,

pages 72–75.

Zhang, D., Yao, L., Zhang, X., Wang, S., Chen, W., Boots,

R., and Benatallah, B. (2018). Cascade and parallel

convolutional recurrent neural networks on eeg-based

intention recognition for brain computer interface. In

Thirty-Second AAAI Conference on Artiﬁcial Intelli-

gence.

Zhang, R. (2019). Making convolutional networks shift-

invariant again. arXiv preprint arXiv:1904.11486.

Zheng, W.-L., Liu, W., Lu, Y., Lu, B.-L., and Cichocki, A.

(2018). Emotionmeter: A multimodal framework for

recognizing human emotions. IEEE transactions on

cybernetics, 49(3):1110–1122.

Zheng, W.-L. and Lu, B.-L. (2015). Investigating criti-

cal frequency bands and channels for eeg-based emo-

tion recognition with deep neural networks. IEEE

Transactions on Autonomous Mental Development,

7(3):162–175.

The Effect of Maxblur-pooling in Neural Networks on Shift-invariance Issue in Various Biological Signal Classiﬁcation Tasks