
The Recipe for Some Invariant Numbers and for a New Projective
Invariant Feature Descriptor
Raphael dos S. Evangelista
a
and Leandro A. F. Fernandes
b
Instituto de Computação, Universidade Federal Fluminense (UFF),
Av. Gal. Milton Tavares de Souza, Niterói, Brazil
Keywords:
Visual Feature, Junction, Invariant Theory, Similarity Map, Affine Map, Projective Map.
Abstract:
The Computer Vision literature provides a range of techniques designed to detect and describe local features
in images. The applicability of these techniques in visual tasks is directly related to the invariance of each
kind of descriptor to a group of geometric transformations. To the best of our knowledge, there is no local
feature descriptor solely based on single intensity images that are invariant to projective transformations. We
present how to use existing monomials invariant to similarity, affine, and projective transformations to compute
invariant numbers from junctions’ geometry. In addition, we present a new junction-based invariant number
and use it to propose a new local feature descriptor invariant to projective transformations in digital images.
1 INTRODUCTION
The ability to recognize visual patterns is essential to
complete our most common daily tasks. Computa-
tional vision systems were developed and applied to a
countless number of problems and, regardless of the
visual challenge, the most basic task is the identifica-
tion, recognition, and classification of objects or parts
of them. Researches have demonstrated that contours
and junctions play an essential role in the recognition
process (Barrow and Tenenbaum, 1981). This affir-
mative does not put texture properties aside on recog-
nition tasks but emphasizes that geometrical features
are of the utmost importance.
The exclusion of junctions from an edge image af-
fects the human visual recognition system more neg-
atively than the elimination of continuous edges, as
exposed by Biederman (1985). Therefore, junctions
and their surrounded regions are assumed to be highly
discriminative. Besides, the perception of this kind
of feature by the human visual system is robust to
changes in viewpoint.
Computer Vision researchers have been chal-
lenged to find ways to detect and describe these par-
ticular regions in such a way that the description be-
comes invariant to the viewpoint of the scene, the
lighting conditions, and other variables. Geomet-
a
https://orcid.org/0000-0002-2808-5865
b
https://orcid.org/0000-0001-8491-793X
rical transformations are classified into groups, de-
pending on its characteristic. The group of linear
projective transformations describes operations that
map primitives between projective planes, after a fi-
nite series of projections. The projective group en-
compasses the affine group (e.g., shearing, and non-
uniform scaling), the similarity group (e.g., uniform
scaling), and the isometric group (e.g., rotations, re-
flexions, and translations). However, most existing
image feature descriptors ignore structural geometry,
preventing the invariance from reaching more general
groups of transformations, e.g., the projective group.
The word invariant means that a value does not
change even when the application of a mapping trans-
forms the element. It is not the same as to affirm
that something has the same behaviour, as usually oc-
curs with regions and textures (Tuytelaars and Miko-
lajczyk, 2008). Some researchers have been study-
ing how to extract geometrical information from im-
ages (e.g., lines, ellipses, and general conic sections)
in such a way that we could acquire actual invari-
ants (Quan, 1995; Luo et al., 2013; Jia et al., 2016).
Many invariant might be used if the extraction suc-
ceeds. For instance, the cross-ratio is a well-known
projective invariant (Hartley and Zisserman, 2004).
In this paper, we show how to use the geometry
of junctions and monomials from the invariant theory
of n ×n matrices (Cayley, 1858) to compute a set of
invariant numbers to similarity and affine mappings.
Also, we show how to use the cross-ratio to calcu-
Evangelista, R. and Fernandes, L.
The Recipe for Some Invariant Numbers and for a New Projective Invariant Feature Descriptor.
DOI: 10.5220/0008894301810188
In Proceedings of the 15th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2020) - Volume 4: VISAPP, pages
181-188
ISBN: 978-989-758-402-2; ISSN: 2184-4321
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
181

late projective invariant values for a subclass of junc-
tions. Finally, we present a new junction-based num-
ber, which is invariant to general homographies. De-
spite the unsuccessful of practical attempts, we hope
that future works might explore the background the-
ory presented in this paper.
2 RELATED WORK
Many techniques address the problem of finding and
describing local discriminative visual features in in-
tensity images. The Scale-Invariant Feature Trans-
form (SIFT) (Lowe, 1999) uses the Difference of
Gaussians operator to achieve invariance to simi-
larity transformations and partial invariance to il-
lumination changes. The Speed-Up Robust Fea-
tures (SURF) (Bay et al., 2008) implements the Hes-
sian Operator, which seems to be more robust against
(but not completely invariant to) affine transforma-
tions (Lindeberg, 2012). The Binary Robust Indepen-
dent Elementary Features (BRIEF) (Calonder et al.,
2012) was the first binary feature descriptor aiming
to be computationally efficient. It uses the FAST
corner detector (Rosten and Drummond, 2006; Ros-
ten et al., 2010) and strings of bits to encode the
features. All these techniques and their extensions
(e.g., Bosch et al. (2008); Ke and Sukthankar (2004);
Yu and Morel (2011); Aldana-Iuit et al. (2016)) take
the textured region around discontinued edges and
corners to build local descriptors from gradient sig-
natures, random difference of intensities and other re-
lations (Tuytelaars and Mikolajczyk, 2008). When
using only texture data, the invariance to each group
of transformations is treated as an independent prob-
lem, which makes the formulation of descriptors
more complicated and less intuitive. The Affine-
SIFT (ASIFT) (Yu and Morel, 2011), for example,
consider the SIFT descriptors extracted from many
random synthetic projections of the input image to re-
trieve affine invariant feature descriptors.
A different approach is to describe interesting con-
tours from the silhouette of objects by using expected
shapes like rectangles, circles, and ellipses (Gdalyahu
and Weinshall, 1999; Alajlan et al., 2007, 2006).
These techniques are strongly based on invariant ge-
ometric relations among the shapes. But they don’t
work well with natural images and usually require
controlled environments, with limited illumination
and points of view. Recent works (Luo et al., 2013;
Fan et al., 2014; Jia et al., 2016; Li et al., 2019)
achieved good results at describing the entire contours
but, despite its limited contour of interest (i.e., the
shape), they are still susceptible to noisy and occlu-
sion. The more localized the feature, the more robust
it may be under projective mappings.
There are several recent solutions based on con-
volutional neural networks (Balntas et al., 2016; Tian
et al., 2017; Mishchuk et al., 2017; Tian et al., 2019)
which outperform the standard unsupervised feature
detection-description-matching algorithms. Despite
their effectiveness, there are still computational sys-
tems with limited resources, that might be interested
in standard and old-fashion algorithms. Thus, the
classical approach still plays an import role in Com-
puter Vision. In this sense, we use projective invariant
geometric relations of the branches of junctions to de-
scribe local discriminative information in images.
3 INVARIANT OF MATRICES
In this section, we review the concept of invariance
when applied to 3 × 3 symmetric matrices, as we can
observe their behavior as if they encode conic sec-
tions. In other words, given any symmetric matrix,
they would be transformed as a primal conic section
or a dual conic section, depending on the situation.
Let M be an invertible n × n matrix. The Cayley-
Hamilton theorem states that every matrix M satisfies
its characteristic polynomial, derived from:
det(M − kI) = k
n
− c
1
k
n−1
+ · ·· + (−1)
n
c
n
,
where I is an identity n × n matrix, k is a unknown lin-
ear coefficient and c
1
,c
2
,··· ,c
n
are the characteristic
coefficients of M. As a generalization, M may be a
linear combination of n matrices
det(k
1
IM
1
+ k
2
IM
2
+ · ·· + k
n
IM
n
) =
f
1
c
1
+ · ·· + k
p
i1
1
k
p
i2
i2
·· ·k
p
in
n
| {z }
f
i
c
i
+ · ·· + f
n
c
n
,
where f
i
denotes the combination of the combinatory
factors k
1
,k
2
,· ·· ,k
n
and p
i1
, p
i2
,· ·· , p
in
are scalar
numbers, to elucidate the general formula.
Assuming that M is symmetric, it encodes a conic
section. The characteristic coefficients are naturally
invariant under the isometric group of transforma-
tions. The characteristic coefficients usually arise as a
function of the determinant, trace, or the combination
of both. One achieves invariance under the similar-
ity group of transformations (excluding translations)
considering the ratio (Semple and Kneebone, 1952):
γ =
dsc(M)
tr(M)
2
, (1)
where tr (M) is the trace and dsc (M) is the second dis-
criminant, defined as the determinant of the leading
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
182

2 × 2 submatrix of M. The discriminant determines
the shape of the curve. When the conic section is de-
generated, the discriminant is zero.
Nevertheless, it is possible to assemble invariant
monomials in a more systematic way, because any
polynomial raised from the combination of charac-
teristic coefficients is also a characteristic polyno-
mial (Forsyth et al., 1991; Quan et al., 1991). There-
fore, conveniently, we can consider the product of all
coefficients
∏
n
i=0
( f
i
c
i
)
a
i
where all a
i
∈ Q are variable
exponents related to the characteristic coefficients c
i
and its combinatorial factors f
i
. We can vary the value
of a
i
as much as we want to build different character-
istic polynomials. But it is important to keep in mind
that not all of them are invariant due to the presence
of the factors f
i
. We are interested in the polynomials
that can neutralize the f
i
effects. So, what we need is:
n
∏
i=0
( f
i
c
i
)
a
i
=
n
∏
i=0
k
p
i1
1
k
p
i2
2
·· ·k
p
in
n
|
{z }
f
i
c
i
a
i
=
n
∏
i=0
c
a
i
i
,
where the above equality is possible if, and only if,
each combinatorial factor f
i
= 1, which leaves the
characteristic coefficients c
i
untouched. Thus, we
want the solution of the homogeneous system Pa = 0,
where P is a square (n + 1) × (n + 1) matrix com-
posed by the scalar powers p
i j
, and a = (a
0
,· ·· ,a
n
)
>
.
Due to space restrictions, see Quan (1995) for details.
The product operator allowed us to find a solution
where
∑
n
i=0
p
i j
= 0, for any given factor k
j
. With this
powerful tool in mind, we can derive as many geomet-
rical quantities of conic sections as intended and com-
bine them to achieve invariance. Quan (1995) proved
that a true projective invariant quantity is only reach-
able with the combination of two curves, so
β
i, j
=
tr
M
−1
i
M
j
det(M
i
)
tr
2
M
−1
j
M
i
det(M
j
)
(2)
where M
i
and M
j
are symmetric matrices related to
any two conic sections.
Section 4 presents our main contribution, which
is how to encode junctions as dual conic sections and
compute invariant numbers for them.
4 THE PROPOSED INVARIANT
MONOMIALS FOR JUNCTIONS
For a given bidimensional intensity image
I : R
2
7→ R
+
, where the function I (x,y) returns
the gray level related to point p = (x, y) ∈ R
2
, the
location of a (continuous) junction correspond to
the intersection of linear ridges in the gradient of I ,
while the branches of a junction are given by the line
segments defined by the ridges. Thus, a continuous
junction J
n
can be defined as the set
J
n
=
{
p | p ∈
p
0
p
i
,∃ i ∈ {1,2,. .., n}
}
, (3)
where n ∈ {2, 3,.. .} is the number of branches or
degree of the junction, p
0
denotes the central ver-
tex (i.e., the point shared by the branches), and
p
i
= (x
i
,y
i
) and p
0
p
i
are, respectively, the delimiter
vertex and the line segment defining the i-th branch,
with p
i
/∈ p
0
p
j
for all i 6= j and i, j ∈ {1,2,. .., n}. We
assume that branches are taken counterclockwise. In
digital images, the branches of digital junctions hav-
ing n ≥ 5 overlap. Thus, n ∈ {2, 3,4} in this case.
By definition, the central vertex p
0
of a junction
is always a proper point (i.e., a point with finite loca-
tion). When the delimiter vertices p
i
are also proper
points, we say that we have a proper junction. How-
ever, when p
i
are ideal points (i.e., points at infinity or
directions), we say that they define an ideal junction.
Section 4.1 presents a similarity invariant mono-
mial adapted for 2-junctions. Affine invariance is
achieved by the monomial used with 3-junctions in
Section 4.2. Sections 4.3 and 4.4 describe projective
invariant numbers for 4-junctions. As shown in Sec-
tion 4.4, only junctions with four (or more) branches
could provide the required input for the projective in-
variant, despite the ambiguous visual connotation re-
lated to them in practice (e.g., occlusions).
4.1 Similarity Invariant for Proper and
Ideal 2-junctions
The key insight in this work was to build symmetric
matrices from the geometry of junctions and use the γ
number defined in (1) as invariant for 2-junctions un-
der similarity transformations. More specifically, we
explore the duality between points in projective space
P
2
and dual conic sections to represent point vec-
tors x = (x,y, w)
>
∈ P
2
as symmetric matrices with
the form (Perwass and Forstner, 2006):
D = xx
>
=
x
2
xy xw
yx y
2
yw
wx wy w
2
, (4)
where
>
denotes matrix transposition.
It is important to notice that rank (D) = 1. There-
fore, D cannot be used directly in (1) since
det(D) = 0. But a net of conics (Semple and Knee-
bone, 1952) computed from at least three dual conic
sections related to linearly independent point vectors
x ∈ P
2
produces a symmetric 3 × 3 matrix with full
The Recipe for Some Invariant Numbers and for a New Projective Invariant Feature Descriptor
183

rank. In our work, we use the following net of conics
to compute invariant γ numbers for 2-junctions:
N = D
0
+ D
1
+ D
2
. (5)
In (5), we assume that the central vertex p
0
is the ori-
gin of the coordinate system. Therefore, (4) relates
the dual conic section matrix D
k
to the point vector
x
k
= (x
k
− x
0
,y
k
− y
0
,1)
>
if p
k
is a proper point, or to
x
k
= (x
k
,y
k
,0)
>
if the vertex is an ideal point.
Proof. Under a point transformation x
0
= T x, a dual
conic matrix D transforms to:
D
0
= T DT
>
. (6)
Using (6), the transformed net of conics (5) is:
N
0
= T D
0
T
>
+ T D
1
T
>
+ T D
2
T
>
= T NT
>
.
Recall that mapping the central vertex p
0
to the
origin (see (5)) cancel out the translation, leaving only
uniform scale and rotation in T . We prove the invari-
ance of γ (1) to similarity transformations S applied to
J
2
by replacing M by N
0
in (1):
γ
0
=
dsc(N
0
)
tr
2
(N
0
)
=
dsc
SNS
>
tr
2
SNS
>
=
dsc(S)dsc (N)dsc
S
>
tr
2
NS
>
S
=
s
4
dsc(N)
s
4
tr
2
(N)
= γ,
where s is the uniform scale factor in S.
4.2 Affine Invariant for Proper and
Ideal 3-junctions
The three vertices of a 2-junction do not provide
enough information for covering the six degrees of
freedom of an affine mapping. Therefore, it is not
possible to define affine invariant values from these
junctions. Using one additional vertex, the proposed
affine invariants for proper 3-junctions (3) are β
1,2
,
β
1,3
, and β
3,1
, from (2). It is important to note that (2)
is proved to be projective-invariant (Quan, 1995), but
that property is lost as soon as the junction is pro-
jected on the image plane after a transformation. De-
spite that, the affine-invariance is preserved.
We define the matrices Q
k
used in (2) from the
coordinates of vertices of a proper 3-junction as:
Q
k
= v
i
v
>
i
+ v
j
v
>
j
, (7)
where v
l
= (x
l
− x
0
,y
l
− y
0
)
>
, for i 6= j 6= k
and i, j,k ∈ {1,2,3}. By doing so, β
1,2
= β
3,2
,
β
1,3
= β
2,3
, β
3,1
= β
2,1
, and β
1,2
+ β
1,3
+ β
3,1
= 1.
As a result, the number of invariant values can be
reduced to two, since β
i, j
= 1 −
β
j,k
+ β
j,i
.
Proof. Let A be an affine transformation whose trans-
lation was canceled out by mapping p
0
to the origin of
the space (see v
l
in (7)). Let Q
0
be the symmetric ma-
trix in (7) after the 3-junction J
3
be transformed by A:
Q
0
k
=
˙
Av
i
v
>
i
˙
A
>
+
˙
Av
j
v
>
j
˙
A
>
=
˙
AQ
k
˙
A
>
,
where
˙
A is the leading 2 × 2 submatrix of A. The in-
variance of β
i, j
to affine mapping is proved by:
β
0
i, j
=
tr
Q
0−1
i
Q
0
j
det(Q
0
i
)
tr
2
Q
0−1
j
Q
0
i
det
Q
0
j
=
tr
˙
A
−>
Q
−1
i
Q
j
˙
A
>
det
˙
AQ
i
˙
A
>
tr
2
˙
A
−>
Q
−1
j
Q
i
˙
A
>
det
˙
AQ
j
˙
A
>
=
tr
Q
−1
i
Q
j
˙
A
>
˙
A
−>
det
2
˙
A
det(Q
i
)
tr
2
Q
−1
j
Q
i
˙
A
>
˙
A
−>
det
2
˙
A
det(Q
j
)
=
tr
Q
−1
i
Q
j
det(Q
i
)
tr
2
Q
−1
j
Q
i
det(Q
j
)
= β
i, j
.
4.3 Projective Invariant for Ideal
4-junctions
The cross-ratio (Hartley and Zisserman, 2004) is a
well-known projective invariant number related to a
list of four collinear points q
i
, for i ∈ {1,2, 3,4}:
λ = (q
1
,q
2
;q
3
,q
4
) =
kq
1
q
3
k
kq
2
q
4
k
kq
2
q
3
k
kq
1
q
4
k
, (8)
where kk is the signed length of a line segment in
Euclidean space. The permutation of the points alter
the cross-ratio, resulting in up to six different values:
λ,
1
λ
,
1
1 − λ
, 1 − λ,
λ
λ − 1
,
λ − 1
λ
(9)
For ideal 4-junctions (3), the central vertex p
0
is a
proper point, while delimiter vertices p
i
= (x
i
,y
i
) are
directions, i.e., x
0
= (x
0
,y
0
,1)
>
and x
i
= (x
i
,y
i
,0)
>
in projective space P
2
, for i ∈ {1,2,3, 4}. Let
r
i
= x
0
× x
i
be the straight line defined by the cen-
tral vertex of the junction and the direction of its i-th
branch. Here, × denotes the cross product. Let l
be a straight line not parallel to any line r
i
. We use
the cross-ratio (8) of points q
i
= l × r
i
shared by l and
r
i
to compute projective invariant values for ideal 4-
junctions. Among all possible results for λ (9), there
is only one in the [−1,0] range. By taking its modu-
lus, we have a projective invariant number in the [0,1]
range that does not depend on the branches’ order.
Proof. The proof for the invariance of λ is presented
by Hartley and Zisserman (2004).
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
184

4.4 Projective Invariant for Proper
4-junctions
Similarity and affine transformations do not affect the
homogeneous coordinate w under a point transforma-
tion x
0
= T x. Thus, for the invariant numbers pre-
sented in Section 4.1 and 4.2, one doesn’t have to
worry about normalizing the homogeneous coordi-
nate of x
0
in order to retrieve the actual location of
the mapped point. Projective transformations, on the
other hand, may change the homogeneous coordinate
of mapped points. The normalization turns the defini-
tion of truly projective invariants a challenging task.
The proposed projective invariant number is ro-
bust to the application of homographies to 4-junctions
and to the subsequent normalization of the homoge-
neous coordinates of vertices. It is computed as:
α =
det(PP)
tr
3
(PP)
, (10)
where
P =
∑
f ∈F
(D
f
1
CD
f
2
CD
f
3
CD
f
4
C). (11)
In (11), F is a set including the 8 cyclic permutations
of the indices of branches in J
4
(3) taken clockwise
and counterclockwise, C is the matrix representation
of the (primal) conic section which passes through the
vertices of J
4
, and D
f
i
is the dual conic section matrix
related to vertex p
f
i
by (4). We have used PP instead
of just P in (10) to force α ≥ 0.
The reason for multiplying matrices D
f
i
C in (11)
is twofold: (i) α must be independent of the selection
of the first branch in J
4
; and (ii) the multiplication al-
lows us to collect from the summation the scalar fac-
tors multiplying D
f
i
and C, making α robust against
the normalization of homogeneous coordinates.
Proof. Recall that under the projective transforma-
tions of points, i.e., x
0
= T x, a primal conic section
matrix C transforms to:
C
0
= T
−>
CT
−1
. (12)
Also, recall that x ≡ δx, C ≡ δC, and D ≡ δD in pro-
jective space P
2
for any real value δ 6= 0, where x, C,
and D denote, respectively, a point vector, a primal
conic section matrix, and a dual conic section matrix.
Using (6) and (12), let D
00
f
i
= δ
f
i
D
0
f
i
= δ
f
i
HD
f
i
H
>
and C
00
= δ
C
C
0
= δ
C
H
−>
CH
−1
be, respectively, the
dual conic related to vertex p
f
i
and the primal conic
defined by the vertices of a 4-junction under a pro-
jective transformation H, for δ
6= 0 being any scalar
factor multiplying these matrices, including the nor-
malization factor of the homogeneous coordinate.
The transformed P matrix is given by:
P
0
=
∑
f ∈F
D
00
f
1
C
00
D
00
f
2
C
00
D
00
f
3
C
00
D
00
f
4
C
00
=
∑
f ∈F
δ
f
HD
f
1
CD
f
2
CD
f
3
CD
f
4
CH
−1
= δ
F
H
∑
f ∈F
(D
f
1
CD
f
2
CD
f
3
CD
f
4
C)
!
H
−1
= δ
F
HPH
−1
,
where δ
F
= δ
f
= δ
4
C
∏
4
i=1
δ
f
i
for all f ∈ F . We prove
the invariance of α by replacing P by P
0
in (10):
α
0
=
det(P
0
P
0
)
tr
3
(P
0
P
0
)
=
det
δ
2
F
HPPH
−1
tr
3
δ
2
F
HPPH
−1
=
δ
6
F
det(H)det(PP) det
H
−1
δ
6
F
tr
3
(PPH
−1
H)
=
det(PP)
tr
3
(PP)
= α.
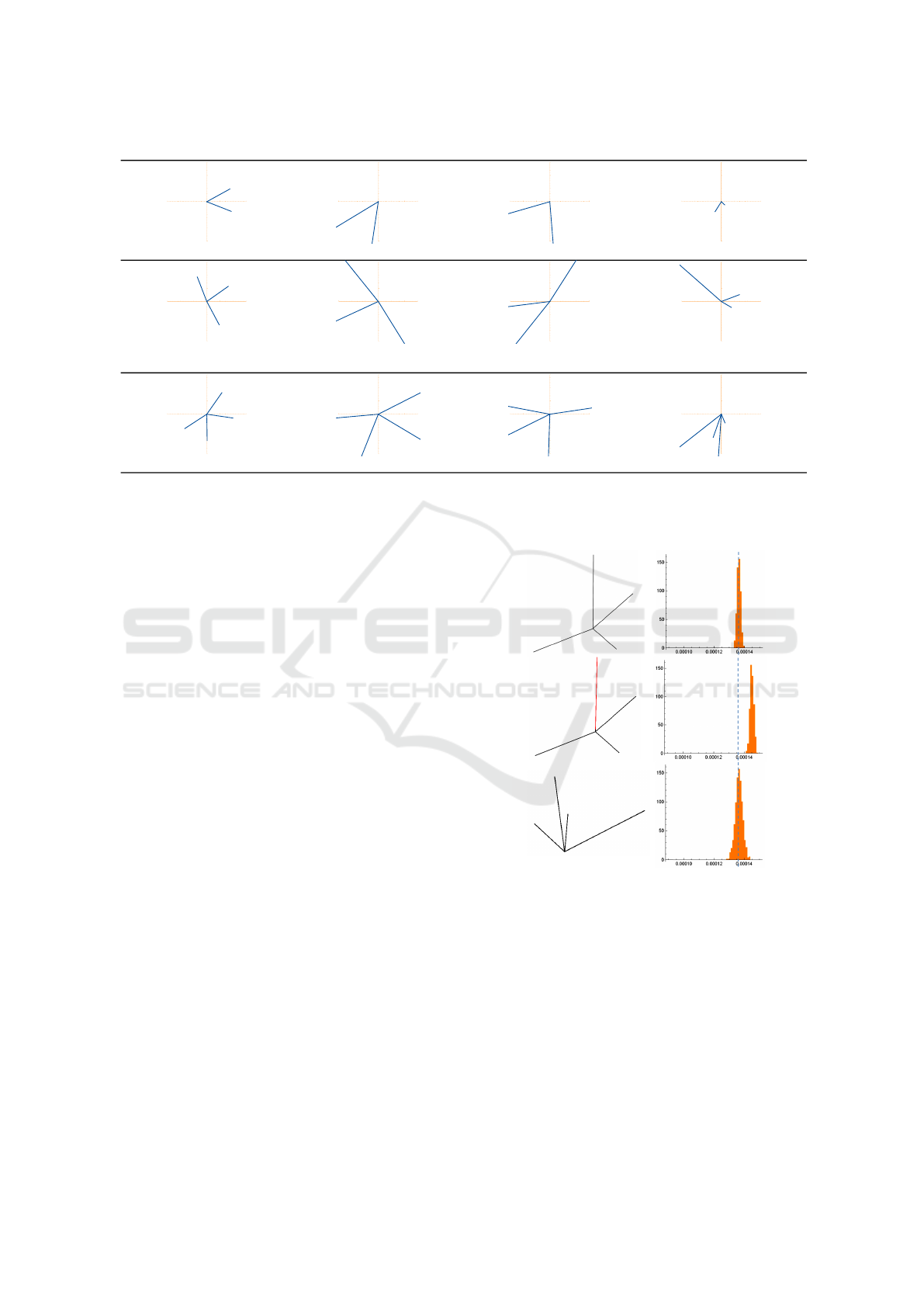
We performed controlled experiments with con-
tinuous junctions and their transformed counterparts
(see Fig. 1). As expected, each proposed number is
invariant to a group of transformations.
To demonstrate the distinctiveness of the given
projective invariant monomial, we built continuous
4-junctions and their projective-transformed counter-
parts (see Fig. 2). For each digital version of each
junction, we took its central and delimiter pixels and
produced 100,000 random continuous junctions by
sampling points in the pixels’ area. Then, we com-
puted the histogram of α numbers related to the set
of random samples and compared the histograms of
original and transformed junctions. Fig. 2 (top) il-
lustrates junctions used as reference and histograms
of invariant values produced using the random sam-
ples. Notice that there is a well-defined peak of votes
close to the actual α number computed for the refer-
ence junction (the dashed line). The distribution of
random α samples produced for an unrelated junc-
tion generates a peak of votes in a different α value
(Fig. 2, middle), while the peak of votes generated
for the transformed version of the reference junction
preserves the signature of the distribution (Fig. 2, bot-
tom). Such behavior suggests that the histogram of
samples may be used to characterize well-defined dis-
crete junctions related by projective transformations.
5 THE PROPOSED PROJECTIVE
INVARIANT DESCRIPTOR
The invariant numbers presented in Section 4 are de-
fined for continuous junctions (J
n
) in bidimensional
The Recipe for Some Invariant Numbers and for a New Projective Invariant Feature Descriptor
185
Reference Similarity Transformation Affine Transformation Projective Transformation
-1.5 -1.0 -0.5 0.5 1.0 1.5
-1.5
-1.0
-0.5
0.5
1.0
1.5
-1.5 -1.0 -0.5 0.5 1.0 1.5
-1.5
-1.0
-0.5
0.5
1.0
1.5
-1.5 -1.0 -0.5 0.5 1.0 1.5
-1.5
-1.0
-0.5
0.5
1.0
1.5
-1.5 -1.0 -0.5 0.5 1.0 1.5
-1.5
-1.0
-0.5
0.5
1.0
1.5
γ = 0.14821 γ = 0.14821 γ = 0.238821 γ = 0.143078
-1.5 -1.0 -0.5 0.5 1.0 1.5
-1.5
-1.0
-0.5
0.5
1.0
1.5
-1.5 -1.0 -0.5 0.5 1.0 1.5
-1.5
-1.0
-0.5
0.5
1.0
1.5
-1.5 -1.0 -0.5 0.5 1.0 1.5
-1.5
-1.0
-0.5
0.5
1.0
1.5
-1.5 -1.0 -0.5 0.5 1.0 1.5
-1.5
-1.0
-0.5
0.5
1.0
1.5
β =
0.15 0.16 0.00
0.13 0.13 0.00
β =
0.15 0.16 0.00
0.13 0.13 0.00
β =
0.15 0.16 0.00
0.13 0.13 0.00
β =
0.02 0.22 0.01
0.01 0.22 0.01
-1.5 -1.0 -0.5 0.5 1.0 1.5
-1.5
-1.0
-0.5
0.5
1.0
1.5
-1.5 -1.0 -0.5 0.5 1.0 1.5
-1.5
-1.0
-0.5
0.5
1.0
1.5
-1.5 -1.0 -0.5 0.5 1.0 1.5
-1.5
-1.0
-0.5
0.5
1.0
1.5
-1.5 -1.0 -0.5 0.5 1.0 1.5
-1.5
-1.0
-0.5
0.5
1.0
1.5
α = 0.496638 α = 0.496638 α = 0.496638 α = 0.496638
Figure 1: Each row presents one type of junction transformed by similarity, affine, and projective transformations (columns).
The respective invariant value, γ, β, and α is at the bottom of each sample junction. Blue and red texts denote when the value
remains the same or changed after the transformation of the reference junctions.
intensity images (I ). For a given bidimensional inten-
sity digital image
ˆ
I : Z
2
7→ R
+
, the discrete domain
of
ˆ
I leads to the definition of digital junctions as:
ˆ
J
n
=
n
ˆp | ˆp ∈
ˆ
B
i
,∃ i ∈ {1,2,. .., n}
o
,
where n ∈ {2,3,4} is the degree of the junction, and
ˆ
B
i
denotes the set of pixels ˆp = (u,v) ∈ Z
2
defining
the i-th branch of the junction having the central pixel
ˆp
0
=
ˆ
B
i
∩
ˆ
B
j
as the only pixel shared by the branches,
for all i 6= j and i, j ∈ {1,2,. .., n}. By definition, the
branches
ˆ
B
i
are digital straight line segments ranging
from the central pixel ˆp
0
to the delimiter pixel ˆp
i
.
The challenges for defining a projective invariant
junction descriptor include: (i) detect well-defined 4-
junctions in images (Section 5.1); (ii) compute de-
scriptors for the detected junctions (Section 5.2); and
(iii) define a matching procedure (Section 5.3).
5.1 Detecting Junctions in Digital
Images
It is quite difficult to perform accurate detection of
well-defined 4-junctions in digital images of natural
scenes using computationally cheap procedures. Our
proposed strategy to accomplish this task is to find
image corners using the Minimum Eigenvalue Cor-
ner Detector (Shi and Tomasi, 1994) and, for each de-
tected corner, define a region of interest (ROI) from
which the analysis of the gradient leads to the identifi-
cation of candidate branches leaving the corner. Can-
didate 4-junctions are produced from the combination
Figure 2: The distributions of α numbers (right) computed
for random junctions samples produced from a digital junc-
tions (left). The junction in the bottom was created by ap-
plying a homography to the junction in the top. The junction
in the middle is not related to the others by a homography.
of those branches. Thus, instead of retrieve one digital
junction for each detected corner, we use each corner
as the central vertex of a set of junctions representing
the image gradient around it. Section 5.2 shows how
the α numbers related to these candidate junctions are
combined to produce a descriptor for the ROI.
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
186

5.2 Computing the Feature Descriptors
Our feature descriptor is a histogram having m bins,
which count the (weighted) frequency of invariant
numbers computed for the set of digital junctions.
However, our experience shows that α numbers close
zero are more frequent (see Fig. 3, left). As a re-
sult, a histogram on the observations of α having a
small m might be unrepresentative (i.e., all resultant
histograms would look the same). We have overcome
this issue by performing a non-linear order-preserving
bijective mapping α 7→
ˆ
α based on the theoretical cu-
mulative distribution of α. Fig. 3 (right) shows the
frequency distribution of
ˆ
α numbers computed from
the α values assumed in Fig. 3 (left). Note that fre-
quencies are better distributed along with the
ˆ
α axis.
Without loss of generality, let
α =
det(PP)
tr
3
(PP)
≡
µ
2
2
µ
2
3
1 + µ
2
2
+ µ
2
3
3
(13)
be the invariant number defined in (10) rewritten in
terms of 1 ≥ µ
2
2
≥ µ
2
3
≥ 0, where 1, µ
2
2
, and µ
2
3
are
the eigenvalues of the symmetric matrix PP after be-
ing divided by the eigenvalue with the largest mag-
nitude (recall that scaling PP does not affect α). Us-
ing (13), it is possible to conclude that α ∈ [0,1/27],
since max
µ
2
,µ
3
α = 1/27. Also, (13) allows us to define the
theoretical cumulative distribution function of α as:
F (α) = 1 − 2
Z
1
˙µ
2
(α)
(µ
2
− ˙µ
3
(µ
2
,α)) dµ
2
,
where functions ˙µ
2
and ˙µ
3
are obtained by solv-
ing (13) for µ
2
= µ
3
and µ
2
= 1, respectively.
For a given α number, we map it to
ˆ
α using:
ˆ
α = F (α), (14)
where
ˆ
α ∈ [0, 1]. We use numerical integration to
evaluate F and its inverse, and keep a lookup list with
m entries to perform fast mapping between α and
ˆ
α.
Each histogram assigned to a given corner pixel
ˆc is computed as follows: (i) each digital junction
ˆ
J
4
is approximated by the continuous junction J
4
whose
vertices correspond to the center of the endpixels of
ˆ
J
4
; (ii) the α value of each J
4
is computed using (10)
and mapped to
ˆ
α using (14); (iii) the
ˆ
α values con-
tribute to the final histogram according to the weight
of their respective digital junctions, which is com-
puted as the product of the strength of the branches.
5.3 Matching Procedure
Given two sets of invariant histograms, namely
A and B, we use the k-Nearest Neighbors algo-
rithm (k -NN) (Friedman et al., 1977) to find the best
0.001 0.002 0.003 0.004 0.005 0.006 0.007
α0
500
1000
1500
2000
Count
0.2 0.4 0.6 0.8 1.0
α
0
200
400
600
800
Count
Figure 3: Distribution of α numbers before (left) and af-
ter (right) applying the non-linear mapping α 7→
ˆ
α. The fre-
quencies concentrate on the left side of the α domain. After
mapping, they distribute better in the [0,1] domain of
ˆ
α.
match in A for each descriptor in B. In our experi-
ments, we have assumed k = 1 and the Earth Mover’s
Distance (EMD) (Rubner et al., 1998) to compare two
histograms. Alternatively, any other algorithms could
be used to match our feature histogram, as long as an
appropriate distance metric is adopted (e.g., Kullback-
Leibler Divergence and Chi-Squared Test).
6 CONCLUSIONS
In this paper, we presented how to compute symmet-
ric matrices from the geometry of junctions having
degree two or three, and how to use these matrices
with monomials invariant to, respectively, similarity
and affine transformations. Using the cross-ratio, we
showed how to compute a projective invariant num-
ber for ideal junctions having degree four. Also, we
presented the derivation of a new projective invariant
number for 4-junctions, which is independent of the
cyclic order assumed for the branches of the junction
and to the normalization of the homogeneous coordi-
nate in projective space. Using the latter invariant,
we defined a new procedure for detecting, describ-
ing, and matching local projective invariant junction-
based features in digital images.
Results show that our descriptor is promising
since it is capable of representing discriminative in-
formation. Unfortunately, the practical attempts to
implement the projective descriptor in natural images
failed due to several reasons, most of them related
to finding digital 4-junctions, which is an open re-
search topic, and that’s why we did not perform com-
parisons with state-of-the-art techniques. We are cur-
rently investigating ways to improve the detection of
junctions’ vertices in digital images. We hope that by
showing connections between the junction’s geome-
try and existing invariant monomials and by present-
ing new invariant numbers and a new descriptor, this
work may stimulate further researches.
The Recipe for Some Invariant Numbers and for a New Projective Invariant Feature Descriptor
187

ACKNOWLEDGEMENTS
This work was partially supported by CNPq-
Brazil (grant 311.037/2017-8) and FAPERJ (grant
E-26/202.718/2018) agencies. Raphael was spon-
sored by a CAPES fellowship.
REFERENCES
Alajlan, N., El Rube, I., Kamel, M. S., and Freeman, G.
(2007). Shape retrieval using triangle-area represen-
tation and dynamic space warping. Pattern Recogn.,
40(7):1911–1920.
Alajlan, N., Kamel, M. S., and Freeman, G. (2006). Multi-
object image retrieval based on shape and topology.
Image Commun., 21(10):904–918.
Aldana-Iuit, J., Mishkin, D., Chum, O., and Matas, J.
(2016). In the saddle: Chasing fast and repeatable
features. In ICPR, pages 675–680.
Balntas, V., Riba, E., Ponsa, D., and Mikolajczyk, K.
(2016). Learning local feature descriptors with triplets
and shallow convolutional neural networks. In BMVC.
Barrow, H. G. and Tenenbaum, J. M. (1981). Interpreting
line drawings as three-dimensional surfaces. Artif. In-
tell., 17(1-3):75–116.
Bay, H., Ess, A., Tuytelaars, T., and Van Gool, L. (2008).
Speeded-up robust features (SURF). Comput. Vis. Im-
age Underst., 110(3):346–359.
Biederman, I. (1985). Human image understanding: recent
research and a theory. Computer Vision, Graphics,
and Image Processing, 32:29–73.
Bosch, A., Zisserman, A., and Muñoz, X. (2008). Scene
classification using a hybrid generative/discriminative
approach. IEEE Trans. Pattern Anal. Mach. Intell.,
30(4):712–727.
Calonder, M., Lepetit, V., Ozuysal, M., Trzcinski, T.,
Strecha, C., and Fua, P. (2012). BRIEF: Computing
a local binary descriptor very fast. IEEE Trans. Pat-
tern Anal. Mach. Intell., 34(7):1281–1298.
Cayley, A. (1858). A memoir on the theory of matrices.
Phil. Trans., 148:17–37.
Fan, X., Luo, Z., Zhang, J., Zhou, X., Jia, Q., and Luo, D.
(2014). Characteristic number: Theory and its appli-
cation to shape analysis. Axioms, 3:202–221.
Forsyth, D., Mundy, J. L., and Zisserman, A. (1991). In-
variant descriptors for 3D object recognition and pose.
IEEE Trans. Pattern Anal. Mach. Intell., pages 971–
991.
Friedman, J. H., Bentely, J., and Finkel, R. A. (1977). An
algorithm for finding best matches in logarithmic ex-
pected time. ACM Trans. Math. Softw., 3(3):209–226.
Gdalyahu, Y. and Weinshall, D. (1999). Flexible syntactic
matching of curves and its application to automatic
hierarchical classification of silhouettes. IEEE Trans.
Pattern Anal. Mach. Intell., 21(12):1312–1328.
Hartley, R. I. and Zisserman, A. (2004). Multiple View Ge-
ometry in Computer Vision. Cambridge University
Press, 2nd edition.
Jia, Q., Fan, X., Liu, Y., Li, H., Luo, Z., and Guo, H.
(2016). Hierarchical projective invariant contexts for
shape recognition. Pattern Recognit., 52:358–374.
Ke, Y. and Sukthankar, R. (2004). PCA-SIFT: A more dis-
tinctive representation for local image descriptors. In
CVPR, pages 506–513.
Li, E., Mo, H., Xu, D., and Li, H. (2019). Image projective
invariants. IEEE Trans. Pattern Anal. Mach. Intell.,
41(5):1144–1157.
Lindeberg, T. (2012). Scale selection properties of gener-
alized scale-space interest point detectors. J. Math.
Imaging Vision, 46(2):177–210.
Lowe, D. G. (1999). Object recognition from local scale-
invariant features. In ICCV, pages 1150–1157.
Luo, Z., Luo, D., Fan, X., Zhou, X., and Jia, Q. (2013). A
shape descriptor based on new projective invariants.
In ICIP, pages 2862–2866.
Mishchuk, A., Mishkin, D., Radenovi
´
c, F., and Matas, J.
(2017). Working hard to know your neighbor’s mar-
gins: Local descriptor learning loss. In NIPS, pages
4829–4840.
Perwass, C. and Forstner, W. (2006). Uncertain Geome-
try with Circles, Spheres and Conics, pages 23–41.
Springer Netherlands.
Quan, L. (1995). Invariant of a pair of non-coplanar con-
ics in space: definition, geometric interpretation and
computation. In ICCV, pages 926–931.
Quan, L., Gros, P., and Mohr, R. (1991). Invariants of a pair
of conics revisited. In BMVC, pages 71–77.
Rosten, E. and Drummond, T. (2006). Machine learning for
high-speed corner detection. In ECCV, pages 430–
443.
Rosten, E., Porter, R., and Drummond, T. (2010). Faster and
better: a machine learning approach to corner detec-
tion. IEEE Trans. Pattern Anal. Mach. Intell., 32:105–
119.
Rubner, Y., Tomasi, C., and Guibas, L. J. (1998). A metric
for distributions with applications to image databases.
In ICCV, pages 59–66.
Semple, J. G. and Kneebone, G. T. (1952). Algebraic Pro-
jective Geometry. Oxford Science Publication.
Shi, J. and Tomasi, C. (1994). Good features to track. In
CVPR, pages 593–600.
Tian, Y., Fan, B., and Wu, F. a. (2017). L2-Net: deep learn-
ing of discriminative patch descriptor in Euclidean
space. In CVPR, pages 6128–6136.
Tian, Y., Yu, X., Fan, B., Wu, F., Heijnen, H., and Balntas,
V. (2019). SOSNet: second order similarity regular-
ization for local descriptor learning. In CVPR, pages
11016–11025.
Tuytelaars, T. and Mikolajczyk, K. (2008). Local invariant
feature detectors: A survey. Found. Trends. Comput.
Graph. Vis., 3(3):177–280.
Yu, G. and Morel, J. (2011). ASIFT: An algorithm for fully
affine invariant comparison. IPOL, 1:11–38.
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
188
