Superpoints in RANSAC Planes: A New Approach for Ground Surface

Extraction Exempliﬁed on Point Classiﬁcation and Context-aware

Reconstruction

Dimitri Bulatov

1 a

, Dominik St

utz

, Lukas Lucks

and Martin Weinmann

Fraunhofer Institute for Optronics, System Technologies and Image Exploitation (IOSB),

Gutleuthausstrasse 1, 76275 Ettlingen, Germany

Institute of Photogrammetry and Remote Sensing, Karlsruhe Institute of Technology (KIT),

Englerstr. 7, 76131 Karlsruhe, Germany

Keywords:

Point Cloud, Classiﬁcation, Surface Reconstruction, Superpoints.

Abstract:

In point clouds obtained from airborne data, the ground points have traditionally been identiﬁed as local

minima of the altitude. Subsequently, the 2.5D digital terrain models have been computed by approximation

of a smooth surfaces from the ground points. But how can we handle purely 3D surfaces of cultural heritage

monuments covered by vegetation or Alpine overhangs, where trees are not necessarily growing in bottom-to-

top direction? We suggest a new approach based on a combination of superpoints and RANSAC implemented

as a ﬁltering procedure, which allows efﬁcient handling of large, challenging point clouds without necessity

of training data. If training data is available, covariance-based features, point histogram features, and dataset-

dependent features as well as combinations thereof are applied to classify points. Results achieved with

a Random Forest classiﬁer and non-local optimization using Markov Random Fields are analyzed for two

challenging datasets: an airborne laser scan and a photogrammetrically reconstructed point cloud. As an

application, surface reconstruction from the thus cleaned point sets is demonstrated.

1 INTRODUCTION

Dense 3D point clouds are more easily accessible than

ever before thanks to increasingly cheap laser tech-

nologies and to advanced pipelines for photogram-

metric reconstruction, available for commercial and

non-commercial use. It is thus not surprising they

ﬁnd many applications in construction industry, civil

engineering, and, as a particular focus of this work,

in cultural heritage preservation. Here the application

ﬁelds range from documentation to monitoring and

from uncovering testimonies of the historic civiliza-

tion (Evans et al., 2013) to elaboration of solutions

for preservation of monuments of cultural heritage as

was the case for the HERACLES project funded by

the Horizon 2020 research and innovation program of

the European Union. To perform analysis of erosions

within in-situ measurements, a large-scale prepara-

tion of data and identiﬁcation of particularly threat-

ened spots is required (Bulatov et al., 2018).

All these applications underline a growing need

for innovative methods for the treatment and analy-

sis of large 3D point clouds. In particular, for moni-

https://orcid.org/0000-0002-0560-2591

toring of cultural heritage, it is important to identify

vegetation areas to be able to differentiate between

those points changing seasonally and those indicat-

ing deterioration of substance. Trees and bushes, not

much relevant for model representation and monu-

ment preservation, should ideally be omitted or mod-

eled by generic models (Lafarge and Mallet, 2012),

while those parts of the scene which are covered by

vegetation may be closed using methods of geometric

inpainting (Guo et al., 2018). This is done because,

on the one hand, data exchange between multinational

partners working on the aforementioned project (Bu-

latov et al., 2018) has turned out to be a non-negligible

issue, and, on the other hand, a gap-free surface for

building models has to be obtained.

The necessary requisite of this semantic surface

modeling representation of a point cloud, namely its

classiﬁcation into semantic categories (terrain, vege-

tation, building parts), must be addressed. Still, in

the literature, see Section 2, we gained an impres-

sion that many previous works relied on a sampling

of the point cloud into an elevation map, that is, as-

signing a z-value to a pair (x,y) within a discrete rect-

angular grid. This is a limitation in presence of ver-

tical walls, balconies, or other purely 3D structures

Bulatov, D., Stütz, D., Lucks, L. and Weinmann, M.

Superpoints in RANSAC Planes: A New Approach for Ground Surface Extraction Exempliﬁed on Point Classiﬁcation and Context-aware Reconstruction.

DOI: 10.5220/0008895600250037

In Proceedings of the 15th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2020) - Volume 1: GRAPP, pages

25-37

ISBN: 978-989-758-402-2; ISSN: 2184-4321

where no such function z(x,y) exists. Another limita-

tion is the necessity to differentiate between different

sources of data (LiDAR-based or stemming from a

photogrammetric reconstruction, among others). This

brings about, ﬁnally, the shortcomings of the point

cloud itself: variable, sometimes very low point den-

sity, noise, and outliers. In order to cope with this,

a particular data structure, called superpoints, will

be proposed in Section 3. This structure, robust to

the variable point density, will allow to decrease the

data volume considerably. Using RANSAC, we will

ﬁnd out which superpoints lie in a dominant plane,

which will allow for a large-scale separation of ter-

rain and non-terrain points without the necessity of

training data generation. Thus, the approach called

SIRP (superpoints in RANSAC plane) is the main

contribution of this article because of being success-

ful, in particular, for challenging scenarios of explicit

three-dimensional structure of the data: The abso-

lute orientation of the planes, or vertical axis direc-

tion, is not supposed, and thus, invariance of SIRP

related to rotations is guaranteed. The superpoints

in planes are clustered and the corresponding points

may be (re)labeled interactively and clusterwise, in

order to correct gross errors or to generate training

data for more than two classes, if necessary. Given

the availability of training data, supervised classiﬁ-

cation approaches may be applied. For a fair com-

parison of their performance with SIRP and as an-

other, minor contribution of this article, we will con-

centrate on two important sets of rotational invariant

features: covariance-based features and those based

on point feature histograms. Additionally to these

features, we will marginally refer to those tailored to

the datasets or applications (source- and application-

dependent). The third important contribution is pre-

sented with post-processing using non-local optimiza-

tion on Markov Random Fields. In Section 4, the per-

formance of SIRP, source-independent features and

post-processing using non-local optimization will be

evaluated. Filtering out non-terrain points allows for

a context-aware surface reconstruction using Poisson

method, which will be presented as an example of an

application. Finally, in Section 5, we will summarize

our work and outline future research directions.

2 RELATED WORK

There is a large amount of methods on 3D point clas-

siﬁcation. Roughly, it was the tendency until 2005

to use rule-based approaches for separation, in par-

ticular, of terrain points from the off-terrain regions.

The pioneering work (Kraus and Pfeifer, 1998) for ex-

tracting ground surface in predominantly ﬂat terrain

presupposes an iterative procedure for robust plane

ﬁtting under the constraint that the off-terrain points

may lie far above but not far below the plane. Since

then, other contributions based on slope-based ﬁlter-

ing (Vosselman, 2000), progressive morphological ﬁl-

tering (Zhang et al., 2003) and hierarchical ﬁltering

(Mongus and

Zalik, 2012), as well as contour analysis

(Elmqvist et al., 2001), have been developed to obtain

the ground surface in non-ﬂat terrain as well. This

last method, brieﬂy summarized as a two-step proce-

dure consisting of ground point detection and surface

ﬁtting, can be considered as a state-of-the-art identi-

ﬁcation of ground in 2.5D data because, since then,

related works are striving to optimize the two steps to

make them less sensitive to outliers, sudden elevation

changes, etc. (Mousa et al., 2019; Perko et al., 2015).

However, both steps of this context will fail for pure

3D point clouds.

With more classes to be differentiated and with

the increasingly challenging scenarios, also the num-

ber of criteria, or features, for differentiation must in-

crease and the manually set thresholds have gradually

been replaced by those computed automatically from

the previously selected training data. In pure 3D point

clouds, using the features planarity, elevation, scat-

tering, and linear grouping has been proposed (La-

farge and Mallet, 2012), and one major concern here

is about the choice of the activation parameters σ for

each of these features. In (West et al., 2004), the

features based on the eigenvalues of the covariance

matrix (also called structure tensor) over the point’s

neighbors are introduced. The thus obtained features

are scale-, translation- and rotation-invariant. They

are used in (Gross and Thoennessen, 2006; Lalonde

et al., 2005; Weinmann, 2016) and other investiga-

tions in order to classify points from remote sensing

data with respect to their geometric saliency. With an

interest in theoretical bounds for neighborhood size

and shape, the results of experimentation with dif-

ferent neighborhood types are presented in (Wein-

mann, 2016; Weinmann et al., 2017): the involved

neighborhood types are given by the k nearest neigh-

bors (kNN), spherical neighborhoods and cylindrical

neighborhoods with varying values of k and varying

radii, while the cylinder height is set to inﬁnity. From

the eigenvector corresponding to the smallest eigen-

value, the information about the local normal vector

can be derived and, similarly, the distribution of the

normals within the neighborhood can be explored. In

(Rusu et al., 2009), angular differences between lo-

cal coordinate systems of pairs of neighboring points

are computed. For each pair of points, there are three

angles, and for a ﬁxed point with k neighbors, these

GRAPP 2020 - 15th International Conference on Computer Graphics Theory and Applications

differences are normalized according to the number

of neighbors and collected into three histograms. An

injective mapping from three integer numbers (bins)

into the one-dimensional index constitutes the com-

putation of Point Feature Histograms (PFHs). This

histogram has one peak in case of an approximately

planar surface point and a uniform distribution for

volumetric point clouds typical for trees.

As one can see from the survey in (Hana et al.,

2018), PFHs are not the only descriptors for point

clouds. This concept gives a hint that successive as-

sessing attributes of neighbors is a key to successful

machine understanding of data, even in challenging

scenarios, since it allows to capture context informa-

tion over considerable shapes. In 2D, this idea cul-

minated in approaches based on Convolutional Neu-

ral Networks. Nowadays, they are commonly applied

in 3D, among others, for classiﬁcation tasks. Cur-

rently, PointNet++ is the state-of-the-art tool for point

classiﬁcation and (Winiwarter et al., 2019) is the ex-

ample of application to remote sensing data. Here,

the visually impressive and quantitatively excellent

results are overshadowed by rather complex models

with many degrees of freedom, which in turn, require

an extensive training procedure, which may take long

for large-scale airborne laser scans.

One common observation of many recent works

is that the high number of 3D points and the point

density are not necessarily beneﬁcial. The vast ma-

jority of points can be actually classiﬁed by rather

simple methods (thresholding) and hence, computa-

tion of higher-level features negatively affects the per-

formance efﬁciency. In (Rusu et al., 2008), it is

shown how to determine “interesting” points, CNN-

based methods like (Qi et al., 2017) perform pool-

ing, while the subsampling of a given point cloud into

voxels is proposed in (Hackel et al., 2016). From a

scale pyramid created by repeatedly down-sampling

the point cloud, a small number of nearest neighbors

is used at each scale for feature computation. The dif-

ference of this inspiring approach to ours is that we

neither compute a kd-structure for setting the voxels

nor use a rigid grid (as e.g. done in (Von Hansen,

2006) for point cloud registration purposes), but em-

ploy a ﬂexible structure of superpoints in which points

are clustered using a ﬁxed tolerance value. For the

particular task of separation of vegetation from the

ground, whereby the ground is not supposed to rep-

resent a horizontal surface but can be vertical or ex-

plicitly three-dimensional, we present the SIRP pro-

cedure specially tailored to this task. Basically, it is a

valuable tool for extraction of training data serving as

the basis of a successive supervised classiﬁcation al-

gorithm, which is applied to the original point cloud.

3 METHODOLOGY

We start this section by describing two main ingre-

dients of the SIRP method, namely, superpoints and

dominant planes computed per superpoint. With these

information, we can easily take a decision for an in-

put point whether it belongs to the ground surface

or not (Section 3.3). Successively, we focus on fea-

ture extraction and describe the details of the super-

vised classiﬁcation, including non-local optimization

on Markov Random Fields. An overview about im-

plementation details concludes this section.

3.1 Superpoints

For acceleration of upcoming computations and re-

duction of data, we introduce the concept of ﬂexible

voxels or (3D) superpoints. The terminology may be

slightly misleading because, in the literature, and also

e.g. in the Point Cloud Library

, grouping takes place

using additional point features, such as Euclidean dis-

tance in normalized RGB space, while in our ap-

proach, feature computation takes place afterwards.

However, because of the functionality and because

such simpler features can be used at a later stage, we

will refer to superpoints from here on. This data struc-

ture allows identiﬁcation of clusters of points within a

pre-deﬁned tolerance ε and is, as we can see in Fig. 1,

left, more efﬁcient as a voxel structure because there

are normally more voxels containing points than su-

perpoints. A fast computation of the structure may

by achieved by the following strategy: It starts by

converting the points scaled by the inverse value of

ε into integers and an injective mapping to a single

non-negative integer keeping in memory the indices:

{x,y,z} → { ˆx, ˆy, ˆz} → j = R

ˆx + ˆy) + ˆz, (1)

where { ˆx, ˆy, ˆz} ∈ Z

+/0

ˆz = round(z/ε), ˆz = ˆz −min(ˆz),R

= max(ˆz)−min(ˆz),

and y and x are treated analogously. Then, sorting the

list and considering the differences of successive list

elements yields the break-points, between which the

list members of points belonging to the same super-

points are stored. Via the original indices, we ﬁnally

access the coordinates, from which we compute the

superpoints’ coordinates as centroids of voxels. In

the next step, we will compute the RANSAC plane

for the data points within a predeﬁned radius around

the centroid. The radius should be a multiple of the

voxel size ε, so that the signatures of vegetation be-

come clear. This is visualized in Fig. 1, middle.

http://pointclouds.org/documentation/tutorials/

supervoxel clustering.php

Superpoints in RANSAC Planes: A New Approach for Ground Surface Extraction Exempliﬁed on Point Classiﬁcation and Context-aware

Reconstruction

Figure 1: Overview of the procedure for ground surface ex-

traction. In the left image, we compare the traditional voxel

structure (Von Hansen, 2006) with our superpoints (cyan

circles). Middle: Computation of RANSAC planes for each

superpoint and clustering procedure, whereby outliers are

indicated by yellow circles. Right: back-projection to the

original point cloud (red color for inliers).

3.2 RANSAC-based Plane Computation

Random Sample Consensus (Fischler and Bolles,

1981) is a well-known method for model ﬁtting in

data with many outliers. Even though many modi-

ﬁcations of this method exist (Raguram et al., 2008),

we give a short description of our acceleration of this

method for the special case of plane ﬁtting in the sense

that it only contains matrix multiplications. Thus, it

can be efﬁciently run with software optimized for ma-

trix processing (e.g. MATLAB), parallelized or even

implemented on GPUs.

The input 3D point cloud has a homogeneous

representation X =

{

,1)

}

m=1

. Since three

points are required for a minimum sample for plane

computation, we consider U triplets of integer num-

bers T =

{

)

}

u=1

, where all a

, b

, and c

lie between 1 and M. Other sampling strategies, such

as random choice of the ﬁrst point followed by a

choice according to normal distribution for the two

remaining points, are possible, too. We deﬁne by

{i}

(T ),i = {1, ...,4} a U-tupil of 3 × 3 matrices. Its

columns correspond to the triplets of indexes in T and

their rows to X in which the i-th row has been omitted.

The computation of 4 ×U determinants (e.g., i = 4)

det



{4}



= x

− x

+ ... − x

(2)

is carried out simultaneously by element-wise multi-

plications and yields U plane hypotheses equations

= (−1)

det



{i}



, (3)

which are stored in a U ×4 matrix Π with Π

u,i

= p

(u)

from (3) and normalized normal vector. In order to

have a ﬁxed number of hypotheses, U must be chosen

higher than this number. The degenerated conﬁgura-

tions can be ﬁltered out easily since they yield p

= 0

for i = 1,...,4. In certain situations, additional ﬁlter-

ing is performed with respect to the slope of the plane

| to discard nearly vertical surfaces. The U × M

matrix R

contains the residuals R thresholded by the

tolerance t:

R = Π · X → R

= R < t. (4)

This yields the number of inliers (column-wise sum

of R

) for all planes, and, therefore, the plane with the

highest number of inliers. Thus, RANSAC is now im-

plemented as a ﬁltering procedure and multiplication

of two matrices. The output of this step is the infor-

mation whether the superpoint lies in its own plane or,

in other words, is part of the terrain. The remaining

superpoints are removed.

3.3 Cluster Analysis and

Back-propagation to the Point

Cloud

The goal of the previous step was to remove the mid-

dle and lower vegetation layers. The problem are the

tree canopies which may often be approximated by

planes. By considering clusters over remaining super-

points and suppressing clusters with less than 1000

members, we get rid of these superpoints as well.

Here, the number 1000 corresponds to the size of the

largest non-terrain objects divided by the voxel size ε.

Finally, the input point cloud is analyzed by con-

sidering the plane p = [v − n

v] through the super-

point v. The normal vector n

of p is obtained from

the covariance matrix (Weinmann, 2016) of a small,

ﬁxed number of points in the cloud which are neigh-

bors of v, whereby the trade-off should be made be-

tween a better localization of the points and indepen-

dence on the local density of points. The third eigen-

value λ

is the measure of the local dispersion of this

plane. From a data point x, we search for the nearest

superpoints within a spherical neighborhood around

v and denote their number by N, whereby N ≤ 8 to

provide the analogy with image pixels. Each of these

superpoints has its own plane p

and we record the

number J of planes p of which x is an inlier (see Fig. 1

right). A point x is classiﬁed as terrain if and only if

J := # (d(x, p

) < t) > λ

· N. (5)

The best way to interpret this equation is to reﬂect a

borderline scenario. Is p the plane computed from an

absolutely planar point subset, then λ

= 0. In this

case, it is sufﬁcient for a point x in the superpoint

merely to be the inlier of its own plane (p) because

the left hand side of (5) will be at least 1.

Using (5), we separate the terrain from non-terrain

objects (in particular vegetation) without the need for

training data. However, in case of multi-class prob-

lems, we need to specify training data labels, a feature

set, and a classiﬁer. Since the availability of training

data depends on the dataset, we postpone this aspect

GRAPP 2020 - 15th International Conference on Computer Graphics Theory and Applications

until the results section and focus on the features and

learning algorithm in the remainder of this section.

3.4 Feature Extraction

There are two groups of generic features considered

in this work. On the one hand, the eight covariance-

based features are derived from the structure tensor,

already mentioned in Section 2: planarity, omnivari-

ance, linearity, scattering, anisotropy, eigenentropy,

curvature change, and sum of the eigenvalues (see

(Weinmann, 2016) for more details). These features

may be computed for different radii of the spheri-

cal/cylindrical neighborhood or number of neighbors

resulting from the kNN algorithm. On the other hand,

the Fast Point Feature Histograms (FPFHs) (Rusu

et al., 2009) yield 33 (alternative or additional) fea-

tures. They are known to be widely invariant to

changes of search radii and can be computed in lin-

ear time with respect to both the number of points in

the list and the neighborhood size. This is the big

difference to the originally implemented PFHs (Rusu

et al., 2008), where the dependence on the neighbor-

hood size is quadratic. Besides, we used multicore

processing in order to further accelerate the compu-

tations. Moreover, the points must be normalized to

have their centroid in the origin of the coordinate sys-

tem. It remains to note that the cardinality of point

neighbors required for computation of (F)PFHs must

not be smaller than that required for normal vector

computation. The dependence of the results and run-

time on different conﬁgurations of features will be

subject of evaluation.

Classiﬁcation can be greatly improved if the prop-

erties of the underlying data are taken into account.

With available pulse number, intensities, and their dis-

tributions over neighborhoods in laser point clouds

as well as color values of points for results of pho-

togrammetric reconstruction, very valuable informa-

tion is given. In case of available color values, we nor-

malize them to have the unity L

-norm ([R,G, B] →

[R,G, B]/(R + G + B)), which allows for a better per-

formance in shadow regions (Weinmann and Wein-

mann, 2018). Besides, signed vertical distances of a

point to the 2.5D DTM surface computed by a state-

of-the-art method (Bulatov et al., 2012) provide large

values for overhanging points and medium values for

vegetation points.

3.5 Learning and Post-processing

Some of the features considered so far may be redun-

dant or even irrelevant for a particular classiﬁcation

task. Ideally, the applied classiﬁer should ignore these

features internally and show robust performance, even

if there is a moderate proportion of such bad features.

We use the Random Forest classiﬁer (Breiman, 2001)

allowing the estimation of out-of-bag features. An ad-

ditional advantage of this classiﬁer is that it is proba-

bilistic. This means that it outputs the probability of

a 3D point x to belong to a class l(x). This probabil-

ity P(l) corresponds to the percentage of trees in the

Random Forest voting for either class.

In the literature, it is popular to introduce a

smoothness prior that neighboring instances should

be encouraged to have the same labels. By interpret-

ing the instances as random variables on a Markov

Random Field (MRF), an energy function

E =

∑





−log P (l(x)) + λ

∑

y∈N (x)

(l(x ) 6= l(y))





(6)

is efﬁciently minimized using e.g. graph cuts (Boykov

et al., 2001), whereby we chose the alpha-expansion

algorithm available online (Delong et al., 2012). Note

that because of the two-class problem and a trivial

smoothness function, the result of the non-local op-

timization is the global minimum. The inﬂuence of

the smoothness parameter λ and the neighborhood N

will be addressed in the results section.

3.6 Implementation Details

In this section, we will refer to the choice of parame-

ter values. Some of them were mentioned in Sections

3.1-3.5 and remained ﬁxed for both datasets of the re-

sults section. The voxel density ε depends on the size

of the smallest object to be detected and on the ex-

tension of the terrain that constitutes approximately a

plane. If ε is too small, then the terrain points will

be very scarce and if it is too large, then low vegeta-

tion, in particular, pasture may be excessively added.

Still, the choice of this parameter may deviate up to

20% with respect to the default value. We worked

with ε = 1 m and ε = 0.2 m for both point clouds –

the LiDAR-based respectively photogrammetric one

– which will be presented next. Surprisingly, not even

the computing time is dramatically dependent on this

parameter: With a larger ε, less superpoints must be

evaluated, on the one hand. On the other hand, they

contain more points, and since the value of U (number

of triplets in Section 3.2) corresponds to the number

of points, more time is needed. The RANSAC thresh-

old t was computed analytically depending on the su-

perpoint size and origin of the point cloud. It cor-

responds roughly to ε/2 while the radius for search

of points for RANSAC was 8ε. The clustering dis-

tance factor depends on the similarity of classes; val-

ues around 2ε are a good choice in our datasets, while

Superpoints in RANSAC Planes: A New Approach for Ground Surface Extraction Exempliﬁed on Point Classiﬁcation and Context-aware

Reconstruction

the cluster cardinality is supposed to rule out outliers.

Its value represents the trade-off between the size of

possible off-terrain objects (density of tree crowns)

and sudden changes of steepness of the terrain. As

a rule of thumb, if classes are badly separated, like

for photogrammetric point clouds because of over-

smoothing, one should tend to lower values of clus-

ter distances in order to prevent points from different

classes to lie in the same cluster. For well-separable

points, one could set the threshold for cluster distance

high. To compute the ﬁnal plane, we used points in

the range of 2ε in the default case of nearest neighbors

in singular cases (isolated cluster center); the plane-

damping factor depends on the noise level. It should

be set to a higher value if parts of the terrain are less

likely to be approximated by a plane (stones on the

ground), or if less accurate points were produced by

the photogrammetric reconstruction. The number of

decision trees in Random Forests was set to 20 in all

experiments to guarantee relatively fast computation

with equal initial conditions for all experiments.

4 RESULTS

4.1 Datasets

The ﬁrst discussed dataset is a point cloud obtained by

an airborne laser scan from an Alpine area in Southern

Germany. The main application here was the creation

of a photo-realistic database, which is usable for train-

ing and education in areas of disaster management

and other quick response applications (H

aufel et al.,

2017). An interesting detail of this dataset, denoted

here and further as Oberjettenberg (as a neighboring

settlement is called), is that a 3D overhang does not

allow to describe the elevation z as a function of x and

y. Even though, according to the data provider, the

point density was 5 to 15 points per m

(while there

were some 81 millions of points in total), it varied

strongly from 10 to 100 responses; and, as Fig. 2, top,

shows, the regions belonging to the chinks and gorges

of the overhang are sparsely covered. To provide sur-

face reconstruction from an unorganized point cloud

(see e.g. (Guo et al., 2018) and references therein), it

is important to clean it from the points belonging to

trees. Around the overhang, deviations of growth di-

rections of trees from the vertical direction are almost

arbitrary, contrary to what we are used to in urban

scenery.

Our second dataset focuses on the medieval wall

surrounding the center of Gubbio, a town in Cen-

tral Italy. The point cloud was obtained by a pho-

togrammetric reconstruction from a sequence of high-

Figure 2: Input point clouds for Oberjettenberg (top) and

Gubbio (bottom).

resolution daylight images. These images had been

captured from the ground and via an unmanned aerial

vehicle, and 3D reconstruction wass performed inde-

pendently from both groups of imagery by means of a

commercial software

. This was followed by interac-

tively transforming the individual reconstructions into

a common coordinate system. The relevant proper-

ties of this point cloud were: cardinality around 58

million and density about 3700 points/m

. The over-

reaching objective of the project was developing au-

tomatic algorithms for monitoring and preservation of

cultural heritage while an important intermediate goal

was to retrieve highly compressed and still very de-

tailed 3D models of the object of interest, as in the

case of Gubbio wall, for monitoring its state (Car-

valho et al., 2018). Therefore, our idea was to iden-

tify vegetation points and to either remove them or to

replace them by generic models of trees, bushes, and

grass areas. For the details about of the project and, in

particular, data acquisition and pre-processing of the

Gubbio dataset, we refer to (Bulatov et al., 2018; Car-

valho et al., 2018). Here, the challenge is to retrieve

the vertical (walls) and even real 3D structures (due

to erosion), keeping in mind that 3D point clouds re-

trieved from passive sensors are sometimes noisy and

sometimes oversmoothed in areas of repetitive pat-

https://www.agisoft.com/

GRAPP 2020 - 15th International Conference on Computer Graphics Theory and Applications

Figure 3: Input data: Oberjettenberg (top) and Gubbio (bottom). In the middle, a detailed view on the rock is shown (Oberjet-

tenberg). The vegetation points are denoted in green (top left) and blue color (bottom left) and removed in the right images.

terns, occlusions, and weak textures. The positive as-

pect, which we intend to exploit, is that RGB values

are available for points together with their XYZ coor-

dinates, as Fig. 2, bottom, shows.

4.2 Ground Surface Filtering

We start by presenting qualitative results for the al-

gorithm based on superpoints. In Fig. 3, we can see

the visually successful ﬁltering result. Most trees and

bushes visible on the left have been ﬁltered out while

the density of points in non-vegetation regions re-

mains approximately the same. In the middle frag-

ment, it seems that from the abundant forest on the

mountain slope, only one single tree trunk remains.

What happens with a small alpine hut in the top im-

age is certainly worth discussion: the lower parts of

it (those which have contact with the ground) remain

while the higher parts have been ﬁltered away: In our

model assumption, there are no other points as terrain

or vegetation. In the Gubbio dataset, it is clear that

some tufts of grass on the wall remain since intensity

was not used for ﬁltering.

For quantitative results, we had to cope with the

fact that both datasets, Oberjettenberg and Gubbio,

are lacking the ground truth. One obvious strategy,

which is chosen in the scope of this work, is to select

a fragment of the data, consisting of some 325 and

500 thousands points, and to create the ground truth

by ourselves, using a (couple of) very salient char-

acteristics of the point cloud followed by an exten-

sive manual relabeling. In order to avoid correlation-

based falsiﬁcation of results, these salient character-

istics should ideally not have much in common with

our methodology based on superpoints. Thus, we re-

lied on dataset-speciﬁc features presented at the end

of Section 3.4: Distance to the DTM (Bulatov et al.,

2012) for the ﬁrst dataset and spectral indices of RGB

values of 3D points were thus selected.

Tables 1 and 2 reveal that the proposed method

allows to obtain good, plausible, and well-balanced

results. In particular, for the Oberjettenberg dataset,

the accuracy is quite high because a lion’s share of

points belong to the class terrain. As a source for er-

rors, we identiﬁed trenches: these are points lying be-

low the plane proposed by RANSAC. In the Gubbio

dataset, porosity and erosion of the wall rock, being

two important aspects why the whole project was in-

stituted, is one of reasons why the algorithm struggles

in its performance. The most important reason, how-

ever, are biases the point cloud itself brings about: as

a result of the photogrammetric procedure for dense

Superpoints in RANSAC Planes: A New Approach for Ground Surface Extraction Exempliﬁed on Point Classiﬁcation and Context-aware

Reconstruction

Table 1: Quantitative results of SIRP for the Oberjettenberg

dataset. Bottom right entry: Overall accuracy (in %). Right

column and bottom row: percentages for precision and re-

call; other entries correspond to the numbers of points. Ter.

= terrain.

True/pred Ter. Non-ter. Total Prec.

Ter. 265867 124 265991 100.0

Non-ter. 4112 55033 59145 93.0

Total 269979 55157 325136 -

Recall 98.5 99.8 - 98.7

Table 2: Quantitative results of SIRP for the Gubbio dataset.

Please refer to Table 1 for additional explanations.

True/pred Ter. Non-ter. Total Prec.

Ter. 131714 7711 139425 94.5

Non-ter. 106091 245768 351859 69.8

Total 237805 253479 491284 -

Recall 55.4 97.0 - 76.9

reconstruction, tree crowns tend to be approximated

by a smooth surface, similar to ground and wall.

4.3 Point Classiﬁcation

The point sets selected for evaluation in the previ-

ous section were subdivided to nearly equal parts into

training and validation set. The training data was bal-

anced to a relationship not exceeding 2:1. For quali-

tative evaluation, we colored the points of any of the

four categories by a separate color in Fig. 4. For the

Oberjettenberg dataset, we see that, despite of over-

all plausible results, covariance-based classiﬁcation

leads to more points along the mountain slope that

were spuriously classiﬁed as vegetation. For FPFHs,

points atop of the trees are sometimes assigned to

a wrong class. Fortunately, the wrongly classiﬁed

points lie mostly isolated, and thus one can expect that

using neighborhood relations (MRFs), we can easily

correct their labels. Different is the situation for the

Gubbio dataset, where the wrongly classiﬁed points

build clusters. They are visible on the margin of the

dataset as well as in the regions bordering classes.

But also here, it is clearly visible that FPFHs perform

much better than covariance-based features.

As for quantitative evaluation, we derived the

numbers of true/false positives/negatives and, consis-

tently, the usual metrics like precision, recall, and

overall accuracy. It could be conﬁrmed that the Gub-

bio dataset is much more complicated than the Ober-

jettenberg dataset. While for the latter, the most fa-

vorable parameters of FPFH features yield an over-

all accuracy of 94.6%, it was only around 81.5% for

the former. Analogously, for covariance-based fea-

tures, the difference between some 93% and 77.2% is

considerable as well. With respect to parameter set-

tings of single sets of the features, most of the ﬁnd-

ings of (Weinmann, 2016) and (Rusu et al., 2009)

are conﬁrmed. kNN with larger neighborhoods usu-

ally performs slightly faster than using radius search

and the quantitative results are comparable; only in

the qualitative results, misclassiﬁcations tend to lie

more in clusters and are therefore better visible. In-

teresting is the combination of covariance-based and

FPFH-based features. The results become more sta-

ble (around 95% overall accuracy for Oberjettenberg

and 82% for Gubbio), even though the combination

covariance-based + kNN + small neighborhoods is

non-conductive for the Gubbio dataset. As for includ-

ing dataset-speciﬁc features into the conﬁgurations,

they helped creating the ground truth and are there-

fore biased. Already local results exhibit a value of

overall accuracy exceeding 95% and thus we exclude

these conﬁgurations from the subsequent analysis of

non-local optimization with MRFs.

Considering the quantitative results for MRFs, we

decided to seek answers for two questions: First,

for the parameter set leading to the so far best lo-

cal result (FPFH features with kNNs and 500 neigh-

bors), how much performance improvement can still

be achieved? Second, for a conﬁguration leading to

a fair result (covariance-based features), to what ex-

tent MRFs can help to improve it? In Fig. 5, we note

a somehow similar performance for both datasets and

conﬁgurations. The overall accuracy increases until a

certain point and then it decreases or stagnates with

some ﬂuctuations caused, probably, by randomness

of methods and inaccuracies of training data. The de-

crease is even much more visible and signiﬁcant if the

overall accuracy is replaced by the Cohen κ coefﬁ-

cient, which considers the fact that the classes are not

necessarily well-balanced. Even though the curves do

not differ strongly in their courses, we can see that

the results for the Oberjettenberg dataset remain bet-

ter for all values of λ than for the Gubbio dataset.

More speciﬁcally, for the Gubbio dataset, covariance-

based features are not sufﬁcient, and even the best im-

provement with MRFs does not reach the quality of

the local result with FPFHs, but is approximately 5%

lower. For the Oberjettenberg dataset, however, ap-

plying MRFs to the covariance-based features, which

are simpler as well as easier to compute and to in-

terpret than FPFHs, leads to almost the same result

even though that of local conﬁguration is four per-

cent points below. Thus, a good performance of the

tried-and-true MRFs with a negligible runtime and

with quite a few parameters to determine (λ and N ) is

an encouraging fact. Two reasons why the improve-

ment of the FPFH result is not that signiﬁcant are:

the point neighborhoods are already extensively taken

GRAPP 2020 - 15th International Conference on Computer Graphics Theory and Applications

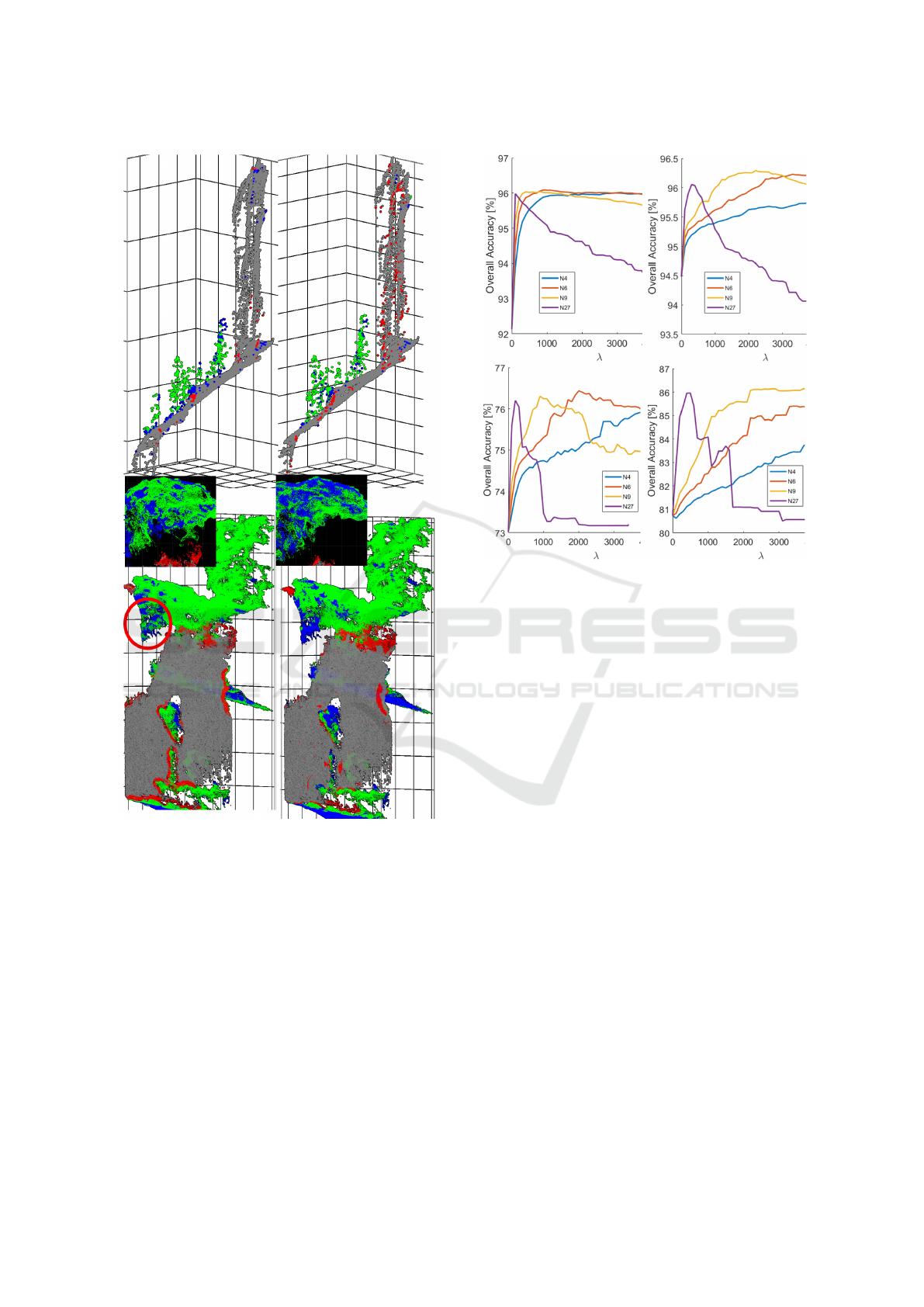
Figure 4: Qualitative classiﬁcation results for fragments of

datasets Oberjettenberg (top row) and Gubbio (bottom row)

using FPFHs and covariance-based features (left and right

images, respectively). By gray and green points, we de-

noted the correctly classiﬁed parts of the terrain (wall in the

case of Gubbio) and vegetation. Blue are points spuriously

classiﬁed as terrain and red as vegetation. Middle: a more

detailed view of the tree crown over the Gubbio city wall

(as indicated by the red circumference).

into account and the smoothness prior is less sophis-

ticated. Analogously, if more neighbors (N from (6))

are taken into account, the decay will be faster, as the

violet curves in all images show.

Figure 5: Results for MRF-based classiﬁcation (Oberjetten-

berg (top) and Gubbio (bottom)) for different feature sets

(left: covariance-based features, right: FPFHs), and differ-

ent neighborhood sizes (colors of the curves with N denot-

ing the number of neighbors). In all curves, overall accuracy

as a function of smoothness parameter λ is shown.

4.4 Application: Surface

Reconstruction

As a possible application, we considered surface re-

construction from points by means of the state-of-the-

art procedure (Kazhdan et al., 2006) and representa-

tion of the surface in different spectral ranges. In the

visualization of Fig. 6, the overhang looks impres-

sively and the 3D character of the point cloud is obvi-

ous. Using an advanced renderer (Feldmann, 2015),

bottom, we believe that the goal of photo-realistic rep-

resentation of this part of the data was achieved. Once

vegetation points have been ﬁltered out, computation

of oriented normal vector ﬁeld and iso-surface extrac-

tion are relatively robust. The size of the cleaned

point cloud yields 4.4 millions faces while the original

mesh has 5.5 millions faces (almost 26% more) and it

is clear from Fig. 6 that, if we compress point clouds

by means of a mesh decimation algorithm, the image

on the right will be by far more appealing and accu-

rate than that on the left, because it is smoother and

no faces connecting different trees will be built. For

Gubbio (compression factor 30%), the cleaned point

cloud probably looks less appealing than the colored

Superpoints in RANSAC Planes: A New Approach for Ground Surface Extraction Exempliﬁed on Point Classiﬁcation and Context-aware

Reconstruction

one in Fig. 2, bottom. However, this has probably less

to do with aforementioned problems than with the fact

that texturing was not in the scope of this work.

4.5 Computing Times

The method for superpoint-based ground surface ﬁl-

tering is able to process some 6700/7800 points or,

alternatively, 450/53 superpoints (in case of Oberjet-

tenberg/Gubbio) per second. For this, a MATLAB

implementation on a server was used, whereby some

acceleration took place for RANSAC (as described in

Section 3.2). Surprisingly, this was almost that fast

than for 5-core FPFHs using a C++ implementation

in the Point Cloud Library employed for feature com-

putation, for which we recorded some 8200 points/s

and which allowed feature collection in less than one

minute for the test point cloud consisting of almost

500,000 points. We can conclude that a single core

implementation would need some 5 minutes. Other

feature sets are more computationally expensive: For

PFHs, the computation time explodes quadratically

with the neighborhood size while the performance

was roughly the same (factor 36 for kNN of a neigh-

borhood size of 150). Even the covariance-based fea-

tures needed longer using a single-core neighborhood

computation (factor of speed 0.47 for small and 1.4

for large neighborhoods). Classiﬁcation (tree bag-

ging) and non-local optimization (on MRFs) require

negligible time. Bearing the application of surface re-

construction in mind, the pipeline including ground

surface extraction using our method and point classi-

ﬁcation using multi-core FPFHs needs negligible time

in comparison with Poisson reconstruction (Kazhdan

et al., 2006) and should therefore be carried out in

order to guarantee an acceptable input for this com-

putationally expensive method.

4.6 Concluding Remarks on

Comparison with Other Approaches

One should always be cautious while comparing the

results of different approaches applied to different

datasets, because one is always a bit more difﬁcult

than another. Even within our datasets, we cannot

completely be sure that the manually created ground

truth is good enough. Assuming that there are few

errors in the reference, the most interesting insight

of our work is that, at least for the LiDAR dataset,

the proposed method, which does not need any train-

ing points, outperforms the rotation-invariant feature

sets used for supervised classiﬁcation. Taking into ac-

count quite comparable computation times, the bene-

ﬁt of SIRP is evident. For the second dataset, its per-

formance is slightly worse than that of FPFHs (76.9%

in Table 2 vs. 81 to 87 % in Fig. 5, bottom right). At

least, the covariance-based features could be left be-

hind (Fig. 5, bottom left). The fact that SIRP does not

need any training data is beneﬁcial for the alternative

evaluation strategy: To run it – with the same param-

eters – on a less challenging dataset, however, with

labeled ground truth. This strategy is currently being

implemented. Finally, one of the newest approaches

on CNN-based multi-class semantic segmentation on

airborne remote sensing data (Winiwarter et al., 2019)

has produced the results of roughly the same order of

magnitude.

5 DISCUSSION AND OUTLOOK

We start this section with the critical discussion about

the newly presented SIRP method. It basically relies

on the fact that the terrain is locally planar whereby

plane orientation is of secondary importance. The

size of the inﬁnitesimal planar patch is given by the

superpoint while the plane search is accomplished by

a smart, loopless implementation of the RANSAC

procedure. On the one hand, generalizing this method

for second degree surfaces (conics) – in order to deal

with abrupt changes of terrain curvature and model-

ing tree shapes – would represent a mathematical-

theoretical challenge. On the other hand, RANSAC

already occupies the major resources of the comput-

ing time of SIRP even though, in the future, it can

be parallelized. Concerning the performance, we ob-

served a quite high overall accuracy given that we in-

tentionally worked with 3D information and did not

use intensity or knowledge about the z axis: SIRP is

widely rotation-invariant. We could say that SIRP,

in combination with other source- or application-

dependent features is a very suitable tool for extrac-

tion of ground truth. For a photogrammetric dataset,

RGB colors may provide a great alleviation. For the

Oberjettenberg dataset, where we already mentioned

the problem of trenches, one could allow more tol-

erance into the direction of superpoint interior. How-

ever, our RANSAC planes are not oriented and impos-

ing consistent orientation is a non-trivial task (Hoppe

et al., 1992). The clustering step is particularly help-

ful because it allows cutting away (possibly) large

parts of data assigned to a wrong class using an in-

teractive tool, such as Cloud Compare

Coming to the features, we could see that applica-

tion of covariance-based features, Fast Point Feature

Histograms, and Markov Random Fields is reason-

https://www.danielgm.net/cc/

GRAPP 2020 - 15th International Conference on Computer Graphics Theory and Applications

Figure 6: Surface reconstruction results from the original point cloud (left) and from the cleaned point cloud (right) for the

Oberjettenberg dataset (part of the data, top) and for the Gubbio dataset (middle). The mesh on the left is colored according to

the vertical distance to the mesh on the right, truncated by the maximum value of 30 m. Bottom: fragments of photo-realistic

representations of Oberjettenberg and Gubbio datasets (left and right, respectively) using a path-tracer (Feldmann, 2015),

(courtesy of Eva Burkard).

able, however, the impacts are different. Covariance-

based features are easier to interpret and to compute,

but FPFHs are faster and better. It is worth men-

tioning that, after post-processing, the performance of

covariance-based features is quite comparable to that

of FPFHs in the case of laser point clouds. For pho-

togrammetric point clouds, there is still a gap in the

performance. Also, we saw that for a high number

Superpoints in RANSAC Planes: A New Approach for Ground Surface Extraction Exempliﬁed on Point Classiﬁcation and Context-aware

Reconstruction

of neighbors, MRFs have not contributed to an im-

provement. Here, their replacement with Conditional

Random Fields, which additionally take into account

the strength of inferences, may help. Finally, it must

be mentioned that feature sets and MRFs are appli-

cable to multi-class problems as well. Testing their

performance is clearly a subject of our future work.

ACKNOWLEDGEMENTS

We wish to thank all those people who made avail-

able for public the software for: (F)PFH (Point Cloud

Library), Graph Cuts on MRFs (Delong et al., 2012),

and interactive point clouds processing (Cloud Com-

pare). We also thank Ms. Eva Burkard (IOSB) for

visualizing the 3D meshes in the path-tracer.

REFERENCES

Boykov, Y., Veksler, O., and Zabih, R. (2001). Fast ap-

proximate energy minimization via graph cuts. IEEE

Transactions on Pattern Analysis and Machine Intel-

ligence, 23(11):1222–1239.

Breiman, L. (2001). Random forests. Machine Learning,

45(1):5–32.

Bulatov, D., Lucks, L., Moßgraber, J., Pohl, M., Solbrig,

P., Murchio, G., and Padeletti, G. (2018). HERA-

CLES: EU-backed multinational project on cultural

heritage preservation. In Earth Resources and Envi-

ronmental Remote Sensing/GIS Applications IX, vol-

ume 10790, pages 78–87. International Society for

Optics and Photonics.

Bulatov, D., Wernerus, P., and Gross, H. (2012). On ap-

plications of sequential multi-view dense reconstruc-

tion from aerial images. In Proceedings of the Inter-

national Conference on Pattern Recognition Applica-

tions and Methods, pages 275–280.

Carvalho, F., Lopes, A., Curulli, A., da Silva, T., Lima, M.,

Montesperelli, G., Ronca, S., Padeletti, G., and Veiga,

J. (2018). The case study of the medieval town walls

of Gubbio in Italy: ﬁrst results on the characterization

of mortars and binders. Heritage, 1(2):468–478.

Delong, A., Osokin, A., Isack, H. N., and Boykov, Y.

(2012). Fast approximate energy minimization with

label costs. International Journal of Computer Vision,

96(1):1–27.

Elmqvist, M., Jungert, E., Lantz, F., Persson, A., and

oderman, U. (2001). Terrain modelling and analy-

sis using laser scanner data. International Archives

of the Photogrammetry, Remote Sensing and Spatial

Information Sciences, 34(3/W4):219–226.

Evans, D. H., Fletcher, R. J., Pottier, C., Chevance, J.-B.,

Soutif, D., Tan, B. S., Im, S., Ea, D., Tin, T., Kim, S.,

et al. (2013). Uncovering archaeological landscapes

at angkor using lidar. Proceedings of the National

Academy of Sciences, 110(31):12595–12600.

Feldmann, D. (2015). Accelerated ray tracing using R-

trees. In International Joint Conference on Computer

Vision, Imaging and Computer Graphics Theory and

Applications, pages 247–257. INSTICC.

Fischler, M. A. and Bolles, R. C. (1981). Random sample

consensus: A paradigm for model ﬁtting with appli-

cations to image analysis and automated cartography.

Commun. ACM, 24(6):381–395.

Gross, H. and Thoennessen, U. (2006). Extraction of lines

from laser point clouds. International Archives of the

Photogrammetry, Remote Sensing and Spatial Infor-

mation Sciences, 36(3):86–91.

Guo, X., Xiao, J., and Wang, Y. (2018). A survey on al-

gorithms of hole ﬁlling in 3D surface reconstruction.

The Visual Computer, 34(1):93–103.

Hackel, T., Wegner, J. D., and Schindler, K. (2016). Fast se-

mantic segmentation of 3D point clouds with strongly

varying density. ISPRS Annals of the Photogramme-

try, Remote Sensing and Spatial Information Sciences,

3(3):177–184.

Hana, X.-F., Jin, J. S., Xie, J., Wang, M.-J., and Jiang, W.

(2018). A comprehensive review of 3d point cloud

descriptors. arXiv preprint arXiv:1802.02297.

aufel, G., Bulatov, D., and Solbrig, P. (2017). Sensor data

fusion for textured reconstruction and virtual repre-

sentation of alpine scenes. In Earth Resources and

Environmental Remote Sensing/GIS Applications VIII,

volume 10428, pages 33–46.

Hoppe, H., DeRose, T., Duchamp, T., McDonald, J., and

Stuetzle, W. (1992). Surface reconstruction from un-

organized points. ACM SIGGRAPH Computer Graph-

ics, 26(2):71–78.

Kazhdan, M., Bolitho, M., and Hoppe, H. (2006). Poisson

surface reconstruction. In Proceedings of the Fourth

Eurographics Symposium on Geometry Processing,

pages 61–70.

Kraus, K. and Pfeifer, N. (1998). Determination of terrain

models in wooded areas with airborne laser scanner

data. ISPRS Journal of Photogrammetry and Remote

Sensing, 53(4):193–203.

Lafarge, F. and Mallet, C. (2012). Creating large-scale city

models from 3D-point clouds: a robust approach with

hybrid representation. International Journal of Com-

puter Vision, 99(1):69–85.

Lalonde, J.-F., Unnikrishnan, R., Vandapel, N., and Hebert,

M. (2005). Scale selection for classiﬁcation of point-

sampled 3D surfaces. In Proceedings of the Fifth In-

ternational Conference on 3-D Digital Imaging and

Modeling (3DIM’05), pages 285–292. IEEE.

Mongus, D. and

Zalik, B. (2012). Parameter-free ground

ﬁltering of LiDAR data for automatic DTM genera-

tion. ISPRS Journal of Photogrammetry and Remote

Sensing, 67:1–12.

Mousa, Y. A., Helmholz, P., Belton, D., and Bulatov, D.

(2019). Building detection and regularisation using

DSM and imagery information. The Photogrammetric

Record, 34(165):85–107.

Perko, R., Raggam, H., Gutjahr, K., and Schardt, M. (2015).

Advanced DTM generation from very high resolution

GRAPP 2020 - 15th International Conference on Computer Graphics Theory and Applications

satellite stereo images. ISPRS Annals of the Pho-

togrammetry, Remote Sensing and Spatial Informa-

tion Sciences, 2(3/W4):165–172.

Qi, C. R., Yi, L., Su, H., and Guibas, L. J. (2017). Point-

Net++: Deep hierarchical feature learning on point

sets in a metric space. In Advances in Neural Infor-

mation Processing Systems, pages 5099–5108.

Raguram, R., Frahm, J.-M., and Pollefeys, M. (2008). A

comparative analysis of RANSAC techniques lead-

ing to adaptive real-time random sample consensus.

In Proceedings of the European Conference on Com-

puter Vision, pages 500–513. Springer.

Rusu, R. B., Blodow, N., and Beetz, M. (2009). Fast point

feature histograms (FPFH) for 3D registration. In

Proceedings of the 2009 IEEE International Confer-

ence on Robotics and Automation, pages 3212–3217.

IEEE.

Rusu, R. B., Marton, Z. C., Blodow, N., and Beetz, M.

(2008). Persistent point feature histograms for 3D

point clouds. In Proceedings of the 10th International

Conference on Intelligent Autonomous Systems, pages

119–128.

Von Hansen, W. (2006). Robust automatic marker-free

registration of terrestrial scan data. International

Archives of the Photogrammetry, Remote Sensing and

Spatial Information Sciences, 36(3):105–110.

Vosselman, G. (2000). Slope based ﬁltering of laser altime-

try data. International Archives of Photogrammetry

and Remote Sensing, 33(B3):935–942.

Weinmann, M. (2016). Reconstruction and Analysis of 3D

Scenes: From Irregularly Distributed 3D Points to

Object Classes. Springer International Publishing, 1st

edition.

Weinmann, M., Jutzi, B., Mallet, C., and Weinmann, M.

(2017). Geometric features and their relevance for

3D point cloud classiﬁcation. ISPRS Annals of the

Photogrammetry, Remote Sensing and Spatial Infor-

mation Sciences, 4(1/W1):157–164.

Weinmann, M. and Weinmann, M. (2018). Geospatial com-

puter vision based on multi-modal data – how valuable

is shape information for the extraction of semantic in-

formation? Remote Sensing, 10(1):2:1–2:20.

West, K. F., Webb, B. N., Lersch, J. R., Pothier, S., Triscari,

J. M., and Iverson, A. E. (2004). Context-driven auto-

mated target detection in 3D data. In Automatic Target

Recognition XIV, volume 5426, pages 133–144. Inter-

national Society for Optics and Photonics.

Winiwarter, L., Mandlburger, G., Pfeifer, N., and S

orgel, U.

(2019). Classiﬁcation of 3D point clouds using deep

neural networks. In Dreil

andertagung der DGPF, der

OVG und der SGPF, pages 663–674.

Zhang, K., Chen, S.-C., Whitman, D., Shyu, M.-L., Yan,

J., and Zhang, C. (2003). A progressive morphologi-

cal ﬁlter for removing nonground measurements from

airborne lidar data. IEEE Transactions on Geoscience

and Remote Sensing, 41(4):872–882.

Superpoints in RANSAC Planes: A New Approach for Ground Surface Extraction Exempliﬁed on Point Classiﬁcation and Context-aware

Reconstruction