Interrelations between Drug Prescriptions and Diagnoses for SHI

Diabetes Patients using Graph Theoretic Methods and a Markov Model

Reinhard Schuster

, Marc Heidbreder

, Timo Emcke

and Martin Schuster

Chair of Department of Health Economics, Epidemiology and Medical Informatics,

Medical Advisory Board of Statutory Health Insurance in Northern Germany (MDK), 23554 L

ubeck, Germany

Department of Health Economics, Epidemiology and Medical Informatics,

Medical Advisory Board of Statutory Health Insurance in Northern Germany (MDK), 23554 L

ubeck, Germany

Chair of Department of Prescription Analysis, Association of Statutory Health Insurance Physicians,

Bismarckallee 1-6, 23812 Bad Segeberg, Germany

Faculty of Epidemiology, Christian-Albrechts University Kiel, 24105 Kiel, Germany

Keywords:

Diabetes, Drugs, Diagnoses, Outpatient Treatment, SHI, Graph Communities, Manhattan Distance, ILP,

CPLEX, Markov Model.

Abstract:

We analyze large data sets of diabetes patients in order to get new insights into the dependencies between

drug groups and diagnoses using age, polypharmacy and multimorbidity as covariates. Diagnostic data using

the ICD-10 classiﬁcation are available with the resolution of quarters. For drugs the exact day of prescription

is available. The analysis uses all co-medication and all diagnoses of all physicians a patient has consulted

within a quarter and is thereby wider than the point of view related to a special physician. The communication

between physicians may be confounded by information deﬁcits due to informal self-diagnostics by the patients.

Differently specialized physicians may apply different guidelines which point to speciﬁc diseases. Interactions

between different drugs and different therapy schemes may lead to new diseases for multimorbid patients.

Large data sets create opportunities to detect such interactions. We use a graph theoretic approach with drug

groups as nodes. Using a diagnose vector edges are given by therapeutic neighborhood using the Manhattan

distance. A graph clustering determines drug groups for similarly sick patients which contains indirectly age

and multimorbidity. This can explain cost effects due to the degree of sickness. The graph clustering uses the

modularity method. The underlying algorithm leads to an integer linear program (ILP) which is in general NP-

hard. For the calculations we use Mathematica from Wolfram Research in combination with a python program

using CPLEX from IBM. Drug innovations may lead to changes in drug therapy. Therefore we compare the

steady state solution of the related Markov model with the status quo of drug prescription.

1 INTRODUCTION

In 2017, 425 million people were suffering from dia-

betes worldwide, risen up steadily from an estimated

382 million people in 2013, cf. (International Dia-

betes Federation, 2017), (Shi and Hu, 2014), (World

Health Organization, 2016). Diabetes mellitus crea-

tes a signiﬁcant clinical and economic burden on so-

ciety, cf. (Songer et al., 1998), (American Diabetes

Association, 1998), (Klein, 2007). Given those num-

bers and economic effects, improving care for patients

with diabetes mellitus has become a priority to natio-

nal health plans, payers, and patients in many coun-

tries. The number and complexity of services requi-

red to manage such patients in accord with the ac-

cepted guidelines chose diabetes mellitus to become

the target of multiple disease management efforts and

initiatives, as well in the ﬁelds of professional edu-

cation as in case management. In the present analy-

sis comorbidities for diabetic patients and their re-

lation to the drugs prescribed are considered using

the ICD-10- (International Statistical Classiﬁcation

of Diseases and Related Health Problems 10th Re-

vision) and ATC-classiﬁcations (Anatomic Therapeu-

tic Chemical). We consider how the related diagno-

ses differ with respect to different antidiabetic drugs

at ATC 5th level (Chemical substance). On the one

hand the drug treatment quality depends on the dia-

Schuster, R., Heidbreder, M., Emcke, T. and Schuster, M.

Interrelations between Drug Prescriptions and Diagnoses for SHI Diabetes Patients using Graph Theoretic Methods and a Markov Model.

DOI: 10.5220/0008911603450352

In Proceedings of the 13th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2020) - Volume 5: HEALTHINF, pages 345-352

ISBN: 978-989-758-398-8; ISSN: 2184-4305

345

gnoses related national and international guidelines.

On the other hand one has to pay attention to aspects

of drug prescription efﬁciency is of crucial importan-

ce. Both result in management tools for the statutory

health insurance like regional target agreements. Mo-

dels should help to ﬁnd optimal solutions with respect

to both aspects. The considered drugs are taken as no-

des of a graph and edges are given by the most equal

diagnostic structure. Starting with the local neighbor-

hood, we get a global graph structure and analyze cha-

racteristics such as graph center or graph periphery

and the graph community structure, cf. (Schuster and

Emcke, 2018). Multimorbidity and polypharmacy are

major problems in elderly patients. On average, pati-

ents above 70 years of age have drugs from more than

seven drug groups at 3rd ATC level (four digits) ad-

ministrated as a daily regime. We analyze the change

of the prescriptions from one quarter to the next by a

Markov Model in order get information about the sta-

bility of the present medication in 2018 and compare

the years 2013 and 2018 with respect to the patients

age and sex.

2 MATERIAL AND METHODS

We analyze all treatments and prescriptions of phy-

sicians for patients of the statutory health insurance

(SHI) by SHI physicians in Schleswig-Holstein, an

administration district in northern Germany (Bundes-

land). Thereby, we compare treatment and prescrip-

tion data from the ﬁrst and second quarter of 2018

(two successive quarters with respect to the Markov

model) and the second quarter of 2013 in order to

get a ﬁve year comparison. The analysis is patient-

centered, meaning that the datasets of all treatments

and prescriptions of all physicians regarding an in-

dividual patient are used. The dataset of the second

quarter of 2018 covers 1,690,683 patients with dia-

gnoses and 1,383,489 patients with drug prescripti-

ons using a pseudonymized patient identity with age

and sex informations. We utilize the three-character

level of the International Statistical Classiﬁcation of

Diseases and Related Health Problems [ICD]. The sa-

me diagnoses for the same patient by different phy-

sicians are not counted repeatedly. For the prescrip-

tion analysis the International Anatomic Therapeu-

tic Chemical (ATC) classiﬁcation system with Ger-

man speciﬁcations provided by the German Institute

of Medical Documentation and Information (DIMDI)

is used. As antidiabetic drugs, we deﬁne the drugs of

the ATC drug groups A10A (insulins and analogues)

and A10B (blood glucose lowering drugs, excl. insu-

lins). There are 208,265 patients with diabetes E10-

E14 (Diabetes mellitus) or O24 (Diabetes mellitus in

pregnancy) and 131,296 patients of 65 years of age

and older among them. Thereby the diabetes preva-

lence regarding all patients within the statutory health

insurance and diagnosed with diabetes is 8.4 % and

the rate of persons insured beneﬁtting from antidiabe-

tic drug therapy is 4.7 %, respectively. For persons of

65 years of age and older, we obtain prevalence values

of 23.5 % regarding diagnoses and 18.3 % regarding

antidiabetic drug therapy. For each drug d by ATC 5th

level we consider which fraction of patients has cer-

tain diagnoses (ICD at the three digit level). Thereby

we get an n-dimensional vector v

(n the number of

diagnoses) and a Manhatten distance of two such vec-

tors. We use drugs d by ATC 5th level(7 digits) as

vertices of a graph. With respect to each drug d we

can select m=1, 2, 3 other drug(s) at that ATC 5th le-

vel with smallest distance and get the top 1 to top 3

directed graphs with edges determined by that distan-

ce neighborhood and the induced undirected graphs

G. For these graphs we construct graph communities

using the modularity method. This is done by an ILP

(integer linear program) which is NP-hard. A related

LP (linear program) can be solved in polynomial time

and ﬁnally we have to apply a post-processing step:

the rounding of the LP to an ILP result, cf. (Shinano

et al., 2003), (Newman, 2006), (Agarwal and Kem-

pe, 2008). Further graph characteristics are the ver-

tex eccentricity which gives the length of the longest

shortest path from the source u to every other vertex

v in the graph G, the graph periphery gives vertices

that are maximally distant to at least one vertex in the

graph G and the graph center gives the set of verti-

ces with minimum eccentricity in the graph G. If we

use transition coefﬁcients for the change of antidia-

betic drugs of patients from one quarter the next, we

obtain a Markov model. We solve the related eigenva-

lue problem for the resulting 32-dimensional matrix.

We look for an eigenvector of a maximal eigenvalue

with components of the same sign in order to get a

stable solution, which we can compare with the pre-

sent fractions of antidiabetic drugs. These drugs will

be considered in relation to patients’ diagnoses, age,

multimorbidity and polypharmacy.

3 RESULTS

36.8 % of the diabetes patients with drug therapy are

treated with metformin having average drug costs of

18.73 Euro per quarter (2nd quarter of 2018). 41.6

% of the patients are treated with cost rising up to

50.00 Euros using glibenclamide (A10BB01), metfor-

min (A10BA02), glimepiride (A10BB12), gliquidone

HEALTHINF 2020 - 13th International Conference on Health Informatics

346

(A10BB08) and gliclazide (A10BB09) in ascending

order to their costs. All these are in the drug group

of sulfonylureas. The next interval from 50 to 100

Euro of pharmakological costs includes only 0.3 %

of the patients. In the range of 100 to 150 (150 to

200, above 200) Euros of drug costs, there are 29.5 %

(15.1 %, 13.5 %) of the patients. Mean drug costs per

quarter above 200 Euros are needed for empagliﬂozin

(A10BK03), insulin aspart fast-acting (A10AB05),

insulin lispro intermediate- or long-acting combi-

ned with fast-acting (A10AD04), insulin lispro fast-

acting (A10AB04), dulaglutide (A10BJ05), exenatide

(A10BJ01) and liraglutide (A10BJ02) again in ascen-

ding order to their cost per quarter. The inequality of

costs is described with a Lorentz curve (cf. ﬁgure 1

right) having a Gini coefﬁcient of 0.428. If different

drug groups have been prescribed for the same pati-

ent she or he is assigned to the drug group with the

highest costs.

0.2 0.4 0.6 0.8 1.0

frac.patients

0.2

0.4

0.6

0.8

1.0

frac.costs

Figure 1: Lorentz curve for fractions of costs and patients

for antidiabetic drug treatment.

The drugs differ in mean age and mean polyphar-

macy degree (number of different ATC codes at four

digit level) for the related patient group. We consi-

der the convex hull in the age-polypharmacy-plane

for drugs which are prescribed at least 1,000 times

per quarter. The convex hull (cf. Figure 2) is span-

ned by insulin aspart fast-acting (A10AB05), met-

formin and dapagliﬂozin (A10BD15), glibenclamide

(A10BB01), insulin (human) intermediate- or long-

acting combined with fast-acting (A10AD01) and du-

laglutide (A10BJ05). The most frequently prescribed

metformin (A10BA02) has a middle age und a lower

polypharmacy position in the convex hull, cf. Figure

The correlation between degree of multimorbidity

(number of different ICD codes at three digit level)

and polypharmacy (number of different ATC codes at

four digit level (3rd level of ATC)) is 0.52. Multmor-

bidity and polypharmacie are related, but do not fol-

low a linear relationship. Not every disease had to be

treated by drugs and interaction of drugs may result

A10AB01

A10AB04

A10AB05

A10AB06

A10AC01

A10AD01

A10AE04

A10AE05

A10BA02

A10BB01

A10BB12

A10BD07

A10BD15

A10BH01

A10BJ02

A10BJ05

A10BK01

A10BK03

A10AB01

A10AB04

A10AB05

A10AB06

A10AC01

A10AD01

A10AE04

A10AE05

A10BA02

A10BB01

A10BB12

A10BD07

A10BD15

A10BH01

A10BJ02

A10BJ05

A10BK01

A10BK03

55 60 65 70 75

age

5.5

6.0

6.5

7.0

7.5

8.0

polypharmacy

Figure 2: Diabetic ATC codes in dependence of mean age

and mean polypharmacy.

in complications, therefore the physicians try to redu-

ce the number of drugs as much as possible. We look

at the number of diabetes patents with i drugs and j

diseases at the mentioned level in Figure 6.

A10AB01

A10AB04

A10AB06

A10AC01

A10AE04

A10AE05

A10BA02

A10BB01

A10BB12

A10BD07

A10BH01

A10BJ02

A10BJ05

A10BK01

A10BK03

A10AB01

A10AB04

A10AB05

A10AB06

A10AC01

A10AD01

A10AE04

A10AE05

A10BA02

A10BB01

A10BB12

A10BD07

A10BD15

A10BH01

A10BJ02

A10BJ05

A10BK01

A10BK03

5.5 6.0 6.5 7.0 7.5 8.0

Polypharmazie

Multimorbidität

Figure 3: Diabetic ATC codes in dependence of mean mul-

timorbidity and mean polypharmacy.

In Figure 3 we consider the substances at the 5th

level of ATC prescribed at least 1,000 times per quar-

ter in the multimorbidity-polypharmacy plane again

with its convex hull. With the aggregation on the

substance level, we obtain a correlation coefﬁcient

of 0.85 which is much higher than on the indivi-

dual level. Extreme low positions of multimorbidity

and polypharmacy show the combination treatment

by metformin and dapagliﬂozin (A10BD15) and in-

sulin aspart fast-acting (A10AB05). The highest posi-

tion in polypharmacy and multimorbidity has insulin

human intermediate- or long-acting combined with

fast-acting (A10AD01). Sometimes, in one quarter a

patient is prescribed different antidiabetic drugs. In

this case, we chose the drug at the 5th level of ATC

with the highest cost per quarter as main drug label.

Interrelations between Drug Prescriptions and Diagnoses for SHI Diabetes Patients using Graph Theoretic Methods and a Markov Model

347

We compare the drug cost per day with respect to the

main antidiabetic drug, with respect to all other anti-

diabetic drugs and with respect to all other drugs. The

total drug cost is an economic measure of illness and

can be compared with polypharmacy and multimor-

bidity. The characteristic values are shown in Table 1.

In Figure 4 the convex hull in the plane spanned by

costs per day for antidiabetic drugs on one axis and

costs of other drug on the other.

Table 1: Daily patient costs for main antidiabetic drug, other

antidiabetic drugs and other drugs in Euro.

ATC cost.

main

anti.

diab.

other

anti.

diab.

cost

other

drugs

number

pati-

ents

drug

A10AB01 1.68 0.60 6.30 6,449 insulin (human) fast-

acting

A10AB04 3.01 0.68 6.05 4,718 insulin lispro fast-acting

A10AB05 2.70 0.85 4.98 5,620 sulin aspart fast-acting

A10AB06 2.64 1.20 5.07 1,123 insulin glulisin fast-acting

A10AC01 1.15 2.23 2.81 2,019 insulin (human)

intermediate-acting

A10AD01 1.49 0.19 5.76 4,268 insulin (human)

intermediate- or long-

acting

A10AE04 2.00 0.79 5.08 12,973 insulin glargin long-

acting

A10AE05 2.08 1.05 5.26 3,225 insulin detemir long-

acting

A10BA02 0.20 0.11 2.74 42,149 metformin

A10BB12 0.31 0.34 2.44 3,021 glimepiride

A10BD07 1.49 0.38 2.78 8,795 metformin and sitagliptin

A10BH01 1.42 0.33 4.24 11,394 sitagliptin

A10BJ02 5.79 0.39 5.27 1,276 liraglutid

A10BJ05 3.62 0.57 5.11 1,057 dulaglutide

A10BK01 1.41 1.53 1.63 1,350 dapagliﬂozin

A10BK03 2.25 0.67 3.88 3,655 empagliﬂozin

A10AB01

A10AB04

A10AB05

A10AB06

A10AC01

A10AD01

A10AE04

A10AE05

A10BA02

A10BB12

A10BD07

A10BH01

A10BJ02

A10BJ05

A10BK01

A10BK03

A10AB01

A10AB04

A10AB05

A10AB06

A10AC01

A10AD01

A10AE04

A10AE05

A10BA02

A10BB12

A10BD07

A10BH01

A10BJ02

A10BJ05

A10BK01

A10BK03

1 2 3 4 5 6

antidibetics

other drugs

Figure 4: Diabetic ATC codes: dependence of costs per day

for antidiabetic drugs and other drugs.

The related graph structure of Figure 5 illustra-

tes which other antidiabetic drugs are most frequently

prescribed if another antidibetic drug for the same pa-

tient in the same quarter is already administrated to

the patient. The graph has two components.

A10AB01

A10AC01

A10AB04

A10AB05

A10AB06

A10AE04

A10AD01

A10AD04

A10BA02

A10AE05

A10BB01

A10BB12

A10BD07

A10BH01

A10BH03

A10BJ02

A10BJ05

A10BK01

A10BK03

Figure 5: Pairs of different antidiabetic drugs prespribed for

the same patient in the same quarter (top position).

One can aggregate the drug costs of a patient on

the 3rd level of ATC. The top position in this procedu-

re is called (basic) Morbidity Related Group (MRG),

cf. (Schuster et al., 2016), (Schuster et al., 2018). With

respect to drug efﬁcieny review of physicians, this

is usually done with respect to ﬁx pairings of phy-

sicians and patients. In our context, it is worthwile to

use the patient centered consideration without a refe-

rence to a physician. If we analyse, in which MRG

groups the considered antidibetics will be assigned,

the top position is always occupied by the antidiabe-

tic MRG groups A10A (insulines and analogues) and

A10B (blood glucose lowering drugs, excl. insulines).

The next two positions are assigned to comorbidities

related to drug groups. In descending order we get

B01A (antitrombotic agents), V04C (other diagnostic

agents, here tests for diabetes), C09D (angiotensin II

receptor blocjers, combinations), R03A (adrenergics,

inhalants), N02A (opioids), C10B (lipid modifying

agents, combinations), L04A (immunosuppressants),

C01E (other cardic preparations), J05A (direct ac-

ting antivirals), L01X (other antineoplastic agents),

R03B (other drugs for obstructive airway diseases,

inhalants) and S01E (antiglaucoma preparations and

miotics).

For each age i we consider the vector v(i) of frac-

tion v(i)

of diabetes patient with diagnose k, the di-

mension of the vector is determined by the number of

ICD codes at three digit level. Figure 7 describes the

Manhattan diagnostic distance of diabetes patients of

HEALTHINF 2020 - 13th International Conference on Health Informatics

348

Figure 6: Number of patients with combinations of drugs

and diseases.

Figure 7: Age determined diagnostic Manhattan distance.

age 40 ≤ i, j ≤ 90.

We look for diagnoses, which appear more fre-

quently for diabetes patients than for all patients. The

same question can be adressed to consider subgroups

with respect to the patients age or sex. One can arran-

ge the results in a proper order with respect to relative

or absolute increase or a combination of both (cf. Ta-

ble 2).

We consider the graph with diabetes drugs as no-

des which are related to other top one and top three

drugs with the most similar diagnostic spectra of the

related patient group and graph communities by the

modular method (cf. ﬁgure 3).

The modularity matrix of a undirected graph G =

(V, E) with vertices V and edges E has the entries

u,v

= a

u,v

−

with the adjacency matrix a

u,v

of G, the degree d

vertex u and m as the total number of edges. We look

Table 2: Increased possibilities of diagnoses for diabetes pa-

tients.

no. ICD frac.

diab.

pat.

frac.

all

pat.

diff.

rel.

diff.

abs.

diagnoses

1 G63 22.8 % 2.2 % 1019.2 % 20.6 % Polyneuropathy in diseases

classiﬁed elsewhere

2 E66 33.4 % 10.7 % 312.5 % 22.7 % Obesity

3 E79 13.0 % 4.4 % 296.6 % 8.6 % Disorders of purine and py-

rimidine metabolism

4 I25 24.6 % 8.6 % 285.9 % 16.0 % Chronic ischaemic heart disea-

5 E78 43.2 % 18.8 % 229.4 % 24.3 % Disorders of lipoprotein meta-

bolism and other lipidaemias

for a partition of V into k clusters. For each pair (u, v)

of vertices we consider a variable x

u,v

with value 0 if

u and v are in the same cluster and value 1 otherwi-

se. One can easily prove that the consistency of the

clustering is guaranteed by the triangle inequality

u,w

≤ x

u,v

+ x

v,w

for each triple (u, v, w) of vertices. The modularitiy

methods maximizes

∑

u,v

(1 − x

u,v

)

under the mentioned constraint of triangle inequality

and x

u,v

∈ {0, 1} as an integer linear problem (ILP).

Solving ILP is NP-hard and thus it is unlikely to sol-

ve it in polynomial time. We use the modularity im-

plementation in Mathematica by Wolfram research

and alternatively the commercial package CPLEX by

IBM, cf. (Shinano et al., 2003)). Integer linear pro-

grams (ILP) allows us to formulate an optimization

problem with a linear objective function and cons-

traints given by a series of linear inequalities. Then,

an integer value assignment of the variables is deter-

mined that fulﬁlls all the constrains. Although solving

ILP problems is computationally hard (NP-hard to be

more speciﬁc), there are powerful solvers available

that perform well regarding our precise problem for-

mulations, cf.(Shinano et al., 2003).

At the top one level, there are ﬁve connected

components, one of them splits into three commu-

nities. At the top 3 level the graph is connected

and has ﬁve graph communities. It has a graph dia-

meter of 6. The graph center consists of metfor-

min (A10BA02), the most frequently used drug and

glimepiride (A10BB12) another low cost drug. The

graph periphery consist of six drugs (insulin human

intermediate-acting, insulin lispro fast-acting, insulin

detemir long-acting, insulin aspart fast-acting, insulin

glulisine fast-acting, insulin aspart intermediate- or

long-acting combined with fast-acting) out of the drug

group A10A (insulins and analogues) and two drugs

Interrelations between Drug Prescriptions and Diagnoses for SHI Diabetes Patients using Graph Theoretic Methods and a Markov Model

349

A10AB01

A10AC01

A10AB04

A10AE05 A10AB05

A10AB06

A10AE04

A10AD01

A10AD04

A10AD05

A10BA02

A10BD07

A10BB01

A10BB12

A10BB08

A10BB09

A10BX03

A10BD05

A10BD10

A10BD15

A10BK01

A10BD24

A10BF01

A10BF02

A10BG03

A10BH01

A10BH03

A10BJ01

A10BJ05

A10BJ02

A10BK03

A10BX02

Figure 8: Diabetes drug neighborhood graph with commu-

nities given by the modular method at top 1 level.

Figure 9: Diabetes drug neighborhood graph with commu-

nities given by the modular method at top 3 level.

from the group A10B (blood glucose lowering drugs,

excl. insulins). Table 3 compares mean age, polyphar-

macy, mulimorbidity, pharmacotherapeutic costs and

the number of prescriptions of the drug groups and

their cluster components.

Patients of cluster 1 have the smallest mean value

of multomorbidity, followed by cluster 3. In cluster 2

the fraction of patients with ICD code G63 (Polyneu-

ropathy in diseases classiﬁed elsewhere) is increased

by 31%. In cluster 4 there are increased fractions of

patients with E78 ICD code (disorders of lipoprote-

in metabolism and other lipidaemias, 11%) and E66

(obesity, 30%). Cluster 5 has an increased value in

F32 code (depressive episode, 31%).

A Markov model with transition coefﬁcients from

quarter 1 of 2018 to quarter 2 of 2018 with respect

to drug changes of patients leads to an eigenvalue 1

and the related eigenvalue has components of the sa-

Table 3: Interaction parameters for antidiabetic drugs.

ATC clu-

ster

age poly-

phar.

mul-

ti-

morb.

nr.

pre-

scr.

cost

Eu-

drug

A10AB01 2 68.6 7.4 16.4 10,020 135.45 insulin (human) fast-

acting

A10AB04 2 56.2 6.0 12.2 6,628 241.78 insulin lispro fast-

acting

A10AB05 2 53.0 5.6 11.2 8,681 211.64 sulin aspart fast-

acting

A10AB06 2 62.0 6.6 14.1 2,017 196.90 insulin glulisin fast-

acting

A10AC01 2 67.0 6.8 14.9 6,178 101.90 insulin (human)

intermediate-acting

A10AD01 5 76.8 8.2 18.4 4,987 132.43 insulin (human)

intermediate- or

long-acting combi-

ned with fast-acting

A10AE04 2 64.3 6.9 14.7 19,134 173.93 insulin glargin long-

acting

A10AE05 2 60.2 6.3 13.5 5,140 180.39 insulin detemir long-

acting

A10BA02 3 67.1 5.6 13.6 64,886 18.73 metformin

A10BB01 1 72.5 5.4 13.1 1,877 17.53 glibenclamide

A10BB12 3 70.2 5.5 14.1 6,397 28.31 glimepiride

A10BD07 1 65.6 5.4 13.0 11,131 136.04 metformin and sitag-

liptin

A10BD15 1 60.4 5.2 12.1 1,159 132.30 metformin and da-

pagliﬂozin

A10BH01 3 69.9 6.6 16.0 14,426 126.80 sitagliptin

A10BJ02 4 58.4 6.3 15.4 1,403 516.78 liraglutid

A10BJ05 4 58.2 6.4 15.8 1,272 320.82 dulaglutide

A10BK01 4 61.6 5.5 13.3 2,979 122.76 dapagliﬂozin

A10BK03 4 62.3 6.1 14.5 4,885 201.45 empagliﬂozin

me sign which thereby can be adjusted to the total

number of diabetes patients. The sum of absolute dif-

ferences of the model result and the observed data is

4.15 % of the total size. The observed data are almost

at equilibrium. The differences in edge distributions

of the diabetes patients are caused mainly by popu-

lation changes in elderly people (decline in the birth

rate nearby the end of World War II in 1945).

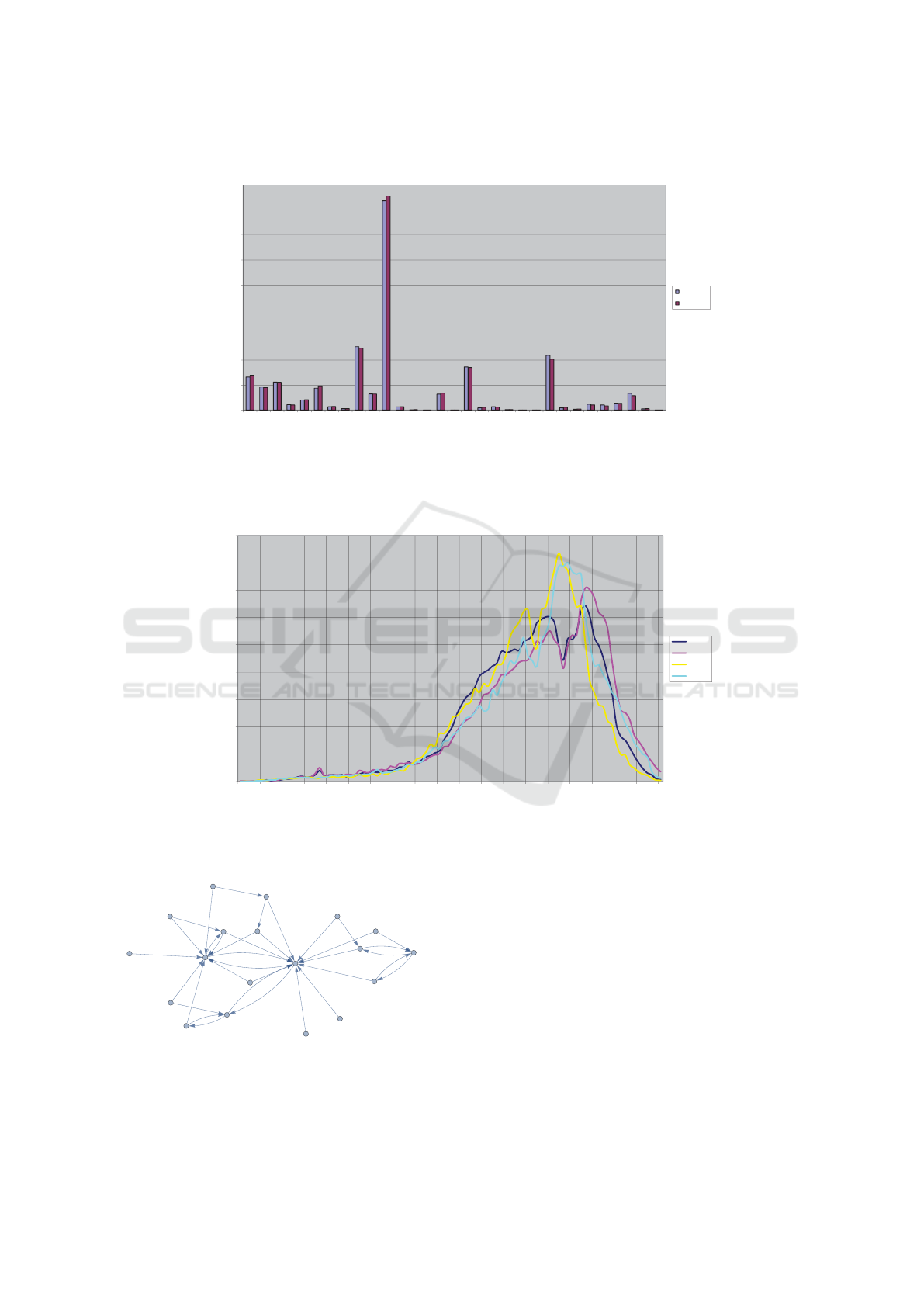
Even though transitions are nearly stable, there

are much less transitions from one substance to ano-

ther substance without loops with at least 30 patients

within the top two transitions (cf. Figure 12). The

top target substances are A10BA02 (metformin) and

A10AE04 (insulin glargin long-acting).

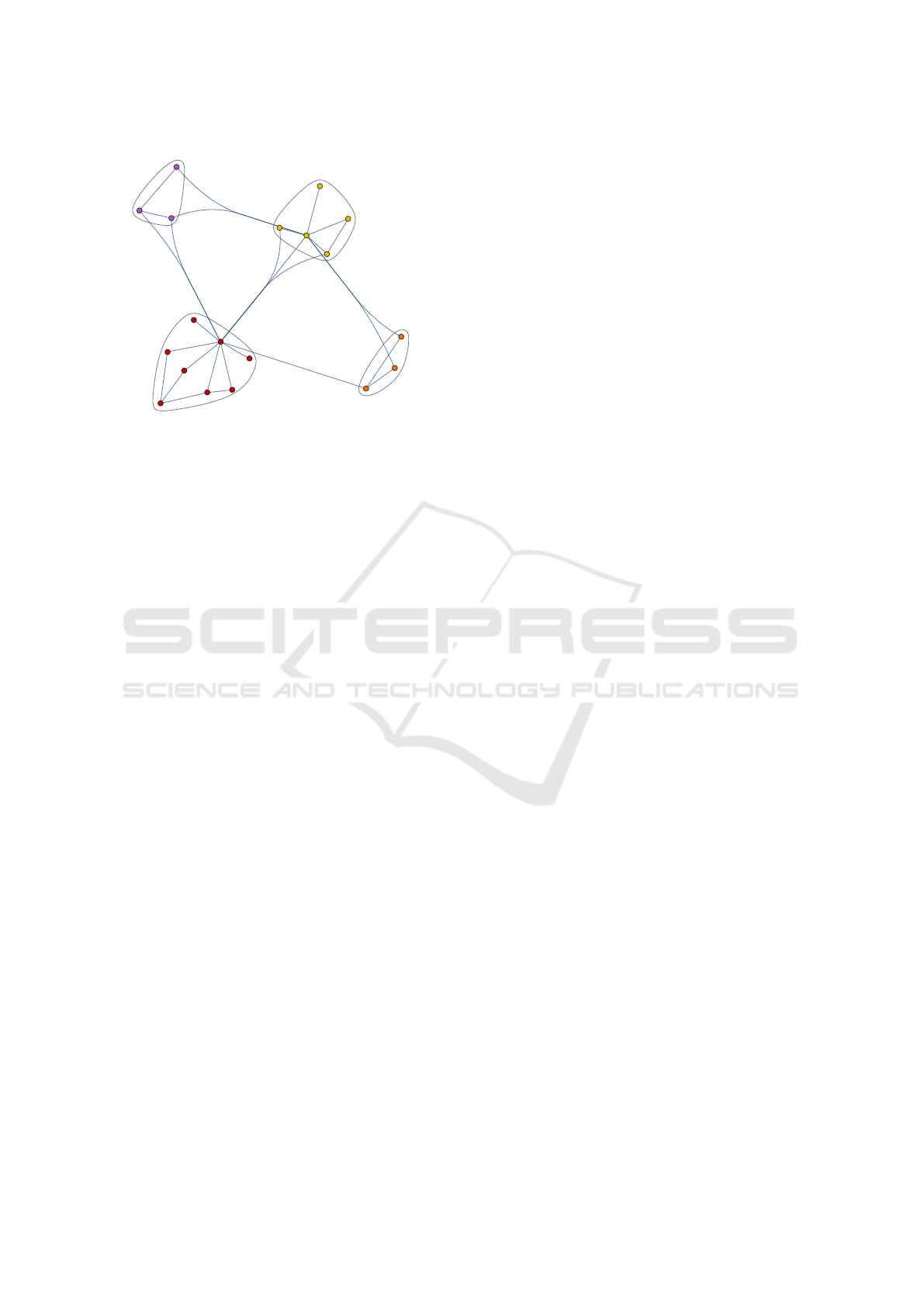
The related undirected graph has four graph com-

munities using the modularity method (cf. Figure 13).

The graph periphery only consists of A10AE04

(insulin glargin long-acting), the graph periphery con-

tains A10BK01 (dapagliﬂozin), A10BB12 (glimepi-

ride), A10BB01 (glibenclamide), A10AE05 (insu-

lin detemir long-acting), A10AD01 (insulin (human)

intermediate- or long-acting combined with fast-

acting) and A10AC01 (insulin (human) intermediate-

acting).

HEALTHINF 2020 - 13th International Conference on Health Informatics

350

5.000

10.000

15.000

20.000

25.000

30.000

35.000

40.000

45.000

A10AB01

A10AB04

A10AB05

A10AB06

A10AC01

A10AD01

A10AD04

A10AD05

A10AE04

A10AE05

A10BA02

A10BB01

A10BB08

A10BB09

A10BB12

A10BD05

A10BD07

A10BD10

A10BD15

A10BF01

A10BF02

A10BG03

A10BH01

A10BH03

A10BJ01

A10BJ02

A10BJ05

A10BK01

A10BK03

A10BX02

A10BX03

no of patients

drug

markov result

observed

model

Figure 10: Markov stable solution compared with the observed data.

0,0%

0,5%

1,0%

1,5%

2,0%

2,5%

3,0%

3,5%

4,0%

4,5%

0 5 10 15 20 25 30 35 40 45 50 55 60 65 70 75 80 85 90 95

fraction

adge

adge distribution of diabetes patient in dependence of sex (m,f ) for 2013 and 2018

m 2018

f 2018

m 2013

f 2013

Figure 11: Edge distribution with respect to sex for 2013 and 2018.

A10BK03

A10BA02

A10AE04

A10BK01

A10BD07

A10BJ05

A10AB04

A10BJ02

A10BH03

A10BH01

A10BD15

A10BB12

A10BB01

A10AE05

A10AB05

A10AB01

A10AD01

A10AC01

A10AB06

Figure 12: Changes of substances from quarter one to quar-

ter two in 2018.

4 CONCLUSIONS

Community structures of graphs offer new insights in

therapeutic backgrounds of prescribed drugs. This of-

fers the opportunity to improve health care decisions

at the negotiation level, to improve medical decisi-

ons from a patient centered point of view and to ad-

apt national and international guidelines from a uni-

ﬁed point of view. Patients’ age, sex, multimorbidi-

ty and further parameters can be used to get neigh-

borhood information as a informational base to opti-

mize personal and health political decisions within a

global context. Network analysis with graph theoretic

methods against the background of big data combi-

Interrelations between Drug Prescriptions and Diagnoses for SHI Diabetes Patients using Graph Theoretic Methods and a Markov Model

351

A10BK03

A10BA02

A10AE04

A10BK01

A10BD07

A10BJ05

A10AB04

A10BJ02

A10BH03

A10BH01

A10BD15

A10BB12

A10BB01

A10AE05

A10AB05

A10AB01

A10AD01

A10AC01

A10AB06

Figure 13: Graph communities for changes of substances

from quarter one to quarter two in 2018.

ned with therapeutic innovations are a powerful tool

for theoretical analyzes as well as for practical acti-

ons. The analysis was done as a patient centered point

of view with the background of the entire informa-

tion with respect to drugs and diseases of all physi-

cians that treated an individual patient in the conside-

red quarter. But the information background of a spe-

cial physician may be informationally rather scare in

comparison. There are principal limitations with re-

spect to data protection. Missing information about

other drugs and other diseases may restrain or pre-

vent the treatment success with substantial risks for

the patient and resulting follow-up costs for complica-

tion treatment further burdening ﬁnancially the health

system. Further research is necessary especially for

identiﬁcation of critical situations. The possibilities of

sharing information with modern digital communica-

tion structures are currently underused. Most guide-

lines are geared towards special diseases and drugs.

Multimorbidity and polypharmacie require priorities

and compromises between beneﬁts and side effects.

Further research is necessary to use the analyzed dif-

ferent degrees of multimorbidity and polypharmacy

for individual informed decision making. The analy-

sis shows that large differences in drug costs can lar-

gely be explained by different diseases and multimod-

bidity. It should be analyzed in which situations large

differences of therapeutic decisions made by an indi-

vidual physician that differ from other physicians at

a statistically assured level are related to drug econo-

mic problems or if they are related to more innovative

treatment at the currently secured scientiﬁc level.

REFERENCES

Agarwal, G. and Kempe, D. (2008). Modularity-

Maximizing Graph Communities via Mathematical

Programming. The European Phisical Journal B,

66:409–418.

American Diabetes Association (1998). Economic conse-

quences of diabetes mellitus in the us in 1997. Diabe-

tes Care, 21:296–309.

International Diabetes Federation (2017). IDF Diabetes At-

las, 8th edn. Brussels, Belgium: International Diabe-

tes Federation 2017.

Klein, B. E. (2007). Overview of epidemiologic studies

of diabetic retinopathy. Ophthalmic Epidemiology,

14:179–183.

Newman, M. (2006). Finding community structure in net-

works using the eigenvectors of matrices. Physical

Review E, 74.

Schuster, R. and Emcke, T. (2018). Graph-theoretic network

analysis of interactions between patients, physicians

and prescribed drugs. submitted to Archives of Data

Science, Series A.

Schuster, R., Emcke, T., Arnstedt, E., and Heidbreder, M.

(2016). Morbidity Related Groups (MRG) for epide-

miological analysis in outpatient treatment. IOS Press,

pages 783–787.

Schuster, R., Ostermann, T., Heidbreder, M., and Emcke,

T. (2018). Relations of Morbidity Related Groups

(MRG), ICD-10 Codes and Age and Gender Structure

in Outpatient Treatment. In Proceedings of the 11th

International Joint Conference on Biomedical Engi-

neering Systems and Technologies - Volume 5: HEAL-

THINF, pages 322–328.

Shi, Y. and Hu, F. (2014). The global implications of diabe-

tes and cancer. Lancet, 383(9933):1947–8.

Shinano, Y., Fujie, T., and Kounoike, Y. (2003). Effectiven-

ess of Parallelizing the ILOG-CPLEX Mixed Integer

Optimizer in the PUBB2 Framework. In Euro-Par

2003 Parallel Processing, pages 451–460. Springer

Berlin Heidelberg.

Songer, T., L, E., and of Diabetes Project Panel, E. (1998).

Studies on the Costs of Diabetes. Atlanta, Ga: Centers

for Disease Control and Prevention.

World Health Organization (2016). Report on Diabetes

(PDF). WHO.

HEALTHINF 2020 - 13th International Conference on Health Informatics

352