Measuring the Similarity of Proteomes using Grammar-based
Compression via Domain Combinations
Morihiro Hayashida
1
, Hitoshi Koyano
2
and Jose C. Nacher
3
1
Department of Electrical Engineering and Computer Science, National Institute of Technology, Matsue College,
Matsue, Shimane, Japan
2
School of Life Science and Technology, Tokyo Institute of Technology, Meguro-ku, Tokyo, Japan
3
Department of Information Science, Faculty of Science, Toho University, Funabashi, Chiba, Japan
Keywords:
Grammar-based Compression, Kolmogorov Complexity, Protein Domain Combination.
Abstract:
Revealing evolution of organisms is one of important biological research topics, and is also useful for un-
derstanding the origin of organisms. Hence, genomic sequences have been compared and aligned for finding
conserved and functional regions. A protein can contain several domains, which are known as structural and
functional units. In the previous work, a proteome, whole kinds of proteins in an organism, was regarded
as a set of sequences of protein domains, and a grammar-based compression algorithm was developed for a
proteome, where production rules in the grammar represented evolutionary processes, mutation and duplica-
tion. In this paper, we propose a similarity measure based on the grammar-based compression, and apply
it to hierarchical clustering of seven organisms, Homo sapiens, Mus musculus, Drosophila melanogaster,
Caenorhabditis elegans, Saccharomyces cerevisiae, Arabidopsis thaliana, and Escherichia coli. The results
suggest that our similarity measure could classify the organisms very well.
1 INTRODUCTION
To understand evolutionary processes of organisms is
important, and many researchers are interested in the
origin of organisms. DNA sequences are changed by
mutation, recombination, gene duplication, and so on,
which are responsible for genetic variation as well as
evolution of new genes and species. For classifying
the evolutionary lineage of an organism, 16S riboso-
mal RNA is often used because the gene is included in
every organism and the evolution rate is slow (Woese
and Fox, 1977).
Comparing DNA and protein sequences is a fun-
damental task in molecular biology and bioinformat-
ics field, and many sequence search tools such as
FASTA (Lipman and Pearson, 1985) and BLAST
(Altschul et al., 1990) have been developed. Re-
cent high-throughput sequencing technologies pro-
duce very long, full-length reads and very large
datasets, and need more efficient alignment methods.
Minimap2 was three times as fast as existing meth-
ods at comparable accuracy to map DNA or long
mRNA sequences against a large reference database
(Li, 2018). Compression techniques are often useful
for efficient analyses of DNA and protein sequences,
and for saving storage space. GReEn was devel-
oped for compressing genome resequencing data us-
ing a reference genome sequence, and outperformed
several existing methods in storage space require-
ments and running times (Pinho et al., 2012). LFQC
is a lossless non-reference compression method for
FASTQ files, and achieved better compression ratios
on several datasets (Nicolae et al., 2015). For our
purpose, however, it is difficult to extract evolution-
ary construction of DNA and protein sequences using
compression in a simple manner.
Protein domains are part of a protein, often form
globular structures, and are known as functional units
(Doolittle, 1995). It is observed that the same kind of
domain can be contained in distinct proteins. Several
computational methods that make use of domain com-
binations have been developed for prediction of inter-
acting proteins (Hayashida et al., 2011), identification
of small protein complexes (Ruan et al., 2013), analy-
sis of the scale-free behavior of protein-protein inter-
action networks (Nacher et al., 2009) among others.
As an evolutionary model of domain combinations in
a proteome, a model with mutation and duplication
of domains was proposed (Nacher et al., 2006). They
defined a specific network, called protein domain net-
Hayashida, M., Koyano, H. and Nacher, J.
Measuring the Similarity of Proteomes using Grammar-based Compression via Domain Combinations.
DOI: 10.5220/0008913101170122
In Proceedings of the 13th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2020) - Volume 3: BIOINFORMATICS, pages 117-122
ISBN: 978-989-758-398-8; ISSN: 2184-4305
Copyright
c
 2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
117

work, constructed from domain combinations of pro-
teins in an organism. In the network, a node repre-
sents a protein, and an edge is added if two proteins
corresponding to the two nodes of the edge have the
same domain. Then, it was reported that the degree
distribution of the protein domain network generated
by their evolutionary model had the same tendency
as those by actual proteomes such as H. sapiens and
M. musculus obtained from Pfam and InterPro do-
main databases (El-Gebali et al., 2018; Mitchell et al.,
2018).
From the viewpoint of information theory, a simi-
larity measure between data structures can be derived.
The Kolmogorov complexity of an object was defined
as the length of a shortest program outputs the object
(Li and Vitanyi, 1997), which cannot be computed re-
alistically, and has been approximated by the com-
pressed size. The conditional Kolmogorov complex-
ity of an object relative to another object was similarly
defined, which means the length of a shortest program
outputs an object using another object. If two objects
are very similar, the conditional Kolmogorov com-
plexity becomes small. The normalized compression
distance (NCD) was proposed using the conditional
Kolmogorov complexity (Li et al., 2004). They com-
pressed several whole mitochondrial DNA sequences
using string compressors such as bzip2 and GenCom-
press (Chen et al., 2001), and constructed a hierarchi-
cal tree based on the distance. In addition to NCD,
the universal compression distance (UCD) and com-
pression distance (CD) were used for classifying bi-
ological sequences, structures, and networks (Ferrag-
ina et al., 2007; Hayashida and Akutsu, 2010).
For the purpose of finding the genetic entropy that
an individual organism contains, a compression al-
gorithm based on evolutionary processes was devel-
oped (Hayashida et al., 2014). In their method, a pro-
teome, that is, whole kinds of proteins in an organ-
ism was regarded as a family of sets of domains, and
a grammar on sets was introduced based on evolu-
tionary processes such as mutation, gene duplication,
and gene fusion for compressing proteomes. In real-
ity, domains, however, are lined in an adequate order
in a protein. Hence, the modified compression algo-
rithm was developed, where a protein was regarded
as a sequence of domains (Hayashida et al., 2018).
In this paper, we propose a similarity measure based
on the modified grammar-based compression, and ap-
ply it to hierarchical clustering of seven organisms, H.
sapiens, M. musculus, D. melanogaster, C. elegans, S.
cerevisiae, A. thaliana, and E. coli. The results sug-
gest that our similarity measure could classify the or-
ganisms very well.
2 METHODS
We briefly review the modified grammar-based com-
pression of a proteome, and a similarity measure
based on the Kolmogorov complexity, and explain
our approach for measuring a similarity between pro-
teomes using the grammar-based compression.
2.1 Grammar-based Compression
Let D and P be a set of domains and a set of proteins,
respectively. We regard a protein P
i
(∈ P ) to be a se-
quence of domains D
j
(∈ D). Then, for all D
j
∈ D, P
i
exists such that D
j
is included in P
i
. We consider the
following problem: Given P and D, find a minimum
grammar G with two types R
m
and R
d
of production
rules constructing all proteins P
i
∈ P from domains
D
j
(∈ D), where the size of the grammar G is defined
by the sum of costs of all production rules of G, R
m
and R
d
correspond to evolutionary processes, muta-
tion and gene duplication, respectively.
In a production rule of R
m
for a protein P
i
, P
i
is constructed from only domains D
i
j
(∈ D) ( j =
1, ..., |P
i
|), where |P
i
| denotes the length of sequence
P
i
. Then, the production rule is written as P
i
←
D
i
1
···D
i
|P
i
|
. The cost for R
m
is defined by
cost
R
m
(P
i
) = dlog |D|e|P
i
|, (1)
where dxe denotes the ceiling function that returns the
least integer greater than or equal to x, the base of the
logarithm is two, and dlog|D|e means the amount in
bits to specify one domain.
In a production rule of R
d
for a protein P
i
, P
i
is
constructed by duplicating another protein P
j
. In the
duplication, domains contained in P
j
are duplicated,
and several domains can be inserted and deleted.
We calculate the Levenshtein distance (Levenshtein,
1965) for finding the minimum number of edit opera-
tions, insertion and deletion from P
j
to P
i
. Then, the
cost for R
d
is defined by
cost
R
d
(P
i
, P
j
) = dlog |P |e + |P
i
|
+d
L
(P
j
, P
i
)(dlog|D|e + dlog(|P
j
| + 1)e), (2)
where d
L
(P
j
, P
i
) denotes the Levenshtein distance
from P
j
to P
i
with insertion cost one, and dlog|P|e
means the amount in bits to specify one protein to
be duplicated. For example, Figure 1 shows an ex-
ample of finding the Levenshtein distance from P
1
=
D
1
D
2
D
1
to P
2
= D
1
D
2
D
3
D
1
. D
3
is inserted to P
1
.
Then, d
L
(P
1
, P
2
) = 1. P
1
has |P
1
| + 1 = 4 candidate
positions to insert domains, and D
3
is inserted in be-
tween the second domain and the third domain of P
1
.
Then, cost
R
d
(P
2
, P
1
) = dlog |P |e+4+ 1 · (dlog|D|e +
dlog4e).
BIOINFORMATICS 2020 - 11th International Conference on Bioinformatics Models, Methods and Algorithms
118

P
1
= D
1
D
2
D
1
P
2
= D
1
D
2
D
3
D
1
Figure 1: Example of finding the Levenshtein distance
from P
1
= D
1
D
2
D
1
to P
2
= D
1
D
2
D
3
D
1
. In this example,
d
L
(P
1
, P
2
) = 1.
For all P
i
∈ P , exactly one production rule is se-
lected for each protein if the size of grammar G is
the smallest. The problem of finding the minimum
grammar G for a proteome P with domains D can
be transformed into the minimum spanning tree prob-
lem for an edge-weighted directed graph G(V, E, w)
with a set V of vertices, a set E of edges, and edge
weight w(e) of e(∈ E) as follows. Suppose that
v
0
is a special vertex representing a protein with-
out any domain, and v
i
is corresponding to a protein
P
i
. Then, V = {v
0
} ∪ {v
i
|P
i
∈ P }, E = {(v
0
, v
i
)|P
i
∈
P } ∪ {(v
i
, v
j
)|P
i
, P
j
∈ P }, and w(v
0
, v
i
) = cost
R
m
(P
i
),
w(v
i
, v
j
) = cost
R
d
(P
j
, P
i
). The minimum spanning
tree problem can be solved in polynomial time, and
at least one edge for each protein belongs to the mini-
mum spanning tree. From the solution, the production
rule for P
i
in the minimum grammar, and the com-
pressed size C(P ) can be obtained.
C(P ) =
∑
P
i
∈P
{δ
R
m
P
i
cost
R
m
(P
i
)
+
∑
P
j
∈P
δ
R
d
P
i
,P
j
cost
R
d
(P
i
, P
j
)}, (3)
where δ
R
m
P
i
= 1 if a mutation-type production rule is
selected to P
i
in the optimal solution, otherwise 0, and
δ
R
d
P
i
,P
j
= 1 if a duplication-type production rule from
P
j
is selected, otherwise 0. The uncompressed size is
calculated by δ
R
m
P
i
= 1, δ
R
d
P
i
,P
j
= 0 for all P
i
.
2.2 Similarity Measure
We can compress a proteome P by finding the mini-
mum grammar as mentioned in the previous section.
The compressed size is the size of the minimum gram-
mar. In general, the conditional Kolmogorov com-
plexity K(o
i
|o
j
) of an object o
i
given another object
o
j
is defined as the size of a minimum program that
takes o
j
and returns o
i
(Li and Vitanyi, 1997). If o
i
is
similar to o
j
, K(o
i
|o
j
) becomes small. The normal-
ized information distance is defined by
max{K(o
i
|o
j
), K(o
j
|o
i
)}
max{K(o
i
), K(o
j
)}
, (4)
where K(o
i
) is the Kolmogorov complexity defined
as K(o
i
|ε) given no objects. Since K(o
i
) and K(o
i
|o
j
)
are not computable, the size C(o
i
) compressed by a
compressor is used for K(o
i
), and K(o
i
|o
j
) is approx-
imated by C(o
i
· o
j
) − C(o
j
), where o
i
· o
j
means a
concatenation of o
i
and o
j
. Thus, the universal com-
pression distance (UCD) is defined by
UCD(o
i
, o
j
)
=
max{C (o
i
· o
j
) −C(o
j
), C(o
j
· o
i
) −C(o
i
)}
max{C (o
i
), C(o
j
)}
.(5)
2.3 Our Compression Approach
For our purpose of measuring the similarity of pro-
teomes, we introduce the sizes of the minimum gram-
mars for two proteomes P
i
and P
j
as the compressed
sizes C(P
i
) and C(P
j
), respectively. Since P
i
∪ P
j
=
P
j
∪ P
i
, substituting C(P
i
∪ P
j
) to Eq.(5), we have the
distance between P
i
and P
j
as
d(P
i
, P
j
) =
C(P
i
∪ P
j
) − min{C(P
i
), C(P
j
)}
max{C (P
i
), C(P
j
)}
. (6)
It is noted that dlog|P
i
∪ P
j
|e can be different
from dlog|P
i
|e or dlog |P
j
|e in Eqs (1) and (2).
Hence, we calculate C(P
i
), C(P
j
) and C(P
i
∪ P
j
)
using dlog |P
i
∪ P
j
|e and dlog |D
i
∪ D
j
|e instead of
dlog|P
i
|e, dlog|D
i
|e and so on, where D
i
and D
j
de-
note sets of domains included in P
i
and P
j
, respec-
tively.
3 COMPUTATIONAL
EXPERIMENTS
As protein domains, we used ProRule entries (Sigrist
et al., 2005) included in UniProt database (release
2019 03) (The UniProt Consortium, 2019), which is
a set of manually created rules concerning domains
identified by PROSITE motifs, and contains the po-
sition of structurally and functionally critical amino
acids. The PROSITE database uses two kinds of de-
scriptors, patterns and profiles, to detect conserved re-
gions. For biologically significant, highly conserved
regions such as enzyme catalytic sites and regions in-
volved in binding a metal ion, patterns or regular ex-
pressions are used. For other motifs, profiles that are
represented by tables of position-specific amino acid
weights and gap costs are used.
For seven organisms, Homo sapiens, Mus
musculus, Drosophila melanogaster, Caenorhabdi-
tis elegans, Saccharomyces cerevisiae, Arabidopsis
thaliana, and Escherichia coli, we got ProRule iden-
tifiers and positions for each protein, and calcu-
lated the compressed sizes, C(P
i
) and C(P
i
∪ P
j
),
Measuring the Similarity of Proteomes using Grammar-based Compression via Domain Combinations
119

for each proteome and pairs of proteomes. Then,
the minimum spanning tree problem for the gener-
ated graph G(V, E, w) was solved using Edmonds’s
optimum branching algorithm (Tarjan, 1977), which
runs in time O(E logV ) for sparse graphs and O(V
2
)
for dense graphs. We performed hierarchical clus-
tering using hclust function in R statistics software
(https://www.r-project.org). In the clustering, accord-
ing to the distance D(X , Y ) between clusters X and
Y , two clusters with the smallest distance are merged
into one cluster. For single linkage clustering, the dis-
tance is defined by
D(X, Y ) = min
i∈X, j∈Y
d(P
i
, P
j
). (7)
For complete linkage clustering, the distance is de-
fined by
D(X, Y ) = max
i∈X, j∈Y
d(P
i
, P
j
). (8)
For the unweighted pair group method with arithmetic
mean (UPGMA) that is used in phylogenetic analy-
ses, the distance is defined by
D(X, Y ) =
∑
i∈X, j∈Y
d(P
i
, P
j
)
|X||Y |
. (9)
4 RESULTS
Table 1 shows the results on the number |P | of pro-
teins, the number |D| of domains, the uncompressed,
compressed sizes, and the compression ratio for sin-
gle proteomes of seven organisms, H. sapiens, M.
musculus, D. melanogaster, C. elegans, S. cerevisiae,
A. thaliana, and E. coli, where the uncompressed size
means the sum of cost
R
m
(P
i
) for all P
i
∈ P , that is, ev-
ery protein is represented by a domain sequence. It is
confirmed that the ratio of the compressed size to the
uncompressed size for higher organisms was smaller
than that for others. It means that higher organisms
use gene duplication more frequently.
Table 2 shows the results on the compressed size
C(P
i
∪ P
j
) between proteomes of the seven organ-
isms. From this table, the distances d(P
i
, P
j
) between
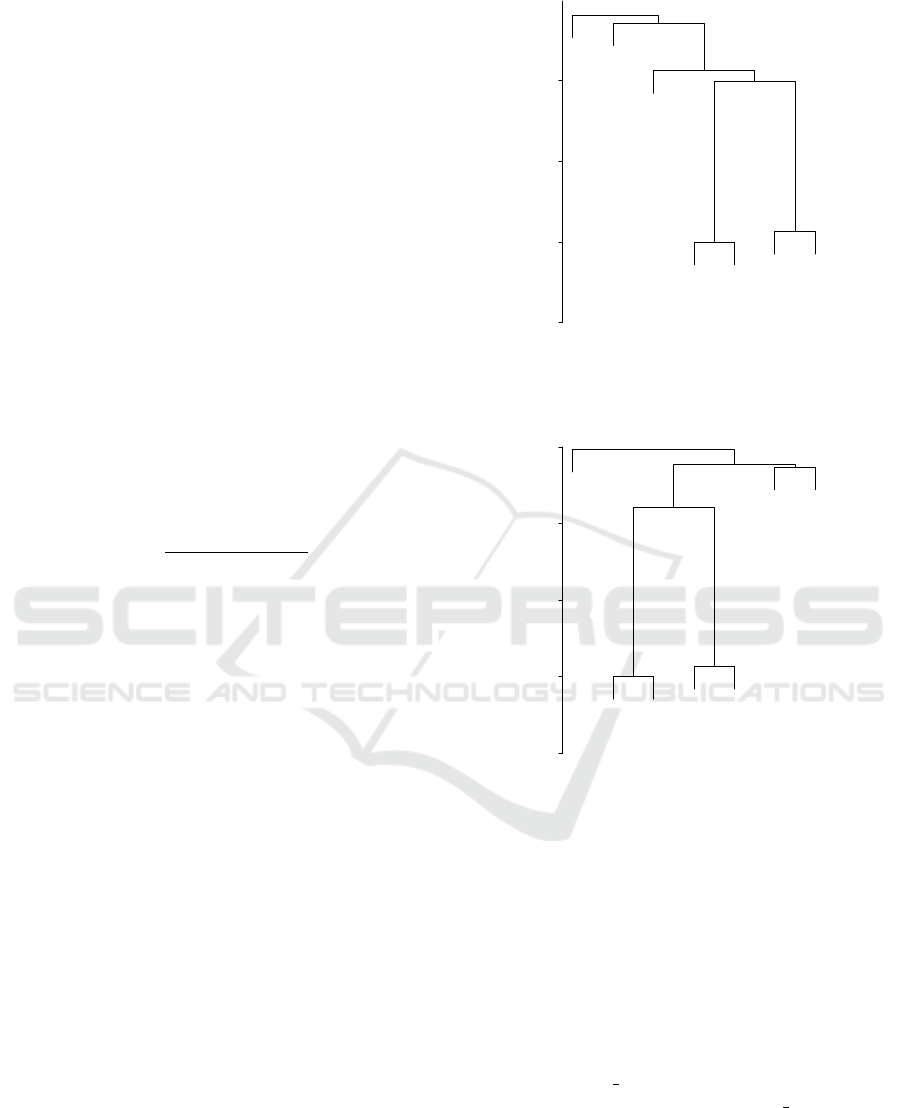
proteomes were calculated. Figures 2, 3, and 4 show
the results on the dendrogram using the single link-
age, complete linkage, and UPGMA clustering, re-
spectively, for proteomes of the seven organisms. The
structure of the hierarchical tree by the single linkage
clustering was the same as that by the UPGMA and
generally known phylogenetic trees, and was slightly
different from that by the complete linkage clustering.
Table 3 shows the results on the rate of the number
of duplication-type production rules including two
E.coli
A.thaliana
S.cerevisiae
M.musculus
H.sapiens
C.elegans
D.melanogaster
0.80 0.85 0.90 0.95
Height
Figure 2: Result on the dendrogram using single linkage
clustering for proteomes of the seven organisms.
E.coli
M.musculus
H.sapiens
C.elegans
D.melanogaster
A.thaliana
S.cerevisiae
0.80 0.85 0.90 0.95 1.00
Height
Figure 3: Result on the dendrogram using complete linkage
clustering for proteomes of the seven organisms.
proteins from distinct organisms to that from one or-
ganism for each pair of proteomes of the seven or-
ganisms. The rates in between H. sapiens and M.
musculus, and between D. melanogaster and C. el-
egans were over a half. It means that many or-
thologous proteins exist in the organisms. For ex-
ample, the number of rules including two proteins
from distinct organisms in between H. sapiens and
M. musculus was 2,970. Among those, for gener-
ation of ACACA HUMAN protein in UniProt iden-
tifier, the rule that duplicates ACACA MOUSE pro-
tein was selected as an optimal solution, where both
proteins contained ProRule identifiers of PRU00409,
PRU01066, PRU01136, and PRU01137, and are
known as acetyl-CoA carboxylases. Conversely, the
rate in between E. coli and another organism was
small. As a reason, it is also considered that the num-
BIOINFORMATICS 2020 - 11th International Conference on Bioinformatics Models, Methods and Algorithms
120

Table 1: Results on the number of proteins, the number of domains, the uncompressed, compressed sizes, and the compression
ratio for single proteomes of the seven organisms.
organism # proteins # domains uncompressed (A) compressed (B) B/A
H. sapiens 7292 666 164290 114564 0.697
M. musculus 6124 665 138330 97925 0.708
D. melanogaster 1105 415 21609 17560 0.813
C. elegans 1318 416 23985 20466 0.853
S. cerevisiae 1337 372 17217 15481 0.899
A. thaliana 5213 426 69444 59313 0.854
E. coli 896 309 11115 10045 0.904
Table 2: Results on the compressed size between proteomes of the seven organisms.
H. sapiens M. musculus D. melanogaster C. elegans S. cerevisiae A. thaliana
M. musculus 199674 – – – – –
D. melanogaster 132262 112699 – – – –
C. elegans 135310 115765 35613 – – –
S. cerevisiae 133241 113703 35511 38812 – –
A. thaliana 180512 163583 82244 85653 74467 –
E. coli 125742 109104 30061 33595 28153 74683
Table 3: Results on the rate of the number of duplication-type production rules including two proteins from distinct organisms
to that from one organism for each pair of proteomes of the seven organisms.
H. sapiens M. musculus D. melanogaster C. elegans S. cerevisiae A. thaliana
M. musculus 0.57 – – – – –
D. melanogaster 0.26 0.22 – – – –
C. elegans 0.25 0.27 0.53 – – –
S. cerevisiae 0.17 0.18 0.36 0.30 – –
A. thaliana 0.18 0.18 0.15 0.19 0.27 –
E. coli 0.025 0.026 0.062 0.068 0.14 0.059
E.coli
A.thaliana
S.cerevisiae
M.musculus
H.sapiens
C.elegans
D.melanogaster
0.80 0.85 0.90 0.95 1.00
Height
Figure 4: Result on the dendrogram using the unweighted
pair group method with arithmetic mean (UPGMA) for pro-
teomes of the seven organisms.
ber of proteins in E. coli was small. For example,
the number of rules including two proteins from dis-
tinct organisms in between E. coli and H. sapiens was
67. Among those, for generation of ODP2 HUMAN
protein, the rule that duplicates ODP2 ECOLI pro-
tein was selected, where ODP2 HUMAN con-
tained two domains identified by PRU01066 and
one domain by PRU01170, and ODP2 ECOLI con-
tained three domains identified by PRU01066 and
one domain by PRU01170. ODP2 HUMAN and
ODP2 ECOLI are known as dihydrolipoyllysine-
residue acetyltransferase components of pyruvate de-
hydrogenase complex. The production rule from
ODP2 ECOLI to ODP2 HUMAN, rather than the
rule from ODP2 HUMAN to ODP2 ECOLI, was se-
lected because the cost of insertion of PRU01066 is
larger than that of deletion of the domain.
5 CONCLUSIONS
We proposed a similarity measure based on the
grammar-based compression for proteomes with sets
of domain sequences, and applied it to hierarchical
clustering of seven organisms, H. sapiens, M. mus-
culus, D. melanogaster, C. elegans, S. cerevisiae, A.
thaliana, and E. coli. The results suggest that our
Measuring the Similarity of Proteomes using Grammar-based Compression via Domain Combinations
121

similarity measure could classify the organisms very
well. As future work, we would like to analyze more
organisms, to find the minimum grammar for generat-
ing proteomes of more organisms, and to investigate
comprehensive evolutionary processes.
ACKNOWLEDGEMENTS
This work was partially supported by JSPS KAK-
ENHI Grant Number JP19K12228.
REFERENCES
Altschul, S., Gish, W., Miller, W., Myers, E., and Lipman,
D. (1990). Basic local alignment search tool. Journal
of Molecular Biology, 215(3):403–410.
Chen, X., Kwong, S., and Li, M. (2001). A compression
algorithm for dna sequences. IEEE Engineering in
Medicine and Biology Magazine, 20(4):61–66.
Doolittle, R. (1995). The multiplicity of domains in pro-
teins. Annual Review of Biochemistry, 64:287–314.
El-Gebali, S., Mistry, J., Bateman, A., Eddy, S. R., Lu-
ciani, A., Potter, S. C., Qureshi, M., Richardson, L. J.,
Salazar, G. A., Smart, A., Sonnhammer, E. L., Hirsh,
L., Paladin, L., Piovesan, D., Tosatto, S. C., and Finn,
R. D. (2018). The Pfam protein families database in
2019. Nucleic Acids Research, 47(D1):D427–D432.
Ferragina, P., Giancarlo, R., Greco, V., Manzini, G., and
Valiente, G. (2007). Compression-based classification
of biological sequences and structures via the Univer-
sal Similarity Metric: experimental assessment. BMC
Bioinformatics, 8:252.
Hayashida, M. and Akutsu, T. (2010). Comparing biolog-
ical networks via graph compression. BMC Systems
Biology, 4(Suppl. 2):S13.
Hayashida, M., Ishibashi, K., and Koyano, H. (2018).
Analyzing order of domains in grammar-based com-
pression of proteomes. In The 24th International
Conference on Parallel and Distributed Processing
Techniques and Applications, pages 278–281. CSREA
Press.
Hayashida, M., Kamada, M., Song, J., and Akutsu, T.
(2011). Conditional random field approach to predic-
tion of protein-protein interactions using domain in-
formation. BMC Systems Biology, 5(Suppl. 1):S8.
Hayashida, M., Ruan, P., and Akutsu, T. (2014). Proteome
compression via protein domain compositions. Meth-
ods, 67:380–385.
Levenshtein, V. (1965). Binary codes capable of correcting
deletions, insertions and reversals. Doklady Adademii
Nauk SSSR, 163(4):845–848.
Li, H. (2018). Minimap2: pairwise alignment for nucleotide
sequences. Bioinformatics, 34(18):3094–3100.
Li, M., Chen, X., Li, X., Ma, B., and Vitanyi, P. (2004). The
similarity metric. IEEE Transactions on Information
Theory, 50:3250–3264.
Li, M. and Vitanyi, P. (1997). An introduction to Kol-
mogorov complexity and its applications. Springer-
Verlag, New York.
Lipman, D. and Pearson, W. (1985). Rapid and sensitive
protein similarity searches. Science, 227(4693):1435–
1441.
Mitchell, A. L., Attwood, T. K., Babbitt, P. C., Blum,
M., Bork, P., Bridge, A., Brown, S. D., Chang, H.-
Y., El-Gebali, S., Fraser, M. I., Gough, J., Haft,
D. R., Huang, H., Letunic, I., Lopez, R., Luciani,
A., Madeira, F., Marchler-Bauer, A., Mi, H., Natale,
D. A., Necci, M., Nuka, G., Orengo, C., Panduran-
gan, A. P., Paysan-Lafosse, T., Pesseat, S., Potter,
S. C., Qureshi, M. A., Rawlings, N. D., Redaschi,
N., Richardson, L. J., Rivoire, C., Salazar, G. A.,
Sangrador-Vegas, A., Sigrist, C. J., Sillitoe, I., Sut-
ton, G. G., Thanki, N., Thomas, P. D., Tosatto, S. C.,
Yong, S.-Y., and Finn, R. D. (2018). InterPro in 2019:
improving coverage, classification and access to pro-
tein sequence annotations. Nucleic Acids Research,
47(D1):D351–D360.
Nacher, J. C., Hayashida, M., and Akutsu, T. (2006). Pro-
tein domain networks: Scale-free mixing of positive
and negative exponents. Physica A, 367:538–552.
Nacher, J. C., Hayashida, M., and Akutsu, T. (2009). Emer-
gence of scale-free distribution in protein-protein in-
teraction networks based on random selection of in-
teracting domain pairs. BioSystems, 95:155–159.
Nicolae, M., Pathak, S., and Rajasekaran, S. (2015).
LFWC: a lossless compression algorithm for FASTQ
files. Bioinformatics, 31(20):3276–3281.
Pinho, A., Pratas, D., and Garcia, S. (2012). GReEn: a
tool for efficient compression of genome resequencing
data. Nucleic Acids Research, 40(4):e27.
Ruan, P., Hayashida, M., Maruyama, O., and Akutsu, T.
(2013). Prediction of heterodimeric protein complexes
from weighted protein-protein interaction networks
using novel features and kernel functions. PLoS ONE,
8(6):e65265.
Sigrist, C. J. A., De Castro, E., Langendijk-Genevaux,
P. S., Le Saux, V., Bairoch, A., and Hulo, N. (2005).
ProRule: a new database containing functional and
structural information on PROSITE profiles. Bioin-
formatics, 21(21):4060–4066.
Tarjan, R. (1977). Finding optimum branchings. Networks,
7:25–35.
The UniProt Consortium (2019). UniProt: a worldwide
hub of protein knowledge. Nucleic Acids Research,
47:D506–D515.
Woese, C. and Fox, G. (1977). Phylogenetic structure of
the prokaryotic domain: the primary kingdoms. Proc.
Natl. Acad. Sci. USA, 74(11):5088–5090.
BIOINFORMATICS 2020 - 11th International Conference on Bioinformatics Models, Methods and Algorithms
122