
An Autoregressive Multiple Model Probabilistic Framework for the
Detection of SSVEPs in Brain-Computer Interfaces
Rosanne Zerafa
1 a
, Tracey Camilleri
1 b
, Owen Falzon
2 c
and Kenneth P. Camilleri
1,2 d
1
Department of Systems and Control Engineering, Faculty of Engineering, University of Malta, Msida, Malta
2
Centre for Biomedical Cybernetics, University of Malta, Msida, Malta
Keywords:
Steady-State Visually Evoked Potential, BCI, Electroencephalography, Single-channel, Univariate, Multiple
Modelling, Autoregressive Modelling.
Abstract:
This work investigates a novel autoregressive multiple model (AR-MM) probabilistic framework for the de-
tection of steady-state visual evoked potentials (SSVEPs) in brain-computer interfaces (BCIs). The proposed
method is compared to standard SSVEP detection techniques using a 12-class SSVEP dataset recorded from
10 subjects. The results, obtained from a single-channel analysis, reveal that the AR-MM probabilistic frame-
work significantly improves the SSVEP detection performance compared to the standard single-channel power
spectral density analysis (PSDA) method. Specifically, an average classification accuracy of 82.02 ± 16.21
% and an information transfer rate (ITR) of 48.22 ± 17.25 bpm are obtained with a 2 s period for SSVEP
detection with the AR-MM probabilistic framework. These results are found to be on average only 2.29 %
and 3.73 % lower in classification accuracy compared to the state-of-the-art multichannel SSVEP detection
methods, specifically the canonical correlation analysis (CCA) and the filter bank canonical correlation analy-
sis (FBCCA) methods, respectively. In terms of training, it is shown that the proposed approach requires only
a few seconds of data to train each model. This study revealed the potential of using the AR-MM probabilistic
approach to distinguish between different classes using single-channel SSVEP data. The proposed method is
particularly appealing for practical use in real-world BCI applications where a minimal amount of channels
and training data are desirable.
1 INTRODUCTION
Brain-computer interface (BCI) systems offer an al-
ternative means of communication and control, re-
moving dependence on the peripheral nervous sys-
tem, opening up accessibility to individuals suffer-
ing from motor disabilities, and providing alternative
access methods to healthy individuals. Non-invasive
BCIs are typically based on electroencephalography
(EEG) where brain activity is acquired through scalp
electrodes. Specific patterns of electrical brain activ-
ity are then translated into commands to control spe-
cific equipment. There are various brain signals hav-
ing distinctive characteristics that are suitable as con-
trol signals for BCIs. This work focuses on SSVEPs,
which are electrical potentials evoked in the brain in
a
https://orcid.org/0000-0003-1640-9882
b
https://orcid.org/0000-0002-4908-1863
c
https://orcid.org/0000-0002-3680-3089
d
https://orcid.org/0000-0003-0436-6408
response to a repetitive visual stimulus that is flick-
ering at a specific frequency. This neural response
consists of oscillatory activity at the fundamental fre-
quency and harmonics of the visual stimulus, and is
prominent in the occipital region of the brain (Regan,
1966). An SSVEP-based BCI exploits this response
by uniquely associating each flickering visual stimuli
to a specific command. These stimuli are presented
to the user who may select a command by attending
to the corresponding stimulus. The BCI identifies the
SSVEP response in the EEG signal and generates the
particular command to control a software application
or an external device (Vialatte et al., 2010).
Parametric modelling, particularly autoregressive
modelling and its variants have been used extensively
to analyse EEG signals (Pardey et al., 1996; Cerutti
et al., 1988; Fabri et al., 2011). For example, AR
models have been used in spectral analysis (Krusien-
ski et al., 2006), feature extraction (Zhang et al., 2015;
Chen et al., 2013), artifact/noise rejection (Wang
et al., 2014; Friman et al., 2007) and for the estima-
68
Zerafa, R., Camilleri, T., Falzon, O. and Camilleri, K.
An Autoregressive Multiple Model Probabilistic Framework for the Detection of SSVEPs in Brain-Computer Interfaces.
DOI: 10.5220/0008924400680078
In Proceedings of the 13th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2020) - Volume 4: BIOSIGNALS, pages 68-78
ISBN: 978-989-758-398-8; ISSN: 2184-4305
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

tion of the cortical functional connectivity (Babiloni
et al., 2005). These techniques fit a model to a time
series signal, having parameters that characterise the
dynamics of the data being modelled. In SSVEP stud-
ies, parametric AR models have been typically used
to provide a power spectrum from which the SSVEP
frequency components are enhanced and used as fea-
tures for SSVEP detection (Herrmann, 2001; Guger
et al., 2012; Safi et al., 2018). The encouraging re-
sults of AR models applied to several EEG-based ap-
plications, has motivated this work to investigate the
use of AR models in a multiple model probabilistic
approach to detect SSVEPs.
In a multiple modelling framework, different
states or modes of operation are represented by spe-
cific models, known as expert models (Liehr et al.,
1999). For an SSVEP-based BCI application, each
expert model would represent an SSVEP class that
is attributed to a specific flickering stimulus. In this
work, each expert model is represented as a linear
Gaussian state space model (Ghahramani and Hinton,
1998) which is autoregressive in nature. The use of
AR parameters as features for classification is com-
mon in EEG based BCI related literature (Galka et al.,
2010; Zhang et al., 2016; Wenchang et al., 2019;
Samdin et al., 2013; Zhang et al., 2016; Miran et al.,
2018), however in this work we use the AR models for
prediction. The residual between the actual and pre-
dicted data is used to determine which model from the
available set best represents the data at each point in
time. Since in an SSVEP-based BCI the subject is ex-
pected to attend to a sequence of stimuli, the dynam-
ics of the EEG signals are expected to switch from
one model to another in time. This residual is incor-
porated within a probabilistic framework in order to
provide a probabilistic decision for classification.
The proposed autoregressive multiple modelling
probabilistic framework works on a single channel of
EEG data and provides classification of SSVEPs in
batch mode, that is segmenting EEG data into a spe-
cific time window which is then processed and la-
belled. The framework is thus compared to power
spectral density analysis (PSDA) which is also a com-
monly used single channel SSVEP detection tech-
nique (M
¨
uller-Putz et al., 2008) as well as to canoni-
cal correlation analysis (CCA) (Lin et al., 2007) and
filter bank CCA (FBCCA) (Chen et al., 2015), both
of which are multi-channel techniques. The results
of the proposed framework showed significant im-
provement in classification performance compared to
PSDA for 1.5-3.5 s window lengths and on average
decreased slightly in classification performance com-
pared to CCA and FBCCA, with the added advantage
of requiring only a single channel. The latter is an im-
portant criterion for the practicality of real-time BCIs
applications.
The paper is organized as follows. In Section 2,
the SSVEP EEG data used for this analysis is pre-
sented and a mathematical description of the AR-
MM framework is given. This is followed by a brief
mathematical description of standard SSVEP detec-
tion methods found in the literature and which are
used here as reference methods. Section 3 presents
the results obtained when incorporating AR models
into a multiple model framework for the identifica-
tion and labelling of SSVEP data. Classification is
initially based on the prediction error alone and then
based on a probability measure. This is followed by
a discussion and conclusion, highlighting the benefits
of using the proposed AR-MM approach as an alter-
native SSVEP detection method.
2 MATERIALS AND METHODS
The first part of this section presents the SSVEP
dataset used for analysis and then presents the the-
ory of the proposed autoregressive multiple modelling
(AR-MM) framework as well as that of the SSVEP
detection techniques being used as baseline for com-
parison purposes.
2.1 SSVEP Dataset
The dataset used in this work contains frequency and
phase modulated SSVEP data from 12 classes, ac-
quired from 10 subjects. This data is used to estimate
the performance of a BCI virtual keyboard (Nakan-
ishi et al., 2015) and is freely available online (Nakan-
ishi, 2015). The 12 stimuli were presented simultane-
ously in matrix form as white squares on a black back-
ground, each having different frequencies ranging be-
tween 9.25 Hz to 14.75 Hz and phases between 0 π to
1.5 π. EEG data were recorded with eight Ag/AgCl
electrodes covering the occipital area. Each subject
was asked to gaze at each of the 12 visual stimuli in a
random order for 15 repetitions. At the beginning of
each trial, a red square appeared for 1 s at the position
of the target stimulus. Subjects were asked to shift
their gaze to the target within the same 1 s duration.
After that, all stimuli started to flicker simultaneously
for 4 s. To reduce eye movement artifacts, subjects
were asked to avoid eye blinks during the stimulation
period. The EEG data was down-sampled to 256 Hz
and then band-pass filtered from 6 Hz to 80 Hz. A
latency delay in the visual system of 135 ms was con-
sidered after each stimulus onset.
An Autoregressive Multiple Model Probabilistic Framework for the Detection of SSVEPs in Brain-Computer Interfaces
69

2.2 Autoregressive Multiple Modelling
(AR-MM) Framework
In this section a mathematical description is given
of the AR-MM framework, where each model is as-
sumed to be autoregressive, specifically applied to de-
tect SSVEPs from a single channel of EEG data. Clas-
sification of the multiple modelling framework is first
based on the AR models used for prediction. A differ-
ent approach is then taken where the AR models are
incorporated within a probabilistic MM framework to
provide a probability measure.
2.2.1 Fitting AR Models for Prediction
In the time domain a univariate AR(p) model of order
p is represented by:
y
t
= −
p
∑
j=1
a
j
y
t− j
+ e
t
, (1)
where y
t
represents data from a single channel at time
t, a
j
represent the AR parameters, and e represents
a zero mean white Gaussian noise process. This is
expressed in the z-domain by:
Y (z) =
E(z)
A(z)
, (2)
where E(z) is the error term and A(z) = 1 + a
1
z
−1
+
... + a
p
z
−p
. Since all the model parameters lie in the
denominator of the rational transfer function, the AR
process is also typically known as an all-pole process.
SSVEP signals are typically characterised by spectra
with narrow peaks at the fundamental and harmonic
components of the stimulus frequency. In autoregres-
sive models, these spectra are characterised by poles
located close to the unit circle in the z-domain. Fur-
thermore, since over short time windows the SSVEP
data is relatively stationary it is reasonable to assume
non-adaptive AR models, where the model parame-
ters remain fixed over time. Non-adaptive parameter
estimation techniques, such as the Yule-Walker (YW),
Burg, and Least Squares (LS) methods (Pardey et al.,
1996; Stoica and Moses, 2005), can be used to find
the optimal parameters that best fit the EEG data.
The parameters of the AR models that have been
fit to SSVEP data may be used as features in a typ-
ical SSVEP classification approach. However, here
the AR models will be used to forecast future data
and analyse the residual between the actual data and
the predicted data.
If ˆy
t
denotes the predicted value of y
t
, then Equa-
tion (1) may be expressed as (Pardey et al., 1996):
ˆy
t
= −
p
∑
j=1
a
j
y
t− j
. (3)
The error between the actual value and the predicted
value is known as the forward prediction error and is
given by:
r
t
= y
t
− ˆy
t
= y
t
+
p
∑
j=1
a
j
y
t− j
. (4)
This residual error r may be used to determine the fit
of the model to the actual data. Specifically, a window
of SSVEP data can be labelled to one of the possible
classes by estimating and comparing the root mean
square error (RMSE) of each respective model.
2.2.2 AR-MM Probabilistic Framework
Let {y
1
,...,y
T
} be a sequence of observed EEG data
having dynamics that depend upon the p-dimensional
latent state variable x
x
x
t
. At time t, the joint distribu-
tion between x
x
x
t
and y
t
of a linear Gaussian state space
model that follows a Bayesian network is given by
(Ghahramani, 2001):
p(x
x
x
t
,y
t
) = p(x
x
x
1
)
T
∏
t=2
p(x
x
x
t
|x
x
x
t−1
)
T
∏
t=1
p(y
t
|x
x
x
t
), (5)
where p(·) denotes the probability density function
and x
x
x
t
is assumed to be a continuous real-valued hid-
den state variable. Assuming linearity and Gaussian-
ity, the state space model is represented by the follow-
ing state and measurement equations:
x
x
x
t
= Φ
Φ
Φx
x
x
t−1
+ w
w
w
t
(6)
y
t
= H
H
H
t
x
x
x
t
+ v
t
, (7)
where y
t
is the observed EEG data from a single
channel at time t, x
x
x
t
= [−a
1
,...,−a
p
]
T
is the hidden
state vector made up of p autoregressive parameters,
H
H
H
t
= [y
t−1
,...,y
t−p
] is the observation vector made up
of p past EEG data samples, Φ
Φ
Φ represents the state
transition matrix and w
w
w
t
and v
t
are two independent
Gaussian noise processes assumed to have zero mean
and covariance Q
Q
Q and variance R, respectively. In this
work, H
H
H
t
is taken to consist of the past p narrow band
pass filtered EEG data, specifically filtered around the
first H harmonic frequency components correspond-
ing to the SSVEP class being modelled by that state
space model, and y
t
is made up of unfiltered EEG data
at time t. Apart from the unknown AR parameters x
x
x
t
,
the unknown parameters that characterise the model
are collectively represented by Θ
Θ
Θ = [R,Q
Q
Q,Φ
Φ
Φ,µ
µ
µ,Σ
Σ
Σ],
where µ
µ
µ represents the initial hidden state vector and
Σ
Σ
Σ its corresponding covariance.
In a MM system, a set of N expert models each
represented by unique state space equations (6) and
(7) and having system parameters Θ
Θ
Θ
i
for i = 1, ...,N
need to be trained. The training process to learn these
BIOSIGNALS 2020 - 13th International Conference on Bio-inspired Systems and Signal Processing
70

system parameters Θ
Θ
Θ shall be described in Section
3.3. Once the different models are trained to represent
each of the states or classes in the system, a proba-
bilistic approach may be used to identify which of the
candidate models best represents the data.
Under this framework, the posterior probability
for each model M
i
given Y
Y
Y
t
, which represents the ob-
served EEG data up till time t, is given by Bayes’ rule
as follows (Fabri and Kadirkamanathan, 2001):
Pr(M
i
|Y
Y
Y
t
) = Pr(M
i
|y
t
,Y
Y
Y
t−1
)
=
p(y
t
|M
i
,Y
Y
Y
t−1
)Pr(M
i
|Y
Y
Y
t−1
)
∑
N
j=1
p(y
t
|M
j
,Y
Y
Y
t−1
)Pr(M
j
|Y
Y
Y
t−1
)
,
(8)
where Pr(M
i
|Y
Y
Y
t−1
) is the prior probability and
p(y
t
|M
i
,Y
Y
Y
t−1
) is the likelihood function which is as-
sumed to be Gaussian and hence estimated as follows:
p(y
t
|M
i
,Y
Y
Y
t−1
) = −
1
(2π)
1
2
|C
C
C
i
t
|
1
2
exp
−
1
2
(y
t
− ˆy
i
t
)
0
(C
C
C
i
t
)
−1
(y
t
− ˆy
i
t
)
.
(9)
In Equation (9), (y
t
− ˆy
i
t
) represents the difference be-
tween the observation y
t
and its mean estimate ˆy
i
t
, re-
ferred to as the residual. The mean estimate of the
observation ˆy
i
t
is given by:
ˆy
i
t
= H
H
H
i
t
ˆ
x
x
x
i
t|t−1
, (10)
where
ˆ
x
x
x
i
t|t−1
denotes the conditional expectation of
state x
x
x
t
. In Equation (9) C
C
C
i
t
is the variance of ˆy
i
t
es-
timated as follows:
C
C
C
i
t
= H
H
H
i
t
P
P
P
i
t|t−1
H
H
H
i
T
t
+ R
i
, (11)
where P
P
P
i
t|t−1
denotes the corresponding state estima-
tion error covariance.
When evaluating the posterior probability
Pr(M
i
|Y
Y
Y
t
) in Equation (8), the prior probability of
the model Pr(M
i
|Y
Y
Y
t−1
) is taken into consideration.
The prior probabilities are here set to be uniformly
distributed, that is, each model has equal chance of
modelling new data. This was done by setting all
prior probabilities equal to 1/N, where N represents
the number of models.
Given the assumption of stationarity within a fixed
time window, a non-adaptive approach is consid-
ered, where the hidden state vector and its covari-
ance are not updated but remain constant over time.
Therefore, the initial state vector and its correspond-
ing covariance remain the same µ
µ
µ = x
x
x
t
and Σ
Σ
Σ = Q
Q
Q.
Consequently in Equations (10) and (11), the initial
state vector and corresponding covariance are used
to calculate the posterior probability,
ˆ
x
x
x
i
t|t−1
= µ
µ
µ
i
and
P
P
P
i
t|t−1
= Σ
Σ
Σ
i
for all t. It follows that Φ
Φ
Φ = I in Equation
(6).
MAP
ExpertmodelN
Expertmodel1
Figure 1: AR-MM probabilistic framework with N expert
models acting as candidates to model the observed sequence
y
t
. The model M
∗
that has the highest posterior probability
is considered as the model that best represents the data.
Under this framework, N probabilities corre-
sponding to the N models are obtained at each time
instance with Equation (8). The model M
∗
that has
the maximum a posteriori (MAP) probability is then
considered as the model that best represents the in-
coming data from the set of available models. Figure
1 shows a block diagram of the AR-MM probabilistic
framework.
2.3 Standard SSVEP Detection
Methods
For the purpose of creating a reference against which
the new proposed method can be evaluated, a num-
ber of standard SSVEP detection techniques found in
the literature (Zerafa et al., 2018) were also imple-
mented. Similar to the proposed AR-MM probabilis-
tic framework, the following methods exploit only the
frequency information of the SSVEP signal, whereas
the phase information is not considered. The PSDA
method was chosen as a reference for the univari-
ate case since this is the simplest and most widely
used single-channel feature extraction method. For
the multivariate case, the CCA and FBCCA were se-
lected as reference methods. In the literature, the
CCA method is generally used as a reference method
against which new SSVEP methods are compared to,
while the FBCCA method, which is an extension of
CCA, has been shown to improve the frequency de-
tection of SSVEPs. A brief mathematical description
of these methods is presented below to better covey
the requirements of each technique and the frame-
work on which each is based.
An Autoregressive Multiple Model Probabilistic Framework for the Detection of SSVEPs in Brain-Computer Interfaces
71

2.3.1 Power Spectral Density Analysis (PSDA)
In PSDA a Fourier representation is used to transform
an EEG signal from the time domain to the frequency
domain and extract specific SSVEP features from the
resulting spectral content. The fast Fourier transform
(FFT) is performed on a single-channel EEG sig-
nal, from which the one-sided power spectral density
(PSD) (M
¨
uller-Putz et al., 2008) is estimated. A fea-
ture vector is constructed from the PSD values at the
fundamental frequencies and harmonics correspond-
ing to the flickering stimuli. A harmonic sum decision
(HSD) method (M
¨
uller-Putz and Pfurtscheller, 2008)
is adopted to construct SSVEP feature vectors, where
the sum of harmonic power values for each stimulus
frequency f
s
is computed as:
H
∑
h=1
max
f
(PSD( f | f ∈ [h f
s
− 0.125,h f
s
+ 0.125])), (12)
where h represents the harmonic number being con-
sidered and H represents the number of harmonic fre-
quencies considered. The feature vector is log nor-
malised to make the features normally distributed.
The largest power amplitude is expected to corre-
spond to the frequency of the target stimulus, repre-
senting the SSVEP response.
2.3.2 Canonical Correlation Analysis (CCA)
CCA is a multivariable statistical method used to find
the underlying correlation between two sets of data
(Lin et al., 2007), used to detect SSVEPs in multi-
channel EEG data. Let Y
Y
Y and X
X
X
f
be two multidimen-
sional variables representing the multi-channel EEG
signals of length T samples and a set of SSVEP ref-
erence signals which have the same length as Y
Y
Y , re-
spectively. The sine-cosine reference signals X
X
X
f
for
the target stimulus frequency f are defined by:
X
X
X
f
=
sin(2πh f
t
F
s
)
cos(2πh f
t
F
s
)
.
.
.
sin(2πH f
t
F
s
)
cos(2πH f
t
F
s
)
T
,
t = 1,... ,T
h = 1,.. .,H
, (13)
where F
s
is the sampling frequency, T is the num-
ber of samples and H is the number of harmonics.
CCA finds the linear combinations y = Y
Y
Y
T
W
W
W
y
and
x
f
= X
X
X
T
f
W
W
W
x
f
, such that the correlation between the
two canonical variants y and x
f
is maximized (Lin
et al., 2007). The weight vectors W
W
W
y
and W
W
W
x
f
are
found by solving the following optimization problem
(Bin et al., 2009):
max
W
W
W
y
,W
W
W
x
f
ρ
f
(y, x
f
) =
E[y
T
x
f
]
q
E[y
T
y]E[x
T
f
x
f
]
=
E[W
W
W
T
y
Y
Y
Y X
X
X
T
f
f
f
W
W
W
x
f
]
q
E[W
W
W
T
y
Y
Y
YY
Y
Y
T
W
W
W
y
]E[W
W
W
T
x
f
X
X
X
f
f
f
X
X
X
T
f
f
f
W
W
W
x
f
]
.
(14)
For each reference signal, a maximum canonical cor-
relation ρ
f
is obtained and used as an SSVEP feature.
The hypothesis is that the reference signal with the
largest correlation contains SSVEP at the same fre-
quency as the stimulus signal.
2.3.3 Filter Bank Canonical Correlation
Analysis (FBCCA)
The FBCCA method is a CCA variant that decom-
poses SSVEPs into multiple sub-band components.
FBCCA performs separate CCAs between each of the
sub-band components and sine-cosine reference sig-
nals (Chen et al., 2015). The filter bank used consists
of sub-bands covering multiple harmonic frequency
bands. The correlation values between the sub-band
components Y
Y
Y
SB
k
, k = 1,...,K from the original EEG
signals Y
Y
Y and the reference signals X
X
X
f
correspond-
ing to all stimulation frequencies f are estimated to
form a correlation vector ρ
ρ
ρ
f
= [ρ
1
f
,..., ρ
K
f
]
T
, where
K is the number of sub-bands. A weighted sum of
squares of the correlation values corresponding to all
sub-band components is then calculated as the feature
for SSVEP detection as follows:
˜
ρ
f
=
K
∑
k=1
w
w
w(k) · (ρ
k
f
)
2
, (15)
where w
w
w(k) are the weights of the sub-band compo-
nents. These weights are set by the observation that
the signal to noise ratio (SNR) of SSVEP harmonics
decreases as the response frequency increases:
w
w
w(k) = k
−a
+ b, k = 1,.. .,K , (16)
where a and b are constants that maximize the clas-
sification performance. The frequency of the refer-
ence signals having the maximum correlation is then
considered to be the target stimulus. The FBCCA
method requires three parameters to be optimized,
namely the number of harmonics to be considered in
the reference signals, the weight vector for the sub-
band components and the number of sub-bands in the
filter bank. Since these may interact with each other in
influencing the BCI performance (Chen et al., 2015;
Nakanishi et al., 2018), a grid search involving the si-
multaneous optimization of these parameters is con-
ducted using training data from various subjects. In
BIOSIGNALS 2020 - 13th International Conference on Bio-inspired Systems and Signal Processing
72
5 10 15 20 25 30 35 40 45 50
Frequency (Hz)
0
2
4
6
8
10
12
Amplitude
10
7
A
1
A
2
A
3
A
4
A
5
A
6
A
7
A
8
A
9
A
10
A
11
A
12
Figure 2: Spectra of the 12 AR models.
this work, based on the findings in the literature, the
number of harmonics, the weight vector, i.e. a and b
in Equation (16), and the number of sub-bands were
fixed to 3, 1.25, 0.25 and 5, respectively.
3 RESULTS
In this section the application of AR models to
SSVEP data is first described. Classification results
of the AR-MM framework are then presented. This
is followed by a description of the training require-
ments of the probabilistic multiple model framework
and its classification results compared to that of stan-
dard SSVEP detection methods.
3.1 AR Models Applied to SSVEP Data
The SSVEP data described in Section 2.1 consisted of
12 different classes, hence an AR model was trained
for each respective class. Training data was narrow
band pass filtered around the first H = 3 harmonic
frequency components corresponding to the actual
SSVEP response such that background activity not
corresponding to the SSVEP response is filtered out
and hence not modelled. An AR model of order 20
was then fit to the data. Given the narrow band filter-
ing done at the pre-processing stage, this model order
was found to give a good representation of the data ir-
respective of the stimulus class. A set of AR parame-
ters A
i
= {a
1
,...,a
p
}, for each model i = 1,..,N
f
was
then obtained using Burg’s method, where N
f
= 12
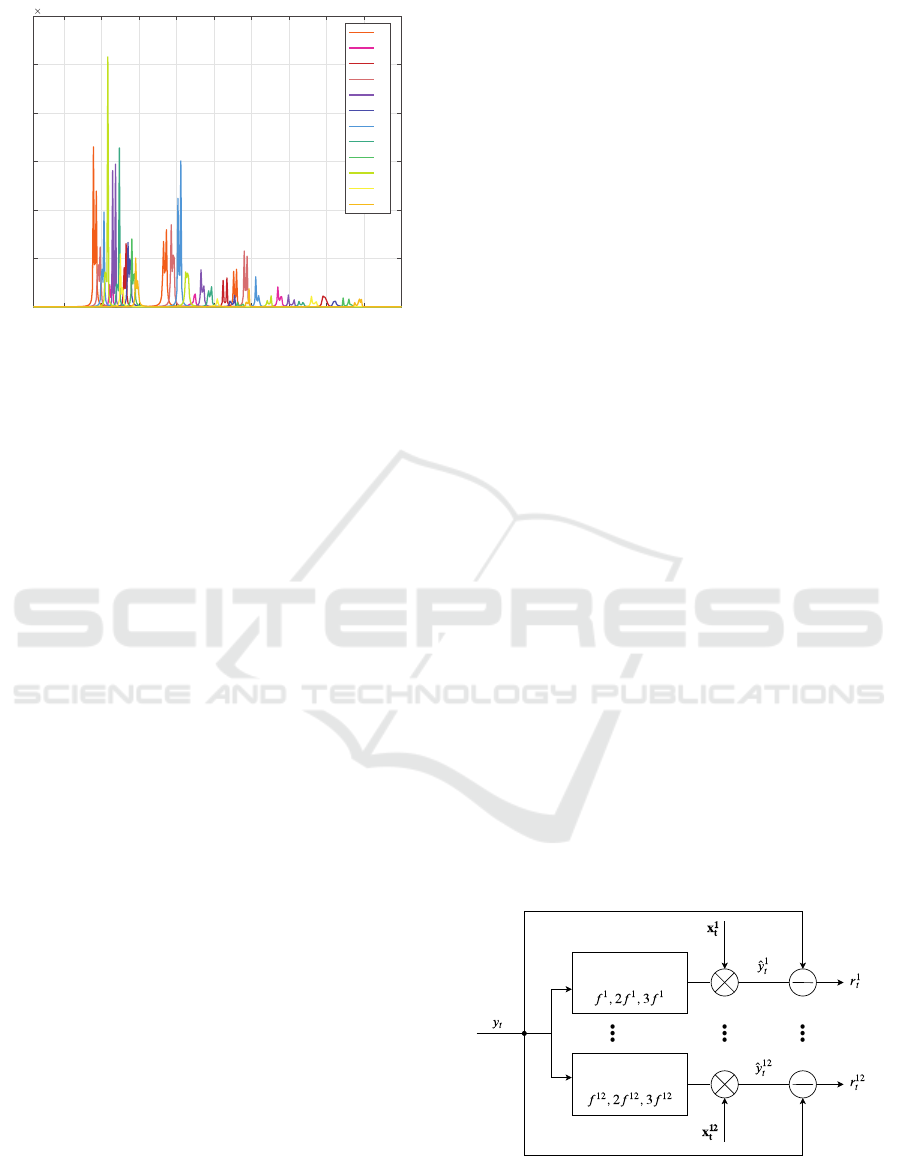
is the number of stimuli classes. Figure 2 shows the
spectra of 12 trained AR models, as an example.
When assigning a class to a new test trial y
t
, the
data is first narrow band pass filtered around the first
three harmonic frequency components corresponding
to each of the 12 stimuli classes. Each trained AR
model, having AR parameter vectors x
x
x
i
t
, is then used
to estimate ˆy
t
, the predicted value of y
t
using Equation
(3). This process is shown in Figure 3.
As an example, Figure 4a shows the original un-
filtered signal and the narrow band pass filtered sig-
nals estimated by each AR model for a 10.25 Hz test
trial. The errors between the original test signal y
t
and
the predicted signals ˆy
i
t
were estimated and the lowest
RMSE across the 2 s window was found. In this case
the minimum error was that between y
t
and ˆy
7
t
, shown
in Figure 4b. A difference between the two signals
can still be observed since the estimated signal is nar-
row band pass filtered around the expected frequency
while the original signal is unfiltered. Hence any ac-
tivity outside the bands of interest will not be mod-
elled. The correct model, however, is expected to best
represent the SSVEP related activity and hence result
in the smallest residual error. In the case being shown
here, this trial was correctly labelled as a class 7 trial,
corresponding to the 10.25 Hz SSVEP response.
3.2 Classification Results of the
AR-MM Method
This section presents the classification accuracy re-
sults when using the lowest RMSE of the 12 trained
models to classify each trial into one of the 12 avail-
able classes. The classification accuracy was esti-
mated by considering only 1 trial per class as train-
ing data to generate the AR models, with the re-
maining 14 trials per class being used as testing data.
Cross validation was then carried out by repeating
the process such that each of the 15 trials was used
once for training purposes, and finally the average
classification accuracy was computed. This analysis
was carried out on each bipolar channel combination
and the highest performance associated with the best
Filterfor
Filterfor
Figure 3: Process to find residual errors between original
signal y
t
and estimated signals ˆy
i
t
for i = 1,..., 12 using 12
different AR models having parameter vectors x
x
x
1
t
to x
x
x
12
t
.
An Autoregressive Multiple Model Probabilistic Framework for the Detection of SSVEPs in Brain-Computer Interfaces
73

0 0.5 1 1.5 2
Time (s)
-12
-10
-8
-6
-4
-2
0
2
4
6
8
Amplitude
(a) Test data y
t
and estimated ˆy
i
t
in the time domain.
0 0.5 1 1.5 2
Time (s)
-12
-10
-8
-6
-4
-2
0
2
4
6
8
Amplitude
(b) Test data y
t
and estimated ˆy
7
t
in the time domain.
Figure 4: A 2 s SSVEP test trial at 10.25 Hz, represented
by class number 7 in the 12-class dataset.
bipolar channel (BBC) was found. The classification
accuracy was also evaluated using different window
lengths for SSVEP detection. Apart from classifica-
tion accuracy, the information transfer rate (ITR) in
bits per minute (bpm) (Wolpaw et al., 2002) was used
as a performance measure and was calculated as:
IT R =
60
T
log
2
N
f
+ Plog
2
P + (1 −P)log
2
1 − P
N
f
− 1
,
(17)
where P is the classification accuracy, and T is the
average time for selection in seconds. An additional
gaze shifting time of 1 s was included in the estima-
tion of the ITR.
Figure 5 shows the average accuracy obtained
with the AR-MM framework, across all subjects and
sessions, for different data lengths ranging between
0.5 s to 4 s, in steps of 0.5 s. The proposed ap-
Table 1: AR-MM results for 12 classes (8.33 % chance clas-
sification accuracy) with 2 s window and 1 s gaze shift.
Subject Accuracy (%) ITR (bpm)
1 47.78 15.60
2 78.33 41.63
3 55.00 20.71
4 71.11 34.37
5 93.33 60.02
6 83.89 47.81
7 96.11 64.27
8 90.56 56.14
9 98.89 69.17
10 93.89 60.83
Mean ± STD 80.89 ± 16.88 47.05 ± 17.61
proach was compared to the PSDA method for which
the performance obtained with the BBC is also be-
ing reported for fair comparison. The PSDA re-
sults obtained are in line with those found in litera-
ture (Lin et al., 2007; Bin et al., 2009), although it
must be noted that direct comparison is difficult due
to variations in BCI setups, such as the number of
stimuli being used. As expected, for both methods,
the SSVEP classification increases with the length of
time window for detection. Paired t-tests were con-
ducted to analyse the difference in performance be-
tween the two methods across all the time windows.
These revealed that there is a statistically significant
(p < 0.05) increase in performance for the AR-MM
method compared with the PSDA for time windows
between 1.5 s and 3 s.
To provide insight on individual subjects’ perfor-
mance, the results in Figure 5 for a time window of 2
s were expanded in Table 1.
This demonstrates that there is a large variation in
performance between subjects. In fact, the classifica-
tion accuracy for 5 subjects is above 90%, for 3 sub-
jects this is between 70% and 90% and for 2 subjects
0.5 1 1.5 2 2.5 3 3.5 4
Time window (s)
0
10
20
30
40
50
60
70
80
90
100
Accuracy (%)
0.5 1 1.5 2 2.5 3 3.5 4
Time window (s)
5
10
15
20
25
30
35
40
45
50
ITR (bpm)
PSDA AR-MM
Figure 5: Performance comparison of PSDA and AR-MM
methods. (a) Average classification accuracy (%) and (b)
ITR (bpm) across all subjects for different time windows
(s).
BIOSIGNALS 2020 - 13th International Conference on Bio-inspired Systems and Signal Processing
74

this is in the range of 50%.
These initial findings demonstrate that AR models
provide a good fit for the SSVEP data and may be
used as a model structure in the multiple modelling
probabilistic framework.
3.3 Training for the Probabilistic
AR-MM Framework
Given the results obtained with the AR-MM approach
presented in the previous section, the AR multiple
models were incorporated within a probabilistic mul-
tiple modelling framework. The process of learning
the AR parameters x
x
x
i
t
and system parameters Θ
Θ
Θ in a
multiple modelling framework requires SSVEP train-
ing data for each class. Let z
i
t
be a vector of a sin-
gle channel SSVEP EEG data, with i = 1,...,N
f
rep-
resenting the number of target stimulus frequencies.
This data is then narrow band pass filtered around
the fundamental frequency f and the first H harmonic
components corresponding to the SSVEP class i and
is represented here by z
i
f
t
. The estimation of parame-
ters x
x
x
i
t
and Θ
Θ
Θ is then being carried out as follows:
• With reference to Section 3.1, the AR parameters
x
x
x
i
t
for the expert model M
i
are found using the fil-
tered training data z
i
f
t
. AR parameters are esti-
mated using Burg’s method and the length of x
x
x
i
t
represents the AR model of order p which was
here set to 20.
• The unknown variance R is estimated from Equa-
tion (7), where the observation vector y
t
is re-
placed with training data z
t
, i.e. v
t
= z
t
− H
H
H
t
x
x
x
t
. In
this case H
H
H
t
represents p past narrow bandpass fil-
tered training data, i.e. H
H
H
t
= [z
f
t−1
,...,z
f
t−p
]. The
variance σ
i
l
of the resulting v
t
is obtained from
each training trial of all the classes i = 1, ...,N
f
,
where l = 1, ...,L represents the number of train-
ing trials. The mean variance across all the train-
ing trials gives R, i.e. R = 1/(N
f
L)
∑
N
f
i=1
∑
L
l=1
σ
i
l
.
• The unknown covariance Q
Q
Q
i
for model M
i
is es-
timated from Equation (6), where for the non-
adaptive approach x
x
x
i
t
= Ix
x
x
i
t
+ w
w
w
t
. Therefore, the
covariance of x
x
x
i
t
∈ R
p
obtained from AR param-
eters across different training trials gives Q
Q
Q
i
∈
R
p×p
.
• As discussed earlier, following the non-adaptive
approach, the rest of the unknown system param-
eter are defined as µ
µ
µ = x
x
x
t
, Σ
Σ
Σ = Q
Q
Q and Φ
Φ
Φ = I.
3.4 AR-MM Probabilistic Framework
In order to compare the performance of the AR-
MM probabilistic approach with that of the state-
of-the-art methods, batch mode classification is con-
sidered in which each trial is first segmented and
then passed through the AR-MM probabilistic pro-
cess. Labelling of one trial is done by finding
argmax
M
∑
N
t
t=1
Pr(M
i
|Y
Y
Y
t
), where N
t
is the total number
of samples in the time window.
Figure 6 shows the average classification accu-
racy and ITR obtained with the AR-MM probabilistic
framework across all subjects and sessions for differ-
ent data lengths from 0.5 s to 4 s, in steps of 0.5 s.
The classification accuracy was estimated by con-
sidering 2 trials per class as training data to generate
the AR models x
x
x
t
, R and Q
Q
Q and the remaining were
used for testing. A minimum of 2 training trials were
necessary to estimate the covariance Q
Q
Q of the state
vector. This process was then repeated seven times
such that all trials were considered for training and an
average classification accuracy was computed. The
performance of the AR-MM probabilistic approach is
compared with that of the PSDA, CCA and FBCCA
methods. In the case of both the AR-MM probabilis-
tic approach and the PSDA method, the performance
for each bipolar channel combination was computed
and the highest performance associated with the BBC
was found. On the other hand, all 8 channels were
used in the estimation of the CCA and FBCCA mul-
tivariate methods.
Two-way repeated measures ANOVA were per-
formed to compare the performance of the proposed
0.5 1 1.5 2 2.5 3 3.5 4
Time window (s)
0
10
20
30
40
50
60
70
80
90
100
Accuracy (%)
0.5 1 1.5 2 2.5 3 3.5 4
Time window (s)
0
10
20
30
40
50
60
ITR (bpm)
PSDA AR-MM probabilistic framework CCA FBCCA
Figure 6: Performance comparison of PSDA, AR-MM
probabilistic framework, CCA and FBCCA methods. (a)
Average classification accuracy (%) and (b) ITR (bpm)
across all subjects for different time windows (s).
An Autoregressive Multiple Model Probabilistic Framework for the Detection of SSVEPs in Brain-Computer Interfaces
75

AR-MM probabilistic framework with each of the ref-
erence SSVEP detection methods across all the differ-
ent time windows. This indicated that there was a sta-
tistically significantly (p < 0.05) improvement in the
overall SSVEP classification accuracy with the AR-
MM probabilistic framework when compared with
the PSDA method. Post-hoc paired t-tests, which
considered the results from different time windows,
revealed that the AR-MM probabilistic method ob-
tained statistically significantly (p < 0.05) higher ac-
curacies compared to PSDA method for time win-
dows 1.5 s - 3.5 s. The overall classification accura-
cies of the multichannel methods, CCA and FBCCA,
were slightly higher than that of the single-channel
AR-MM probabilistic framework. In the case of the
FBCCA method, the accuracy was found to be sta-
tistically significantly higher (p < 0.05) than the AR-
MM probabilistic approach for time windows of 1 s,
1.5 s and 4 s. These results indicate that the AR-
MM probabilistic approach can significantly enhance
the performance of the single-channel PSDA method.
These results also show a slight decrease in perfor-
mance, specifically 2.29 % compared to the multi-
channel CCA method and 3.73 % compared to its
extension the FBCCA method on average over all
time windows, with the advantage of requiring only
a single-channel for SSVEP detection.
4 DISCUSSION
The results presented in Section 3 demonstrate that
the multiple model probabilistic framework is a
promising technique for the detection of SSVEPs in
BCIs.
Autoregressive models that capture the dynamics
of the underlying SSVEP signal in the EEG data were
used as a model structure for the AR-MM framework.
Initially an investigation was conducted to evaluate
whether AR models provide a good fit for the data.
The standard approach of using AR models in EEG
analysis is to find AR parameters for incoming EEG
data to form features which can then be used for clas-
sification (Guger et al., 2012; Safi et al., 2018). In
this work however, AR expert models were trained
for each SSVEP class, each of which has a distinct
frequency, and then used for prediction on new EEG
data. The residual between the true and the recon-
structed signals was evaluated and used for classifica-
tion. This was done since the MM framework is based
on the analysis of this residual which is specifically
used to calculate the likelihood function in Equation
(9). The initial classification results of the AR-MM
framework using the RMSE as a basis for classifica-
tion were compared to the PSDA method. The latter
is the simplest and one of the most commonly used
SSVEP detection methods, which similarly to the pro-
posed approach, operates on bipolar EEG channels.
It is worth pointing out that the classification of the
PSDA method is done using features in the frequency
domain, specifically by analysing the power ampli-
tude of respective harmonics, while the classifica-
tion of the AR-MM approach is done in the time do-
main, specifically by analysing the residual between
the original and the predicted signals. The results ob-
tained by the AR-MM approach showed a significant
improvement in performance compared to the PSDA
method.
The second part of the analysis involved the re-
structuring of the AR-MM approach within a proba-
bilistic framework. In this case, a probability measure
for each model in representing incoming data was ob-
tained at each time instance and this result was then
evaluated to find which model gave the best repre-
sentation within a fixed time window, allowing batch
mode classification as done with other state-of-the-art
techniques. In this case, apart from comparing the
performance of the AR-MM probabilistic framework
to a similar single bipolar channel PSDA method,
the framework was also compared to the multivariate
CCA and FBCCA methods. Similar to the proposed
AR-MM probabilistic framework, these methods ex-
ploit only the frequency information of the SSVEP
signal, whereas the phase information is not consid-
ered. This is particularly useful in BCI setups that
do not have phase coded stimuli. It must be high-
lighted that multichannel SSVEP detection methods
are known to benefit from an optimized combination
of multiple signals. In fact it has been shown that this
results in a greater robustness against noise and hence
improved performance compared to single channel
methods (Friman et al., 2007; Bin et al., 2009). The
results obtained for the single-channel AR-MM prob-
abilistic framework showed significant improvement
over the single-channel PSDA method but even more
promising, the results obtained were only slightly
lower compared to the multichannel methods for most
time windows of SSVEP detection. This means that
a BCI requires only a pair of electrodes to function
with the AR-MM probabilistic approach, making it
more practical for the user.
Various studies have shown that incorporating a
user’s training data significantly improves the detec-
tion performance (Nakanishi et al., 2015). However,
the amount of training data significantly varies be-
tween methods and this may result in long and tedious
training sessions (Zerafa et al., 2018). In this work it
was shown that the AR-MM probabilistic method re-
BIOSIGNALS 2020 - 13th International Conference on Bio-inspired Systems and Signal Processing
76

quires only 2 trials per class of training data to model
the AR models, hence only a few seconds of training
are actually required for a new BCI user. From a pre-
liminary analysis we have carried out, we identified
that increasing the number of training trials for the
AR-MM framework did not show statistical improve-
ments in performance. The transferability of train-
ing data in the AR-MM probabilistic approach from
one subject to another will also be addressed in future
work.
5 CONCLUSIONS
A novel autoregressive multiple model (AR-MM)
probabilistic framework for the detection of SSVEPs
for BCIs was presented in this paper. Through this
work we have shown that the univariate AR-MM
probabilistic approach can yield a significant im-
provement in performance over PSDA, a standard
single-channel SSVEP detection method and is only
2.29 % and 3.73 % lower in classification perfor-
mance compared to CCA and FBCCA, respectively,
two standard multichannel SSVEP detection meth-
ods. The proposed framework also provides a mea-
sure of probability for each SSVEP class, which can
be used as a measure of certainty in the decision mak-
ing process.
ACKNOWLEDGEMENTS
This work was partially supported by the project
BrainApp, financed by the Malta Council for Science
& Technology through FUSION: The R&I Technol-
ogy Development Programme 2016.
REFERENCES
Babiloni, F., Cincotti, F., Babiloni, C., Carducci, F., Mat-
tia, D., Astolfi, L., Basilisco, A., Rossini, P. M., Ding,
L., Ni, Y., Cheng, J., Christine, K., Sweeney, J., and
He, B. (2005). Estimation of the cortical functional
connectivity with the multimodal integration of high-
resolution EEG and fMRI data by directed transfer
function. Neuroimage, 24(1):118–131.
Bin, G., Gao, X., Yan, Z., Hong, B., and Gao, S.
(2009). An online multi-channel SSVEP-based brain-
computer interface using a canonical correlation anal-
ysis method. J. Neural Eng., 6(4):046002.
Cerutti, S., Chiarenza, G., Liberati, D., Mascellani, P., and
Pavesi, G. (1988). A Parametric Method of Identifica-
tion. IEEE Trans. Biomed. Eng., 35(9):701–711.
Chen, L. L., Madhavan, R., Rapoport, B. I., and Ander-
son, W. S. (2013). Real-time brain oscillation detec-
tion and phase-locked stimulation using autoregres-
sive spectral estimation and time-series forward pre-
diction. IEEE Trans. Biomed. Eng., 60(3):753–762.
Chen, X., Wang, Y., Gao, S., Jung, T.-P., and Gao,
X. (2015). Filter bank canonical correlation
analysis for implementing a high-speed SSVEP-
based brain–computer interface. J. Neural Eng.,
12(4):46008.
Fabri, S., Camilleri, K., and Cassar, T. (2011). Paramet-
ric Modelling of EEG Data for the Identification of
Mental Tasks. In Biomed. Enigeering Trends Electron.
Commun. Softw., pages 367–386.
Fabri, S. G. and Kadirkamanathan, V. (2001). Functional
Adaptive Control : an Intelligent Systems Approach.
Springer London.
Friman, O., Volosyak, I., and Gr
¨
aser, A. (2007). Mul-
tiple channel detection of steady-state visual evoked
potentials for brain-computer interfaces. IEEE Trans.
Biomed. Eng., 54(4):742–750.
Galka, A., Wong, K. K. F., and Ozaki, T. (2010). Modeling
Phase Transitions in the Brain. Model. Phase Transi-
tions Brain, pages 27–53.
Ghahramani, Z. (2001). An Introduction to Hidden Markov
Models and Bayesian Networks. J. Pattern Recognit.
Artif. Intell., 15(1):9–42.
Ghahramani, Z. and Hinton, G. E. (1998). Switching State-
Space Models. Dep. Comput. Sci. Univ. Toronto,
pages 1–28.
Guger, C., Allison, B. Z., Großwindhager, B., Pr
¨
uckl, R.,
Hinterm
¨
uller, C., Kapeller, C., Bruckner, M., Krausz,
G., and Edlinger, G. (2012). How many people could
use an SSVEP BCI? Front. Neurosci., 6(169):1–6.
Herrmann, C. S. (2001). Human EEG responses to 1-100
Hz flicker: Resonance phenomena in visual cortex
and their potential correlation to cognitive phenom-
ena. Exp. Brain Res., 137(3-4):346–353.
Krusienski, D. J., McFarland, D. J., and Wolpaw, J. R.
(2006). An evaluation of autoregressive spectral es-
timation model order for brain-computer interface ap-
plications. Conf. Proc. IEEE Eng. Med. Biol. Soc.,
1:1323–6.
Liehr, S., Pawelzik, K., Kohlmorgen, J., and M
¨
uller, K. R.
(1999). Hidden Markov mixtures of experts with an
application to EEG recordings from sleep. Theory
Biosci., 118(3-4):246–260.
Lin, Z., Zhang, C., Wu, W., and Gao, X. (2007). Frequency
recognition based on canonical correlation analysis
for SSVEP-Based BCIs. IEEE Trans. Biomed. Eng.,
54(6):1172–1176.
Miran, S., Akram, S., Sheikhattar, A., Simon, J. Z., Zhang,
T., and Babadi, B. (2018). Real-time tracking of se-
lective auditory attention from M/EEG: A Bayesian
filtering approach. Front. Neurosci., 12(MAY):1–20.
M
¨
uller-Putz, G. R., Eder, E., Wriessnegger, S. C., and
Pfurtscheller, G. (2008). Comparison of DFT and
lock-in amplifier features and search for optimal elec-
trode positions in SSVEP-based BCI. J. Neurosci.
Methods, 168(1):174–181.
An Autoregressive Multiple Model Probabilistic Framework for the Detection of SSVEPs in Brain-Computer Interfaces
77

M
¨
uller-Putz, G. R. and Pfurtscheller, G. (2008). Control
of an electrical prosthesis with an SSVEP-based BCI.
IEEE Trans. Biomed. Eng., 55(1):361–364.
Nakanishi, M. (2015). 12-class joint frequency-
phase modulated SSVEP dataset for
estimating online BCI performance
[https://github.com/mnakanishi/12JFPM SSVEP].
Nakanishi, M., Wang, Y., Chen, X., Wang, Y.-t., Gao,
X., and Jung, T.-p. (2018). Enhancing Detection of
SSVEPs for a High-Speed Brain Speller Using Task-
Related Component Analysis. IEEE Trans. Biomed.
Eng., 65(1):104–112.
Nakanishi, M., Wang, Y., Wang, Y.-t., and Jung, T.-p.
(2015). A comparison study of canonical correlation
analysis based methods for detecting steady-state vi-
sual evoked potentials. PLoS One, 10(10):e0140703.
Pardey, J., Roberts, S., and Tarassenko, L. (1996). A review
of parametric modelling techniques for EEG analysis.
Med. Eng. Phys., 18(1):2–11.
Regan, D. (1966). Some characteristics of average
steady-state and transient responses evoked by mod-
ulated light. Electroencephalogr. Clin. Neurophysiol.,
20(3):238–248.
Safi, S. M. M., Pooyan, M., and Motie Nasrabadi, A.
(2018). SSVEP recognition by modeling brain activ-
ity using system identification based on Box-Jenkins
model. Comput. Biol. Med., 101(August):82–89.
Samdin, S. B., Ting, C. M., Salleh, S. H., Ariff, A. K., and
Mohd Noor, A. B. (2013). Linear dynamic models
for classification of single-trial EEG. Proc. Annu. Int.
Conf. IEEE Eng. Med. Biol. Soc. EMBS, (July):4827–
4830.
Stoica, P. and Moses, R. (2005). Spectral Analysis of Sig-
nals. Pearson Prentice Hall.
Vialatte, F. B., Maurice, M., Dauwels, J., and Cichocki, A.
(2010). Steady-state visually evoked potentials: Focus
on essential paradigms and future perspectives. Prog.
Neurobiol., 90(4):418–438.
Wang, Z., Xu, P., Liu, T., Tian, Y., Lei, X., and Yao,
D. (2014). Robust removal of ocular artifacts by
combining Independent Component Analysis and sys-
tem identification. Biomed. Signal Process. Control,
10(1):250–259.
Wenchang, Z., Fuchun, S., Chuanqi, T., and Shaobo, L.
(2019). Linear Dynamical Systems Modeling for
EEG-Based Motor Imagery Brain-Computer Inter-
face. 1006(December 2018).
Wolpaw, J. R., Birbaumer, N., Mcfarland, D. J.,
Pfurtscheller, G., and Vaughan, T. M. (2002).
Brain–computer interfaces for communication and
control. Clin. Neurophysiol., 113:767–791.
Zerafa, R., Camilleri, T., Falzon, O., and Camilleri, K. P.
(2018). To train or not to train? A survey on training
of feature extraction methods for SSVEP-based BCIs.
J. Neural Eng., 15(051001).
Zhang, W., Sun, F., Tan, C., and Liu, S. (2016). Low-Rank
Linear Dynamical Systems for Motor Imagery EEG.
Comput. Intell. Neurosci., 2016.
Zhang, Y., Ji, X., and Zhang, Y. (2015). Classification of
EEG signals based on AR model and approximate en-
tropy. Proc. Int. Jt. Conf. Neural Networks, 2015-
Septe.
BIOSIGNALS 2020 - 13th International Conference on Bio-inspired Systems and Signal Processing
78
