
User-controllable Multi-texture Synthesis with Generative Adversarial
Networks
Aibek Alanov
1,2,3
, Max Kochurov
2,4
, Denis Volkhonskiy
4
, Daniil Yashkov
5
,
Evgeny Burnaev
4
and Dmitry Vetrov
2,3
1
National Research University Higher School of Economics, Moscow, Russia
2
Samsung AI Center Moscow, Moscow, Russia
3
Samsung-HSE Laboratory, National Research University Higher School of Economics, Moscow, Russia
4
Skolkovo Institute of Science and Technology, Moscow, Russia
5
Federal Research Center ”Computer Science and Control” of the Russian Academy of Sciences, Moscow, Russia
Keywords:
Texture Synthesis, Manifold Learning, Deep Learning, Generative Adversarial Networks.
Abstract:
We propose a novel multi-texture synthesis model based on generative adversarial networks (GANs) with a
user-controllable mechanism. The user control ability allows to explicitly specify the texture which should be
generated by the model. This property follows from using an encoder part which learns a latent representation
for each texture from the dataset. To ensure a dataset coverage, we use an adversarial loss function that
penalizes for incorrect reproductions of a given texture. In experiments, we show that our model can learn
descriptive texture manifolds for large datasets and from raw data such as a collection of high-resolution
photos. We show our unsupervised learning pipeline may help segmentation models. Moreover, we apply our
method to produce 3D textures and show that it outperforms existing baselines.
1 INTRODUCTION
Textures are essential and crucial perceptual elements
in computer graphics. They can be defined as im-
ages with repetitive or periodic local patterns. Texture
synthesis models based on deep neural networks have
recently drawn a great interest to a computer vision
community. Gatys et al.(Gatys et al., 2015; Gatys
et al., 2016b) proposed to use a convolutional neu-
ral network as an effective texture feature extractor.
They proposed to use a Gram matrix of hidden layers
of a pre-trained VGG network as a descriptor of a tex-
ture. Follow-up papers (Johnson et al., 2016; Ulyanov
et al., 2016) significantly speed up a synthesis of tex-
ture by substituting an expensive optimization process
in (Gatys et al., 2015; Gatys et al., 2016b) to a fast for-
ward pass of a feed-forward convolutional network.
However, these methods suffer from many problems
such as generality inefficiency (i.e., train one network
per texture) and poor diversity (i.e., synthesize visu-
ally indistinguishable textures).
Recently, Periodic Spatial GAN (PSGAN)
(Bergmann et al., 2017) and Diversified Texture Syn-
thesis (DTS) (Li et al., 2017) models were proposed
Figure 1: One can take 1) New Guinea 3264 × 4928 landscape photo, learn 2) a manifold of 2D texture embeddings for this
photo, visualize 3) texture map for the image and perform 4) texture detection for a patch using distances between learned
embeddings.
First two authors have equal contribution.
214
Alanov, A., Kochurov, M., Volkhonskiy, D., Yashkov, D., Burnaev, E. and Vetrov, D.
User-controllable Multi-texture Synthesis with Generative Adversarial Networks.
DOI: 10.5220/0008924502140221
In Proceedings of the 15th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2020) - Volume 4: VISAPP, pages
214-221
ISBN: 978-989-758-402-2; ISSN: 2184-4321
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Legend
- encoder
- generator
- texture pair
discriminator
- texture
discriminator
- latent
discriminator
Prior distribution
sample
Texture sample
Prior distribution
sample
Same texture
samples
Fake Real
Texture sample
Pair
Matching
Generation
Matching
Encoder
Matching
Texture sample
Figure 2: Training pipeline of the proposed method.
as an attempt to partly solve these issues. PSGAN
and DTS are multi-texture synthesis models, i.e.,
they train one network for generating many textures.
However, each model has its own limitations (see
Table 1). PSGAN has incomplete dataset coverage,
and a user control mechanism is absent. Lack of
dataset coverage means that it can miss some textures
from the training dataset. The absence of a user
control does not allow to explicitly specify the texture
which should be generated by the model in PSGAN.
DTS is not scalable with respect to dataset size,
cannot be applied to learn textures from raw data and
to synthesize 3D textures. It is not scalable because
the number of parameters of the DTS model linearly
depends on the number of textures in the dataset. The
learning from raw data means that the input for the
model is a high-resolution image as in Figure 1 and
the method should extract textures in an unsupervised
way. DTS does not support such training mode
(which we call fully unsupervised) because for this
model input textures should be specified explicitly.
The shortage of generality to 3D textures in DTS
model comes from inapplicability of VGG network
to 3D images.
We propose a novel multi-texture synthesis model
which does not have limitations of PSGAN and DTS.
Table 1: Comparison of multi-texture synthesis methods.
PSGAN DTS Ours
multi-texture X X X
user control X X
dataset coverage X X
scalability with respect
to dataset size
X X
ability to learn textures
from raw data
X X
unsupervised texture
detection
X
applicability to 3D X X
Our model allows for generating a user-specified tex-
ture from the training dataset. This is achieved by
using an encoder network which learns a latent repre-
sentation for each texture from the dataset. To ensure
the complete dataset coverage of our method we use
a loss function that penalizes for incorrect reproduc-
tions of a given texture. Thus, the generator is forced
to learn the ability to synthesize each texture seen dur-
ing the training phase. Our method is more scalable
with respect to dataset size compared to DTS and is
able to learn textures in a fully unsupervised way from
raw data as a collection of high-resolution photos. We
show that our model learns a descriptive texture mani-
fold in latent space. Such low dimensional representa-
tions can be applied as useful texture descriptors, for
example, for an unsupervised texture detection (see
Figure 1) or improving segmentation models. Also,
we can apply our approach to 3D texture synthesis be-
cause we use fully adversarial losses and do not utilize
VGG network descriptors.
We experimentally show that our model can learn
large datasets of textures. We check that our generator
learns all textures from the training dataset by condi-
tionally synthesizing each of them. We demonstrate
that our model can learn meaningful texture mani-
folds as opposed to PSGAN (see Figure 6). We com-
pare the efficiency of our approach and DTS in terms
of memory consumption and show that our model is
much more scalable than DTS for large datasets. We
also provide proof of concept experiments showing
that embeddings learned in an unsupervized way may
help segmentation models.
We apply our method to 3D texture-like porous
media structures which is a real-world problem from
Digital Rock Physics. Synthesis of porous structures
plays an important role (Volkhonskiy et al., 2019) be-
cause an assessment of the variability in the inherent
material properties is often experimentally not feasi-
ble. Moreover, usually it is necessary to acquire a
number of representative samples of the void-solid
User-controllable Multi-texture Synthesis with Generative Adversarial Networks
215

structure. We show that our method outperforms a
baseline (Mosser et al., 2017) in the porous media
synthesis which trains one network per texture.
Briefly summarize, we can highlight the following
key advantages of our model:
• user control (conditional generation),
• full dataset coverage,
• scalability with respect to dataset size,
• ability to learn descriptive texture manifolds from
raw data in a fully unsupervised way,
• applicability to 3D texture synthesis.
2 PROPOSED METHOD
We look for a multi-texture synthesis pipeline that can
generate textures in a user-controllable manner, en-
sure full dataset coverage and be scalable with respect
to dataset size. We use an encoder network E
ϕ
(x)
which allows to map textures to a latent space and
gives low dimensional representations. We use a sim-
ilar generator network G
θ
(z) as in PSGAN.
The generator G
θ
(z) takes as an input a noise ten-
sor z ∈ R
d×h
z
×w
z
which has three parts z = [z
g
, z
l
, z
p
].
These parts are the same as in PSGAN:
• z
g
∈ R
d
g
×h
z
×w
z
is a global part which determines
the type of texture. It consists of only one vec-
tor ¯z
g
of size d
g
which is repeated through spatial
dimensions.
• z
l
∈ R
d
l
×h
z
×w
z
is a local part and each element
z
l
ki j
is sampled from a standard normal distribu-
tion N (0, 1) independently. This part encourages
the diversity within one texture.
• z
p
∈ R
d
p
×h
z
×w
z
is a periodic part and z
p
ki j
=
sin(a
k
(z
g
) · i + b
k
(z
g
) · j + ξ
k
) where a
k
, b
k
are
trainable functions and ξ
k
is sampled from
U[0, 2π] independently. This part helps generat-
ing periodic patterns.
We see that for generating a texture it is sufficient
to put the vector ¯z
g
as an input to the generator G
θ
be-
cause z
l
is obtained independently from N (0, 1) and
z
p
is computed from z
g
. It means that we can consider
¯z
g
as a latent representation of a corresponding texture
and we will train our encoder E
ϕ
(x) to recover this la-
tent vector ¯z
g
for an input texture x. Further, we will
assume that the generator G
θ
(z) takes only the vector
¯z
g
as input and builds other parts of the noise tensor
from it. For simplicity, we denote ¯z
g
as z.
The encoder E
ϕ
(x) takes an input texture x and
returns the distribution q
ϕ
(z|x) = N (µ
ϕ
(x), σ
2
ϕ
(x)) of
the global vector z (the same as ¯z
g
) of the texture x.
Then we can formulate properties of the generator
G
θ
(z) and the encoder E
ϕ
(x) we expect in our model:
• samples G
θ
(z) are real textures if we sample z
from a prior p(z) (in our case it is N (0, I)).
• if z
ϕ
(x) ∼ q
ϕ
(z|x) then G
θ
(z
ϕ
(x)) has the same
texture type as x.
• an aggregated distribution of the encoder E
ϕ
(x)
should be close to the prior p(z), i.e. q
ϕ
(z) =
R
q
ϕ
(z|x)p
∗
(x)dx ≈ p(z) where p
∗
(x) is a true dis-
tribution of textures.
• samples G
θ
(z
ϕ
) are real textures if z
ϕ
is sampled
from aggregated q
ϕ
(z).
To ensure these properties we use three types of
adversarial losses:
• generator matching: L
x
for matching the distri-
bution of both samples G
θ
(z) and reproductions
G
θ
(z
ϕ
) to the distribution of real textures p
∗
(x).
• pair matching: L
xx
for matching the distribu-
tion of pairs (x, x
0
) to the distribution of pairs
(x, G
θ
(z
ϕ
(x))) where x and x
0
are samples of the
same texture. It will ensure that G
θ
(z
ϕ
(x)) has the
same texture type as x.
• encoder matching: L
z
for matching the aggre-
gated distribution q
ϕ
(z) to the prior p(z).
We consider exact definitions of these adversar-
ial losses in Section 2.1. We demonstrate the whole
pipeline of the training procedure in Figure 2.
2.1 Generator & Encoder Objectives
Generator Matching. For matching both samples
G
θ
(z) and reproductions G
θ
(z
ϕ
) to real textures we
use a discriminator D
ψ
(x) as in PSGAN which maps
an input image x to a two-dimensional tensor of spa-
tial size s × t. Each element D
i j
ψ
(x) of the discrimi-
nator’s output corresponds to a local part x and esti-
mates probability that such receptive field is real ver-
sus synthesized by G
θ
. Then a value function V
x
(θ, ψ)
of such adversarial game min
θ
max
ψ
V
x
(θ, ψ) will be the
following:
V
x
(θ, ψ) =
1
st
s,t
∑
i, j
h
E
p
∗
(x)
logD
i j
ψ
(x) (1)
+E
p(z)
log(1 − D
i j
ψ
(G
θ
(z)))
+ E
q
ϕ
(z)
log(1 − D
i j
ψ
(G
θ
(z
ϕ
)))
i
As in (Goodfellow et al., 2014) we modify the
value function V
x
(θ, ψ) for the generator G
θ
by sub-
stituting the term log(1 − D
i j
ψ
(·)) to − log D
i j
ψ
(·). So,
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
216
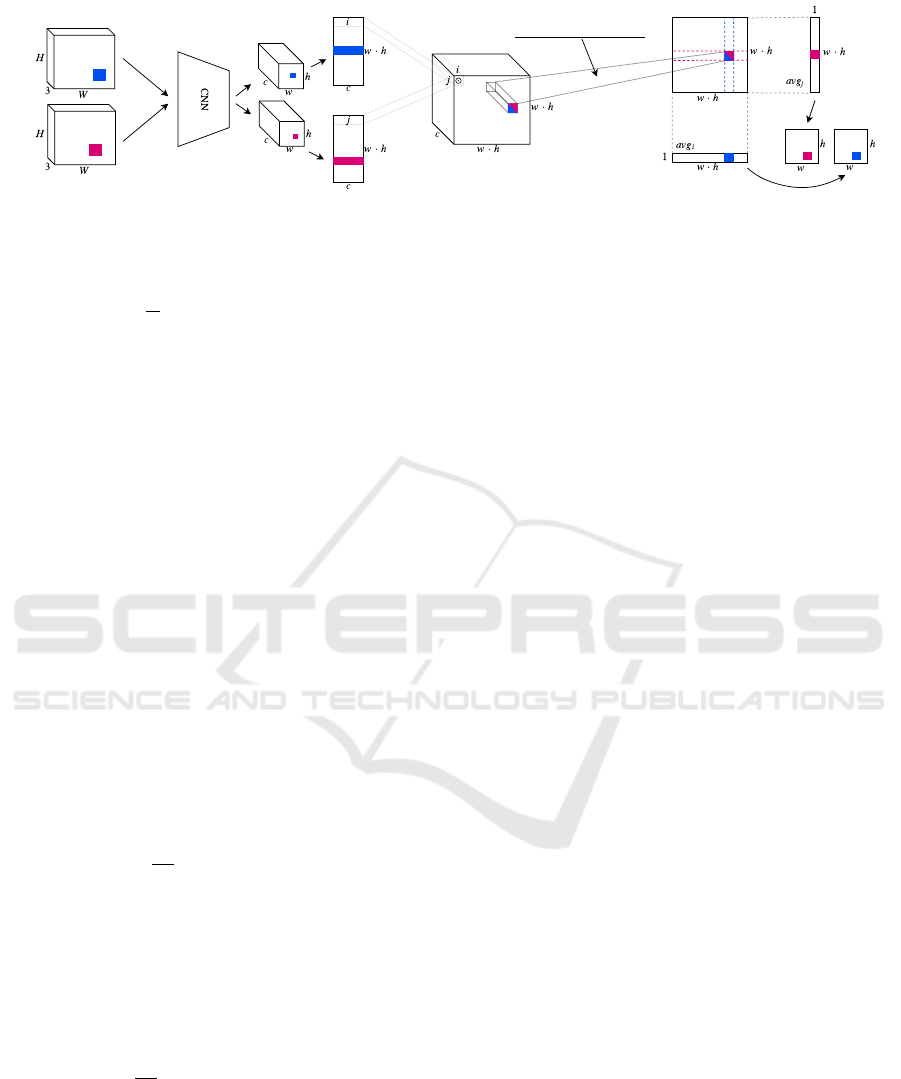
image 1
image 2
conv1x1 + ReLU + conv1x1
logits 1 logits 2
Figure 3: The architecture of the discriminator on pairs D
τ
(x, y).
the adversarial loss L
x
is
L
x
(θ) = −
1
st
s,t
∑
i, j
h
E
p(z)
logD
i j
ψ
(G
θ
(z))+ (2)
+E
q
ϕ
(z)
logD
i j
ψ
(G
θ
(z
ϕ
))
i
→ min
θ
Pair Matching. The goal is to match fake pairs
(x, G
θ
(z
ϕ
(x))) to real ones (x, x
0
) where x and x
0
are
samples of the same texture (in practice, we can ob-
tain real pairs by taking two different random patches
from one texture). For this purpose we use a discrim-
inator D
τ
(x, y) of special architecture which is pro-
vided in Figure 3.
We consider the following distributions:
• p
∗
xx
(x, y) over real pairs (x, y) where x and y are
examples of the same texture;
• p
θ,ϕ
(x, y) over fake pairs (x, y) where x is a
real texture and y is its reproduction, i.e., y =
G
θ
(z
ϕ
(x)).
We denote the dimension of the discriminator’s
output matrix as p × q and D
i j
τ
(x, y) as the i j-th ele-
ment of this matrix. The value function V
xx
(θ, ϕ, τ)
for this adversarial game min
θ,ϕ
max
τ
V
xx
(θ, ϕ, τ) is
V
xx
(θ, ϕ, τ) =
1
pq
p,q
∑
i, j
h
E
p
∗
xx
(x,y)
logD
i j
τ
(x, y) +
+ E
p
θ,ϕ
(x,y)
log(1 − D
i j
τ
(x, y))
i
(3)
The discriminator D
τ
tries to maximize the value
function V
xx
(θ, ϕ, τ) while the generator G
θ
and the
encoder E
ϕ
minimize it.
Then the adversarial loss L
xx
is
L
xx
(θ, ϕ) = −
1
pq
p,q
∑
i, j
E
p
θ,ϕ
(x,y)
logD
i j
τ
(x, y) → min
θ,ϕ
(4)
Encoder Matching. We need to use encoder match-
ing because otherwise if we use only one objective
L
xx
(θ, ϕ) for training the encoder E
ϕ
(x) then embed-
dings for textures can be very far from samples z that
come from the prior distribution p(z). It will lead
to unstable training of the generator G
θ
(z) because it
should generate good images both for samples from
the prior p(z) and for embeddings which come from
the encoder E
ϕ
.
Therefore, to regularize the encoder E
ϕ
we match
the prior distribution p(z) and the aggregated encoder
distribution q
ϕ
(z) =
R
q
ϕ
(z|x)p
∗
(x)dx using the dis-
criminator D
ζ
(z). It classifies samples z from p(z)
versus ones from q
ϕ
(z). The minimax game of E
ϕ
(x)
and D
ζ
is defined as min
ϕ
max
ζ
V
z
(ϕ, ζ), where V
z
(ϕ, ζ)
is
V
z
(ϕ, ζ) = E
p(z)
logD
ζ
(z) (5)
+E
q
ϕ
(z)
log(1 − D
ζ
(z))
To sample from q
ϕ
(z) we should at first sample some
texture x then sample z from the encoder distribution
by z = µ
ϕ
(x) + σ
ϕ
(x) ∗ ε, where ε ∼ N (0, I). The ad-
versarial loss L
z
(ϕ) is
L
z
(ϕ) = −E
q
ϕ
(z)
logD
ζ
(z) → min
ϕ
(6)
Final Objectives. Thus, for both the generator G
θ
and the encoder E
ϕ
we optimize the following objec-
tives:
• the generator G
θ
loss
L(θ) = α
1
L
x
(θ) + α
2
L
xx
(θ, ϕ) → min
θ
(7)
• the encoder E
ϕ
loss
L(ϕ) = β
1
L
z
(ϕ) + β
2
L
xx
(θ, ϕ) → min
ϕ
(8)
In experiments, we use α
1
= α
2
= β
1
= β
2
= 1.
3 RELATED WORK
Deep learning methods were shown to be an efficient
parametric model for texture synthesis. Papers of
Gatys et al.(Gatys et al., 2015; Gatys et al., 2016b)
are a milestone: they proposed to use Gram matrices
of VGG intermediate layer activations as texture de-
scriptors. This approach allows for generating high-
quality images of textures (Gatys et al., 2015) by
User-controllable Multi-texture Synthesis with Generative Adversarial Networks
217

(a) PSGAN-5D samples (b) Our-2D model samples
(c) Our-2D model reproductions. Columns 1,4,7,10 are real
textures, others are reproductions
Figure 4: Examples of generated/reproduced textures from
PSGAN and our model.
running an expensive optimization process. Subse-
quent works (Ulyanov et al., 2016; Johnson et al.,
2016) significantly accelerate a texture synthesis by
approximating this optimization procedure by fast
feed-forward convolutional networks. Further works
improve this approach either by using optimization
techniques (Frigo et al., 2016; Gatys et al., 2016a;
Li and Wand, 2016), introducing an instance normal-
ization (Ulyanov et al., 2017; Ulyanov et al., ) or ap-
plying GANs-based models for non-stationary texture
synthesis (Zhou et al., 2018). These methods have
significant limitations such as the requirement to train
one network per texture and poor diversity of samples.
Multi-texture Synthesis Methods. DTS (Li et al.,
2017) was introduced by Li et al.as a multi-texture
synthesis model. Spatial GAN (SGAN) model
(Jetchev et al., 2016) was introduced by Jetchev
et al.as the first method where GANs are applied to
texture synthesis. It showed good results, surpass-
ing the results of (Gatys et al., 2015). Bergmann
et al.(Bergmann et al., 2017) improved SGAN by in-
troducing Periodic Spatial GAN (PSGAN) model.
Our model is based on GANs with an encoder net-
work which allows mapping an input texture to a la-
tent embedding. We use the adversarial loss for this
purpose inspired by (Xian et al., 2018) where it is
used for image synthesis guided by sketch, color, and
texture. The benefit of such loss is that it can be eas-
ily applied to 3D textures. Previous works (Mosser
et al., 2017; Volkhonskiy et al., 2019) on synthesiz-
ing 3D porous material used GANs with 3D convolu-
tional layers inside a generator and a discriminator.
4 EXPERIMENTS
In experiments, we train our model on scaly, braided,
honeycomb and striped categories from Oxford De-
scribable Textures Dataset (Cimpoi et al., 2014).
These are datasets with natural textures in the wild.
We use the same fully-convolutional architecture for
D
ψ
(x), G
θ
(z) as in PSGAN (Bergmann et al., 2017).
We used a spectral normalization (Miyato et al., 2018)
for discriminators that significantly improved training
stability.
4.1 Inception Score for Textures
It is a common practice in natural image generation
to evaluate a model that approximates data distri-
bution p
∗
(x) using Inception Score (Szegedy et al.,
2016). For this purpose Inception network is used
to get label distribution p(t|x). Then one calculates
IS = exp
E
x∼p
∗
(x)
KL
p(t|x)kp(t)
, where p(t) =
E
x∼p
∗
(x)
p(t|x) is aggregated label distribution. The
straightforward application of Inception network does
not make sense for textures. Therefore, we train a
classifier with an architecture similar
∗
to D
ψ
(x) to
predict texture types for a given texture dataset. To do
that properly, we manually clean our data from dupli-
cates so that every texture example has a distinct label
and use random cropping as data augmentation. Our
trained classifier achieves 100% accuracy on a scaly
dataset. We use this classifier to evaluate Inception
Score for models trained on the same texture dataset.
4.2 Unconditional and Conditional
Generation
For models like PSGAN we are not able to obtain re-
productions, we only have access to texture genera-
tion process. One would ask for the guarantees that a
model is able to generate every texture in the dataset
from only the prior distribution. We evaluate PSGAN
and our model on a scaly dataset with 116 unique tex-
tures. After models are trained, we estimate the In-
ception Score. We observed that Inception Score dif-
Table 2: Inception Scores for conditional and unconditional
generation from PSGAN and our model. Classifier used to
compute IS achieved perfect accuracy on train data.
Model Uncond. IS Cond. IS
PSGAN-5D 73.68±0.6 NA
Our-2D 73.74±0.3 103.96±0.1
∗
The only difference is the number of output logits
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
218

(a) PSGAN-5D samples
(b) Our-2D model samples
(c) Our-2D model reproductions
Figure 5: Histogram of classifier predictions on 50000 gen-
erated samples from PSGAN (a) and Our model (b) and for
500 reproductions per class for our model (c). Each bin rep-
resents a separate texture class from scaly dataset.
fers with d
g
and thus picked the best d
g
separately
for both PSGAN and our model obtaining d
g
= 5
and d
g
= 2 respectively. Both models were trained
with Adam (Kingma and Ba, 2015) (betas=0.5,0.99)
with batch size 64 on a single GPU. Their best per-
formance was achieved in around 80k iterations. For
both models, we used spectral normalization to im-
prove training stability (Miyato et al., 2018).
Both models can generate high-quality textures
from low dimensional space. Our model additionally
can successfully generate reproductions for every tex-
ture in the dataset. Figure 5 and Table 2 summarise
the results for conditional (reproductions) and uncon-
ditional texture generation. Figure 5a indicates PS-
GAN may have missing textures, our model does not
suffer from this issue. Inception Score suggests that
conditional generation is a far better way to sample
from the model. In Figure 4 we provide samples and
texture reproductions for trained models.
4.3 Texture Manifold
Autoencoding property is a nice to have feature for
generative models. One can treat embeddings as low
dimensional data representations. As shown in sec-
tion 4.2 our model can reconstruct every texture in
the dataset. Moreover, we are able to visualize the
manifold of textures since we trained this model with
d
g
= 2. To compare this manifold to PSGAN, we train
a separate PSGAN model with d
g
= 2. 2D manifolds
(a) PSGAN 2D manifold (b) Ours 2D manifold
Figure 6: 2D manifold for 116 textures from scaly dataset.
Our model gives paces one texture to a distinct location.
Grid is taken over [−2.25, 2.25] × [−2.25, 2.25] with step
0.225.
near prior distribution for both models can be found
in Figure 6. Our model learns visually better 2D man-
ifold and allocates similar textures nearby.
4.4 Spatial Embeddings Structure
As described in sections 4.5 and 4.3, our method can
learn descriptive texture manifold from a collection
of raw data in an unsupervised way. The obtained
texture embeddings may be useful. Consider a large
input image X, e.g.as the first in Figure 1, and the
trained G(z) and E(x) on this image. Note that at
the training stage encoder E(x) is a fully convolu-
tional network, followed by global average pooling.
Applied to X as-is, the encoder’s output would be
”average” texture embedding for the whole image X.
Replacing global average pooling by spatial average
pooling with small kernel allows E(X ) to output tex-
ture embeddings for each receptive field in the input
image X. We denote such modified encoder as
e
E(x).
Z =
e
E(X) is a tensor with spatial texture embed-
dings for X. They smoothly change along spatial di-
mensions as visualized by reconstructing them with
generator
˜
G(Z) on the third picture in Figure 1.
One can take a reference patch P with a texture
(e.g., grass) and find similar textures in image X. This
is illustrated in the last picture in Figure 1. We picked
a patch P with grass on it and constructed a heatmap
M: M
i j
= exp(−αd(
e
E(X)
i j
, E(P))
2
), where d(·, ·) is
Euclidean distance and α = 3 in our example. We
then interpolated M to the original size of X.
This example shows that
e
E(x) allows using
learned embeddings for other tasks that have no re-
lation to texture generation. We believe supervised
methods would benefit from adding additional fea-
tures obtained in an unsupervised way.
User-controllable Multi-texture Synthesis with Generative Adversarial Networks
219

Table 3: KL divergence between real, our and the baseline distributions of statistics (permeability, Euler characteristic, and
surface area) for size 160
3
. The standard deviation was computed using the bootstrap method with 1000 resamples.
Permeability Euler characteristic Surface area
KL(p
real
, p
ours
) KL (p
real
, p
baseline
) KL (p
real
, p
ours
) KL (p
real
, p
baseline
) KL (p
real
, p
ours
) KL (p
real
, p
baseline
)
Ketton 5.06 ± 0.35 4.68 ± 0.56 3.66 ± 0.73 1.86 ± 0.42 1.85 ± 0.62 7.73 ± 0.18
Berea 0.49 ± 0.07 0.50 ± 0.12 0.34 ± 0.08 1.36 ± 0.25 0.33 ± 0.11 5.91 ± 0.54
Doddington 0.42 ± 0.10 3.41 ± 1.68 2.65 ± 2.29 3.35 ± 1.13 4.83 ± 2.06 7.92 ± 0.27
Estaillades 0.80 ± 0.24 3.41 ± 0.46 1.85 ± 0.29 2.05 ± 1.05 4.62 ± 0.66 6.93 ± 0.39
Bentheimer 0.47 ± 0.08 1.38 ± 0.49 1.24 ± 0.41 3.44 ± 1.91 1.20 ± 0.73 1.25 ± 0.12
Figure 7: Merrigum House 3872 × 2592 photo and its
learned 2D texture manifold using our model.
4.5 Learning Texture Manifolds from
Raw Data and Texture Detection
The learned manifold in section 4.3 was obtained
from well prepared data and a single image in sec-
tion 4.4. Real cases usually do not have clean data
and require either expensive data preparation or un-
supervised methods. Our model can learn texture
manifolds from raw data such as a collection of high-
resolution photos. To cope with training texture man-
ifolds on raw data, we suggest to construct p
∗
(x, x
0
) in
equation 3 with two crops from almost the same loca-
tion. In Figure 7 we provide a manifold learned from
House photo.
4.6 Application to 3D Synthesis
In this section, we demonstrate the applicability of our
model to the Digital Rock Physics. We trained our
model on 3D Porous Media structures
†
(i.e. see Fig.
8a) of five different types: Ketton, Berea, Dodding-
ton, Estaillades and Bentheimer. Each type of rock
has an initial size 1000
3
binary voxels. As the base-
line, we considered Porous Media GANs (Mosser
et al., 2017), which is deep convolutional GANs with
3D convolutional layers.
For the comparison of our model with real sam-
ples and the baseline samples, we use permeability
statistics and two so-called Minkowski functionals.
†
All samples were taken from Imperial College
database
(a) Real (b) Ours (c) Baseline
Figure 8: Real, synthetic (our model) and synthetic (base-
line model) Berea samples of size 150
3
.
We used the following experimental setup. We
trained our model on random crops of size 160
3
on
all types of porous structures. We also trained five
baseline models on each type separately. Then we
generated 500 synthetic samples of size 160
3
of each
type using our model and the baseline model. We also
cropped 500 samples of size 160
3
from the real data.
As a result, for each type of structure, we obtained
three sets of objects: real, synthetic and baseline.
The visual result of the synthesis is presented in
Fig. 8 for Berea. In the figure, there are three sam-
ples: real (i.e., cropped from the original big sample),
ours and a sample of the baseline model. Because our
model is fully convolutional, we can increase the gen-
erated sample size by expanding the spatial dimen-
sions of the latent embedding z. The network struc-
ture allows to produce larger texture sizes.Then, for
each real, synthetic and baseline objects we calculated
three statistics: permeability, Surface Area and Euler
characteristics. To measure the distance between dis-
tributions of statistics for real, our and baseline sam-
ples we approximated these distributions by discrete
ones obtained using the histogram method with 50
bins. Then for each statistic, we calculated KL diver-
gence between the distributions of the statistic of a)
real and our generated samples; b) real and baseline
generated samples.
The comparison of the KL is presented at Tab. 3
for the permeability and for Minkowski functionals.
As we can see, our model performs better accordingly
for most types of porous structures.
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
220

5 CONCLUSIONS AND FUTURE
WORK
In this paper, we proposed a novel model for multi-
texture synthesis. We showed it ensures full dataset
coverage and can detect textures on images in the un-
supervised setting. We provided a way to learn a man-
ifold of training textures even from a collection of raw
high-resolution photos. We also demonstrated that the
proposed model applies to the real-world 3D texture
synthesis problem: porous media generation. Our
model outperforms the baseline by better reproduc-
ing physical properties of real data. In future work,
we want to study the texture detection ability of our
model for improving segmentation in an unsupervised
way and seek for its new applications.
ACKNOWLEDGEMENTS
Aibek Alanov, Max Kochurov, Dmitry Vetrov were
supported by Samsung Research, Samsung Electron-
ics. The work of Dmitry Vetrov was supported by the
Russian Science Foundation grant no.17-71-20072.
The work of E. Burnaev and D. Volkhonskiy was sup-
ported by the MES of RF, grant No. 14.615.21.0004,
grant code: RFMEFI61518X0004. The authors E.
Burnaev and D. Volkhonskiy acknowledge the usage
of the Skoltech CDISE HPC cluster Zhores for ob-
taining some results presented in this paper.
REFERENCES
Bergmann, U., Jetchev, N., and Vollgraf, R. (2017). Learn-
ing texture manifolds with the periodic spatial gan.
ICML.
Cimpoi, M., Maji, S., Kokkinos, I., Mohamed, S., and
Vedaldi, A. (2014). Describing textures in the wild.
In Proc. IEEE CVPR, pages 3606–3613, Washington,
DC, USA. IEEE Computer Society.
Frigo, O., Sabater, N., Delon, J., and Hellier, P. (2016). Split
and match: Example-based adaptive patch sampling
for unsupervised style transfer. In Proc. IEEE CVPR,
pages 553–561.
Gatys, L., Ecker, A. S., and Bethge, M. (2015). Texture syn-
thesis using convolutional neural networks. In NIPS,
pages 262–270.
Gatys, L. A., Bethge, M., Hertzmann, A., and Shechtman,
E. (2016a). Preserving color in neural artistic style
transfer. arXiv preprint arXiv:1606.05897.
Gatys, L. A., Ecker, A. S., and Bethge, M. (2016b). Image
style transfer using convolutional neural networks. In
Proc. IEEE CVPR, pages 2414–2423.
Goodfellow, I., Pouget-Abadie, J., Mirza, M., Xu, B.,
Warde-Farley, D., Ozair, S., Courville, A., and Ben-
gio, Y. (2014). Generative adversarial nets. In NIPS,
pages 2672–2680.
Jetchev, N., Bergmann, U., and Vollgraf, R. (2016). Texture
synthesis with spatial generative adversarial networks.
arXiv preprint arXiv:1611.08207.
Johnson, J., Alahi, A., and Fei-Fei, L. (2016). Perceptual
losses for real-time style transfer and super-resolution.
In ECCV, pages 694–711. Springer.
Kingma, D. P. and Ba, J. (2015). Adam: A method for
stochastic optimization. In International Conference
on Learning Representations (ICLR).
Li, C. and Wand, M. (2016). Combining markov random
fields and convolutional neural networks for image
synthesis. In Proceedings of the IEEE Conference
on Computer Vision and Pattern Recognition, pages
2479–2486.
Li, Y., Fang, C., Yang, J., Wang, Z., Lu, X., and Yang,
M.-H. (2017). Diversified texture synthesis with feed-
forward networks. In Proc. CVPR.
Miyato, T., Kataoka, T., Koyama, M., and Yoshida, Y.
(2018). Spectral normalization for generative adver-
sarial networks. ICLR.
Mosser, L., Dubrule, O., and Blunt, M. J. (2017). Re-
construction of three-dimensional porous media using
generative adversarial neural networks. Physical Re-
view E, 96(4):043309.
Szegedy, C., Vanhoucke, V., Ioffe, S., Shlens, J., and Wojna,
Z. (2016). Rethinking the inception architecture for
computer vision. In 2016 IEEE Conference on Com-
puter Vision and Pattern Recognition, CVPR 2016,
Las Vegas, NV, USA, June 27-30, 2016, pages 2818–
2826.
Ulyanov, D., Lebedev, V., Vedaldi, A., and Lempitsky, V. S.
(2016). Texture networks: Feed-forward synthesis of
textures and stylized images. In ICML, pages 1349–
1357.
Ulyanov, D., Vedaldi, A., and Lempitsky, V. Instance nor-
malization: the missing ingredient for fast stylization.
corr abs/1607.0 (2016).
Ulyanov, D., Vedaldi, A., and Lempitsky, V. (2017). Im-
proved texture networks: Maximizing quality and di-
versity in feed-forward stylization and texture synthe-
sis. In Proceedings of the IEEE Conference on Com-
puter Vision and Pattern Recognition, pages 6924–
6932.
Volkhonskiy, D., Muravleva, E., Sudakov, O., Orlov, D.,
Belozerov, B., Burnaev, E., and Koroteev, D. (2019).
Reconstruction of 3d porous media from 2d slices.
arXiv preprint arXiv:1901.10233.
Xian, W., Sangkloy, P., Agrawal, V., Raj, A., Lu, J., Fang,
C., Yu, F., and Hays, J. (2018). Texturegan: Con-
trolling deep image synthesis with texture patches. In
Proceedings of the IEEE Conference on Computer Vi-
sion and Pattern Recognition, pages 8456–8465.
Zhou, Y., Zhu, Z., Bai, X., Lischinski, D., Cohen-Or,
D., and Huang, H. (2018). Non-stationary texture
synthesis by adversarial expansion. arXiv preprint
arXiv:1805.04487.
User-controllable Multi-texture Synthesis with Generative Adversarial Networks
221
