
Pre- and Post-processing Strategies for Generic Slice-wise
Segmentation of Tomographic 3D Datasets Utilizing U-Net Deep
Learning Models Trained for Specific Diagnostic Domains
Gerald A. Zwettler
1,2
, Werner Backfrieder
3
and David R. Holmes III
1
1
Biomedical Analytics and Computational Engineering Lab, Department of Physiology and Biomedical Engineering,
Mayo Clinic College of Medicine, 200 First St. SW, 55905 Rochester, MN, U.S.A.
2
Research Group Advanced Information Systems and Technology (AIST), Department of Software Engineering,
University of Applied Sciences Upper Austria, Softwarepark 11, 4232 Hagenberg, Austria
3
Medical Informatics, Department of Software Engineering, University of Applied Sciences Upper Austria,
Softwarepark 11, 4232 Hagenberg, Austria
Keywords: Deep Learning, U-Net, Model-based Segmentation in Medicine, Computed Tomography.
Abstract: An automated and generally applicable method for segmentation is still in focus of medical image processing
research. Since a few years artificial inteligence methods show promising results, especially with widely
available scalable Deep Learning libraries. In this work, a five layer hybrid U-net is developed for slice-by-
slice segmentation of liver data sets. Training data is taken from the Medical Segmentation Decathlon
database, providing 131 fully segmented volumes. A slice-oriented segmentation model is implemented
utilizing deep learning algorithms with adaptions for variable parenchyma shape along the stacking direction
and similarities between adjacent slices. Both are transformed for coronal and sagittal views. The
implementation is on a GPU rack with TensorFlow and Keras. For a quantitative measure of segmentation
accuracy, standardized volume and surface metrics are used. Results DSC=97.59, JI=95.29 and NSD=99.37
show proper segmentation comparable to 3D U-Nets and other state of the art. The development of a 2D-slice
oriented segmentation is justified by short training time and less complexity and therefore massively reduced
memory consumption. This work manifests the high potential of AI methods for general use in medical
segmentation as fully- or semi-automated tool supervised by the expert user.
1 INTRODUCTION
Automated and precise segmentation of anatomical
structures for computer-assisted diagnostics is still
field of ongoing research. Only for particular domains,
off-the-shelf applications are available (Christensen
and Wake, 2018) but generally computer-aided
diagnostic is achieved in a user-centric process
utilizing frameworks providing tools for semi-
automated processing (Strakos et al. 2015). The
manual processing of the datasets thereby necessitates
a lot of experience in both, the technical and the
medical domain and is exposed to subjective
processing, even if following a rather standardized
segmentation process (Zwettler et al. 2013).
1.1 Medical Background
The precise segmentation of specific anatomical
structures from 3D data forms the basis for quantita-
tive analysis in computer-assisted diagnostics. The
quantitation aspect is relevant for assessing disease
progression or general scoring (Aggarwal et al. 2011).
Based on segmented anatomical structures, the
visualization and inspection in 3D, as well as
utilization in AR and VR environments becomes
feasible. Segmentations are further relevant for surgery
planning, building up anatomical atlas models,
evaluating image acquisition protocols or as input data
for nowadays widely available 3D print (Squelch
2018).
1.2 Sate of the Art
Since the appearance of the first CT scanners, in the
early 1970s, intensive research in the field of medical
image processing targeting at fully automated
segmentation approaches has been initiated and is still
going on.
66
Zwettler, G., Backfrieder, W. and Holmes III, D.
Pre- and Post-processing Strategies for Generic Slice-wise Segmentation of Tomographic 3D Datasets Utilizing U-Net Deep Learning Models Trained for Specific Diagnostic Domains.
DOI: 10.5220/0008932100660078
In Proceedings of the 15th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2020) - Volume 5: VISAPP, pages
66-78
ISBN: 978-989-758-402-2; ISSN: 2184-4321
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

A priori knowledge about the target shape, lead to
deformable models (McInerney and Terzopoulos
1996). With statistical shape (Cootes et al. 1992),
adaptive models are calculated from a large set of
reference datasets with corresponding reference
positions, thus representing the statistical shape
variability of the target anatomical structure in a
sophisticated way. Statistical Shape models allow for a
very compact representation of the target’s structure
due to PCA but the precise and generic determination
of corresponding landmarks is still unsolved and
necessitates specific approaches in particular
diagnostic domains. Incorporating the input dataset
intensity profiles besides shape, Active Appearance
Models (Cootes et al. 1998) can be trained for
automated segmentation in specific anatomical
domains but attracted interest and significance in a
non-diagnostic domain, namely human face
comparison and recognition.
In recent years, improvements in GPU speed,
massive efforts in AI research of large companies and
availability of machine learning frameworks such as
Tensorflow to the research community were the trigger
for significant improvements in Deep Learning and to
allow for technical implementation of some concepts,
since then only theoretically documented. The most
significant developments are thereby Feed Forward
networks with several hidden layers that are applicable
in many computer vision and also speech recognition
tasks. Nevertheless, Feed Forward networks are also
applied for medical multi-modal image fusion (Zhang
and Wang 2011). The concept of self-organizing
neural networks first introduced by Kohonen
(Kohonen 1995) for clustering in complex domains
was successfully applied to classification of renal
diseases too (Van Biesen 1998). With recurrent neural
networks and long/short-term-memories (LSTM)
(Hochreiter and Schmidhuber 1997) semantic
processing of input data sequences as relevant for OCR
and voice analysis, c.f. DeepVoice, became feasible
(Arik et al. 2017). One of the most significant
developments in Deep Learning in recent years are
convolutional neural networks, training kernels and
weights of multi-resolution filter pyramids and thus
clearly outperforming classic convolutional-layer
based approaches such as Haar Cascades (Viola and
Jones 2001). Some of the most relevant CNN
architectures are LeNet, AlexNet, GoogLeNet or
ResNet showing more than 1200 layer. New fields of
application opened generative adversial networks
(GAN) (Goodfellow et al. 2014). It is applied for
mimicking of natural data in domains as generating
paintings, hand written letters or medical data (Yi et al.
2019). The latter are used for automated liver
segmentation (Yang et al., 2017) or generation of test
data to prevent from over-fitting (Frid-Adar 2018).
1.3 Related Work
The U-Net architecture was initially developed for 2D
cell border classification (Ronneberg et al. 2014) but
soon transformed to processing 3D data too (Cicek et
al. 2016), applicable for brain tumor segmentation
(Amorim et al. 2017), liver segmentation (Meine et al.
2018) and various other medical diagnostic domains.
Recent notable advances in 3D U-Net architectures
are 3D dilated convolution kernels to significantly
speed-up the processing and allow for real-time
application (Chen et al. 2019) as well as generic
models for semantic segmentation on different
imaging modalities and anatomical structures (Huang
et al. 2019).
1.4 Generic Deep Learning Models
In this work, several approaches for utilizing
conventional U-Net architectures for slice-wise
processing of tomographic 3D datasets are presented.
Due to the utilized pre-processing strategy with ROI
selection and adjusting the intensity profile, the
approach evaluated on liver CT datasets is applicable
to different domains like lung, kidney or other
modalities such as brain MRI too.
Besides a sufficient amount of at least 100 volumes
along with precise reference segmentations, for the
generic segmentation approach no additional domain-
specific knowledge is incorporated.
Due to the slice-wise processing, important aspects
of the 3D dataset such as position within the patient get
lost. In this work several strategies are adressed and
evaluated to utilize positional information for the slice-
wise processing.
2 MATERIAL
For this research work, the liver datasets from the
Medical Segmentation Decathlon database (Simpson
et al., 2019) are utilized for training, validation and test.
The use of the database is restricted to the 131 liver
datasets that are provided together with reference
segmentations as ground truth. All 3D volumes are
available in NIFTI1 image format (DFWG, 2005), a
modification of the Analyze 7.5 format (BIR, 1986).
The medical image analysis software Analyze (Robb et
al. 1989) is utilized to convert the datasets from NIFTI1
to Analyze 7.5 and to perform the data preparation and
pre-processing subsequently described in section 2.2.
Pre- and Post-processing Strategies for Generic Slice-wise Segmentation of Tomographic 3D Datasets Utilizing U-Net Deep Learning
Models Trained for Specific Diagnostic Domains
67
2.1 Analytic Inspection of the
Task03_Liver Datasets
The 3D volumes are available as axial slices of matrix
size 512×512 with an average number of slices
µ
sliceCnt
=447.62±275.25 [74;987]. The iso-spacing in
x/y-direction is given with µ
spacingXY
=0.793±.118
[.1557;1.000] and the inhomogeneous slice thickness
is described with µ
spacingXY
=1.506±1.177 [.699;5.000].
The intensities of the CT slices range between
µ
intMIN
=-1103.26±204.93 [-2048;-1000] to
µ
intMAX
=3334.70±3566.96 [1023;27748]. The vendor-
related suspicious low and high values are not further
addressed as they are out of the relevant intensity
context for the liver segmentation domain.
The reference segmentations provided for the liver
datasets represent a three-class non-overlapping
discrimination of the volume, namely background (0),
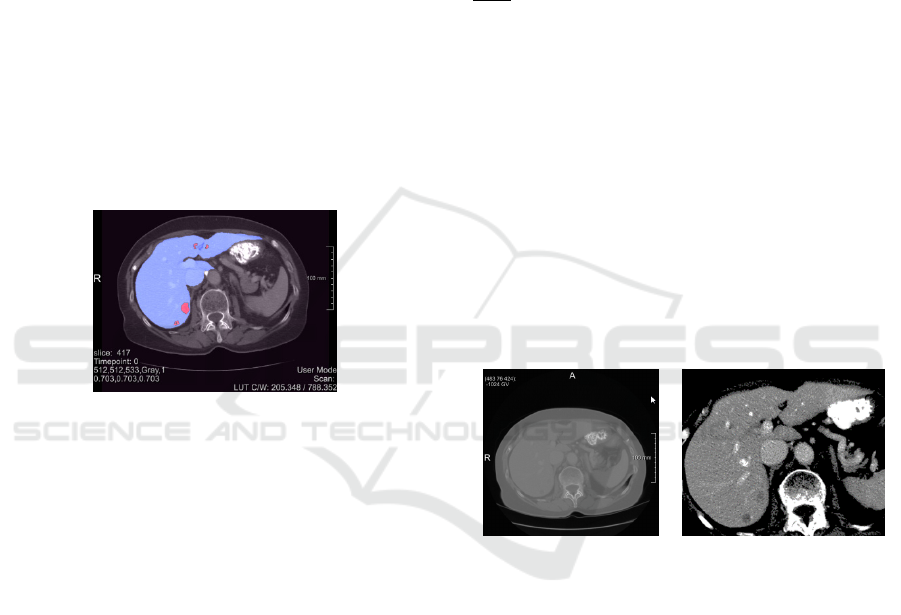
liver (1) and liver tumour (2) as shown in Fig.1 for slice
417 of dataset #0.
Figure 1: Med Decathlon slice 417 of liver dataset #0 with
parenchyma (blue) and the tumour (red) respectively.
2.2 Data Preparation and
Pre-processing
In this work a binary segmentation of the liver
parenchyma is the objective target. Thus, the ground
truth for liver and tumour areas are merged leading to
an encapsulated liver shape.
To balance the significant mismatch in slice
thicknesses, the z spacing is adjusted to the x/y inter-
slice spacing utilizing cubic interpolation for the
intensity dataset and shape interpolation (Rajagopalan
et al. 2003) for the binary reference masks. In case of
the slice thickness being below the in plane resolution,
the data remains unchanged to conserve the axial slices
at extent 512×512.
Due to the up-sampling, the number of slices is
increased to µ
sliceCnt
=639.55±248.77 [74;998].
Analysing the extent of the liver within the particular
datasets, the size of the enclosing ROI extent is given
with µ
widthLiver
=285.02±42.54,
µ
heightLiver
=246.50±31.83 and µ
widthLiver
=208.84± 57.87.
To process the input data almost at original resolution
and nevertheless limiting the size of the model to be
trained, all axial slices are scaled to an extent of
352×288 pixels, thereby conserving the aspect ratio
and placing the image content at the centre. A total
number of 27,358 slices is available, segregated into
train, validation and test datasets.
Besides normalization with respect to the extent,
the intensity profile is adjusted utilizing a scalar
transfer function similar to common windowing. Based
on the average intensity µ
liver
and σ
liver
, the transfer
function is applied according to Eqn. (1) for scale
∙
σ
to restrict all values to a range of [12;243].
T
127
|
μ
|
∙,0
μ
127
|
μ
|
∙,255
μ
(1)
The scale ratio thereby does not transform values to
full range of [0;255] to allow for some adaptability
with respect to data augmentation. For training, µ
liver
and σ
liver
are derived from statistical analysis with
given binary reference segmentation mask, while for
testing the range is derived from manual windowing.
As shown in Fig. 2, all axial slices are scaled to the
target extent of 352×288 pixels with the intensity
profile of the target structure normalized around midst
position 127 of utilized data type unsigned char in
terms of data normalization, see Fig. 2 for slice 100 of
pre-processed dataset #0.
(a) (b)
Figure 2: The original slice 424 of dataset #0 (a) is cropped
according to reference segmentation mask with the average
pixel intensity of the liver parenchyma.
The given reference segmentations are of
acceptable accuracy and thus stay untouched with one
exceptional case, namely dataset #102 where around
slice 323 there is an invalid small blob classified
offshore the parenchyma that is removed.
3 METHODOLOGY
For liver segmentation based on tomographic 3D
volume data, several approaches for slice-wise
processing are evaluated and finally combined in a
hybrid model. For the segmentation task a U-net
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
68

architecture comprising 5 levels of hierarchy is
adjusted to input image size of 352×288 pixels for axial
slices, see Fig. 3. To prevent implicit shrinking by each
convolution operation, padding is applied, thus
ensuring intermediate image size reduced by a factor
of two at each hierarchy level, namely 176×144,
88×72, 44×36 and 22×18 respectively. The network
complexity is manifested by 31,031,685 trainable
parameters with kernel size 3×3 and considering the
bias parameters for each of the in total 23 layers.
3.1 Data Augmentation
With the liver dataset from the Medical Segmentation
Decathlon database only 131 tomographic CT volumes
are available. Nevertheless, as the volume is processed
in a slice-wise manner, the CT volumes result in at least
27,358 axial slices available for training, validation and
test. Due to the high resolution, differences between
neighbouring slices are low and thus redundancy is
present in the dataset. Thus, data augmentation is
needed to enrich the number of input slices to prevent
from over-fitting at higher epoch counts and to reduce
the gap between training and testing accuracy.
Data augmentation is implemented in an original
way to keep full control of the nature of the artificial
images generated compared to out of the box
Keras/Tensorflow functionality. The following
parameters are used to manipulate the slices chosen for
the current batch and thus to enrich the amount of data
available for training:
transX and transY: translation in x-direction and y-
direction of the current slice
rot: rotation around the image center
intMul: linear scale of the image intensities leading
to brighter or darker pixel values within the borders
of the windowing range
intAdd: additive manipulation of the intensities
within the window, leading to a uniform shift for
full scalar range
For all of these parameters, a valid range is configured
a priori. The parameter set to apply for a particular
image is then given as randomly selected values
(uniform distribution) within the valid range of the
augmentation parameters.
Pixel values of the augmented image are thereby
calculated as shown in Eqn. (2).
,
,
∙
1
0.5
∙
0.5
∙intAdd
(2)
Figure 3: Network layout of the U-Net architecture utilized in this paper adapted from (Ronneberg et al. 2015). The intermediate
results on each of the five hierarchy layer are visualized for slice 72 of dataset #0. At full resolution of 352×288 two layers with
64 convolution kernels are applied while after reducing the size to 176×144 two layers with 128 convolution kernels each are
applied. To reconstruct the original size, four concat operators and up-sampling are applied.
Pre- and Post-processing Strategies for Generic Slice-wise Segmentation of Tomographic 3D Datasets Utilizing U-Net Deep Learning
Models Trained for Specific Diagnostic Domains
69

2
2
∙
0.5
∙
0.5
∙
(3)
with in
0.0;1.0
and
0.5
∙.
A drawback of common data augmentation is the
loss of image information when rotating and
translating the image content while introducing
background regions with lack of information confusing
the model training process. To adress this problem and
to dampen the effects, a safety margin of
paddingOffset =10 is used to provide a
surrounding frame with original image data to use for
the augmented images, see Fig. 4.
(a) (b)
Figure 4: Although the axial slices utilized are of size
352×288, due to the paddingOffset the virtual image size is
372×308 thus introducing a safety margin for transformations
(a). With transX=15.5, transY=-23.8 and
rot=8.1 the relevant image content is still within the
processed as visible for the sinister rib cage (b).
3.2 Deep Learning based Classification
3.2.1 Classification of Axial Slices
In a straight-forward approach the tomographic input
datasets are sliced in axial direction to provide one-
channel input tensors of size 352×288 for the
modelAxial.h5 axial U-Net (ax) weights to be trained.
Due to the a priori defined ROI of the parenchyma area,
the axial parenchyma shape grows and shrinks in
caudal-to-cranial direction with moving position
according to a significant trend. Nevertheless, this
positional information within the slices is not utilized
in this approach.
According to the chosen pre-processing, the aspect
ratio of the axial slices is conserved with the width,
height scaled to the target tensor size utilizing cubic
interpolation. In z-direction there is no interpolation
required. All axial slices are varied with respect to data
augmentation parameters 16,16,10,.1,30 for
transX, transY, rot, intMul and intAdd respectively.
For model training, a learning rate of 5∙10
is configured for the Adam Optimizer (Kingma and Ba
2014) with 10.9 , 20.999 and
10
using cross-entropy as loss. The
training runs for 200 epochs at most using
32 and 12 preventing
from pre-mature stopping (validation loss).
3.2.2 Discrete Axial Model for Specific
Z-ranges within the ROI
With the model modelAxial.h5 neither 3D information
nor the characteristic axial liver shape according to the
position within the ROI are incorporated. Especially in
the caudal and cranial section of the ROI the
parenchyma size is low and varying intensity profiles
observed. Thus, the position within the ROI, denoted
as sliceRatio with values scaled to
0;1
should be
incorporated too.
For the chosen U-net architecture, it is hard to
provide the relevant sliceRatio parameter as additional
input to the network. It is possible to attach a FCN layer
with medium depth at the end of U-Net probability
mask classification to use the sliceRatio parameter for
automatic derivation of the locally best threshold value
for final binarization of the segmentation.
Nevertheless, there the positional impact would be
marginal.
As both the shape and position of the parenchyma
areas vary heavily within an entire 3D volume, splitting
the slice range into smaller sections increases the local
homogeneity at the cost of reduced amount of training
data, see Fig. 5.
To smooth transitions, the reduced amount of
training data for each of the sections as well as the
sharp border areas between them, the segments are
defined to overlap by 0.05 with [0;0.25[, [0.15;0.45[,
[0.35;0.65[, [0.55;0.85[ and [0.75;1.00] for the
sections 1-5 respectively.
To further utilize the predictability of neighbouring
segments close to the border sections, the final result is
combined in a linear interpolation way as shown in
Eqn. (4) with only the at most two sections
neighbouring the particular sliceRatio
are
incorporated for number of classes 5 and model
predictions
.
,
∑
,
∙
,
with
(4)
,
1
1
,
1
2∙
∙
1
1
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
70

Figure 5: The axial slice stack is devided into overlapping
sections 1-5. As shown on the right chart, the position-related
trend in size for the first n=5 datasets is highly correlated and
thus motivates splitting into model sections.
3.2.3 Slice Propagation Incorporating
Neighbouring Results
Due to the high inter-slice-resolution of the employed
CT data, neighbouring slices show a high correlation
with respect to position, size and orientation of the
segmentations. Incorporating this given fact, the actual
slice segmentations are expected to get stabilized. A
similar semantic plausibility check is used with LSTM
deep learning for natural language processing or for
robust video object retrieval. Certainly, LSTM
concepts would be applicable too but enriching the
neighbouring slices with the right amount of
uncertainty at all memory layers is a challenging task.
Consequently, another 2D U-Net approach is
chosen and enriched with the neighbouring slices.
Besides the input
to be segmented, also
autonomous segmentation results of the previous and
next slice as ,
and
,
are added to the input
tensor that is reshaped to
1,288,352,3
extent
similar as applicable for RGB images, c.f. Fig. 6.
A crucial aspect is how to define the neighbouring
slices for training. With the ground truth provided, the
influence of the particular intensity profile slice is
marginalized, thus only the proximate slices are
utilized.
The data augmentation for this 3-slice concept is of
high importance. The transformation of the mid slice is
performed with the same parameter set
16,16,10,.1,30
as used in section 3.1. To conserve
the inter-slice-correlation it would neither be a good
idea to randomly transform the proximate slices nor to
move them along with the mid slice to sustain a small
but crucial level of variability. Thus, for the previous
and next slice, a ¼ of the mid slice data augmentation
range is utilized and applied relative to the mid slice
transformation.
With the presented 3-slice model of
1, and
1 denoted as
, the results of a first run can be
improved by bottom-up and top-down processing.
Furthermore, the slice-wise propagation opens rich
possibility for manual adjustment of the results.
Figure 6: The training tensor for the mid slice is enriched by
neighbouring single-slice predictions.
3.2.4 Incorporating Axial and Sagittal Views
for Overall Classification Building up a
Hybrid Position-based Model
The drawback of slice-wise data processing are the
outer sections, where the target structure continuously
vanishes in mass. For the axial slices, this is the case in
the top and bottom rows. To overcome this limitation,
it makes sense to incorporate sagittal and coronal slices
too. Although the sagittal and coronal slices show
weaknesses in the left/right and front/back areas
respectively, with respect to the overall information a
significant gain is expected. Axial slices are
transformed to sagittal (256x376) and coronal
(256x308) with z-dimension scaled to 256 for each of
the 3D datasets. Two U-net models, sagittal (ax
s
) and
coronal (ax
c
), are trained and applied as described in
section 3.2.1 with results back-transformed to axial
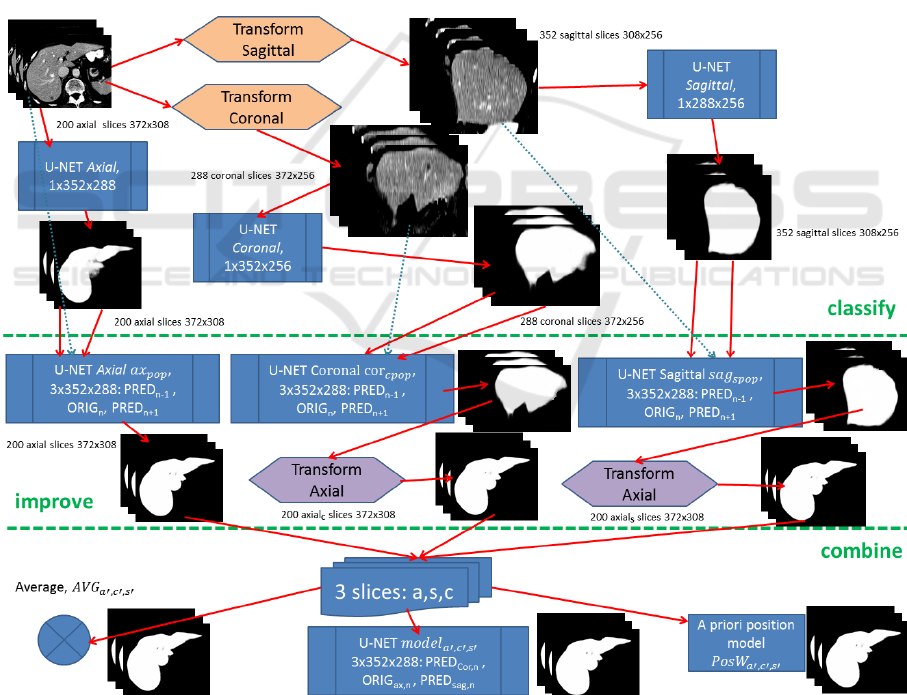
view. In Fig. 7 the preparation of segmentation results
for axial, sagittal and coronal can be seen in the
classify-section.
The 3-slice model ax
pop
, incorporating
neighbouring slices and thus a marginally perspective
aspect is expected to be capable of further improving
slice-by-slice results, c.f. improve section of Fig. 7.
With ax
pop
applied to reconstructions from sagittal and
coronal, axial segmentation information is thereby
already incorporated lowering the benefit for
combination of the three orthogonal views. Thus,
sagittal and coronal predictions are improved with
specific 3-slice models denoted as ax
spopSAG
and ax
spopCOR
respectively, see Fig. 7.
Now, as for each slice a good segmentation result
from axial, sagittal and coronal view is achieved, they
get combined for the final result.
The most straight forward approach thereby is
averaging of the three particular slices, denoted as
,,
. As for the border areas two of three views are
Pre- and Post-processing Strategies for Generic Slice-wise Segmentation of Tomographic 3D Datasets Utilizing U-Net Deep Learning
Models Trained for Specific Diagnostic Domains
71
expected to contribute good results, averaging or
majority voting seem to be a functional approach.
Alternatively, a 3-layer U-Net model can be trained
as decision tree, denoted as
,,
.
A third approach (
,,
) for combining the
orthogonal slices focuses on the position-based
evaluation of the prediction accuracy of the axial,
sagittal and coronal models calculated from pixel-wise
error as a normalized volume of size 100×100×100.
Smoothing (Gaussian kernel, r=1, 8 runs) is applied to
get a dense weight-map for position-dependent
accuracy of axial, coronal and sagittal slices.
4 IMPLEMENTATION
For the manually performed pre-processing steps such
as converting the image type, resampling to isotopic
voxels as well as for visualization of the results the
image processing frameworks and tools Analyze,
MeVisLab and ImageJ are utilized.
The model training and testing is implemented in
Python version 3.7.3 with separate parameterizable
scripts
for the various process steps using
Tensorflow 2.0 beta together with Keras.
The Python image processing is largely built upon
OpenCV or numpy for fast matrix operations.
To provide the model with training data, a
DataGenerator class is derived from Sequence
base class.
With a data generator, the batches can be loaded
from the file system on demand and one gets full
control on the data augmentation and on the batch-
randomization.
Figure 7: Axial slices are first transformed into sagittal and coronal views too, all to get classified by an individual U-Net. After
this classification section, results can further be improved by using a generic 3-slice U-Net (ax
pop
) after reconstruction to axial
view or specific ones (sag
pop
, cor
pop
) prior to axial reconstruction. The improved results finally get combined by one of the three
proposed strategies, averaging, U-net trained for merging or a position-based weighting algorithm.
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
72

5 RESULTS
5.1 Evaluation Metrics
For evaluation, in this work the same metrics as
proposed by the medical decathlon challenge are used
(MedDecathlon 2018). These are the Sørensen-Dice
coefficient (DSC)(Dice, 1945) for evaluation of the
spatial overlap and the normalized surface distance
(NSD) (Laplante, 2019) evaluating the spatial
proximity of test and reference shape to compare.
Additionally, the Jaccard index (Jaccard, 1912) as a
stricter metric for area match compared to the Dice
coefficient is evaluated too to allow for comparability
with further research papers. The metrics are calculated
according to Eqs. (5)-(7) for foreground reference
segmentation R and foreground test region S of image
I with ⊆,⊆ and pixels
,
∈∪.
,
2⋅
|
∩
|
|
|
|
|
(5)
,
1
∑
,
,
∙
,,
∑
,,
,
,
(6)
,
|
∩
|
|
|
|
|
|
∩
|
(7)
Metric
,
∈
0;1
thereby calculates for error
pixels the distance to the correct border of the reference
shape and normalizes with pixels in ∪.
For the overall accuracy of a dataset, i.e. 3D
volume, the metrics DSC, NSD and JI are caclulated
by summing up the FP, FN and correct results of all the
slices. To adress the statistics per slice, for the same
metrics a median slice accuracy is evaluated per dataset
denoted as DSC
med
, NSD
med
and JI
med
respectively.
Testing on several 3D volumes, the partciular results of
the six mentioned metrics are statistically analyzed too
for getting an overall evidence.
5.2 Hardware Infrastructure
All of the process steps discussed in this paper, namely
data preparation, pre-processing, model training and
validation/test are performed on a Colfax SX9600 GPU
Rack with 2×Intel Xeon Gold 6148 2.4GHZ processors
and 768GB of DDR4 memory with 2667MHZ clock
frequency split into 24 partitions of 32GB each. The
system runs CentosOS 7.6 operating system and
provides for fast tensor calculation 8 GPU cores,
namely 4× NVIDIA Volta Titan V 12G and 4× NVIDIA
Tesla V100 32G.
5.3 Results on Pre-processing and Data
Augmentation
The safety margin of 10 pixels used to enlarge the input
axial slices from 352×288 to 372×308 successfully
helped to prevent from black-areas due to rotation and
translation outside the image borders for the effective
image range. The intensity profile manipulation for the
data augmentation process does not result in a value
overflow, see Fig. 8.
To preserve the binary reference segmentation
masks, as interpolation strategy the modes Area and
Nearest Neighbour are to be utilized only.
(a)
(b)
(c)
(d)
Figure 8: Axial slice 276 (a) and reference segmentation (c)
get transformed by transX=-6.64, transY=3.51,
rot=3.00, intMul=1.02 and intAdd=-5.74 (b),
(d).
5.4 Slice-wise Classification Utilizing a
Single Model
The following axial, sagittal and coronal models are
trained with 22,000 (axial), 40,000 (sagittal) and
32,000 (coronal) augmented datasets while validation
is performed with the remaining datasets, namely
4,858 (axial), 8,232 (sagittal) and 7,848 (coronal). The
imbalance in train and test data results from different
dataset dimensionality in the main viewing directions
and is implicitly balanced utilizing data augmentation.
For results of the evaluation metrics on the axial,
sagittal and coronal model, c.f. Table 1. Furthermore,
the models ax
s
and ax
c
are evaluated after
reconstruction and resampling from sagittal/axial to
axial slices.
Although the axial, cornal and sagittal model show
similar accuracy, their particular strength is located in
various sections as shown in Fig. 9. The axial model is
weak in the caudal sections but outperforming in the
cranial sections.
Pre- and Post-processing Strategies for Generic Slice-wise Segmentation of Tomographic 3D Datasets Utilizing U-Net Deep Learning
Models Trained for Specific Diagnostic Domains
73
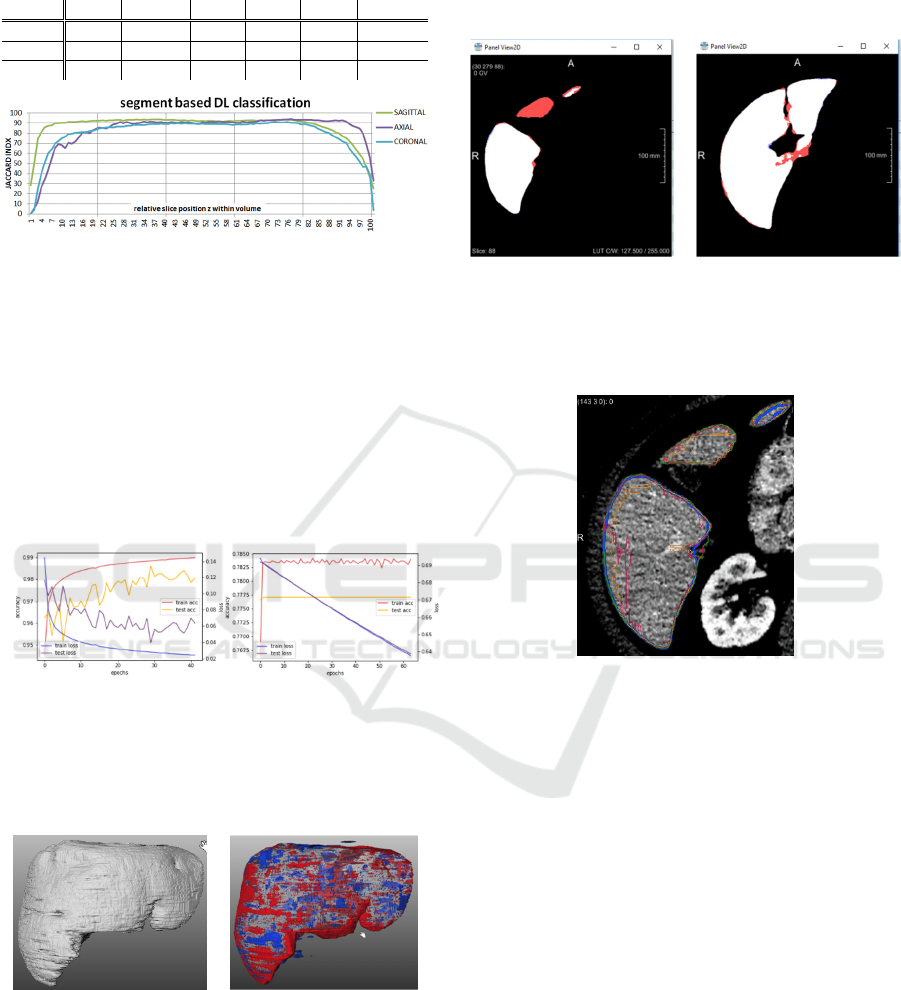
Table 1: Results for the particular slice-wise models
evaluated on the test datasets.
model DSC DSC
med
JI JI
med
NSD NSD
med
96.2 96.6 92.6 93.4 98.2 99.0
96.8 96.9 93.8 93.9 96.2 99.3
96.5 96.5 93.2 93.3 97.9 98.6
Figure 9: JI metric evaluated for axial, sagittal and coronal
model per 1% intervals with respect to relative z-position
within the volume.
The training process for the final axial model is
shown in Fig.10 (a) while in Fig.10 (b) an premature
stagnation with identical settings is visible. With each
epoch on full training data lasting for 35:10 minutes the
overall training of a large model took 15-20 hours. In
contrast, model evaluation takes place in millisecond
range and is only affected by file loading and pre-
processing demand.
(a) (b)
Figure 10: While in (a) the axial model approaches good
results within 36 epochs, depending on the initial random
batch and random the training gets early stuck in about 50%
of the cases (b).
(a)
(b)
Figure 11: Correctly segmented liver area for dataset #101 in
(a) and FP, FN visualization at surface and vena porta areas
in (b).
The achievable segmentation accuracy is
visualized for dataset #111 in Fig. 11 with the matching
volume in (a) and the FP and FN areas in blue and red
respectively. Axial segmentation results are rather
weak in the caudal and cranial areas, see Fig. 12. This
deficiency is easily levelled by incorporating sagittal
and coronal too, see Fig. 13.
(a) (b)
Figure 12: Axial view of segmentation mismatch of slice 88
and 135 of dataset #111 for model ax (a-b). In caudal
direction the starting slices of new morphological islands
sometimes stay unclassified.
Figure 13: Axial view of segmentation mismatch of slice 88
of dataset #111 with ground truth (green), axial (blue),
sagittal (red) and coronal (orange) incorporating the midst
parenchyma part (red FN region in Fig. 12 (a)) in caudal
direction in contrast to the axial result.
5.5 Classification with Discrete Axial
Models for Specific Z-ranges
Results on the section-based models are listed in Tab.
2. As the training data of 22.000 slices gets split up into
5 sections, the quality of these specific models are
marginally below the full axial model ax. Only if the
axial model is trained with a reduced amount of data
too for reason of compensation (axial small, ax
small
), the
section models are significantly outperforming. The
mode with linearly combining the classification results
of the neighbouring sections for a particular slice (e.g.
ax
1,nb
) outperform the use of only the nearest section
(e.g. ax
1
).
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
74

Table 2: Section based evaluation of various models,
namely full axial model ax trained with 22,000 datasets,
axsmall only trained with 4,400 datasets such as the section
models ax1- ax5. Model axnb incorporates neighbouring
sections for linear interpolation.
S
model
DSC DSC
med
JI JI
med
NSD NSD
med
1
ax 89.8 93.0 81.5 86.9 88.1 96.4
ax
small
67.0 62.5 50.3 45.5 41.9 45.2
ax
1
87.4 88.4 77.6 79.3 82.2 89.5
ax
1,nb
88.0 89.3 78.5 80.6 83.6 90.9
2
ax 96.2 97.0 92.6 94.2 97.7 99.3
ax
small
86.5 88.2 76.2 78.9 85.5 88.7
ax
2
96.0 97.0 92.2 94.1 97.3 99.3
ax
2,nb
96.2 97.2 92.6 94.5 97.6 99.4
3
ax 96.2 96.7 92.6 93.5 98.2 99.1
ax
small
87.3 88.1 77.5 78.7 87.3 89.9
ax
3
96.9 97.2 93.9 94.6 98.8 99.4
ax
3,nb
96.9 97.1 93.9 94.4 98.8 99.4
4
ax 96.8 97.2 93.8 94.5 98.7 99.2
ax
small
88.1 90.1 78.8 81.9 85.8 90.7
ax
4
96.6 97.0 93.5 94.1 98.4 99.2
ax
4,nb
96.9 97.2 94.0 94.6 98.7 99.4
5
ax 96.0 96.5 92.3 93.2 98.6 98.9
ax
small
86.7 88.6 76.5 79.6 85.4 89.9
ax
5
94.1 94.7 88.9 90.0 88.6 92.6
ax
5,nb
94.6 95.1 89.7 90.7 90.2 94.5
all
ax 96.2 96.6 92.6 93.4 98.2 99.0
ax
small
86.8 86.9 76.6 76.8 85.2 87.6
ax
1-5
95.9 96.4 92.1 93.0 96.7 98.7
ax
nb
96.1 96.6 92.5 93.4 97.1 99.0
5.6 Slice to Slice Result Propagation
Results on the 3-slice U-Net implementing predictions
of the previous and the next slice are found in Table 3.
Table 3: Test runs on 3-slice model expecting prediction for
(n-1), original axial slice and prediction for (n+1).
model DSC DSC
med
JI JI
med
NSD NSD
med
96.2 96.6 92.6 93.4 98.2 99.0
95.2 95.6 90.8 91.5 95.1 98.6
97.0 97.3 94.1 94.7 98.7 99.4
98.6 98.5 97.2 97.0 99.9 99.9
96.8 96.9 93.8 93.9 96.2 99.3
97.2 97.3 94.5 94.7 98.0 99.2
97.1 97.1 94.4 94.4 97.2 99.1
96.5 96.5 93.2 93.3 97.9 98.6
96.9 97.1 94.0 94.4 98.3 99.1
96.9 97.0 93.9 94.1 98.2 99.0
The model is thereby trained to get the intensity
profile for slice n and a first rough prediction for the
slices n-1 and n+1. In Table 3 there are test runs for
three predictions as ax
ppp
, the expected input ax
pop
together with neighbouring predictions and ground
truth for previous (ax
top
). Furthermore, the
reconstructed sagittal and coronal slices are tested, too,
utilizing the same model. For the coronal and sagittal
view,
the axial 3-slice model (ax
spop
, ax
cpop
) leads to
similar improvements after reconstruction to axial
view as applying specific trained 3-slice models for
coronal and sagittal before the reconstruction (sag
spop
,
cor
cpop
), cf. Fig. 7.
5.7 Hybrid Position Model of Axial,
Coronal and Sagittal Segmentation
Combining the particular results from axial, coronal
and sagittal the overall quality of results gets improved
for the a priori position model and a U-Net trained for
combination.
Table 4: Quality of results for the segmentations ax, ax
c
and
ax
s
is improved by combining with average (AVG), position
model (PosW) or U-net model trained for combination
(model). As input, the pre-classified slices without (a, s, c)
and with 3-slice improvement (a’, s’, c’) are applied.
model DSC
DSC
med
JI JI
med
NSD
NSD
med
96.2 96.6 92.6 93.4 98.2 99.0
96.8 96.9 93.8 93.9 96.2 99.3
96.5 96.5 93.2 93.3 97.9 98.6
,,
97.2 97.3 94.6 94.7 99.1 99.4
,,
97.2 97.3 94.6 94.7 99.1 99.4
,,
97.5 97.6 95.2 95.2 99.3 99.5
,,
97.4 97.5 94.9 95.1 99.2 99.5
,,
97.4 97.5 94.9 95.1 99.2 99.5
,,
97.6 97.7 95.3 95.5 99.4 99.6
Results on the entire liver dataset can be found in Table
4. Comparing the simple averaging (AVG) and the
complex position-based a priori model (PosW), the
results are almost equal.
(a) (b)
Figure 14: Axial view of segmentation mismatch of slice 88
and 135 of dataset #111 for model model
a’,c’,s’
(a-b). The 3-
slice model and combination of orthogonal views corrects the
error (model
a’,c’,s’
) of ax model, c.f. Fig. 12.
Pre- and Post-processing Strategies for Generic Slice-wise Segmentation of Tomographic 3D Datasets Utilizing U-Net Deep Learning
Models Trained for Specific Diagnostic Domains
75

It is shown that U-net models are applicable for result
migration too and highest accuracy is achieved for
utilizing both, the 3-slice-improvement and the
combination of the orthogonal views, c.f. Fig. 14 (a-b)
for slices 88 and 135 of dataset #111.
5.8 Comparison to Other Approaches
The highest achieved accuracy in this paper is to be
quantified with DSC=97.59, JI=95.29 and
NSD=99.37 for PosW
a’,c’,s’
.
A similar slice-based approach utilizing LevelSets
for result propagation and a Statistical Shape Model for
initial parametrization achieved an average
JI=93.6±3.3 and a volume match of 96.82±1.72%
(Zwettler et al. 2009). At the medical decathlon 2018,
the top team achieved DSC=0.95 and NSD=0.98
evaluated for L1 region utilizing a nnU-Net (Isensee et
al. 2019).
6 DISCUSSION
With precise pre-processing and post-processing, the
domain of 3D segmentation in medicine can be
addressed with 2D slice-by-slice models, too
approaching similar level of quality. Classification
with 2D models has some significant advantages with
respect to calculation power required for model
training and memory consumption. Furthermore, for
user-centric approaches in the medical domain, the
interaction with 2D slices is more common with a
broader range of interaction paradigms.
Surprisingly the sectional models did not pay of as
expected. It was shown that this fact results from the
reduced amount of testing data. Thus, if a sufficient
amount of slices is available, splitting into sectors is a
reasonable strategy, training only on a subset of the
axial shapes and positions besides the intensity profile.
With the data augmentation strategy presented in this
paper, the lack in training data could not be
compensated. Instead, real medical image data or
results of GANs should be utilized.
With the 3-slice model, the perfect basis for user-
centric and interactive post-processing is provided. In
this paper it was shown that the improved results can
be propagated from slice to slice. Nevertheless, the
axial
pop
model perfectly worked out for improving the
initially segmented slices at similar accuracy compared
to the particular models (sag
spop
, cor
cpop
). Marginal
incorporation of a mini 3D-subvolume of 3 slices
significantly improved results. In future incorporating
5 or 7 slices will be investigated, possibly a higher step
increment will allow further improvement.
The combination of the axial and reconstructed
coronal and sagittal results is a crucial point. As for all
positions two of the main views lead to robust results,
it is not a huge surprise that a simple averageing model
can compete with the presented complex a priori
position model. The concept, that axial is weak at
caudal and cranial directions with sagittal and coronal
weak at front/back and left/right respectively was
proven by deeper analysis.
Nevertheless, these aspects were not corrrectltly
adressed with the position-based model. The caudal
and cranial sections are not only axial slices at the very
begin or end as they might arise inside the volume too.
Thus, it would be a better strategy to analyze the local
gradients, e.g. utilizing eigenvalue analysis. If the x, y
or z-gradients are high in local neighborhood, one can
conclude the adapted weights for axial, coronal and
sagittal then.
With the chosen ROI size of 288×352×256 it was
shown that tensors for deep learning not necessarily
need to be isotropic as stated in other papers.
7 CONCLUSIONS
Utilizing powerful Deep Learning as a small image
processing module, most of its black box nature
vanishes. If these modules are integrated into
conventional image processing chains in an adequate
way, significant improvements on the date pre- and
post-processing become feasible.
Furthermore, it is shown that in spite of iteratively
improving deep learning architectures and processing
power it still might be a reasonable decision to
decompose a 3D segmentation problem into slice-by-
slice processing.
Future work will focus on user-centric interaction
paradigms. Up to now powerful deep learning models
are available for a broad community but rather as a
black box. Thus, one has to accept the most often good
results as they are provided by the model.
Nevertheless, in computer-based medical analytics
the human diagnostician always should have powerful
tools for overruling the machine made decisions. With
slice-wise processing of the input volume, many
human-computer interaction paradigms become
realizable.
Another aspect to address in ongoing research is the
genericity of this concept. Besides the parenchyma-
optimized ROI dimensionality all other aspects of the
model are very generic. With definition of a priori ROI
and windowing, one axial sagittal, coronal model
should be able to not only handle parenchyma data, but
also datasets with kidney, lung, gall bladder and many
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
76

more in focus too if getting re-trained on a sufficient
amount of reference data.
REFERENCES
Aggarwal, A., Vig, R., Bhadoria, S., and Dethe, C.G., 2011.
Role of Segmentation in Medical Imaging: A
Comparative Study. In: Int. Journal of Comp. Applic.
29(1).
Amorim, P.H.A., Chagas, V.S., Escudero, G.G., Oliveira,
D.D.C., Pereira, S.M., Santos, H.M., and Scussel, A.A.,
2017. 3D U-Nets for Brain Tumour Segmentation. In:
MICCAI 2017 BraTS Challenge. In: Proc. of the
MICCAI 2017.
Arik, S.O., Chrzanowski , M., Coates, A., Diamos , G.,
Gibiansky, A., Kang, Y., Li, X., Miller, J., Raiman, J.,
Sengupta, S., and Shoeybi , M., 2017. Deep voice: Real
time neural text to speech. In: ICML 2017
BIR, 1986. ANALYZE
TM
Header File Format, available from
http://www.grahamwideman.com/gw/brain/analyze/for
matdoc.htm, last visted 11.9.2019.
Chen, C., Liu, X., Ding, M., Zheng, J., and Li, J., 2019. 3D
Dilated Multi-Fiber Network for Real-time Brain Tumor
Segmentation in MRI. In: CoRR, available from
https://arxiv.org/pdf/1904.03355.pdf, last visited
1.10.2019.
Christensen, A., and Wake, N., 2018. Wohler Report:
Medical image processing software, Available from
http://www.wohlersassociates.com/medical2018.pdf ,
last visited 1.10.2019 .
Cicek, Ö., Abdulkadir, A., Lienkamp, S.S., Brox, T., and
Ronneberg, O. 2016. 3D U-Net: Learning Dense
Volumetric Segmentation from Sparse Annotation. In:
MICCAI 2016.
Cootes, T.F., Taylor, C.J., Cooper, D.H., and Graham, J.,
1992. Training Models of Shape from Sets of Examples.
In Proc. of the British Machine Vision Conference, 9-18.,
Leeds, U.K.
Cootes, T.F., Edwards, G.J., and Taylor, C.J., 1998. Active
Appearance Models. In Proc. of the 5th Europ. Conf. on
Computer Vision, 484- 498. June 2-6, Freiburg,
Germany.
DFWG, 2005. NIFTI - Neuroimaging Informatics
Technology Initiative, available from
https://nifti.nimh.nih.gov/, last visited 11.9.2019
Dice, L.R., 1945. Measures of the Amount of Ecologic
Association Between Species. In: Ecology. 26 (3).
Frid-Adar, M., Diamant, I., Klang, E., Amitai, M.,
Goldberger, J., and Greenspan, H., 2018. GAN-based
synthetic medical image augmentation for increased
CNN performance in liver lesion classification. In:
Neurocomputing, pp. 321-331.
Goodfellow , I.J., Pouget Abadie , J., Mirza, M., Xu, B.,
Warde Farley, D., Ozair, S., Courville, A., and Bengio,
Y., 2014. Generative Adversarial Nets. In Proc. of the
27th Int. Conf. on Neural Information Processing
Systems, vol. 2.
Hochreiter, S., and Schmidhuber, J., 1997. Long Short-Term
Memory. In: Neural Computation 9(8), pp. 1735-1780.
Huang, C., Han, H., Yao, Q., Zhu, S., and Zhou, S.K., 2019.
3D U
2
-Net: A 3D Universal U-Net for Multi-Domain
Medical Image Segmentation. In: Proc. of the MICCAI
2019.
Isensee, F., Petersen, J., Kohl, S.A.A., Jäger, P.F., and Maier-
Hain, K.H., 2019. nnU-Net: Breaking the Spell on
Successful Medical Image Segmentation. In: CoRR.
Jaccard, P., 1912. The Distribution of the flora in the alpine
zone, In: New Phytologist, 11.
Kingma, D.P., and Ba, J.L., 2014. Adam : A method for
stochastic optimization. In: Int. Conf. on Learning
Representations (ICLR), available from
https://arxiv.org/abs/1412.6980, last visited 1.10.2019.
Laplante, P.A. (ed.), 2019. Encyclopedia of Image
Processing. In: CRC Press/Taylor & Francis Publishing.
McInerney, T., and Terzopoulos, D., 1996. Deformable
Models in Medical Image Analysis : A Survey. In
Medical Image Analysis 1 (2): pp. 91-108.
MedDecathlon, 2018. MSD-Ranking Scheme, available
from: http://medicaldecathlon.com/files/MSD-Ranking-
scheme.pdf, last visited 19.9.2019.
Meine, H., Chlebus, G., Ghafoorian, M., Endo, I., and
Schenk, A., 2018. Comparison of U-net-based
Convolutional Neural Networks for Liver Segmentation
in CT. In: Computer Vision and Pattern Recognition,
available from https://arxiv.org/abs/
1810.04017, last visited 1.10.2019.
Rajagopalan, S., Karwoski, R.A., Robb, R.A., Ellis, R.E., and
Peters, T.M., 2003. Shape-Based Interpolation of Porous
and Tortuous Binary Objects. In: MICCAI 2003, pp.
957-958.
Robb, R.A., Hanson, D.P., Karwoski, R.A., Larson, A.G.,
Workman, E.L. and Stacy, M.C., 1989. Analyze: a
comprehensive, operator-interactive software package
for multidimensional medical image display and
analysis. In: Comput Med Imaging Graph 13(6): 433–
454.
Ronneberg, O., Fischer, P., and Brox, T., 2015. U-Net:
Convolutional Networks for Biomedical Image
Segmentation. In: MICCAI 2015, Springer, LNCS,
Vol.9351: 234—241.
Simpson, A., Antonelli, M., Bakas, S., Bilello, M., Farahani,
K., Ginneken, B., Kopp-Schneider, A., Landman, B.,
Litjens, G., Menze, B., Ronneberger, O., Summers, R.,
Bilic, P., Christ, P., Do, R., Gollub, M., Golia-Pernicka,
J., Heckers, S., Jarnagin, W. and Cardoso, M.J., 2019. A
large annotated medical image dataset for the
development and evaluation of segmentation algorithms.
In CoRR.
Squelch, A., 2018. 3D printing and medical imaging. In:
Journal Med Radiat Sci. 65(3).
Stegmaier, J., 2017. New Methods to Improve Large-Scale
Microscopy Image Analysis with Prior Knowledge and
Uncertainty. In: KIT Scientific Publishing, Karlsruhe.
Strakos, P., Jaros, M., Karasek, T., Kozubek, T., Vavra, P.,
and Jonszta, T., 2015. Review of the Software Used for
3D Volumetric Reconstruction of the Liver. In: Int.
Journal of Computer and Information Engineering 9(2).
Pre- and Post-processing Strategies for Generic Slice-wise Segmentation of Tomographic 3D Datasets Utilizing U-Net Deep Learning
Models Trained for Specific Diagnostic Domains
77

Van Biesen, W., Sieben, G., Lameire, N., and Vanholder, R.,
1998. Application of Kohonen neural networks for the
non-morphological distinction between glomerular and
tubular renal disease. In: Nephrol Dial Transplant 13(1),
pp. 59-66
Viola, P., and Jones, M., 2001. Rapid Object Detection using
a Boosted Cascade of Simple Features. In: Conf. on
Computer Vision and Pattern Recognition 2001
Yang, D., Xu, D., Zhou, S.K., Georgescu, B., Chen, M.,
Grbic, S., Metaxas, D., and Comaniciu, D., 2017.
Automatic Liver Segmentation Using an Adversarial
Image-to-Image Network. In: MICCAI 2017.
Yi, X., Walia, E., and Babyn, P., 2019. Generative
Adversarial Network in Medical Imaging: A Review. In:
Medical Image Analysis vol. 58.
Zhang, J., and Wang, X.W. 2011. The application of feed
forward neural network for the X ray image fusion. In: J.
Phys.
Zwettler, G., and Backfrieder, W., 2013. Generic Model-
Based Application of Modular Image Processing Chains
for Medical 3D Data Analysis in Clinical Research and
Radiographer Training. In: Proc. of IWISH 2013, pp. 58-
64
Zwettler, G., Backfrieder, W., Swoboda, R., and Pfeifer, F.,
2009. Fast Fully-automated Model-driven Liver
Segmentation Utilizing Slicewise Applied Levelsets on
Large CT Data. In: Proc. of the 21
st
EMSS 2009, pp. 161-
166.
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
78
