
Clothing Category Classification using Common Models Adaptively
Adjusted to Observation
Jingyu Hu
1,∗
, Nobuyuki Kita
2
and Yasuyo Kita
2
1
Technology Platform Center, IHI Corporation Technology & Intelligence Integration, Japan
2
Intelligent Systems Research Institute, National Institute of Advanced Industrial Science and Technology (AIST),
Tsukuba, Japan
Keywords:
Clothing Categorization, Active Recognition, Recognition of Deformable Objects, Automatic Handling of
Clothing, Robot Vision.
Abstract:
This paper proposes a method of automatically classifying the category of clothing items by adaptively ad-
justing common models subject to each observation. In the previous work(Hu and Kita, 2015), we proposed a
two-stage method of categorizing a clothing item using a dual-arm robot. First, to alleviate the effect of large
physical deformation, the method reshaped a clothing item of interest into one of a small number of limited
shapes by using a fixed basic sequence of re-grasp actions. The shape was then matched with shape potential
images of clothing category, each of which was configured by combining the clothing contours of various
designed items of the same category. However, there was a problem that the shape potential images were too
general to be highly discriminative. In this paper, we propose to configure high discriminative shape potential
images by adjusting them subject to observation. Concretely, we restrict the contours used for potential images
according to simply observable information. Two series of experiments using various clothing items of five
categories demonstrate the effect of the proposed method.
1 INTRODUCTION
As home and rehabilitation robots are expected to
play an important role in an aging society, it will
become necessary for robots to automatically han-
dle daily objects including clothing items. The large
deformation of clothing items that is accompanied
by complex self-occlusion makes it more difficult to
recognize items. There have been many studies on
the recognition for handling clothes, such as those
on classification(B. Willimon and Walker, 2013)(Stria
and Hlavac, 2018), and automatic folding (J. Maitin-
Shepard and Abbeel, 2010)(S. Miller and Abbeel,
2011)(Y. Kita and Kita, 2014)(P. Yang and Ogata,
2017).
The present paper focuses on the automatic classi-
fication of clothing items into a category (e.g., shirts,
trousers) using a dual-arm robot without flattening the
items on a table. Unlike most existing methods, we
aim at a method that can work with general mod-
els of the category without requiring preregistration
of the clothing items to be recognized. Considering
the almost infinite variation in clothing shape, it is
∗
Was a student in the Department of Intelligent Interaction
Technologies of the University of Tsukuba, Tsukuba, Japan
extremely difficult to make the model of each cat-
egory that is highly discriminating among different
categories and at the same time is tolerant of intra-
category shape variation. To overcome this problem,
in the previouswork(Hu and Kita, 2015) we proposed
a two-stage method to separately deal with the shape
variation due to design variation of a category from
that caused by physical deformation. First, to lessen
the effect of physical deformation, the item of inter-
est is reshaped into one of a small number of limited
shapes in the air. Then, to absorb the shape varia-
tion of each limited shape due to the different size,
design and material within the category, we match the
shape with a potential image, which is made by com-
bining contours of clothing items of various design
and material. The feasibility tests of the work demon-
strated a high potential of the strategy. However, we
also found the defect of the shape model represented
by the potential image: while the model can cover
variation caused by large individual size, design and
materials, it has low discriminative power.
To overcome this weak point, this paper proposes
to add a feedback process from observation to the
model building process, as illustrated in Fig. 1. Al-
though we, human, naturally do such feedback, few
310
Hu, J., Kita, N. and Kita, Y.
Clothing Category Classification using Common Models Adaptively Adjusted to Observation.
DOI: 10.5220/0008936903100317
In Proceedings of the 15th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2020) - Volume 5: VISAPP, pages
310-317
ISBN: 978-989-758-402-2; ISSN: 2184-4321
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Figure 1: Strategy for clothing category classification: parts colored by red are the contribution of this paper.
works take this approach: most works prepare the
model at the first and just directly use it to match with
observations.
The contribution of the present paper is to build
discriminating common models in response to each
observation. Owing to this improvement, the pro-
posed method well classifies clothing category with-
out requiring either the preregistration of individual
clothing information or a learning stage using huge
training data.
This paper is organized as follows. After survey-
ing related works in Section 2, in Section 3, we briefly
explain a base two-stage method. Section 4 describes
how to configure potential images that are adjusted
to each observed case. Section 5 presents the results
of experiments conducted using both a manual setting
and a humanoid system, and then finally, the paper is
concluded with discussions of the current status and
future direction of research in Section 6.
2 RELATED WORK
Miller et al. (S. Miller and Abbeel, 2011) used pa-
rameterized models as general models for the analysis
of clothing items flattened on a desk. However, flat-
tening an item itself is not an easy task, as shown in
other studies (e.g., (B. Willimon and Walker, 2011)),
and requires extra procedures.
Classifying the category of clothing items held
in the air has also been studied from the early
days(Hamajima and Kakikura, 2000)(F. Osawa and
Kamiya, 2007). Recently, many researchers ap-
plied a learning approach for handling clothing
items, some of which are dealing with hang-
ing clothes(A. Doumanoglou, 2014)(I. Mariolis
and Malassiotis, 2015)(Stria and Hlavac, 2018).
Doumanoglou et al. (A. Doumanoglou, 2014) used
3D features extracted from depth images of cloth-
ing items to classify the clothing category and to
detect the position to hold according to the random
forests algorithm. Although they obtained good re-
sults even for items different from those used in the
learning stage, their methods require approximately
30,000 observation data for training to achieve the re-
sults. It is uncertain if the learned classifier still works
when the situation (i.e., the robots and 3D sensors)
changes. Mariolis et al. (I. Mariolis and Malassio-
tis, 2015) applied a deep learning approach to auto-
matically extract efficient features from 3D clothing
shapes, aiming at classifying the pose and category
of clothing. They reduced the burden of the learning
stage using a synthetic database obtained by physics
based simulation. In the learning stage, however, the
method requires the model of the individual clothing
item to be recognized and does not target the general
categorization of arbitrary items. Stria et al. (Stria
and Hlavac, 2018) proposed to use 3D point clouds
of the whole circumference of a garment held by a
robot hand as input for category classification. They
extracted auto-encoder features from the point clouds
using a convolutional neural network (CNN) and use
the features for SVM classification of garment cate-
gories. When using the 3D shape of a garment after
grasping its lowest part, high success ratio was re-
ported. However, the shape held by only one hand
originally shows small difference between different
categories especially in the case of garments made of
soft materials. In addition, the output of their method
is just a type of category and does not indicate any in-
formation of the clothing state. Before taking specific
Clothing Category Classification using Common Models Adaptively Adjusted to Observation
311

Figure 2: Two-stage method for overcoming two types of
shape variations of clothing.
handling actions such as folding and spreading, an ad-
ditional method to recognize the state is required.
For the purpose of classification of category at the
same time of recognizing the clothing state, we take
the two-stage approach shown in Fig. 2, where a
clothing item of interest is first brought into one of a
small number of limited shapes and the type of limited
shape is then recognized. Osawa et al. (F. Osawa and
Kamiya, 2007) proposed a method that re-grasps the
lowest point of clothing items twice to limit the phys-
ical deformation. The difference between their way
and ours is that we bring clothing items into more dis-
criminative shapes by finding a proper grasping posi-
tion.
3 BASE METHOD
3.1 Bringing an Item into a Limited
Shape
Fig. 2 shows the flow of our two-stage method. To
bring any item into a shape that is as discriminating
as possible without prior knowledge of the item, we
select the following sequence of actions: 1. Pick up
an item at an arbitrary point; 2. Grasp the lowest
point and release the first hand; 3. Grasp the con-
vex point closest to the currently grasped point and
spread the item. After the application of this basic se-
quence of actions, an item of any category is brought
into one of a few types of shapes. We refer to such
possible shapes as the set of limited shapes. In the
case of the five categories that we deal with in this pa-
per, all categories are brought into two types of lim-
ited shapes. Figure 3(a)–(d) shows the two limited
shapes of four of the five categories, namely long-
sleeve shirts, trousers, skirts and half-sleeve shirts,
where pink and green points illustrate the two grasp-
ing points after the sequence is executed. We refer to
Figure 3: Limited shapes of various categories.
a limited shape as, for example, “Shape A of a long-
sleeve shirt”, abbreviated as LS-A as shown in Fig. 3.
For A types, left-right symmetrical shapes also exist.
These actions are automatically done by a dual-
arm robot by the method proposed in (Hu and Kita,
2015). To detect the convex point of items such as
shoulder of shirts stably, a sequence of 3D depth im-
ages from different view directions are used to track
possible convex points during the sequential observa-
tion.
3.2 Potential Image for Representing
Intra-category Shape Variation
After bringing the clothing item of interest into one of
the set of limited shapes, the proposed method classi-
fies the type of limited shape, such as LS-A in Fig. 3,
according to the shape of the observed clothing area.
To absorb variations of the contour shape of a type
of limited shape depending on the size, design and
softness of clothing items in the category, we use a
potential image to represent each limited shape.
First, several typically designed clothing models
are built for each category. For this, we take the
shapes from different clothing items on the Inter-
net. The clothing model is represented by a simpli-
fied planar surface that deforms three-dimensionally.
As examples, pictures of long-sleeve shirts from the
Internet and the models built manually from their
shapes are shown in Fig.4(a). Limited shapes of each
category are then physically simulated using these
models by manually giving two holding positions.
For this simulation, we use the “n-cloth” function in
Maya(GOULD, 2004). To consider different fabrics
of clothing, we also change parameters of the softness
in the models, such as stretch resistance of dynamic
properties. Fig.4(b) show examples of 3D shapes for
Shape A of long-sleeve shirts obtained after the simu-
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
312

Figure 4: Building a database of 3D shapes (long-sleeve
shirts (LS-A)): (a) pictures of long-sleeve shirts from the
Internet and the models built from their shapes; (b) limited
shapes physically simulated using the models and different
elastic property.
Figure 5: Calculation of potential images: (a) collection of
different contours in an image; (b) smoothing of the possi-
ble shape.
lations. The two-dimensional (2D) contours extracted
from the projection of the simulated 3D shapes are
normalized based on the distance between two grasp-
ing points and integrated on a image as shown Fig.
5(a). Then the area enclosed by the contours are filled
with the value of 1.0 (the middle figure of Fig.5(b))
for the purpose of compensating the small number of
samples for infinite shape variation. Then the poten-
tial image is obtaining by smoothing the image using
a Gaussian filter (the right figure of Fig.5(b)). We re-
fer to the calculated image as the “potential image of
limited shape”. P(i, j), where (i, j) is the 2D coordi-
nates of the image.
In the observation stage, the contour of the cloth-
ing area in an observed depth image is extracted and
Figure 6: Ambiguity of potential images considering all
possible variations: (a) Shape B of trousers (TR-B); (b)
Shape B of skirts (SK-B).
normalized in the same way as the model building
process. The consistency between the extracted con-
tour and the potential image of each limited shape is
then measured using R:
R =
∑
N
n=1
P(i
n
, j
n
)
N
, (1)
where N is the number of pixels of the observed
contour and (i
n
, j
n
) denotesthe coordinatesof contour
point n(n = 1,...,N).
4 ADAPTIVE ADJUSTMENT OF A
POTENTIAL IMAGE
The potential image described above can represent
large intra-category variations in each limited shape,
but on the other hand, its generality weakens the abil-
ity to discriminate from other categories. Figure 6
shows an example, an ambiguity of potential images
between Shape B of trousers (TR-B) and Shape B of
skirt (SK-B). Because the potential image of TR-B
covers a large area owing to the high variance of the
ratio of the width and the length of trousers for chil-
dren and adults, contours of limited shapes other than
TR-B also have a high value of R (shown under each
figure) in the matching with it, and the recognition
thus becomes unreliable.
Here, we propose to feedback observed informa-
tion to the model-building process for obtaining more
discriminating models. Some information obtained
from observation using simple image processing can
lead the constraint of shape variation. Model contours
that is inconsistent to the constraint can be removed
Clothing Category Classification using Common Models Adaptively Adjusted to Observation
313

Figure 7: Potential image adjusted to observation: (a) stable
simple features specifying the clothing region; (b) improve-
ment gained using adjusted potential images.
from candidates. Concretely, we measure the three
lengths as shown in Fig. 7(a): B (base) is the horizon-
tal distance between two holding positions; L (length)
is the vertical distance between a holding position and
the lowest point of the observed item;W (width) is the
horizontal distance between the leftmost and right-
most points of the observed item. The simple ratios
between them are calculated:
k
1
= L/B, k
2
= W/B.
For each 2D model contour, m, obtained in
the process described in Section 3.2, (k
1m
,k
2m
) is
calculated and recorded in advance. When catego-
rizing an observation, (k
1
,k
2
) of the observed item
is calculated and only the model contours that are
consistent with these ratios are integrated into one
potential image. Considering the length variation
caused by the difference in how strongly stretched the
clothing item, some allowable differences, L
d
,W
d
,
from observed values of L,W are introduced. A
2D model contour m is selected only if its ratio,
(k
1m
,k
2m
), satisfies
(L− L
d
)/B < k
1m
< (L+ L
d
)/B
(W −W
d
)/B < k
2m
< (W +W
d
)/B.
(2)
Figure 7(b) and (c) shows examples of potential
images built using L,W calculated from the observa-
tion of Fig. 6(a) and (b), respectively. Through this
adjustment, potential images become more specific,
resulting discriminating against different categories,
while still absorbing intra-category shape variations.
We see the values of R of incorrect potential images
become low, while ones of correct potential images
keep high.
In all experiments of this paper, we assume the
length variation affected by the strength of pulling as
+- 3.5cm and set both L
d
and W
d
at 7 cm.
Figure 8: Observation setting for Experiments using man-
ual setting: (a) observed image; (b) 3D data of the clothing
item.
5 EXPERIMENTS
We conducted two types of experiments to separately
examine the performance of the classification method
using adjusted potential images and the practical po-
tency of the two-stage strategy using the classification
method. In both experiments, we deal with clothing
items of five categories: long-sleeve shirts, trousers,
skirts, half-sleeve shirts and towels. Because clothing
of each category is brought into two limited shapes
after the basic sequence of actions described in Sec-
tion 3.1, the task of the experiments is classification
of clothing items into one of 10 limited shapes.
In advance of the experiments, a database of 2D
contours of various limited shapes was built as ex-
plained in Section 3.2. Specifically, we chose nine
items of different design and size for each category
from pictures on the Internet and gave two types of
softness to each shape, resulting in 18 different con-
tours for each limited shape besides the towel. Be-
cause the towel has less variation in design, only 12
contours were used. Therefore, the database consists
of (18 (contours) × 4 (categories) + 12 (contours for
the towel)) × 2 (limited shapes) = 168 contours. As
we noted in Section 4, the potential images are adap-
tively calculated after observation.
5.1 Experiments using Manual Setting
We conducted experiments with different clothing
items by manually setting the items into limited
shapes. Specifically, a clothing item was hung by
being pinched at two points as shown in Fig. 8(a).
The 3D data of clothing items were obtained using a
trinocular vision system (Ueshiba, 2006) as shown in
Fig. 8(b) and (c) for the texture-mapped 3D data and
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
314
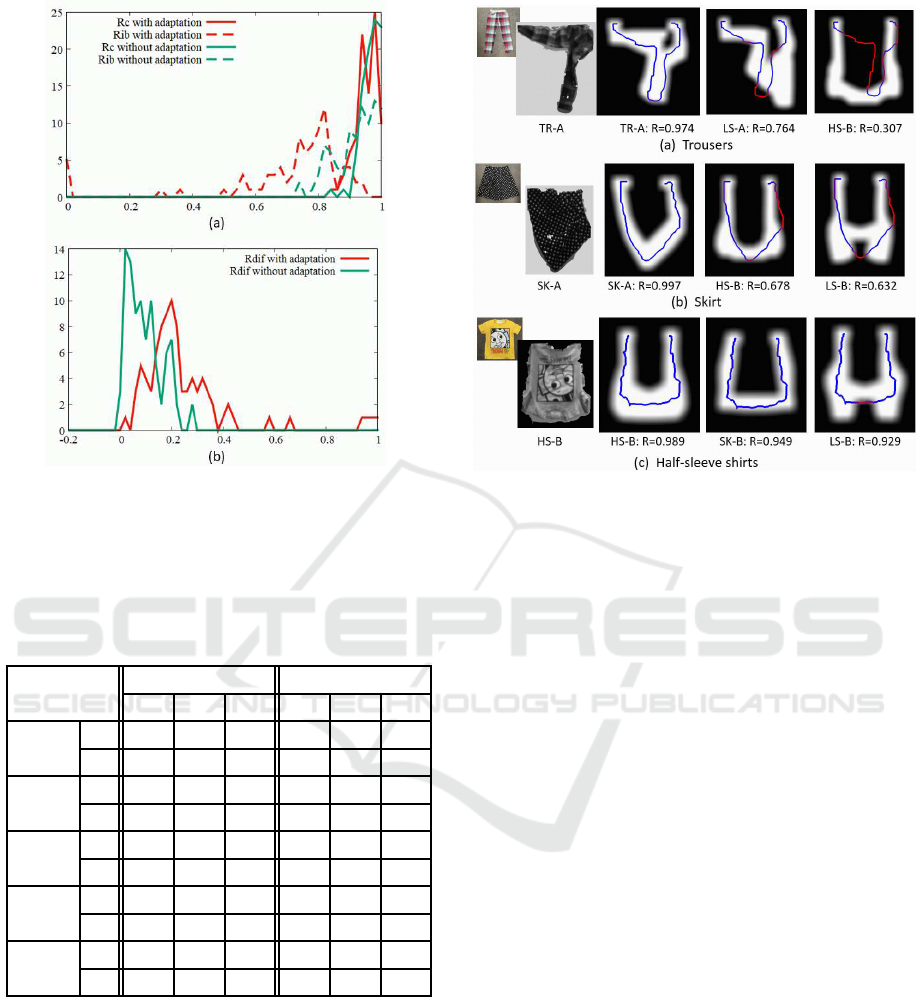
Figure 9: Variance of R
c
and R
ib
:(a) comparison of the dis-
tribution of R with (red) and without (green) model adjust-
ment; (b) distribution of the difference between R
c
and R
ib
with/without model adjustment.
Table 1: Classification results for a manual setting: the
number of success, failure and confusing (conf.) cases
when using potential images non-adjusted P(i, j) and ad-
justed P(i, j) respectively.
Limited non-adjusted adjusted
shape Success Failure Conf. Success Failure Conf.
L-sleeve A 10 0 0 10 0 0
shirts B 10 0 10 10 0 1
Trousers A 10 0 7 10 0 0
B 10 0 3 10 0 0
Skirts A 10 0 1 10 0 0
B 10 0 1 10 0 0
H-sleeve A 10 0 1 10 0 0
shirts B 3 7 3 10 0 2
Towel A 4 1 4 5 0 1
B 5 0 1 5 0 0
the 3D observed points (gray dots).
In this experiment, we used 10 long-sleeve shirts,
10 pairs of trousers, 10 skirts, 10 half-sleeve shirts
and five towels. We formed two limited shapes for
each piece of clothing, and a total of 90 observations
were thus made. The experimental results are sum-
marized in Table 1. To evaluate the effect of model
adjustment, experiments without the adjustment pro-
cess (i.e., using all contours of the database to make
potential images) were also conducted; these results
are listed in the column “non-adjusted”.
Figure 10: Results of Experiment using manual setting: the
potential image of the limited shapes with the three highest
R of (a) Shape A of trousers, (b) Shape A of skirt and (c)
Shape B of half-sleeve shirt.
The diagram of Fig. 9(a) shows the distributions
of R of the correct type, R
c
and the largest R among
the incorrect types, R
ib
. The former and latter are
plotted with solid and dashed lines respectively, while
the color red/green indicates the result with/without
model adjustment. In contrast to the result that the
distribution of R
c
does not change greatly with model
adjustment, the distribution of R
ib
largely shifted to
lower values. Figure 9(b) shows the distribution of
the difference between R
c
and R
ib
with/without the
model adjustment (red/green). The difference clearly
became large with the adjustment; the average of the
distribution increases from 0.165 to 0.238. The im-
provement in discriminant efficiency is also clearly
shown in Table 1. In all experiments, the correct
types of the limited shape were successfully selected
as shown in the column “adjusted”.
Three examples of classification results are shown
in Fig.10. The first and second columns of Fig.10
show the clothing item and the 3D observation data
of its limited shape. The last three columns show
the potential image of the limited shapes with the
three highest R in descending order. The blue and
red colored lines superposed on the potential images
show the contour extracted from the observation data.
The RGB color of each contour point (i, j), (R, G, B),
is determined as ((1 − P(i, j)),0.0,P(i, j)); contour
points with higher P(i, j) are colored more blue, while
those with lower P(i, j) are colored more red. The
Clothing Category Classification using Common Models Adaptively Adjusted to Observation
315

consistency R calculated for each potential image is
shown under the image. As shown in the examples of
Shape A of trousers (TR-A, Fig.10 (a)) and Shape A
of skirt (SK-A, Fig.10 (b)), R of the correct type was
clearly the largest in most cases. The column “con-
fusing (conf.)” in Table 1 shows the number of cases
where the difference between the largest and second
largest R is less than 0.05. There were four confusing
cases of the proposed method. Two were ambiguity
between Shape B of half-sleeve shirts (HS-B) with
very short sleeves and Shape B of skirts (SK-B) as
shown in Fig.10(c).
Owing to inaccurate 3D observation data around
the boundary of clothing regions, extracted contours
are not so smooth even after several dilation/erosion
image processes. Insensitivity to such disturbance is
one advantage of using potential images. The compu-
tational time for adaptively configuring potential im-
ages is 0.2 s (using an Intel Xeon 3.47-GHz proces-
sor) on average, which is sufficiently short for real-
time processing.
5.2 Experiments using a Humanoid
System
We examined the practical potency of the total strat-
egy, using the humanoid robot HRP-2 (Kaneko et al.,
2004) and the same trinocular vision system as used
in the first experiment set in front of the robot at a
distance of 3 m. In this experiment, we used six long-
sleeve shirts, five pairs of trousers, six skirts, seven
half-sleeve shirts and eight towels. By using some of
the items multiple times, 52 trials were done in total.
Figure 11 shows some examples of the case where
items were successfully reshaped into one of the lim-
ited shapes and then correctly classified. All experi-
mental results are summarized in Table 2. From the
third to the fifth columns, the denominator and nu-
merator are the number of experiments and success-
ful cases respectively, whereas the third, fourth and
fifth columns give the results of detection of the close
convex point, spreading the item using the detected
points, and classification using the spread shapes.
Table 2: Experimental results using a humanoid.
Category Num.
of expt.
Selection SpreadingClassifi-
cation
LS shirts 10 7/10 7/7 7/7
Trousers 11 9/11 9/9 9/9
Skirts 11 6/11 6/6 5/6
HS-shirts 10 6/10 5/6 4/5
Towels 10 6/10 4/6 4/4
Figure 11: Examples of successful spreading in Experi-
ment using a humanoid system: (a) Shape B of trousers;
(b) Shape A of skirts; (c) Shape B of long-sleeve shirts.
Figure 12: Examples of failures in Experiment using a hu-
manoid system: (a) spreading failure of a skirt; (b) classifi-
cation failure due to unexpected shape deformation.
The overall success rate of reshaping an item into
one of the limited shapes was not high, 60% (31/52).
Most of failures happened in the case of skirts, half-
sleeve shirts and towels, because we just applied the
reshaping method developed for the other two cate-
gories, long-sleeve shirts and trousers. Figure 12(a)
shows an example of the failure in detecting close
convex point of skirts. Although the current method
detects only convex points at a planar part, waist parts
of skirts were often spread into a round shape, causing
detection failures.
Once clothing items were successfully spread into
one of the limited shapes, the items were successfully
classified into the correct type of limited shape except
in the two in 31 cases. Fig 12(b) shows one failure
case: a half-sleeve shirt was spread into a perfectly
flattened shape by chance, which is not expected as
typical shapes. In this case, even the largest R became
very low and indicative of such special situation.
6 CONCLUSION
We proposed a method of clothing category classifi-
cation that builds discriminating common models us-
ing the feedback from current observation. Under the
framework where a dual-arm robot first reshapes a
clothing item into one of a small number of limited
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
316

shapes, two series of experiments using many dif-
ferent clothing items of five clothing categories were
conducted. Although the method of bringing cloth-
ing items into one of the limited shapes is still in a
stage of development, the classification is highly cor-
rect once the items are successfully reshaped into a
limited shape. Though we need more thorough exper-
iments for assertion, the current results showed that
the feedback of observed information to model build-
ing process enables common category models that is
highly discriminating among different categories and
at the same time is tolerant of intra-category shape
variation.
Because, in the proposed framework, the state of
the clothing item is also known at the same time as
the classification, such as Shape A of trousers in Fig.
10(a), the method can be directly connected to sub-
sequent actions for specific tasks such as folding or
spreading into a fixed shape. The results also have
high affinity with the model-drivenmethod of (Y. Kita
and Kita, 2014) to perform further tasks.
ACKNOWLEDGEMENTS
The authors thank Dr. Y. Kawai, Mr. T. Ueshiba
for their support of this research. This work was
supported by a Grant-in-Aid for Scientific Research,
KAKENHI (16H02885).
REFERENCES
A. Doumanoglou, A. Kargakos, T.-K. K. S. M. (2014). Au-
tonomous active recognition and unfolding of clothes
using random decision forests and probabilistic plan-
ning. In International Conference in Robotics and Au-
tomation (ICRA) 2014, pages pp.987–993.
B. Willimon, S. and Walker, I. (2013). Classification of
clothing using midlevel layers. ISRN Robot, pages pp.
1–17.
B. Willimon, S. B. and Walker, I. (2011). Model for un-
folding laundry using interactive perception. Int’l
Conf. on Intelligent Robots and Systems (IROS11), pp.
4871–4876.
F. Osawa, H. S. and Kamiya, Y. (2007). Unfolding of mas-
sive laundry and classification types by dual manip-
ulator. Journal of Advanced Computational Intelli-
gence and Intelligent Informatics, Vol. 11, No.5:457–
463.
GOULD, D. A. D. (2004). Complete Maya Programming.
Morgan Kaufmann Pub.
Hamajima, K. and Kakikura, M. (2000). Planning strat-
egy for task of unfolding clothes (classification of
clothes). Journal of Robotics and Mechatronics, Vol.
12, No.5:pp. 577–584.
Hu, J. and Kita, Y. (2015). Classification of the category
of clothing item after bringing it into limited shapes.
In Proc. of International Conference on Humanoid
Robots 2015, pages pp.588–594.
I. Mariolis, G. Peleka, A. K. and Malassiotis, S. (2015).
Pose and category recognition of highly deformable
objects using deep learning. In International Confer-
ence in Robotics and Automation (ICRA) 2015, pages
pp.655–662.
J. Maitin-Shepard, M. Cusumano-Towner, J. L. and Abbeel,
P. (2010). Cloth grasp point detection based on
multiple-view geometric cues with application to
robotic towel folding. In Proc. of IEEE Int’l Conf.
on Robotics and Automation (ICRA ’10).
Kaneko, K., Kanehiro, F., Kajita, S., Hirata, M., Akachi, K.,
and Isozumi, T. (2004). Humanoid Robot HRP-2. In
Proc. of IEEE Int’l Conf. on Robotics and Automation
(ICRA ’04), pages pp.1083–1090.
P. Yang, K. Sasaki, K. S. K. K. S. S. and Ogata, T. (2017).
Repeatable folding task by humanoid robot worker us-
ing deep learning. IEEE Robotics and Automation Let-
ters, Vol. 2:pp.397–403.
S. Miller, M. Fritz, T. D. and Abbeel, P. (2011). Parameter-
ized shape models for clothing. In Proc. of IEEE Int’l
Conf. on Robotics and Automation (ICRA ’11), pages
pp. 4861–4868.
Stria, J. and Hlavac, V. (2018). Classification of hang-
ing garments using learned features extracted from
3d point clouds. In Proc. of Int. Conf. on Intelligent
Robots and Systems (IROS 2018), pages pp.5307–
5312.
Ueshiba, T. (2006). An efficient implementation tech-
nique of bidirectional matching for real-time trinocu-
lar stereo vision. In Proc. of 18th Int. Conf. on Pattern
Recognition, pages pp.1076–1079.
Y. Kita, F. Kanehiro, T. U. and Kita, N. (2014). Strategy for
folding clothing on the basis of deformable models. In
Proc. of International Conference on Image Analysis
and Recognition 2014, pages pp.442–452.
Clothing Category Classification using Common Models Adaptively Adjusted to Observation
317
