Generation of Tree Surface Mesh Models from Point Clouds using Skin

Surfaces

Chi Wan Lim

, Like Gobeawan

, Sum Thai Wong

, Daniel J. Wise

, Peng Cheng

Hee Joo Poh

and Yi Su

Institute of High Performance Computing, A*STAR, Singapore

Keywords:

Tree Modelling, Point-based Processing, Skin Surfaces.

Abstract:

This work focuses on the extraction and reconstruction of the tree branching models from large scale 3D

LiDAR point clouds, utilizing the concept of skin models for modelling tree joints. Tree joints are one of

the most challenging components to model due to its potential for highly intricate morphology and complex

branching topology. During the reconstruction process, point clouds ﬁrst undergo a classiﬁcation process to

remove leaves and then skeletonization to derive the branching morphology and estimate individual branch

thicknesses. The tree branching model can then be modelled as a collection of cylindrical volumes connected

by fused tree joints. The novelty of this work lies in the usage of skin surfaces as a proxy for modelling the

tree joints. The generated tree triangular mesh surface is smooth and continuous, and we further propose a

method to convert it into quadrilateral patches. The beneﬁts of having piecewise components of branches and

joints are such that it facilitates the subsequent generation of 3D ﬁnite elements, as they can be handled and

meshed independently.

1 INTRODUCTION

With the advent of laser scanning technologies and

larger storage capabilities, there is a growing inter-

est in digitization of entire cities, including its dis-

tinctive ﬂora landscape. This not only serves the pri-

mary purpose of visualization but also affords multi-

ple possibilities for urban climatology-related simula-

tions. The range of computation and simulation that

municipal arborists are interested in includes measur-

ing the leaf area index, studying the morphology of

various tree species (Gobeawan et al., 2019), deter-

mining the effect of pruning on structural integrity,

and the effect of torrential winds on trees planted near

coastal regions.

The motivation for this work arises from the need

for a simulation-ready 3D ﬁnite element mesh, of-

ten required for computer simulations such as wind-

https://orcid.org/0000-0002-8319-9742

https://orcid.org/0000-0001-6501-6394

https://orcid.org/0000-0003-1131-3646

https://orcid.org/0000-0002-0347-6827

https://orcid.org/0000-0002-9594-0120

https://orcid.org/0000-0003-3029-7012

https://orcid.org/0000-0001-5416-7138

loading (Poh et al., 2019). A tree can be modelled

as a collection of connected cylinders, similar to a

skeletal model with thickness. However, at the point

of joint connection, different trees can exhibit very

diverse morphology, with some species having com-

pressed inter-node distance resulting in multiple child

branches sprouting from a single point. From a mesh-

ing viewpoint, this can be challenging to model while

maintaining a smooth manifold surface, which is crit-

ical for 3D meshing. In this work, our contribution is

a computational geometry approach that models each

branch joint as a skin surface model (Edelsbrunner,

1999), separately from the other connecting branches.

Each branch joint is then handled and meshed inde-

pendently, with a localized half-sphere region cutout

for a seamless connection with its connected branches

in order to create a full tree mesh surface.

1.1 Objective

To address the growing need for fast processing of

large laser scanned data comprising of hundreds of

trees in a single LiDAR scan and generate simulation-

ready individual tree models, our work focuses on two

main components:

• An automated classiﬁcation and segmentation of

Lim, C., Gobeawan, L., Wong, S., Wise, D., Cheng, P., Poh, H. and Su, Y.

Generation of Tree Surface Mesh Models from Point Clouds using Skin Surfaces.

DOI: 10.5220/0008937100830092

In Proceedings of the 15th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2020) - Volume 1: GRAPP, pages

83-92

ISBN: 978-989-758-402-2; ISSN: 2184-4321

woody structures from LiDAR point clouds of

trees.

• Usage of skin models as a proxy for modelling

tree joints in order to produce a smooth continu-

ous mesh surface of an entire tree.

2 RELATED WORK

Modelling of tree branching structures that are based

on point clouds acquired from laser scanners is typ-

ically dependent on a few stages. The ﬁrst stage

separates the point clouds into leaf and branch re-

gions. During the laser acquisition process, the in-

tensity value of the surface which the laser comes

into contact with can indicate whether it is a leaf or

branch surface (Li et al., 2017). Other approaches for

classiﬁcation includes using ﬁlters such as Gaussian

mixture model (Belton et al., 2013) based on parame-

ters extracted by using principal component analysis,

clustering based on small surface patches (Raumo-

nen et al., 2013) formed using local neighbourhood,

supervised classiﬁcation based on photographs (Xie

et al., 2018), or voxelization-based branch structure

detection (Hu et al., 2017).

After the removal of the leaves, the remaining

point cloud goes through a skeletonization process to

construct a connectivity graph. This facilitates not

only the ﬁnal model generation but provides a sec-

ondary structural map of the branching morphologi-

cal structure. A popular approach is to make use of

Dijkstra’s shortest path algorithm to create a branch-

structure graph (BSG), which is a spatially embed-

ded and connected acyclic graph (Xu et al., 2007;

Livny et al., 2010). This approach is particularly ro-

bust even on sparse point clouds. Other graph con-

struction approaches include using laplacian-based

contraction (Cao et al., 2010; Su et al., 2011) and

voxel/octree thinning (Hu et al., 2017; Bucksch and

Lindenbergh, 2008). For point cloud with normals,

the work on curve skeleton extraction (Tagliasacchi

et al., 2009) using the concept of rotational symmetry

axis is specially catered for cylindrical-like objects.

A more generalized skeleton extraction (Huang et al.,

2013) using L

-medial is subsequently proposedwith-

out prior assumption regarding topology or shape ge-

ometry, but parameter adjustments might be required

for point clouds under different scanning conditions.

Once a skeletal graph is obtained, the point cloud

can be segmented into smaller groups and replaced

with a cylindrical shape form. Chains of cylinders are

often used as an approximation for tree branches by

ﬁtting cylinders onto the point clouds itself (Pfeifer

et al., 2004; Hackenberg et al., 2014). Few works,

however, go into detail of how to merge the resulting

set of cylinders into a single polygonal mesh model

with smooth surfaces, especially at the tree joint re-

gions. Bloomenthal (Bloomenthal, 1985) was one of

the ﬁrst to model tree joint surfaces using a ramiform

shape, but with only two outgoing branching outlets.

The work of (Yan et al., 2009) uses a B-splines loft-

ing method to approximate the cylinders and can be

converted into a piecewise linear mesh representation

that is suitable for simulation. Another work by Zhu

et al. (Zhu et al., 2015) uses a local convolution sur-

face approximation method based on B-Meshes (Ji

et al., 2010) to create a combined high-quality quad-

only mesh.

Our work differs by modeling tree joints individ-

ually using skin surfaces as an intermediary model,

before joining them to the cylindrical branch models.

This provides two signiﬁcant beneﬁts. The ﬁrst is that

each joint can be modeled to fully accommodate any

number of branches that are joined to it while main-

taining a smooth surface overall. Secondly, breaking

down a tree model into branches (sequence of cylin-

ders) and joints (skin models) facilitates the genera-

tion of 3D ﬁnite elements, as compared to a combined

tree model which might have multiple thin branches

that are complicated to mesh as a single tree. In terms

of classiﬁcation between leafy and woody regions of

the points cloud, an automatic approach is proposed

based on each point’s intensity value and the sparsity

of their local neighbourhood. Lastly, our work pro-

poses an approach to convert the existing triangular

tree joint mesh into quadrilateral patches that further

improves its viability for downstream simulation ap-

plications.

3 PRE-PROCESSING OF POINT

CLOUDS

LiDAR scans, both in ALS (airborne) and MLS

(mobile) format, were acquired as referenced in the

work by Soon & Khoo (Soon and Khoo, 2017).

The point clouds used in this work are mostly MLS

data, collected using a Riegl VMX-450 at around

40 points/m

, typically around 70m range at a speed

of 60 km/hr. The point clouds are contained in the

LAS format, which is a public ﬁle format for the

interchange of 3-dimensional point cloud data be-

tween data users. Typically for LiDAR MLS data,

point clouds covering entire streets with multiple trees

are captured in a single LAS ﬁle. The individual

tree isolation procedure is performed by generating

best-ﬁtting ellipses around each identiﬁed tree trunks

enveloping their respective canopy, see (Gobeawan

GRAPP 2020 - 15th International Conference on Computer Graphics Theory and Applications

et al., 2018) for a more detailed description of the

procedure. Once the point cloud of a single tree is

isolated, the goal is to decimate it further such that it

only contains points that are lying on the woody sur-

face. A skeletal graph model of the tree branching can

then be generated. This whole process is fully auto-

mated.

3.1 Trunk Data Sampling

In order to remove the leafy regions from each iso-

lated tree point cloud, the 3-dimensional position and

intensity parameter of each data point are used. There

is a characteristic differencebetween points generated

by the laser scanner as it strikes a woody surface or

a leafy surface. First, points lying on woody surfaces

havea slightly higher intensities. Second, the sparsity,

as measured by the distance to the nearest neighbour,

is also different, with points on woody structures hav-

ing a denser group of nearest neighbours. Although

both factors can be used as a means to classify woody

structures, the separation limit differs from tree to

tree. Hence, to automate the classiﬁcation process for

large datasets, there is a need to acquire some initial

sampling results.

Figure 1: Histogram of Intensity and Neighbourhood Spar-

sity. The normalised spread of both parameters taken from

a portion of the trunk region as compared to the full tree

point cloud.

Based on the tree isolation procedure in (Gob-

eawan et al., 2018), the location of the trunk base

can be found. This information can be used to sep-

arate the tree from the ground surface reliably. Once

the base/root of the tree is identiﬁed, points that are

within a distance above it (based on 20% of the

tree height) can be used to sample for their inten-

sity ranges and neighbourhood sparsity. Since this re-

gion can be generally assumed to be the trunk region,

the sampling result is indicative for the rest of the

woody structures throughout the point cloud. Fig. 1

shows the distribution of the two parameters between

points taken from the trunk region and the full point

cloud data of the tree. It can be clearly seen that

points from the trunk region have a higher intensi-

ties and denser neighbourhood distance. The double

peak phenomenon is attributed to the fact that multi-

ple scans taken at different instances, which can be af-

fected by other factors such as weather conditions, are

merged together to form the full point cloud. Taking

the combined distribution of all points, the separation

limit for intensity is set at mean value plus two times

the standard deviation, while the neighbourhoodspar-

sity is set at mean value minus two times the standard

deviation. Additionally, the sampling can be further

improved by gradually increasing the contribution the

closer the points are to the trunk base, lessening the

arbitrary selection based on 20% of tree height.

3.2 Classiﬁcation of Woody Structures

The classiﬁcation procedure operates in a few stages.

The ﬁrst stage extracts all the points that are within

the limits of both the pre-sampled intensity range

and neighbourhood sparsity. Selected points that are

within a k-nearest neighbourhood of each other are

clustered together, where k is typically a small num-

ber between 6 to 12. Small clusters under the size of 3

are discarded to removethe outliers. The second stage

expands each cluster by creeping outwards, achieved

through incorporating points into the clusters that are

within the neighbourhood distance limit, regardless of

the intensity. At this juncture, the points in all the

clusters are deemed to be lying on woody structure,

see Fig. 2(b). The next stage attempts to trace the

path from each point down to the root of the tree us-

ing the connected acyclic graph formed using Dijik-

stra’s shortest path algorithm. All the points traversed

by each path are absorbed into the clusters, forming

the full set of points classiﬁed as woody structure, see

Fig. 2(c).

3.3 Forming Branch Connectivity

The distance to the root of the tree for each woody

point can be calculated and used as a means to re-

cluster the points. A binning distance of around 1-2%,

depending on the required resolution, of the height of

the tree is employed. Each cluster of points have the

same binning distance and are grouped together based

on neighbourhood connectivity. In Fig. 2(c), the clus-

ters are colour-coded in an alternate fashion to illus-

trate the clustering approach using distance binning.

As each point has a connected path downwards to

the base of the tree, it can be used to establish cluster-

to-cluster connectivity. Let C = {C

···C

} be the set

of clusters. Each cluster has one single downward

Generation of Tree Surface Mesh Models from Point Clouds using Skin Surfaces

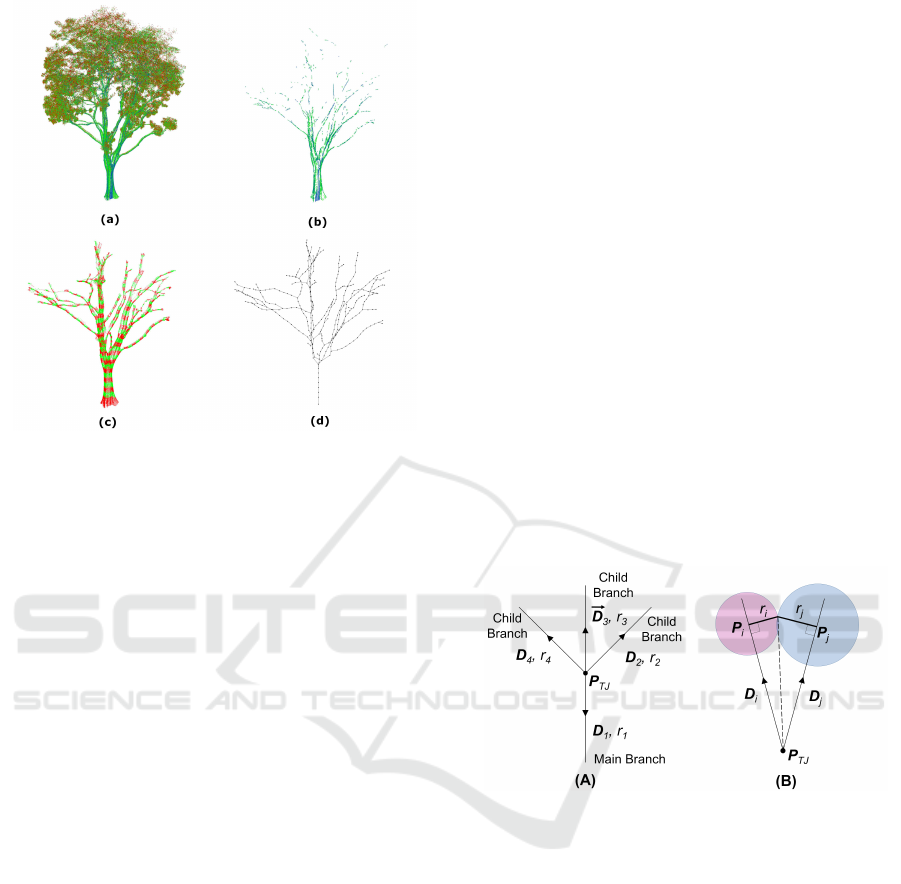
Figure 2: Stages of Branch Reconstruction. The different

stages of branch reconstruction is shown: (a) Original Point

Cloud, (b) Classiﬁcation by Trunk-sampled Parameters, (c)

Shortest Path Tracing and (d) Cluster Connectivity Graph.

connectivity, represented by the function →, with the

exception of the cluster containing the root of the tree.

To establish the downward connectivity for C

, a path

traversal to the root for each point within the cluster

is performed. Once the path reaches a point of a dif-

ferent cluster, C

, a downward connection is formed,

i.e., C

→ C

. However, it is possible that points in the

same cluster have different paths to the root, thereby

forming connections with multiple clusters. In this

situation, the cluster which has the highest number

of connections forms the ﬁnal downward connectivity

with it. Upward connectivity for the clusters can then

be inversely inferred. Clusters with multiple upward

connectivities are termed as joint nodes, while those

with single upward connectivity are termed as branch

nodes. An illustration depicting the connectivities of

clusters is shown in Fig. 2(d).

The centroid of each node can be computed as the

average location of all the points located within it. An

additional thickness parameter is attached to all the

branch nodes. The thickness parameter is estimated

by ﬁrst projecting all the points onto a plane deﬁned

by its centroid and a normal direction, estimated us-

ing the vector direction from itself to clusters which it

has a connection with. The average distance of all the

projected points to the centroid is taken to the node

thickness. Both the centroid and the thickness param-

eter are used in the subsequent sections for generating

the surface mesh of the tree branch model. The full

connectivity graph is termed the skeletal tree model.

4 SKIN SURFACES

Skin surfaces were introduced as a new paradigm for

deﬁning smooth surfaces through the simple combi-

natorial of spheres. A skin surface S

is deﬁned by

a set of spheres B in R

and a shrink factor s, where

0 ≤ s ≤ 1. It is the closed group of the inﬁnite set of

spheres derived from B formed through convex com-

bination and shrinking. For further reading on the

mathematical formulation, we refer to (Edelsbrunner,

1999). There have been efﬁcient algorithms, such as

(Cheng and Shi, 2009), which allow mesh surfaces

with guaranteed quality to be generated. In our imple-

mentation, we make use of an available package from

CGAL (CGAL, 2019) (Computational Geometry Al-

gorithm Library) which provides a closed manifold

surface mesh over the skin surface as deﬁned through

an input array consisting of a group of spheres and a

shrink factor. The shrink factor allows for the con-

trol and tuning of the contouring surface shrinkage

between spheres. Other works such as (Li et al.,

2015) uses direct interpolation instead to form sur-

faces, which would require more sphere placements

to achieve the same contouring effect.

Figure 3: Computation of Sphere Position. A partial il-

lustration of the tree joint connectivity is shown in (A). The

ideal geometrical conﬁguration for a pair of spheres B

and

is shown in (B).

4.1 Modelling Tree Joints

In a skeletal tree model, any node that is connected

to three or more distinct nodes is deﬁned as a tree

joint. Each node has an associated thickness and a

centroid location. Using the thickness and position

of its connected nodes, a skin surface is constructed

around the tree joint node. Once the skin surface

for the tree joint is generated, a half-sphere region

corresponding to each connecting branch is identiﬁed

and removed from the skin surface, creating a circu-

lar opening. This circular opening would be used as a

mesh-connecting conduit with the cylindrical surface

mesh used for the mesh model of the branches, i.e.,

nodes with only two or fewer connections.

GRAPP 2020 - 15th International Conference on Computer Graphics Theory and Applications

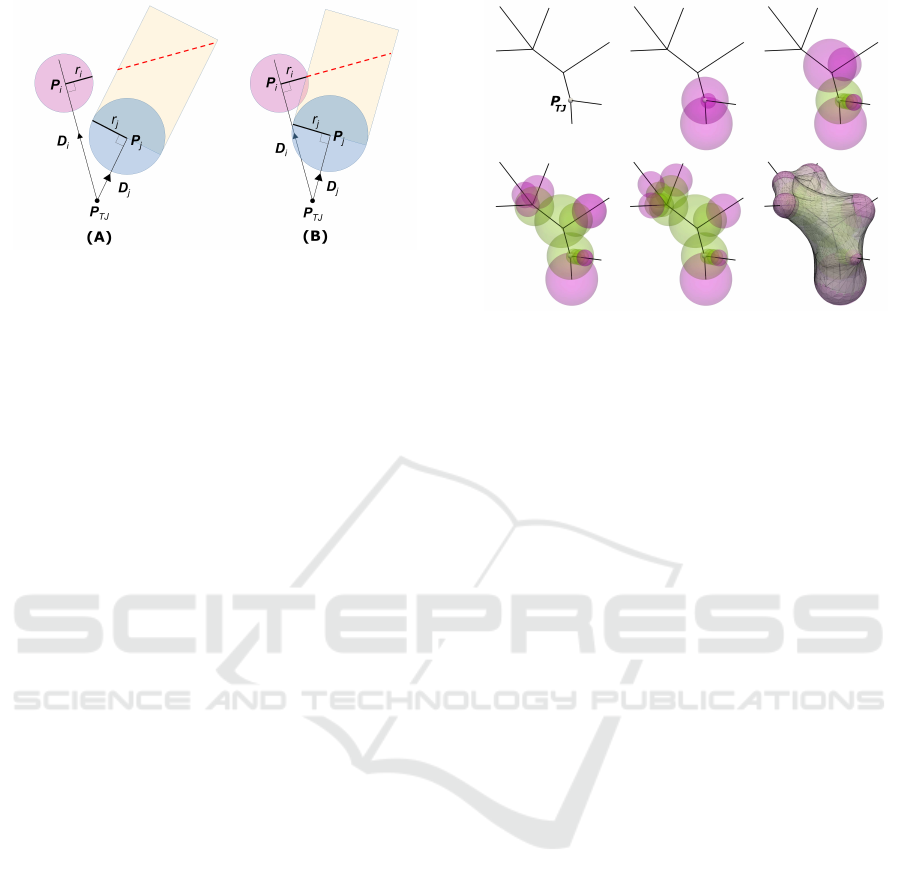
Figure 4: Intersection Test. Two different ball conﬁguration

with different intersection outcomes. There is no intersec-

tion in (A) while there is one in (B).

4.1.1 Ideal Balls Placement

To generate the skin surface, a set of spheres B =

·· ·B

} must be speciﬁed, along with a shrink fac-

tor s. Each B

contains two parameters, its position P

and radius r

. For s, a constant of 0.25 is employed

throughout our implementation for a look similar to

actual trees. Let P

be the centroid of a tree joint

TJ with n number of connecting branches, with their

vector directions termed as

−→

and radii as

to r

(see Fig. 3A). Let

−→

be the main branch

while

−→

are the child branches. The resulting

skin surface mesh should be such that when the set of

cylindrical rays, as deﬁned by

−→

and r

to r

are projected onto it, it will result in distinct and non-

intersecting patches. To achieve this goal, the set of

spheres placement to construct the skin surface should

be such that a half-sphere region for each sphere, cor-

responding to each branch, should be unobstructed by

other spheres.

The test can be conducted to check for intersection

based on the 2D illustration shown in Fig. 4. In (A),

a rectangular projection based on

−→

is intersected

with the perpendicular line deﬁned by the orthogonal

line to

−→

and the point P

. The result of that inter-

section is the red dotted line. If the red dotted line

comes within a distance of r

to P

as shown in (B),

then an intersection is deemed to have occurred. In

the 3D case, the intersection test is between an ellipse

(resulting from an angled planar cut of the cylinder)

and a sphere.

4.1.2 Ball Generation

In Figure 3B, the ideal position of B

and B

can be

solved geometrically. However, the restriction lies in

the length of the branch, which might not be able to

accommodate in cases of tight angle difference. As

can only lie along the vector P

+ k

−→

, where k

Figure 5: Ball Generation Process. The series of images

depict the ball generation process for a single joint. Green

sphere are in the dormant set, while pink spheres are in the

active set. The ﬁnal image on the lower right shows the skin

surface model.

is a scalar, there is a limit to the value of k. This is

constrained by the length of the immediate distance to

the next branch node. Hence, the path which B

can

lie upon follows the upward connectivity from branch

node to branch node. Therefore, an iterative approach

is required to generate the spheres.

The sequence of images, as depicted in Fig. 5,

shows the sequence of ball placements used to form

the skin surface for a tree joint. At the start of the

process, n number of spheres (equal to the number

of connected nodes) are generated and placed in set

active

(pink spheres). Each P

is initialized to the po-

sition P

+ r

−→

. The sphere’s radius parameters fol-

low directly from its corresponding branch’s radius.

This ensures that each half-sphere region is distinct

on the eventual skin surface mesh. We then iteratively

compare each possible pair of spheres in B

active

, using

the cylindrical projection approach shown in Fig. 4.

Once the projection from B

is determined to intersect

with another sphere B

, B

is duplicated and placed in

another set B

dormant

(green spheres). The B

in B

active

is then updated with its new position with k

= k

+ r

4.1.3 Merging of Tree Joints

In the event where k

> |P

− P

|, where BN is the

next upward connected branch node, B

is similarly

duplicated and added to B

dormant

while updated with

its new position with P

. We then merge the tree

joint with the newly intersected tree joint, spawning

m number of new child branches and the associated

new set of spheres B

new

= {B

·· ·B

}. The inter-

sected sphere B

is added to B

dormant

and discarded

from B

active

, while B

new

is added to it. The process

of testing for cylindrical intersection repeats. The ﬁ-

Generation of Tree Surface Mesh Models from Point Clouds using Skin Surfaces

Figure 6: Half-Sphere Region Removal. In (A), a cylindri-

cal projection based on the connecting branch direction and

radius is projected onto the skin model. Based on an inter-

section test made at every 45

◦

interval as illustrated in (B), a

new point is added to the skin mesh surface. A planar walk

connecting all the points is executed and the half-surface

region is removed in (C).

nal tree joint model is created by using the two sets of

spheres listed in B

active

and B

dormant

. In Fig. 5, three

joints are shown and merged together as a single one.

The whole process stops when none of the spheres in

active

intersects with another.

4.2 Half Sphere Removal

To create a half-sphere opening for attachment with

the cylindrical mesh surfaces of the branch nodes,

the half-sphere region corresponding to each ball in

active

is required to be removed for connecting to the

branches. To identify the set of surface triangle ele-

ments corresponding to that half-sphere region, a con-

nected edge path delineating the border of the half-

sphere region has to be formed on the skin mesh sur-

face. Due to the nature of how the skin surface is

formed, using a planar cut would not likely provide a

satisfactory result due to the smoothed curved surface

resulting from multiple nearby spheres. Instead, we

ﬁrst project points and add points onto the skin sur-

face at every 45

◦

interval based on a cylindrical ray

projection with the corresponding

−→

D and r parame-

ters of the child branch (see Fig. 6A & 6B). Next,

a planar walk on the surface creates the edge path

connectivity between each pair of adjacent projected

points. Each planar path lies on the intersection be-

tween the skin model and the plane formed by the pair

of adjacent projected points and the center of the inci-

dent sphere. The resulting mesh with the half-sphere

region removed is shown in Figure 6C.

5 QUADRILATERAL PATCH

GENERATION

Structured quadrilateral meshes offer many numeri-

cal advantages over unstructured meshes due to their

tensor product structures. However, the generation of

quadrilateral meshes is not trivial. In this section,

we explore a potentially viable approach to gener-

ate 6-sided patches on the tree joint triangular-based

meshes that are constructed based on an intrinsic De-

launay triangulation of the points at the tip of the

spheres in B

active

. Our approach takes reference from

works (Boier-Martin et al., 2004; Daniels II et al.,

2011), which use the concept of Voronoi regions to

decompose the underlying triangular base mesh into

separate domains, where further parametrization into

quadrilaterals can take place.

The quadrilateral patch decomposition is applied

to a tree joint node taken from the Khaya senegalen-

sis example, see Figure 8. Prior to the removal of the

half-sphere region (Figure 6B), tip-points are placed

for each B

at the position P

+ (k

+ r

)

−→

. Using

these tip-points, a Voronoi decomposition of the tree

joint model is applied (Figure 8A). The dual Delaunay

graph constitutes triangular connectivity between the

tip points. Geodesic paths are then plotted between

points with such connectivity (Figure 8B). Once the

half-sphere regions are removed from the base-mesh

(Figure 6C), the intersected portions of the geodesic

paths are removed and merged with the boundary, ef-

fectively forming 6-sided patches (Figure 8C).

A particular case can arise when one of the

geodesic path intersects with the half-sphere from the

opposite vertex in the triangulation, resulting in the

formation of two distinct quadrilateral patches. In

most cases, the 6-sided patches can be split relatively

easily into quadrilaterals using a 6-valence singular-

ity at the barycentric point. However, other conﬁg-

urations such as using two 5-valence singularities or

methods such as multi-block decomposition (Fogg

et al., 2013) can be adopted depending on the skew-

ness of the 6-sided patch. Each quadric patch can

then be quad-meshed with added singularity points,

depending on its aspect ratio.

6 RESULTS

We implemented our algorithm on a LiDAR scan

dataset of a group of trees along a roadside in Sin-

gapore. Each individual tree underwent the branch-

leaf classiﬁcation process and the result is shown in

Fig 7. Based on the estimated parameters from the

lower trunk regions of each tree, most of the ﬁrst

few branching orders can be seen to be classiﬁed (red

coloured) with good accuracy. For trees with sparser

leaf densities, especially for larger trees, the classiﬁ-

cation can even reach the higher-order (and thinner)

branches.

GRAPP 2020 - 15th International Conference on Computer Graphics Theory and Applications

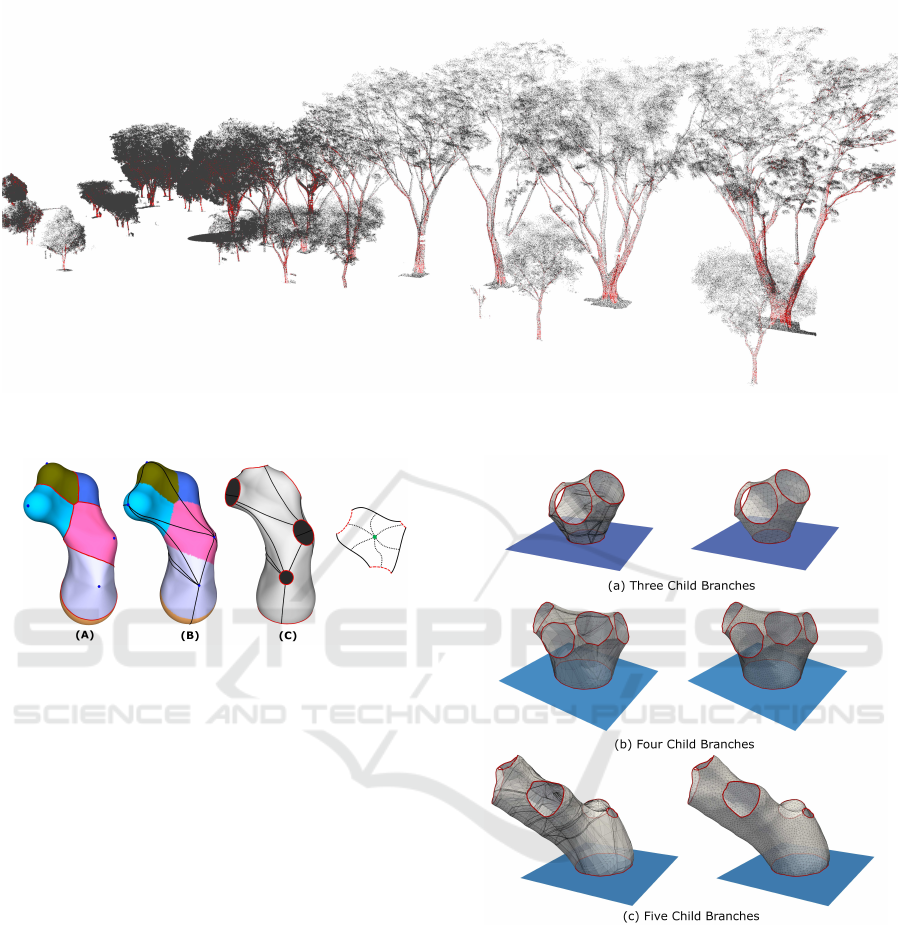
Figure 7: Branch Classiﬁcation. The classiﬁcation result of a group of trees, the points corresponding to woody regions are

coloured red.

Figure 8: Generating Quadrilateral Patches. The series of

images illustrate the patch generation process - (A) Voronoi

patches based on sphere tips, (B) Intrinsic Delaunay trian-

gulation, (C) 6-sided patches and the proposed quadrilateral

conﬁguration (left to right).

Using the classiﬁed branch points, the skeletal

tree model and the tree surface model are recon-

structed. The tree joint generation algorithm is imple-

mented using C++, utilizing packages from CGAL.

The two main packages used are skin surface mesh

for skin surface generation, fast intersection and dis-

tance computation (AABB Tree) for point projection

on the surface mesh.

To test the validity of our tree joint construction

approach, we generate tree joints using multiple ran-

domly generated child branch directions and radii.

The results are shown in Fig. 9 for three, four, and

ﬁve child branches. The meshes on the left are di-

rectly generated using the CGAL skin surface pack-

age. CGAL offers further functionalities for a pro-

gressive surface subdivision that reduces the error

with respect to the mathematical formulation of the

skin surface. However, the resulting mesh quality can

be quite poor (see Figure 6 for an example). Hence,

a CGAL remeshing operation is applied to achieve a

smooth mesh surface with good qualities, as shown

on the right of Fig. 9.

Figure 9: Tree Joint Meshes. The following tree joint

meshes were created randomly with varying number of

child branches. The original mesh created using CGAL’s

skin surface is shown on the left, while the resmeshed ver-

sion is shown on the right.

6.1 Classiﬁcation and Tree Skeletal

Model

We tested our algorithm on ﬁve commonly found tree

species in Singapore from the LiDAR dataset. These

are Tabebuia rosa, Swietenia macrophylla, Samanea

saman, Peltophorum pterocarpum and Khaya sene-

galensis. The result of the classiﬁcation process and

the subsequent skeletal tree extraction is shown in

Generation of Tree Surface Mesh Models from Point Clouds using Skin Surfaces

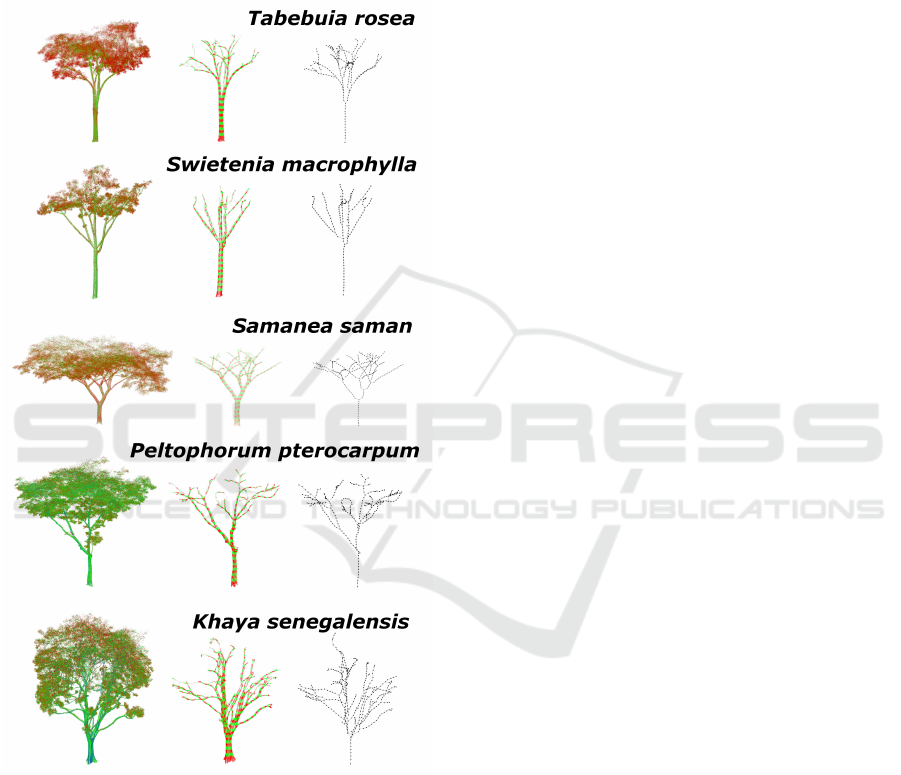
Fig 10. The original points are shown and coloured

based on their intensity values. From lowest to high-

est intensities, the corresponding color gradient goes

from red to green and then ﬁnally blue. As high-

lighted based on the color distribution, it can be seen

that the range of intensities differs from tree to tree,

depending on conditions such as the amount of sun-

light, temperature, or weather conditions.

Figure 10: Skeletal Tree Generation. The original point

clouds are shown on the left, the classiﬁcation results in the

middle, and the skeletal tree model are shown on the right.

The classiﬁcation is often most robust at the trunk

region since the sampling parameters were taken from

there. However, the fuzziness grows as it moves in-

wards in the crown region. This is to be expected:

the foliage affects the surface region of the branches

which the laser scanner can reach. A further pruning

operation is performed on the skeletal model to en-

sure that awkward (usually erroneous) connectivities

with large bending angles are removed.

Typically for point clouds acquired through laser

scanner, multiple passes are often merged together to

cover all sides of a tree. Slight variation during regis-

tration can result in overlapping surfaces. Depending

on other factors such as occlusion or weather condi-

tions, it can cause unevenness in the distribution of

points throughout the tree. Very often, manual adjust-

ment of parameters of intensity and sparsity can result

in superior classiﬁcation results. In our case, we are

able to recover the ﬁrst few tree branching order quite

accurately just by using the automated trunk-based

parameter estimation approach. Our current tree clas-

siﬁcation approach is a ”quick-and-dirty” that works

relatively well, and noted other more involved algo-

rithms such as (Vicari et al., 2019) and usage of ma-

chine learning approaches for point cloud classiﬁca-

tion (Wang et al., 2017).

6.2 Surface Mesh Generation

Each of the ﬁve skeletal models generated from the

point clouds is used to generate a surface mesh of the

tree branching structure. A skin model is created for

each joint node in the skeletal model. The ﬁve surface

mesh tree models are shown in Fig 11. A few exam-

ples of the tree joints created using skin surface model

are shown on the right. A real tree can have very intri-

cate branching morphology, and some tree joints can

have up to 6 to 8 child branches. The generated tree

joints shown have smooth surfaces that mimic the ac-

tual tree surfaces. Furthermore, its simple construc-

tion approach based on a collection of spheres allows

it to be employed as a suitable intermediary model for

generating the complex branching structures of trees,

no matter the morphology.

Like any real-world data acquisition, it can be

subjected to noise and other external environmental

variables such as occlusion, leading to partial cov-

erage of branches. As such, radius estimate might

vary widely even along the same branch. Hence, all

radii along a branch (i.e., branch nodes that lies be-

tween two joints) are averaged out. This is why cylin-

ders are used as an approximation shape model rather

than cones. Additionally between the child and par-

ent branches, the general rule to follow is by using

Leonardo da Vinci’s rule (i.e., the sum of the cross-

sectional area of all tree branches above a branch-

ing point at any height is equal to the cross-sectional

area of the trunk or the branch immediately below the

branching point). An initial check of all node radii

is conducted, and in cases where signiﬁcant discrep-

ancies occur, usually due to inadequate sampling, a

ﬁltering operation is applied to ensure that it adheres

to this rule.

GRAPP 2020 - 15th International Conference on Computer Graphics Theory and Applications

Figure 11: Full Meshed Model of the Trees. The ﬁve point

cloud test data is meshed and a few of the tree joint models

used are shown on the right.

The remeshing operation applied on the meshed

skin model can be adjusted to select for edge length.

Since the lower part of the tree can be substantially

larger in size than the upper region, a size-invariant

measurement has to be applied to preserve the mod-

elling accuracy, especially for the thinner branches.

For consistent preservation of details, the average

edge length of a tree joint mesh is set to be 1/30

of the smallest circular boundary created by the half-

sphere removal. This ensures that all cylindrical

branches, no matter the size, will have the same mesh-

ing density.

7 DISCUSSION AND

CONCLUSION

The intent of this work is to address the issue of con-

structing a simulation-ready 3D ﬁnite element mesh

model from point clouds of trees. A surface mesh

model of a tree typically has multiple long slender

branches that can be quite challenging to generate a

volumetric mesh. Hence, a piecewise model approach

such as ours wouldfacilitate the volumetric mesh gen-

eration process as the cylindricalbranches and the tree

joint models can be handled separately. By using a

template surface on each of the half-sphere openings,

and also on the cylindrical branch models, both can

be meshed separately and then merged. Furthermore,

a piecewise model facilitates the assignment of dif-

ferent material properties on various parts of the tree,

such as between trunk and branches.

We have also applied the tree surface mesh

generation for various tree species models which

were procedurally created based on L-system growth

rules (Gobeawan et al., 2019). The artiﬁcially created

tree is often written into an MTG ﬁle format (Godin

et al., 1999), which contains branching connectivities

and radii data that are sufﬁcient for our method.

In conclusion, this paper describes an approach

to make use of skin surfaces as a representation of

tree joints. It facilitates the construction of a full tree

surface mesh from a skeletal model extracted from a

laser-scanned point cloud. Among the many works,

we ﬁnd that the approach of (Ji et al., 2010) has

many similarity with our skin surface approach for

modelling complex joints, as used in (Zhu et al.,

2015). A proposed extension is to make comparison

studies between their approach and ours. Our future

work includes both improving our quadrilateral patch

formulation and exploring the formation of 3D ﬁnite

elements, both tetrahedral and hexahedral, using our

proposed piecewise tree joint construction method.

REFERENCES

Belton, D., Moncrieff, S., and Chapman, J. (2013). Process-

ing tree point clouds using gaussian mixture models.

Proceedings of the ISPRS Annals of the Photogram-

metry, Remote Sensing and Spatial Information Sci-

ences, Antalya, Turkey, pages 11–13.

Bloomenthal, J. (1985). Modeling the mighty maple. In

ACM SIGGRAPH Computer Graphics, volume 19,

pages 305–311. ACM.

Boier-Martin, I., Rushmeier, H., and Jin, J. (2004). Pa-

rameterization of triangle meshes over quadrilateral

domains. In Proceedings of the 2004 Eurograph-

Generation of Tree Surface Mesh Models from Point Clouds using Skin Surfaces

ics/ACM SIGGRAPH symposium on Geometry pro-

cessing, pages 193–203. ACM.

Bucksch, A. and Lindenbergh, R. (2008). Campino—a

skeletonization method for point cloud processing. IS-

PRS journal of photogrammetry and remote sensing,

63(1):115–127.

Cao, J., Tagliasacchi, A., Olson, M., Zhang, H., and Su,

Z. (2010). Point cloud skeletons via laplacian based

contraction. In 2010 Shape Modeling International

Conference, pages 187–197. IEEE.

CGAL (2019). CGAL User and Reference Manual. CGAL

Editorial Board, 4.14 edition.

Cheng, H.-L. and Shi, X. (2009). Quality mesh generation

for molecular skin surfaces using restricted union of

balls. Computational Geometry, 42(3):196 – 206.

Daniels II, J., Lizier, M., Siqueira, M., Silva, C. T., and

Nonato, L. G. (2011). Template-based quadrilateral

meshing. Computers & Graphics, 35(3):471–482.

Edelsbrunner, H. (1999). Deformable smooth surface de-

sign. Discrete & Computational Geometry, 21(1):87–

115.

Fogg, H. J., Armstrong, C. G., and Robinson, T. T. (2013).

Multi-block decomposition using cross-ﬁelds. Pro-

ceedings of adaptive modelling and simulation, Lis-

bon, pages 254–267.

Gobeawan, L., Lin, E., Tandon, A., Yee, A., Khoo, V., Teo,

S., Yi, S., Lim, C., Wong, S., Wise, D., et al. (2018).

Modeling trees for virtual singapore: From data ac-

quisition to citygml models. International Archives of

the Photogrammetry, Remote Sensing & Spatial Infor-

mation Sciences, 42.

Gobeawan, L., Wise, D. J., Yee, A. T. K., Wong, S. T.,

Lim, C., Lin, E. S., and Su, Y. (2019). Convenient

tree species modeling for virtual cities. In Advances

in Computer Graphics - 36th Computer Graphics

International Conference, CGI 2019, Calgary, AB,

Canada, June 17-20, 2019, Proceedings, pages 304–

315.

Godin, C., Ccostes, E., and Sinoquet, H. (1999). A

method for describing plant architecture which in-

tegrates topology and geometry. Annals of Botany,

84(3):343–357.

Hackenberg, J., Morhart, C., Sheppard, J., Spiecker, H., and

Disney, M. (2014). Highly accurate tree models de-

rived from terrestrial laser scan data: A method de-

scription. Forests, 5:1069–1105.

Hu, S., Li, Z., Zhang, Z., He, D., and Wimmer, M.

(2017). Efﬁcient tree modeling from airborne lidar

point clouds. Comput. Graph., 67(C):1–13.

Huang, H., Wu, S., Cohen-Or, D., Gong, M., Zhang, H., Li,

G., and Chen, B. (2013). L1-medial skeleton of point

cloud. ACM Trans. Graph., 32(4):65–1.

Ji, Z., Liu, L., and Wang, Y. (2010). B-mesh: a modeling

system for base meshes of 3d articulated shapes. In

Computer Graphics Forum, volume 29, pages 2169–

2177. Wiley Online Library.

Li, P., Wang, B., Sun, F., Guo, X., Zhang, C., and Wang, W.

(2015). Q-mat: Computing medial axis transform by

quadratic error minimization. ACM Transactions on

Graphics (TOG), 35(1):8.

Li, R., Bu, G., and Wang, P. (2017). An automatic tree

skeleton extracting method based on point cloud of

terrestrial laser scanner. International Journal of Op-

tics, 2017:1–11.

Livny, Y., Yan, F., Olson, M., Chen, B., Zhang, H., and

El-Sana, J. (2010). Automatic reconstruction of tree

skeletal structures from point clouds. ACM Trans.

Graph., 29(6):151:1–151:8.

Pfeifer, N., Gorte, B., Winterhalder, D., et al. (2004). Au-

tomatic reconstruction of single trees from terrestrial

laser scanner data. In Proceedings of 20th ISPRS

Congress, volume 35, pages 114–119. ISPRS Istan-

bul.

Poh, H., Lim, C., Ge, Z., Wise, D., Lou, J., Eng, Y., Lin, E.,

Burcham, D., Li, K., Lee, I., Chang, S., Chan, W.-L.,

Lee, H., and Khoo, B. (2019). Fractal tree geometry

reconstruction and meshing: From point cloud model

to tree aerodynamic simulation. In The Eighth Inter-

national Symposium on Physics of Fluids (ISPF8).

Raumonen, P., Kaasalainen, M.,

Akerblom, M.,

Kaasalainen, S., Kaartinen, H., Vastaranta, M.,

Holopainen, M., Disney, M., and Lewis, P. (2013).

Fast automatic precision tree models from terrestrial

laser scanner data. Remote Sensing, 5:491–520.

Soon, K. and Khoo, V. (2017). Citygml modelling for singa-

pore 3d national mapping. The International Archives

of Photogrammetry, Remote Sensing and Spatial In-

formation Sciences, 42:37.

Su, Z., Zhao, Y., Zhao, C., Guo, X., and Li, Z. (2011).

Skeleton extraction for tree models. Math. Comput.

Model., 54(3-4):1115–1120.

Tagliasacchi, A., Zhang, H., and Cohen-Or, D. (2009).

Curve skeleton extraction from incomplete point

cloud. ACM Trans. Graph., 28(3):71:1–71:9.

Vicari, M. B., Disney, M., Wilkes, P., Burt, A., Calders,

K., and Woodgate, W. (2019). Leaf and wood clas-

siﬁcation framework for terrestrial lidar point clouds.

Methods in Ecology and Evolution, 10(5):680–694.

Wang, D., Hollaus, M., and Pfeifer, N. (2017). Feasibility

of machine learning methods for separating wood and

leaf points from terrestrial laser scanning data. ISPRS

Annals of Photogrammetry, Remote Sensing & Spatial

Information Sciences, 4.

Xie, D., Wang, X., Qi, J., Chen, Y., Mu, X., Zhang, W., and

Yan, G. (2018). Reconstruction of single tree with

leaves based on terrestrial lidar point cloud data. Re-

mote Sensing, 10:686.

Xu, H., Gossett, N., and Chen, B. (2007). Knowledge and

heuristic-based modeling of laser-scanned trees. ACM

Trans. Graph., 26(4).

Yan, D., Wintz, J., Mourrain, B., Wang, W., Boudon, F., and

Godin, C. (2009). Efﬁcient and robust reconstruction

of botanical branching structure from laser scanned

points. In 2009 11th IEEE International Conference

on Computer-Aided Design and Computer Graphics,

pages 572–575.

Zhu, X., Jin, X., and You, L. (2015). High-quality tree

structures modelling using local convolution surface

approximation. The Visual Computer, 31(1):69–82.

GRAPP 2020 - 15th International Conference on Computer Graphics Theory and Applications