DataShiftExplorer: Visualizing and Comparing Change

in Multidimensional Data for Supervised Learning

Bruno Schneider

, Daniel A. Keim and Mennatallah El-Assady

University of Konstanz, Germany

Keywords:

Dataset Shift, Information Visualization, Classiﬁcation.

Abstract:

In supervised learning, to ensure the model's validity, it is essential to identify dataset shifts, i.e., when the

data distribution changes from the one the model encountered at the time of training. To detect such changes,

a comparative analysis of the multidimensional data distributions of the training data and new, unseen datasets

is required. In this paper, we span the design space of visualizations for multidimensional comparative data

analytics. Based on this design space, we present DataShiftExplorer, a technique tailored to identify and an-

alyze the change in multidimensional data distributions. Throughout examples, we show how DataShiftEx-

plorer facilitates the identiﬁcation and analysis of data changes, supporting supervised learning.

1 INTRODUCTION

Supervised learning is ubiquitous in diverse appli-

cation domains, ranging from image recognition to

health-care and disease prevention. The success of

its application depends on the data used to train a

model. However, even when a classiﬁcation or re-

gression model achieve high accuracy during the

model building phase, their performance might drop

when applied on new data that has not been seen

during training. This issue is known as the dataset

shift problem in machine learning (Moreno-Torres

et al., 2012). Common causes for this problem are

non-stationary environments (due to temporal or spa-

tial change) and the sample selection bias (Herrera,

2011). Under these scenarios, it is particularly help-

ful if we can foresee and analyze the change in new

data, especially when we do not have the new data

labels or cannot track the model’s performance. Nu-

merical methods can produce the same statistics for

data with entirely different properties (Matejka and

Fitzmaurice, 2017). A way to reveal and convey what

statistics alone can not capture is through data visual-

ization and analytics (Tukey, 1977; Chambers, 2017).

This paper spans the design space of visualiza-

tions for multidimensional comparative data ana-

lytics. Based on this space, we identify an under-

explored problem, namely, the explicit encoding of

https://orcid.org/0000-0001-5679-3781

https://orcid.org/0000-0001-8526-2613

change in multidimensional data. In our work, we ad-

dress the general problem of how to capture and vi-

sualize changing data properties in multidimensional

data distributions. The application to the dataset shift

problem in supervised learning guided our efforts in

developing a visual analytics technique to analyse

change between two multidimensional datasets, the

DataShiftExplorer.

We visually integrate different data representa-

tions and facilitate the comparison in a single view,

instead of analyzing separate visualization compo-

nents. Our approach also enables interactions, e.g.,

local data selections that reveal shift-patterns that

conventional visualization techniques may not ﬁnd.

Regarding the data preparation, we simplify the rep-

resentation of each multidimensional data record in

order to further create a visual hierarchy that empha-

sizes the most recurring data structures. Hence, our

tailored visual representations and data ﬁltering en-

able the analysis and comparison of the changes in

data distributions at different levels of detail, both,

during the training and testing (with unseen data)

phases of supervised learning.

In this paper, we contribute with a design space

for developing visual methods that explicitly encode

the change in multidimensional data, for comparing

two or more data subsets. Both, the visualization

of data distributions, as well as the dataset shift are

well-studied problems in the visual analytics and

machine learning ﬁelds, respectively. However, in

this work we attempt to connect both sides through

Schneider, B., Keim, D. and El-Assady, M.

DataShiftExplorer: Visualizing and Comparing Change in Multidimensional Data for Supervised Learning.

DOI: 10.5220/0008940801410148

In Proceedings of the 15th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2020) - Volume 3: IVAPP, pages

141-148

ISBN: 978-989-758-402-2; ISSN: 2184-4321

141

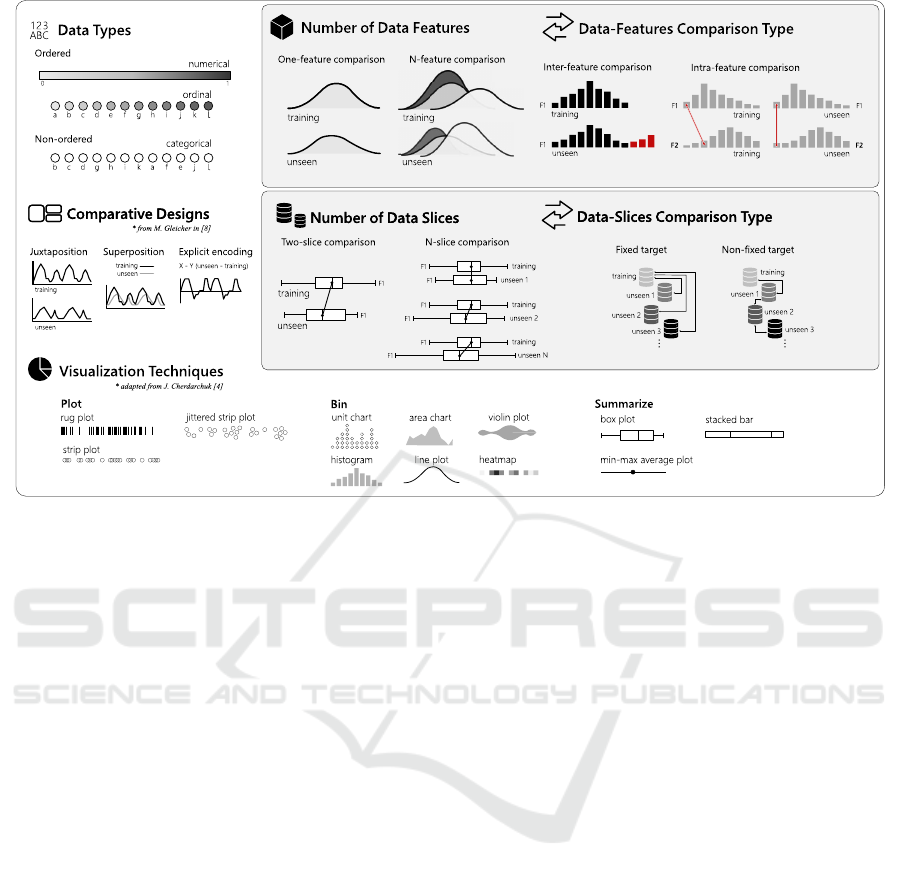
Figure 1: The design space for multidimensional comparative data analysis. This space spans seven dimensions to

structure the design of comparative VA solutions. It provides a systematization of all aspects to be considered for the visual

comparison of two or more data distributions. It also facilitates the identiﬁcation of under-studied alternatives, opening gaps,

and providing directions and opportunities for future research.

an explicit visualization of data change. We present

the DataShiftExplorer, an interactive visual analyt-

ics technique to identify, analyze, and compare the

change in multidimensional data distributions, in

general.

2 RELATED WORK

We present what the dataset shift problem in machine-

learning is, and brieﬂy revise the existing approaches

for visualizing data distributions, respectively in the

two next subsections.

2.1 The Dataset Shift Problem

Many machine learning algorithms follow the as-

sumption that the training data is governed by the

same distribution which the model will later be ex-

posed. (Bickel et al., 2009). However, in real-

life settings, the data a system faces after deploy-

ment does not necessarily have the same proper-

ties of the data available during development. This

issue is called dataset shift (Moreno-Torres et al.,

2012). It is a well-investigated real-world problem, by

machine-learning practitioners and researchers (Her-

rera, 2011), (Storkey, 2009), (Kull and Flach, 2014).

Regarding the terminology, most of the dataset

shift literature uses training, validation and test sets

when they refer to data subsets. The ﬁrst two ones are

different splits of the labeled data one has at hand to

build a model, by training and evaluating it. Then, the

test set corresponds to the unlabeled data for classiﬁ-

cation after model building. The shift, when it occurs,

happens between training and test sets. We prefer to

use the term unseen, instead of test. We want to make

a distinction because the test data is also used to refer

to a data split available at the time of model building,

in which the labels are omitted temporarily. On the

other hand, our deﬁnition of unseen encompasses data

that come after the process of model building, and are

not available during its construction.

The most basic form of dataset shift is the covari-

ate shift, when only the distribution of the input data

variables changes, comparing training to unseen data

(Herrera, 2011), (Storkey, 2009). One example is data

collected from a population for predictive analysis of

consumer behavior that, due to budget constraints,

did not consider all the regions of its relevant mar-

ket. Then, after building a model for this task, more

data comes, this time with all the relevant areas. In

this case, the performance of the model may drop be-

cause it has to deal with data not seen at the time of

training. Another common form of dataset shift is the

prior probability shift. It occurs when only the dis-

IVAPP 2020 - 11th International Conference on Information Visualization Theory and Applications

142

tributions of the target output variable change (Kull

and Flach, 2014). In classiﬁcation, the target variable

is the class label. A typical example is a system for

spam-detection that deals with different proportions

of spam and no-spam messages during development

and in production.

The most common causes of dataset shift are non-

stationary environments (due to a temporal or spatial

change) and sample selection biases (Herrera, 2011;

Moreno-Torres et al., 2012). There are more sophisti-

cated types of shift, like the concept-drift (or concept-

shift), when the relationship between the input and

target variables change, and what the model has to

learn changes over time. The latter type is out of our

scope. Our aim is providing novel visual exploratory

methods to support the identiﬁcation and analysis of

the two most basic dataset shift scenarios.

2.2 Visualization of Data Distributions

The use of graphical methods for exploratory data

analysis received a lot of attention over the last

decades (Tukey, 1977; Tufte, 2001; Chambers, 2017).

Among these methods, we focus on the visualizations

of data distributions, alone or in comparative layouts.

Approaches that enable the selection and visualiza-

tion of data subsets (Lex et al., 2010) are out of our

scope. We are interested in visualizing all the data.

We use the categorization of data-distribution visual-

izations proposed by Cherdarchuk in (Cherdarchuk,

2016). The categories describe what to do with the

data, plot, bin or summarize (see Visualization Tech-

niques in Figure 1). The three categories comple-

ment each other and offer different perspectives on the

same data. Individually, the techniques inside each

category have limitations (Correll et al., 2018). The

author proposes a forth category, rank, that we con-

sider an operation over the existing ones, and we do

not use.

In the ﬁrst category, plot the data, examples are the

rug-plot (Hilﬁger, 2015) and the strip-plot (Waskom,

2018). The idea is directly representing each data

point using the graphic element of choice. It provides

direct information on the number of points as well

as its distribution, but overplotting is an issue if the

dataset is vast. Jittering (Chambers, 2017) may alle-

viate that issue, by randomly changing the position of

the graphical elements in the axis that does not en-

code the data value.

The second category of data-distribution visual-

izations proposed in (Cherdarchuk, 2016) includes

techniques based on binning and on the estimation

of densities. The histogram (Poosala et al., 1996)

is a typical example of a visualization based on bin-

ning. The density-plots, another technique, produce a

smoothed representation of the histogram. However,

instead of directly representing the number of counts

in each bin, they use more sophisticated estimation

methods (Silverman, 2018) to represent a probability

density function. Variations of the density plot ex-

ist, like the violin-plot and the bean-plot (Wickham

and Stryjewski, 2011; Kampstra et al., 2008; Correll

and Gleicher, 2014; Hintze and Nelson, 1998; McGill

et al., 1978). They add a mirrored density plot, pro-

ducing a symmetrical ﬁgure that helps in compar-

ing certain types of distributions. Dot plots (Sasieni

and Royston, 1996) also use binning but representing

the counts with circles instead of rectangles. In (Ro-

drigues and Weiskopf, 2017), Rodrigues et al. present

a technique to construct non-linear dot plots for a high

dynamic range of data frequencies.

In the last category, summarize, box-plots (Wick-

ham and Stryjewski, 2011; Benjamini, 1988) are an

example. In this visualization, the idea is represent-

ing the second and third quartiles, together with the

median, to communicate where half of the data is in

the distribution. Additionally, it can also show out-

liers, for instance, or minimum and maximum val-

ues, depending on the variations of box-plot used.

Enhancements exist, like adjusting the box-plot to

show skewed distributions (Hubert and Vandervieren,

2008). There are plots which combine summarizing

with density curves. The vase-plot (Wickham and

Stryjewski, 2011) is an example, which shows sum-

mary statistics like the box-plot, together with the

shape of the distribution for the middle-half of the

data. We can also ﬁnd examples in which violin-

plots and bean-plots appear with additions of sum-

mary statistics on top of them.

3 VISUALIZING CHANGE

We propose a design-space for multidimensional

comparative data analysis (details in Figure 1). It

helps in the systematization of which are the main

aspects that we should consider when approaching

the problem of visualizing the change in multidimen-

sional data, and what options are available for each of

those aspects, or problem dimensions. This system-

atization also helps to identify options that are not ex-

plored yet in its full potential.

3.1 Design Space for Comparative Data

Analysis

The task of comparing data distributions may sound

not too complicated. However, if we consider our ap-

DataShiftExplorer: Visualizing and Comparing Change in Multidimensional Data for Supervised Learning

143

plication context, one may need to analyze and com-

pare an initial set of training data with a series of dif-

ferent incoming unseen data sets, for instance. In this

analysis, it may also happen that the data has not only

a few but dozens of features. So, the problem we in-

vestigate demands scalability in different directions,

one or N-feature, and one or N-data slices in our par-

ticular case.

To cope with a dynamic scenario and the compara-

tive needs our application brings, we work with seven

problem dimensions. In the following, we describe

one-by-one.

Data Types: the data are either numerical, or-

dinal, or categorical. The ﬁrst two ones, numerical

and ordinal, are ordered types. However, the ordinal

data fall into categories, while the numerical data fall

into a continuous or discrete numerical scale. Exam-

ples are one person's weight for numerical data or rat-

ing a hotel from one to ﬁve starts for the ordinal data

type. The categorical type also falls into categories

but does not have an implicit order. One example is

the hair color of individuals (e.g., blonde, red, brown,

and black). The type of data directly impacts which

statistical methods and visualization techniques are

available in each case. In (Kosara et al., 2006), for in-

stance, Kosara et al. present Parallel sets, a technique

based on the parallel-coordinates plot, but tailored to

deal with categorical data.

Number of Data Features: How many data fea-

tures (also called data attributes, or dimensions) take

part in the comparison. Each feature in each data sub-

set (e.g., training or unseen) has its distribution. We

want to compare them, and as the number of features

increase, more difﬁcult is ﬁnding a suitable visualiza-

tion solution that does not overload the analyst and

hinder the comparative analysis.

Data-features Comparison Type: One can com-

pare the distributions of the same feature in different

data subsets (inter-feature comparison). Another pos-

sibility is comparing the relationships between two or

more feature in one subset, versus the same relation-

ships in another subset (intra-feature comparison).

By relationships, we mean, for instance, analyzing if

a given range of values in a numerical feature majorly

connects to a particular range in another feature and

if this behavior changes across different data subsets.

Number of Data Slices: In our application for su-

pervised learning, typically there are two data slices,

the training set, and another set of unseen data. How-

ever, an increasing number of unseen data subsets

may appear in a supervised learning problem. We call

this the N-slice scenario, which turns the comparison

of a growing number of sets even more challenging.

Data-slices Comparison Type: If we have more

than two data slices for comparison, then one possibil-

ity is to have a ﬁxed target, i.e., comparing the incom-

ing sets always with the training data. Another op-

tion is comparing the next slice always with the pre-

vious one, and we call it the non-ﬁxed target compar-

ison type.

Comparative Designs: Regarding the data visu-

alization and how to organize a layout for visual com-

parison, we use the categorization proposed by Gle-

icher in (Gleicher, 2018). There are three possible

arrangements: juxtaposition, in which different plots

appear side-by-side, the superposition, in which two

or more plots appear on top of each other, and the ex-

plicit encoding. In this last case, an example is the

subtraction of values between two data series to ob-

tain and visualize the change. Explicit in this case

means that we directly represent and visualize the

amount of change, instead of inferring it by looking to

what is different between two side-by-side plots, for

instance. The three arrangements do not exist only in

isolation. One can combine them in the same visual

comparison, supported by a set of visualizations.

Visualization Techniques: We consider three

types from the categorization of data-distribution

visualizations proposed by Cherdarchuk in (Cher-

darchuk, 2016): plot, bin or summarize the data, as we

discuss in Section 2.2. They complement each other

and may appear in combination, in superposed lay-

outs, for instance. If one uses a box-plot, which sum-

marize the data, the goal is not showing in detail value

ranges are distributed, but a few descriptive statistics.

On the other hand, to see data counts per value range,

the bin type is an alternative, using a histogram. The

ﬁrst strategy, to directly plot the data, provides a very

compact representation of the distributions, but over-

plotting is an issue.

3.2 Under-explored Comparative

Approaches

The design-space we propose served to the purpose

of systematizing how we approach the problem of vi-

sualizing the data-shift. The problem-dimensions we

present and the options inside each of those also ac-

cept combinations. For instance, the same application

may contain more than one data type, combinations

of comparative designs, and a set of different visual-

ization techniques.

Among the alternatives we illustrate in the design-

space ﬁgure, we want to draw attention to the intra-

feature comparison type (in Figure 1, Data-Features

Comparison Type). In this comparison, it is necessary

to show not only the data distributions shapes in isola-

IVAPP 2020 - 11th International Conference on Information Visualization Theory and Applications

144

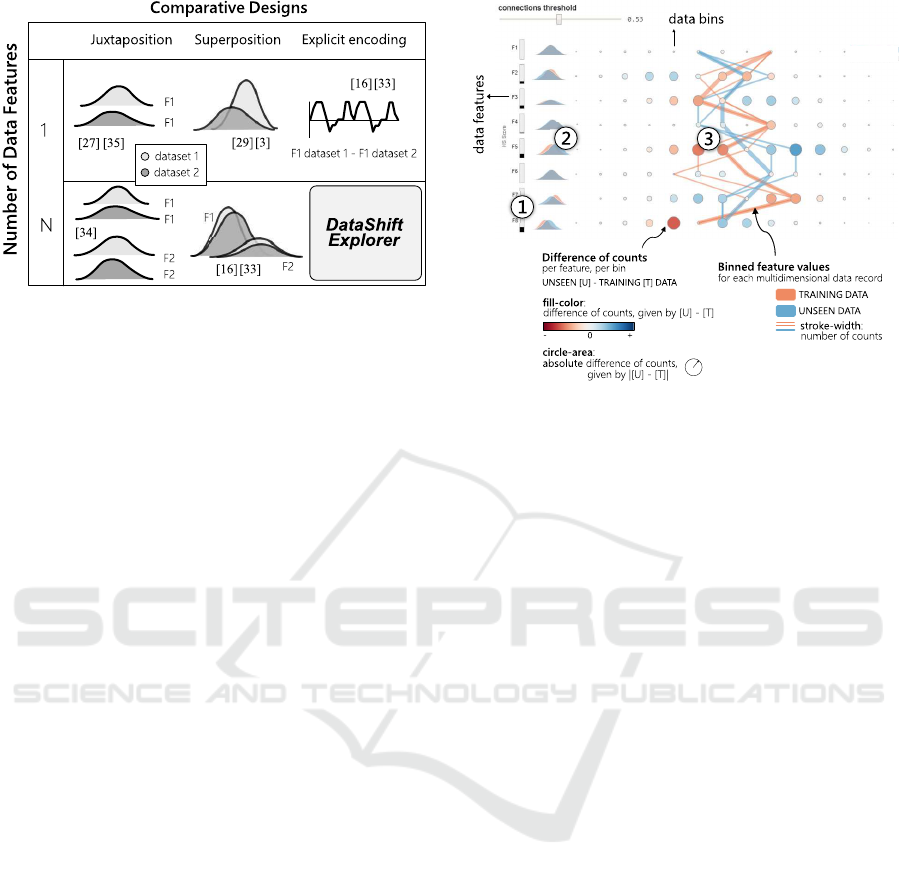
Figure 2: Using the terminology we propose in our design-

space (Figure 1), we identify an under-served task in com-

parative data analysis, namely the explicit visualization

of change in multidimensional datasets. We present the

DataShiftExplorer to support this task.

tion but also how the values across different features

and corresponding distributions connect. And not

only how they are connected in a single data slice, but

what are the main changes between these connections

in two different data slices, for instance. That compar-

ison is one of the goals we pursue with our DataShif-

tExplorer, which we present in the following section.

Finally, we identify, using the terminology from

the design-space, a visual comparison type of multi-

dimensional data that, to the best of our knowledge,

is still under-explored (Figure 2), taking into account

the existing techniques we revise in Section 2.2. This

type is about visualizing the change in multidimen-

sional datasets using a single visualization, instead

of replicating series of visualizations for each fea-

ture and putting them side-by-side. Starting from this

opportunity, we develop our approach to experiment

with new ideas and solutions to support this compar-

ison. The data preprocessing requirements and the

visual-encoding decisions appear in detail in the fol-

lowing section.

4 THE DataShiftExplorer

We present the DataShiftExplorer, a visualization

technique to identify and analyze the dataset shift in

supervised learning. This technique is tailored to en-

code the change in data distributions explicitly, be-

tween the training data and the unseen set, for N-

feature comparison in a single and compact visual-

ization. It is also model-agnostic because it does not

need the classiﬁcation data labels, as well as it sup-

ports binary and multiclass problems.

Figure 3: Identiﬁcation and analysis of change in mul-

tidimensional data distributions. We present DataShift-

Explorer, a visual analytics technique to analyze the data

shift between two multidimensional distributions. It enables

users to (1) sort the features by data change; (2) compare

the shapes of the data distributions in superimposed den-

sity plots; and (3) explore in detail the data-shift patterns in

a tailored visualization, composed of a parallel-coordinates

style plot and a difference-plot in a compact form. The tar-

get application domain is the comparison between training

and unseen data for supervised learning.

4.1 Basic Idea

The DataShiftExplorer main visualization has three

components. The ﬁrst one (Figure 3.1) is a bar chart

that shows the magnitude of change between training

and unseen data per feature. The second (Figure 3.2)

is a series of superimposed density plots to com-

pare the shapes of the data distributions. Finally, the

third component (Figure 3.3) is a tailored visualiza-

tion to explore in detail the data-shift patterns, com-

posed of two layers of information. The ﬁrst layer is a

difference-plot, which shows the (normalized) differ-

ence of counts between data bins per feature, in un-

seen and training sets. In this layer, we use the ex-

plicit encoding comparative design. The second layer

shows the connections among binned feature values in

training and unseen sets using the superposition com-

parative design, for all the data instances in both sets.

In the difference of counts layer (Figure 3.3

again), we show in a very compact form, in a single

plot, where are the more signiﬁcant data changes be-

tween two datasets. We inform, based on a diverg-

ing color scale and dots of varying size, if new data

ranges per feature appeared for the ﬁrst time in the un-

seen data. Conversely, we show if data ranges appear

in training but do not exist in unseen data. However,

DataShiftExplorer: Visualizing and Comparing Change in Multidimensional Data for Supervised Learning

145

despite the compact form of a difference-plot, it can-

not communicate the amounts of data which gener-

ated the differences. To overcome this limitation, we

have an additional layer with the lines that show the

connection among all the binned feature values for

every multidimensional data record, like a parallel-

coordinates plot. Therefore, these lines give an idea

of the amount of data in each set that respond to the

differences in counts.

To align the layers of information in the visual-

ization and simplify the data representation, we use

data binning in both cases (dots and lines). Instead

of using the exact value for each feature, we substi-

tute it by to which bin the value belongs for every fea-

ture, in case of numerical data. With this new rep-

resentation, we group the data by the same (trans-

formed) value for every feature and count the num-

ber of occurrences of multidimensional data-records

with that same representation. Lastly, we give more

importance to the data-records with more counts, by

increasing the stroke-width in the visualization using

a non-linear exponential scale. This visual hierarchy

has a signiﬁcant impact on the simpliﬁcation of the

visualization, and helps the visual comparison of data

in different sets. In contrast, directly plotting the data

without preprocessing in bins result in overplotting.

Figure 4: We use different datasets to show which pat-

terns the DataShiftExplorer produces when there is a data

change and when there is not, between training and unseen

sets. In the left example (1), the lines follow a very similar

path, which corresponds to the no data-shift pattern. In the

right (2), there are crossings between training and unseen

data lines, and they follow opposite directions. We can also

see blue and red circles in the difference-plot, which corre-

sponds to the data-shift pattern.

4.2 Visual Encoding

We build our difference-plot (Figure 3.3) by ﬁrst com-

puting, for each bin (value range) in each feature, the

normalized number of counts in both training (T) and

unseen (U) data. Then, we build, in both cases, ma-

trices of counts per bin per feature and compute [U]

- [T], element-wise. We use a diverging color scale

to map the result of the subtraction to the ﬁll color

of the dots in the difference-plot. Negative values ap-

pear in red, zero in white, and positive values in blue.

Regarding the data preprocessing before the construc-

tion of our difference-plot, we normalize the num-

ber of counts using simple proportional scaling, tak-

ing into account differences of size between training

and unseen data. Then, we compute [U] - [T]. How-

ever, before plotting the resulting matrix, we ﬁrst look

back individually in [U] and [T] counts per row. For

each row, which corresponds to one feature, we take

the maximum value we ﬁnd. This number gives us

the magnitude of change per feature, and we map this

maximum (maxPerFeature) to the extremes of the di-

verging color scale before plotting each row, using [-

maxPerFeature, maxPerFeature]. The normalization

per feature avoids that an outlier makes the changes

in other features almost imperceptible.

We organize the layout of the difference-plot in

the following way: each feature corresponds to one

row in the visualization along the vertical axis, and

each bin corresponds to one column in the horizontal

axis. Then, each dot, which corresponds to one pos-

sible combination of feature and value range, has the

ﬁll color mapped to the result of the subtraction [U]

- [T], normalized per feature as we explained before.

Shades of blue mean that more data appear in unseen

for the given feature and bin. Conversely, red corre-

sponds to a negative value and means that, in training

data, there are more counts for the respective dot than

in unseen data. Also, the absolute value of unseen mi-

nus training, | [U ]− [T ] | , is mapped to the size (area)

of the circles.

In the parallel-coordinates style plot (Figure 3.3

again) that show all feature value ranges for each data

record, we use distinct solid colors to set the stroke

color, salmon for training and blue for unseen data.

We then use a non-linear exponential scale to map

the number of counts to the stroke-width, because we

want to emphasize the data-records with more counts

and make the lines of the less frequent connections

appear with much less visual importance. Regard-

ing the data preprocessing for the parallel-coordinates

style plot, we also use simple proportional scaling to

normalize the data instances counts and consider dif-

ferences of size between datasets.

4.3 Interaction, Data-ﬁltering, and

Details-on-demand

On top of the data preprocessing steps and visual en-

coding, the interaction plays an essential role in the

DataShiftExplorer, facilitating our visual comparison

task. Interactive components allow us to support three

subtasks (see Figure 5). The ﬁrst one, identifying the

most recurring feature vectors (T1), works by reduc-

IVAPP 2020 - 11th International Conference on Information Visualization Theory and Applications

146

Figure 5: We use the DataShiftExplorer to compare training and unseen sets. We generate synthetic classiﬁcation data with

eight features and two classes. From left to right, we ﬁrst ﬁlter the data to show only the most recurring data-instances in both

training and unseen sets (1), which reduces the number of lines and the over-plotting in our main visualization. Then, we can

identify the dataset shift pattern we describe in Figure 4. After, we sort the features to see the ones that most change next

to each other in the visualization (2). We also support the task of locally selecting feature value ranges (3). This selection

triggers a ﬁlter that shows only the data instances, both in training and unseen sets, in which the values for the data feature

under analysis ﬁt into the selection. Using this resource, we can investigate in which other features there is less overlap

between training and unseen data lines in the visualization for a given selected range. Lastly, auxiliary visualizations reveal

additional information on the distributions of one particular data feature.

ing overplotting and keeping only the most recurring

changes among feature values. Then, by sorting fea-

tures by data change (T2), we organize the visualiza-

tion layout and see signiﬁcant changes ﬁrst. The third

subtask, locally selecting feature value ranges (T3),

proﬁts from the interaction capabilities to reveal local

changes, besides the overall view.

To support the ﬁrst task (T1), the interactive com-

ponent we use is a data-ﬁlter that controls the number

of lines to appear in our visualization, the ones that

show the value ranges for all features in the training

and unseen sets. This ﬁlter interactively updates the

threshold of the minimum number of counts, so that

lines representing multidimensional data instances

with fewer counts than this threshold do not appear.

There is a clear trade-off between seeing all data, and

in this case with poor legibility for comparison, or ﬁl-

tering it and keeping only the most recurring struc-

tures for comparison in both sets, for better legibility.

Regarding the possibility to sort the features

by data change (T2), we use the two-sample

Kolmogorov-Smirnov (KS) statistic (Cieslak and

Chawla, 2009), which tests whether two samples are

drawn from the same distribution. The KS statistics

lies between 0 and 1 and works as a distance measure

between data distributions. The smaller the KS statis-

tics value is, more similar are the distributions. We

precompute the KS for each feature between train-

ing and unseen sets and allow the interactive selec-

tion of this sorting criterion, which updates our visu-

alization accordingly. As an auxiliary plot, we show

next to the rectangle bars that encode the KS statistics

for each feature a small superposition of two density

plots, showing the shapes of the distributions in train-

ing and unseen sets. The density plots are efﬁcient for

comparing differences in shape between both distri-

butions, as well as conﬁrm the data-shift indicated by

the KS statistic.

For the third task (T3), we provide an interaction

on mouse-click that shows, for a selected data range

per feature in the difference plot, only the lines in

training and unseen data that ﬁts into this selection.

It also works as a ﬁlter, but this time we are ﬁltering

by a range of values in one feature. The mouse-click

on a particular circle in the difference-plot determines

which feature and which value range to ﬁlter (exam-

ple in Figure 5). Using this interaction, we can se-

lect one data range we know is new in unseen data by

looking for the biggest blue circle in the difference-

plot, for instance. Then, we inspect where the lines

go, analyzing where there is no overlap between train-

ing and unseen data lines. This way, we identify, for

a given selection, in which features and value ranges

the dataset shift occurs.

Finally, we also work with three linked visualiza-

tions: one rug-plot, a simpliﬁed version of a box-

plot, and one density-plot (Figure 5.3, on the bot-

tom). The density plot is the same one that appear in a

much smaller version next to the KS statistics rectan-

gle bars. We use these visualizations to show the data-

distribution of one feature at each time, both in train-

ing (in red color) and unseen sets (in blue color). They

offer three different perspectives on the same data dis-

tributions. As we present in Section 3, there are the

plot, bin and summarize data distribution visualiza-

tion types, which correspond respectively to our aux-

iliary rug plot, density plot and simpliﬁed box-plot.

DataShiftExplorer: Visualizing and Comparing Change in Multidimensional Data for Supervised Learning

147

5 FUTURE WORK

After spanning the design-space of multidimensional

comparative data analytics, we identify a potential re-

search gap, and develop an interactive visualization

prototype, the DataShiftExplorer

However, our work has limitations. The main one

is that user studies are missing. We plan to vali-

date our prototype in controlled environments as fu-

ture work. Regarding the prototype, one limitation is

that we do not let the user change the number of data

bins interactively. Binning is a necessary preprocess-

ing step in our pipeline. However, a different number

of bins may affect the visual outcome signiﬁcantly.

A necessary extension is letting the user interactively

update this number.

Lastly, in the user studies, it will also be important

to explore real datasets with our tool. So far, in the

examples we provide in this paper, we generate the

data using a synthetic classiﬁcation data generator

to have complete control over the generation process.

REFERENCES

Benjamini, Y. (1988). Opening the box of a boxplot. The

American Statistician, 42(4):257–262.

Bickel, S., Br

uckner, M., and Scheffer, T. (2009). Discrimi-

native learning under covariate shift with a single opti-

mization problem. In Dataset Shift in Machine Learn-

ing, pages 161–177. MIT.

Chambers, J. M. (2017). Graphical Methods for Data Anal-

ysis. Chapman and Hall/CRC.

Cherdarchuk, J. (2016). Visualizing distribu-

tions. http://www.darkhorseanalytics.com/blog/

visualizing-distributions-3.

Cieslak, D. A. and Chawla, N. V. (2009). A framework for

monitoring classiﬁers’ performance: when and why

failure occurs? Knowledge and Information Systems,

18(1):83–108.

Correll, M. and Gleicher, M. (2014). Error bars considered

harmful: Exploring alternate encodings for mean and

error. IEEE transactions on visualization and com-

puter graphics, 20(12):2142–2151.

Correll, M., Li, M., Kindlmann, G., and Scheidegger, C.

(2018). Looks good to me: Visualizations as sanity

checks. IEEE transactions on visualization and com-

puter graphics, 25(1):830–839.

Gleicher, M. (2018). Considerations for visualizing com-

parison. IEEE transactions on visualization and com-

puter graphics, 24(1):413–423.

Herrera, F. (2011). Dataset shift in classiﬁcation: Ap-

proaches and problems. http://iwann.ugr.es/2011/pdf/

InvitedTalk-FHerrera-IWANN11.pdf.

http://datashiftexplorer.dbvis.de

http://scikit-learn.org/stable/modules/generated/

sklearn.datasets.make classiﬁcation.html

Hilﬁger, J. J. (2015). Graphing Data with R: An Introduc-

tion. O’Reilly Media, Inc.

Hintze, J. L. and Nelson, R. D. (1998). Violin plots: a box

plot-density trace synergism. The American Statisti-

cian, 52(2):181–184.

Hubert, M. and Vandervieren, E. (2008). An adjusted box-

plot for skewed distributions. Computational statis-

tics & data analysis, 52(12):5186–5201.

Kampstra, P. et al. (2008). Beanplot: A boxplot alternative

for visual comparison of distributions. Journal of Sta-

tistical Software.

Kosara, R., Bendix, F., and Hauser, H. (2006). Parallel sets:

Interactive exploration and visual analysis of categori-

cal data. IEEE transactions on visualization and com-

puter graphics, 12(4):558–568.

Kull, M. and Flach, P. (2014). Patterns of dataset shift. In

First International Workshop on Learning over Multi-

ple Contexts (LMCE) at ECML-PKDD.

Lex, A., Streit, M., Partl, C., Kashofer, K., and Schmalstieg,

D. (2010). Comparative analysis of multidimensional,

quantitative data. IEEE Transactions on Visualization

and Computer Graphics, 16(6):1027–1035.

Matejka, J. and Fitzmaurice, G. (2017). Same stats, differ-

ent graphs: Generating datasets with varied appear-

ance and identical statistics through simulated anneal-

ing. In Proceedings of the 2017 CHI Conference on

Human Factors in Computing Systems, pages 1290–

1294. ACM.

McGill, R., Tukey, J. W., and Larsen, W. A. (1978).

Variations of box plots. The American Statistician,

32(1):12–16.

Moreno-Torres, J. G., Raeder, T., Alaiz-Rodr

ıGuez, R.,

Chawla, N. V., and Herrera, F. (2012). A unifying

view on dataset shift in classiﬁcation. Pattern Recog-

nition, 45(1):521–530.

Poosala, V., Haas, P. J., Ioannidis, Y. E., and Shekita, E. J.

(1996). Improved histograms for selectivity estima-

tion of range predicates. SIGMOD Rec., 25(2):294–

305.

Rodrigues, N. and Weiskopf, D. (2017). Nonlinear dot

plots. IEEE transactions on visualization and com-

puter graphics, 24(1):616–625.

Sasieni, P. D. and Royston, P. (1996). Dotplots. Journal of

the Royal Statistical Society: Series C (Applied Statis-

tics), 45(2):219–234.

Silverman, B. W. (2018). Density estimation for statistics

and data analysis. Routledge.

Storkey, A. J. (2009). When training and test sets are dif-

ferent: characterizing learning transfer. In In Dataset

Shift in Machine Learning, pages 3–28. MIT Press.

Tufte, E. R. (2001). The visual display of quantitative in-

formation, volume 2. Graphics press Cheshire, CT.

Tukey, J. (1977). Exploratory data analysis. Addison-

Wesley Publishing Company.

Waskom, M. (2018). Seaborn: statistical data visualization.

http://seaborn.pydata.org.

Wickham, H. and Stryjewski, L. (2011). 40 years of box-

plots. Am. Statistician.

IVAPP 2020 - 11th International Conference on Information Visualization Theory and Applications

148