Regularization in Higher-order Photometric Stereo Inspection for
Non-Lambertian Reflections
Doris Antensteiner
a
and Svorad
ˇ
Stolc
Austrian Institute of Technology, Giefinggasse 4, Vienna, Austria
Keywords:
Photometric Stereo, Surface Normals, Higher-order Polynomials, Depth Reconstruction, Non-Lambertian
Materials.
Abstract:
In this paper we present and compare two regularized higher-order photometric stereo approaches for the
reconstruction of varying albedos and surface normals of non-Lambertian materials. We evaluate the two
different higher-order polynomial methods, which we additionally regularize with Tikhonov’s method. The
reconstruction of surface properties is essential for a vast amount of industrial applications, such as the iden-
tification of surface defects, the analysis of security features or the detection of forged documents. For the
reconstruction of Lambertian objects, lower order models can be used to achieve an accurate representation,
while higher-order models allow the description of non-Lambertian behaviors accurately. Qualitative and
quantitative results on a ground truth dataset as well as on real-world data show that the use of a regularized
higher-order polynomial model can significantly improve the surface normal and albedo reconstructions.
1 INTRODUCTION
Analyzing the surface normals and illumination inde-
pendent reflectance (albedo) from multiple reflections
of an object presents one of the most important prob-
lems in computer vision. Especially in industrial ap-
plications, the surface normals and albedo give essen-
tial information for a number of challenges. Such ap-
plications lie in the field of defect detection for inline
production setups, the analysis of complex print struc-
tures (e.g. optically variable security features) as well
as in the inspection and detection of forged documents
and banknotes. However, such surface reflections
behave usually in a complex non-Lambertian man-
ner, while a vast amount of reconstruction algorithms
only consider diffuse reflection elements. This leads
to systematic errors in reflective regions. We tackle
this issue by formulating two second-order polyno-
mial models and pairing them with a Tikhonov regu-
larization to analyze the non-Lambertian reflectance.
The Tikhonov regularization is a widely-used regu-
larization approach that was invented independently
in various fields, e.g. (Tikhonov, 1943). We com-
pare both higher-order polynomial models and ex-
plain their differences, along with comparing the pho-
tometric stereo reconstructions with standard Lam-
bertian models.
a
https://orcid.org/0000-0003-2083-0135
(a) Lambertian model. (b) HO-Poly model.
Figure 1: Illustration of the suppression of errors in sur-
face normals due to a shiny metal surface on a bandage-
pin using regularized second-order polynomials (HO-Poly)
compared to the reconstruction with a standard Lambertian
model. Note the compensation of the strong non-smooth
deviations along the metal piece in HO-Poly in contrast to
the non-compensated Lambertian reference method.
Photometric stereo is a well-studied computer vi-
sion approach which emerged in the early 80s (Wood-
ham, 1980). It describes using the Lambertian re-
flectance model to recover the surface normals and
albedo, with several images taken from a fixed
scene under various calibrated illumination condi-
tions. However, real world surface reflections which
show specularities, benefit from higher-order models.
Alternatively, those specular reflections can be treated

as outliers by a lower order approximation (Mallick
et al., 2005).
Polynomial approximations were previously used
on texture maps (PTMs) (Malzbender et al., 2001)
in order to achieve increased photo-realism of re-
constructed surface textures. These are second-order
models defined on the xy-domain. We build on
that idea and advance this approach to a second-
order polynomial defined on the full xyz-domain,
which naturally expands upon the standard Lamber-
tian model. We label this approach as higher-order
polynomial (HO-Poly). This formulation is a natural
higher-order extension of the Lambertian model for-
mulation.
Spherical harmonics follow the same idea with
different second-order basis functions and were pre-
viously studied in the context of photometric stereo.
The projection onto a spherical basis to derive har-
monics was used in (Basri et al., 2007). Later,
face shapes were analyzed using spherical har-
monics (Kemelmacher-Shlizerman and Basri, 2011),
where the light coefficients and albedo were estimated
from one reference face shape. We utilize and regular-
ize the higher-order spherical harmonics (HO-SH) to
reach a more accurate non-Lambertian model. This is
a more established formulation compared to our HO-
Poly and benefits from the orthogonal behavior of the
basis functions. In contrast, HO-Poly does not have
full orthogonality but in contrast offers one more de-
gree of freedom for the second-order case.
We demonstrate two L2 regularized polynomial
representations (HO-Poly and HO-SH) of the light
source vectors, formulated to achieve a more precise
photometric stereo representation. Their benefit in re-
gards to the surface normal calculation is illustrated in
Fig. 1 in comparison to a full Lambertian model. The
shown bandage-pin was acquired with a light dome
using 32 illumination sources. The surface normals
show a strong bias on the highly reflective metal pin
element in the image center. This effect is strongly
suppressed using a regularized higher-order model.
In this paper, differences and properties of the two
proposed polynomial representations are discussed.
We outline the importance of regularization using
higher-order photometric stereo models. For both
methods, we propose and investigate polynomial rep-
resentations consisting of up to second-order compo-
nents. The zero-order elements represent the ambient
component which can help dealing with illumination
behaviours such as stray light. The first-order compo-
nents of the light polynomials are utilized to extract
the varying albedo and surface normals of the object.
Second-order elements comprise higher-order infor-
mation, such as specular lobes. We use a Tikhonov
regularization to restrict the behaviour of the second-
order components as well as the ambient zero-order
component simultaneously.
2 REFLECTANCE
REPRESENTATION
For Lambertian surfaces, low order spherical har-
monics can be utilized to represent the illumination
conditions accurately. A simple extension for non-
Lambertian surfaces can be approximated by filter-
ing specular regions (Shashua, 1997). Another ap-
proach of formulating the irradiance in terms of spher-
ical harmonic coefficients of the incident illumination
was explored in (Ramamoorthi and Hanrahan, 2001),
building on that work, low order spherical harmonics
were utilized by (Basri et al., 2007). Non-Lambertian
surfaces require higher-order models to allow for an
accurate representation.
In this paper we formulate polynomial functions
which were frequently used in the fields of optics,
modelling surface reflectance and textures in order to
synthesize geometric details from images.
Zernike polynomials (Zernike, 1934) are an or-
thogonal polynomial sequence which are used in op-
tics for modelling optical aberrations. Since they are
represented on a unit disk they are not directly ap-
plicable to our task. Instead, we formulate spher-
ical harmonic polynomials which can be used to
represent smooth surface reflectance functions on a
sphere (MacRobert, 1948; Haindl and Filip, 2013).
For polynomial methods, the representation of
specular peaks can not be estimated fully, if solely
the lower-order polynomial function is considered.
Higher-order functions are required for more accurate
representations. In the field of photometric stereo,
such higher-order representations are used to reach
a compact formulation and stable analysis of the ob-
served reflectance.
Having sufficient data, another characterization
can be tailored by learning the reflectance behavior
using convolutional neural networks. This allows
weights to capture even complex reflectance distribu-
tion functions (Haindl and Filip, 2013; Antensteiner
and
ˇ
Stolc, 2017).
In our work we propose regularized higher-order
formulations. Using regularization for higher-order
models is essential to control the higher-order com-
ponents. In our presented methods we propose the
use of a Tikhonov regularizer. This traditional regu-
larization allows for a high performance implementa-
tion while remaining within a least-squares approach.
A local per-pixel computation does not require any it-

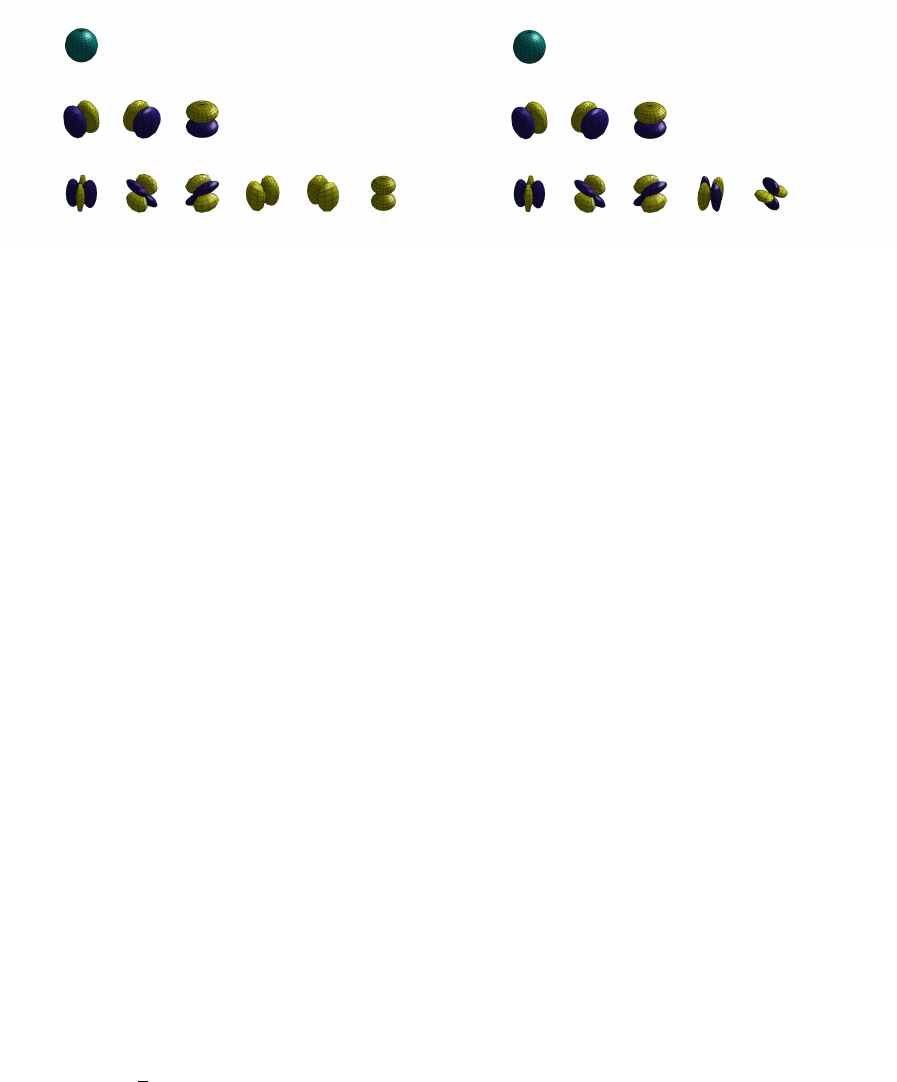
Order
0
1
st
2
st
1,
X, Y, Z,
X Y, X Z, Y  Z, X X , Y Y, Z  Z
(a) HO-Poly
Order
0
1
st
2
st
1,
X, Y, Z,
X Y, X Z, Y  Z, X  X −Y Y, X X − Z Z
(b) HO-SH
Figure 2: Basis functions of the proposed regularized polynomial HO-Poly and the spherical harmonics formulation HO-SH,
represented are the elements of the polynomials as described in Eq. 2 and Eq. 3 . These plots show the basis functions as they
would appear for a large number of elements n.
erative optimization or sorting as it can be solved via
a closed-form method. This makes our method apt for
industrial inline applications which require real-time
processing. We will evaluate a Tikhonov regulariza-
tion on both, such polynomials which are a natural
extension of the Lambertian formulation and PTMs
(HO-Poly) as well as a spherical harmonics represen-
tation (HO-SH). These approaches are well-fitting for
the reconstruction of surface normals and the vary-
ing albedo of non-Lambertian surfaces. We compare
the results of our proposed regularized methods to the
outcome reached by a standard Lambertian model.
3 PHOTOMETRIC STEREO
Photometric stereo methods reconstruct the surface
orientation and albedo of an object, acquired under
varying lighting conditions. In standard photomet-
ric stereo we consider a Lambertian surface capture
of the dimensions of M × N pixels, with surface nor-
mals N
i, j
∈ R
3
at the discretized locations (i, j) ∈
M × N and an albedo ρ
i, j
∈ R. These are recon-
structed under defined illumination sources L ∈ R
n×3
with n observed intensities E
i, j
∈ R
n
. The matrix
M
i, j
= ρ
i, j
N
i, j
with vectors at each location, repre-
senting albedo scaled surface normal vectors can be
recovered using a standard least squares (LS) formu-
lation, solved with a conjugate gradient approach:
min
M
i, j
1
2
||L · M
i, j
− E
i, j
||
2
. (1)
The depth consequently can be recovered using
e.g. the (generalized) method of Nehab, which was
previously described in (Nehab et al., 2005; Anten-
steiner et al., 2018).
4 OUR REGULARIZED
HIGHER-ORDER
PHOTOMETRIC STEREO
We analyze two different higher-order functions for
the photometric stereo light source modelling. First,
we approach the description by a natural extension
of the Lambertian formulation by higher-order terms
with utilizing the Tikhonov regularization for behav-
ing the second-order and zero-order terms (HO-Poly).
We illustrate (Fig. 2a), that the corresponding basis
functions show partial non-orthogonal behavior and
hence possibly result in ambiguities. We evaluate
this behavior and solve the problem by evaluating the
more common spherical harmonics second approach
with our proposed Tikhonov regularization extension
(HO-SH). The spherical harmonics model is consist-
ing of orthogonal basis functions (see Fig. 2b), while
HO-Poly has the benefit of boasting one more degree
of freedom.
4.1 Higher-order Polynomial
We are expressing the regularized higher-order poly-
nomial HO-Poly in Cartesian coordinates. The terms
of the HO-Poly are expressed as P ∈ R
n×10
, which
we limit to the reconstruction of up to second-order
elements. We define our light vector L by it’s compo-
nents {X,Y , Z} ∈ R
n×3
as follows:
L = [X ,Y , Z], with (2)
X = [x
1
, ..., x
n
],
Y = [y
1
, ..., y
n
], and
Z = [z
1
, ..., z
n
].
We utilize the light vector components to formu-
late our polynomial as follows:

Albedo
HO-Poly HO-SH Lambertian
Normals
Depth
HO-Poly HO-SH Lambertian
Figure 3: Comparison of the reconstruction using the proposed regularized higher-order methods HO-Poly and HO-SH in
reference to the standard Lambertian model. Both on the PCB board (left) and the coin (right) the systematic surface normal
errors (and as a result errors in the depth reconstruction) in the Lambertian reconstruction are suppressed by the use of higher-
order models.
P = [P
2
, P
1
, P
0
], where (3)
P
2
= [X  X,Y Y , Z  Z, ...
X Y , X  Z,Y  Z],
P
1
= [X,Y , Z],
P
0
= [1],
with 1 defining a one-valued vector of length n and 
denoting the Hadamard product. We formulate an en-
ergy function to solve for our extended M
i, j
∈ R
10
.
min
M
i, j
1
2
||P · M
i, j
− E
i, j
||
2
+ λ||Γ · M
i, j
||
2
(4)
A Tikhonov regularizer Γ ∈ R
7×10
represents an
identity matrix for [P
2
, P
0
] with a linear scaling fac-
tor λ.
We extract the albedo and surface normals us-
ing the first-order components of our light polyno-
mial P
1
. The second-order components of the poly-
nomial are holding non-Lambertian elements, which
we filter out. The length of the vector M
i, j,l
is defined
by the albedo, as per definition all normals are unit
vectors, hence we can extract the albedo and normals
simultaneously:
q
N
2
i, j,x
+ N
2
i, j,y
+ N
2
i, j,z
= 1, (5)
ρ
i, j
=
q
M
2
i, j,l
1
+ M
2
i, j,l
2
+ M
2
i, j,l
3
. (6)
The basis elements of this method (Eq. 3) are illus-
trated in Fig. 2a. We show that the last three second-
order polynomials are not behaving perfectly orthogo-
nal to the first-order components. Therefore, an over-
lap of these terms in the achieved representation is
possible. To overcome these limitations, we propose
the use of spherical harmonic polynomials, which ful-
fill the orthogonality of the basis functions but have
a disadvantage in containing one degree of freedom
less.
4.2 Spherical Harmonic Polynomials
We are expressing our regularized spherical higher-
order harmonics (HO-SH) in Cartesian coordinates as
homogeneous polynomials (Gallier, 2009). For the
photometric stereo estimation, we use bases of the
higher-order spherical harmonic polynomials up to
the second-order with a polynomial P ∈ R
n×9
as fol-
lows:
P
n
= [P
2
, P
1
, P
0
], where (7)
P
2
= [X  X −Z  Z,Y Y − Z  Z, ...
X Y , X  Z,Y  Z],
P
1
= [X,Y , Z], and
P
0
= [1].
Contrary to our polynomial in Eq. 3, spheri-
cal harmonics show orthogonality in the basis func-
tions. This shows in the second-order polynomials or
higher-order polynomial functions. Note that the to-
tal number of polynomial elements is reduced by one
compared to our HO-Poly approach.
We are solving for the extended M
i, j
∈ R
9
contain-
ing the surface normals and albedo using a squared
energy function (properties described in Eq. 5 and
Eq. 6) with a Tikhonov regularization as described in
Eq. 4, albeit with distinct dimensions with Γ ∈ R
7×9
.
The regularizer Γ is representing an identity matrix
for [P
2
, P
0
] with a linear scaling factor λ. The first-

Side Top
Figure 4: Illumination positions of the DiLiGenT dataset,
used for our quantitative evaluation. Of the given 96 total
positions, we chose 10 of the extended central arch (marked
in blue). The positions are shown from a side-view with
connected arches to indicate the scan pattern as well as from
the top view.
order components of our light polynomial P
1
are used
to extract the albedo and surface normals.
5 RESULTS
We analyzed the difference between two regularized
polynomial representations of higher-order photomet-
ric stereo inspection, namely a natural extension of
the Lambertian formulation with higher-order terms
(HO-Poly) and a spherical harmonic polynomial rep-
resentation (HO-SH), which we described in Sec. 4,
quantitatively and qualitatively. We show that regu-
larization in higher-order photometric stereo formu-
lations is essential and evaluate it’s influence using
a Tikhonov regularizer. In our model, we activate
the regularization on the second-order and zero-order
components. The latter represent the ambient compo-
nent, which is needed to deal with effects stemming
from stray light.
Lower order photometric stereo descriptions can
represent diffuse surface reflections. Higher-order es-
timates are necessary for surfaces which show non-
Lambertian behavior. This is the case for most real-
world materials. We showed the difference between
our HO-Poly light source representation and the HO-
SH in Fig. 2a and Fig. 2b. Where the former can re-
sult in ambiguous representations due to a partial non-
orthogonal behavior of the basis but has one more de-
gree of freedom and the latter has orthogonal basis
functions. We investigate this difference and the in-
fluence of the regularization.
5.1 Quantitative Evaluation
We use the DiLiGenT dataset (Shi et al., 2019) to
quantitatively evaluate our regularized higher-order
methods in reference to a Lambertian photometric
stereo model. The quality is measured by the mean
0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8
Regularization Weight
6.5
7
7.5
8
8.5
9
MSE
10
-3
HO-SH
Lambertian
HO-Poly
Figure 5: Influence of the regularization weight λ. Higher-
order photometric stereo polynomials (HO-SH and HO-
Poly) require a regularization to weight the Lambertian in-
fluence. The best result was reached at λ
1
= 0.19 for HO-
Poly, both representations show equal results at λ
2
= 0.5.
We show numerical evaluation at both points λ
1
and λ
2
as
well as for λ
3
= 1 in Tab. 1.
squared error (MSE) between the given ground truth
(GT) surface normals and our results. Note that
surface normals vectors have unit length by defini-
tion, which allows a quite accurate comparison using
the MSE distance. The DiLiGenT non-Lambertian
photometric stereo dataset contains general materials
with various degrees of shine as well as ground truth
surface normals which were acquired using a high
precision laser scanner. It consists of 10 scenes (ball,
cat, pot1, bear, pot2, buddha, goblet, reading, cow and
harvest), each illuminated from 96 directions. These
96 directions are organized into 12 arches (see Fig. 4),
each arch consisting of 8 illumination directions. We
used the first 10 light directions and acquisitions from
the dataset for each scene, since we usually deal with
a limited number of illumination sources in industrial
environments. These 10 light sources cover the whole
central acquisition arch and two points of the neigh-
bouring arch.
Our quantitative evaluation of the influence of the
regularization parameter λ on our higher-order mod-
els is represented in Fig. 5. We show the importance
of the regularization for higher-order models. Nu-
meric results for the chosen regularization parameter
values λ
1
= 0.19, λ
2
= 0.5, λ
3
= 1 are presented in
Tab. 1. A smaller MSE value indicates a result closer
to the GT surface normals.
Over all examples in the dataset, the sufficiently
regularized HO-SH and HO-Poly performed supe-
rior to the traditional Lambertian model. For a reg-
ularization of λ > 0.5 the HO-SH model performs
best. We explain this by the orthogonality of the ba-
sis functions. While ambiguous results can occur us-
ing the HO-Poly functions, HO-SH allows for a non-
ambiguous solution. Though, for a lower regulariza-
tion of 0.05 < λ < 0.5 the best result is achieved by
the HO-Poly model. This model has one additional
degree of freedom which allows for a superior re-

Table 1: Quantitative evaluation of the proposed algorithms using the DiLiGenT dataset. For both proposed regularized
methods as well as the standard Lambertian reconstruction we evaluate the MSE to the ground truth surface normals.
MSE ball cat pot1 bear pot2 buddha goblet reading cow harvest mean
λ
1
Lambertian 0.0192 0.0201 0.0280 0.0321 0.0627 0.0495 0.0889 0.1046 0.1385 0.1838 0.0727
HO-SH 0.0128 0.0255 0.0284 0.0257 0.0601 0.0527 0.1043 0.1127 0.1329 0.1903 0.0745
HO-Poly 0.0122 0.0197 0.0231 0.0226 0.0558 0.0438 0.0856 0.0943 0.1243 0.1724 0.0654
λ
2
Lambertian 0.0192 0.0201 0.0280 0.0321 0.0627 0.0495 0.0889 0.1046 0.1385 0.1838 0.0727
HO-SH 0.0148 0.0198 0.0264 0.0246 0.0586 0.0475 0.0876 0.1024 0.1296 0.1792 0.0690
HO-Poly 0.0165 0.0191 0.0259 0.0269 0.0593 0.0465 0.0852 0.0999 0.1321 0.1790 0.0690
λ
3
Lambertian 0.0192 0.0201 0.0280 0.0321 0.0627 0.0495 0.0889 0.1046 0.1385 0.1838 0.0727
HO-SH 0.0174 0.0196 0.0272 0.0287 0.0607 0.0484 0.0874 0.1031 0.1344 0.1811 0.0708
HO-Poly 0.0184 0.0197 0.0274 0.0304 0.0616 0.0486 0.0876 0.1031 0.1365 0.1822 0.0715
sult in a low-regularized setting. Regularizing too
low however, when dealing with higher-order pho-
tometric stereo methods, results in a reconstruction
performance far below the one achieved by a simple
Lambertian model. By this we can clearly show the
importance of regularization for higher-order models.
The function of the regularization is to enforce the
higher-order and zero-order components to contain
lower values.
5.2 Qualitative Evaluation
Using a light dome with n = 32 known illumination
sources (as illustrated in Fig. 6), we extracted the
surface normals and albedos using the HO-Poly and
HO-SH models. We compare the results obtained for
these models to estimates stemming from the standard
Lambertian formulation of Eq. 1. Reconstructions
using the regularized higher-order polynomial (HO-
Poly), the regularized higher-order spherical harmon-
ics (HO-SH) and the Lambertian model are shown in
Fig. 3. It is visible that the Lambertian reconstruction
both on the PCB and the coin shows strong systematic
offsets. This deviation can be observed in the surface
normals and demonstrates its effects in the resulting
depth map, achieved by the method of Nehab (Ne-
hab et al., 2005). Considering the varying albedo, a
more stable result can be subjectively observed us-
ing higher-order spherical harmonics compared to the
other two methods. The surface normal reconstruc-
tion both as achieved by the HO-Poly and the HO-
SH approach show similar behaviors when regular-
ized sufficiently (λ = 0.7 was used for our example).
6 SUMMARY AND
CONCLUSIONS
We proposed and compared two regularized higher-
order photometric stereo approaches to reconstruct
the varying albedo and surface normals from an ob-
ject. Utilizing higher-order terms allows superior re-
sults when regularized sufficiently. We demonstrate
this on two formulations, where one is a well-known
compact model which boasts orthogonality of the ba-
sis functions (HO-SH) and the other one has an addi-
tional degree of freedom (HO-Poly). We demonstrate
why regularization is essential in higher-order mod-
els and show an evaluation of both proposed regular-
ized formulations in reference to a Lambertian model
qualitatively and quantitatively.
Our regularization of choice is achieved by
Tikhonov’s method. Since this fits well in a least-
squares formulation, we can solve it very fast and ef-
ficiently, which is essential for industrial applications.
In the presence of shadows our formulation has addi-
tional benefits compared to an L1-formulation (such
as presented by (Zhang and Drew, 2015)), since they
behave non-sparse. In areas with sparse outliers such
as spikes produced by glass or highly reflective sur-
faces, our approach might show numerical disadvan-
tages compared to an L1 regularization.
We tested all methods on non-Lambertian real
world data, acquired with a light dome with 32 illumi-
nation sources. Our experiments demonstrate that our
regularized methods can significantly improve the re-
construction of the albedo, surface normals and depth
compared to a Lambertian model, provided that suffi-
cient regularization is used. We demonstrate that non-
regularized higher-order models are not well-behaved
and show high error rates. Additionally we show that
while normals can be more accurately reconstructed
using orthogonal basis functions and proper regular-
ization (HO-SH), using our polynomial formulation
with an additional degree of freedom (HO-Poly) with
lower regularization shows the best numeric accuracy.
We prove this by evaluating the approaches on the
DiLiGenT dataset, which contains GT surface normal
data. With our regularized HO-SH approach we can
approximate a wide variety of surface reflectance be-

Light dome
Side Top
Figure 6: Illustration of our photometric light dome acquisition setup used in our real world qualitative experiments, with
32 illumination sources. The side view shows the connected light source positions to indicate the scan pattern, the top view
marks single light source locations.
haviors.
Achieving highly accurate results on non-
Lambertian surfaces is essential for industrial appli-
cations. Stable approaches allow highly accurate re-
sults in the field of detection and analysis of surface
defects, material analysis as well as the inspection of
security features and high precision prints.
In future projects we will consider extending regu-
larized higher-order methods further beyond second-
order models. Such an extension might lead to ad-
ditional advantages for specific materials which are
hard to fit using second-order models.
REFERENCES
Antensteiner, D. and
ˇ
Stolc, S. (2017). Full brdf reconstruc-
tion using cnns from partial photometric stereo-light
field data. In The IEEE Conference on Computer Vi-
sion and Pattern Recognition (CVPR) Workshops.
Antensteiner, D.,
ˇ
Stolc, S., and Pock, T. (2018). A review
of depth and normal fusion algorithms. Sensors.
Basri, R., Jacobs, D., and Kemelmacher, I. (2007). Photo-
metric stereo with general, unknown lighting. Inter-
national Journal of Computer Vision, 72:239–257.
Gallier, J. (2009). Notes on spherical harmonics and linear
representations of lie groups.
Haindl, M. and Filip, J. (2013). Visual Texture: Accu-
rate Material Appearance Measurement, Representa-
tion and Modeling. Advances in Computer Vision and
Pattern Recognition. Springer London.
Kemelmacher-Shlizerman, I. and Basri, R. (2011). 3d face
reconstruction from a single image using a single ref-
erence face shape. IEEE Transactions on Pattern
Analysis and Machine Intelligence, 33(2):394–405.
MacRobert, T. (1948). Spherical Harmonics: An Elemen-
tary Treatise on Harmonic Functions, with Applica-
tions. Dover Publ.
Mallick, S. P., Zickler, T. E., Kriegman, D. J., and Bel-
humeur, P. N. (2005). Beyond lambert: Reconstruct-
ing specular surfaces using color. 2005 IEEE Com-
puter Society Conference on Computer Vision and
Pattern Recognition (CVPR’05), 2:619–626 vol. 2.
Malzbender, T., Gelb, D., and Wolters, H. (2001). Polyno-
mial texture maps. In Proceedings of the 28th An-
nual Conference on Computer Graphics and Inter-
active Techniques, SIGGRAPH ’01, pages 519–528,
New York, NY, USA. ACM.
Nehab, D., Rusinkiewicz, S., Davis, J., and Ramamoorthi,
R. (2005). Efficiently combining positions and nor-
mals for precise 3d geometry. ACM Trans. Graph.,
24(3):536–543.
Ramamoorthi, R. and Hanrahan, P. (2001). On the rela-
tionship between radiance and irradiance: Determin-
ing the illumination from images of a convex lamber-
tian object. Journal of the Optical Society of America.
A, Optics, image science, and vision, 18:2448–59.
Shashua, A. (1997). On photometric issues in 3d visual
recognition from a single 2d image. International
Journal of Computer Vision, 21(1):99–122.
Shi, B., Mo, Z., Wu, Z. H., Duan, D., Yeung, S.-K., and Tan,
P. (2019). A benchmark dataset and evaluation for
non-lambertian and uncalibrated photometric stereo.
IEEE Transactions on Pattern Analysis and Machine
Intelligence, 41:271–284.
Tikhonov, A. N. (1943). On the stability of inverse problem.
Doklady Akademii Nauk SSSRe, 39:195–198.
Woodham, R. J. (1980). Photometric Method For Determin-
ing Surface Orientation From Multiple Images. Opti-
cal Engineering, 19(1):139 – 144.
Zernike, v. F. (1934). Beugungstheorie des Schneidenver-
fahrens und seiner Verbesserten Form, der Phasenkon-
trastmethode. Physica, 1:689–704.
Zhang, M. and Drew, M. S. (2015). Robust surface normal
estimation via greedy sparse regression. EURASIP
Journal on Image and Video Processing, 2015(1):42.