
A Hierarchical Loss for Semantic Segmentation
Bruce R. Muller
a
and William A. P. Smith
b
Department of Computer Science, University of York, York, U.K.
Keywords:
Semantic Segmentation, Class Hierarchies, Scene Understanding.
Abstract:
We exploit knowledge of class hierarchies to aid the training of semantic segmentation convolutional neural
networks. We do not modify the architecture of the network itself, but rather propose to compute a loss that is
a summation of classification losses at different levels of class abstraction. This allows the network to differen-
tiate serious errors (the wrong superclass) from minor errors (correct superclass but incorrect finescale class)
and to learn visual features that are shared between classes that belong to the same superclass. The method
is straightforward to implement (we provide a PyTorch implementation that can be used with any existing
semantic segmentation network) and we show that it yields performance improvements (faster convergence,
better mean Intersection over Union) relative to training with a flat class hierarchy and the same network
architecture. We provide results for the Helen facial and Mapillary Vistas road-scene segmentation datasets.
1 INTRODUCTION
The visual world is full of structure, from relation-
ships between objects to scenes and objects composed
of hierarchical parts. For example, at the most ab-
stract level, a road scene could be segmented into
three parts: ground plane, objects on the ground plane
and the sky. The next finer level of abstraction might
differentiate the ground plane into road and pavement,
then the road into lanes, white lines and so on. Hu-
man perception exploits this structure in order to rea-
son abstractly without having to cope with the deluge
of information when all features and parts are consid-
ered simultaneously. Moreover, it is quite easy for a
human to describe this structure in a consistent way
and to reflect it in annotations or labels. It is therefore
surprising that the vast majority of work on learning-
based object recognition, object detection, semantic
segmentation and many other tasks completely ig-
nores this structure. Classification tasks are usually
solved with a flat class hierarchy, but in this paper
we seek to utilise this structure. Another motivation
is that there is often inhomogeneity between datasets
in terms of labelling. For example, the LFW parts
label database (Kae et al., 2013) segments face im-
ages into background, hair and skin, while the seg-
ment annotations (Smith et al., 2013) for the Helen
dataset (Le et al., 2012) define 11 segments. Util-
a
https://orcid.org/0000-0003-3682-9032
b
https://orcid.org/0000-0002-6047-0413
ising both datasets to train a single network, while
retaining the richness of the labels in the latter one,
is not straightforward. Depending on the applica-
tion, we may also wish to be able to vary the gran-
ularity of labels provided by the same network.
In this paper, we tackle the problem of semantic
segmentation and introduce the idea of hierarchical
classification loss functions. The idea is very sim-
ple. Any existing semantic segmentation architecture
that outputs one logit per class per pixel (and which
would conventionally be trained using a single classi-
fication loss such as cross entropy) can compute a sum
of losses at each level of abstraction within the class
hierarchy. The benefit is to differentiate serious errors
from less serious. In the toy example shown in Fig. 1,
a face/hair error would be penalised less severely than
a background/face error since both face and hair be-
long to the superclass head and so L
1
would not pe-
nalise the error. This encourages the network to learn
visual features that are shared between classes be-
longing to the same superclass, i.e. the knowledge
conveyed by the class hierarchy allows the network to
exploit regularity in appearance. Since coarser classi-
fication into fewer abstract classes is presumably sim-
pler than finescale classification, it also means that the
learning process can naturally proceed in a coarse to
fine manner, learning the more abstract classes earlier.
The approach is very simple to implement, requiring
only a few lines of code to compute the hierarchical
losses once the tree has been constructed.
260
Muller, B. and Smith, W.
A Hierarchical Loss for Semantic Segmentation.
DOI: 10.5220/0008946002600267
In Proceedings of the 15th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2020) - Volume 4: VISAPP, pages
260-267
ISBN: 978-989-758-402-2; ISSN: 2184-4321
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Any semantic
segmentation architecture
Σ
L
1
L
2
head
background
face
hair
0.3
0.4
0.3
0.7
L
1
L
2
Total loss = L
1
+L
2
Class hierarchy
Hierarchical Loss Layer
p(c)
p(c
1
)
Figure 1: Overview of our idea. Given the output of any semantic segmentation architecture and a class hierarchy, we compute
losses for each level of abstraction within the hierarchy, inferring probabilities of superclasses from their children.
2 RELATED WORK
Semantic Segmentation. The state-of-the-art in se-
mantic segmentation has advanced rapidly in the last
5 years thanks to end-to-end learning with fully con-
volutional networks (Long et al., 2015). The field is
large, so we provide only a brief summary here. A
landmark paper was SegNet (Badrinarayanan et al.,
2017) which utilised an encoder-decoder architec-
ture with skip connections with a novel unpooling
operation for upsampling. Wu et al. (Wu et al.,
2019) recently explored extensions of this architec-
ture. G
¨
uc¸l
¨
u et al. (G
¨
uc¸l
¨
u et al., 2017) perform fa-
cial semantic segmentation by augmenting a convo-
lutional neural network (CNN) with conditional ran-
dom fields and an adversarial loss. Ning et al. (Ning
et al., 2018) achieve very fast performance using hier-
archical dilation units and feature refinement. Cur-
rent state-of-the-art facial segmentation is achieved
by Lin et al. (Lin et al., 2019) using a spatial fo-
cusing transform and a Mask R-CNN/Resnet-18-FPN
region-of-interest network for segmenting facial sub-
components into a whole. Rota Bul
`
o et al. (Rota Bul
`
o
et al., 2018) achieve state-of-the-art road scene se-
mantic segmentation performance. They combine a
DeepLabv3 head with a wideResNExt body and pro-
pose a special form of activated batch normalisation
which saves memory and allowing for a larger net-
work throughput. Zhao et al. (Zhao et al., 2017)
proposed Pyramid Scene Parsing Network (PSPNet)
which utilises a new architecture module to capture
contextual information. Chen et al. (Chen et al., 2018)
extend DeepLabv3 by adding a decoder module based
on atrous separable convolution. None of these meth-
ods exploit scene structure provided by class hierar-
chies.
Hierarchical Methods. Existing hierarchy-based
methods have focused on hierarchical architectures,
i.e. methods that specifically adapt the architecture of
the network to the specific hierarchy for a particular
task. This is typified by Branch-CNN (Zhu and Bain,
2017) and Hierarchical Deep CNN (Yan et al., 2015)
in which a network architecture is constructed to re-
flect the classification hierarchy. Luo et al. (Luo et al.,
2012) use face and component detections to constrain
face segmentation.
Deng et al. (Deng et al., 2014) encode class rela-
tionships in a Hierarchy and Exclusion (HEX) graph.
This enables them to reason probabilistically about la-
bel relations using a CRF. While very powerful, this
also makes inference on their model more expensive
and defining a HEX graph requires richer information
than we use.
Srivastava and Salakhutdinov (Srivastava and
Salakhutdinov, 2013) similarly take a probabilistic
approach and attempt to learn a hierarchy as part of
the training process. This does not necessarily reflect
the semantic class structure but is rather chosen to op-
timise subsequent classification performance. Again,
inference is more complex and expensive.
Meletis et al. (Meletis and Dubbelman, 2018) use
a restricted set of classifiers in a hierarchical fashion
on the output of a standard deep learning architecture
to harness differing levels of semantic description.
3 HIERARCHY DESIGN
Our approach requires a predefined hierarchy, which
we assume is designed based on expert human knowl-
edge. In the case of objects composed of parts, this
is straightforward since the parts can naturally be de-
scribed hierarchically. For more general scenes this
may require specific domain knowledge in order to be
able to group related objects together into the same
A Hierarchical Loss for Semantic Segmentation
261

image
background
foreground
hair
face
eyebrows
right-eyebrow
left-eyebrow
eyes
right-eye
left-eye
skin
nose
face-skin
mouth
lower-lip
inner-mouth
upper-lip
Figure 2: Our hierarchy for the Helen segment classes. Note that the classes in the original dataset (Smith et al., 2013) are the
leaves in our hierarchy.
superclass. We emphasise two points. First, the prac-
tical effort of doing this is extremely low. We do not
require any new annotation of the training images,
there is simply a one off task to design a hierarchy
for the classes already used in the labelling. Second,
many existing datasets were annotated with a hierar-
chical class structure in mind (even if this is rarely
used). For example, the COCO-stuff dataset (Chen
et al., 2018) clusters each of the 172 classes into 11
abstract groups, providing a shallow hierarchy.
For the experiments in this paper we use two
datasets that represent each of the cases above. The
segment annotations (Smith et al., 2013) for the Helen
dataset (Le et al., 2012) are not provided with any hi-
erarchy. However, there is an obvious parts-based par-
titioning such that the classes used in the dataset cor-
respond to the leaves of a hierarchy tree (see Fig. 2).
To emphasise again: we do not need to relabel the
Helen annotations. We simply use the original anno-
tations in conjunction with the hierarchy. The sec-
ond case is the Mapillary Vistas road scene dataset.
This was originally designed with a hierarchical class
structure (see (Neuhold et al., 2017) for details) for
which some superclasses are based on clustering re-
lated objects (for example, the vehicle superclass).
4 HIERARCHICAL LOSS
Our method is based on computing a sum of classi-
fication losses over each level of abstraction within a
classification hierarchy. In order to use the approach,
one simply needs a class hierarchy defined by a tree
and a segmentation architecture that outputs a classi-
fication for each of the classes corresponding to leaf
nodes in the tree. In this section we describe our rep-
resentation and the hierarchical losses.
Tree-based Representation. We represent our
class hierarchy using a tree (V, E), with V =
{v
1
, . . . , v
n
} the set of vertices and E ⊂ V ×V the set
of ordered edges such that (v
i
, v
j
) ∈ E encodes that
v
i
is a parent of v
j
. We assume that the first m nodes
correspond to leaves in the tree, i.e. @ v
j
∈ V, (v
i
, v
j
) ∈
E ⇒ 1 ≤ i ≤ m. These nodes correspond to the finest
scale classes. If (v
i
, v
j
) ∈ E then v
i
is a more gen-
eral, more abstract, superclass of v
j
. The label for a
pixel, c, should be at the finest level of classification,
i.e. c ∈ {1, . . . , m}.
We define depth(v
i
) to mean the number of edges
between vertex v
i
and the root node. Hence, the depth
of the tree is given by D
max
= max
i
depth(v
i
). We
define ancestor(v
i
, v
j
) to be true if v
i
is an ancestor of
v
j
, i.e. that v
i
is a superclass of v
j
and false otherwise.
Inferring Coarse Classes from Fine. We assume
that the segmentation CNN outputs one logit, x
i
, per
pixel per leaf node, i.e. the output of the network is
of size H × W × m. Hence, the probability, p
i
, as-
sociated with node i can be computed by applying the
softmax function, σ : R 7→ [0, 1], to x
i
. The probability
associated with non-leaf nodes is defined recursively
by summing the probabilities of its children until leaf
nodes are reached:
p
i
=
σ(x
i
) if 1 ≤ i ≤ m
∑
(v
i
,v
j
)∈E
p
j
otherwise
(1)
Note that any summation is over a subset of leaf-
nodes whose total sum is one so any p
i
is ≤ 1.
Depth Dependent Losses. The appropriate label
varies depending on the level of abstraction, i.e. the
depth considered in the tree. We define the correct
class at a depth d ∈ {0, . . . , D
max
} to be:
c
d
=
(
c if depth(v
c
) ≤ d
i, depth(v
i
) = d ∧ anc(v
i
, v
c
) otherwise
(2)
where anc(v
i
, v
c
) denotes the ancestor of nodes v
i
and
v
c
. The classification loss at depth d is computed us-
ing the negative log loss as L
d
= −log(p
c
d
). Note that
L
0
= 0. The total hierarchical loss is then a summa-
tion over all depths in the tree: L =
∑
D
max
d=0
L
d
.
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
262

background
foreground
hair
face
mouth
upper_lip
inner_mouth
lower_lip
skin
face_skin
nose
eyes
left_eye
right_eye
eyebrows
left_eyebrow
right_eyebrow
precomputed_hierarchy_list = [
[ [background],[hair],[upper_lip],[inner_mouth],[lower_lip],[face_skin],
[nose],[left_eye],[right_eye],[left_eyebrow],[right_eyebrow] ],
[ [background],[hair],[upper_lip],[inner_mouth],[lower_lip],
[face_skin,nose],[left_eye,right_eye],[left_eyebrow,right_eyebrow] ],
[ [background],[hair],[upper_lip,inner_mouth,lower_lip,face_skin,nose,
left_eye,right_eye,left_eyebrow,right_eyebrow] ],
[ [background],[hair,upper_lip,inner_mouth,lower_lip,face_skin,nose,
left_eye,right_eye,left_eyebrow,right_eyebrow] ] ]
Figure 3: Class hierarchy implementation example for the hierarchy in Fig. 2. In our implementation the classification
hierarchy is provided as a text file (left). From this, we precompute lists of leaf nodes (right) for each abstraction depth
corresponding to the summations required for computing internal node probabilities (e.g. Fig. 1 bottom-left: hair and face
class probabilities infer a value of 0.7 for the abstract class head). The four sub-lists in precomputed hierarchy list
correspond to the four abstraction depths for the hierarchy depicted in Fig. 2.
5 IMPLEMENTATION
In this section we describe implementation details for
our hierarchical loss function. Our implementation is
written using standard PyTorch layers and we make it
publicly available
1
in a form that is easy to integrate
with any existing semantic segmentation architecture.
We also explain how to ensure numerical stability in
the computation of these losses.
Tree Structure. The hierarchical class structure is
provided as a text file using indentation to signify par-
ent/child relationships. For example the Helen hierar-
chy we use in Fig. 2 is written as a text file as shown in
Fig. 3 (left). Loading the text file, we internally store
the tree as a structure of linked python objects called
nodes. Each leaf-node in the hierarchy represents a
class in our dataset and encapsulates an integer rep-
resenting the channel it will use in the output of the
neural network. Additionally we ensure to keep con-
sistent the integer numbering between class labels in
the training data and python hierarchical leaf-nodes.
To implement our hierarchical loss, we precom-
pute lists representing the set of leaf node classes
that belong to each superclass (see Fig. 3 (right)
for an example on the Helen dataset). We may
think of the hierarchy in terms of various levels of
abstraction. For example, the hierarchy in Fig. 1
has two abstraction levels: the base level where
we take all leaf-nodes, and the level up where we
have background and head (which is inferred from
1
github.com/brucemuller/HierarchicalLosses
hair and face). In that case we could precom-
pute the lists [ [background], [hair], [face]]
and [[background], [hair, face]] for the base
and more abstract level respectively. For our Helen
dataset we have four levels of abstraction as shown
by the hierarchy in Figures 2 and 3.
It is important to note that every leaf class will
contribute to the same number of losses regardless of
the hierarchical depth, and we are not assigning dif-
ferent weights to different classes based on how deep
they are in the class hierarchy.
To illustrate the simplicity and generalisability of
our idea, we have included the code snippet in Listing
1. Note that for clarity, we ignore the numerical sta-
bility issues (discussed below) in this snippet. Here
we illustrate exactly how the output of any neural net-
work semantic segmentation classification layer can
be processed to compute hierarchical loss from an
easily designed semantic hierarchy. The output from
the CNN is deep copied for each depth in the tree to
compute the separate level losses.
Each level loss list represents the branches with
which we need to sum probabilities. We use the level
loss list for a particular abstraction level to extract the
softmaxed CNN output channels to be summed over
(lines 7 to 12 of Listing 1). Every summed slice of
a branch is inserted into each channel associated with
that branch for ease of implementation (lines 19 and
20 of Listing 1). While this step duplicates probabil-
ity slices in summed probabilities for a particular
abstraction level, it allows us to easily pass into any
PyTorch loss. Finally to compute the loss for each ab-
A Hierarchical Loss for Semantic Segmentation
263
1 p r o b a b i l i t i e s = s o f t m a x ( c n n o u t p u t , dim = 1 ) ; l o s s = 0
2
3 f o r l e v e l l o s s l i s t i n p r e c o m p u t e d h i e r a r c h y l i s t
4
5 p r o b a b i l i t i e s t o s u m = p r o b a b i l i t i e s . c l o n e ( )
6 s u m m e d p r o b a b i l i t i e s = p r o b a b i l i t i e s t o s u m
7 f o r b r a nc h i n l e v e l l o s s l i s t :
8
9 # E x t r a c t t h e r e l e v a n t p r o b a b i l i t i e s a c c o r d i n g t o a b ra nc h i n o ur h i e r a r c h y .
10 b r a n c h p r o b s = t o r c h . F l o a t T e n s o r ( )
11 f o r c h a nn e l i n b r a n ch :
12 b r a n c h p r o b s = t o r c h . c a t ( ( b r a n c h p ro b s , p r o b a b i l i t i e s t o s u m [ : , c h a n n e l , : , : ] . u ns qu ee ze ( 1 ) ) , 1 )
13
14 # Sum t h e s e p r o b a b i l i t i e s i n t o a s i n g l e s l i c e ; t h i s i s h i e r a r c h i c a l i n f e r e n c e .
15 s u m m e d t r e e b r a n c h s l i c e = b r a n c h p r o b s . sum (1 , k e epdim =Tr ue )
16
17 # I n s e r t i n f e r r e d p r o b a b i l i t y s l i c e i n t o ea c h c h a n n e l o f s u m m e d p r o b a b i l i t i e s g iv e n by b ra n c h .
18 # T hi s d u p l i c a t e s p r o b a b i l i t i e s f o r e a s y p a s s i n g t o s t a n d a r d l o s s f u n c t i o n s su ch a s n l l l o s s .
19 f o r c h a nn e l i n b r a n ch :
20 s u m m e d p r o b a b i l i t i e s [ : , c h an n e l : ( c h a nn e l +1) , : , : ] = s u m m e d t r e e b r a n c h s l i c e
21
22 l e v e l l o s s = n l l l o s s ( l o g ( s u m m e d p r o b a b i l i t i e s ) , t a r g e t )
23 l o s s = l o s s + l e v e l l o s s
24 r e t u r n ( l o s s )
Listing 1: PyTorch snippet for computing the inferred probabilities at the abstraction levels in our hierarchy. The hierarchy
of classes is represented by level loss list, which is a list of lists composed of integers representing our branching
classes.
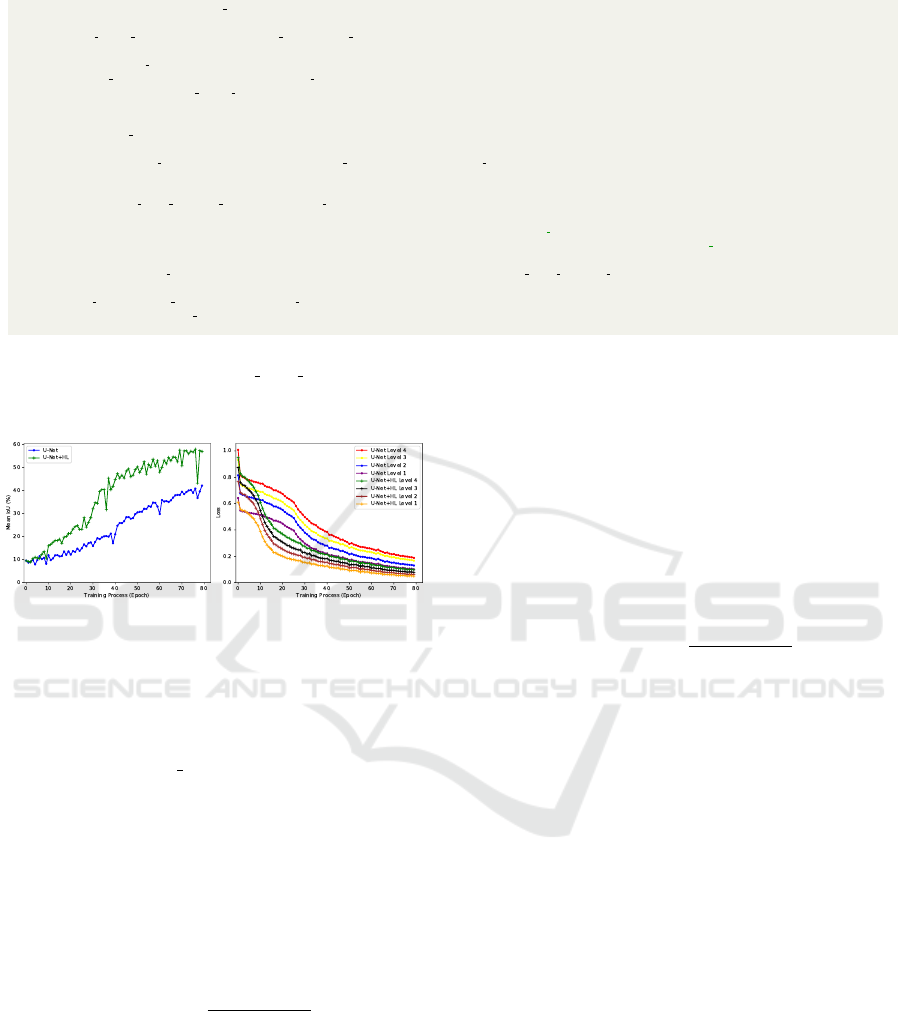
Figure 4: Training behaviour versus epoch on the Helen
dataset. Left: Mean IOU. In both cases we show results
trained with vanilla (U-Net) and hierarchical (U-Net+HL)
losses. Right: Classification loss for each depth D = 1..4.
straction level, we take the log of the summed proba-
bility tensor, which is passed to the negative log like-
lihood loss layer (nll loss) along with labels.
Numerical Stability. Evaluating cross entropy
(log) loss of a probability computed using softmax
is numerically unstable and can easily lead to over-
flow or underflow. In most implementations, this is
circumvented using the “log-sum-exp trick” (Murphy,
2006) derived from the identity exp(x) = exp(x − b +
b) = exp(x − b) exp(b):
L = − log p
i
= − log
exp(x
i
)
∑
n
j=1
exp(x
j
)
!
=
− x
i
+ b + log
n
∑
j=1
exp(x
j
− b), (3)
where b = max
i∈{1,...,n}
x
i
is chosen so that the maxi-
mum exponential has value one and thus avoids over-
flow, while at least one summand will avoid under-
flow and hence avoid taking a logarithm of zero.
Our hierarchical classification losses involve com-
puting log losses on internal nodes in the class hierar-
chy tree. The probabilities in these nodes are in turn
formed by summing probabilities computed by apply-
ing softmax to CNN outputs. This leads to evaluation
of losses of the form −log(
∑
i∈C
p
i
) where C is the set
of leaf nodes contributing to the superclass. This can
be made numerically stable by double application of
the log-sum-exp trick:
L = − log
∑
i∈C
p
i
= − log
∑
i∈C
exp(x
i
)
∑
n
j=1
exp(x
j
)
=
b + log
n
∑
j=1
exp(x
j
− b) − b
C
− log
∑
i∈C
exp(x
i
− b
C
).
(4)
b is defined as before while b
C
= max
i∈C
x
i
. The use
of two different shifts for the two logarithm terms is
required to avoid underflow when b
C
b.
6 EXPERIMENTS
We seek to investigate the relative performance gain
in using the hierarchical loss versus training simply
on a flat hierarchy. To this end, in our experiments we
train two networks for each task. One is a “vanilla”
U-net (Ronneberger et al., 2015), the other is exactly
the same U-net architecture but trained with hierarchi-
cal loss (referred to as U-net+HL). We train U-Net/U-
Net+HL models simultaneously such that they receive
identical data input at each iteration. Note that we
do not seek nor achieve state-of-the-art performance.
A more complex architecture, problem-specific tun-
ing and so on would lead to improved performance
but our goal here is to assess relative performance
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
264
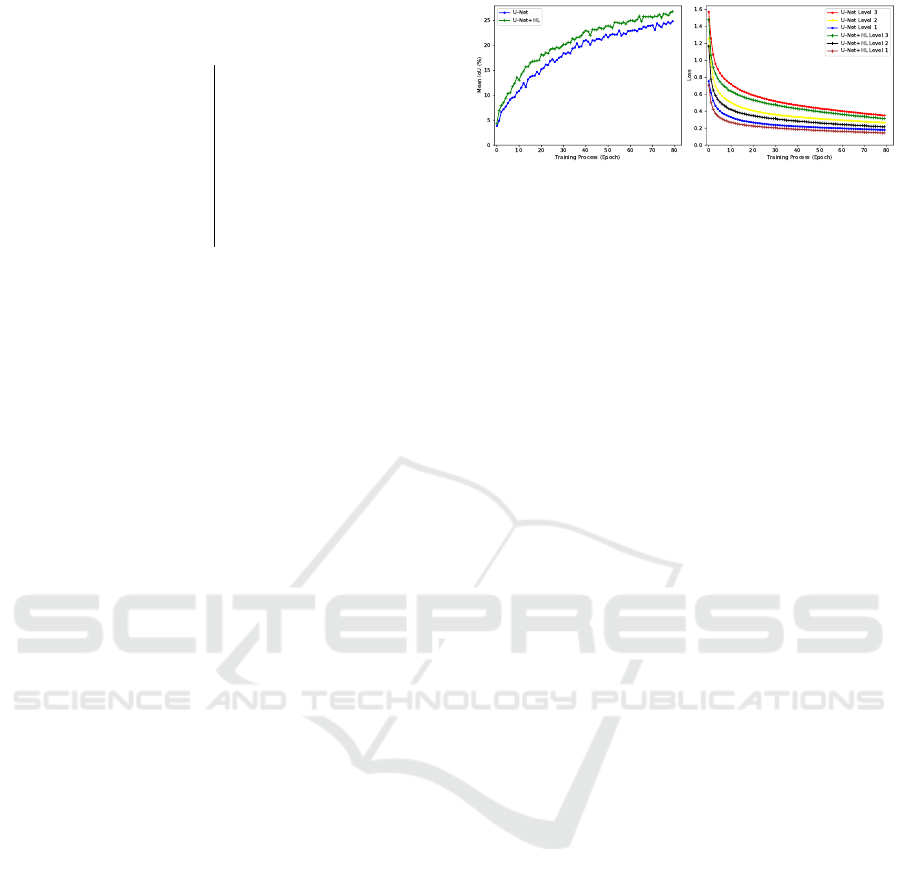
Table 1: Mean and class IOU (%) on Helen and Vistas (sub-
set selected) datasets at training convergence.
Helen Dataset Vistas Dataset
Class U-Net U-Net+HL Class U-Net U-Net+HL
Background 92.04 92.653 Car 80.35 80.91
Face skin 86.53 87.04 Terrain 54.21 56.07
Left eyebrow 63.12 62.68 Lane Marking 49.14 51.69
Right eyebrow 63.65 64.25 Building 77.31 79.67
Left eye 63.98 67.81 Road 82.31 82.69
Right eye 64.92 72.72 Trash Can 5.38 18.63
Nose 84.05 82.55 Manhole 2.25 16.96
Upper lip 52.88 56.48 Catch Basin 1.58 13.59
Inner mouth 62.17 67.94 Snow 56.97 71.46
Lower lip 65.64 67.92 Person 39.23 48.3
Hair 65.41 66.11 Water 29.87 16.1
Mean 69.49 71.65 Mean 24.74 26.51
gain using a simple baseline architecture. Networks
use Kaiming uniform initialisation with the same ran-
dom seed (to equally initialise vanilla and hierarchi-
cally trained networks). Pre-training is not utilised.
We use Stochastic Gradient Decent with a learning
rate of 0.01 and a batch size of 5 (due to memory
constraints). During training, images/labels were ran-
domly square-cropped using the shortest dimension
and re-sized to 256
2
. The only further augmentation
used was random flipping (p = 0.5).
Datasets. For experimenting with hierarchical
losses on segmentation we chose two very different
datasets: the Helen (Le et al., 2012) facial dataset and
Mapillary’s Vistas (Neuhold et al., 2017) road scene
dataset. The Helen dataset covers a wide variety
of facial types (age, ethnicity, colour/grayscale,
expression, facial pose), originally built for facial
feature localisation (Le et al., 2012). We use an
augmented Helen (Smith et al., 2013) dataset with
semantic segmentation labels. Helen contains
2000, 230 and 100 images/annotations for training,
validation and testing respectively, for 11 classes
(10 facial and background, see Tab. 1(left)). It
should be noted that the ground truth annotations are
occasionally inaccurate, particularly for hair which
makes it challenging to learn. The road scene Vistas
dataset (Neuhold et al., 2017) is composed of 25000
images/annotations (18000 training, 2000 validation,
5000 testing), with 66 classes. As Vistas contains too
many classes to easily illustrate we have chosen only
a representative subset in Tab. 1 (right) which show
most significant difference in performance and given
the mean over all classes. Further, our intention is
to indicate the performance improvement by using
hierarchical learning, rather than to compare between
datasets. The Vistas hierarchy is three levels deep,
contains 66 leaf nodes, and 11 internal nodes.
Results. Fig. 4 (right) shows losses for each ab-
straction depth of the class hierarchy for the He-
len experiment. Note that the deeper loss is always
Figure 5: Training behaviour on Vistas. Left: mean IOU
versus epoch. Right: classification loss for each abstraction
depth D = 1..3 versus epoch. We show results trained with
vanilla (U-Net) and hierarchical (U-Net+HL) loss.
larger than a shallower one, suggesting that our hier-
archically trained method significantly benefits from
the hierarchical structure in the class labels, partic-
ularly in the early phase of training, learning much
faster than the vanilla model. Fig. 4 (left) illus-
trates the mean Intersection over Union (IOU) during
training. Performance gain is most significant post
epoch 35 and can be observed in the qualitative re-
sults from Fig. 6. At performance convergence we
observe some qualitative differences between the hi-
erarchically trained network and the vanilla. For ex-
ample, in Fig. 6 U-net+HL predictions at epoch 200
have somewhat less hair artefacts, while the 1st exam-
ple shows improvement over a difficult angled facial
pose. Epoch 50 results clearly show faster conver-
gence.
For Vistas, the IOU performance gain is less no-
table than on Helen, but we show the hierarchi-
cally trained model outperforming the vanilla model
in both level losses and mean IOU (Fig. 5 and
Tab. 1(right)). The qualitative results in Fig. 7 illus-
trate predictions for both methods at epoch 1 and 80.
Most interestingly, after 1 epoch the hierarchically
trained model is able to classify correctly a signifi-
cant proportion of lane-markings whereas the vanilla
trained model cannot, showing how quickly our hi-
erarchical model is learning. Relative to the vanilla
model, our hierarchically trained model achieves a
3% and 7% relative improvement for Helen and Vis-
tas respectively (see Tab. 1).
7 CONCLUSIONS
Our results illustrate the great potential of using losses
that encourage semantically similar classes within a
hierarchy to be classified close together, where the
model parameters are guided towards a solution not
only better quantitatively, but faster in training than
using a standard loss implementation. We speculate
that the hierarchically trained models perform better
due to learning more robust features from visually
A Hierarchical Loss for Semantic Segmentation
265

Input Ground Truth 30 Epochs 50 Epochs 200 Epochs
U-net U-net+HL U-net U-net+HL U-net U-net+HL
Figure 6: Prediction comparisons on the Helen dataset. From left to right: raw input image, ground truth annotation, vanilla
trained U-Net prediction at 30 epochs, hierarchically trained U-Net prediction at 30 epochs , vanilla trained U-Net prediction at
50 epochs, hierarchically trained U-Net prediction at 50 epochs, vanilla trained U-Net prediction at 200 epochs, hierarchically
trained U-Net prediction at 200 epochs.
similar classes which are close within the tree struc-
ture. The hierarchy is providing the network with
more information (e.g. a pixel belongs to an eye-brow,
which belongs to a face and so on), which can be
exploited to learn shared and more robust features.
There is a possible link to metric learning here where,
rather than positive and negative class labels, we are
provided with classes that can be more or less simi-
lar within a hierarchy. A particular advantage of this
work is its generality and self-contained nature allows
the possibility of plugging this hierarchical loss on the
end of any deep learning architecture. Taking advan-
tage of the hierarchical cues readily apparent to us can
help train a deep network faster and with greater ac-
curacy. Moreover any hierarchical structure can be
provided to help train your model. We also contribute
a numerically stable formulation for computing log
and softmax of a network output separately, a neces-
sity for summing probabilities according to a hierar-
chical structure. Future work could include learning
the hierarchy itself which best solves your task. Addi-
tionally we would like to use our ideas to construct a
level of abstraction segmenter for tree based labels on
hierarchically trained models. Ability to extract seg-
mentations at multiple levels in a hierarchy describing
your data is quite useful, intuitive and is not some-
thing commonly achieved by semantic segmentation
solvers in the current community.
REFERENCES
Badrinarayanan, V., Kendall, A., and Cipolla, R. (2017).
Segnet: A deep convolutional encoder-decoder archi-
tecture for image segmentation. IEEE TPAMI.
Chen, L.-C., Zhu, Y., Papandreou, G., Schroff, F., and
Adam, H. (2018). Encoder-decoder with atrous sep-
arable convolution for semantic image segmentation.
In Proc. ECCV, pages 801–818.
Deng, J., Ding, N., Jia, Y., Frome, A., Murphy, K., Bengio,
S., Li, Y., Neven, H., and Adam, H. (2014). Large-
scale object classification using label relation graphs.
In Proc. ECCV, pages 48–64.
G
¨
uc¸l
¨
u, U., G
¨
uc¸l
¨
ut
¨
urk, Y., Madadi, M., Escalera, S., Bar
´
o,
X., Gonz
´
alez, J., van Lier, R., and van Gerven,
M. A. (2017). End-to-end semantic face segmenta-
tion with conditional random fields as convolutional,
recurrent and adversarial networks. arXiv preprint
arXiv:1703.03305.
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
266

Input Ground truth 1 epoch 80 epochs
U-net U-net+HL U-net U-net+HL
Figure 7: Qualitative comparisons on Vistas. From left to right: raw input image, ground truth annotation, vanilla trained
U-Net prediction at 1 epoch, hierarchically trained U-Net prediction at 1 epoch, vanilla trained U-Net prediction at 80 epochs,
hierarchically trained U-Net prediction at 80 epochs.
Kae, A., Sohn, K., Lee, H., and Learned-Miller, E. (2013).
Augmenting crfs with boltzmann machine shape pri-
ors for image labeling. In Proc. CVPR, pages 2019–
2026.
Le, V., Brandt, J., Lin, Z., Bourdev, L., and Huang, T. S.
(2012). Interactive facial feature localization. In Proc.
ECCV, pages 679–692.
Lin, J., Yang, H., Chen, D., Zeng, M., Wen, F., and Yuan, L.
(2019). Face parsing with roi tanh-warping. In Proc.
CVPR, pages 5654–5663.
Long, J., Shelhamer, E., and Darrell, T. (2015). Fully con-
volutional networks for semantic segmentation. In
Proc. CVPR, pages 3431–3440.
Luo, P., Wang, X., and Tang, X. (2012). Hierarchical
face parsing via deep learning. In Proc. CVPR, pages
2480–2487. IEEE.
Meletis, P. and Dubbelman, G. (2018). Training of convo-
lutional networks on multiple heterogeneous datasets
for street scene semantic segmentation. In IVS (IV).
Murphy, K. P. (2006). Naive bayes classifiers. Technical
Report 18, University of British Columbia.
Neuhold, G., Ollmann, T., Rota Bulo, S., and Kontschieder,
P. (2017). The mapillary vistas dataset for semantic
understanding of street scenes. In Proc. ICCV, pages
4990–4999.
Ning, Q., Zhu, J., and Chen, C. (2018). Very fast seman-
tic image segmentation using hierarchical dilation and
feature refining. Cogn. Comput., 10(1):62–72.
Ronneberger, O., Fischer, P., and Brox, T. (2015). U-net:
Convolutional networks for biomedical image seg-
mentation. In Proc. MICCAI, pages 234–241.
Rota Bul
`
o, S., Porzi, L., and Kontschieder, P. (2018).
In-place activated batchnorm for memory-optimized
training of dnns. In Proc. CVPR, pages 5639–5647.
Smith, B. M., Zhang, L., Brandt, J., Lin, Z., and Yang, J.
(2013). Exemplar-based face parsing. In Proc. CVPR,
pages 3484–3491.
Srivastava, N. and Salakhutdinov, R. R. (2013). Discrimina-
tive transfer learning with tree-based priors. In Proc.
NIPS, pages 2094–2102.
Wu, Z., Shen, C., and Van Den Hengel, A. (2019). Wider or
deeper: Revisiting the resnet model for visual recog-
nition. Pattern Recognition, 90:119–133.
Yan, Z., Zhang, H., Piramuthu, R., Jagadeesh, V., DeCoste,
D., Di, W., and Yu, Y. (2015). Hd-cnn: hierarchical
deep convolutional neural networks for large scale vi-
sual recognition. In Proc. ICCV, pages 2740–2748.
Zhao, H., Shi, J., Qi, X., Wang, X., and Jia, J. (2017). Pyra-
mid scene parsing network. In Proc. CVPR, pages
2881–2890.
Zhu, X. and Bain, M. (2017). B-cnn: Branch convolutional
neural network for hierarchical classification. arXiv
preprint arXiv:1709.09890.
A Hierarchical Loss for Semantic Segmentation
267
