A Real-time Ultrasound Rendering with Model-based Tissue

Deformation for Needle Insertion

Charles Barnouin

, Florence Zara

1 a

and Fabrice Jaillet

2 b

Universit

e de Lyon, CNRS, Universit

e Lyon 1, LIRIS, SAARA Team, UMR5205, F-69622, France

Universit

e de Lyon, IUT Lyon 1, Computer Science Department, F-01000, Bourg-en-Bresse, France

Keywords:

Ultrasound Rendering, 2D Texture, Haptic Devices, Physically based Tissue Deformation, Needle Insertion.

Abstract:

In the course of developing a training simulator for puncture, a novel approach is proposed to render in real-

time the ultrasound (US) image of any 3D model. It is combined with the deformation of the soft tissues (due

to their interactions with a needle and a probe) according to their physical properties. Our solution reproduces

the usual US artifacts at a low cost. It combines the use of textures and ray-tracing with a new way to efﬁciently

render ﬁbrous tissues. Deformations are handled in real-time on the GPU using displacement functions. Our

approach goes beyond the usual bottleneck of real-time deformations of 3D models in interactive US simula-

tion. The display of tissues deformation and the possibilities to tune the 3D morphotypes, tissue properties,

needle shape, or even speciﬁc probe characteristics, is clearly an advantage in such a training environment.

1 INTRODUCTION

Ultrasound (US) is a radiation-free, non-invasive and

real-time imaging medical device. Widely used in

clinical practice, it is a mechanical wave propagating

in ﬂuids and solids generally at 20 kHz. Multiple tis-

sue interactions create the ﬁnal image, such as spec-

ular reﬂection and refraction, absorption and scatter-

ing. Relatively cost-effective, it is relevantly used for

both diagnosis and image-guided interventions (Heer

et al., 2004). Nevertheless, extensive training is re-

quired to acquire and interpret ultrasound images, es-

pecially when paired with the insertion of a needle.

For example, the puncture necessitates spatial rea-

soning, hand-eye and left/right hand coordination, all

skills developed through extensive training.

In the rheumatology domain, a relevant training

simulator for needle insertion has to enable students

to learn how to puncture from multiple points of

view, and to identify tissues which properties may

differ from a patient to another, or when tissues are

inﬂamed. Moreover, the training environment has

to provide interactive and accurate forces feedback

through haptic devices: during puncture, the rheuma-

tologists adapt their gesture to the deformations in-

duced by the probe and needle movements. Thus,

https://orcid.org/0000-0002-0118-7204

https://orcid.org/0000-0002-7330-8116

two challenges emerge to develop such a simulator:

(i) render a realistic enough ultrasound image in any

probe/tissues conﬁguration, embedding all the prop-

erties to clearly identify the biological tissues; (ii)

provide real-time interactions between the soft tissues

and the medical devices through force feedback and

visible deformations on the ultrasound image.

In this paper, we propose a new strategy to address

these two points. We will describe our proposed solu-

tion for ultrasound rendering, haptic forces feedback

and display of tissues deformation on the ultrasound

images. All the components of our solution are linked

and embodied in a coherent framework. At the end,

our approach based on the GPU permits:

• a real-time ultrasound rendering including tissues

ﬁbrosity according to their geometrical properties.

We used an original texture-dependent oriented

blur to enhance realism.

• a visualization of tissues deformation directly on

the ultrasound image. We used some displace-

ment functions accounting for the tissues proper-

ties and the interaction forces between the haptic

devices and the 3D scene.

Our solution has been designed to be easily trans-

ferable to multiple medical cases and areas of interest,

such as the shoulder or ankle joints. It combines tech-

niques from Computer Graphics rendering and Vir-

tual Reality in a complementary way to provide re-

Barnouin, C., Zara, F. and Jaillet, F.

A Real-time Ultrasound Rendering with Model-based Tissue Deformation for Needle Insertion.

DOI: 10.5220/0008947302350246

In Proceedings of the 15th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2020) - Volume 1: GRAPP, pages

235-246

ISBN: 978-989-758-402-2; ISSN: 2184-4321

235

alistic visual and touch sensations at the same time.

Ray-tracing and texture manipulation provide accu-

rate enough tissue rendering for a real-time simulator,

while the collision and haptic algorithms are suitable

for a fast update necessary for a smooth touch feeling.

2 STATE OF THE ART

This section presents previous work on ultrasound

rendering and simulation of needle insertion. Both

are combined to provide realistic tissue deformations

and haptic feedback within an ultrasound view.

Ultrasound Rendering. The techniques to create US

image can be separated in two approaches: interpola-

tion of real images or generation of realistic images.

The ﬁrst approach uses pre-recorded 3D ultra-

sound volume, generally acquired with a 3D probe, or

by combining multiple 2D slices. In some cases, the

3D volume can also be reconstructed from Computed

Tomography (CT scan) or MRI acquisition. Dur-

ing the ultrasound rendering simulation, the volume

is sliced along the plane created with the ultrasound

probe. With this approach, in (Magee and Kessel,

2005), an augmented reality simulator matched a real

CT scan with a mannequin body, whereas the probe

was calibrated to ﬁnd the location and orientation

of the ultrasound plane to slice the volume. Later

on, they improved the image quality with 3D tex-

tures obtained from real images (Magee et al., 2007).

In (Ni et al., 2011), a biopsy simulator was embedding

several ultrasound volumes scanned with a dedicated

probe and stitched together to form a panorama. This

panorama is then resampled to match a previously ac-

quired CT scan of the same volume. Spacial trans-

formations may be applied afterwards, to create res-

piratory motion for example. In (Vidal et al., 2008),

an ultrasound guided needle puncture simulator with

patient speciﬁc CT scan is proposed, which also re-

quires an acquisition phase and remains very patient-

dependent. They added several post-processing ef-

fects like shadows, but did not implement tissue de-

formation. In (Goksel and Salcudean, 2009), they

used 3D ultrasound volumes matched to a 3D elas-

ticity model to perform a fast B-Mode ultrasound im-

age in deformable tissues. While being realistic for

obvious reasons, this class of approach imposes con-

straints on the model, which needs to roughly match

the database and to be created for every considered

joint. Moreover, it requires to create a 3D volume for

each new case, such as speciﬁc location of inﬂamma-

tory tissues or patient speciﬁc geometry or morphol-

ogy (aged or fat inﬂamed shoulders considerably dif-

fer from a healthy and young one). The speciﬁcity of

the probe (ﬁeld of view, frequency, area of effect, etc.)

is also imposed by the acquisition probe.

The second approach to synthetic ultrasound im-

ages consists in simulating the ultrasonic wave prop-

agation in the media, with accurate models of the

probe, tissue scatterers, and interface models. Usu-

ally, generating a single frame is simply too time con-

suming for real-time applications. The older models

may take up to several hours (Bamber and Dickinson,

1980; Jensen, 1991). However, new approaches are

getting closer to real-time, such as (Marion and Vray,

2009), where a linear convolution model and a 3D set

of moving scatterers were used, combined with bet-

ter hardware. Others physical ray-tracing methods us-

ing GPU such as presented in (Mattausch and Goksel,

2016; Burger et al., 2013) are seen as very promising

despite a loss of performance while dealing with tis-

sue deformations. They used a combination of convo-

lution and ray-tracing to create their render. Another

interesting idea was presented in (Law et al., 2011)

to render ultrasound images on deformable meshes,

using two opposite rays for each pixel that needs to

be rendered, one of them going towards the probe.

They register the traversed materials to deduce the

pixel color, and thus are able to create effects like at-

tenuation. However, performances of this approach

are not compatible with the requirements of a training

simulator, especially when the probe is moving con-

tinuously. Finally, the ray-tracing methods don’t take

tissue ﬁber into account: as the number of surfaces

goes higher, it would increase the number of bounces

and thus the calculus time.

To go beyond the limitations of both approaches,

such as the rigidity of 3D data volume for the former

and computation time for the latter, we propose a

novel approach combining the use of textures and

ray-tracing to render ultrasound effects like shadows,

speckle, and ﬁber orientation. Moreover, in the

context of the development of a training medical

simulator, real-time computation, as well as the pos-

sibility to tune the 3D models, the physical properties

of tissues, or the probe characteristics (ﬁeld of view,

attenuation, etc.) are important points to consider.

Needle Insertion Simulation. Modeling techniques

for puncture also face the accuracy vs real-time trade-

off. Soft tissue cutting, due to the needle insertion,

involves three types of force: frictional, elastic, and

actual cutting forces. However, the cutting force is of-

ten modeled as a constant acting at the tip of the nee-

dle, and no actual tissue cutting is performed for per-

formance reasons. In a review on cutting mechanics

and techniques (Takabi and Tai, 2017), the cohesive

zone model is seen as the most promising technique,

though requiring to set up the cohesive zone before

GRAPP 2020 - 15th International Conference on Computer Graphics Theory and Applications

236

the cutting. Moreover, the step-by-step remeshing,

used to prepare the zone, may be time-consuming,

and the simulation itself is not performed in real-time.

Yet, needle insertion modeling for real-time applica-

tion has been presented in (Abolhassani et al., 2007),

which aims to address the modeling of the force as

well as the needle path.

In one of the precursor works in puncture model-

ing (DiMaio and Salcudean, 2003), the force distri-

bution is estimated along the shaft and a 2D model is

proposed for force/displacement relationship. Later,

Okamura et al. investigated the in vitro needle forces

using sensors, and presented models for cutting, fric-

tion and elastic forces during puncture (Okamura

et al., 2004). The strength of those models is that they

are simple enough for real-time applications. A new

method was presented in (Duriez et al., 2009) for the

insertion of ﬂexible needle using constraint models.

They achieved a real-time simulation with deformable

needle and tissue, while adding effect like steering.

However, only a simple model was presented, and

there is no evidence the method will keep working

with more complex ones.

(Crouch et al., 2005), and later on (Gao et al.,

2013) chose to study the tissue deformation in regard

of time and insertion velocity. The former focuses on

the insertion force once the needle is inside the tis-

sue, while the latter insists on the deformation of the

surface during puncture. Both studies are of partic-

ular interest: assuming the needle velocity being ap-

proximately constant during puncture, they can link

tissue deformation and needle insertion with a simple

mathematical function. Both authors assure a good

approximation of force and deformation, even if the

ﬁdelity of the relaxation phase could be improved.

In our approach, the force feedback, due to the

needle insertion in tissues, is calculated without

changing the topology of the meshes involved in the

3D scene. Our solution is based on the use of dis-

placement ﬁeld models allowing us to handle de-

formation according to both physical properties (the

force intensity) of the tissues and the organ shape (via

the geometric mesh). It allows us a real-time display,

and an accurate force model compatible with haptic

requirements.

3 GENERAL APPROACH

To propose a relevant training simulator of needle

puncture, one of the challenges remains in generat-

ing an interactive 2D view of the 3D scene with a re-

alist ultrasound rendering which must exhibit the tis-

sues deformation involved by the manipulation of two

haptic devices (simulating the probe and the needle).

At the beginning of each time frame, the ﬁrst step

consists in computing a 2D slice of the 3D scene ac-

cording to the probe position. To that aim, a new sur-

face is created for each 3D mesh of the scene using

the Capping Clipped Solids method (McReynolds and

Blythe, 2005, chapter 16). This OpenGL based solu-

tion enables a fast computation of the slices, and the

new surfaces hence created will serve as support for

the effects during the rendering pass, to integrate the

tissues deformation and create the ﬁnal ultrasound im-

age. Moreover, the 2D slice is rendered in the same

render pass as the 3D scene, which means both can

be displayed concurrently without performance loss.

This enables a nice two-views display inside the med-

ical simulator Next. Fig. 1 illustrates our pipeline

strategy of creating, in real-time, a relevant ultrasound

rendering with tissues deformation.

Haptic rendering

(section 5)

US rendering

(section 4)

Tissue deformation

(section 6)

US rendering with

deformation

(section results)

Figure 1: Our pipeline to obtain an ultrasound image of our

3D scene during the manipulation of the two haptic devices.

Ultrasound Rendering (see section 4). The ultra-

sound view requires two steps. Firstly, we deal with

a solution based on an ultrasound database limited

to textures, to compute the ultrasound rendering on

the 2D slice. Note that, no complete pre-recorded

ultrasound volume is required. Secondly, some extra

treatments are performed to consider the orientation

of the tissues (with an original way to show ﬁber

orientation for tendon using a texture-dependent

oriented blur) or to add artifacts (like shadow or

reﬂection) resulting from the manipulation of a

probe. This approach enables the generation of the

ultrasound view of any joints (shoulder, knee) in

all directions according to the manipulation of the

probe. Moreover, it only requires a few number of

real ultrasound images.

Haptic Rendering (see section 5). To reproduce the

sense of touch and to improve the realism of the

simulator, we provide haptic feedback of the probe

and of the needle used during puncture. As these

devices exhibit distinct behavior, the force-feedback

algorithm would differ: the probe only experiences

contact, while the needle goes through contact and

A Real-time Ultrasound Rendering with Model-based Tissue Deformation for Needle Insertion

237

insertion. Thus, frictional, elastic and cutting force

are modeled for the needle, which is also path

constrained with a tunnel effect. While the forces

calculation is already well-known, the precision of

our collision algorithm and our tunnel effect allow

us to easily transfer the force information to produce

accurate visual deformations due to the interactions.

Tissue Deformation (see section 6). The ultrasound

view must display the deformations undergone by

tissues due to the needle insertion during the puncture

gesture, as well as probe/tissue interactions. To that

end, we use the haptic devices feedback and we

deﬁne two displacement functions that link the force

to the displacement of the surrounding tissues. Then,

the calculus of these deformations is performed on

the GPU to create a speciﬁc output image. Finally,

this 2D output image will be used to integrate

these deformations into the ultrasound view. This

approach, which is based on the deformation of the

2D image (rather than the simulation of 3D mesh

deformations), enables us a real-time rendering of the

tissues deformation.

Fig. 2 gives an illustration of the modules in our

framework and the communications between them.

Scenes

(Simulation goal)

3D meshes,

physical properties

US textures

Collision detection

(section 5)

Force model

(section 5)

Device position

Collision detection

(section 5)

Force model

(section 5)

Device position

User

VAO/VBO

Shadow testing

Clipping

Texturing

Displacement

(section 6)

US effects

(section 4)

Final output

(section results)

Needle Probe

Hand Hand

Haptic thread

Database

Render thread

Monitor

Figure 2: The modules of our framework.

4 ULTRASOUND RENDERING

In this section, we will detail our solution to create an

US rendering of a 3D scene in real-time. It deals with

ultrasound texture and additional treatments to further

integrate usual ultrasound artifacts (Law et al., 2011).

Creation of Our 3D Scene. A simpliﬁed scene

based on a young and healthy shoulder will serve to

illustrate our rendering process. To create this scene,

all tissues but subcutaneous fat were segmented from

a reference US image. Then, the layers were extruded

and turned into 3D meshes. At the end, it contains

Ultrasound reference image

Figure 3: 3D view of the shoulder scene made from a US

reference image. The probe and the needle have been added.

4,004 tetrahedral elements for all the involved tissues

(Fig. 3(3-8)). Next, our US rendering process runs

in several steps, as illustrated on Fig. 4. It starts

from the 2D slice of the 3D scene (Fig. 4a) on which

several effects (reﬂection, shadow, attenuation, noise,

blur, orientation) are added to obtain the US view

(Fig. 4f).

2D Slice with Diffuse Color. The process starts from

Fig. 4a with the 2D slice of our 3D scene (obtained

according to the probe position). The 2D surfaces

created by the Capping Clipped Solids method were

given a diffuse color, except for the deltoid. Indeed,

for thick tissue (like deltoid), we can directly apply a

texture acquired from the reference image (Fig. 3(4)),

by selecting a zone with a representative pattern

for the tissue, and using a texture synthesis algo-

rithm (Harrison, 2001). Thus, we use the similarity

of the ﬁbrous pattern in thick muscles for a given

orientation to ﬁll a texture data bank from reference

images, and use those textures as a basis for the US

images of any thick muscle. Two orientations were

considered: lateral and longitudinal (respectively

perpendicular and parallel to the US plane), due to

differences in patterns. The diffuse color given to

each of the other tissues is its target mean color in

the ﬁnal render, at the exception of the bone tissue,

whose white color is the the reﬂection one.

Reﬂection and Shadow. Reﬂection and refraction

occur at the boundary of two media. In ﬂuid/ﬂuid

interfaces, the reﬂection ratio increases with the dif-

ference of acoustic impedance between the media.

The intensity reﬂected I

at the interface from an

incoming intensity I

is deﬁned according to the

acoustic impedance Z

of each media with: I

((Z

− Z

)/(Z

+ Z

))

Visually, a bright area appears at most of tissue in-

terfaces (skin/muscle, muscle/tendon - Fig. 3(B)) due

to this reﬂected intensity. For ﬂuid/solid interfaces,

when the ultrasound wave encounters a bone, most

of the energy will be reﬂected. As a result, a darker

area/shadow (Fig. 3(C)) appears below the bone sur-

face, with a bright area on the bone interface itself.

GRAPP 2020 - 15th International Conference on Computer Graphics Theory and Applications

238

(a) 2D slice (b) = (a) + ref./sh. (c) = (b) + noise (d) ﬁber orientation (e) = (c) + (d) (f) = (b) + (e)

Figure 4: Illustration of the rendering pass effects to generate an US image. Contrast has been modiﬁed for a better view.

To create both effects at the same time, a typical

depth map is ﬁlled into a texture, before any other ren-

der pass (the US probe acting as a spotlight). This

depth map contains information relative to the dis-

tance of the surfaces of objects to the probe. It pro-

vides feedback regarding which parts are lying under-

neath bones, for example. Later on, a ray-tracing is

performed to trigger shadows in appropriate places.

Let’s note that a small bias was added to the depth

testing to acknowledge the reﬂection phenomenon.

While inside this bias, the render appears brighter.

This method allows us to create both the reﬂec-

tion and shadow rendering in one step for ﬂuid/solid

interfaces. For a ﬂuid/ﬂuid interface, only the bright

area is rendered: e.g. tendons appear as hyperechoic

(bright) but get no shadow. In our example, applying

these effects on Fig. 4a leads to Fig. 4b.

Attenuation. When the US wave propagates through

the tissues, the acoustic pressure undergoes an attenu-

ation of its global amplitude. Attenuation gathers two

ultrasound phenomena: scattering and absorption.

Scattering. The scattering effect results from the

interaction of the wave with the small particles or

defaults in the biological tissue. Their physical

properties are different enough from the surrounding

medium to lead to the emission of a secondary wave.

It creates the speckle effect in the US images, which

is computationally intensive to recreate accurately.

In our rendering, the speckle is approximated by a

Perlin noise: from Fig. 4b, we obtained Fig. 4c.

Absorption. This effect depends on the frequency f of

the probe, the biological tissue characteristics and the

distance to the wave emission point. With attenuation

coefﬁcient α and depth z , the attenuation intensity I

from an incoming intensity I

is deﬁned by:

= I

· 10

−αz f /20

. (1)

Visually, it generates darker pixels as the wave

propagates further. A non physically-realistic but

cost effective and accurate enough visual effect can

be achieved with the help of the same ray-tracing

as in the shadow rendering pass. Indeed, knowing

the distance between the pixel to be rendered and

the probe, it is enough to use only the average soft

tissue attenuation for each tissue in the scene. The

attenuation effect is added at the end of the rendering

process: with Fig. 5a (identical to Fig. 4f), we

obtained Fig. 5b (using α = 0.54 db/(MHz.cm)).

Fiber Orientation. As previously explained for del-

toid, longitudinal and lateral 2D textures are ex-

tracted and synthesized beforehand from real ultra-

sound recording to consider the orientation of some

biological thick tissues like muscles. Then, the right

texture blending ratio is computed relatively to the

tissue orientation with the probe. However, the tex-

ture synthesis failed for thin tissues (like tendons -

Fig. 3(A-6)) since the input data are too scarce. A

way to achieve the desired visual orientation would

be to model all lines inside the ﬁbrous model. How-

ever, this would force us to create numerous lines in-

side each ﬁbrous tissue prior to the rendering pass,

thus dramatically reducing performances. Instead, we

proposed a new method that we called oriented blur.

(a) w/o absorption (b) w/ absorption

Figure 5: US image without (a) or with (b) absorption.

Pre-computation. The ﬁrst (pre-computed) step is to

retrieve the orientation of the ﬁber. It is calculated

for all vertices thanks to the speciﬁc geometry

of tendon-like tissue. Indeed, tendons present

a curved cylindrical shape, in which the ﬁbrous

lines follow the direction of the curve. Thus, the

direction is set by the smallest principal curvatures

via quadratic ﬁtting (Panozzo et al., 2010). This

direction is then normalized and stored as a 3D vector.

Then, during the generation of the ultrasound

view, the oriented blur used for thin tissues works in

two phases (see Fig. 6).

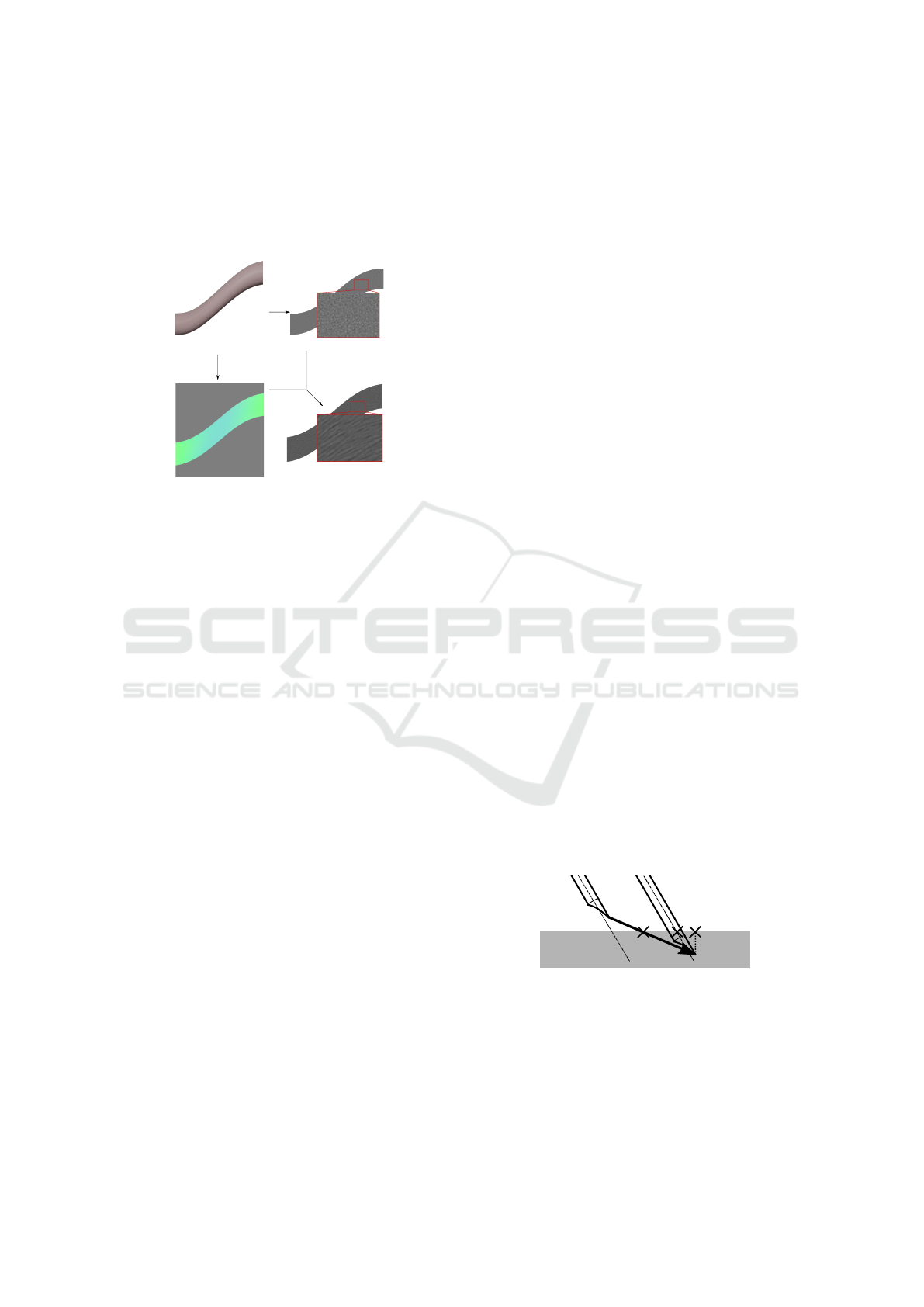
First GPU pass. The considered 3D tissue (Fig. 6a)

is clipped in the ultrasound plane according to the

probe position, and its surface is colored according

to the orientation of the ﬁbers (Fig. 6b). For our 3D

scene, Fig. 4d displays the orientation of the ﬁbers

of the tendon. This created image will be readable

by the GPU later on. For this result, the normalized

A Real-time Ultrasound Rendering with Model-based Tissue Deformation for Needle Insertion

239

three-dimensional curvature direction is mapped into

the three-dimensional (RGB) color space. Hence, the

gray color corresponds to the null vector. Since it ac-

counts for the orientation of the probe, this step can-

not be pre-calculated.

(a) (c)

(d)(b)

Figure 6: Oriented blur method: (a) a 3D tendon-like tissue

is transformed into (d) a ﬁbrous tissue on the 2D US view

using (b) its RGB curvature map and (c) its noisy 2D image.

Second GPU Pass. The created image (Fig. 6b) is

used as an input to post-process the noisy image

(Fig. 6c) to create the oriented blur (Fig. 6d): an

inverse mapping on the input image gives the blur

direction for each pixel of the noisy image. Then,

a 1D convolution kernel to calculate the mean of 9

pixel values in the direction is used.

This technique fully uses the noise coming from

the non homogeneous properties of the tissue (for a

tissue with a plain original color, the oriented blur

would not change the color of the pixel). Let’s note

that some US images are also being subject to a more

classic radial blur. While this effect is more noticeable

in abdominal ultrasound where the probe will scan for

deep tissues, the distortion of the bottom part of the

US image is still present in the reference image.

To achieve this, the image from Fig. 4c is

post-processed to be rendered multiple times with

radial offset. The center of rotation is given by the

ultrasound probe, and the higher the angle, the less

sharp the image is rendered. For our 3D scene, both

the oriented and radial blur can be seen in Fig. 4e:

the radial blur effect is more noticeable at the bottom

of the picture, while our oriented blur effect is only

present in the tendon.

Final US Image w/o Absorption. To end the render-

ing pass, the blurred picture (Fig. 4e) was mixed with

the image obtained with the reﬂection and shadow ef-

fects (Fig. 4b) to create the ﬁnal picture (Fig. 4f). See

Fig. 5b for the same ﬁnal image with absorption.

5 HAPTIC RENDERING

As previously said, two haptic devices were inte-

grated in our framework. They simulate the manip-

ulation of the needle and the probe to give the user

the sense of touch thanks to forces applied to the de-

vices. To get a smooth haptic feedback, the contact

forces must be updated at around 1,000 Hz. As a

result, the force feedback algorithm runs in its own

thread for both the needle and the probe. Further-

more, their behaviors differ enough to handle them

separately within the simulator (see Fig. 2): the probe

interacts with the surface skin and supplies the plane

for the ultrasound rendering, while the needle pro-

vides puncture forces and interacts with all tissues.

In this section, we will present the force feedback

algorithms for both devices. The generated forces

presented here will be used in the next section to

create the tissue deformation in the ultrasound view.

Collision Detection. The ﬁrst step in haptic rendering

is the detection of the collision between the haptic de-

vice and the objects in the 3D scene. We use the same

collision thread for both the needle and the probe, as

long as the needle does not pierce the ﬁrst layer of an

object. Usually, the collision is detected after it al-

ready occurred, by using volumes interpenetration or

by checking if the haptic point is inside an object.

For example, Fig. 7 illustrates the collision detec-

tion with a needle having a velocity v. A collision

point is calculated afterward, using the minimal dis-

tance to surface (leading to point C), or the intersec-

tion of the needle shaft and the surface (leading to

point B). However, it means that the real collision

point is actually never registered, which could gen-

erate accuracy errors in its exact position if the needle

is moving before registration. While this inaccuracy

may be ﬁne for the sole haptic thread, the visualiza-

tion of the deformation that depends on this collision

point would suffer: an offset could appear between

the needle and the deformed tissues.

Figure 7: Collision point detection using a ray-casting fol-

lowing the velocity v. A is our detection point, B is the

detection point along the shaft, C is the detection point with

minimal distance to the surface of the virtual object.

To prevent this, we use a ray-casting method

and a Bounding Volume Hierarchy on the surface

triangles to detect precisely the collision point, even

though this level of precision will mostly be used

GRAPP 2020 - 15th International Conference on Computer Graphics Theory and Applications

240

for the force feedback and accuracy of the needle.

Below a critical distance between the device and the

triangular surface of the virtual object, a collision

point is created (and constantly updated) by taking

into account the direction of the device’s velocity

(leading to point A). Then, barycentric coordinates

in the detected triangle of the collision point are

stored, along with the normal of the triangle. This

information allows us to detect whether the device is

above or touching the object during haptic rendering.

After that, the behaviors of the devices naturally

differ when they are moving below the plane contain-

ing the detected triangle.

Probe Haptic Rendering. During the penetration of

the surface plane by the haptic device, a classic God-

Object (Zilles and Salisbury, 1995) is created for the

probe. It is constrained to remain above the plane, to

avoid unwanted display with the probe penetrating the

tissues.

Then, to get the haptic rendering of the probe, a

simple stiffness force is calculated based on the elas-

tic properties of the biological tissue, characterized

by a stiffness K. This force f

is normal to the probe

and depends on the distance x between the haptic

interface and the God-Object, with: f

(x) = Kx n,

where n is the unit vector following the normal of

the collided triangle, K = 0.5 N/mm for the skin (Ni

et al., 2011). The force is null above the tissue.

Moreover, as transmission gel is applied between the

skin and the probe, the tangential part of the friction

force is kept to 0 N. As a result, the probe can move

freely on the object surface (and small friction force

may be added on demand).

Needle Haptic Rendering. During insertion, the nee-

dle involves several force models and may go through

multiple tissues. We followed Okamura which thor-

oughly studied this phenomena for liver tissue (Oka-

mura et al., 2004). Let f

, f

be the forces due to

stiffness, cutting and friction, respectively. Let x be

the distance between the puncture point and the tip of

the needle. The global force f

along the needle shaft

(with u its corresponding unit vector) is deﬁned by:

(x) = f

(x) + f

(x).

Stiffness Force. During the pre-puncture step, the

stiffness force intensity kf

k is steadily increasing un-

til the puncture occurs (i.e. as long as kf

(x)k < f

with f

the intensity of the necessary force to punc-

ture the interface). At this point, a sharp resistance

loss is detected involving kf

(x)k = 0 until a new in-

terface is met. Following Okamura, we chose to ap-

proximate the pre-puncture stiffness force f

with a

second-order polynomial leading to: f

(x) = (K

x +

) u, where K

are parameters chosen accord-

ing to tissues. Even if this force modeling is vastly

used, speciﬁc parameter data per tissues are rarely

given. Indeed, even in (Okamura et al., 2004), those

parameters differed for the same tissue between tests.

This problem has been tackled in a survey (van Ger-

wen et al., 2012): without massive experimental data,

the only option is to trust the haptic sense from multi-

ple experts to tune the parameters K

according to

their own feedback sensation during their experiment

on the simulator.

Cutting Force. After puncture, the cutting force is in-

volved to slice through the tissue. It combines the

fracture force needed to create the path for the needle,

and the stiffness force of the tip of the needle on the

tissue. It is usually isolated by puncturing the exact

same path twice and subtracting the two global forces.

The cutting force is approximated by a constant, if the

needle velocity is not zero, with: f

(x) = f

Friction force. A wide number of friction models ex-

ists (Yang et al., 2018). Following (Okamura et al.,

2004), a modiﬁed Karnopp model is used. For more

information, we advise to see the corresponding arti-

cle.

Tunnel Effect. In addition to the usual forces in hap-

tic needle insertion, we constrain the needle on a path

during the puncture (see Fig. 8). It serves the purpose

of improving the force feedback realism with the ad-

dition of a force perpendicular to the needle shaft.

Figure 8: Constraint points and tunnel effect.

The ﬁrst constraint (P

) is the skin collision point.

It is acting as a ball joint combined with a sliding part.

The needle can only slide at the collision point and no

tangential movement is allowed. While right under

the skin surface, the user is free to rotate the needle

to adapt his direction path. But as soon as the user

is exceeding a given depth (P

) or when another tis-

sue is punctured (P

), a new constraint is created. The

two combined constraints create a linear path that the

needle will be constrained to follow. Any deviation

creates a force feedback f

simulating the elastic be-

havior of the tissue with the same stiffness K. This

force is the only one perpendicular to the needle shaft

direction. It is deﬁned by:

= −



x − (x · P

)

||P



, (2)

with x the vector of length x between P

and the tip

A Real-time Ultrasound Rendering with Model-based Tissue Deformation for Needle Insertion

241

of the needle, l the full length of the needle. The

ﬁrst constraint P

is of signiﬁcant importance, as it

will dictate the overall behavior of the needle (hence

the need for precision in the collision thread). This

constraint is linked to the collided triangle and must

be updated during any displacement or deformation

of the considered triangle.

Furthermore, when multiple layers of tissue are

punctured, the force is the sum of the combined ef-

forts of the tissues. For each tissue, the friction force

is weighted by the needle length traversing it. Note

that stiffness and cutting forces only appear at the

layer of the needle tip (and that the stiffness force will

disappear as soon as no layer interface is intersected).

6 TISSUE DEFORMATION

SHADER

The last step consists in taking into account the veloc-

ity and the force feedback of the two haptic devices

in the rendering process. Indeed, the challenge is

to visualize the tissue deformation in the ultrasound

view during gesture. We detail here our original

solution based on displacement ﬁelds.

General Approach. The force feedback and velocity

of the needle/probe can be linked to the displacement

of the surrounding tissues by simple equations.

This approach is based on observation and function

ﬁtting (Gao et al., 2013; Crouch et al., 2005). Then,

the 3D displacement function is directly mapped to

the 2D image. It avoids the 3D physical simulation

of soft tissues and interactions with medical instru-

ments, that is barely compatible with real-time.

Rendering Pipeline. In our rendering, there are two

phases to obtain the deformations in the US view:

(i) the 2D ultrasound is rendered into an image (see

Section 4); (ii) this image is displayed on the screen.

However, between these two steps, post-processing

effects may be applied on the GPU.

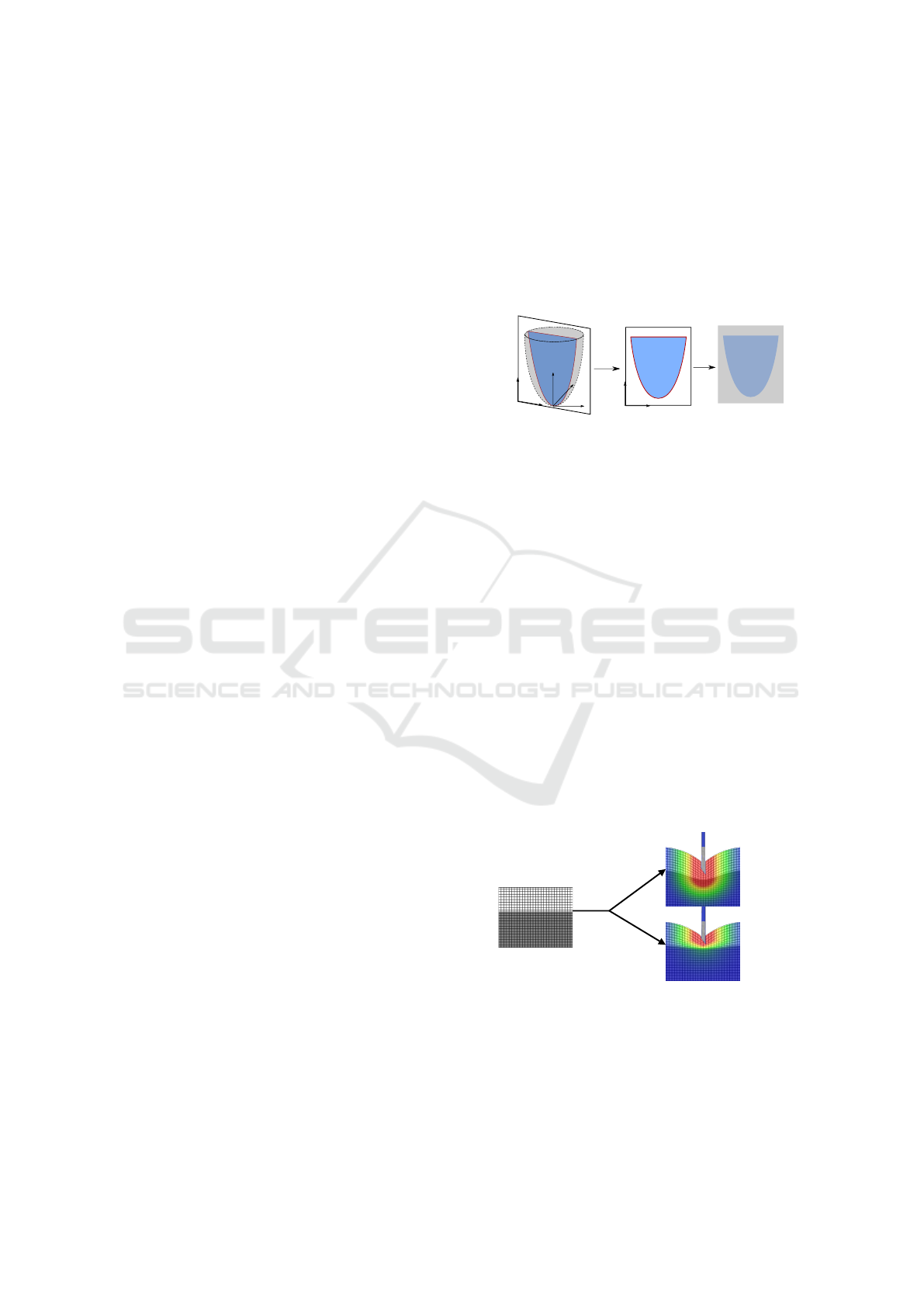
Let’s consider a pixel P of the 2D image with

basic coordinates (u,v). With no additional effect,

the screen exactly displays the image of the rendered

scene. Now if we want to render the pixel P with an

offset given by a displacement function d, we only

have to apply this displacement at P. Thus, we obtain

its new position d(P) = P

of coordinates (u

). A

heatmap is often used to highlight the displacement

intensity (Fig. 10b or c, with a blue-red scale).

The ﬁrst step consists in deﬁning the 3D displace-

ment function (noted d(x,y,z) in the world space) cor-

responding to the wanted effect (needle insertion or

probe contact); then, the 2D section corresponding

to the ultrasound plane is retrieved and we apply the

corresponding displacement (noted d(u,v) in the im-

age space) on each pixel. Note that the displacement

function is ﬁrst computed in 3D, allowing us to see

the inﬂuence of the needle on the tissues, even if the

needle itself is not visible in the 2D plane. At the end,

the conversion (much like for the orientation blur pro-

cess) transforms the sectioned deformation function

into a texture readable by the GPU (see Fig. 9).

d(x, y,z)

d(u, v)

RGB

Figure 9: (i) The displacement function d(x,y,z) is deﬁned

in the 3D world space. (ii) It is transformed in d(u,v) in the

US image space. (iii) The corresponding texture is stored.

To improve realism, we consider several elastic

behaviors of soft tissues. To illustrate our process,

Fig. 10 presents an example for one section of a sim-

ple 2-layered 3D scene, where a texture grid was

added to better follow the displacement. The Young

modulus E of each tissue is given by its gray value.

Each pixel of the image (Fig. 10a) is moved follow-

ing the value of the displacement function, which de-

pends of the Young modulus. Moreover, a mean value

with neighbor pixels is performed to ensure displace-

ment continuity at the interface between two highly

different values of E. At the end, the difference could

be appreciated when using a single (Fig. 10b) or sev-

eral values (Fig. 10c) of E. Under normal conditions,

the texture grid is replaced by the US render and the

Young modulus information is given by a 2D slice im-

age with a gray shading for each tissue (calculated and

stored at the same time as the diffuse color - Fig. 4a).

= 0.5 N/mm

= 5 N/mm

(b)

(c)

d(u,v,E)

(a)

Figure 10: Displacement function d(u, v,E) applied on im-

age (a) resulting to image (b) or (c) according to E value.

At this point, the issue is to ﬁnd ﬁtting and

conﬁgurable displacement functions d(x, y,z, E) in

the world space to simulate the deformation due to

the needle insertion and the probe according to the

elastic behavior of the tissue.

GRAPP 2020 - 15th International Conference on Computer Graphics Theory and Applications

242

Displacement Due to the Needle. The deformation

due to the needle can be decomposed into two parts:

(i) the skin deformation before and during puncture;

(ii) the inner tissues deformation after puncture.

Skin Deformation. Intensive work on the deformation

of the skin has been made by Gao et al. (Gao et al.,

2013). Even though the experiment took place with

an artiﬁcial tissue and at ﬁxed velocity of 2.5 mm/s, it

shows a relationship between the needle displacement

and the deformed volume of the skin. We used those

results to simulate the deformation of the skin and

subcutaneous tissues during elastic deformation due

to the stiffness force.

Inner Tissues Deformation. The deformation of

subcutaneous tissues is only visible in the 2D ultra-

sound view. During needle displacement, friction

forces between the needle and the biological tissue

cause a deformation of the latter that only affects the

surrounding area, with no (or negligible) deformation

outside of it. This area has been studied in (Crouch

et al., 2005). Their model allows us to use the

deformation function of the tissue close to the needle

during displacement, and to display it in real-time

during the US image rendering step.

Displacement Functions. To further match the obser-

vation and forces calculated by haptic rendering, the

displacement function for the needle insertion is split

into two: before/after puncture of its layer. And, the

displacement functions are deﬁned to visually ﬁt the

model of (Gao et al., 2013) and (Crouch et al., 2005).

Let ˜r be the smallest distance to the needle shaft

(Fig. 11). Before puncture, as the needle pushes the

surface, the displacement of the tissue at the tip of

the needle is exactly equal to the displacement of this

same tip. Indeed, the pre-puncture elastic force is

dominant until the puncture occurs. This displace-

ment also affects the tissues under the puncture point.

It is deﬁned by:

d(˜r,z, E) =











max



2 −

˜r

max



, z < z

max



˜r

max



, z > z

max

0, ˜r > R

max

(3)

where g(t) = 1 − (3t

− 2t

), f

is the stiffness force,

E is the Young modulus of the tissue at the point

(˜r,z). R

max

is the inﬂuence radius of the needle from

Crouch’s model (with R

max

= 2cm).

After puncture, the friction and cutting forces af-

fect the tissues along the shaft and the ones below the

needle. Locally, the friction force is dominant along

the shaft, while the cutting force is dominant under

the tip. It means that we can also split our displace-

max

˜r

Figure 11: Two zones of effect for the displacement func-

tion: along (light gray) / beneath (dark gray) the needle tip.

ment function in two. It is deﬁned by:

d(˜r,z, E) =











max



2 −

˜r

max



, z < z

max



˜r

max



, z > z

max

0, ˜r > R

max

(4)

where f

and f

are the friction and cutting force given

by the haptic device simulating the needle. Let’s

remark that f

is divided by z

max

as the friction force

is spread along the needle.

Displacement Due to the Probe. The probe deforms

the tissue on a global scale, proportionally to the pres-

sure exerted on the skin. An interesting study has

been made by (Flack et al., 2016), which records the

probe position during acquisition to deduce the ex-

erted pressure, and apply reverse displacement onto

the US images. However, the studied abdominal im-

age exhibit much larger deformations than ours. Due

to US images generation process and pressure of the

probe, the soft tissue are always subject to displace-

ment during acquisition. At the difference of abdom-

inal probe, the ones used for shoulder joint are ﬂat.

Thus, an uniform force could be applied at the sur-

face of the skin, and the displacement function results

in: d(z) = kf

k/(E(1 + z)), where f

is the stiffness

force given by the haptic device simulating the probe.

Let’s note that this displacement function is added to

the one of the needle.

7 RESULTS

Our Complete Simulator. Fig. 12 presents a pic-

ture of our simulator. For this ﬁrst prototype, we

used an Intel

Core™ i7-6800K CPU, an NVIDIA

GeForce

1070GTX and 31.3 GB of memory. The

haptic devices were respectively a Touch™ 3D sty-

lus and a Geomagic

Touch™. Fig. 12 also shows the

two main views proposed by the graphical rendering:

(i) a pedagogical 3D views (showing interactions be-

tween organs and needle) which permit to infer inter-

nal location of the tissues and needle, with their dis-

placements; (ii) our 2D ultrasound view, including the

A Real-time Ultrasound Rendering with Model-based Tissue Deformation for Needle Insertion

243

Figure 12: Our simulator which couples a graphical render-

ing with two haptic devices simulating probe and needle.

(up) 3D models (shoulder-probe-needle); (down) zoom on

tissue deformation with ultrasound view.

tissue deformation, similar to the one provided by the

probe used by rheumatologists during the gesture.

US rendering. Fig. 13 presents the reference image

used to create our 3D scene and the US image gen-

erated by our method for the clipping zone of the 3D

scene deﬁned according to the probe position. The

adaptability of our model is presented on a pseudo-

anatomical scene on Fig. 14, coupled with its peda-

gogical US view.

Figure 13: (left) US reference image. (right) The ultrasound

image generated by our process (without deformation).

Figure 14: A scene model seen from behind (left) and the

corresponding pedagogical US view (right).

Fig. 15 shows some results obtained for the dis-

placement of the soft tissues, due to the needle or the

probe, considering a single or two values of E for the

tissues (E = 0.5 and 5N/mm for top and bottom lay-

ers). Fig. 16 presents our ﬁnal US rendering. On this

ﬁgure, we can see the tissue deformation due to the

forces involved by haptic devices (probe or needle):

they are used to alter the texture, allowing a realistic

real-time display of the tissue deformation on the US

image.

Figure 15: Deformation due to (a) the needle and (b) the

probe considering a single (top row) or two values of E (bot-

tom row) for tissues.

Performance. Several tests were performed on a

simple scene, involving a sphere with an increasing

amount of triangles. The sphere acted as a ﬁbrous ob-

ject under deformation. The recorded times (Fig. 17)

are the mean of the ﬁrst 120 simulation frames. The

results are presented for all render steps.

Even for 7, 864,320 triangles, our rendering runs

in about 0.002 s with all the effects, which is more

than enough for real-time simulation (≈0.06 s). To

compare those results with other existing approaches

on US image generation with mesh deformation, we

ran the tests again and ﬁlled the GPU buffer at each

frame (Fig. 18), which takes up to to 99% of frame

rendering time.

We avoid this time consuming step, which would

be mandatory in case of an update of the vertex po-

sitions, as in classical methods. This comparison is

the closest we were able to imagine while avoiding

a tedious implementation of a physically-based soft

tissue deformation system.

The haptic thread itself always runs at around

500 Hz. While lower than the usual frequency of

1,000 Hz, none of the 2 haptic devices has shown par-

asitic vibrations.

8 DISCUSSION

The pipeline presented here allows us to create an US

image from any biological tissue model and from any

GRAPP 2020 - 15th International Conference on Computer Graphics Theory and Applications

244

Figure 16: Final US images showing the probe or the needle tissue deformation (w/ or w/o the superposed heatmap).

0.0000

0.0005

0.0010

0.0015

0.0020

Number of triangles

Time (s)

Legend

Add blur

Add deformation

Draw probe and needle

Draw sliced scene

Fill deformation texture

Fill fiber texture

Fill mask texture

Fill reflection map

Fill shadow map

Figure 17: Cumulated time (in seconds) of all the render

steps versus the numbers of triangles (log scale).

Figure 18: Loss in performances using the classical ap-

proach. Loss of FPS (green) and percentage of time to reﬁll

the buffer relative to frame rendering time (red) vs the num-

ber of triangles (in log scale).

probe location and orientation. We avoid the con-

struction of a speciﬁc database that might be very de-

pendent on a considered joint or on the location of in-

ﬂammatory tissues. The rendering goes through sev-

eral steps, including shadow, reﬂection, noise, attenu-

ation and it includes the rendering of ﬁber orientation,

which to our knowledge has never been presented be-

fore in a real-time simulation. Instead of modeling

the ﬁbrous tissue, we used a texture-based oriented

blur. In related work, we have seen the beneﬁts of the

generative approach to create the ultrasound image,

thanks to its ﬂexibility, even if they still lack some re-

alism when done in real-time environment. To over-

come this, we managed to add the ﬁbrous structure to

better identify the biological tissue.

Some inner structure of non-ﬁbrous tissue, such as

the subcutaneous fat, still lacks details. Voronoi noise

is a possible solution to add realism. Moreover, strong

echoes in some probe orientations produce repetitive

light pattern that are not yet generated in our model

(see Fig. 13).

Concerning the evaluation and comparison of our

images with previous work, it is proved to be difﬁ-

cult due to the different choices of body region and

the subjectiveness on the quality. Therefore, the de-

tails, ultrasound effects and overall evaluation of our

images is in course with subject-matter experts. We

present here the technical novelties in ultrasound ren-

dering, ﬁber orientation and real-time image deforma-

tions.

Few real-time needle insertion simulation with

haptic were seen in related works and all on reduced

models. The use of displacement function directly

on the image allows us to work with complex mod-

els without increasing computational time. However,

the displacement functions accuracy depends of a de-

formation model. For example, the current model is

not appropriate for very low of fast velocities, and

lack realism in the relaxation phase. This trade-off

is believed to be the price to pay to cope with perfor-

mances required in real-time environment.

9 CONCLUSION AND

PERSPECTIVE

In this paper, we presented a new way to create an

ultrasound rendering suitable for a needle insertion

training simulator. Our strategy enables to show, in

the ultrasound view, the deformation induced by the

use of two haptic devices which correspond to the

probe and the needle usually used by rheumatologists.

Our proposition brings some breakthroughs.

Firstly, it avoids the use of a 3D volume texture

database. This permits to easily consider several

joints (knee, shoulder), various patient morphology,

various pathologies with inﬂamed tissues, etc. Sec-

ondly, it permits to display the tissue ﬁbers and their

orientation in the US view. This point visually im-

proves the existing solutions in ultrasound rendering.

Thirdly, our approach enables to show the tissue de-

formations due to the needle insertion. To that end,

our solution deals with the use of textures and dis-

placement models to take advantage of the GPU for

a complete real-time solution. The haptic puncture

forces were calculated using the constrained points

found by continous detections and allow a realistic

A Real-time Ultrasound Rendering with Model-based Tissue Deformation for Needle Insertion

245

deformation inside the US view, leading to improve

the learner immersion sense.

Next step will aim to further improve the visual

rendering of the US image by adding others arti-

facts, and add more complex and precise displace-

ment force, based on physically-based simulations.

ACKNOWLEDGMENTS

This work was supported by French state funds

managed by the ANR within the IDEFI-SAMSEI

(Strat

egies d’Apprentissage des M

etiers de Sant

e en

Environnement Immersif) project. We thank rheuma-

tologist Dr.Coury-Lucas for her valuable feedback,

and E. Galin and J-C. Iehl for their help.

REFERENCES

Abolhassani, N., Patel, R., and Moallem, M. (2007). Needle

insertion into soft tissue: A survey. Medical engineer-

ing & physics, 29(4):413–431.

Bamber, J. and Dickinson, R. (1980). Ultrasonic B-scanning:

a computer simulation. Physics in Medicine & Biology,

25(3):463.

Burger, B., Bettinghausen, S., Radle, M., and Hesser, J.

(2013). Real-time gpu-based ultrasound simulation us-

ing deformable mesh models. IEEE transactions on

medical imaging, 32(3):609–618.

Crouch, J. R., Schneider, C. M., Wainer, J., and Okamura,

A. M. (2005). A velocity-dependent model for needle

insertion in soft tissue. In International Conference on

Medical Image Computing and Computer-Assisted In-

tervention, pages 624–632. Springer.

DiMaio, S. P. and Salcudean, S. E. (2003). Needle inser-

tion modeling and simulation. IEEE Transactions on

robotics and automation, 19(5):864–875.

Duriez, C., Gu

ebert, C., Marchal, M., Cotin, S., and Grisoni,

L. (2009). Interactive simulation of ﬂexible nee-

dle insertions based on constraint models. In In-

ternational Conference on Medical Image Computing

and Computer-Assisted Intervention, pages 291–299.

Springer.

Flack, B., Makhinya, M., and Goksel, O. (2016). Model-

based compensation of tissue deformation during data

acquisition for interpolative ultrasound simulation. In

Biomedical Imaging (ISBI), 2016 IEEE 13th Interna-

tional Symposium on, pages 502–505. IEEE.

Gao, D., Lei, Y., and Yao, B. (2013). Analysis of dynamic tis-

sue deformation during needle insertion into soft tissue.

IFAC Proceedings Volumes, 46(5):684–691.

Goksel, O. and Salcudean, S. E. (2009). B-mode ultrasound

image simulation in deformable 3-D medium. IEEE

transactions on medical imaging, 28(11):1657–1669.

Harrison, P. (2001). A non-hierarchical procedure for re-

synthesis of complex textures. WSCG ’2001: Confer-

ence proceedings: University of West Bohemia, Plzen,

Czech Republic, pages 190–197.

Heer, I., Middendorf, K., M

uller-Egloff, S., Dugas, M., and

Strauss, A. (2004). Ultrasound training: the virtual

patient. Ultrasound in Obstetrics and Gynecology,

24(4):440–444.

Jensen, J. A. (1991). A model for the propagation and scat-

tering of ultrasound in tissue. The Journal of the Acous-

tical Society of America, 89(1):182–190.

Law, Y. C., Ullrich, S., Knott, T., Kuhlen, T., and Weg, S.

(2011). Ultrasound image simulation with gpu-based

ray tracing. Virtuelle und Erweiterte Realit

at, 8:183–

194.

Magee, D. and Kessel, D. (2005). A computer based simula-

tor for ultrasound guided needle insertion procedures.

IEE International Conference on Visual Information

Engineering (VIE 2005), pages 301–308.

Magee, D., Zhu, Y., Ratnalingam, R., Gardner, P., and Kessel,

D. (2007). An augmented reality simulator for ultra-

sound guided needle placement training. Medical & bi-

ological engineering & computing, 45(10):957–967.

Marion, A. and Vray, D. (2009). Toward a real-time simula-

tion of ultrasound image sequences based on a 3-d set

of moving scatterers. IEEE transactions on ultrason-

ics, ferroelectrics, and frequency control, 56(10):2167–

2179.

Mattausch, O. and Goksel, O. (2016). Monte-carlo ray-

tracing for realistic interactive ultrasound simulation. In

Proceedings of the Eurographics Workshop on Visual

Computing for Biology and Medicine, pages 173–181.

Eurographics Association.

McReynolds, T. and Blythe, D. (2005). Advanced graphics

programming using OpenGL. Elsevier.

Ni, D., Chan, W. Y., Qin, J., Chui, Y.-P., Qu, I., Ho, S. S.,

and Heng, P.-A. (2011). A virtual reality simulator

for ultrasound-guided biopsy training. IEEE Computer

Graphics and Applications, 31(2):36–48.

Okamura, A. M., Simone, C., and O’leary, M. D. (2004).

Force modeling for needle insertion into soft tis-

sue. IEEE transactions on biomedical engineering,

51(10):1707–1716.

Panozzo, D., Puppo, E., and Rocca, L. (2010). Efﬁ-

cient multi-scale curvature and crease estimation. Pro-

ceedings of Computer Graphics, Computer Vision and

Mathematics (Brno, Czech Rapubic, 1(6).

Takabi, B. and Tai, B. L. (2017). A review of cutting me-

chanics and modeling techniques for biological materi-

als. Medical engineering & physics, 45:1–14.

van Gerwen, D. J., Dankelman, J., and van den Dobbelsteen,

J. J. (2012). Needle–tissue interaction forces–a survey

of experimental data. Medical engineering & physics,

34(6):665–680.

Vidal, F. P., John, N. W., Healey, A. E., and Gould, D. A.

(2008). Simulation of ultrasound guided needle punc-

ture using patient speciﬁc data with 3D textures and vol-

ume haptics. Computer Animation and Virtual Worlds,

19(2):111–127.

Yang, C., Xie, Y., Liu, S., and Sun, D. (2018). Force

modeling, identiﬁcation, and feedback control of robot-

assisted needle insertion: a survey of the literature. Sen-

sors, 18(2):561.

Zilles, C. B. and Salisbury, J. K. (1995). A constraint-based

god-object method for haptic display. In Intelligent

Robots and Systems 95.’Human Robot Interaction and

Cooperative Robots’, Proceedings. 1995 IEEE/RSJ In-

ternational Conference on, volume 3, pages 146–151.

IEEE.

GRAPP 2020 - 15th International Conference on Computer Graphics Theory and Applications

246