Impact of Threshold Values for Filter-based Univariate Feature

Selection in Heart Disease Classification

Houda Benhar

, Ali Idri

1,2

and Mohamed Hosni

Software Project Management Research Team, ENSIAS, Mohammed V University, Rabat, Morocco

Complex Systems Engineering and Human Systems, Mohammed VI Polytechnic University, Ben Guerir, Morocco

Keywords: Data Preprocessing, Feature Selection, Univariate, Filter Technique, Heart Disease, Classification.

Abstract: In the last decade, feature selection (FS), was one of the most investigated preprocessing tasks for heart

disease prediction. Determining the optimal features which contribute more towards the diagnosis of heart

disease can reduce the number of clinical tests needed to be taken by a patient, decrease the model cost,

reduce the storage requirements and improve the comprehensibility of the induced model. In this study a

comparison of three filter feature ranking methods was carried out. Feature ranking methods need to set a

threshold (i.e. the percentage of the number of relevant features to be selected) in order to select the final

subset of features. Thus, the aim of this study is to investigate if there is a threshold value which is an

optimal choice for three different feature ranking methods and four classifiers used for heart disease

classification in four heart disease datasets. The used feature ranking methods and selection thresholds

resulted in optimal classification performance for one or more classifiers over small and large heart disease

datasets. The size of the dataset takes an important role in the choice of the selection threshold.

1 INTRODUCTION

Heart disease (HD) is a general term referring to a

variety of conditions and disorders that affect the

heart and blood vessels (Mendes et al., 2015). HD

types include coronary artery disease, valvular heart

disease, cardiomyopathy, heart rhythm disturbances

(arrhythmias) and heart infections. According to the

World Health Organization, an estimation of 17.9

million people died due to HD in 2016, representing

31% of all global deaths. An accurate and early

detection of cardiac diseases can save many lives by

monitoring heart activities (Mustaqeem, Anwar,

Majid, & Khan, 2017). Data mining (DM) offers a

set of powerful techniques that allow the

identification and extraction of relevant information

embedded in large data sets (Ting, Shum, Kwok,

Tsang, & Lee, 2009). DM can be very beneficial for

doctors and patients particularly in the case of

diseases with high mortality and morbidity rates

such as HD. Nonetheless, the quality of the

knowledge extracted highly depends on the quality

of the data used (Idri, Benhar, Fernández-Alemán, &

Kadi, 2018). A rigorous preprocessing of data before

using DM techniques is, therefore, mandatory (Ting

et al., 2009). A previous study on data preprocessing

tasks in heart disease knowledge discovery (Benhar,

Idri, & Fernández-Alemán, 2019), showed that

researchers were mainly interested in data reduction

and particularly in feature selection in order to

improve the performance of DM-based decision

support systems for HD prediction.

Feature selection is defined as the process of

detecting relevant features and discarding irrelevant

and redundant ones with the goal of obtaining a

subset of features that accurately describe a given

problem (Guyon, Steve, Masoud, & Lotfi, 2006). In

addition to its ability to improve the performance of

a DM model (Bolón-Canedo, Sánchez-Maroño, &

Alonso-Betanzos, 2015), FS has other advantages

such as shortening the number of measurements,

reducing the execution time and improving

transparency and compactness of the suggested

diagnosis (Huan & Lei, 2005; Jaganathan &

Kuppuchamy, 2013). FS algorithms are generally

classified as filter, wrapper or embedded models

(Jovic, Brkic, & Bogunovic, 2015). Filter feature

selection techniques consist of evaluating the

characteristics of the training data to select feature

subsets independently of any learning algorithm,

while wrappers use a targeted learning algorithm in

order to assess the performance of the selected

Benhar, H., Idri, A. and Hosni, M.

Impact of Threshold Values for Filter-based Univariate Feature Selection in Heart Disease Classiﬁcation.

DOI: 10.5220/0008947403910398

In Proceedings of the 13th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2020) - Volume 5: HEALTHINF, pages 391-398

ISBN: 978-989-758-398-8; ISSN: 2184-4305

391

subsets (Bolón-Canedo, Sánchez-Maroño, &

Alonso-Betanzos, 2013). Embedded methods embed

the process of FS into the training process of the

learning algorithm. In addition to these three types

of FS techniques, researchers proposed new hybrid

approaches in order to consolidate the advantages

and eliminate the drawbacks of the individual ones

(Peter & Somasundaram, 2012).

FS methods can also be classified according to:

(1) univariate techniques (i.e. rankers) which provide

a ranking of features and the subset of selected

features can be determined by setting a cutoff

threshold or specify how many attributes to retain;

and (2) multivariate techniques which produce the

best subset of features based on a specific search

strategy using some performance measures. Several

studies in the literature made use of feature ranking

techniques to classify heart disease without

providing information about the threshold used to

select the final subset (Jabbar, Deekshatulu, &

Chandra, 2013, 2015; Peter & Somasundaram,

2012), or used a default threshold (Almuhaideb &

Menai, 2016) (e.g. selecting the 10 top ranked

attributes) for all feature ranking methods and over

all datasets.

The main purpose of this study is, therefore, to

evaluate and compare the impact of ReliefF, Info

Gain and Correlation feature ranking techniques

using different threshold values on the performance

of heart disease classification using four classifiers:

(K-Nearest Neighbor (KNN), Support Vector

Machine (SVM), Multilayer Perceptron (MLP)

neural network architecture and Decision Trees

(DT). The rationale behind choosing these four

classifiers is that they were the most frequently

employed techniques when developing classifiers to

diagnose HD patients (Kadi, Idri, & Fernandez-

Aleman, 2017; Shouman, Turner, & Stocker, 2012).

The experiments were performed using the Weka

3.8.3 software (Hall et al., 2009) using four heart

disease datasets taken from the UCI Machine

Learning Repository (Dua & Graff, 2019). The

classifiers were evaluated using three performance

criteria: accuracy, kappa statistic and area under the

ROC curve, and a 10-fold cross validation method.

The rest of the paper is organized as follows:

Section 2 presents an overview of the feature

selection and classification techniques used. The

experimental design is described in Section 3.

Results are presented and discussed in Section 4.

Findings and future work are presented in Section 5.

2 FEATURE SELECTION AND

CLASSIFICATION

TECHNIQUES

2.1 Feature Selection Techniques

2.1.1 ReliefF

ReliefF (Kononenko, Robnik-Šikonja, & Pompe,

1996) is an extension of the original Relief

algorithm (Kenji & A., 1992) that works by

randomly sampling an instance from the dataset and

then locating its nearest neighbor from the same

class (called nearest hit) and the opposite one (called

nearest miss). The rationale is that a good attribute

should have the same value for instances from the

same class and should differentiate between

instances from different classes.

2.1.2 Correlation

Correlation based feature selection, also known as

linear correlation or Pearson correlation coefficient,

measures linear correlation between two variables.

The resulting value ranges between -1 and 1, with -1

meaning perfect negative correlation, +1 meaning

perfect positive correlation and 0 meaning no linear

correlation between the two variables (Gooch,

2011).

2.1.3 Info Gain

Information Gain (Quinlan, 1986) is one of the most

common attribute evaluation methods. It uses

entropy to measure how much “information” a

feature gives us about the class considering a single

feature at a time.

2.2 Threshold Values

Several studies in the literature used different

thresholds that retain different percentages of

features (Bolón-Canedo et al., 2013; Hosni, Idri, &

Abran, 2017; Jaganathan & Kuppuchamy, 2013;

Seijo-Pardo, Porto-Díaz, Bolón-Canedo, & Alonso-

Betanzos, 2017). In (Bolón-Canedo et al., 2013), the

authors suggested selecting 40% of features if the

initial number of features ranges from 10 to 75.

Studies on fault prediction and software effort

estimation recommended the use of the top

Log_2(N) features of feature ranking techniques in

the Weka tool (Hosni et al., 2017), where N is the

number of features in the initial set. In this study, a

comparison between five different thresholds,

HEALTHINF 2020 - 13th International Conference on Health Informatics

392

including the aforementioned ones, is conducted.

The selected thresholds used are:

▪ Log_2(N): where N is the number of features in a

given dataset.

▪ 10%, 20%, 40%, and 50%: these thresholds select

the top 10%, 20%, 40%, and 50% of the most

relevant features of the final ordered rankings

respectively.

2.3 Classification Techniques

2.3.1 K-Nearest Neighbor

The k-nearest neighbor (KNN) algorithm assumes

that similar instances have similar classifications:

novel instances are classified according to the

classifications of their most similar neighbors. K is a

positive, and typically small, integer. An object is

classified by a plurality vote of its neighbours

(Cover & Hart, 1967).

2.3.2 Support Vector Machine

Support Vector Machines (SVMs) are a set of

related methods for supervised learning which

consist of creating a maximum-margin hyperplane

that lies in a transformed input space and splits the

example classes, while maximizing the distance to

the nearest cleanly split examples (Vapnik, 2000).

2.3.3 Multilayer Perceptron

Multilayer perceptron (MLP) is a feedforward neural

network model used for classification and regression

tasks and consists of, at least, three layers of nodes:

an input layer, a hidden layer and an output layer. In

the input layer each node represents an independent

variable. The outputs of the first layer are used as

inputs of the next layer and this procedure is

repeated recursively until finally the output layer is

reached (Gardner & Dorling, 1998).

2.3.4 Decision Trees

A decision tree (DT) is a decision support tool that

uses a tree-like model of decisions and their possible

consequences (Bhargava, Sharma, Bhargava, &

Mathuria, 2013). In a DT each node represents a

feature (attribute), each link (branch) represents a

decision (rule) and each leaf represents an outcome.

The variant of DTs used in this paper is C4.5 known

as J48 in Weka.

3 EXPERIMENTAL DESIGN

3.1 Datasets Description

Statlog Heart Dataset: This dataset contains 270

instances belonging to two classes: the absence

(class absent) or presence (class present) of heart

disease. The number of instances belonging to the

class absent is 150 while 120 instances belong to the

class present. The dataset contains 13 attributes in

addition to the class attribute.

Cleveland Heart Disease Dataset: Experiments

published on this dataset refer to using its processed

version which contains 13 attributes in addition to

the class attribute and 303 instances. In addition to

this version we used the unprocessed dataset which

contains 75 attributes and 282 instances, as we

believe it might contain valuable information. The

instances of both datasets belong to five classes

integer valued from 0 (no presence of heart disease)

to 4. Experiments with the Cleveland database have

concentrated on simply attempting to distinguish

presence (values 1, 2, 3, 4) from absence (value 0) of

heart disease. Therefore, all values from 2 to 4 were

replaced by 1 to determine patients with heart

disease. The number of healthy patients (belonging

to class 0) in the processed and the unprocessed

datasets is 164 and 157 respectively while the

number of heart disease patients is 139 and 125

respectively. The processed and unprocessed

datasets contain a total of 6 and 5968 missing values

respectively.

Arrhythmia Dataset: This database contains 452

instances belonging to 16 classes integer valued

from 1 (no presence of heart disease) to 16. In this

study we only concentrate on binary classification to

distinguish between the presence and absence of

heart disease. Therefore, the absence of heart disease

was indicated with the value 0 by replacing values of

1, and its presence with 1 by replacing all values

from 2 to 16. The number of healthy patients

(belonging to class 0) is 245 while 207 patients have

heart disease (class 1). The dataset contains 279

attributes in addition to the class attribute. The

dataset contains a total of 408 missing values.

3.2 Performance Measures

Three criteria were used to evaluate the performance

of the classifiers (Ferri, Hernández-Orallo, &

Modroiu, 2009): Accuracy, Kappa statistic and Area

Under the ROC (Receiver Operating Characteristics)

Curve or simply AUC.

Impact of Threshold Values for Filter-based Univariate Feature Selection in Heart Disease Classiﬁcation

393

Accuracy is the rate of correct predictions made by a

classifier. The Area Under the Receiver Operating

Characteristics (ROC) Curve known as Area under

the curve (AUC) is an evaluation metric which

calculates the performance of a binary classifier by

adjusting the appearance of true positive results and

false positive results in the model. Furthermore, the

Kappa statistic measures the agreement between two

raters who each classify N items into C mutually

exclusive categories.

3.3 Methodology

In this study 10-fold cross validation method is used

to evaluate the performances of the classifiers (Arlot

& Celisse, 2010). KNN, SVM, MLP and DT

classifiers were applied using the default parameters

of the Weka tool. The procedure of the experiments

is as follows:

Step 1: For each dataset and each feature ranking

method, a feature ranking list is returned and the top

ranked features are selected using five thresholds.

Step 2: Build the different classifiers with each

feature subset as well as the entire feature set and

evaluate the classification performance using a10-

fold cross validation method to obtain accuracy,

kappa statistic and AUC scores.

Step 3: Cluster the classifiers using Scott-Knott test

(Scott & Knott, 1974) based on the Kappa criterion

in order to assess whether there is a significant

difference between the different classifiers.

Step 4: Rank the classifiers that belong to the best

Scott-Knott (SK) cluster using the Borda Count

voting system based on three performance criteria:

Accuracy, Kappa and AUC.

For the sake of clarity, the following

abbreviations were used: the feature ranking

technique ReliefF was denoted R, Info Gain was

denoted I and Correlation was denoted C.

Furthermore, to describe a feature subset selected

with a threshold and a ranker, the first number or

letter of the threshold was used along with the

abbreviation of the ranker. Furthemore, the entire

feature set was denoted ORG. For instance, SVMI4

means the classifier SVM trained using the subset

obtained with Info Gain and the threshold 40%.

4 RESULTS AND DISCUSSIONS

This section presents the empirical results of the

experiments. In order to apply feature selection and

train the different classifiers, a software prototype

based on Weka API was developed using Java

programming language under a Microsoft

environment, while the SK statistical test was

performed using R Software.

4.1 Missing Data Handling

The unprocessed Cleveland dataset contains twenty

attributes with a percentage of 100% of missing

values and two attributes with a percentage of 92%

and 24% missing values. As high percentages of

missing values can severely degrade the

classification performance (Almuhaideb & Menai,

2016), those attributes were removed from the

dataset along with the patient’s identification

number (id), the social security number (ccf) and the

name (name) attributes. Nine other attributes

contained a few missing values that did not

exceed 2%, and thus were not removed. After this

step, we are left with a total of 50 features in

addition to the class attribute. Furthermore, an

attribute containing 376 missing values (83%) was

removed from the Arrhythmia dataset resulting in a

total of 278 attributes in addition to the class

attribute.

4.2 Feature Ranking Results

Due to the limit number of pages, the datasets that

was further preprocessed by the authors to handle

missing values in addition to the datasets obtained

with feature selection will be available upon request.

4.3 Classification Results and

Discussions

For each dataset, a total of 64 variants were

evaluated. The SK test results in terms of kappa

measure for the four datasets are depicted in Fig. 1-

Fig.4. The SK identified two clusters in processed

Cleveland and Statlog datasets, four clusters in

unprocessed Cleveland and three clusters in

Arrhythmia dataset.

Fig. 1 shows that the best cluster contains a total

of 31 variants (lines in black) for the processed

Cleveland dataset. A diversity of classifiers trained

using different subsets appear in this cluster. Eight

SVM classifiers trained on subsets selected with I4,

I5, R4, R5, C4, CL, C5 and R5, in addition to

SVMORG, appear in this cluster. Furthermore, nine

MLP classifiers based on the original feature set and

subsets obtained with CL, IL, R4, R5, C4, C5, I4

and I5 belong to this cluster. The rest of the

classifiers belonging to the best cluster consist of

eight DTs based on subsets selected with I4, I5, C4,

HEALTHINF 2020 - 13th International Conference on Health Informatics

394

C5, R4, R5, IL, CL and five KNNs trained with

subsets obtained with C4, R4, R5, CL and IL.

From Fig. 2, it can be noticed that the best cluster

contains 32 classifiers for the Statlog dataset. As can

be observed, nine MLP classifiers induced from

subsets selected with IL, CL, R4, R5, I4, I5, C4, C5

and C2, in addition to MLPORG, appear in this

cluster. Moreover, eight SVM classifiers trained on

the original feature set and subsets selected with C4,

C5, I4, I5, R4, R5 and CL belong to this cluster. The

rest of the classifiers of the best cluster consist of

eight DTs based on subsets selected with R4, R5, I4,

I5, IL, CL, C5 and C2 and six KNNs trained with

subsets obtained with I4, R4, R5, IL, CL, C2.

Fig. 3 shows that the best cluster contains a total

of 29 best classifiers for the unprocessed Cleveland

dataset. Among these 29 classifiers we find ten

MLPs and ten SVMs induced from the original

feature set and subsets obtained using C2, C4, C5,

R2, R4, R5, I2, I4 and I5, and eight DT classifiers

trained using the original feature set and subsets

selected with R2, R4, R5, I4, I5, C4 and C5.

Besides, only KNNC5 belong to the best cluster.

As can be seen from Fig. 4, a total of 39 variants

are present in the first cluster for the Arrhythmia

dataset. In this cluster we can notice the presence of

fourteen SVM classifiers based on the original

feature set and reduced subsets selected with CL ,

C1, C2, C4, C5, R1, R2, R4, R5, I1, I2, I4, I5. In

addition, thirteen MLP classifiers based on subsets

selected with RL, R1, R2, R4, R5, IL, I1, I2, I4, I5,

CL, C1 and C4 belong to the best cluster. The rest of

the classifiers of the best cluster are DTs trained

with the original features and feature subsets

obtained with IL , I1, I2, I4, I5, R1, R2, R4, C4, R5,

C5. Note that no KNN classifier appears in the best

cluster for this dataset.

The first ten ranks of the best classifiers

according to the Borda count voting system are

given in Table 1.Borda count ranks the classifiers of

the best cluster based on kappa, accuracy and AUC

measures in order to gain more insight into the

results. Classifiers marked with the same letter (e.g.

ᵃ) have the same rank.

From Table 1, we observe that four classifiers

based on reduced feature subsets gave the best

performance for the Cleveland dataset. These

classifiers include SVMI5, SVMC5, MLPCL and

KNNCL with accuracies of 83.81%, 83.81%,

83.15% and 82.82% respectively. For the Statlog

dataset, the first ranked classifier is MLPIL

achieving an accuracy of 85.19%. For the

unprocessed Cleveland dataset all the ten first

classifiers achieved an accuracy of 100% while for

Arrhythmia dataset the best classifier is DTI2 with

an accuracy of 80.92%.

From the obtained results, different remarks can

be made:

- SVM classifiers proved to be very powerful

since even SVMs trained on the whole feature set

belonged to the best SK clusters for all datasets.

- The larger the dataset is the poorer KNN

classifiers perform since only one KNN

classifier(KNNC2) appears in the best SK cluster of

the unprocessed Cleveland dataset and no KNN

classifier belongs to the best cluster for Arrhythmia

which is not surprising since KNN is a memory-

based method..

- From the Borda count results we can notice that

the different subsets on which the best ten

classifiers, for Statlog and Cleveland datasets, were

based were mainly obtained with Log, 40% or 50%

thresholds which selected more attributes than 10%

and 20%. For the unprocessed Cleveland the subsets

were mainly obtained with 20%, 40% and 50%

which select more attributes than 10% and Log

while for Arrhythmia the selected subsets were

mostly obtained with 10%, 20%, 40% which

selected more attributes than Log and less than 50%.

Therefore, the size of the datasets plays an important

role in the choice of the thresholds.

- We believe that the different thresholds and

feature ranking methods presented in this study can

be tested with different datasets and classifiers in

other domains in order to obtain optimal results. In

fact, the results we obtained are very promising. For

example, for Cleveland dataset SVMI5 and SVMC5

trained on six attributes outperformed the results of

other studies, such as those of RBF trained on

subsets selected with Fuzzy Entropy and Mean

selection (81.75% with six selected attributes) or

Half selection (83.44% with seven selected

attributes) (Jaganathan & Kuppuchamy, 2013).

Furthemore, our SVM classifiers outperformed the

accuracy of fuzzy AHP and feed-forward neural

network (83%) trained on nine attributes selected

form Cleveland dataset with a modified differential

evolution algorithm (Vivekanandan & Sriman,

2017). Also for Statlog dataset MLPIL with only

three features achieved the same results of RBF

(85.19% with four selected attributes) with Fuzzy

Entropy feature ranking and Neural Network for

threshold selection. Moreover the MLPIL classifier

achieved the same accuracy of MLP classifier with

a hybrid feature selection method which also

selected three features in

Impact of Threshold Values for Filter-based Univariate Feature Selection in Heart Disease Classiﬁcation

395

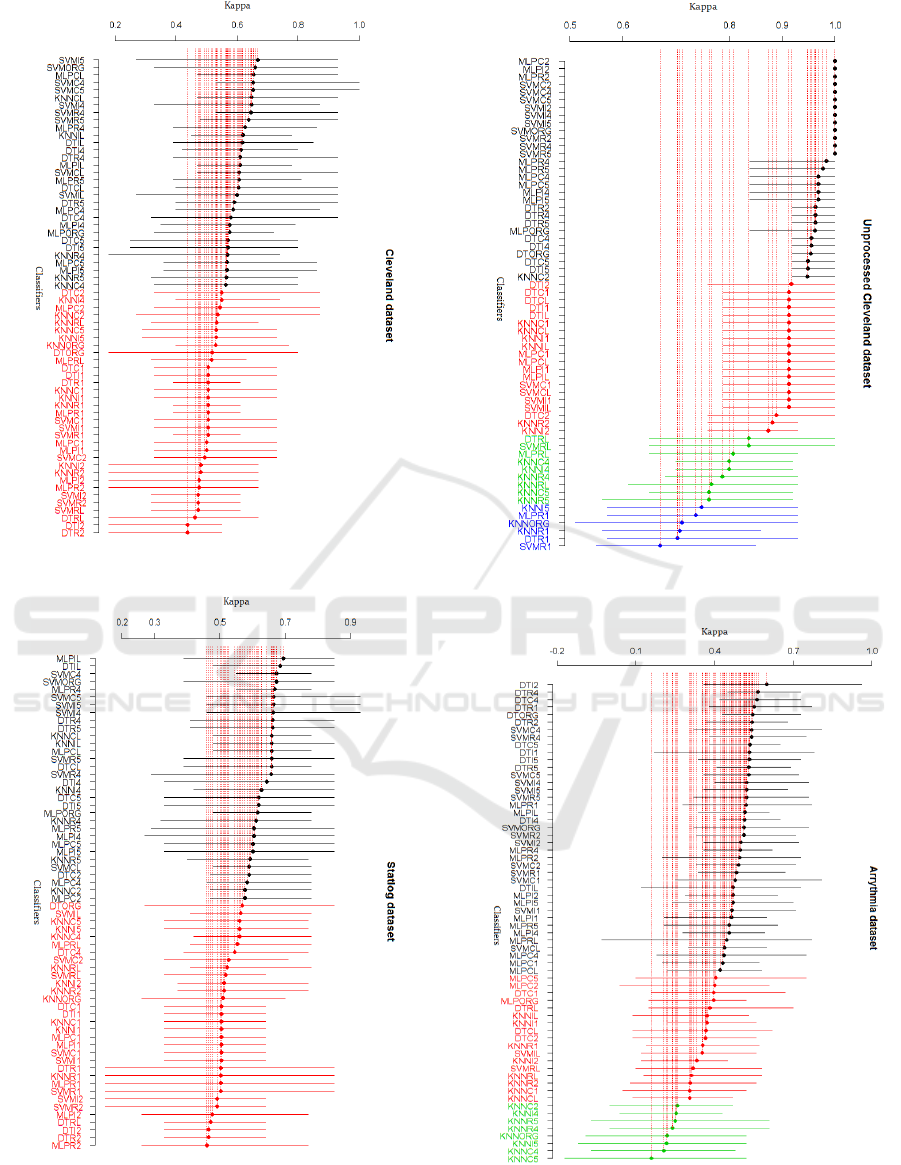
Figure 1: SK test results on processed Cleveland dataset.

Figure 2: SK test results on Statlog dataset.

Figure 3: SK test results on unprocessed Cleveland

dataset.

Figure 4: SK test results on Arrhythmia dataset.

HEALTHINF 2020 - 13th International Conference on Health Informatics

396

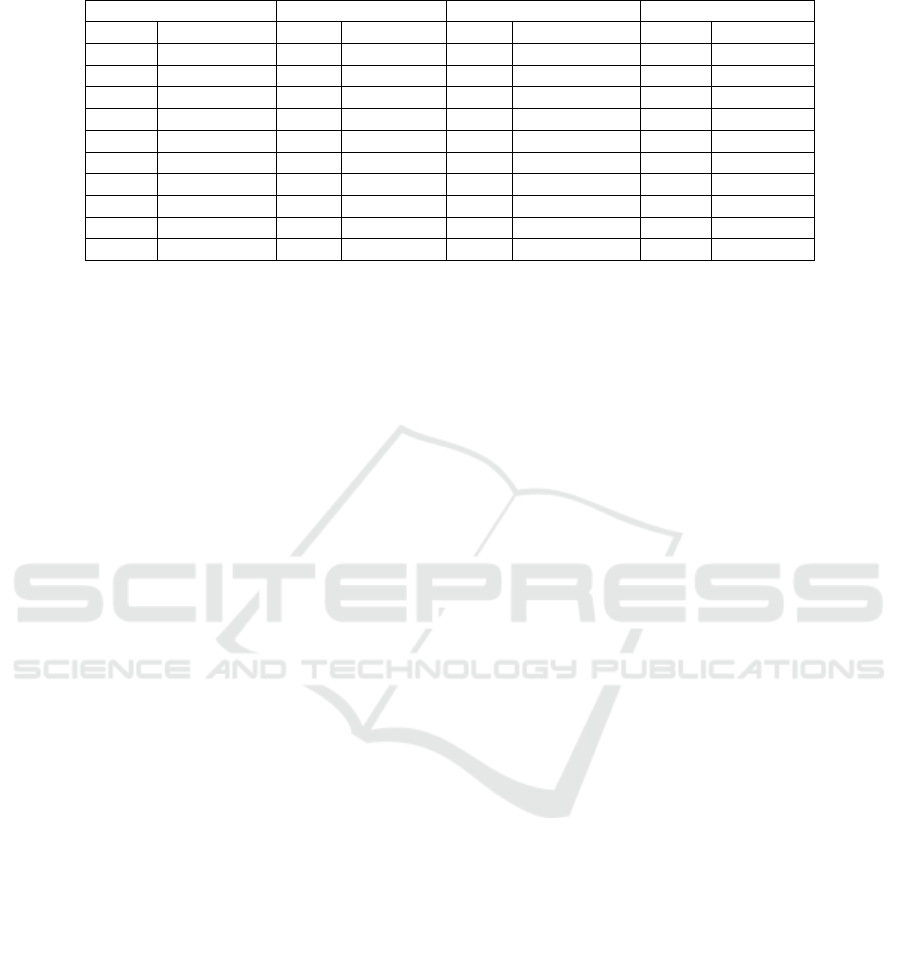
Table 1: Classifiers ranked at the top ten positions of Borda count.

Cleveland

Statlog

Unprocessed cleveland

Arrhythmia

Rank

Classifiers

Rank

Classifiers

Rank

Classifiers

Rank

Classifiers

ᵃSVMI5

MLPIL

ᵃMLPC2

DTI2

ᵃSVMC5

ᵃDTIL

ᵃMLPI2

ᵃDTC4

ᵃMLPCL

ᵃMLPR4

ᵃMLPR2

ᵃDTR4

ᵃKNNCL

ᵇSVMC4

ᵃSVMC2

DTR1

SVMORG

ᵇSVMORG

ᵃSVMC4

SVMC4

MLPR4

ᵇDTR4

ᵃSVMC5

ᵇSVMR4

SVMC4

ᵇDTR5

ᵃSVMI2

ᵇDTR2

ᵇSVMI4

ᵇKNNCL

ᵃSVMI4

DTORG

ᵇSVMR4

ᵇKNNIL

ᵃSVMI5

SVMC5

SVMR5

ᵇMLPCL

ᵃSVMORG

DTI1

(Peter & Somasundaram, 2012). For Arrhythmia

dataset, the accuracy of DTI2 outperformed the

accuracy results of DT and four other classifiers

obtained in (Sasikala, Appavu, & Geetha, 2014) with

feature extraction and hybrid feature selection.

- The results obtained for unprocessed Cleveland

considerably outperform those obtained for the

processed Cleveland dataset which shows that this

dataset contains features that can be very informative

about heart disease and thus this dataset should be

more investigated.

5 CONCLUSION

The use of univariate filter methods with different

thresholds for feature selection resulted in optimal

classification performance for one or more classifiers

over small and large heart disease datasets. The best

results obtained in this study are very competitive

with results of other methods in the literature which

used multivariate filters, hybrid or multivariate

wrapper feature selection methods on the same heart

disease datasets. The results of this study suggest that

the unprocessed Cleveland dataset might contain

highly informative features about heart disease

diagnosis.

Ongoing work aims to investigate more feature

ranking techniques to construct ensemble feature

ranking methods along with hyper-parameter tuning

for better results.

ACKNOWLEDGEMENTS

This work was conducted within the research project

MPHR/PPR1-2016-2020. The authors would like to

thank the Moroccan MESRSFC and CNRST for their

support.

REFERENCES

Almuhaideb, S., & Menai, M. E. B. (2016). Impact of

preprocessing on medical data classification.

Frontiers of Computer Science, 10(6), 1082–1102.

https://doi.org/10.1007/s11704-016-5203-5

Arlot, S., & Celisse, A. (2010). A survey of cross-validation

procedures for model selection. Statistics Surveys, 4,

40–79. https://doi.org/10.1214/09-SS054

Benhar, H., Idri, A., & Fernández-Alemán, J. L. (2019). A

Systematic Mapping Study of Data Preparation in

Heart Disease Knowledge Discovery. Journal of

Medical Systems, 43(1), 17. https://doi.org/10.1007/

s10916-018-1134-z

Bhargava, N., Sharma, G., Bhargava, R., & Mathuria, M.

(2013). Decision Tree Analysis on J48 Algorithm for

Data Mining. International Journal of Advanced

Research in Computer Science and Software

Engineering, 3(6), 1114–1119. https://doi.org/10

.23956/ijarcsse

Bolón-Canedo, V., Sánchez-Maroño, N., & Alonso-

Betanzos, A. (2013). A review of feature selection

methods on synthetic data. Knowledge and

Information Systems, 34(3), 483–519. https://doi.

org/10.1007/s10115-012-0487-8

Bolón-Canedo, V., Sánchez-Maroño, N., & Alonso-

Betanzos, A. (2015). Recent advances and emerging

challenges of feature selection in the context of big

data. Knowledge-Based Systems, 86, 33–45.

https://doi.org/10.1016/j.knosys.2015.05.014

Cover, T., & Hart, P. (1967). Nearest neighbor pattern

classification. IEEE Transactions on Information

Theory, 13(1), 21–27. https://doi.org/10.1109/

TIT.1967.1053964

Dua, D., & Graff, C. (2019). UCI Machine Learning

Repository. Retrieved from http://archive.ics.

uci.edu/ml

Ferri, C., Hernández-Orallo, J., & Modroiu, R. (2009). An

experimental comparison of performance measures

for classification. Pattern Recognition Letters, 30(1),

27–38. https://doi.org/10.1016/j.patrec.2008.08.010

Gardner, M. ., & Dorling, S. . (1998). Artificial neural

networks (the multilayer perceptron)—a review of

Impact of Threshold Values for Filter-based Univariate Feature Selection in Heart Disease Classiﬁcation

397

applications in the atmospheric sciences. Atmospheric

Environment, 32(14–15), 2627–2636. https://doi.org/

10.1016/S1352-2310(97)00447-0

Gooch, J. W. (2011). Pearson Product-Moment Correlation

Coefficient. In Encyclopedia of Measurement and

Statistics. https://doi.org/

10.4135/9781412952644.n338

Guyon, I., Steve, G., Masoud, N., & Lotfi, A. Z. (2006).

Feature Extraction: Foundations and Applications (I.

Guyon, M. Nikravesh, S. Gunn, & L. A. Zadeh, Eds.).

https://doi.org/10.1007/978-3-540-35488-8

Hall, M., Frank, E., Holmes, G., Pfahringer, B., Reutemann,

P., & Witten, I. H. (2009). The WEKA data mining

software. ACM SIGKDD Explorations Newsletter.

https://doi.org/10.1145/1656274.1656278

Hosni, M., Idri, A., & Abran, A. (2017). Investigating

heterogeneous ensembles with filter feature selection for

software effort estimation. Proceedings of the 27th

International Workshop on Software Measurement and

12th International Conference on Software Process and

Product Measurement, 207–220.

https://doi.org/10.1145/3143434.3143456

Huan, L., & Lei, Y. (2005). Toward integrating feature

selection algorithms for classification and clustering.

IEEE Transactions on Knowledge and Data

Engineering, 17(4), 491–502. https://doi.org/

10.1109/TKDE.2005.66

Idri, A., Benhar, H., Fernández-Alemán, J. L., & Kadi, I.

(2018). A systematic map of medical data preprocessing

in knowledge discovery. Computer Methods and

Programs in Biomedicine, 162, 69–85.

https://doi.org/10.1016/j.cmpb.2018.05.007

Jabbar, M. A., Deekshatulu, B. L., & Chandra, P. (2013).

Heart disease classification using nearest neighbor

classifier with feature subset selection. ANNALS

.COMPUTER SCIENCE SERIES, Vol. XI fa, 47–54.

Jabbar, M. A., Deekshatulu, B. L., & Chandra, P. (2015).

Computational intelligence technique for early

diagnosis of heart disease. 2015 IEEE International

Conference on Engineering and Technology

(ICETECH), 1–6. https://doi.org/10.1109/

ICETECH.2015.7275001

Jaganathan, P., & Kuppuchamy, R. (2013). A threshold

fuzzy entropy based feature selection for medical

database classification. Computers in Biology and

Medicine, 43(12), 2222–2229. https://doi.org/10.1016/

j.compbiomed.2013.10.016

Jovic, A., Brkic, K., & Bogunovic, N. (2015). A review of

feature selection methods with applications. 2015 38th

International Convention on Information and

Communication Technology, Electronics and

Microelectronics (MIPRO), 1200–1205. https://doi.

org/10.1109/MIPRO.2015.7160458

Kadi, I., Idri, A., & Fernandez-Aleman, J. L. (2017).

Knowledge discovery in cardiology: A systematic

literature review. International Journal of Medical

Informatics, 97, 12–32. https://doi.org/10.1016/j.ijmed

inf.2016.09.005

Kenji, K., & A., R. L. (1992). The Feature Selection

Problem : Traditional Methods and a New Algorithm.

AAAI-92 Proceedings. https://doi.org/10.1016/S0031-

3203(01)00046-2

Kononenko, I., Robnik-Šikonja, M., & Pompe, U. (1996).

ReliefF for estimation and discretization of attributes in

classification, regression, and ILP problems. Artificial

Intelligence: Methodology, Systems, Applications, 31–

40. https://doi.org/DOI 10.1016/

j.chroma.2012.01.030

Mendes, D., Paredes, S., Rocha, T., Carvalho, P.,

Henriques, J., Cabiddu, R., & Morais, J. (2015).

Assessment of cardiovascular risk based on a data-

driven knowledge discovery approach. 2015 37th

Annual International Conference of the IEEE

Engineering in Medicine and Biology Society (EMBC),

6800–6803. https://doi.org/10.1109/EMBC.2015.7319

955

Mustaqeem, A., Anwar, S. M., Majid, M., & Khan, A. R.

(2017). Wrapper method for feature selection to classify

cardiac arrhythmia. Proceedings of the Annual

International Conference of the IEEE Engineering in

Medicine and Biology Society, EMBS, 3656–3659.

https://doi.org/10.1109/EMBC.2017.8037650

Peter, T. J., & Somasundaram, K. (2012). Study and

Development of Novel Feature Selection Framework

for Heart Disease Prediction. International Journal of

Scientific and Research Publications, 2(10), 1–7.

Quinlan, J. R. (1986). Induction of Decision Trees. Machine

Learning, 1(1), 81–106. https://doi.org/

10.1023/A:1022643204877

Sasikala, S., Appavu, A. B. S., & Geetha, S. (2014). RF-

SEA-Based Feature Selection for Data Classification in

Medical Domain. Intelligent Computing, Networking,

and Informatics, 243, 599–608.

https://doi.org/10.1007/978-81-322-1665-0_59

Scott, A. J., & Knott, M. (1974). A Cluster Analysis Method

for Grouping Means in the Analysis of Variance.

Biometrics. https://doi.org/10.2307/2529204

Seijo-Pardo, B., Porto-Díaz, I., Bolón-Canedo, V., &

Alonso-Betanzos, A. (2017). Ensemble feature

selection: Homogeneous and heterogeneous approaches.

Knowledge-Based Systems, 118, 124–139.

https://doi.org/10.1016/j.knosys.2016.11.017

Shouman, M., Turner, T., & Stocker, R. (2012). Using data

mining techniques in heart disease diagnosis and

treatment. 2012 Japan-Egypt Conference on

Electronics, Communications and Computers, 173–177.

https://doi.org/10.1109/JEC-ECC.2012.6186978

Ting, S. L., Shum, C. C., Kwok, S. K., Tsang, A. H. C., &

Lee, W. B. (2009). Data Mining in Biomedicine:

Current Applications and Further Directions for

Research. Journal of Software Engineering and

Applications, 02(03), 150–159. https://doi.org/10.

4236/jsea.2009.23022

Vapnik, V. N. (2000). The Nature of Statistical Learning

Theory. https://doi.org/10.1007/978-1-4757-3264-1

Vivekanandan, T., & Sriman, N. I. N. C. (2017). Optimal

feature selection using a modified differential evolution

algorithm and its effectiveness for prediction of heart

disease. Computers in Biology and Medicine, 90, 125–

136. https://doi.org/10.1016/j.compbiomed.2017.09.011

HEALTHINF 2020 - 13th International Conference on Health Informatics

398