Learning Geometrically Consistent Mesh Corrections

tefan S

aftescu and Paul Newman

Mobile Robotics Group, Oxford Robotics Institute, University of Oxford, U.K.

{stefan, pnewman}@robots.ox.ac.uk

Keywords:

3D Reconstruction, Depth Reﬁnement, Deep Learning.

Abstract:

Building good 3D maps is a challenging and expensive task, which requires high-quality sensors and careful,

time-consuming scanning. We seek to reduce the cost of building good reconstructions by correcting views of

existing low-quality ones in a post-hoc fashion using learnt priors over surfaces and appearance. We train a

convolutional neural network model to predict the difference in inverse-depth from varying viewpoints of two

meshes – one of low quality that we wish to correct, and one of high-quality that we use as a reference.

In contrast to previous work, we pay attention to the problem of excessive smoothing in corrected meshes. We

address this with a suitable network architecture, and introduce a loss-weighting mechanism that emphasises

edges in the prediction. Furthermore, smooth predictions result in geometrical inconsistencies. To deal with

this issue, we present a loss function which penalises re-projection differences that are not due to occlusions.

Our model reduces gross errors by 45.3%–77.5%, up to ﬁve times more than previous work.

1 INTRODUCTION

Dense 3D maps are a crucial component in many sys-

tems and better maps make robots easier to build and

safer to operate. Despite recent progress in hardware

such as the wide availability of GPUs, and algorithms

that scale with the amount of data and the available

hardware, high-quality maps, especially at large scales

and outdoors, remain difﬁcult to build cheaply, often

requiring expensive sensors such as 3D lidars, and

careful, dense scans.

The main motivation of our work is to reduce the

cost of building good dense 3D maps. The reduction

in cost can come from either: a) cheaper but nosier

sensors, such as stereo cameras; b) less data, and there-

fore less time spent densely scanning an area. There

are two ways in which we can produce better recon-

structions with cheaper data. We can learn the kinds of

errors a certain modality produces. For a stereo cam-

era, for example, there will be missing data in areas

without a lot of texture (walls, roads), and the ambi-

guity in depth is usually along the viewing rays. In

addition, we can learn priors for a target environment:

cars usually have known shapes, roads and buildings

do not have holes in them, surfaces tend to be vertical

or horizontal in an urban environment, etc.

We tackle the problem of correcting dense recon-

structions with a convolutional neural network (CNN)

that operates on rasterised views of a 3D mesh as a

post-processing step, following a classical reconstruc-

Mesh Features (View 2)Mesh Features (View 1)

Shared

Weights

abs

Resample from

Element-wise addition

Element-wise subtraction

Element-wise multiplication

Corrected inverse-depth Corrected inverse-depth

Resampled inverse-depth

Geometric Consistency Error

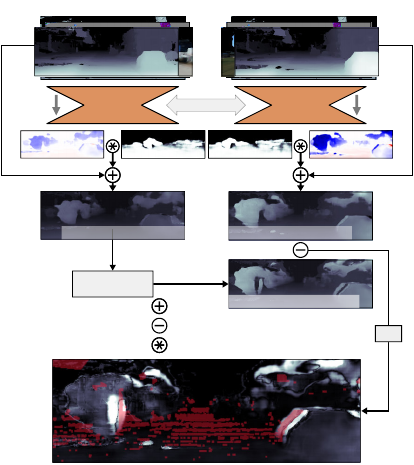
Figure 1: Illustration of geometric consistency for two views

of the same scene a few meters apart. The predictions of our

model can be used to compute corrected depth maps for a

set of views. The corrected depth-maps should be consistent:

they should be describing the same scene. To enforce this,

we densely reproject inverse-depth from View 1 to View 2,

using the corrected depth of View 2. The absolute differ-

ence (bottom) is the inconsistency of View 1 with respect to

View 2. This is minimised during the training of our model,

which enforces geometrically consistent predictions. The

red overlay is the occlusion mask.

tion pipeline. To train this model, we start with two

meshes, a low-quality one and a reference high-quality

one. From each reconstruction, we render multiple

types of images (such as inverse-depth, normals, etc.),

referred to as mesh features, from multiple viewpoints.

We then train the model on the mesh features to pre-

dict the difference in inverse-depth between the high-

quality reconstruction and the low-quality one, thus

enabling us to correct the low-quality mesh.

Previous work (Tanner et al., 2018) has demon-

strated the idea of correcting meshes post-hoc via 2D

rasterised views. We address its two main limitations.

Firstly, we deal with the issue of overly smooth pre-

dictions. We propose changes to the architecture and

training more suitable for our task: we add skip con-

nections from the encoder to the decoder in our

CNN

which are known to help in localising edges in pre-

dictions; we propose a loss-weighting method that pe-

nalises incorrect predictions more the closer they are

to an edge. Secondly, predictions on nearby views are

not always consistent, i.e. when applying the predicted

corrections the geometry of the scene is not always

the same. To improve consistency, we employ a view

synthesis based loss, and show that this also improves

the performance of the network. An illustration of the

geometric consistency loss is shown in Figure 1, while

Figure 2 shows an overview of our method.

Our contributions are as follows:

Error correction: We propose a

CNN

model that

is able to correct 2D views of a dense 3D reconstruc-

tion. We propose a novel weighting mechanism to

improve performance around edges in the prediction.

We evaluate it against existing work and show that

we outperform it, especially when images are from

multiple viewpoints.

Geometric consistency: We adapt the photometric

consistency loss that features in related tasks such as

depth-from-mono (Godard et al., 2017) to the task of

correcting reconstructions. This is a novel use of the

loss, which has thus far only been employed on RGB

images. We leverage the existing reconstruction to

compute occlusion masks, and thus exclude from the

loss areas where geometric consistency is impossible.

We show that this use of geometric consistency as an

auxiliary loss further improves our model.

2 RELATED WORK

Several systems for building 3D reconstructions have

been proposed, such as BOR

G (Tanner et al., 2015) or

KinectFusion (Newcombe et al., 2011). Our approach

is to correct the output of such a system by looking

at the meshes it builds. As we operate on inverse-

depth images, our work is similar to depth reﬁnement.

Below, we review some of the literature on that topic,

as well as some other methods that our system draws

inspiration from.

Filtering and Optimisation of Depth

Improving depth or disparity images is a well-

researched area, with various methods proposed, some

of which are guided by an additional aligned colour

image. The most straightforward unguided techniques

are based on minimising either on a joint bilateral ﬁl-

ter (

JBF

) (Tomasi and Manduchi, 1998) when ﬁltering,

or Total Generalised Variation (

TGV

) (Bredies et al.,

2010) for optimisation. Guided techniques use another

image aligned with the depth-map to inform the re-

ﬁnement. The guide image is used especially around

edges, to modulate the smoothing effect of ﬁltering

or optimisation. For example, Kopf et al. (2007) or

Matsuo et al. (2013) propose variants of a

JBF

for re-

ﬁning depth, while Tanner et al. (2016) demonstrates

TGV

-based method that uses both magnitude and di-

rection of colour images to regularise depth maps. An

interesting combination of learning and optimisation

is proposed by Riegler et al. (2016). The Primal-Dual

algorithm (Chambolle and Pock, 2011) normally em-

ployed for

TGV

optimisation is unrolled and included

into a

CNN

model that learns to upsample depth im-

ages. Our work relies on an existing 3D reconstruc-

tion pipeline (Tanner et al., 2015), in which some of

these depth reﬁnement techniques have already been

employed. We focus on post-processing meshes and

ﬁxing errors that cannot easily be ﬁxed in single, live

depth images.

Learnt Depth Reﬁnement and Completion

Some methods for learning depth map reﬁnement and

completion have been recently proposed. Eldesokey

et al. (2018); Uhrig et al. (2017) propose

CNN

model

for solving the KITTI Depth Completion Challenge,

where sparse depth maps produced from laser data

are densiﬁed. Hua and Gong (2018) use normalised

convolutions (Knutsson and Westin, 1993) to predict

dense depth maps that have been sparsely sampled.

These methods all rely on having some sort of high-

quality, usually laser, depth information (albeit sparse)

at run-time, and are only designed to ﬁll in the missing

data. In contrast, we only require high-quality data

during training, and our method aims to reﬁne depth

from a low-quality mesh in a more general sense – both

ﬁlling in blanks, as well as reﬁning existing surfaces.

A few other methods more closely related in spirit

to ours aim to learn depth reﬁnement using meshes as

reference. Kwon et al. (2015) use dictionary learning

Extracted

mesh features

Stereo Reconstruction

Corrected Reconstruction

3D Fusion (BOR²G)

Geometric

Consistency

Regression

(data, ∇)

Regression

(data, ∇)

Rened

Inverse-depth

Predicted ErrorPredicted Error

Predicted Mask

CNN

Shared

Weights

Extracted

mesh features

Inverse-depth

labels

Stereo Reconstruction

Lidar Reconstruction

Correction

Training

Rened

Inverse-depth

Predicted ErrorPredicted Error

Predicted Mask

CNN

Shared

Weights

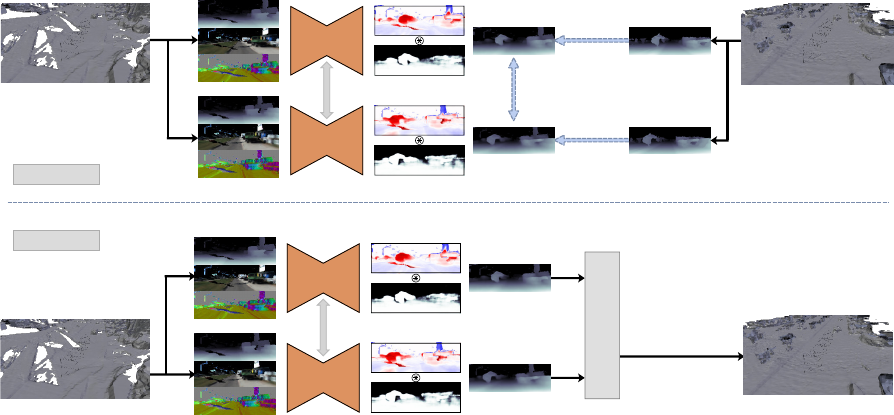
Figure 2: Overview of our method. Our network learns to correct meshes by observing 2D renderings of mesh features and

predicting the error in inverse-depth. In addition to error, our network also predicts a soft mask that is multiplied element-wise

with the error to control which regions of the input inverse-depth image are corrected. During training, inverse-depth images

from a high-quality reconstruction are used to supervise our network, and a geometric consistency loss is applied between

predictions on nearby views, as described in Section 3.2. When using our model to correct meshes, the reﬁned inverse-depth

images of the input mesh are fused into a new 3D reconstruction of higher quality.

to model the statistical relationships between raw RGB-

D images, and high-quality depth data obtained by

fusing multiple depth maps with KinectFusion (New-

combe et al., 2011). Two other recent works use fused

RGB-D reconstruction to obtain high-quality reference

data and train

CNN

s to enhance depth. Zhang and

Funkhouser (2018) uses a colour image to predict nor-

mals and occlusion boundaries, supervised by the 3D

reconstruction, and then formulates an optimisation

problem to ﬁll in holes in an aligned depth image.

Jeon and Lee (2018) introduce a 4000-image dataset

of raw/clean depth image pairs, and train a

CNN

enhance raw depth maps. Furthermore, they show

that 3D reconstructions can be obtained with fewer

data and quicker when using their depth-enhancing

network. These methods all rely on live colour images

to guide the reﬁnement or completion of live depth.

That means that only limited data is available for train-

ing. In contrast, our purely mesh-based formulation

allows us to extract many more training pairs from any

viewpoint, removing any viewpoint-speciﬁc bias that

might otherwise surface while learning.

Learnt Depth Estimation

Another related line of research has been monocular

depth estimation, which inspires our choices of net-

work architecture and the use of geometry as a source

of self-supervision. Dharmasiri et al. (2019); Godard

et al. (2017); Klodt and Vedaldi (2018); Laina et al.

(2016); Mahjourian et al. (2018); Ummenhofer et al.

(2017); Zhou et al. (2017), etc. propose various

CNN

models for depth estimation from single colour im-

ages. When explicit depth ground-truth is unavailable,

the training is self-supervised using multiview geom-

etry: the predicted depths and relative poses should

maximise the photometric consistency of nearby input

images. In this work, we show how the photometric

consistency loss can be adapted to ensure consistency

between inverse-depth predictions directly, without

need for colour images.

3 METHOD

3.1 Training Data

In contrast to many existing approaches, this work is

about correcting existing reconstructions, and there-

fore we assume the existence of 3D meshes of a scene.

In addition to the low-quality reconstruction we wish

to correct, we also have a high-quality reconstruction

of the same scene. For example, we learn to correct

3D reconstructions from depth-maps using laser recon-

structions as a reference. To build the meshes we train

on, we use the BOR

G (Tanner et al., 2015) system.

The training data consists of 2D views of the

(a) Colour Reconstruction

(b) Inverse-depth

(d) Triangle Area

(e) Triangle Edge Length Ratios

(f) Surface to Camera Angle

Figure 3: Example mesh features. We ﬂy a camera through

an existing mesh and at each location produce mesh features.

During training, inverse-depth images of a high-quality mesh

are available, and our model learns a mapping from the mesh

features pictured above to the high-quality inverse-depth.

meshes. We use the same virtual camera to gener-

ate aligned views of the low-quality mesh and the

high-quality mesh for each scene. Because a mesh is

available, we can generate multiple types of images

at each viewpoint. In particular, we generate inverse-

depth, normals, mesh triangle area, mesh triangle edge

ratio (ratio between the shortest and the longest edge

of each triangle), and surface-to-camera angle (Fig-

ure 3). We refer to these images as mesh features. The

ground-truth labels (

∆

) are computed as the difference

in inverse-depth between high-quality and low-quality

reconstructions:

∆(p) = d

(p) − d

(p) (1)

where

is a pixel index, and

and

are inverse-

depth images for the high-quality and low-quality re-

construction, respectively. For notational compactness,

∆(p)

is referred to as

∆

, and future deﬁnitions are over

all values of p, unless otherwise mentioned.

Inverse-depth is used instead of depth for several

reasons. Firstly, it emphasises surfaces close to the

camera where more information is available per pixel.

Secondly, background (non-surface) pixels are not pro-

cessed separately – they are assigned a value of zero,

corresponding to points inﬁnitely far away from the

camera. If we used depth, those pixels would either

have to be assigned an arbitrary ﬁnite value, which

would result in semantic discontinuities in the output,

or learnt to be ignored by the network, since there is

no standard way to deal with inﬁnite values in a

CNN

Finally, another advantage of inverse-depth is that re-

sampling it, which is needed to compute geometric

consistency, is simpler than resampling depth images.

3.2 Geometric Consistency

Intuitively, since the reconstructions we wish to cor-

rect are static, the predictions made from overlapping

views should be geometrically consistent. In other

words, surfaces that appear in a certain location accord-

ing to a prediction should appear in the same location

in all predictions where they are in view.

We resample nearby predicted views according

to the predicted geometry of the current view, and

minimise the absolute difference in inverse-depth. This

dense warping is similar to reprojecting nearby views

into the current view, but has the advantage of being

differentiable, and of generating dense images instead

of sparse reprojected pointclouds. An illustration of

this idea is shown in Figure 1.

Normally, dense warping is used in conjunction

with colour images, where the values of the pixels

are view-independent. Since we are warping inverse-

depth images, where the pixel values depend on the

viewpoint, we need to compute the absolute difference

in the same camera frame.

Concretely, for a view

, a nearby view

, let

∆

∗

be a

CNN

prediction for the target view, let

∆

∗

be a

prediction for the nearby view, and let

∗

= d

+ ∆

∗

and

∗

= d

+ ∆

∗

the corrected inverse-depth images

for the two views. Furthermore, let

be pixel coor-

dinates in the target view,

the intrinsic matrix of

the virtual camera, and

n,t

the SE(3) transform from

view

to view

. We can then deﬁne the geometric

(a) Front-left view. (b) Front-right view.

Figure 4: Visibility masks for views generated at a location. The image regions highlighted in red, green, blue, and cyan

are also visible in the (a) left, (b) right, (c) back, and (d) top views, respectively. (a): inverse-depth view from a dense 3D

reconstruction; the regions visible in the left, and top views are respectively highlighted in green and cyan. (b): a view of the

same scene as (a), 2 m to the right; the regions visible in the left, and top views are respectively highlighted in red and cyan. (c):

a view of the same scene as (a), looking back; the region visible in top view is highlighted in cyan. (d): a view of the same

scene as (a), looking down from 25 m above; the regions visible in the left, right, and back views are respectively highlighted in

red, green, and blue. Areas outside the highlighted regions are occluded – they are not visible from the other view. For example,

distant areas of (a)–(c), such as the sky, are not visible from the top view; the region behind the car on the right in (a) is not

visible from (b). These occluded parts of the image are ignored when computing the geometric consistency loss (Section 3.3.2).

For visualisation purposes, morphological closing has been applied to the visibility masks shown here, to remove some of the

small-scale noise.

inconsistency

∗

n,t

−

∗

n,t

where

∗

n,t

is the predicted

inverse-depth from view

in the frame of view

and

∗

n,t

is the warped inverse-depth from view n.

They are deﬁned as follows:

∗

n,t

) = d

∗

), (2)

∗

n,t

) =

(4)

(3)

+ ε

, (3)

where superscripts indicate vector elements,

is the

3D homogeneous point in view

corresponding to

pixel p

, and p

its projection:

(3)

+ ε



(1)

(2)



, (4)

= F

, (5)

= (p

1 d

∗

))

, (6)

= K

n,t

−1

, (7)



K 0



. (8)

The sample pixel

does not necessarily have in-

teger coordinates, and thus may lie in-between pixels

in the

∗

grid. Note that we add a small value

with

the same sign as

(3)

in Equations 3 and 4 to avoid

dividing by zero. Under the mild assumption that sur-

faces between pixels are planar, we can sample

∗

linearly interpolating the four pixels nearest to

–

another advantage of the inverse-depth formulation.

Occlusion Masks

A common problem with this approach is that views

cannot be consistent in the presence of occlusions. In

our setting, however, since the views are synthetic

(and therefore the intrinsic and extrinsic parameters

are perfectly known), we are able to create occlusion

masks and only apply the geometric consistency loss

where there are no occlusions, as noted in Equation 11.

We compute occlusion masks from the reference

high-quality reconstruction. Each mesh triangle is as-

signed an index by hashing its world frame coordinates.

Then, in addition to mesh features, an image with mesh

triangle indices is generated at each location. For each

pair of views, each pixel of the triangle index image

is resampled from one view into the other in a similar

fashion to the inverse-depth above. Instead of interpo-

lating between the four nearest neighbours, these are

returned as four separate samples. The pixels where

the indices match at least one of the four samples are

considered unoccluded, and the pixels where they do

not are considered occluded (see Figure 4).

Small errors appear due to rasterisation when mesh

triangles are too small, often those that are far away

from the camera. We could avoid these errors by gen-

erating occlusion masks with the OpenGL rasterisation

Table 1: Overview of the

CNN

architecture for error predic-

tion.

Block Type Filter Size/Stride Output Size

Input - 96 ×288 × F

Convolution 3 ×3/1 96 ×288 × 64

Residual 3 ×3/1 96 ×288 × 64

Convolution 5 ×5/1 48 ×144 × 64

Max Pool 3 ×3/2 24 × 72 × 64

Residual×2 3 ×3/1 24 × 72 × 64

Projection 3 ×3/2 12 × 36 × 256

Residual×2 3 ×3/1 12 × 36 × 256

Projection 3 ×3/2 6 × 18 × 512

Residual×2 3 ×3/1 6 × 18 × 512

Projection 3 ×3/2 3 × 9 × 1024

Residual×8 3 ×3/2 3 × 9 × 2048

Up-projection 3 ×3/

6 × 18 ×1024

Up-projection 3 ×3/

12 × 36 × 512

Up-projection 3 ×3/

24 × 72 × 256

Up-projection 3 ×3/

48 ×144 × 128

Up-projection 3 ×3/

96 ×288 × 32

Residual 3 ×3/1 96 ×288 × 32

Convolution 3 ×3/1 96 ×288 × 2

pipeline when the rest of the data is generated. How-

ever, this greatly increases the space required to store

training data – the number of occlusion masks scales

quadratically with the number of views we want to en-

force consistency between. Generating the occlusion

masks on the ﬂy means that geometric consistency

can be enforced between arbitrary views, so more set-

tings can be explored without regenerating part of the

training data.

3.3 Model

3.3.1 Network Architecture

The model used is an encoder-decoder

CNN

similar to

the one proposed in Tanner et al. (2018). The encoder

is composed of residual blocks based on the ResNet-

50 architecture (He et al., 2016), and the decoder uses

up-convolutions proposed by Shi et al. (2016). U-Net

Ronneberger et al. (2015) style skip connections are

added between the encoder and the decoder to improve

the sharpness of predictions. As a simple way to offer

our model some introspective capabilities, we predict

a soft attention mask (with values

∈ [0, 1]

) in addition

to the error in inverse-depth, as a second output of the

network. This mask is multiplied pixel-wise with the

error prediction to modulate which parts are going to

be used and does not require extra supervision. Table 1

provides an overview for each of the layers of the

proposed CNN.

3.3.2 Loss

The objective function has several components, as fol-

lows. The ﬁrst term is the data loss that minimises the

error between the output and the label. To compute

this loss, we use berHu norm (Owen, 2007). For large

errors, this behaves in the same way as an

norm.

For small errors, where the gradients of

become too

small to drive the error completely to zero,

norm is

used instead. The advantages of this norm have also

been observed in Laina et al. (2016); Ma and Karaman

(2018). The data loss is deﬁned as follows:

data

∑

p∈V

W ·

∆

∗

− ∆

berHu

, (9)

where

is the pixel index,

is the set of valid pixels

(to account for missing data in the ground-truth),

is a per-pixel weight detailed in Section 3.3.3,

∆

∗

and

∆

are the prediction and the target, respectively, and

k · k

berHu

is the berHu norm.

To improve small-scale details and prevent arte-

facts in the prediction, while also allowing for sharp

discontinuities, we also apply a loss on the gradient of

the predictions:

∇

∑

p∈V

W·



∂

∆

∗

− ∂

∆



∂

∆

∗

− ∂

∆





. (10)

We use the Sobel operator (Sobel and Feldman,

1968) to approximate the gradients in the equation

above.

The geometric consistency loss guides nearby pre-

dictions to have the same 3D geometry, and relies on

reprojected nearby views

∗

n,t

. For a target view

, a set

of nearby views

, the set of pixels unoccluded in a

nearby view

(see Figure 4), this loss is deﬁned as:

∑

n∈N

∑

p∈U



∗

n,t

− d

∗

n,t



. (11)

Note that

has no relation to the set of valid pixels

(

) from the previous losses, since this loss is only

computed between predictions. This enables the net-

work to make sensible predictions even in parts of the

image which have no valid label.

Finally, we also include an

weight regulariser,

reg

, to reduce overﬁtting by keeping the weights

small. The overall objective is thus deﬁned as:

L = λ

data

+ λ

∇

+ λ

reg

, (12)

where

is the scale, and the

s are weights for each

of the components (see Table 2 for values).

3.3.3 Loss Weight

Inspired by the work of Ronneberger et al. (2015) on

U-Nets, we use a loss-weighting mechanism based on

Table 2: Summary of Hyperparameters Used in System.

Symbol Value Description

data

1 Weight of the data loss.

∇

0.1 Weight of the smoothness loss.

0.1

Weight of the geometric consis-

tency loss.

reg

−6

Weight of the

variable regu-

lariser.

min

0.1 Minimum per-pixel loss scaling.

max

5 Maximum per-pixel loss scaling.

max

−4

Initial learning rate.

min

5 ·10

−6

Final learning rate.

max

1.2 ·10

Learning rate decay steps.

0.9

Adam exponential decay rate for

ﬁrst moment estimates.

0.999

Adam exponential decay rate for

second moment estimates.

Norm at witch gradients are

clipped during training.

16 Batch size.

5 ·10

Number of training steps.

the Euclidean Distance Transform (Felzenszwalb and

Huttenlocher, 2012) to emphasise edge pixels when

regressing to the error in depth. We ﬁrst extract Canny

edges (Canny, 1986) from the ground-truth labels.

Based on these edges, we then compute the per-pixel

weights as:

d(p) = ln(1 + EDT(p))

W(p) = (w

max

− w

min

)



1 −

d(p)

max

d(p)



+ w

min

(13)

where

W(p)

is the loss weight for pixel

EDT(p)

the Euclidean Distance Transform at pixel

, and

min

and

max

are the desired range of the per-pixel weight.

This will assign

max

weight to edge pixels, and lower

weights the farther pixels are from an edge, down to

min

for the farthest pixels.

4 EXPERIMENTS

4.1 Experimantal Setup

Training and Inference

The network is implemented in Python using Tensor-

Flow v1.12. Each model is trained on an Nvidia Ti-

tan V GPU. The weights are optimised for 500 000

steps with a batch size of 16 using the Adam opti-

miser (Kingma and Ba, 2015). The learning rate (

)

is decayed linearly for the ﬁrst 120 000 steps. Gener-

ating the mesh features takes an average of 52 ms per

view using OpenGL on an Nvidia GTX Titan Black,

# gross error pixels

1.05 1.15 1.25 1.25

1.25

Threshold

Ours (full)

Ours w/o geometric consistency

Uncorrected

Baseline (Tanner et al., 2018)

Model

Figure 5: Gross error correction. For each threshold (Equa-

tion 14), we count how many pixels are incorrect in the

predictions over the test set. Our full model removes 45.3%

of the smaller errors and 77.5% of the gross errors. The

baseline model is unable to effectively handle the multi-view

setup, and fails to correct gross errors.

and inference takes an average of 12.5 ms on the Ti-

tan V. All the training hyper-parameters are deﬁned in

Table 2. The optimiser parameters are the ones sug-

ested by Kingma and Ba (2015), while the rest have

been chosen after a small search to improve validation

metrics.

Dataset

Three sequences from the KITTI visual odometry

(

KITTI-VO

) dataset were used as the input to the re-

construction pipeline. For each sequence, two recon-

structions are built: one from the stereo camera depth-

maps, and one from the laser data. Both the meshes

are generated with a ﬁxed voxel width of 0.2 m. In

the experiments, we show how to learn a correction

of the depth-map reconstruction using the laser recon-

struction as reference. Using OpenGL Shading Lan-

guage (

GLSL

), we create a virtual camera and project

each dense reconstruction into mesh features. We

sample locations along the original trajectory in each

sequence every 0.3m, and at each location we gener-

ate mesh features from four different viewpoints. An

illustration of the viewpoints is shown in Figure 4. For

all experiments, the

KITTI-VO

sequences 00, 05, and

06 are used, from which a total of 96 728 training ex-

amples of size

96 × 288

are generated. We split each

of the mesh feature sequences into three distinct parts:

the ﬁrst 80% we use as training data, the next 10%

we use for validating hyperparameter choices, and the

last 10% we use for evaluation. All three sequences

are predominantly in urban environments with small

amounts of visible vegetation.

Performance Metrics

We use some metrics common in literature for assess-

ing inverse-depth predictions.

Table 3: Generalisation Capability of Depth Error Correction.

Model Train Test iMAE iRMSE δ < 1.05 δ < 1.15 δ < 1.25

δ < 1.25

Uncorrected – 00 1.76 ·10

−2

8.10 · 10

−2

52.71% 79.00% 84.02% 88.73% 90.71%

– 05 1.57 · 10

−2

8.15 · 10

−2

55.11% 80.61% 84.27% 88.30% 90.46%

– 06 2.81 · 10

−2

1.24 · 10

−1

49.47% 72.71% 75.07% 78.64% 80.49%

Ours 05; 06 00 1.45 ·10

−2

8.03 · 10

−2

66.14% 85.27% 89.93% 94.76% 96.82%

00; 06 05 1.19 ·10

−2

7.67 · 10

−2

70.38% 86.31% 90.25% 94.86% 96.99%

00; 05 06 2.37 ·10

−2

1.15 · 10

−1

62.27% 78.14% 81.72% 85.85% 88.20%

Table 4: Depth Error Correction Ablation Study Results.

Model iMAE iRMSE δ < 1.05 δ < 1.15 δ < 1.25 δ < 1.25

δ < 1.25

Uncorrected 1.85 · 10

−2

8.73 ·10

−2

50.90% 80.77% 85.38% 89.72% 91.35%

Baseline 1.47 · 10

−2

6.25 ·10

−2

63.92% 81.65% 85.90% 90.72% 92.69%

w/ our losses; no GC 1.28 · 10

−2

6.26 ·10

−2

67.77% 84.35% 89.05% 94.16% 96.17%

w/ our losses; GC 1.17 ·10

−2

5.44 ·10

−2

68.66% 84.64% 89.45% 94.81% 96.65%

Ours (no attn; no GC) 1.12 · 10

−2

5.49 ·10

−2

70.47% 87.68% 92.08% 96.35% 97.72%

Ours (no GC) 1.12 · 10

−2

5.63 ·10

−2

71.31% 88.34% 92.41% 96.41% 97.81%

Ours (no attn) 1.02 · 10

−2

5.31 ·10

−2

72.93% 89.27% 93.20% 96.87% 98.10%

Ours (full) 1.06 · 10

−2

5.37 · 10

−2

73.16% 88.94% 92.91% 96.76% 98.05%

Our ﬁrst metric measures the accuracy of our net-

work’s ability to estimate errors under a given thresh-

old, serving as an indication of how often our estimate

is correct. The thresholded accuracy measure is essen-

tially the expectation that a given pixel in

is within

a threshold thr of the label:

δ = E

p∈V





max



∗



< thr



, (14)

where

is the reference inverse-depth,

∗

is the

predicted inverse depth,

is the set of valid pix-

els, and

is the cardinality of

, and

I(·)

repre-

sents the indicator function. For granularity, we use

thr ∈ {1.05, 1.15, 1.25, 1.25

, 1.25

In addition, the mean absolute error (

MAE

) and

root mean square error (

RMSE

) metrics provide a quan-

titative measure of per pixel error and are computed as

follows:

iMAE =

∑

p∈V



∗

− d



, (15)

iRMSE =

∑

p∈V

∗

− d

)

, (16)

where the ‘i’ indicates that the metrics are computed

over inverse-depth images.

4.2 Gross Error Correction

We ﬁrst look at how well our model corrects gross

errors in inverse-depth. Equation 14 can be used to

classify pixels in an image as either correct or incor-

rect at a given threshold. Using this method, we count

the number of incorrect pixels in our predictions, and

compare it to the number of incorrect pixels in the

input inverse-depth. As a baseline, we train the model

proposed in Tanner et al. (2018) on our dataset, and

compare it to our full model, trained with and without

the geometric consistency loss (Figure 5). Our pro-

posed model outperforms the baseline at correcting

both small errors (

thr = 1.05

) as well as larger errors,

reducing the number of errors at

thr = 1.25

by 77.5%.

4.3 Generalisation Capability

To be useful in practice, the model needs to be able

to generalise to new data. For example, separate mod-

els could be trained for indoor scenes and outdoor

scenes, or other different types of environments, but

certainly within the same kind of environment, one

model should work well for a variety of scenes.

To evaluate this, we train the full model on a subset

of the available sequences, and test it on the rest (ex-

cluding the frames used for validation in Section 4.2).

Sequences 00 and 05 represent different suburban

scenes of the same city, while the scene in sequence

06 is in an area where the road is much wider and the

buildings are much farther apart. Table 3 shows the

data splits and the performance of the models on the

test sequences. Interestingly, the model trained only on

the suburban scenes of sequences 00 and 05 performs

particularly well on the visually distinct sequence 06.

(a) Ground truth (b) Baseline

(e) Ours (full)

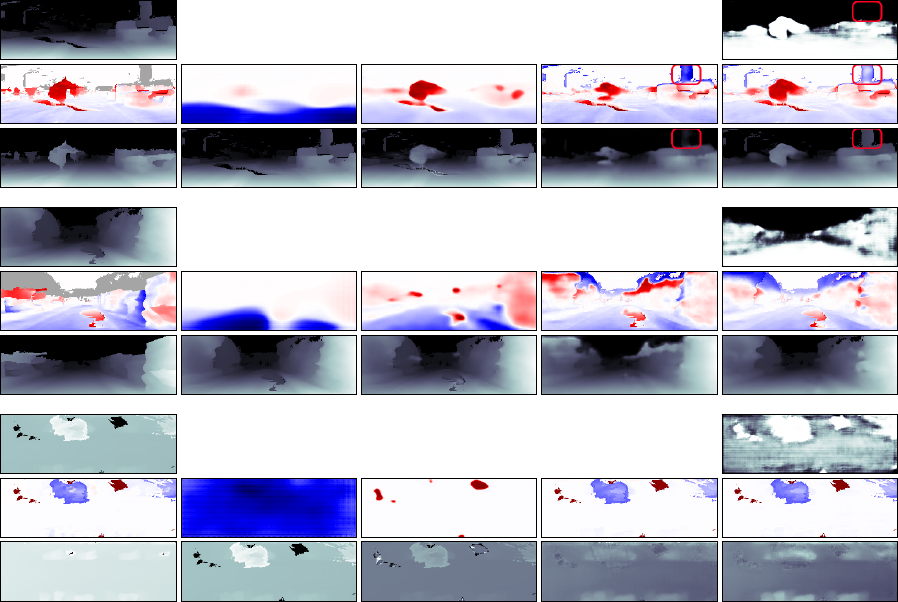
Figure 6: Illustration of how the quality of the predictions changes as different components are added to the system. Each three

rows show an example, as follows: (a) Input inverse-depth and ground-truth error, and ground-truth inverse-depth. The shaded

areas in the ground-truth error represent missing data in the reference mesh. (b)–(d) Prediction and corrected inverse-depth.

(e): Attention mask, prediction, and corrected inverse-depth. The baseline model (b) only learns very rough predictions and is

unable to generalise well to the top viewpoint (last example). Our proposed losses help with generalisation across viewpoints,

but without skip connections in the network predictions are not very well localised (c). Our model (d); (e) makes well-localised

predictions. The attention mask removes some of the spurious predictions where there is no reference data (e). For example, the

highlighted background structure in the ﬁrst example is removed when the attention mask is not used (d), while the attention

mask disables edits to that region of the input image (e).

This highlights the ability of our model to reduce gross

errors.

4.4 Ablation Study

To better understand how different components of our

model improve the learnt correction, we perform an

ablation study. The results in Table 4 show that our

proposed geometric consistency loss (rows with GC)

improves performance at all error scales.

The proposed attention mask (rows with attn) im-

proves the performance in the absence of geometric

consistency, but slightly limits the performance espe-

cially with larger errors. However, qualitatively (Fig-

ure 6), the attention mask allows us to better handle

missing training data (that is greyed out in the ground

truth column). In particular, surfaces are not spuri-

ously removed or added in those regions: the model

learns to mask those regions out of the correction and

keep them as they are.

4.5 Corrected Meshes

We demonstrate our method in practice by using the

corrected inverse-depth images to create new, cor-

rected reconstructions of the input meshes. Our model

effectively corrects missing surfaces, particularly on

the road, as illustrated in Figure 7. This results in

higher surface coverage of the original scene.

As is common with neural networks trained for

image regression, predictions can sometimes be too

smooth. While we address this by using skip connec-

(a) Uncorrected mesh

(b) Corrected mesh

Figure 7: Images of 3D reconstructions of KITTI sequence 00 (left) and 06 (right). (a) Shows the uncorrected meshes that our

network processes, built solely from a stereo camera. Note the large missing surfaces due to either poor lighting, or poorly

textured regions. Our model recovers the missing surfaces (b), providing a more complete reconstruction. (c) shows the

corrected meshes with colour copied from the uncorrected input. The models used for this illustration here are trained as

described in Section 4.3, so the corrected meshes are not part of the training data.

tions between the encoder and decoder of the network,

smoothness in predictions can still occur, especially

when there are no edges in the network input to guide

the output. This is not a problem when ﬁlling in closed

holes like the ones in the road, which have clear bound-

aries. However, for regions without clear boundaries,

such as the top of buildings, network predictions are

too smooth. This can be seen in both Figure 6 and

Figure 7.

5 CONCLUSION

In this paper we present a method for correcting gross

errors in dense 3D meshes. We extracted paired 2D

mesh features from two reconstructions and trained a

neural network to predict the difference in inverse-

depth between the two. We addressed the issue

of overly-smooth predictions with a U-Net architec-

ture and a loss-weighting mechanism that emphasises

edges. The geometric consistency of our predictions is

improved with a view-synthesis loss that targets incon-

sistencies. Our experiments show that the proposed

method reduces gross errors in inverse-depth views of

the mesh by up to 77.5%.

While in this paper we focus on correcting meshes

of urban scenes built from street-level sensors, our

method is generally applicable to environments with

strong priors that can be learnt from data.

ACKNOWLEDGEMENTS

The authors would like to acknowledge the support

of the UK’s Engineering and Physical Sciences Re-

search Council (EPSRC) through the Centre for Doc-

toral Training in Autonomous Intelligent Machines

and Systems (AIMS) Programme Grant EP/L015897/1.

Paul Newman is supported by EPSRC Programme

Grant EP/M019918/1.

REFERENCES

Bredies, K., Kunisch, K., and Pock, T. (2010). Total gener-

alized variation. SIAM Journal of Imaging Sciences,

3:4920–526.

Canny, J. F. (1986). A computational approach to edge

detection. IEEE Transactions on Pattern Analysis and

Machine Intelligence, PAMI-8:679–698.

Chambolle, A. and Pock, T. (2011). A ﬁrst-order primal-

dual algorithm for convex problems with applications

to imaging. Journal of Mathematical Imaging and

Vision, 40(1):120–145.

Dharmasiri, T., Spek, A., and Drummond, T. (2019). ENG:

End-to-end neural geometry for robust depth and pose

estimation using CNNs. In Proceedings of the Asian

Conference on Computer Vision (ACCV), pages 625–

642.

Eldesokey, A., Felsberg, M., and Khan, F. S. (2018). Prop-

agating conﬁdences through CNNs for sparse data re-

gression. In Proceedings of the British Machine Vision

Conference (BMVC).

Felzenszwalb, P. F. and Huttenlocher, D. P. (2012). Distance

transforms of sampled functions. Theory of Computing,

8:415–428.

Godard, C., Mac Aodha, O., and Brostow, G. J. (2017). Un-

supervised monocular depth estimation with left-right

consistency. In Proceedings of the IEEE International

Conference on Computer Vision and Pattern Recogni-

tion (CVPR).

He, K., Zhang, X., Ren, S., and Sun, J. (2016). Deep residual

learning for image recognition. In Proceedings of the

IEEE International Conference on Computer Vision

and Pattern Recognition (CVPR), pages 770–778.

Hua, J. and Gong, X. (2018). A normalized convolutional

neural network for guided sparse depth upsampling. In

Proceedings of the International Joint Conference on

Artiﬁcial Intelligence (IJCAI).

Jeon, J. and Lee, S. (2018). Reconstruction-based pairwise

depth dataset for depth image enhancement using CNN.

In Proceedings of the European Conference on Com-

puter Vision (ECCV).

Kingma, D. and Ba, J. (2015). Adam: A method for stochas-

tic optimization. In Proceedings of the International

Conference on Learning Representations (ICLR).

Klodt, M. and Vedaldi, A. (2018). Supervising the new with

the old: Learning SfM from SfM. In Proceedings of

the European Conference on Computer Vision (ECCV).

Knutsson, H. and Westin, C.-F. (1993). Normalized and

differential convolution: Methods for interpolation and

ﬁltering of incomplete and uncertain data. In Proceed-

ings of the IEEE International Conference on Com-

puter Vision and Pattern Recognition (CVPR).

Kopf, J., Cohen, M. F., Lischinski, D., and Uyttendaele, M.

(2007). Joint bilateral upsampling. ACM Transactions

on Graphics, 26:96.

Kwon, H., Tai, Y.-W., and Lin, S. (2015). Data-driven depth

map reﬁnement via multi-scale sparse representation.

In Proceedings of the IEEE International Conference

on Computer Vision and Pattern Recognition (CVPR),

pages 159–167.

Laina, I., Rupprecht, C., Belagiannis, V., Tombari, F., and

Navab, N. (2016). Deeper depth prediction with fully

convolutional residual networks. In Proceedings of the

IEEE International Conference on 3D Vision (3DV),

pages 239–248.

Ma, F. and Karaman, S. (2018). Sparse-to-dense: Depth pre-

diction from sparse depth samples and a single image.

In Proceedings of the IEEE International Conference

on Robotics and Automation (ICRA).

Mahjourian, R., Wicke, M., and Angelova, A. (2018). Un-

supervised learning of depth and ego-motion from

monocular video using 3D geometric constraints. In

Proceedings of the IEEE International Conference

on Computer Vision and Pattern Recognition (CVPR),

pages 5667–5675.

Matsuo, T., Fukushima, N., and Ishibashi, Y. (2013).

Weighted joint bilateral ﬁlter with slope depth compen-

sation ﬁlter for depth map reﬁnement. In Proceedings

of the International Conference on Computer Vision

Theory and Applications (VISAPP).

Newcombe, R. A., Izadi, S., Hilliges, O., Molyneaux, D.,

Kim, D., Davison, A. J., Kohli, P., Shotton, J., Hodges,

S., and Fitzgibbon, A. W. (2011). KinectFusion: Real-

time dense surface mapping and tracking. In IEEE

International Symposium on Mixed and Augmented

Reality, pages 127–136.

Owen, A. B. (2007). A robust hybrid of lasso and ridge

regression. Contemporary Mathematics, 443:59–72.

Riegler, G., R

uther, M., and Bischof, H. (2016). ATGV-Net:

Accurate depth super-resolution. In Proceedings of the

European Conference on Computer Vision (ECCV).

Ronneberger, O., Fischer, P., and Brox, T. (2015). U-Net:

Convolutional networks for biomedical image segmen-

tation. In Medical Image Computing and Computer

Assisted Intervention (MICCAI).

Shi, W., Caballero, J., Husz

ar, F., Totz, J., Aitken, A. P.,

Bishop, R., Rueckert, D., and Wang, Z. (2016). Real-

time single image and video super-resolution using

an efﬁcient sub-pixel convolutional neural network.

In Proceedings of the IEEE International Conference

on Computer Vision and Pattern Recognition (CVPR),

pages 1874–1883.

Sobel, I. and Feldman, G. (1968). A 3

3 isotropic gradi-

ent operator for image processing. presented at the

Stanford Artiﬁcial Intelligence Project (SAIL).

Tanner, M., Pini

es, P., Paz, L. M., and Newman, P. (2015).

BOR

G: Building optimal regularised reconstructions

with GPUs (in cubes). In Proceedings of the Interna-

tional Conference on Field and Service Robotics (FSR),

Toronto, Canada.

Tanner, M., Pini

es, P., Paz, L. M., and Newman, P. (2016).

Keep geometry in context: Using contextual priors for

very-large-scale 3d dense reconstructions. In Robotics:

Science and Systems (RSS). Workshop on Geometry

and Beyond: Representations, Physics, and Scene Un-

derstanding for Robotics.

Tanner, M., S

aftescu,

., Bewley, A., and Newman, P. (2018).

Meshed up: Learnt error correction in 3D reconstruc-

tions. In Proceedings of the IEEE International Con-

ference on Robotics and Automation (ICRA), Brisbane,

Australia.

Tomasi, C. and Manduchi, R. (1998). Bilateral ﬁltering for

gray and color images. In Proceedings of the Interna-

tional Conference on Computer Vision (ICCV), pages

839–846.

Uhrig, J., Schneider, N., Schneider, L., Franke, U., Brox, T.,

and Geiger, A. (2017). Sparsity invariant CNNs. In

Proceedings of the IEEE International Conference on

3D Vision (3DV).

Ummenhofer, B., Zhou, H., Uhrig, J., Mayer, N., Ilg, E.,

Dosovitskiy, A., and Brox, T. (2017). DeMoN: Depth

and motion network for learning monocular stereo.

In Proceedings of the IEEE International Conference

on Computer Vision and Pattern Recognition (CVPR),

pages 5622–5631.

Zhang, Y. and Funkhouser, T. A. (2018). Deep depth com-

pletion of a single RGB-D image. In Proceedings of the

IEEE International Conference on Computer Vision

and Pattern Recognition (CVPR), pages 175–185.

Zhou, T., Brown, M., Snavely, N., and Lowe, D. G. (2017).

Unsupervised learning of depth and ego-motion from

video. In Proceedings of the IEEE International Con-

ference on Computer Vision and Pattern Recognition

(CVPR).