
Parallel Reconstruction of Quad Only Meshes
from Volume Data
Roberto Grosso and Daniel Zint
Visual Computing, Friedrich-Alexander-Universit
¨
at Erlangen-N
¨
urnberg (FAU), Germany
Keywords:
Dual Marching Cubes, Quad Meshing, Parallel Mesh Reconstruction.
Abstract:
We present a method to reconstruct quad only meshes from volume data which mainly consists of two steps:
reconstruction of a quad only mesh and topological simplification to reduce the number of irregular vertices.
A novel algorithm is described that computes Dual Marching Cubes (DMC) meshes without using lookup
tables. The meshes are topologically consistent across cell borders, i.e. they are watertight. The output of the
algorithm is a quad only mesh stored in a halfedge data structure. Due to the transitions between voxel layers
in volume data, meshes have numerous quad elements with vertices of valence 3−X −3 −Y, where X, Y ≥5,
and 3 −3 −3 −3. Hence, we simplify the mesh by eliminating these elements wherever possible. Finally, we
briefly describe a CUDA implementation of the algorithms, which allows processing huge amounts of data on
GPU at almost interactive time rates.
1 INTRODUCTION
Iso-surface reconstruction from volume data is a com-
mon processing step in many engineering and scien-
tific applications, such as surface reconstruction from
range sensor data, analysis and visualization of med-
ical images, or geometry reconstruction of large pro-
tein chains in molecular science. In many cases, vol-
ume data is represented by a hexahedral mesh which
stores a scalar function sampled at the mesh vertices.
In medical applications CT or MRI data are repre-
sented by voxel grids. In this work cell means a voxel
or a hexahedral mesh element. The surface is obtained
by the Marching Cubes (MC) algorithm, which only
requires an iso-value representing the surface as input.
A MC surface shows two major drawbacks. Triangles
are poorly shaped, and the mesh is not topologically
correct, i.e. it might be inconsistent across cell bor-
ders and not homeomorphic to the underlying surface
(Nielson, 2003). The dual marching cubes (DMC) al-
gorithm (Nielson, 2004) generates quad only meshes.
It is based on a lookup table with 23 base cases. A
consistent discretization of the iso-surface across cell
borders requires using the asymptotic decider (Niel-
son and Hamann, 1991; Grosso, 2017) which results
in a large number of special cases, called subconfig-
urations in (Nielson, 2003). An alternative strategy
to generate consistent triangulations of the iso-surface
was presented in (Grosso, 2016a; Renbo et al., 2005;
Pasko et al., 1988) and is based on the following ob-
servations. Given an iso-value ι
0
, the iso-surface is
defined as:
S
ι
0
= {(x, y, z) ∈ R
3
|T (x, y, z) = ι
0
}, (1)
where T : M → R is the trilinear interpolant defined
on the hexahedral mesh M . The intersection of the
iso-surface with a face of a cell is a set of hyperbolic
arcs. The intersection of the iso-surface with a cell is a
set of closed curves, each being a C
0
-continuous col-
lection of hyperbolic arcs. Up to four different com-
ponents or branches of the iso-surface can intersect a
cell, resulting in up to four independent closed curves,
hereafter referred to as MC polygons. They are con-
sistent across cell borders if the asymptotic decider is
applied.
DMC computes a vertex representative for each
MC polygon, which should lie on the iso-surface de-
fined by equation (1). In a hexahedral mesh an edge
is shared by four cells. If we connect the vertex repre-
sentatives of the cells sharing a common edge we ob-
tain a quadrilateral. Thus, DMC generates quad only
meshes. If the intersection of the iso-surface with a
cell is computed using the asymptotic decider, it is
guaranteed that the DMC mesh is topologically con-
sistent across cell borders, i.e. it is watertight.
The main contribution of the work is a new DMC
algorithm which does not require a lookup table, gen-
erates watertight meshes, and is simple to parallelize.
102
Grosso, R. and Zint, D.
Parallel Reconstruction of Quad Only Meshes from Volume Data.
DOI: 10.5220/0008948701020112
In Proceedings of the 15th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2020) - Volume 1: GRAPP, pages
102-112
ISBN: 978-989-758-402-2; ISSN: 2184-4321
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

The algorithm output is a high quality quad only mesh
which accurately represents the underlying geome-
try as defined by equation (1). Neighborhood and
connectivity information is encoded using a halfedge
data structure. Furthermore, we implemented par-
allel smoothing methods to reduce vertices and ele-
ments with valence pattern 3 −X −3 −Y , X, Y ≥ 5
and 3 −3 −3 −3 which commonly appear in DMC
meshes computed from volume data.
In the following, we first present a brief review of
previous work emphasizing the problem of topologi-
cal consistency and parallel reconstruction. In Sec. 3
we present the parallel DMC algorithm, and in Sec. 4
we describe our parallel implementation of two mesh
simplification techniques. In Sec. 5 we show the per-
formance of the methods presented, and in Sec. 6 we
give some comments on the results. The source code
is available at GitHub (Grosso, 2016b).
2 RELATED WORK
Research contributions in the area of iso-surface ex-
traction from volume data can be classified into three
main groups, standard Marching Cubes (MC) and its
extensions to resolve topological correctness and con-
sistency; Dual Marching Cubes which extract quad
meshes dual to the MC polygons; and Dual Contour-
ing, which computes an iso-surface from the dual grid
or the dual of an octree.
Methods for computing iso-surfaces based on the
standard MC have to deal with the problem of in-
consistent meshes across cell borders. Furthermore,
MC methods might generate meshes which are not
homeomorphic to the iso-surface as defined by equa-
tion (1). Methods presented so far are either based on
extended lookup tables, or they first compute the in-
tersection of the iso-surface with a cell, resulting in a
MC polygon which is consistently triangulated.
After D
¨
urst (D
¨
urst, 1988) observed that MC does
not consistently triangulate the iso-surface across cell
borders, Nielson and Hamann (Nielson and Hamann,
1991) introduced the asymptotic decider to resolve
ambiguities at the cell faces. Natarajan (Natarajan,
1994) discovered interior ambiguities and introduced
an extended lookup table. Chernyaev (Chernyaev,
1995) modified the lookup table increasing the num-
ber of cases up to 33 in total, which is commonly
called MC33. Different authors proposed new tech-
niques to improve performance or to solve topological
inconsistencies (Lewiner et al., 2003; Cignoni et al.,
2000; Matveyev, 1999; Montani et al., 1994; Niel-
son, 2003; Custodio et al., 2013; Etiene et al., 2012;
Lopes and Brodlie, 2003). For each ambiguous face,
special subcases have to be considered which results
in a large number of configurations.
Algorithms were presented which resolve ambi-
guities without using a lookup table. The first method
to compute iso-surfaces based on the intersection of
the surface with the cell faces was proposed by Pasko
et al. (Pasko et al., 1988). Renbo et al. (Renbo et al.,
2005) developed a triangulation algorithm which does
not use lookup tables. These methods process un-
ambiguous and ambiguous cells in the same manner,
which is much more computational intensive than the
MC algorithm. Grosso (Grosso, 2016a) developed a
hybrid technique which processes unambiguous cells
with the standard MC. Ambiguous cells are triangu-
lated based on a set of rules applied to the MC poly-
gons. This method has the advantage of not relying
on lookup tables in ambiguous cases.
In order to improve performance and to overcome
the problem of generating a large amount of triangles
many parallel strategies were proposed in literature.
A parallel iso-surface algorithm which is combined
with edge collapses was presented in (Ulrich et al.,
2014; Dupuy et al., 2010). It is a modification of the
tandem algorithm introduced in (Attali et al., 2005).
Parallel implementations become more complex if the
output has to be a data structure with connectivity and
neighborhood information. A GPU-based technique
to reconstruct and smooth the iso-surface by repo-
sitioning the vertices without changing mesh topol-
ogy was introduced in (Chen et al., 2015). A method
to compute standard MC on multiple GPUs was de-
scribed in (D’Agostino and Seinstra, 2015). A ma-
jor problem of these algorithms is that they use large
buffers to compute a consistent numbering of the ver-
tex indices. Usually, a unique vertex index is com-
puted by counting cells or edges via a prefix sum.
This is not viable in our case, as buffers may be-
come very large. We opted for a different technique
which results in a much simpler algorithm that deliv-
ers good performance results and allows to compute
iso-surfaces from very large volume data.
The Dual Marching Cubes algorithm presented by
Nielson (Nielson, 2004) is a different strategy to re-
construct an iso-surface from a volume data. The in-
tersection of the iso-surface with the cell can be ap-
proximated by a polygon on the cell faces. This is
what we call the MC polygon in the previous section.
The DMC algorithm computes the dual of these MC
polygons. The dual to the MC polygons is a quad only
mesh because each edge in the volume mesh is shared
by four cells. This algorithm relies on the lookup ta-
ble introduced in (Nielson, 2003) which consists of
23 basis cases. Ambiguities are resolved by introduc-
ing sub-configurations. This method is a generaliza-
Parallel Reconstruction of Quad Only Meshes from Volume Data
103

ee
77
ee
1111
ee
33
ee
88
ee
55
ee
1010
ee
11
ee
99
ee
44
ee
66
ee
00
ee
22
vv
44
vv
66
vv
22
vv
00
vv
77
vv
33
vv
11
vv
55
Figure 1: Local index convention for vertices and edges in
a cell.
tion of the SurfaceNets proposed in (de Bruin et al.,
2000; Gibson, 1998). A parallel implementation of
the DMC algorithm is presented in (L
¨
offler and Schu-
mann, 2012). The method generates a 1-ring neigh-
borhood data structure and approximates the surface
by using error quadrics. Nevertheless, it relies on
large buffers whose size depends on the number of
edges to compute unique vertex indices via prefix
sums.
Dual Contouring (DC) (Schaefer and Warren,
2004; Ju et al., 2002) is an alternative method for
extracting iso-surfaces from volume data. It first ap-
proximates the data by computing an octree. For each
cell of the octree, the method computes a single ver-
tex representing the surface intersection with the cell.
The vertex is placed within the cell by optimizing
a quadratic functional based on error quadrics. The
method just computes a single vertex for each cell in
the octree, and therefore the resulting mesh might not
be manifold. Subsequently different works were pro-
posed that mainly deal with the problem of comput-
ing manifold meshes out of an octree (Rashid et al.,
2016; Schaefer et al., 2007; Kazhdan et al., 2007;
Zhang et al., 2004). Dual contouring generates tri-
angle meshes from a hierarchical data structure.
3 DUAL MARCHING CUBES
We use the index convention for vertices and edges
shown in Fig. 1. For instance, in the unit reference
cell [0, 1] ×[0, 1] ×[0, 1] we have v
0
= (0, 0, 0), and
e
0
= {v
0
, v
1
}. The restriction of the trilinear inter-
polant T to a unit reference cell has the form
F(u, v, w) =
(1 −w)[ f
0
(1 −u)(1 −v) + f
1
u(1 −v)
+ f
2
(1 −u)v + f
3
uv]
+ w[ f
4
(1 −u)(1 −v) + f
5
u(1 −v)
+ f
6
(1 −u)v + f
7
uv], (2)
(a) Intersection with cell (b) Hyperbolic arcs on faces
(c) 12 sided MC polygon ap-
proximating the hyperbolic
arcs
(d) Three MC polygons
Figure 2: MC polygons approximating the intersection of
the iso-surface with the cell faces.
where (u, v, w) ∈ [0, 1]
3
are local coordinates and f
i
are the function values at the cell vertices v
i
. Up
to four branches of the iso-surface obtained from
F(u, v, w) = ι
0
might intersect the cell. In Fig. 2a
we show an iso-surface with only one component in-
tersecting the cell at all twelve edges. In Fig. 2b
we see the corresponding hyperbolic arcs at the cell
faces, and in Fig. 2c the MC polygon used to approx-
imate the hyperbolic arcs. For each branch of the iso-
surface, DMC selects a single vertex within the cell
which represents the surface. For the case shown in
Fig. 2d three vertices have to be computed.
Each edge in the mesh or voxel grid is shared by
four cells, except for the boundary edges. If a branch
of the iso-surface intersects an edge, it will intersect
all four cells sharing this edge. Therefore, connecting
the representative vertices from each cell will gener-
ate a quadrilateral that is an element of the iso-surface.
If the MC polygons are constructed using the asymp-
totic decider (Nielson and Hamann, 1991), the gener-
ated mesh is topologically consistent across cell bor-
ders. The mesh is called dual, because each vertex in
the MC polygon has a corresponding quadrilateral in
the dual mesh, and each vertex of the dual mesh rep-
resents a MC polygon. The DMC generates meshes
which have less vertices and better shaped elements
than the meshes generated by the standard MC algo-
rithm (Nielson, 2004). Nevertheless, the generated
GRAPP 2020 - 15th International Conference on Computer Graphics Theory and Applications
104

(a) MC case 12 (b) MC case 13
Figure 3: Two configurations which have the topology of a
cylinder (tunnel) for MC cases 12 and 13.
iso-surface might not be topologically correct. For
certain configurations which can typically be found
in medical data, the iso-surface (1) will not be home-
omorphic to the reconstructed mesh. The DMC algo-
rithm as it was formulated above cannot reconstruct
tunnels (Grosso, 2016a), Fig. 3. The standard MC
algorithm cannot reconstruct these tunnels either.
The parallel DMC algorithm we propose gener-
ates an indexed face set for the quadrilateral mesh,
where the elements are all consistently oriented. Op-
tionally, a halfedge data structure carrying neighbor
information can be computed. The global structure of
the algorithm we propose consists of three main steps:
1) initialize buffers; 2) compute the DMC mesh; 3)
generate a halfedge data structure. In the initializa-
tion step buffers are created and default values are set
with the help of simple CUDA kernels. In the next
subsections we briefly describe how to compute the
DMC quadrilateral mesh and subsequently generate
the halfedge data structure.
3.1 DMC Quadrilateral Mesh
The DMC quadrilateral mesh is computed with two
CUDA kernels. The first kernel proceeds cell wise
and computes the vertex representatives and the
quadrilaterals. The indices constituting a quadrilat-
eral are stored by the kernel in a hash table. We opted
to use a hash table to enable processing of volume
data consisting of hundreds of millions of vertices, see
Sec. 5. The second kernel collects the quadrilaterals
from the hash table into an index buffer. Each thread
started by the first kernel has to carry out the follow-
ing processing steps for the cell being processed: 1)
Compute MC polygons, 2) Estimate vertex represen-
tatives for each MC polygon, and 3) Compute and
store quadrilateral indices in a hash table. In order to
improve performance, the kernel returns immediately
if the iso-surface does not intersect the cell.
Figure 4: Two configuration where three branches intersect
the cell, MC case 13.
3.1.1 Computation of MC Polygons
A cell might be intersected by up to four disconnected
branches of the iso-surface. Therefore, we expect
to obtain up to four closed MC polygons. The de-
vice method implemented for this purpose returns the
number of polygons, the size of each of the polygons,
and the indices of the intersected edges. This quan-
tities can be computed in two steps. First, the cell
is processed face wise. The intersection of the iso-
surface with a face is given by a segment, Fig. 2.
For each segment on a face the indices of the start
and end edge are computed. Segments are oriented
such that vertices with function values larger than the
iso-value are located to the left of the segments. Am-
biguous cases are solved with the asymptotic decider
(Nielson and Hamann, 1991). In a second step, seg-
ments are connected to build up closed polygons. The
number of MC polygons, their size, and the indices of
the edges being intersected can be stored in a 64bit
unsigned long integer.
3.1.2 Estimation of Vertex Representatives
Within the cell a vertex that is a representative of the
iso-surface is computed for each surface branch. The
vertex representative must be placed as close as pos-
sible to the iso-surface defined by equation (1). The
different branches intersecting the cell might be very
close to each other, Fig. 4. The estimates for the
vertex representatives must be positioned on the right
surface branch, otherwise the resulting mesh will be
non-manifold, i.e. mesh elements will overlap. We
compute these vertices in two steps. First, an initial
position is estimated. Second, the vertex is moved to-
wards the surface by iteration. The initial position of
the vertex is computed as the mean value (center of
gravity) of the vertices of the MC polygon. This is a
good estimate as can be easily seen from the fact that
branches of the surface within a cell are separated by
asymptotic planes.
Next, the position of the representatives is moved
towards the surface (1) by using the following itera-
Parallel Reconstruction of Quad Only Meshes from Volume Data
105

tion formula:
v
k+1
= v
k
+ λ∇F(v
k
), (3)
where v = (u, v, w) are the local coordinates and λ is
given by
λ = α ·
ι
0
−F(v
k
)
||∇F(v
k
)||
2
,
where α is a damping factor. We choose α = 0.25 and
iterate for a maximum of five steps. Normals are com-
puted at the vertex representative in two steps. First,
the gradient of the scalar function is estimated at the
cell vertices by using central difference. Second, the
gradient is interpolated trilinearly at the position of
the vertex representative and then normalized. We use
central differences because it has a better truncation
error than forward or backward difference. The com-
putation of the gradient using the trilinear interpolant
has the same approximation error as forward differ-
ence, thus producing poor results.
3.1.3 Computation of the Quadrilaterals
Quadrilaterals are computed by connecting vertices of
four neighbor cells sharing a common edge. The edge
must be intersected by the corresponding MC poly-
gons. Quadrilaterals must be consistently oriented. In
contrast to the original MC lookup table (Lorensen
and Cline, 1987), quadrilaterals are oriented such that
their normals point in the same direction as the gradi-
ent of the volume data.
Each quadrilateral is uniquely assigned to an edge
of the volume mesh. Quadrilaterals are stored in a
hash table where the key is the unique index of the
corresponding edge. We use open hashing and lin-
ear probing to find an empty bucket in the hash table.
Hash tables were chosen to be twice as large as the
expected number of elements in table. A quadrilat-
eral is represented by an array of four integers. For
each cell, the index of the vertex representative has
to be stored at the right position within this array
to construct quadrilaterals which are consistently ori-
ented. We are using the naming convention presented
in Fig. 1. Fig 5 demonstrates how to save vertex in-
dices properly. Edge e
0
= {v
0
, v
1
} is shared by four
neighbor cells. In the other three cells it will have the
names e
4
= {v
4
, v
5
}, e
6
= {v
3
, v
7
}, and e
2
= {v
2
, v
3
}.
Assume that f
0
≥ ι
0
and the index B of the vertex is
stored at the first position of the index array. The
thread processing the cell where this edge has the
name e
4
has to store the index C of the vertex repre-
sentative at the second position in the array. Similarly,
the thread processing the cell where the edge has the
name e
6
stores the index D at the third position and
finally, the thread processing the cell where the edge
Table 1: How to build quadrilaterals depending on the edge
configuration. The table indicates the position of the vertex
index in the quadrilateral array.
edge e = {v
i
, v
j
} case f
i
≥ ι
0
case f
j
≥ ι
0
e
0
= v
0
, v
1
0 0
e
1
= v
1
, v
3
0 0
e
2
= v
2
, v
3
3 1
e
3
= v
0
, v
3
3 1
e
4
= v
4
, v
5
1 3
e
5
= v
5
, v
7
1 3
e
6
= v
6
, v
7
2 2
e
7
= v
4
, v
6
2 2
e
8
= v
0
, v
4
0 0
e
9
= v
1
, v
5
3 1
e
10
= v
3
, v
7
2 2
e
11
= v
2
, v
6
2 2
has the name e
2
stores the vertex A at the fourth po-
sition. All possible cases are summarized in Table 1.
Each quadrilateral is computed by four threads and
stored in a hash table as key, [B, A, D, C].
A kernel is in charge of computing the vertex rep-
resentatives from each cell. The kernel processes the
input data cell wise. For each cell it computes the
vertex representatives and corresponding normals for
each branch of the iso-surface. These vertices are in-
terior to the cell, thus the kernel can assign a unique
global index to the vertices which is required by the
mesh data structure. The index corresponds to the po-
sition of vertex and normal within a buffer and is ob-
tained using atomicAdd on an atomic counter. As in-
dicated above this unique address for vertex and nor-
mal is stored in a hash table, where the key is the
unique index of the edge in the voxel grid being in-
tersected by the corresponding surface branch. The
bucket in the hash table has four entries containing
the indices of the vertices which build a quadrilateral.
The vertices are stored in order to build a consistently
oriented quadrilateral according to the scheme given
in Table 1. The hash table is implemented as an array.
Collisions are solved by using open addressing with
linear probing. We use atomicCAS to test for colli-
sions. At the end the hash table contains all quadrilat-
erals in the mesh.
Finally, a second kernel will collect the quadrilat-
erals from the hash table and save the elements into
an index buffer. Boundaries are easily handled by this
kernel. A bucket in the hash table contains a quadri-
lateral or it is empty. If an entry in a bucket is an
invalid index, the cell was a boundary cell. In this
case no quadrilateral is generated.
GRAPP 2020 - 15th International Conference on Computer Graphics Theory and Applications
106

vv
11
vv
00
AA
BB
CC
DD
e
0
(a) case e
0
vv
33
vv
22
AA
BB
CC
DD
e
2
(b) case e
2
vv
55
vv
44
AA
BB
CC
DD
e
4
(c) case e
4
vv
77
vv
66
AA
BB
CC
DD
e
6
(d) case e
6
Figure 5: How to collect vertices from different cells which constitute a quadrilateral.
Figure 6: The distinct threads processing the twin edges
e
i
and e
j
will compute the same key and save them in the
same bucket in the hash table. The neighbor edges will be
connected by the next kernel.
3.2 Halfedge Data Structure
The halfedge data structure is computed using two
kernels. In the first kernel, each thread processes
a quadrilateral and collects the local information re-
quired by the data structure. For each vertex we store
the halfedge which starts at the vertex, and for the
face the first halfedge is stored. For the four halfedges
in a quadrilateral we store the index of the vertex at
which the halfedge starts, the face and the index of
the next halfedge. This kernel saves the indices of the
halfedges in a hash table. The key is constructed us-
ing the indices of the incident vertices and saved in
a 64bit unsigned long int. The smaller index is
saved in the first 32bits, the larger index in the second
32bits. As shown in Fig. 6, distinct threads process-
ing the twin edges e
i
and e
j
will compute the same
key based on the indices of the vertices v
l
, v
k
and save
them in the same bucket in the hash table. The hald-
edge whose starting vertex has the smaller index is
store at the first entry in the bucket, the other at the
second. Global information is collected by a second
kernel which processes the entries of the hash table
and connects twin edges. If a halfedge has no neigh-
bor, it is a boundary edge.
4 MESH SIMPLIFICATION
Due to the transitions between layers in the vol-
ume data, the DMC mesh has numerous quadrilat-
erals with the valence pattern 3 −X −3 −Y , where
X, Y ≥ 5, i.e. two non consecutive vertices with va-
lence 3 and the other two vertices with valence equal
to or larger than 5, Fig. 7a; and quadrilaterals with the
valence pattern 3 −3 −3 −3, Fig. 7b. This elements
can be easily removed from the mesh as follows. For
the case 7a vertices in red are merged into a new ver-
tex and the red element is removed. For the case 7b
edges in red are collapsed moving vertices in red to-
ward vertices in blue. The red elements are removed.
For the configuration 7c no element can be removed
in order to keep the mesh manifold.
4.1 Pattern 3 −X −3 −Y
First note that if two neighbor elements with this va-
lence pattern share a vertex of valence three, the el-
ements can’t be removed from the mesh. Otherwise,
elements with this valence pattern are removed from
the mesh with the following CUDA kernels:
1. Compute vertex valence. For this purpose a ker-
nel iterates through the halfedges and increases
the valence of its vertex by using atomicAdd().
2. Find elements with the valence pattern. For each
quadrilateral a kernel checks the element for the
valence pattern. There is a buffer with an int en-
try for each vertex, a counter, which counts how
often quadrilaterals with this valence pattern share
a vertex with valence three. This way neighbor el-
ements with the same valence pattern that can’t be
removed are identified easily.
3. Merge vertices with valence three. This kernel
works element wise. For elements with this va-
lence pattern the two vertices with valence three
are merged into a new vertex, Fig. 7a, if the
counter is one for both vertices. Otherwise, a
neighbor element with this valence pattern shares
Parallel Reconstruction of Quad Only Meshes from Volume Data
107
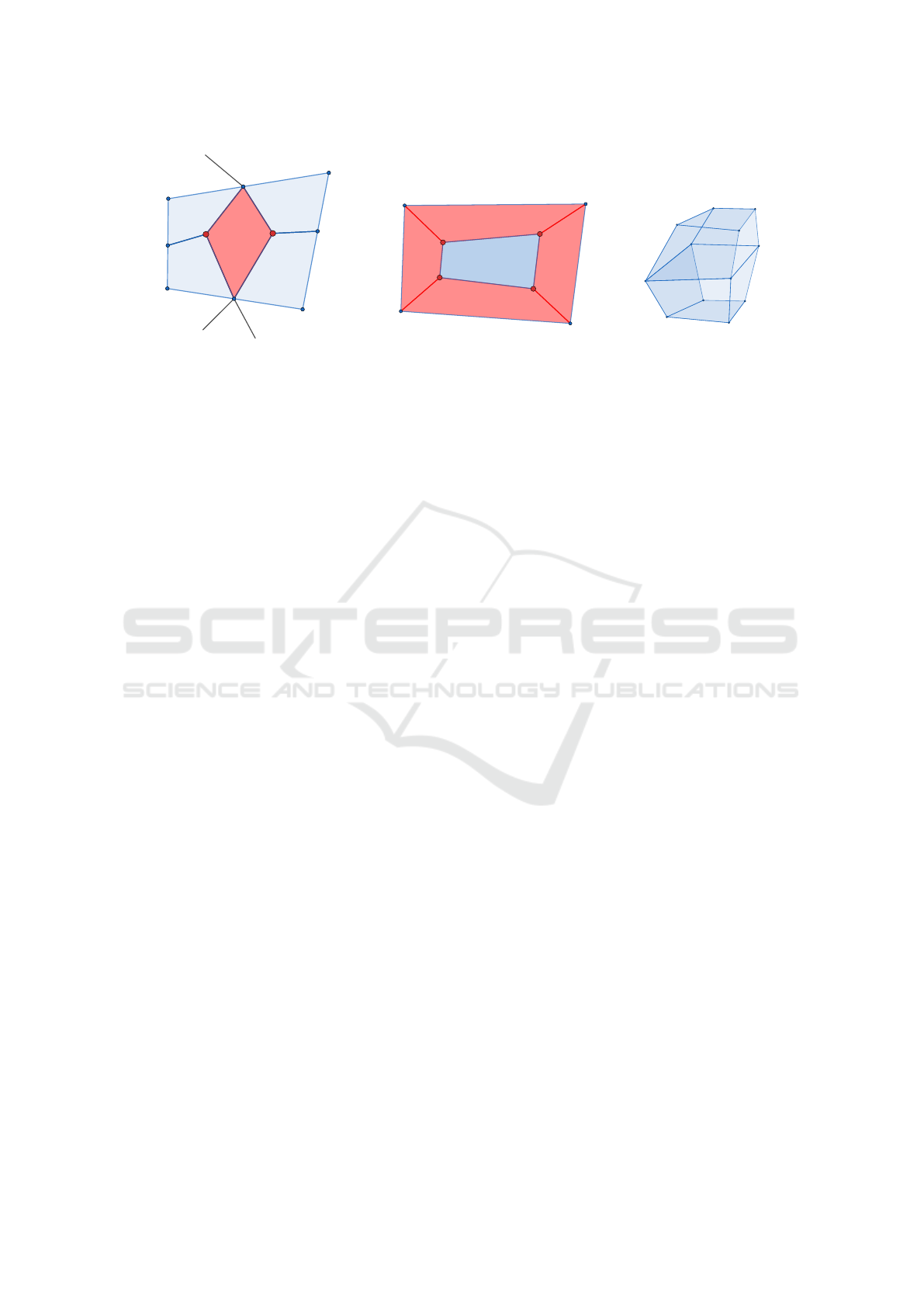
(a) Valence pattern 3 − X − 3 −Y ,
X, Y ≥ 5
(b) Valence pattern 3 −3 −3 −3 (c) This configuration
can’t be removed
Figure 7: Valence pattern 3 −X −3 −Y , where X, Y ≥ 5 and 3 −3 −3 −3. For the case 7a on the left vertices in red are
collapsed into a new vertex, removing the red element. For the case 7b in the middle the edges in red are collapsed moving
the vertices in red toward the vertices in blue. The red elements are removed. For the configuration on the right no element
will be removed in order to keep the mesh manifold.
a vertex of valence three, the element can’t be re-
moved.
4. Remove vertices. This kernel works vertex wise.
It copies vertices to a new vertex buffer, if they
are not marked for removal, and it maps old to
new vertex indices.
5. Remove quadrilaterals. This kernel works ele-
ment wise and copies quadrilaterals to a new el-
ement buffer, if they are not marked for removal.
It uses index mapping from the previous kernel to
connect vertices which form a quadrilateral.
6. Re-build halfedge data structure.
The algorithm requires five kernels to remove vertices
and elements. Afterwards, the halfedge data structure
has to be re-computed.
4.2 Pattern 3 −3 −3 −3
There are two configurations for which elements with
this valence pattern can’t be removed from the mesh:
two neighbor elements have the same valence pattern,
e.g. they are the faces of a hexahedron; or the ele-
ments are faces of a configuration as shown in Fig. 7c.
In the latter case, two quadrilaterals sharing the same
four vertices would remain, i.e. the mesh would be
non-manifold. The following processing steps were
implemented to remove elements with the valence
pattern 3 −3 −3 −3:
1. Compute vertex valence. Similar to the kernel
presented in Sec. 4.1.
2. Mark vertices and elements for removal. This ker-
nel processes the mesh element wise. For each el-
ement it tests if all the vertices have valence three.
In this case, the complete neighborhood is recon-
structed. The kernel checks if the element has a
neighbor with the same valence pattern or if it is
the case shown in Fig. 7c. If not, the element
and its four neighbors, Fig. 7b, are marked for
removal.
3. Remove vertices. Similar to the kernel presented
in Sec. 4.1.
4. Remove elements. Similar to the kernel presented
in Sec. 4.1.
5. Re-compute halfedge data structure.
The algorithm requires four kernels to remove ele-
ments from the mesh. We remark that neighborhood
is reconstructed using the halfedge data structure.
5 RESULTS
We evaluate the performance of the parallel DMC and
simplification algorithms presented in this work. We
compute the iso-surface from two CT data sets, a hu-
man skull of size 512
2
×641 shown in Fig. 8 and a
human torso of size 512
2
×743 for which iso-surfaces
were extracted with different iso-values. For the iso-
value 700, Fig. 9a, we call the data body, and for the
iso-value 1200 skeleton, Fig. 9b. The experiments
were carried out on a desktop computer with an In-
tel Core i7-6700 with 32 GB memory and a NVIDIA
GeForce GTX 1080 8GB. We first analyze the perfor-
mance of the parallel DMC algorithm and afterwards
present the effects of mesh simplification.
5.1 Parallel DMC
The performance of the parallel DMC is evaluated
by measuring computation time and number of ver-
tices and quadrilaterals generated. We compare the
GRAPP 2020 - 15th International Conference on Computer Graphics Theory and Applications
108

Figure 8: DMC mesh of a CT of a human skull after sim-
plification.
results with the corresponding meshes obtained with
the standard MC algorithm. For this purpose we sub-
divide quadrilaterals into triangles. For each element
we select the subdivision which satisfies the MaxMin
angle criterion. We also compare the quality of the el-
ements generated by both algorithms. Element qual-
ity is computed using the mean ratio metric,
q
m
tri
= 4
√
3
A
∑
3
i=1
l
2
i
, (4)
where A is the signed area of the triangle, and l
i
is
the length of their incident edges (Freitag and Knupp,
2002; M. Knupp, 2000).
Performance of the DMC in comparison with the
standard MC is given in Table 2. Times are given
in milliseconds. Both algorithms run on the GPU
and for comparison both generate a shared vertex data
structure. Table 3 gives the number of elements gen-
erated by DMC compared to the standard MC algo-
rithm. DMC generates about 1% less vertices and
correspondingly less elements than the standard MC.
The standard MC algorithm is faster than the DMC
algorithm. Nevertheless, it does not generate consis-
tent meshes and the overall quality of the elements is
worse compared to the elements generated by DMC
as shown in Fig. 10. This figure shows the element
quality for DMC with mesh simplification in cyan,
without mesh simplification in magenta, and for MC
in red. In this figure, elements are sorted accord-
ing to their quality. We clearly see that the standard
MC generates a much larger amount of triangles with
a lower quality than the DMC. Mesh simplification
slightly increases element quality. For comparison,
quadrilaterals were subdivided into two triangles us-
ing the MaxMin angle criterion. Some quadrilaterals
are thin resulting in triangles which don’t have a good
quality. Element quality and mesh consistency has a
high impact in photo realistic high quality rendering
in graphics applications or mesh processing in com-
putational geometry. This is a main reason why dual
methods for surface reconstruction are preferred over
the standard MC algorithm. Performance was com-
Table 2: Processing time to extract an iso-surface with the
DMC and MC algorithms. The table includes the times re-
quired to generate the halfedge data structure from the DMC
mesh.
skull body skeleton
DMC 85 103 109
MC 54 68 74
halfedge 71 59 87
pared with a C++ implementation of DMC including
a OpenMP parallelization using omp pragmas. The
code has many critical areas due to unique index com-
putations and writing operations. The GPU version is
60 to 77 times faster than the C++ OMP implemen-
tations and around 120 times faster than the sequen-
tial version as shown in Table 4. The back projection
method introduced in Sec. 3.1, equation (3), improves
the accuracy of the DMC mesh, Fig. 11. The plot
in red corresponds to the approximation error without
the projection of the vertex to the surface. The plot in
blue is the error after projection. The approximation
error is measured by comparing the function value at
the vertex with the iso-value normalized to [0, 1]. We
clearly see that the point back projection improves the
accuracy of the vertex representatives.
Table 3: Number of elements generated with the DMC and
MC algorithms. The head data set has 512
2
×641 voxels.
The data set used to generate the the torso and body surfaces
has 512
2
×743 cells.
vertices elements
skull DMC 5,052,520 5,072,697
skull MC 5,072,707 10,239,432
body DMC 4,249,113 4,234,305
body MC 4,251,835 8,472,218
skeleton DMC 6,294,356 6,278,397
skeleton MC 6,291,993 12,555,936
Table 4: Processing time to extract an iso-surface with the
DMC algorithm on GPU and CPU, including a CPU parallel
implementation with OpenMP. Times are given in millisec-
onds.
skull body skeleton
CUDA 85 103 109
CPU + OMP 6268 5415 8584
CPU 12204 13591 14523
Parallel Reconstruction of Quad Only Meshes from Volume Data
109
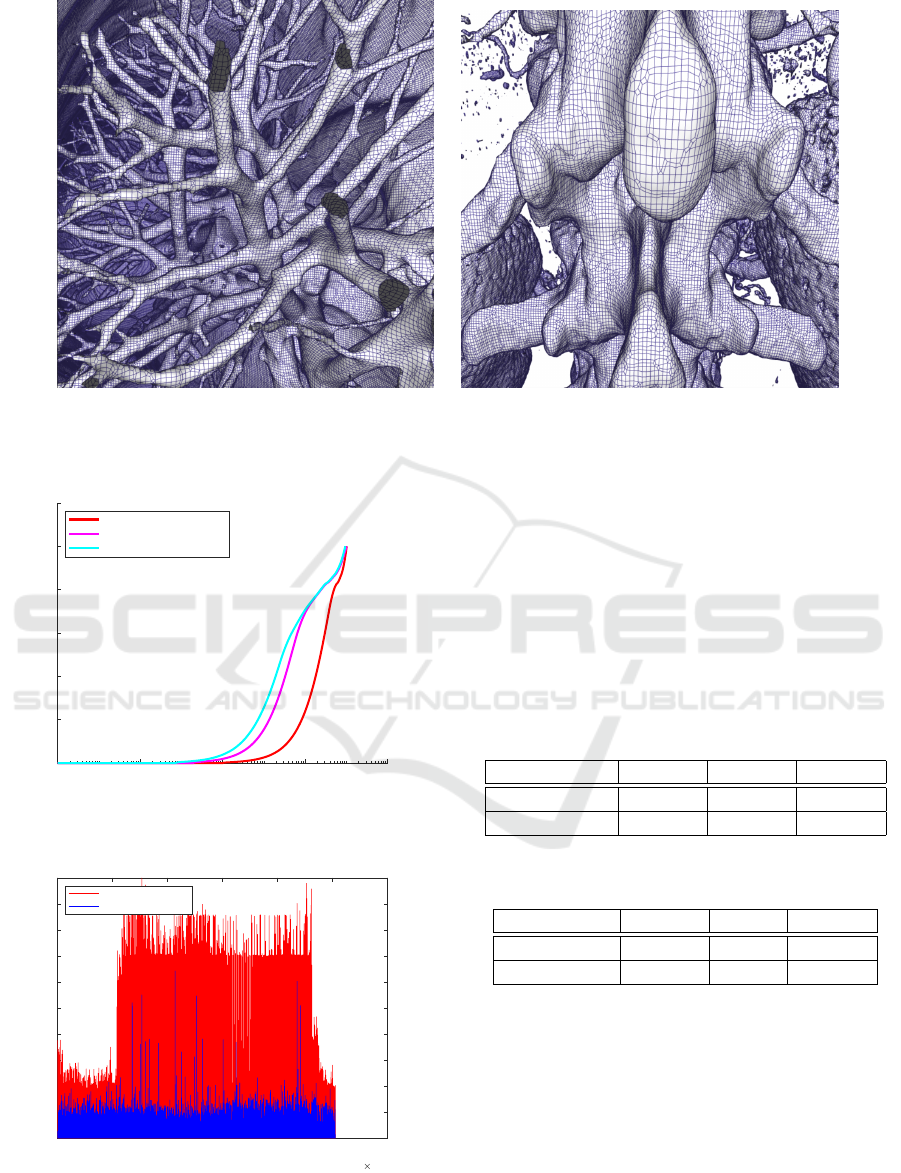
(a) DMC mesh showing respiratory tract, iso-value =
700
(b) DMC mesh showing the spine, iso-value = 1200
Figure 9: DMC mesh of a CT of a human torso.
10
0
10
2
10
4
10
6
10
8
element
0
0.2
0.4
0.6
0.8
1
1.2
element quality
MC
DMC
DMC with mesh simplf.
Figure 10: Element quality of DMC in cyan and magenta
compared to MC in red based on the mean ratio metric.
0 1 2 3 4 5 6
vertices
10
6
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
error
without error handling
with error handling
Figure 11: The red plot gives the error of the vertex rep-
resentatives without back projection. The blue plot is the
error after back projection.
5.2 Mesh Simplification
Simplification algorithms are evaluated by computa-
tional performance and by the number of elements be-
ing eliminated. The histograms presented in Fig. 12
show that the elimination of elements with valence
patterns 3 −X −3 −Y , X, Y ≥ 5, and 3 −3 −3 −3
considerably reduces the number of irregular vertices.
Table 5: Simplification of elements with valence pattern 3 −
X −3 −Y . Times are given in milliseconds.
3 −X −3 −Y skull body skeleton
time 12 9 14
vertices 169,331 161,904 212,795
Table 6: Simplification of the valence pattern 3 −3 −3 −3.
Times are given in milliseconds.
3 −3 −3 −3 skull body skeleton
time 7 5 8
vertices 190,292 18,652 165,908
The method implemented to simplify elements
with the valence pattern 3 −X −3 −Y , where X , Y ≥5
eliminates the same number of vertices and elements.
Table 5 gives runtime and total number of elements
removed from the original DMC mesh. For instance,
for the human skull data set it reduces about 3% of
the total number of elements. We remark that the
halfedge data structure has to be recomputed after
mesh simplification. Table 6 presents the results ob-
tained with the algorithm for the simplification of el-
ements with valence pattern 3 −3 −3 −3. Run times
GRAPP 2020 - 15th International Conference on Computer Graphics Theory and Applications
110

0 2 4 6 8 10 12
valence
0
0.5
1
1.5
2
2.5
vertices
#10
6
(a) Valence distribution before simplification
0 2 4 6 8 10 12
valence
0
0.5
1
1.5
2
2.5
vertices
#10
6
(b) Valence distribution after simplification
Figure 12: Distribution of the vertex valences in the DMC mesh before simplification in blue and after in red.
(a) DMC mesh (b) DMC after simplifica-
tion
Figure 13: DMC mesh after removing elements with va-
lence pattern 3 −X −3 −Y and 3 −3 −3 −3
are comparable to the previous case, also eliminat-
ing a similar number of elements, except for the case
of the human torso with iso-value 700, named body
in the table. Due to the geometric properties of the
iso-surface, the body surface does not have many ele-
ments with this valence pattern.
6 CONCLUSIONS
We presented a parallel implementation of the DMC
algorithm which efficiently processes volume data
consisting of hundreds of millions of voxels. The
DMC meshes are topologically consistent across cell
borders. This is due to the fact that we compute the
intersection of the iso-surface with the cells using the
asymptotic decider to solve ambiguities. The output
of the algorithm is a quadrilateral mesh stored in a
halfedge data structure. We use the fact that the data
is already on the GPU device and perform some mesh
simplification by eliminating vertices and quadrilater-
als with valence pattern 3 −X −3 −Y , X, Y ≥ 5 and
3 −3 −3 −3. This way vertices in the DMC mesh
have better valence distribution. In the implementa-
tion geometric constraints for the simplification were
not considered. The DMC algorithm generate meshes
with a better element quality than the standard MC.
REFERENCES
Attali, D., Cohen-Steiner, D., and Edelsbrunner, H. (2005).
Extraction and simplification of iso-surfaces in tan-
dem. In Proceedings of the Third Eurographics Sym-
posium on Geometry Processing, SGP ’05, Aire-la-
Ville, Switzerland, Switzerland. Eurographics Asso-
ciation.
Chen, J., Jin, X., and Deng, Z. (2015). Gpu-based polygo-
nization and optimization for implicit surfaces. Vis.
Comput., 31(2):119–130.
Chernyaev, E. V. (1995). Marching cubes 33: Construction
of topologically correct isosurfaces. Technical report.
Cignoni, P., Ganovelli, F., Montani, C., and Scopigno, R.
(2000). Reconstruction of topologically correct and
adaptive trilinear isosurfaces. Computers & Graphics,
24:399–418.
Custodio, L., Etiene, T., Pesco, S., and Silva, C.
(2013). Practical considerations on marching cubes
33 topological correctness. Computers & Graphics,
37(7):840 – 850.
D’Agostino, D. and Seinstra, F. J. (2015). A parallel isosur-
face extraction component for visualization pipelines
executing on gpu clusters. J. Comput. Appl. Math.,
273(C):383–393.
de Bruin, P. W., Vos, F. M., Post, F. H., Frisken-Gibson,
S. F., and Vossepoel, A. M. (2000). Improving tri-
angle mesh quality with surfacenets. In Medical Im-
age Computing and Computer-Assisted Intervention
– MICCAI 2000, pages 804–813, Berlin, Heidelberg.
Springer Berlin Heidelberg.
Dupuy, G., Jobard, B., Guillon, S., Keskes, N., and Ko-
matitsch, D. (2010). Parallel extraction and simplifi-
cation of large isosurfaces using an extended tandem
algorithm. Comput. Aided Des., 42(2):129–138.
Parallel Reconstruction of Quad Only Meshes from Volume Data
111

D
¨
urst, M. J. (1988). Re: Additional reference to ”marching
cubes”. SIGGRAPH Comput. Graph., 22(5):243–.
Etiene, T., Nonato, L. G., Scheidegger, C., Tienry, J., Pe-
ters, T. J., Pascucci, V., Kirby, R. M., and Silva, C. T.
(2012). Topology verification for isosurface extrac-
tion. IEEE Transactions on Visualization and Com-
puter Graphics, 18(6):952–965.
Freitag, L. A. and Knupp, P. M. (2002). Tetrahedral mesh
improvement via optimization of the element condi-
tion number.
Gibson, S. F. F. (1998). Constrained elastic surface nets:
Generating smooth surfaces from binary segmented
data. In Medical Image Computing and Computer-
Assisted Intervention — MICCAI’98, pages 888–898,
Berlin, Heidelberg. Springer Berlin Heidelberg.
Grosso, R. (2016a). Construction of topologically correct
and manifold isosurfaces. Computer Graphics Forum,
35(5):187–196.
Grosso, R. (2016b). tmc. https://github.com/
rogrosso/tmc.
Grosso, R. (2017). An asymptotic decider for robust and
topologically correct triangulation of isosurfaces. In
Proceedings of the Computer Graphics International
Conference, CGI ’17, pages 39:1–39:5, New York,
NY, USA. ACM.
Ju, T., Losasso, F., Schaefer, S., and Warren, J. (2002).
Dual contouring of hermite data. In Proceedings of
the 29th Annual Conference on Computer Graphics
and Interactive Techniques (SIGGRAPH 2002), pages
339–346. ACM Press.
Kazhdan, M., Klein, A., Dalal, K., and Hoppe, H. (2007).
Unconstrained isosurface extraction on arbitrary oc-
trees. In Proceedings of the Fifth Eurographics Sym-
posium on Geometry Processing, pages 125–133.
Lewiner, T., Lopes, H., Vieira, A. W., and Tavares, G.
(2003). Efficient implementation of marching cubes’
cases with topological guarantees. Journal of Graph-
ics Tools, 8(2):1–15.
L
¨
offler, F. and Schumann, H. (2012). Generating smooth
high-quality isosurfaces for interactive modeling and
visualization of complex terrains. In VMV.
Lopes, A. and Brodlie, K. (2003). Improving the robust-
ness and accuracy of the marching cubes algorithm
for isosurfacing. IEEE Transactions on Visualization
and Computer Graphics, 9:2003.
Lorensen, W. E. and Cline, H. E. (1987). Marching cubes:
A high resolution 3d surface construction algorithm.
SIGGRAPH Comput. Graph., 21(4):163–169.
M. Knupp, P. (2000). Achieving finite element mesh qual-
ity via optimization of the jacobian matrix norm and
associated quantities. part i—a framework for sur-
face mesh optimization. Int. J. Numer. Meth. Engng,
48:401–420.
Matveyev, S. V. (1999). Marching cubes: surface complex-
ity measure. In Proceedings of SPIE - The Interna-
tional Society for Optical Engineering, volume 3643,
pages 220–225.
Montani, C., Scateni, R., and Scopigno, R. (1994). A
modified look-up table for implicit disambiguation of
marching cubes. The Visual Computer, 10(6):353–
355.
Natarajan, B. K. (1994). On generating topologically con-
sistent isosurfaces from uniform samples. The Visual
Computer, 11(1):52–62.
Nielson, G. M. (2003). On marching cubes. IEEE
Transactions on Visualization and Computer Graph-
ics, 9(3):283–297.
Nielson, G. M. (2004). Dual marching cubes. In Proceed-
ings of the Conference on Visualization ’04, VIS ’04,
pages 489–496, Washington, DC, USA. IEEE Com-
puter Society.
Nielson, G. M. and Hamann, B. (1991). The asymptotic de-
cider: Resolving the ambiguity in marching cubes. In
Proceedings of the 2Nd Conference on Visualization
’91, VIS ’91, pages 83–91, Los Alamitos, CA, USA.
IEEE Computer Society Press.
Pasko, A., Pilyugin, V., and Pokrovskiy, V. (1988). Geo-
metric modeling in the analysis of trivariate functions.
Computers & Graphics, 12(3):457 – 465.
Rashid, T., Sultana, S., and Audette, M. A. (2016). Water-
tight and 2-manifold surface meshes using dual con-
touring with tetrahedral decomposition of grid cubes.
Procedia Engineering, 163:136 – 148. 25th Interna-
tional Meshing Roundtable.
Renbo, X., Weijun, L., and Yuechao, W. (2005). A ro-
bust and topological correct marching cube algorithm
without look-up table. In Proceedings of the The Fifth
International Conference on Computer and Informa-
tion Technology, CIT ’05, pages 565–569, Washing-
ton, DC, USA. IEEE Computer Society.
Schaefer, S., Ju, T., and Warren, J. (2007). Manifold dual
contouring. IEEE Transactions on Visualization and
Computer Graphics, 13(3).
Schaefer, S. and Warren, J. (2004). Dual marching cubes:
Primal contouring of dual grids. In Computer Graph-
ics and Applications, 2004. PG 2004. 12th Pacific
Conference on, pages 70–76. IEEE Computer Society.
Ulrich, C., Grund, N., Derzapf, E., Lobachev, O., and
Guthe, M. (2014). Parallel iso-surface extraction and
simplification. In WSCG 2014 : Communication
Papers Proceedings, pages 361–368. Vaclav Skala –
Union Agency, Plzen.
Zhang, N., Hong, W., and Kaufman, A. (2004). Dual con-
touring with topology-preserving simplification using
enhanced cell representation. In Proceedings of the
Conference on Visualization ’04, pages 505–512.
GRAPP 2020 - 15th International Conference on Computer Graphics Theory and Applications
112
