
Enhancing Deep Spectral Super-resolution from RGB Images by
Enforcing the Metameric Constraint
Tarek Stiebel, Philipp Seltsam and Dorit Merhof
Institute of Imaging & Computer Vision, RWTH Aachen University, Germany
Keywords:
Spectral Reconstruction, Spectral Super-resolution, Metameric Spectral Super-resolution.
Abstract:
The task of spectral signal reconstruction from RGB images requires to solve a heavily underconstrained set of
equations. In recent work, deep learning has been applied to solve this inherently difficult problem. Based on
a given training set of corresponding RGB images and spectral images, a neural network is trained to learn an
optimal end-to-end mapping. However, in such an approach no additional knowledge is incorporated into the
networks prediction. We propose and analyze methods for incorporating prior knowledge based on the idea,
that when reprojecting any reconstructed spectrum into the camera RGB space it must be (ideally) identical to
the originally measured camera signal. It is therefore enforced, that every reconstruction is at least a metamer
of the ideal spectrum with respect to the observed signal and observer. This is the one major constraint that
any reconstruction should fulfil to be physically plausible, but has been neglected so far.
1 INTRODUCTION
Spectral imaging has the advantage compared to RGB
imaging devices, that the acquired data contains more
accurate information on the spectral power distribu-
tion (SPD) of the light captured by the imaging de-
vice (spectral stimulus). This added information can
be useful for a broad variety of computer vision tasks
ranging from object detection and image classifica-
tion to a more accurate color measurement. How-
ever, actually obtaining spectral images, even in the
reduced form of multi-spectral imaging, is still a com-
plicated task. An increased spectral resolution dur-
ing measurement comes at the cost of either a lim-
ited temporal resolution, e.g. filter wheel design
or spectral line scanning, or reduced spatial resolu-
tion, e.g. integrated devices based on macro pixels.
Therefore, alternative approaches have been devel-
oped. One possibility is to pursue a more computa-
tional approach by trying to compensate for an insuf-
ficient measurement in form of a spectral reconstruc-
tion. The underlying idea is straight-forward: Since
it poses a severe challenge to acquire spectral images
directly, only capture images we can easily measure
instead: RGB images. Subsequently, compute the
missing information using adequate signal process-
ing techniques. However, this is an extremely under-
constrained problem.
While the task of recovering spectral images from
a low dimensional (e.g. RGB) spectral measurement
has been within the focus of distinct researchers for
decades (Hardeberg et al., 1999; Hill, 2002; Miyake
et al., 1999), it recently attracted novel attention, in
particular under the name of spectral super-resolution
and the application of deep learning (Arad et al.,
2018; Timofte et al., 2018). Prior to deep learning,
all approaches were more or less based upon the idea
of reducing the dimensionality of the spectral domain
utilizing proper basis functions. One comparably re-
cent example was proposed by Arad et al. (Arad and
Ben-Shahar, 2016) who learn a dictionary based map-
ping which was improved later on by Aeschbacher
et al. (Aeschbacher et al., 2017). The more mod-
ern solution is the application of deep learning, cur-
rently forming the state-of-the-art. A large variety
of approaches based on neural networks can directly
be taken from the 2018 NTIRE challenge on spec-
tral super-resolution (Arad et al., 2018). One of the
major advantages of convolutional neural networks
(CNNs) in particular is the fact, that they are capable
of implicitly incorporating contextual image informa-
tion (Stiebel et al., 2018). Instead of considering pix-
els individually, entire regions are processed and used
to reconstruct only a single SPD, not only leading to
a better performance in comparison to single pixel
based algorithms but also to an increased robustness
against noise. It is also possible to combine learned
basis functions with deep learning, as demonstrated
Stiebel, T., Seltsam, P. and Merhof, D.
Enhancing Deep Spectral Super-resolution from RGB Images by Enforcing the Metameric Constraint.
DOI: 10.5220/0008950100570066
In Proceedings of the 15th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2020) - Volume 4: VISAPP, pages
57-66
ISBN: 978-989-758-402-2; ISSN: 2184-4321
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
57

by Jia et al. (Jia et al., 2017) or Nguyen et al. (Nguyen
et al., 2014). A rather novel approach has been pro-
posed by Kaya et al. (Kaya et al., 2018) who aim
at estimating a spectral image from an RGB image
taken under unknown settings. The approach consists
of a combination of neural networks for respectively
spectral sensitivity estimation from the combination
of an RGB image and a hyper-spectral image as well
as spectral super-resolution given knowledge of the
spectral sensitivity.
Deep learning based approaches usually require ex-
plicit knowledge of the spectral sensitivity function
of the imaging device. This way, a large training
set of corresponding pairs of RGB images and spec-
tral images can be generated from existing spectral
databases. Should the spectral sensitivity be unknown
and, instead, the training set be captured directly us-
ing paired spectral imaging and an RGB device, one
could argue that based on the paired images the spec-
tral sensitivity can be computed anyway. Follow-
ing the creation of the training data, a network (or
a combination of networks) is trained on the gener-
ated data to learn an end-to-end mapping from the
RGB to the spectral domain. However, no further
knowledge is considered, any mathematical or phys-
ical constraints have so far been completely ignored.
While spectral super-resolution is certainly not trivial,
there is one condition that always has to be fulfilled
and remains yet completely unchecked. There is the
metameric constraint that the spectral reconstruction
must be within the so-called metameric set. Every
spectral reconstruction must equal the actually mea-
sured camera signal when reprojected back into the
camera RGB space using the known camera sensitiv-
ity. Assuming knowledge of the spectral sensitivity,
this appears like an obvious choice for constraining
and therefore optimizing the reconstruction. The ex-
ploitation of metamerism was so far only considered
in more traditional approaches, which do not use deep
learning (Bianco, 2010).
The contribution of this work is adapting the neces-
sary theory regarding metamer sets (Finlayson and
Morovic, 2005) and proposing a modification for any
deep neural network in order to enforce the metameric
constraint. A state of the art neural network to
describe the mapping from camera RGB-images to
spectral images is considered and exemplary modi-
fied. The modification is evaluated on an established
benchmark, the ICVL dataset (Arad and Ben-Shahar,
2016). The ICVL dataset does not only provide a
large hyper-spectral database, but it was also used
within the 2018 NTIRE challenge on spectral recon-
struction from RGB images (Timofte et al., 2018) and
therefore offers a valid comparison to a variety of al-
gorithms. It is demonstrated, how the incorporation of
the metameric constraint into the networks prediction
can increase the convergence properties during train-
ing. In the absence of noise, it also yields superior
results in contrast to the original approach. Last, an
analysis on the influence of noise is provided.
2 THEORETICAL FOUNDATION
We will start by summarizing the necessary un-
derlying theory regarding image formation and
metamerism. Assuming a q-dimensional imaging de-
vice, signal formation is modeled using
g = σ ·S
cam
· r, (1)
where r ∈ R
k
denotes a spectral stimulus that results
in the measured camera signal g ∈ R
q
when viewed
by a camera associated with the spectral sensitivity
S
cam
∈ R
q×k
. The scaling factor σ might be inter-
preted as exposure time and is used as normalization
to map general spectral stimuli onto a valid camera
signal range. We assume a spectral sampling rang-
ing from 400nm to 700nm in 10nm steps and only
consider RGB images for the remainder of this work,
resulting in q = 3 and k = 31.
The linear model described by Eq. 1 is on an ab-
stract level a projection of a 31 dimensional space
onto a three dimensional space. Due to the nature
of such a projection, there exists an infinite amount
of distinct spectral stimuli which all project onto an
identical camera signal. All these stimuli are called
metamers with respect to the observed camera signal
as well as the camera sensitivity. The task of spectral
super-resolution amounts to finding a solution to the
inverse mapping of Eq. 1, i.e. predicting a 31 dimen-
sional signal based on the three dimensional signal,
which is an extremely ill-posed problem. Put differ-
ently, any stimulus that is a metamer is a viable solu-
tion.
It is well established, that a reconstructed spectral
stimulus can be separated into two parts: a particu-
lar solution , r
p
, and a metameric black solution, r
b
(Finlayson and Morovic, 2005),
r = r
p
+ r
b
. (2)
An open question to date is the appropriate way to
actually perform this separation. Since there are cer-
tain degrees of freedom involved, a unique separation
does not exist. However, the topic of an adequate ba-
sis is not the focus of this work. We will therefore
settle with the trivial approach to obtain a particular
solution by considering the Moore-Penrose inverse
r
p
= P · g, (3)
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
58

Network Architecture
RGB Image Spectral Image
(a) Original
Network Architecture
r
p
r
b
RGB Image Spectral Image
(b) Proposed Modification
Figure 1: Proposed modification to enforce the metameric constraint.
with
P = S
T
(SS
T
)
−1
∈ R
k×q
. (4)
The matrix P represents a q dimensional basis within
the spectral domain, forming a spectral subspace that
is directly observable by the camera. On the con-
trary, there is the subspace of all metameric blacks,
B ∈ R
k×(k−q)
, which is spanned by the null-space of
S,
B = null(S). (5)
Since the basis of the metameric blacks is by defini-
tion orthogonal to the camera sensitivity, any change
within this subspace remains hidden to the camera
0 = S · r
b
, (6)
thus the name.
3 METHODS TOWARDS
ENFORCING METAMERISM
In this section, we will propose different approaches
for deep learning based spectral reconstruction to con-
sider the metameric constraint in an explicit way.
3.1 Estimating Metameric Blacks
A mathematically enforcing approach is to shift from
directly predicting a spectral image based on an
RGB image to only predicting the position within the
metameric black space. Since the space of metameric
blacks is of dimension n = k − q = 28, the dimen-
sional complexity of signal prediction is reduced from
31 to 28, hopefully leading to an enhancement of the
Algorithm 1: Modification.
1: procedure INITIALIZE
2: B = nullspace(S)
3: P = S
T
(SS
T
)
−1
4: network ← NeuralNetwork(n out = k − q))
5: procedure RECONSTRUCT(rgb img)
6: r
b
= B · network(rgb img)
7: r
p
= P · rgb img
8: r = r
p
+ r
b
9: return r
networks prediction capability. Additionally, any re-
construction achieved in such a way is by definition
guaranteed to be a metamer, since only the metameric
black is predicted by the network. The metameric
black may in turn be chosen arbitrarily, since it does
not effect the observed camera signal.
Original network architectures are designed to learn
an end-to-end mapping from RGB images towards
the 31 dimensional spectral images. In order to apply
the proposed modification, the networks themselves
do not need to be changed. They still assume RGB
images as input, but the amount of output dimensions
is reduced from 31 to 28, i.e. any network now only
predicts the metameric blacks within the metameric
subspace with respect to the sensing device. The pre-
dicted metameric blacks are combined with the par-
ticular solution, r
p
, for each given camera signal ac-
cording to Eq. 2 and 4, resulting in the actual spectral
reconstruction. The necessary steps to modify the net-
works workflow are outlined in Al. 1 and visualized
in Figure 1.
3.2 Metameric Loss
As an alternative, a less strict possibility towards con-
sidering the metameric constraint on the spectral re-
construction is proposed in form of an extended loss
function. An additional term is introduced that is en-
tirely devoted to the metameric constraint. Instead of
only evaluating the spectral reconstruction, I
0
spec
, by
comparing it to the ground truth, I
spec
, using the error
metric M(·), e.g. RMSE, the spectral reconstruction is
additionally reprojected onto the camera signal space
using Eq. 1 and the known camera sensitivity func-
tion. The resulting reconstructed RGB image, I
0
rgb
,
can likewise be compared to the original input RGB
image, I
rgb
. Combining both parts together yields the
newly proposed total loss, L,
L = αM(I
rgb
, I
0
rgb
) + M(I
spec
, I
0
spec
), (7)
with α ∈ [0, ∞) denoting a linear weighting term on
the metameric constraint. An α-value of 0 corre-
sponds to a pure spectral loss with no change at all,
whereas a value of 1 corresponds to an equal weight-
ing of both the spectral and the metameric loss. The
metameric loss should always reach a value of zero,
if the spectral reconstruction is in fact a metamer. In
Enhancing Deep Spectral Super-resolution from RGB Images by Enforcing the Metameric Constraint
59

400 500 600 700
wavelength in nm
0.00
0.25
0.50
0.75
1.00
rel. sensitivity
(a) Kodak DCS 420
400 500 600 700
wavelength in nm
0.00
0.25
0.50
0.75
1.00
rel. sensitivity
(b) Nikon D1X
400 500 600 700
wavelength in nm
0.00
0.25
0.50
0.75
1.00
rel. sensitivity
(c) Sony DXC
Figure 2: The relative spectral sensitivity functions of the considered RGB cameras (Kawakami et al., 2013).
reality, sources for inaccuracies like noise effects or
an imperfect measurement of the spectral sensitivity
function can be expected to ensure metameric loss
values greater than zero.
4 EXPERIMENTAL SETUP
In the following, the evaluation process of the pro-
posed methodologies as well as the precise steps taken
to generate the results are described.
4.1 Training Data
An extended version of the ICVL dataset (Arad and
Ben-Shahar, 2016) is considered, as it was published
1
during the 2018 CVPR Challenge on spectral recon-
struction (Timofte et al., 2018). The database forms
the largest freely available hyper-spectral database to
date. In summary, the training set consists of 256
spectral images mostly having a spatial resolution of
1392 x 1300, whereas there are 5 images within a
respective validation and test set. The spectral reso-
lution ranges from 400nm to 700nm in 10nm steps.
Based on a given camera sensitivity, all spectral im-
ages are projected into a cameras RGB signal space
using Eq. 1. A total of three different cameras are con-
sidered: Sony DXC 930, Kodak DCS 420 and Nikon
D1X. The associated spectral sensitivity functions are
publicly available (Kawakami et al., 2013). Their cor-
responding relative sensitivities are displayed in Fig-
ure 2.
Since the spectral images of the dataset are not nor-
malized in any way but provide the original light in-
tensities as captured in wild, all computed camera im-
ages need to be appropriately scaled. Such a scal-
ing must be performed for each of the three camera
models individually and might be interpreted as a real
cameras exposure time. Typical desired signal ranges
are [0, 1] or [0, 255]. In this work, the latter was
1
http://icvl.cs.bgu.ac.il/ntire-2018/
chosen. The reason is our interest in modeling the po-
tential effect of an 8bit signal encoding. In total, three
different signal scenarios were generated:
• Ideal
The calculated camera signals are used directly
in floating point precision for training and eval-
uation.
• Quantization
In order to consider a more realistic scenario,
quantization was applied to the ideal RGB images
assuming 8bit.
• Quantization & Noise
As a last scenario, the already quantized RGB
images were additionally disturbed using white
noise with a standard deviation of 1.
An open question is still the proper calculation
of the scaling factor. Within previous work, all im-
ages were typically scaled such that the maximal ob-
servable color signal equals the value 255 across the
entire dataset. Since such an approach of normaliz-
ing spectral data has been frequently followed and
already found a wide adaption especially within the
deep learning community, it is also considered within
this work. However, it comes with a couple of im-
portant underlying assumptions. In analogy to the
task of color constancy, which aims at estimating and
compensating the influence of an unknown illuminant
onto basically any image, the described approach of
normalizing spectral data can be seen a max-spectral
algorithm (Gijsenij et al., 2011). It is based on the un-
derlying idea, that at some arbitrary position within
an image, the light source is either directly observ-
able or through the reflection at a white surface. In
a Lambertian world, any object potentially reflecting
the emitted light is expected to not reflect more light
than the incident amount. The maximal observable
signal must therefore correspond to the light source.
A more reasonable approach for determining the scal-
ing factor might be the explicit consideration of a real
white reference. This is especially the case due to
the dataset actually containing images of white boards
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
60
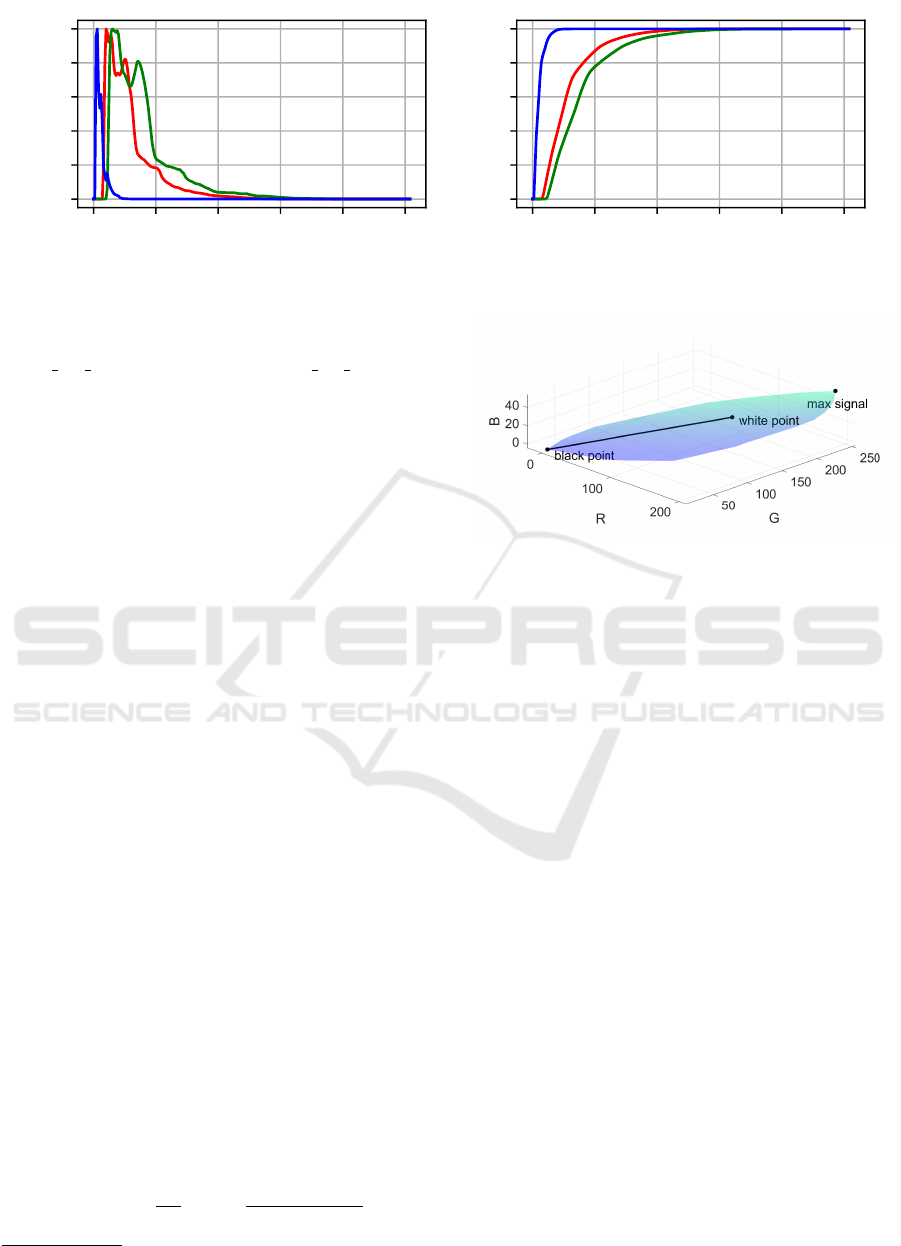
0 50 100 150 200 250
signal value
0.0
0.2
0.4
0.6
0.8
1.0
relative frequency
(a) Histogram
0 50 100 150 200 250
signal value
0.0
0.2
0.4
0.6
0.8
1.0
cumulative density
(b) Cumulative histogram
Figure 3: Histograms on the occurrences of camera signals across the entire dataset for the Kodak camera.
and calibration patterns. For example, image 26
(BGU HS 00026) and image 52 (BGU HS 00052) of
the dataset contain a white reference that can be used
for an estimate on the illuminant. The estimated SPD
of the illuminant is subsequently projected into cam-
era signal space to obtain its white point and used for
signal normalization. The normalization is achieved
by deducing a scaling factor such that the white point,
i.e. the projected illuminant, has at maximum a signal
value of 255. As an alternative approach to the max-
imum signal scaling, the white point based approach
is additionally followed for comparison.
4.2 Network and Training Details
Within this work, we restrict ourselves to the U-Net
based architecture proposed by Stiebel et al. (Stiebel
et al., 2018), because it is publicly available
1
and
therefore guarantees reproducibility. It was shown
to reach state-of-the-art performance for the task of
spectral reconstruction from RGB images (Timofte
et al., 2018) and thus ensures a fair comparison.
While we chose a single architecture for testing pur-
poses, all proposed steps can be applied to any archi-
tecture of choice in an analogous way. The network
is considered in its original version, which from now
on will be called the vanilla network, as well as in
a modified version containing our proposed changes
such that it only predicts the metameric blacks.
All training details were left untouched and are there-
fore identical to the original work (Stiebel et al.,
2018). In summary, every network is trained for 5
epochs using Adam optimization and a learning rate
of 0.0001 in any considered scenario. The batch size
is 10 with a patch size of 32. Both the spectral loss as
well as the metameric loss are computed by the mean
relative absolute error (MRAE),
MRAE(I, I
0
) =
1
mn
m
∑
i=1
n
∑
j=1
|
I(i, j) − I
0
(i, j)
I(i, j)
|, (8)
1
https://github.com/tastiSaher/SpectralReconstruction
Figure 4: The set of all potential camera signals for the Ko-
dak camera.
with I denoting the ground truth image having m rows
and n columns and I
0
the reconstruction.
All implementations were carried out using Python
and Pytorch. The training process itself was run
on a single graphics card of the type NVIDIA GTX
2080TI.
5 RESULTS AND DISCUSSION
First of all, an analysis of the dataset itself is pro-
vided and the influence of a proper scaling factor is
discussed. Considering all the generated images for
the ideal scenario, a closer look is taken upon the dis-
tribution of all potential color signals across the entire
dataset. For starters, a scaling factor corresponding
to the maximum possible signal value is assumed. A
channel wise histogram analysis was conducted. The
results are exemplary visualized for the Kodak camera
in Fig 3. It is immediately visible that the majority of
color signals is within the lower half of the cameras’
dynamic range. Such an uneven data distribution is
not desirable and may lead to a bias in final predic-
tion results. The distributions in case of the other two
camera devices turn out in an analogous way. This is
an issue that can be treated by choosing a scaling ac-
cording to a true white reference.
While all three camera channels are considered sepa-
Enhancing Deep Spectral Super-resolution from RGB Images by Enforcing the Metameric Constraint
61

Table 1: Resulting error metrics for both the vanilla network as well as the modified version only estimating the metameric
blacks. All camera images were scaled according to the maximal signal. The reported values represent the average results
over the test set.
Vanilla Network Metameric Blacks
MRAE RMSE GFC MRAE RMSE GFC
Ideal
Sony DXC 930 0.01677 23.75 0.99916 0.01542 23.96 0.99914
Kodak DCS 420 0.01325 17.08 0.99951 0.01298 16.37 0.99954
Nikon D1X 0.01416 19.84 0.99936 0.01412 19.26 0.99942
Quantization
Sony DXC 930 0.02316 28.18 0.99880 0.04674 41.73 0.99550
Kodak DCS 420 0.01722 17.87 0.99943 0.05400 60.74 0.99615
Nikon D1X 0.01745 18.42 0.99949 0.03130 28.73 0.99800
Quantization & Noise
Sony DXC 930 0.03007 31.73 0.99853 0.07857 74.51 0.98774
Kodak DCS 420 0.02426 20.33 0.99926 0.09700 127.2 0.97909
Nikon D1X 0.02317 22.86 0.99915 0.05518 50.65 0.99367
rately within the histogram analysis, their interaction
is also highly relevant. Of particular interest is the
3 dimensional subspace containing all possibly mea-
surable camera signals. It was estimated by comput-
ing the convex hull over all color signals within the
dataset. The resulting volume is depicted in Fig. 4.
Additionally, the white point as it is observable from
the white reference is explicitly marked in the visual-
ization. The black point is also highlighted for a bet-
ter understanding. The line passing through both the
black and white point might be considered as some
sort of lightness axis. In total, when considering a
scaling according to the white reference, more than
99% of all values were found to be still representable
without being subject to a potential signal clipping.
This is due to all pixels exceeding the white point
showing either dead pixels or local highly specular re-
flections, both of which are limited in numbers. It will
be concluded that a proper scaling according to a true
white reference is advantageous. However, we will
continue using the maximum signal scaling variant,
since it is common practice within the deep learning
community.
5.1 Estimating Metameric Blacks
An extensive study was performed and is provided
to analyze the potential change in performance due
to the proposed network modification. Tab. 1 dis-
plays the reconstruction results for both the vanilla
network and the modified version in case of all con-
sidered scenarios. For every permutation of network
setup, scenario and camera, the network is trained
from scratch upon the training set and evaluated over
the test set. Considered error metrics are the mean
relative absolute error as described by Eq. 8, the root
mean squared error (RMSE) and the goodness-of-fit
coefficient (GFC). A GFC value greater than 0.999
represents a good reconstruction and a value greater
than 0.9999 an excellent reconstruction (Imai et al.,
2002). The reported metrics in Tab. 1 are the com-
puted mean values over the test image set.
Different trends can be observed. The most intuitive
observation is an increasing reconstruction error with
the considered scenarios difficulty, i.e from ideal over
quantization to noisy. This is also independent of the
chosen camera model. The respective camera models
show differences in their performance relative to each
other. For most scenarios, the Kodak camera outper-
forms its contenders. The Nikon camera comes sec-
ond, with the Sony camera closing in last. These dif-
ferences in performance can be attributed to the dif-
ferences in the cameras spectral sensitivities. The best
ranking sensitivities of the Kodak device are probably
closer to some underlying basis function within the
considered spectral dataset and therefore able to cap-
ture more spectral information.
However, opposing trends become apparent when
comparing the metameric constraint network to its
vanilla version. The modified network always outper-
formed its original counterpart within the ideal set-
ting. Restraining the possible solution space by three
dimensions using the metameric constraint does in
fact help the network to reach better results. Ad-
ditionally, the modification also has a positive influ-
ence on the training process itself. Fig. 5 displays an
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
62

Figure 5: Exemplary training process for the original and modified network in an ideal world for the Kodak camera.
0 0.2 0.4
0.6
0.8 1
0
1
2
3
4
5
α
MRAE · 100
(a) Ideal
0 0.2 0.4
0.6
0.8
0
1
2
3
4
5
α
MRAE · 100
(b) Quantization
Figure 6: Evaluation of the metameric loss. The higher the value α, the more is the metameric loss term weighted.
exemplary loss function during the training for both
the modified network (orange) and the vanilla version
(blue). Particularly in the beginning, the influence of
the forced metameric constrained is significant. Since
independent of the networks’ processing the recon-
structed spectra are forced to be at least metameric to
the true spectral stimulus, even the initial approxima-
tion is at least remotely close. This leads to a way
faster convergence due to the better initialization by
design. In total, the modified version converges ap-
proximately four times faster. Even providing an un-
limited amount of training time, the original network
is never able to reach the modified networks predic-
tive capabilities. This behavior is consistent for all
considered cameras and experiments we conducted,
showing great potential for physically motivated re-
strictions on a neural networks prediction.
However, the prediction results of the modified net-
work are actually worse than the vanilla version when
leaving the ideal world. The influence of disturbances
on the prediction is of great interest, since they can
most certainly be expected in a real world applica-
tion. Metamer based spectral reconstruction appears
to be rather sensitive in this regard. The networks’
predictive capability appears insufficient to compen-
sate for noise effects, when limited by the metameric
constraint. This can be seen for both the quantized
and noisy scenario. In fact, the prediction quality sig-
nificantly worsens with the added noise in comparison
to just quantization noise. The fixed initial particular
solution based on a measured camera signal can most
likely be hold accountable for this effect. This way,
any disturbances contained within camera signals are
propagated and possibly enhanced, leading to initial
estimates on the particular solution that are too far off
and cannot be fixed.
Finally, an interesting behavior can be observed for
the quantized and noisy scenario in conjunction with
the metameric constraint network. The relative per-
formance of the different camera devices to each other
changes. In fact, the ranking is almost inverted. The
originally best performing device, the Kodak camera,
achieves now the worst results. It demonstrates that
the choice of sensitivity is of great importance and
should always be optimized for the task at hand.
5.2 Modified Loss
As an alternative to the mathematically strict enforce-
ment of the metameric constraint, a modified loss was
proposed. It might be seen as weaker constraint hope-
fully placing less restrictions on the network to remain
Enhancing Deep Spectral Super-resolution from RGB Images by Enforcing the Metameric Constraint
63
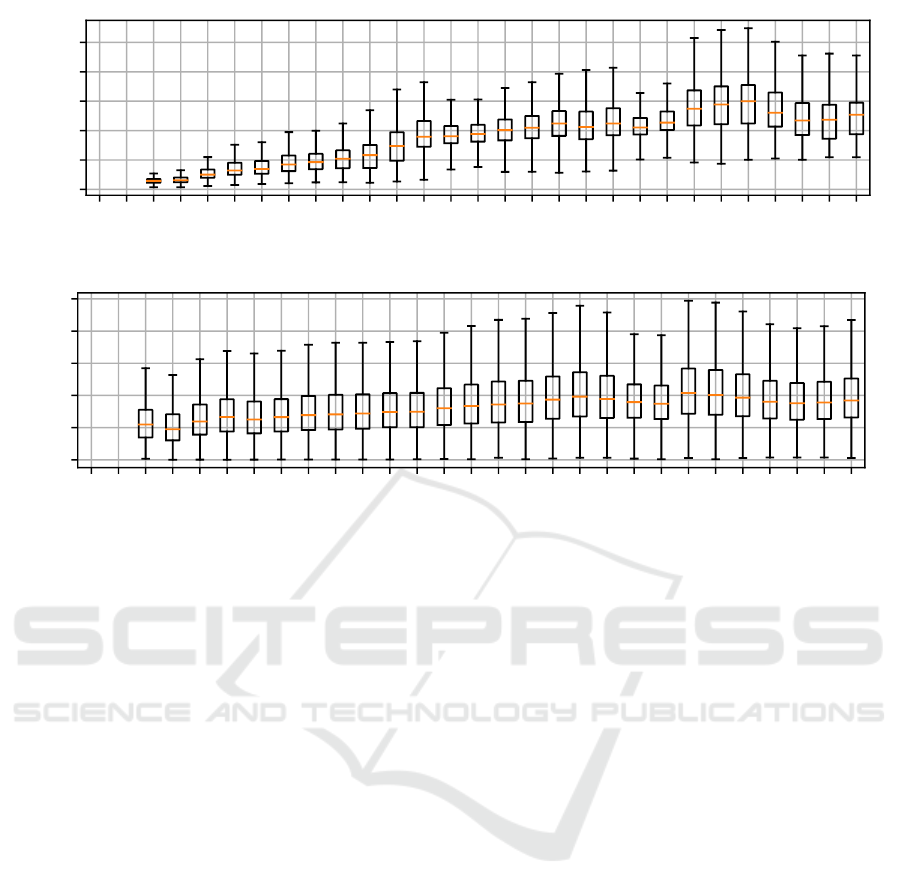
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
position along lightness axis
0
50
100
150
200
250
MAE
(a) Reconstruction error within the spectral domain
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
position along lightness axis
0.0
0.2
0.4
0.6
0.8
1.0
MAE
(b) Reconstruction error within the RGB signal domain
Figure 7: A visualization of the reconstruction error of the vanilla neural network as a box plot depending on the signal
position inside the OCS for the Kodak camera. A higher position on the lightness axis corresponds to a more centralized
signal position inside the OCS. For a better clarification, the lightness axis is explicitly visualized in Fig 4.
robust in the presence of noise. In analogy to the re-
sults presented in Tab. 1 the analysis was performed.
However, an additional parameter needs to be eval-
uated, the metameric loss weight α, as described by
Eq. 7. For a better understanding, the results were vi-
sually processed. The influence of the added loss is
exemplary visualized in Fig. 6 for both the ideal and
quantized scenario for the Kodak camera. In an ideal
world the added metameric term does not appear to
have any influence at all. When considering quantiza-
tion, it can be seen though, that an increasing term of
α, i.e. a higher weighted influence of the metameric
loss component, has a negative impact on the poten-
tial reconstruction of the network. In fact, an α-value
of 0 appears to be ideal, i.e. no metameric loss term
at all. This result is representative and consistent for
all experiments we conducted. When considering the
noisy scenario, the negative impact of the metameric
loss term also only increases. Like the proposed net-
work modification, the metameric loss negatively im-
pacts the result in the presence of noise, but in contrast
to before, it neither has a positive impact in an ideal
world.
5.3 Vanilla Network
Explicitly considering metameric constraints showed
mixed effects on the potential prediction quality of
the neural network. While a significant performance
increase within an ideal world was demonstrated,
the moment any disturbances as little as quantiza-
tion noise are introduced the added constraints seem
counter productive. In order to acquire a better under-
standing as to why, a closer look is taken upon the pre-
diction quality of the vanilla network. It is known that
the corresponding metameric set of a color signal is
the larger the more centralized a camera signal inside
the camera signal space becomes (Finlayson and Mo-
rovic, 2005). Therefore, the average prediction error
of the network is inspected depending on the corre-
sponding color signal position in its 3D signal space.
It can be expected that the more central a camera sig-
nal is located, the harder the reconstruction task be-
comes due to an increasing number of metamers and
therefore the worse the signal prediction gets. In order
to visualize the suspected behavior, every color signal
of the test image set is projected from its 3D signal
space as shown in Fig. 4 onto the lightness axis. The
original signal reconstruction error can then be eval-
uated depending on its relative position on the light-
ness axis. Simply speaking, the higher the position on
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
64

the lightness axis becomes, the more central the color
signal is located. The evolution of the spectral recon-
struction error over the lightness axis is displayed in
Fig. 7a as box plot. The considered error metric is
the mean absolute error (MAE), i.e. the average Eu-
clidean distance of the computed spectral reconstruc-
tion to its ground truth. A direct increase of the error
metric depending on the camera signal position is im-
mediately apparent.
Likewise to the proposed metameric loss, it is also
possible to project all spectral reconstructions back
into camera signal space and compare the result to the
input RGB image. When performing the same anal-
ysis as before but this time inside the camera signal
space, another trend is observed and shown in Fig. 7b.
In contrast to the spectral domain, the reconstruction
error remains rather constant independent of the po-
sition inside the signal space. It is worth highlighting
the average absolute error inside the camera signal do-
main. Since we are assuming an 8bit encoding and
therefore signals ranging from 0 to 255, the average
absolute errors are in fact in the same range as po-
tential quantization noise. One might argue, that the
reconstruction itself is already close to ideal. Any ad-
ditionally introduced reconstruction error within the
spectral domain must thus be along dimensions that
are not observable by the camera system. Therefore,
the limits of spectral reconstruction from RGB image
acquisition appear to be already reached. The map-
ping from one camera signal to many possible spec-
tral signals cannot be easily solved and most likely
only be further optimized in a significant way by em-
ploying multi-spectral imaging. The interesting re-
sult though is, that the neural network appears to
be already capable of implicitly learning the realm
of metameric blacks itself. Made reconstruction er-
rors are mostly introduced in a meaningful way along
spectral dimensions no information is available on.
For further research, it would be highly interesting to
understand how and in what form the network actu-
ally represents the information.
6 CONCLUSION
Within this work, a modification to neural networks
which perform the task of spectral reconstruction
from camera images was proposed. The modification
is based upon the idea to mathematically enforce the
reconstruction to be at least within the metameric sub-
set of spectral stimuli to the true stimulus. The poten-
tial positive impact of the modification was demon-
strated by applying it to a state-of-the-art model and
using it to reconstruct spectral images from differ-
ent simulated RGB cameras. Since the enforced
metameric constraint directly corresponds to a better
initialization, the training process also converges sig-
nificantly faster. However, above findings only hold
true in an ideal world. The metameric based recon-
struction was found to be highly sensitive to noise,
probably preventing an application in the real world.
It was further demonstrated, that a consideration of
metamerism within the loss function does not yield
any positive effects at all. The reason is that knowl-
edge of a cameras’ sensitivity can already be success-
fully learned by directly training a neural network to
learn an end-to-end mapping from the camera signal
space to the spectral domain. As shown within this
work, such self-learned knowledge must be contained
somewhere within a fully trained network. However,
it is unclear in what form, leaving the potential extrac-
tion of a learned camera sensitivity from the network
as an interesting topic for further research.
REFERENCES
Aeschbacher, J., Wu, J., and Timofte, R. (2017). In de-
fense of shallow learned spectral reconstruction from
rgb images. 2017 IEEE International Conference on
Computer Vision Workshops (ICCVW), pages 471–
479.
Arad, B. and Ben-Shahar, O. (2016). Sparse recovery of
hyperspectral signal from natural rgb images. In Eu-
ropean Conference on Computer Vision, pages 19–34.
Springer.
Arad, B., Ben-Shahar, O., Timofte, R., Van Gool, L., Zhang,
L., Yang, M.-H., et al. (2018). Ntire 2018 challenge on
spectral reconstruction from rgb images. In The IEEE
Conference on Computer Vision and Pattern Recogni-
tion (CVPR) Workshops.
Bianco, S. (2010). Reflectance spectra recovery from tris-
timulus values by adaptive estimation with metameric
shape correction. J. Opt. Soc. Am. A, 27(8):1868–
1877.
Finlayson, G. D. and Morovic, P. (2005). Metamer sets. J.
Opt. Soc. Am. A, 22(5):810–819.
Gijsenij, A., Gevers, T., and van de Weijer, J. (2011). Com-
putational color constancy: Survey and experiments.
IEEE Transactions on Image Processing, 20:2475–
2489.
Hardeberg, J. Y., Schmitt, F. J. M., and Brettel, H. (1999).
Multispectral image capture using a tunable filter. In
Proc.SPIE, volume 3963, pages 3963 – 3963 – 12.
Hill, B. (2002). Optimization of total multispectral imag-
ing systems: best spectral match versus least observer
metamerism. In 9th Congress of the International
Colour Association, volume 4421, pages 481–486.
Imai, F. H., Rosen, M. R., and Berns, R. S. (2002). Com-
parative study of metrics for spectral match quality.
In Conference on Colour in Graphics, Imaging, and
Vision (CGIV), pages 492–496.
Enhancing Deep Spectral Super-resolution from RGB Images by Enforcing the Metameric Constraint
65

Jia, Y., Zheng, Y., Gu, L., Subpa-Asa, A., Lam, A., Sato, Y.,
and Sato, I. (2017). From rgb to spectrum for natural
scenes via manifold-based mapping. In International
Conference on Computer Vision (ICCV), pages 4715–
4723.
Kawakami, R., Hongxun, Z., Tan, R. T., and Ikeuchi, K.
(2013). Camera spectral sensitivity and white balance
estimation from sky images. International Journal of
Computer Vision.
Kaya, B., Can, Y. B., and Timofte, R. (2018). Towards
spectral estimation from a single RGB image in the
wild. CoRR, abs/1812.00805.
Miyake, Y., Yokoyama, Y., Tsumura, N., Haneishi, H.,
Miyata, K., and Hayashi, J. (1999). Development
of multiband color imaging systems for recordings of
art paintings. In Color Imaging: Device-Independent
Color, Color Hardcopy, and Graphic Arts.
Nguyen, R. M. H., Prasad, D. K., and Brown, M. S. (2014).
Training-based spectral reconstruction from a single
rgb image. In European Conference on Computer Vi-
sion (ECCV), pages 186–201. Springer.
Stiebel, T., Koppers, S., Seltsam, P., and Merhof, D. (2018).
Reconstructing spectral images from rgb-images us-
ing a convolutional neural network. In The IEEE Con-
ference on Computer Vision and Pattern Recognition
(CVPR) Workshops.
Timofte, R., Gu, S., Wu, J., Van Gool, L., Zhang, L., Yang,
M.-H., et al. (2018). Ntire 2018 challenge on sin-
gle image super-resolution: Methods and results. In
The IEEE Conference on Computer Vision and Pat-
tern Recognition (CVPR) Workshops.
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
66
