
Graph based Method for Online Handwritten Character Recognition
Rabiaa Zitouni
1 a
, Hala Bezine
2
and Najet Arous
1
1
Laboratory LR-SITI ENIT, University Tunis El Manar, B.P.37, 1002 Tunis, Tunisia
2
Laboratory REGIM ENIS, University Sfax, B.P.1173, 3038 Sfax, Tunisia
Keywords:
Fuzzy Attributed Relational Graph, Graph Matching, Structural Pattern Recognition, Handwritten Graphs,
Tree Search Method.
Abstract:
In this research, we attempt to propose a novel graph-based approach for online handwritten character recog-
nition. Unlike the most well-known online handwritten recognition methods, which are based on statistical
representations, we set forward a new approach based on structural representation to overcome the inherent
deformations of handwritten characters. An Attributed Relational Graph (ARG) is dedicated to allowing the
direct labeling of nodes (strokes) and edges (relationships) of a graph to model the input character. Each node
is characterized by a set of fuzzy membership degrees describing their properties (type, size). Fuzzy descrip-
tion is invested in order to guarantee more robustness against uncertainty, ambiguity and vagueness. ARGs
edges stand for spatial relationships between different strokes. At a subsequent stage, a tree-search based
optimal matching algorithm is explored, which allows the search for character structures i.e the minimum cost
of nodes. Experiments performed on ADAB and IRONOFF datasets, reveal promising results. In particular,
the comparison with the state of the art demonstrates the significance of the proposed system.
1 INTRODUCTION
Graphs have emerged as an active area of research
aims to model structural relations of objects and pat-
terns. The graph’s ability to model different parts of
an object as well as its bases on sound mathemati-
cal background can be invested in many diverse fields
(Baldini et al., 2019; Lee et al., 2018). In the domain
of handwritten character recognition, graph drew the
attention and whetted the interest of numerous re-
searchers.
The use of a graph-based handwritten recognition
induces the need to formulate two main required oper-
ations: transforming handwritten graphs into feature
vectors and calculating the graph similarity. From this
perspective, the common task is to compare graphs to
find the similarities between them. This is known as
graph matching (GM). Basically, two types of graph
matching were adopted by researchers(Yan et al.,
2016). The exact graph matching refers to the search
for an exact replication of the test graph in the tem-
plate graph as well as the conservation of all rela-
tionships presented in test one. The complexity of
the exact graph matching has not yet been speci-
fied to be P or NP(Conte et al., 2004), but there are
a
https://orcid.org/0000-0002-7616-8374
polynomial algorithms for solving the isomorphism
problem of certain graph categories. A well-known
method is based on the depth-first search (backtrack-
ing) with a forward checking method which greatly
reduces the number of backtracking steps. The in-
exact graph matching provides a distance value that
indicates graph dissimilarity(Bengoetxea, 2002). One
of the most flexible and versatile approaches to inex-
act graph matching is graph edit distance(Abu-Aisheh
et al., 2017). However, the latter suffers from its high
complexity that limits its applicability to graphs with
small size. For this reason, a number of methods ad-
dressing the high computational complexity of graph
edit distance computation has been established, e.g.
(Darwiche et al., 2019).
Moreover, in recent years many tree-based
methods(Abu-Aisheh et al., 2015) have become of
great interest to researchers since computational time
and even the explored search space can be manage-
able with the impact of the quality of the provided
matching solution. Therefore, the primary motiva-
tion of the paper lies in tree-based methods which can
be explored in GM computation. Besides, owing to
the variability and ambiguity of handwritten charac-
ter strucure (for example: disorder, imprecision, con-
nection, etc) the use of fuzzy graph-based description
could be extremely helpful to add flexibility against
Zitouni, R., Bezine, H. and Arous, N.
Graph based Method for Online Handwritten Character Recognition.
DOI: 10.5220/0008956602630270
In Proceedings of the 15th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2020) - Volume 1: GRAPP, pages
263-270
ISBN: 978-989-758-402-2; ISSN: 2184-4321
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
263

these errors. In this paper, we propose a novel fuzzy
graph-based handwritten method that takes advantage
of the aforementioned tree technique and fuzzy logic
concept merging them together with a Weighted Eu-
clidean Distance (WED) to matching two characters
graphs. Finally, we shall use the fuzzy attributed rela-
tional graph (FARG) matching algorithm to recognize
online hand written characters. The rest of this paper
is organized as follows. Section 2, presents a brief
description about related works. Section 3, illustrates
the graph used to represent the handwritten character
and presents the graph matching algorithm. In section
4, the experimental evaluation is elaborated on ADAB
and IRONOFF datasets. Finally, section 5 wraps up
the conclusion and provides new perspectives for fu-
ture works.
2 LITERATURE REVIEW
Great attention has been paid to graph based method
in many application fields. Among them, we can cite:
image analysis (Cl
´
ement et al., 2018), etc. For in-
stance, a few attempts are performed in online hand-
written character recognition research with graph rep-
resentation or relative concepts. One of the pioneer
attempts to use graph in online handwritten charac-
ter recognition was carried out by Si-Wei Lu et al.(Lu
et al., 1991). To obtain an efficient recognition system
and avoid much of the combinatorial explosion in the
graph matching, the author resorted to a two-level hi-
erarchical graph representation for handwritten Chi-
nese characters. The two-level graph has a special
structure: the lower level is composed of nodes that
denote the strokes of a character to which they at-
tributed through the irrespective orientation on the
one hand. The edges denote relations between nodes
according to the type of junction on the other. Fi-
nally, an error-tolerant graph matching for classifica-
tion framework is provided. This attempt is also con-
ducted with (Huang et al., 1993) to recognize Chi-
nese characters. Indeed, any character class will be
described by a graph where the stroke’s points repre-
sent the nodes and relation between them is defined
by an edge. A constraint-based optimization prob-
lem is formulated using a relaxation matching for re-
solving issues in pattern recognition. Resting upon
Chinese characters, in(Suganthan and Yan, 1998) a
method for recognition of hand printed Chinese char-
acters is defined. Hopfield networks have been used
to solve graph matching problem. In both references
(Rocha and Pavlidis, 1994) and (Rocha and Pavlidis,
1995) the task of recognizing machine printed dis-
torted characters in text lines is tackled. Unlike all
graph methods each node corresponds to a branch,
an ending, a turning points or a sharp corner and the
edges represent strokes. Recognition task of text lines
turns into an error-tolerant subgraph isomorphisms
from character prototype graphs to text line graphs. In
this case, the benefits recorded compared to feature-
based methods are typically two fold: First, mak-
ing optical character recognition to be independent of
segmentation. Second, handling both touching and
broken characters. Ref (Chakravarthy and Kompella,
2003) also tackled the online handwritten recogni-
tion problem using graph-based shape representation.
In this work, the authors aim to build graphs from
a handwritten shape. In this sense, they opted first
for creating a vector out of seven Structural Proper-
ties (SP) related to the shape of handwriting: inte-
rior, end, bump, cross, dot and various other char-
acteristic shape points of the trace of a handwritten
text. Thereafter, each handwritten character is rep-
resented by a graph with SP design the nodes and
edge served as a link between nodes. (Al Mubarok
and Nugroho, 2016) proposed a method using the
skeleton structure of character as a way to design
graph where edges were identified into shape types
and nodes were detected with line simplification al-
gorithm. The graph matching issue is converted into
hierarchical approach and is concepted with the sub-
graph isomorphism principals. To the knowledge of
the underlying authors, these methods are still far
away of being able to deal efficiently with a large and
multilingual dataset of complexe characters. Thus, we
evolve a fuzzy matching algorithm for graph-based
handwriting recognition. The proposed matching al-
gorithm permits efficiency more regarding the vari-
ability of characters, as well as the imprecision and
the ambiguity of their structures.
3 GRAPH REPRESENTATION OF
HANDWRITTEN CHARACTERS
3.1 Introduction of Fuzzy Attributed
Graph
The notion of Attributed relational graph (ARG) was
introduced in 1983 by Tsai and Fu for pattern analy-
sis task (Tsai and Fu, 1983). The nodes of the graph
indicate the different components of objects while the
edges denote the relations between these components.
More recently, this definition has been extended to a
Fuzzy Attributed Relational Graph (FARG) by attach-
ing fuzzy attributes to its nodes and edges. FARG was
introduced by Chang and Cheung (1992)(Chan and
GRAPP 2020 - 15th International Conference on Computer Graphics Theory and Applications
264
Cheung, 1992). These references (Jouili et al., 2009;
Luqman et al., 2013) are suggested for supplementary
reading on ARG and FARG respectively and their ap-
plications.
3.2 Graph Generation
An online character pattern is composed of a se-
quence of an arbitrary number of strokes. A stroke
is defined as an elementary drawn between pen up
and pen down. A handwritten character is approxi-
mated by a graph where stroke is denoted with node.
These nodes are linked by an edge that represents the
relations between them. For a handwritten character
that is composed of n strokes, its associated graph is
also composed of n nodes (same number of strokes)
and n(n- 1)/2 edges. An example of nodes and edges
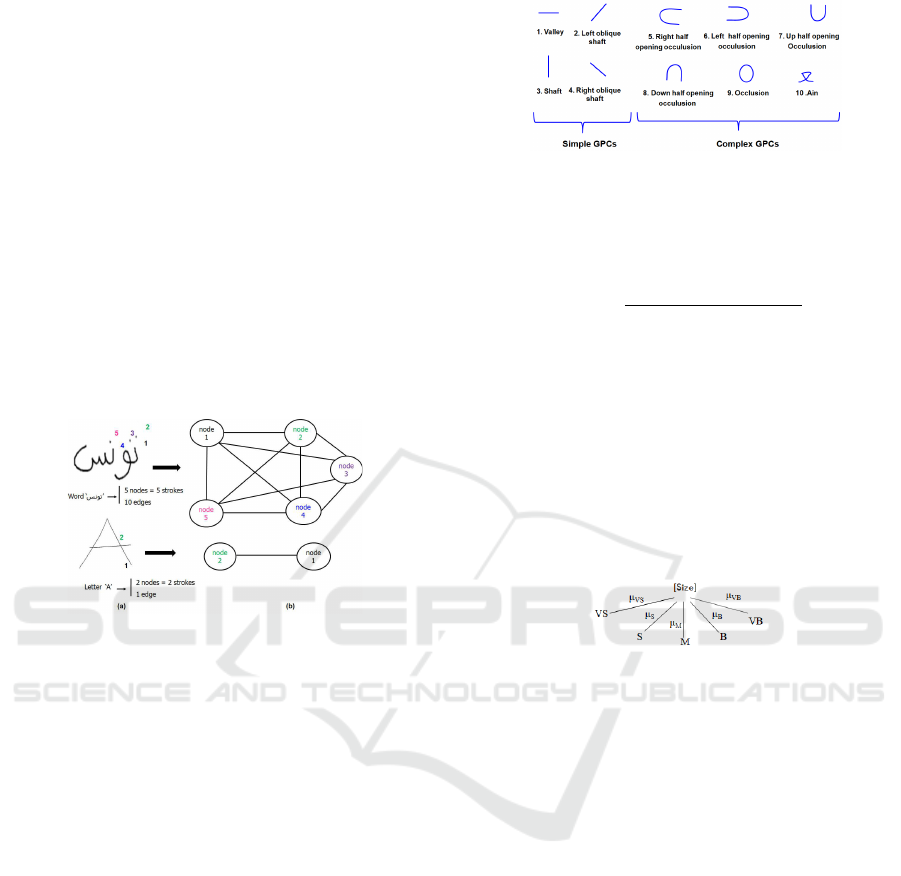
numbers is illustrated in figure 1.
Figure 1: (a) An example of a handwritten character, (b) Its
corresponding graph.
3.3 Computation of Node Attributes
Two nodes attributes are used namely type and size.
3.3.1 Stroke Type Attribute
Based on the βeta-elliptic model, each script in the
segmentation step is modeled in the dynamic domain
by a series of βeta profiles and in the static domain
by a series of elliptic arcs. The reader is referred to
(Bezine et al., 2007) for more details. Firstly, for
each elliptic stroke we assigned an Elementary Per-
ceptual Code (EPC) (Njah et al., 2012). However,
to solve the problems of perception and uncertainty
of assessed EPC, we opted for fuzzy logic representa-
tion(Njah et al., 2012). Based on the human vision we
cannot perceive these EPCs. What we can perceive is
restricted to some general forms labeled Global Per-
ceptual Codes (GPCs)obtained with the combination
of fuzzy EPCs. Due to the variety of possible com-
binations concerning either the number or the type of
EPCs that form a GPC, we opted to use the Genetic
Algorithms (GAs) to detect GPCs easily. Figure 2 ex-
hibits the different GPCs, their classification and the
corresponding shapes.
Figure 2: List of GPCs.
3.3.2 Size Type Attribute
The following equation is used to compute the size of
handwritten stroke :
d =
q
(x
l
− x
f
)
2
+ (y
l
− y
f
)
2
(1)
Where (x
f
,y
f
) and (x
l
,y
l
) denote respectively the start
and end point coordinates. The membership functions
for the linguistic values of this feature are identified
over the domain [0, 1]. The domain is then divided
into 5 fuzzy regions. In order to get more significant
regions and minimum overlapping sets between them.
The linguistic labels associated with it are Very Small
(VS) , Small (S) , Medium (M), Big (B) and Very Big
(VB) as depicted in figure 3 .
Figure 3: Size representation.
3.4 Computation of Edge Attribute
3.4.1 Spatial Relations
Same strokes can appear differently in the same char-
acters and can be placed in different positions, which
may change the characters meaning. For this reason,
defining the spatial relation is necessary. In spite of
the advantages, relationships have not been actively
modeled in many online handwritten character recog-
nition systems. They were tackled in many offline
task (Cl
´
ement et al., 2018). As a matter of fact, in or-
der to infer the relationship within handwriting stroke,
we should first invest strokes’ topological properties
i.e centroid and bounding boxes.
Bounding Box: A stroke bounding box is defined as
the smallest rectangle that firmly encloses the stroke.
Bounding box of stroke ’S’ is represented by four co-
ordinates: x
S
1
= min(x
S
i
), x
S
2
= max(x
S
i
), y
S
1
= min(y
S
i
)
and y
S
2
= max(y
S
i
) as depicted in the figure 4.
Centroid: The most common technique to check the
position of stroke within a region or not is to ana-
Graph based Method for Online Handwritten Character Recognition
265

Figure 4: Bounding box of an Arabic stroke.
lyze the coordinates of its centroid. We define the x-
coordinate of the centroid of a stroke s as x
c
= (x
S
2
−
x
S
1
)/2 and the y-coordinate as y
c
= (y
S
2
− y
S
1
)/2. At
this level, the consideration of two successive hand-
written strokes S and S
1
and the use of the center of
their bounding boxes and the centroids of both strokes
enable us to identify the following geometrical fea-
tures.
i) The angle of the line passes through the two cen-
troids of strokes with respect to the horizontal line
as expressed in the equation below:
θ = tan
−1
(
y
S
1
c
− y
S
c
x
S
1
x
− x
S
p
) (2)
ii) The intersection points
S ∩ S
1
=
1 if (S ∩ S
1
6= ∅) ⇒ intersect
0 otherwise
(3)
iii) The distance between the y-coordinates of the
centroids, denoted by dist
y
(S,S
1
) = y
S
1
c
− y
S
c
iv) The distance between the x-coordinates of the
centroids, denoted by dist
x
(S,S
1
) = x
S
1
c
− x
S
c
v) The distances between the x-coordinates
of the bottom right boundaries, denoted by
dist
bt
(S,S
1
) = x
S
1
2
− x
S
2
vi) The distances between the x-coordinates of the
Top left boundaries, denoted by dist
top
(S,S
1
) =
x
S
1
1
− x
S
1
An illustrative example is presented in figure 5 with
the different calculated metrics.
Figure 5: Geometrical features between two handwritten
strokes S and S
1
of Latin character.
The different features serve as input to a fuzzy con-
troller whose outputs are a spatial relation type.
Therefore a set of ten spatial relations are identified
as illustrated in figure 6.
Figure 6: Strokes relationships.
3.5 Matching Handwritten Graphs and
Recognition
The comparison of two handwritten graphs can be for-
mulated as a problem of inexact graph matching. For
thus, we adopted an algorithm based a tree search of
the node mappings. The following sections describe
the main parts of this algorithm in detail.
3.5.1 Proposed Algorithm
Given two FARGs G
1
which denotes the template
handwritten graph and G
2
the test one. The graph
G
1
has N nodes, which are represented as n
x
i
(i ∈
1,2···N) while graph G
2
has N
0
nodes, which are rep-
resented as n
y
i
(i ∈ 1,2 · · ·N
0
). Assume that any n
x
i
or
n
y
i
can be expressed by a vector of µ
x
i
and µ
y
i
respec-
tively:
µ
i
x
= µ
(i)
x
[1],µ
(i)
x
[2],...,µ
(i)
x
[a],...,µ
(i)
x
[A],a ∈ {1,2, ...A} (4)
µ
i
y
= µ
(i)
y
[1],µ
(i)
y
[2],...,µ
(i)
y
[a
0
],...,µ
(i)
y
[A],a
0
∈ {1,2,...A} (5)
A is the total number of membership degree associ-
ated with nodes regardless of n
i
x
. Different weights
are assigned to each node features according to their
relative importance to describe the node characteris-
tics. We denote by W
n
i
x
the weight of node n
x
i
and W
n
i
y
the weight of node n
y
i
. G
1
and G
2
are represented in
the weight space as a weight vector of W
N
and W
N
0
respectively :
W
N
=
h
W
n
1
x
,W
n
2
x
,...,W
x
N
i
,i ∈ {1,2,...N}and
∑
N
i=1
W
n
i
x
= 1 (6)
W
N
0
=
h
W
n
1
y
,W
n
2
y
,...,W
y
N
0
i
,i ∈ {1,2,...N
0
}and
∑
N
0
i=1
W
n
i
y
= 1 (7)
node n
i
x
and node n
i
y
with the highest value of W
N
and W
0
N
respectively are considered the most impor-
tant nodes during the nodes matching.
The edge between every node n
i
x
and n
j
x
in G
1
is rep-
resented by a vector of e
(i, j)
x
while the edge between
every node n
i
y
and n
j
y
in G
2
is represented by a vec-
tor of e
(i, j)
y
. Similarly, both edges e
(i, j)
x
and e
(i, j)
y
are
represented by a set of vectors denoted below :
e
(i, j)
x
= e
(i, j)
x
[1],e
(i, j)
x
[2],..., e
(i, j)
x
[b],..., e
(i, j)
x
[B],b ∈ {1, 2, ...B} (8)
e
(i, j)
y
= e
(i, j)
y
[1],e
(i, j)
y
[2],..., e
(i, j)
y
[b
0
],..., e
(i, j)
y
[B],b
0
∈ {1, 2, ...B} (9)
GRAPP 2020 - 15th International Conference on Computer Graphics Theory and Applications
266

Where B is the total number of membership associ-
ated with edges regardless of e
(i, j)
x
or e
(i, j)
y
respec-
tively. If we denote by W
e
i
x
the weight of edge e
(i, j)
x
and W
e
i
y
the weight of edge e
(i, j)
y
. G
1
and G
2
are rep-
resented in the weight space as a weight vector W
T
and W
T
0
respectively :
W
T
=
h
W
e
1
x
,W
e
2
x
,...,W
e
T
x
i
,i ∈ {1,2,...T }and
∑
T
i=1
W
e
i
x
= 1 (10)
W
T
0
=
h
W
e
1
y
,W
e
2
y
,...,W
e
T
0
y
i
,i ∈ {1,2, ...T
0
}and
∑
T
0
i=1
W
e
j
y
= 1 (11)
With T and T
0
are the total number of edges in tem-
plate and test character respectively.
The graph matching is carried out by means of a tree
search algorithm provided in algorithm 1.
Algorithm 1: Tree-based search algorithm.
Input: Template graph G
1
and test graph G
2
Output: The lowest cost match between G
1
and G
2
Matching(G
1
,G
2
)
Dist
min
= ∞
P =
/
0
N
min
=NULL
N=
/
0
N’=
/
0
N ← extract
nodes
(G
1
)
N’ ← extract
nodes
(G
2
)
for each node n ∈ N do
for each node n
0
∈ N
0
do
Compute Dist(n,n
0
) using Eq(10)
if (Dist(n,n
0
) ≺ Dist
min
) then
Dist
min
=Dist(n,n
0
)
N
min
=n
0
end if
end for
P ← P ∪ {(n,N
min
)}
N ← N - {(n)}
N
0
← N
0
- {(N
min
)}
end for
Return P
In order to identify the similarity between two entities
a distance metric is needed. From this perspective,
the weighted euclidean distance metrics opts for the
fuzzy attributes. Given a node n
i
x
in G
1
and its pair
node in G
2
is n
j
y
, a distance between the two nodes is
measured using weighted Euclidean metric (WED) as
portrayed below:
Dist
1
= [
A
∑
i=1
W
n
i
× (µ
i
x
− µ
i
y
)
2
]
1
2
(12)
The weights W
N
i
are proposed as:
W
N
i
= max(max(µ
i
x
),max(µ
i
y
)) (13)
It is noticeable that a distance between two paired
edges is computed by the equation below:
Dist
2
= [
∑
B
i=1
W
e
i
× (e
(i, j)
x
− e
(i, j)
y
)
2
]
1
2
(14)
The weights W
e
i
are proposed as:
W
e
i
= max(max(e
(i, j)
x
),e
(i, j)
y
)) (15)
A synthesis distance caused by all nodes is then ex-
pressed by:
Dist
nodes
=
∑
L
1
i=1
Dist
1
(16)
A synthesis distance caused by all edges is then ex-
pressed by:
Dist
edges
=
∑
L
2
i=1
Dist
2
(17)
Where L
1
and L
2
are the number of matched node
pairs and the number of matched edge pairs, respec-
tively. Thus a similarity measure between a pair of
FARG r can be defined directly with
Sim(G
1
,G
2
) = W
G
1
× Dist
nodes
+W
G
2
× Dist
edges
(18)
Where W
G
1
and W
G
2
are properly selected weights of
G
1
and G
2
. The procedure of computation of similar-
ity is summarized below (algorithm 2).
Algorithm 2: The proposed FARG matching algorithm.
Input: Template graph G
1
and test graph G
2
Output: Matching similarity measure Sim
Dist
1
=
/
0
Dist
2
=
/
0
Dist
nodes
=
/
0
Dist
edges
=
/
0
P
1
=
/
0
P
1
=matching( G
1
, G
2
)
for each successor pairs of nodes {(n,n
0
),(n
1
,n
0
1
)} ∈
P1 do
E
1
=extract
edge
(n,n
1
) ∈ G
1
E
2
=extract
edge
(n
0
,n
0
1
) ∈ G
2
Dist
2
=Compute Dist(E
1
,E
2
) using Eq(12)
Dist
edges
← Dist
edges
∪ {(Dist
2
)}
end for
for each pair of nodes (n,n
0
) ∈ P1 do
Dist
1
=Compute Dist(n,n
0
) using Eq(10)
Dist
nodes
← Dist
nodes
∪ {(Dist
1
)}
end for
Dist
nodes
← Dist
nodes
∪ {(Dist
1
)}
Compute Sim using Eq(16)
3.6 Recognition
The proposed approach uses a fuzzy graph matching
algorithm to recognize online handwritten characters.
Graph based Method for Online Handwritten Character Recognition
267

Figure 7: Flowchart of the proposed algorithm for hand-
written recognition characters.
Figure7 illustrates an overview of the framework and
rests upon a set of phases as described below.
In the first phase, the FARG of handwritten characters
for both template and test are extracted as explained in
section 3. In the second phase the similarity of nodes
Sim(nodes)
i j
as well as Sim(edges)
i j
between a graph
FARG
i
of the i
th
test graph and a graph FARG
j
of the
j
th
template graph is calculated as mentioned in al-
gorithm 2. Then the similarity S
j
between the two
graphs is computed by summing up the nodes and
edges similarities. Therefore, the class correspond-
ing to the graph which provides the best match (max-
imum degree of similarity) constituent the recognized
handwritten character.
C = argmax
j
{Sim
j
} (19)
4 EXPERIMENTAL RESULTS
At this stage of analysis, we shall address the obtained
results, discuss them and evaluate them in order to as-
sess the effectiveness and feasibility of our approach.
4.1 Datasets
ADAB Data Base: The data base ADAB (El Abed
et al., 2011) was developed in cooperation between
the Institut fuer Nachrichtentechnik (IfN) and Re-
search Groups in Intelligent Machines,Tunisia at Uni-
versity of Sfax. It was collected by using digital
tablets connected to computers,more than 130 dif-
ferent writers mainly of Tunisian nationality. This
database contains 21575 online Tunisian town and
village names in Arabic languages. IRONOFF
database: The database IRONOFF (Viard-Gaudin
et al., 1999) is created using the mechanism Pen
Tablet which was of a tablet type A4Wacom Ultra Pad
sampling speed of 100 points per second since 1999.
The prototype is recorded in the format UNIPEN.
IRONOFF database is characterized by the domi-
nance of isolated symbols, French and English words
as well as digits.
A set of 1135 handwritten characters are randomly
selected from these data bases to perform fuzzy graph
matching and therefore to carry out the recognition
task. First, each handwritten words is converted into
graphs by representing strokes by nodes and spatial
relationships between them by edges. Table 1 por-
trays the graph and its distribution degree. We denote
the ex, tr and tes as the size of examples, training and
testing of both datasets respectively. Minimum and
maximum of nodes N and edge E degrees for graphs
are also presented. The size varies from small graphs
with under 5 nodes and edges and up to 15 nodes and
edges in both datasets.
Table 1: Graph and their degree distribution.
Size Min Max
Dataset ex tr tes |N| |E| |N| |E|
IRONOFF 634 381 253 2 1 10 45
ADAB 519 312 207 2 1 15 105
4.1.1 Experimental Results
In order to explain why the FARG has such an ex-
cellent performance, time complexity should be ana-
lyzed.
4.1.2 Execution Time
The different experiments were performed on PC with
Intel Core i7-7500, 8 GB RAM. Table 2 displays the
required time of each input character for generating
(building) its corresponding graph related to the nodes
number.
Table 2: Computational time for graph generation.
Number of nodes Graph generation times
≺ 5 ≺ 10s
5-10 10-25 s
10 25s
It can be observed that the method requires less ex-
ecution time for a smaller number of nodes. Ta-
ble 3 introduces the running time for some hand-
written drawing. For each entry we would illustrate
the drawn characters property number of nodes of
template and test graph (N
G
, N
0
G
, respectively) ,the
time for generating both graphs(GG) N
G
and N
0
G
,
the time for graph matching between graphs(M) (sec-
tion 3) and finally the total computational time. Note
that the largest computational times are required for
GRAPP 2020 - 15th International Conference on Computer Graphics Theory and Applications
268

generation (building) graphs mainly due to the pre-
processing step which was performed to reduce the
noise and step needed for calculating nodes/edges at-
tributes.
Table 3: Computational time.
Scripts |N
G
| |N
0
G
| Computational time
GG M Total
”
é¢ËA
®J
.
Ë@” 11 11 56 22 78
”ÉêÓñK
.
” 4 4 18 7 25
ñJ
” 7 7 30 9 39
”
éÓ
QK
.
” 6 6 24 8 32
”
èð@Q
ªÓ” 7 7 40 17 57
”
é
KAK
P
@” 10 10 46 18 64
”A” 3 3 14 6 20
”B” 2 2 12 4 16
”Money” 2 2 14 5 19
”Quiz” 5 5 18 6 24
”quelqu’un” 8 8 42 19 61
”Neptune” 8 8 48 15 63
4.2 Recognition Accuracy
For both dataset, the training and testing sets contain
60% and 40% of graphs respectively, and serve as the
dataset graphs. Referring to table 4 and table 5, we get
an impressive recognition rate which exceeds 98% for
both dataset. Next, our ultimate objective is to eval-
uate our approach which is based on graph matching
with related works. It is worth noting, a large vari-
ety of recognition algorithms has been tested on these
datasets and some of the best results are outlined.
Table 4: Best reported recognition results for the ADAB
dataset.
Systems Recognition rate
HMM (Khlif et al., 2016) 93.33%
MLP-HMM (Elleuch et al., 2016) 96.45%
CNN (Tagougui et al., 2013) 91.8%
AUC-HMM1 (El Abed et al., 2011) 98.45%
FARG matching (present work) 98.62 %
In table 4, we compared our results with re-
sults conducted on ADAB dataset by (Khlif et al.,
2016),(Elleuch et al., 2016), (Tagougui et al., 2013)
and (El Abed et al., 2011) and based on HMM, MLP-
HMM, CNN networks and AUC-HMM1 respectively.
The recognition rate provided by our algorithm ex-
hibits an improvement that varies between 6.82% and
0.17% over the four participating systems.
Table 5 reports also the performance of our recogni-
tion systems on IRONOFF dataset. We achieved a
Table 5: Best reported recognition results for the IRONOFF
dataset.
Systems Recognition rate
ConvLSTM(Akouaydi et al., 2019) 93%
BCP+LSTM(Akouaydi et al., 2019) 98%
FARG matching (present work) 99.24%
very competitive rate with respect to other two pub-
lished result (Akouaydi et al., 2019) based on Con-
vLSTM and BCP+LSTM. We exhibited an improve-
ment that varies between 6.24% and 1.24% over re-
lated systems. This finding which based on the use
of an efficient WED metric jointly with a tree search
process guides the matching solutions and therefore
contributes to a high-rate recognition.
5 CONCLUSIONS
In this paper, we aimed at setting forward a new ap-
proach to perform an online handwritten recognition.
The nodes and edges of the graph are labeled using
fuzzy logic attributes. The graphs are matched us-
ing a WED as the similarity function and based on a
tree search process. The approach is tested on ADAB
and IRONOFF datasets. This approach helps to rec-
ognize the handwritten character and achieve recog-
nition rates of 98.62 % and 99.24% respectively. Our
work is an initial step that can be further developed
as it opens new perspectives and offers different hori-
zons for future works in the domain of handwritten
recognition includes the investigation of a graph em-
bedding method with a new classification schemes
such as deep learning.
REFERENCES
Abu-Aisheh, Z., Ga
¨
uzere, B., Bougleux, S., Ramel, J.-Y.,
Brun, L., Raveaux, R., H
´
eroux, P., and Adam, S.
(2017). Graph edit distance contest: Results and fu-
ture challenges. Pattern Recognition Letters, 100:96–
103.
Abu-Aisheh, Z., Raveaux, R., Ramel, J.-Y., and Martineau,
P. (2015). An exact graph edit distance algorithm for
solving pattern recognition problems. In 4th Inter-
national Conference on Pattern Recognition Applica-
tions and Methods 2015.
Akouaydi, H., Njah, S., Ouarda, W., Samet, A., Dhieb, T.,
Zaied, M., and Alimi, A. M. (2019). Neural archi-
tecture based on fuzzy perceptual representation for
online multilingual handwriting recognition. arXiv
preprint arXiv:1908.00634.
Al Mubarok, A. and Nugroho, H. (2016). Handwritten char-
acter recognition using hierarchical graph matching.
In International Conference on Advanced Computer
Graph based Method for Online Handwritten Character Recognition
269

Science and Information Systems (ICACSIS), pages
454–459. IEEE.
Baldini, L., Martino, A., and Rizzi, A. (2019). Stochastic
information granules extraction for graph embedding
and classification. In Proceedings of the 11th Inter-
national Joint Conference on Computational Intelli-
gence, volume 1, pages 391–402.
Bengoetxea, E. (2002). Inexact Graph Matching Using Es-
timation of Distribution Algorithms. PhD thesis, Ecole
Nationale Sup
´
erieure des T
´
el
´
ecommunications,Paris,
France.
Bezine, H., Kefi, M., and Alimi, A. M. (2007). On the beta-
elliptic model for the control of the human arm move-
ment. International Journal of Pattern Recognition
and Artificial Intelligence, 21(01):5–19.
Chakravarthy, V. S. and Kompella, B. (2003). The shape
of handwritten characters. Pattern recognition letters,
24(12):1901–1913.
Chan, K. and Cheung, Y. (1992). Fuzzy-attribute graph
with application to chinese character recognition.
IEEE transactions on systems, man, and cybernetics,
22(1):153–160.
Cl
´
ement, M., Kurtz, C., and Wendling, L. (2018). Learning
spatial relations and shapes for structural object de-
scription and scene recognition. Pattern Recognition,
84:197–210.
Conte, D., Foggia, P., Sansone, C., and Vento, M. (2004).
Thirty years of graph matching in pattern recognition.
International journal of pattern recognition and arti-
ficial intelligence, 18(03):265–298.
Darwiche, M., Conte, D., Raveaux, R., and T’Kindt, V.
(2019). A local branching heuristic for solving a graph
edit distance problem. Computers & Operations Re-
search, 106:225–235.
El Abed, H., Kherallah, M., M
¨
argner, V., and Alimi, A. M.
(2011). On-line arabic handwriting recognition com-
petition. International Journal on Document Analysis
and Recognition (IJDAR), 14(1):15–23.
Elleuch, M., Zouari, R., and Kherallah, M. (2016). Feature
extractor based deep method to enhance online arabic
handwritten recognition system. In International Con-
ference on Artificial Neural Networks, pages 136–144.
Springer.
Huang, X., Gu, J., and Wu, Y. (1993). A constrained
approach to multifont chinese character recognition.
IEEE transactions on pattern analysis and machine
intelligence, 15(8):838–843.
Jouili, S., Mili, I., and Tabbone, S. (2009). Attributed graph
matching using local descriptions. In International
Conference on Advanced Concepts for Intelligent Vi-
sion Systems, pages 89–99. Springer.
Khlif, H., Prum, S., Kessentini, Y., Kanoun, S., and Ogier,
J.-M. (2016). Fusion of explicit segmentation based
system and segmentation-free based system for on-
line arabic handwritten word recognition. In 15th In-
ternational Conference on Frontiers in Handwriting
Recognition (ICFHR), pages 399–404. IEEE.
Lee, J. B., Rossi, R. A., Kim, S., Ahmed, N. K., and Koh, E.
(2018). Attention models in graphs: A survey. arXiv
preprint arXiv:1807.07984.
Lu, S. W., Ren, Y., and Suen, C. Y. (1991). Hierarchi-
cal attributed graph representation and recognition of
handwritten chinese characters. Pattern Recognition,
24(7):617–632.
Luqman, M. M., Ramel, J.-Y., Llad
´
os, J., and Brouard, T.
(2013). Fuzzy multilevel graph embedding. Pattern
Recognition, 46(2):551–565.
Njah, S., Ltaief, M., Bezine, H., and Alimi, A. M. (2012).
The pertohs theory for on-line handwriting segmenta-
tion. International Journal of Computer Science Is-
sues (IJCSI), 9(5):142–151.
Rocha, J. and Pavlidis, T. (1994). A shape analysis model
with applications to a character recognition system.
IEEE Transactions on Pattern Analysis and Machine
Intelligence, 16(4):393–404.
Rocha, J. and Pavlidis, T. (1995). Character recognition
without segmentation. IEEE Transactions on pattern
analysis and machine intelligence, 17(9):903–909.
Suganthan, P. N. and Yan, H. (1998). Recognition of
handprinted chinese characters by constrained graph
matching. Image and Vision Computing, 16(3):191–
201.
Tagougui, N., Boubaker, H., Kherallah, M., and Alimi,
A. M. (2013). A hybrid mlpnn/hmm recognition sys-
tem for online arabic handwritten script. In World
Congress on Computer and Information Technology
(WCCIT), pages 1–6. IEEE.
Tsai, W.-H. and Fu, K.-S. (1983). Subgraph error-
correcting isomorphisms for syntactic pattern recog-
nition. IEEE Transactions on Systems, man, and cy-
bernetics, (1):48–62.
Viard-Gaudin, C., Lallican, P. M., Knerr, S., and Binter,
P. (1999). The ireste on/off (ironoff) dual handwrit-
ing database. In Proceedings of the Fifth Interna-
tional Conference on Document Analysis and Recog-
nition(ICDAR), pages 455–458. IEEE.
Yan, J., Yin, X.-C., Lin, W., Deng, C., Zha, H., and Yang,
X. (2016). A short survey of recent advances in graph
matching. In Proceedings of International Conference
on Multimedia Retrieval, pages 167–174. ACM.
GRAPP 2020 - 15th International Conference on Computer Graphics Theory and Applications
270
