Filter Learning from Deep Descriptors of a Fully Convolutional Siamese
Network for Tracking in Videos
Hugo de Lima Chaves
1
, Kevyn Swhants Ribeiro
1
, Andr
´
e de Souza Brito
1
, Hemerson Tacon
1
,
Marcelo Bernardes Vieira
1
, Augusto Santiago Cerqueira
1
, Saulo Moraes Villela
1
,
Helena de Almeida Maia
2
, Darwin Ttito Concha
2
and Helio Pedrini
2
1
Department of Computer Science, Federal University of Juiz de Fora (UFJF), Juiz de Fora, MG, Brazil
2
Institute of Computing, University of Campinas (UNICAMP), Campinas, SP, Brazil
Keywords:
Video Tracking, Siamese Network, Deep Descriptors.
Abstract:
Siamese Neural Networks (SNNs) attracted the attention of the Visual Object Tracking community due to
their relatively low computational cost and high efficacy to compare similarity between a reference and a
candidate object to track its trajectory in a video over time. However, a video tracker that purely relies on
an SNN might suffer from drifting due to changes in the target object. We propose a framework to take into
account the changes of the target object in multiple time-based descriptors. In order to show its validity,
we define long-term and short-term descriptors based on the first and the recent appearance of the object,
respectively. Such memories are combined into a final descriptor that is the actual tracking reference. To
compute the short-term memory descriptor, we estimate a filter bank through the usage of a genetic algorithm
strategy. The final method has a low computational cost since it is applied through convolution operations
along the tracking. According to the experiments performed in the widely used OTB50 dataset, our proposal
improves the performance of an SNN dedicated to visual object tracking, being comparable to the state of the
art methods.
1 INTRODUCTION
Video Object Tracking (VOT) is one of the fundamen-
tal problems in computer vision. It consists of provid-
ing an object trajectory along a video given its initial
coordinates. VOT is a key component in many ap-
plications: surveillance system, robotics, autonomous
driving, intelligent traffic control, augmented real-
ity, sports video analysis. The traditional approaches
to this problem are grounded on mathematical mod-
els designed to detect and extract features of a tar-
get. These features are manually designed, or hand-
crafted, beforehand by human experts for very spe-
cific issues such as: occlusions, illumination changes
and many others (Nanni et al., 2017).
However, since the advent of Deep Learning
approaches through Convolutional Neural Networks
(CNNs), the Computer Vision community has made
a notorious effort to obtain feature descriptors based
on data instead of those designed by experts. A spe-
cific type of Deep Neural Network (DNN) employed
in the feature design task is the Siamese Neural Net-
work (SNN). Designed for template comparison, it
is used for a wide range of applications, including:
signature verification, audio analysis and face recog-
nition (Bromley et al., 1994; Taigman et al., 2014;
Manocha et al., 2018). The capability to generate de-
scriptors for similarity comparison between a refer-
ence and candidate image has inspired works for VOT
applications (Valmadre et al., 2017).
In this paper, the VOT problem is addressed by en-
hancing a specific type of SNN for visual tracking, the
SiamFC (Bertinetto et al., 2016). Our premise is that
one may obtain tracking improvements by combining
the descriptor outputted by this SNN along the video.
More specifically, we propose a method to learn a
set of linear time-invariant filters from a video sub-
set. The supervised filter learning is performed by a
Genetic Algorithm (GA). By filtering the descriptors
provided by the network over time, we capture the
short-term memory of the tracked object. We also use
a reliable descriptor obtained from the initial frames
of the video. This is the long-term object memory to
be used along the whole tracking. As our results show,

the combination of the long-term and short-term de-
scriptors outperforms the SiamFC tracker and is com-
parable to the state-of-the-art methods.
The main contributions of this work are the filter
learning approach and the framework to use multiple
representations of the object to improve video track-
ing. The combination of long and short-term memory
descriptors is also a major contribution, improving the
tracking with a very low computational cost.
2 RELATED WORK
The usage of SNN for VOT problems is a very recent
approach, presenting noticeable performance in the
latest public evaluations (Kristan et al., 2017; Kris-
tan et al., 2018). The SINT was the first tracker that
relied on an SNN (Tao et al., 2016) with a simplis-
tic framework to compare a reference image patch,
the Region Of Interest (ROI) in the first frame, with
each frame of the video. It compares several Bound-
ing Boxes (BB) close to the region where the object
was detected in the previous frame and picks the most
similar as output for the current frame. This sim-
ple model reached the state-of-the-art performance
in its time, outperforming well-established methods,
such as TLD (Kalal et al., 2012), which has occlu-
sion detection and object model updating. Likewise,
Bertinetto et al. (Bertinetto et al., 2016) proposed a
fully convolutional SNN that compares a frame to an
object image. It only uses a pre-trained SNN to local-
ize the object. No model update is included. Its inno-
vation is the use of a Fully Convolutional Neural Net-
work (FCNN). The SiamFC shows a score-map that
indicates the confidence of the object to be found in a
particular image region. Due to its simplicity, perfor-
mance and the strong evidence that SNNs are a very
promising approach for VOT, the SiamFC has been
used as baseline to many works to demonstrate new
tracking concepts, as online weight adaptiveness, cor-
relational filters, rotation invariance and others (Guo
et al., 2017; Rout et al., 2018; Valmadre et al., 2017).
Another SNN for template matching is proposed by
(Guo et al., 2017). They argue that the SiamFC lacks
adaptiveness during tracking. They apply an online
transformation on the weights of the static SNN based
on the information of recent frames, adding tempo-
ral information. It also learns a background suppres-
sion transformation for the query image. In a differ-
ent way, Rout et al. (Rout et al., 2018) improved the
SiamFC by providing a rotation-invariant framework.
They assume smooth rotations of the object along
consecutive frames. Then, several images are pre-
sented with different rotation angles, giving it more
robustness when compared to SiamFC.
The representation of objects based on deep de-
scriptors is a common point in recent VOT works (Tao
et al., 2016; Wang and Yeung, 2013; Bertinetto et al.,
2016; Danelljan et al., 2016; Danelljan et al., 2017).
Some of them process the deep descriptors using a
correlation filter with the drawback of having high
computational cost. The main concern is to extract
spatial relations from feature maps of deep descrip-
tors. In contrast, temporal component analysis and
descriptor filtering is an open branch to be explored
(Huang, 2017).
Recently, Valmandre et al. (Valmadre et al., 2017)
adapted the SiamFC to use a correction filter and pro-
posed an adaptive method to weight the temporal vari-
ation of feature maps. Instead of having a single rep-
resentation of the object based only on the first frame,
a new template is computed for each frame. The
templates are combined with the previous ones in a
moving average. That work showed evidence that the
performance can be improved by temporal filtering.
Since the moving average is a linear time-invariant
filter, we argue that it is possible to find filters more
suitable for tracking purposes. Our motivation is to
explore methods to weight the consecutive descriptors
obtained during tracking. We estimate filters based on
observations of annotated tracking data. In summary,
our goal is to learn a set of filters to process deep de-
scriptors in time.
In this context, Cemes and Ait-Boudaoud (Cemes
and Ait-Boudaoud, 1993) showed a comparison be-
tween GA and other methods to find FIR (Finite Im-
pulse Response) filters. Similarly, Dey et al. (Dey
et al., 2010) showed the advantages of FIR filter de-
sign using GA. Despite the GA computational cost, it
has a strong potential to overcome local minima and
is a suggestive choice to find filters. Details about the
encoding scheme used in our work that is useful for
GA convergence are presented by (Ahmad and Anto-
niou, 2006).
3 PROPOSED METHOD
Our proposed method is based on a frozen version
of the SiamFC pre-trained on the ImageNet Video
dataset. Originally, the SiamFC is composed of
two twin networks, i.e. identical networks sharing
weights, where the first one processes a reference im-
age (the first frame) and the second one processes
the current frame. The networks are inspired by the
AlexNet architecture (Krizhevsky et al., 2012). Both
networks output descriptors from the images that are
used in an object localization module. This module is

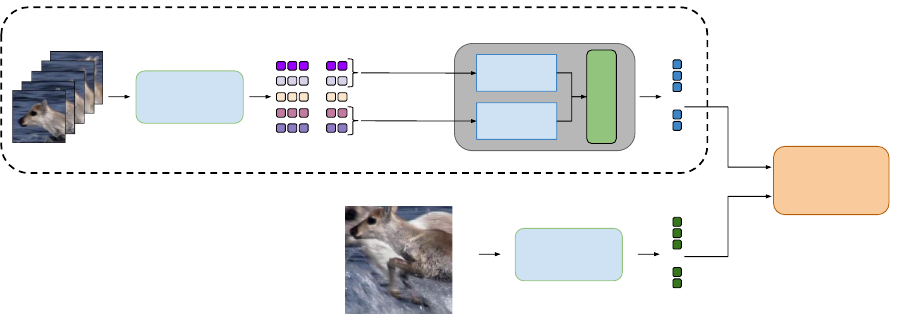
SiamFC
(Encoding)
Reference
Estimated BBs
Signal of descriptors
Long-term
Memory
Short-term
Memory
...
...
...
...
...
Combination
First q frames
Previous m frames
...
Updated
object
descriptor
SiamFC
(Encoding)
...
Candidate
descriptor
SiamFC
(Object
Localization)
Current frame
Figure 1: Method overview. The BBs identified in the video are encoded by the SiamFC, resulting in a signal of descriptors.
Memories cover different parts of the video to provide suitable descriptors for different appearances of the object. Descriptors
are combined to better represent the original object. Notice that the target localization is performed as defined by the original
SiamFC.
composed of a cross-correlation layer that generates
a score map indicating the likelihood of the object in
the reference image to be found in a given region of
the candidate image.
Trackers based on SNNs, as SINT and SiamFC,
rely only on the descriptor generated in the first frame,
computed from the ROI contents. The SNNs do not
consider the multiple dynamic instances of the object
along the video. They also tend to fail when objects
from the ROI background eventually appear. One way
to overcome the mapping limitation of these SNNs is
to use more than one instance of the same object to
compose the final target descriptor. To this end, in our
method (Figure 1), we propose a novel module that
considers the available BBs estimated by the tracker
to update the reference descriptor at each time. The
reference descriptor is computed through the combi-
nation of a long and a short-term memory.
A sequence of descriptors z[n] is generated by the
encoded BBs outputted by the tracker along the video,
as shown in Figure 1. The descriptor for the frame n
is defined as
z[n] = w(BB
n
), (1)
where BB
n
is the n-th BB into which the tracked ob-
ject is estimated to be, and w is a function encoding
the object into a k-dimensional feature vector from the
weights of the twin networks.
Thus, a descriptor z[n] is a k-dimensional feature
vector representing the object in a given frame n.
The consecutive set of descriptors are interpreted in
this work as k independent unidimensional signals in
function of time.
3.1 Object Memory: Combining
SiamFC Descriptors
This work is based on the VOT-dedicated SNN
SiamFC. However, the following concepts can be
adapted to other VOT SNNs. Given a sequence of
descriptors (z[0], ··· , z[n − 1]), one may define an op-
eration O to generate a combined descriptor that bet-
ter represents the object for use in frame n. In other
words, the operation O takes into account the n − 1
previous feature vectors to compute a combined vec-
tor z
comb
[n]. It is analogous to take into account the
n − 1 BBs returned by the tracker as
z
comb
[n] = O(z[0], ..., z[n − 1]). (2)
The goal is to find a combination of descriptors
that improves the performance of the system instead
of relying on the information of a single descriptor
z[0].
We propose to use limited sequences of descrip-
tors to capture different mappings of the object over
time. Each sequence is referred to as an object mem-
ory. As shown in Figure 1, multiple memories can be
used to better track the object.
This work focuses on two types of memories. The
first one is a long-term object representation. It has
to keep the original object information from the early
frames of the video. It works as an anchor memory
for not losing the reference to the target object. The
second one is a short-term object representation that
combines the most recent descriptors. Its goal is to
capture the latest appearances of the object. We pro-
pose the use of linear time-invariant filters to compute
the short-term descriptor. A filter bank of k filters,
one for each descriptor component, is learned from a

training set of videos using a GA approach. The mul-
tiple memory combination and the filter based mem-
ory are the main contributions of our work.
3.2 Computing the Long-term Memory
The long-term memory comprises the set of descrip-
tors of the earliest appearances in the video to pre-
serve the original object information. Therefore, it
provides a reliable static representation of the object,
instead of using only a imprecise descriptor z[0]. It is
based on two assumptions:
1. the tracker provides fair outputs (BB) for the first
frames of the video;
2. the object appearance is roughly the same in the
initial frames.
Considering that two similar inputs cannot be
mapped into a very different location in feature space
by definition (Koch et al., 2015), the long-term mem-
ory is the expected value E() of the q descriptors of
the first BBs provided by the tracker
z
long
[n] = E([z[0], ..., z[q − 1]]). (3)
Notice that, for n ≥ q, the long-term memory is
a constant signal based on the first q frames of the
video. Therefore, any change in the object appearance
in a frame n ≥ q is not considered.
3.3 Computing the Short-term Memory
We propose the short-term memory to be based on
the m previous frames, computed by filtering the de-
scriptors. The filter bank h[n] is composed of k unidi-
mensional FIR filters h
i
= {c
m−1
, ··· , c
1
, c
0
}, where
m is the filter order, 1 ≤ i ≤ k, c
j
∈ R, and the ori-
gin c
0
corresponds to the frame n − 1. Let S[n] =
(z[n − m], ··· , z[n − 1]) be the sequence of the m pre-
vious descriptors, from the oldest to the newest. The
filtered signal of descriptors is given by the convolu-
tion of the sequence and the filter bank
z
short
[n] = S[n] ∗ h[n]. (4)
It is required to extend the videos for the first m−1
frames, to complete the sequence S[n]. We extend the
video by filling the missing positions with the descrip-
tor z[0] of the first frame.
Different from the long-term memory z
long
[n], the
short memory z
short
[n] changes according to the latest
appearance of the tracked object.
3.4 Final Object Descriptor from
Memory Combination
The memory descriptors have complementary infor-
mation about the tracked object and can be combined
as
z
comb
[n] = α · z
long
[n] + (1 − α) · z
short
[n], (5)
where 0 ≤ α ≤ 1 is a conservative factor to balance
the reliability of the long-term memory and the adap-
tiveness of the filtered memory. This k-dimensional
descriptor is used to localize the object in the cur-
rent frame, as shown in Figure 1. More precisely,
the improved descriptor z
comb
[n] is plugged into the
SiamFC’s cross-correlation module in order to local-
ize the object, providing an adapted representation of
the original object for detection in frame n.
3.5 Filter Bank Estimation
We propose to learn the filter bank h[n] from Ground
Truth (GT) videos with known object BBs. Let g
(v)
[n]
be the evaluation of labeled GTs in a video v by a
fully convolutional SNN. Also, consider the sequence
of descriptors z
(v)
[n] obtained from the BBs generated
by the tracker using the same SNN. We seek a filter
bank h[n] that, applied to z
(v)
[n], generates the com-
bined descriptor z
comb(v)
[n] that is closer to the GT
descriptors g
(v)
[n], as expressed by the minimization
problem
argmin
h[n]
∑
v
||g
(v)
[n] − z
comb(v)
[n]||
2
, (6)
where z
comb(v)
[n] is given by Equation (5).
Therefore, it is assumed that the signal of descrip-
tors from a set of videos have components that are
universally present in the tracking performed by an
SNN. So the goal is to estimate a filter bank that keeps
frequency components of accurate trackings and at-
tenuate the incorrect ones.
3.6 Filter Learning
Considering the literature, we have chosen a GA to
find the desired filter bank. The GA is individually ap-
plied to find each of the k filters of h[n] that minimize
Equation (6). However, since the BBs that generate
z
comb(v)
[n] can be very close to those which generate
g
(v)
[n], it may lead to impulsive filters as trivial solu-
tions. We propose to add white noise to the descrip-
tors z
(v)
[n] returned by the SNN before minimization
in order to avoid the trivial solution.
Each individual genotype is composed of a string
of integers, where the genes that form a chromosome

represent the filter coefficients. Thus, a filter of or-
der m is represented by a chromosome of m integers.
We generate a population of P
s
individuals where the
genetic operators are performed.
The selection attempts to discard individuals with
lower fitness values and keep the ones with the highest
fitness as:
Θ(h
i
) =
∑
v,n

||g
(v)
i
[n] − z
comb(v)
i
[n]||
2
+ δ

−1
, (7)
where δ is a small number to guarantee a finite fitness
and 1 ≤ i ≤ k. This step is probabilistic and not all of
the best individuals pass to the next generation. This
randomness eliminates local minima in the optimiza-
tion process (Dey et al., 2010). After selection, the
crossover and mutation are computed to generate new
individuals for a new population. This is repeated un-
til a number of iterations is reached. The whole pro-
cess is performed k times to find the complete filter
bank h[n].
4 EXPERIMENTAL RESULTS
In this Section, we present and evaluate the experi-
mental results obtained with our method.
4.1 Experimental Setup
The SiamFC and the proposed method were written
in Python3.5. We use the public implementation of
the SiamFC provided by (Zhang, 2017). We also
used: TensorFlow 1.10.0 for the implementation of
the SiamFC, Numpy 1.14.5 for numerical computa-
tion, OpenCV 3.4.3, and the evolutionary computa-
tion framework DEAP 1.2.2. Experiments were run
in two Intel E5-4607 @ 2.20GHz processors with 24
cores and 32 GB Memory. In this setup, the SiamFC
gives the tracking rate of 0.1 frames per second in av-
erage.
Two datasets are used in this work. The VOT2015
provides videos for training the filter learning step,
while the performance is evaluated in the OTB50
dataset. The training videos from VOT2015 are:
''bag'', ''racing'', ''ball1'', ''octopus'', ''bolt2'', ''pedes-
trian'', ''road''. The SiamFC presented outputs close to
the GT for these videos, i.e., the tracking had a good
average performance.
The performance is compared by the location pre-
cision and overlap success rates given their respective
thresholds (Tao et al., 2016).
Regarding the GA parameters, the probability of
gene mutation is p
g
=
1
m
to introduce about one mu-
tation in the filter each time it is selected. The proba-
bility of selecting an individual for mutation is p
m
=
90%. The crossover probability is p
c
= 95%. The
convergence criterion is the maximum number of it-
erations m
i
= 600. The population size is P
s
= 5M.
4.2 Parameter Setting and Method
Evaluation
The number of descriptors q, for the long-term mem-
ory, the filter order m, for the short-term memory,
and the conservative factor α can be better evalu-
ated in conjunction. But in this work, they are ex-
plored empirically due to the high computational cost
of the learning step. For the filter order m = 31, each
learning run took 16 hours to complete. The num-
ber of training videos also strongly impacts the run-
time since each population is computed with com-
plete track evaluations over them. But it is worthy
to mention that, once the filter is learned, our method
requires unidimensional convolutions along the track-
ing with very low overhead.
Table 1: Varying the filter order m for short-term memory.
Filter Order m
Precision Plots
(AUC)
Success Plots
(AUC)
21 0.792 0.563
31 0.809 0.577
41 0.788 0.559
51 0.768 0.556
Table 2: Varying the number of descriptors for the long-
term memory.
Number of
Descriptors q
Precision Plots
(AUC)
Success Plots
(AUC)
1 0.785 0.569
10 0.765 0.552
15 0.778 0.563
17 0.805 0.578
20 0.794 0.574
30 0.809 0.577
After preliminary tests, we fixed q = 17 and α =
0.65 and varied the filter order m to test the short-term
memory. As shown in Table 1, m = 31 presented the
best Area Under Curve (AUC). Considering the av-
erage frame rate of 25 FPS of the dataset videos, it
means that 1.24s of past descriptors are used to repre-
sent the object as short-term memory.
In Table 2, m = 31 and α = 0.65 were fixed and
q varied to show other results. Considering several
combinations of m and α, better results were achieved
around q = 30 which averages the first 1.2s of the
videos as long-term memory.

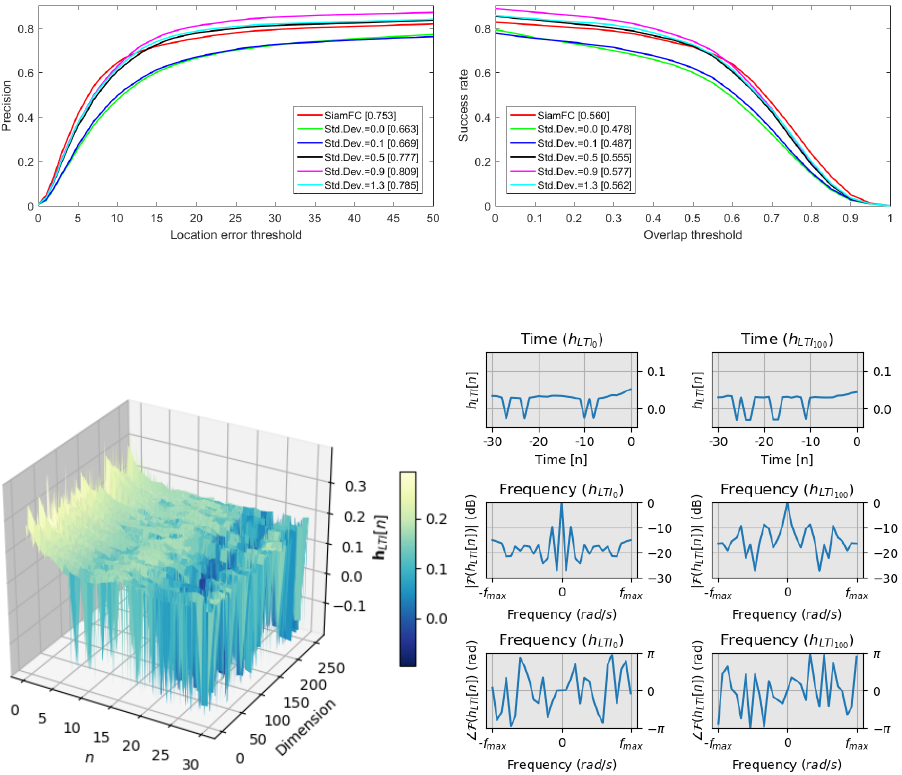
(a) (b)
Figure 2: Results for the white noise standard deviation.
(a) (b)
Figure 3: Representation of the learned filter bank. a) the 256 filters in the time domain. b) filters from tracks 0 and 100.
From top to bottom: time domain, magnitude response in the frequency domain, phase response in the frequency domain.
Figure 2(a) and Figure 2(b) present the perfor-
mance curves with multiple levels of white noise
added in the filter learning step. The poor perfor-
mance with σ = 0 in all thresholds shows the im-
portance of the noise addition to avoid the trivial im-
pulsive filters. The performance is improved as the
standard deviation grows up to σ = 0.9. Beyond
this value, the noise starts corrupting the signal and
the performance decreases. Since only videos hav-
ing high F-measure with the SiamFC are used, the
detected BB has a high overlap with the GT. The ad-
dition of noise forces the GA to find filters capable of
rejecting the white noise plus the SiamFC imprecise
descriptors.
Based on previous experiments, the best filter
bank obtained has order m = 31, conservative factor
α = 0.65 and white noise standard-deviation σ = 0.9.
The resulting 256 filters in the time domain are illus-
trated in Figure 3(a). Notice that the filters have a
similar distribution in time. Figure 3(b) shows two
filters from the bank to a more in-depth analysis. No-
tice the strong DC component in the two filters that
can be verified by their Fourier transform at the bot-
tom. Although we have discussed the limits of per-
formance of an SNN, one of its fundamental charac-
teristics is keeping the descriptor insensitive for dif-
ferent instances of the objects. Also, notice that the
strongest coefficients of the filters are usually the first
ones. This means that the last descriptors in the video
are the most relevant ones on average. It is an in-
tuitive consideration, as the change in the appearance
of ROI in the latest frames looks to be more important

Table 3: Location Error precision and IoU success for different thresholds. From the fourth row, each line corresponds to the
performance of one category of the OTB50 dataset. The best performance for each category and for each of the thresholds is
highlighted in bold.
Location Error Precision Intersection over Union (IoU) Success
Threshold 50 30 10 0.25 0.50 0.75
Method Ours SiamFC Ours SiamFC Ours SiamFC Ours SiamFC Ours SiamFC Ours SiamFC
Category
Abrupt Motion 0.877 0.830 0.837 0.795 0.469 0.580 0.857 0.817 0.692 0.686 0.260 0.307
Background Clutter 0.835 0.763 0.817 0.727 0.645 0.575 0.809 0.727 0.736 0.636 0.388 0.321
Blur
0.846 0.816 0.806 0.787 0.420 0.551 0.812 0.794 0.623 0.666 0.207 0.291
Deformation 0.847 0.784 0.831 0.763 0.556 0.568 0.834 0.764 0.684 0.648 0.239 0.258
Illumination Variation 0.855 0.769 0.829 0.741 0.534 0.571 0.814 0.739 0.668 0.649 0.291 0.341
In-Plane Rotation 0.836 0.772 0.804 0.739 0.570 0.592 0.804 0.751 0.697 0.675 0.302 0.336
Low Resolution 0.819 0.782 0.776 0.744 0.531 0.548 0.795 0.762 0.666 0.674 0.257 0.317
Occlusion 0.842 0.795 0.819 0.775 0.530 0.592 0.816 0.774 0.687 0.678 0.238 0.297
Out-of-Plane Rotation 0.848 0.792 0.824 0.763 0.590 0.608 0.819 0.765 0.699 0.672 0.290 0.318
Out-of-View 0.735 0.713 0.689 0.693 0.358 0.481 0.730 0.708 0.638 0.645 0.312 0.387
Scale Variation 0.883 0.834 0.863 0.804 0.670 0.682 0.856 0.813 0.716 0.721 0.308 0.368
than the earlier ones. For most filters, we observed in
the frequency domain that low-frequency components
tend to be higher than the high-frequency ones. It can
be understood as a fast change in ROI appearance is
less important than a consistent and smoother one.
4.3 Comparison with the SiamFC
The long and short memories are complementary to
the SiamFC. In this section, we use SiamFC as base-
line to show how it is improved. Using the mean
threshold of 25 for the Location Error (LE) (Figure
2(a)), our method improves the baseline from 0.778
to 0.827, a gain of 6.4%. Likewise, with the threshold
of 0.5 for the overlap error (Figure 2(b)), our method
improves the baseline from 0.683 to 0.7, a gain of
2.5%.
For a deeper understanding, we applied the post-
hoc Nemenyi test to the whole curves of SiamFC (red)
and our method with σ = 0.9 (magenta) in Figure 2.
The location precision rate has p-value = 4.95 · 10
−4
,
meaning that both curves are statistically different.
However, the p-value for the success rate of overlap
is 0.406 meaning that the curves are statistically sim-
ilar. Interestingly, a visual comparison of both results
shows that our method tends to better track the object
but with less precise BBs. This is due to the averaging
nature of the long and short memories. The SiamFC
loses the object more often but when it finds it, the
resulting BB is more precise.
Besides, our method obtained the AUC location
precision rate of 0.809 and overlap success rate of
0.577. Considering the performance of SiamFC,
which is 0.753 and 0.560 respectively, our method
improves the overall location precision rate in about
7.6% and the overlap success rate about in 3.0% with-
out increasing the computational cost.
Finally, we present the Location Error precision
and Intersection over Union success for the 11 cate-
gories of the OTB50 dataset (Table 3). The LE pre-
cision was computed for the thresholds 50, 30 and 10
and the IoU success for the thresholds 0.25, 0.50 and
0.75. For the LE precision, our method has some-
what the same performance in all categories, except
the Out-of-View since it does not deal with object
absences. The numbers reinforce that our method
obtains BBs containing the object’s center more of-
ten than the SiamFC. Observing the IoU success, our
method outperforms the SiamFC in all categories for
low thresholds. However, the SiamFC has superior
performance for thresholds above 0.50. Thus, the
SiamFC is indicated when more precision and tighter
BBs are required, provided that occasional wrong ob-
ject detection along the whole tracking is not critical.
4.4 Comparison with the State of the
Art
Our method enhances the SiamFC performance, as
observed in Figure 5. One of the advantages is its
adherence to the Ground Truth BB, i.e. our method
sticks to the object along the tracking (Figures 4(a)
and 4(b)). Thus, it has higher precision and suc-
cess rates for high threshold tolerance. The original
SiamFC, is more precise in defining the BB that con-
tains the object (Figure 4(c)). In Figure 4(d) shows

(a)
(b)
(c)
(d)
Figure 4: Proposed method (green) visually compared to the SiamFC (red). The GT is blue. OTB50 Dataset sequences: (a)
lemming (b) skiing (c) singer1 (d) motorRolling.
(a) (b)
Figure 5: State-of-the-art methods: (a) Precision plots (b) IoU Success plots.
how our method tracks the object correctly but in most
cases gives a BB greater or smaller than the ground
truth. As a general rule, our method is more appro-
priate when good object localization throughout the
whole video is paramount.
Figures 4(a) and 4(b) provide examples of the bet-
ter adherence to the tracked object of the proposed
method. Notice that it does not lose the object when

SiamFC fails. Nevertheless, the SiamFC usually out-
puts a more precise BB of the object, as shown in Fig-
ure 4(c). It explains higher precision and success rates
by the SiamFC for small thresholds.
Figure 5 shows a comparison to several state-of-
the-art trackers. Notice that MDNET, CCOT, ECO
and SINT have higher AUC than our tracker. Due
to its simple and effective approach, however, our
method is lightweight with fairly comparable results.
We remark that the lack of object occlusion detection
greatly impairs our precision and success rates.
5 CONCLUSION
We proposed the use of two object descriptors for im-
proving tracking using an SNN. A long-term mem-
ory, based on the first object appearances, is combined
with a short-term memory, based on recent appear-
ances, to form an updated object descriptor. Its dy-
namic nature adapts to the object and is more suit-
able for long tracking. We applied the method to
the SiamFC descriptors but it can be adapted to other
SNNs.
The proposed short-term memory is obtained by
low-cost convolutions with a filter bank. The filter
bank is learned by a GA strategy from videos with
high F-measure. More specifically, only seven videos
from the VOT2015 dataset were used for training:
''bag'', ''racing'', ''ball1'', ''octopus'', ''bolt2'', ''pedes-
trian'', ''road''. Despite the high computational cost
for the GA step, the learned filter bank showed to be
general enough for tracking over the 50 videos of the
OTB50 dataset. Our filter learning proposal is thus ca-
pable to generalize object descriptor variations along
tracking.
Our novel approach presented promising results,
showing a consistent gain for object localization. The
obtained BBs on well-known datasets proved to be
adherent to the tracked object over time. Compared to
the state of the art trackers, our method has fair preci-
sion and success rates with a very low computational
cost. Our method is appropriate when good object lo-
calization throughout the whole video is paramount,
but low BB precision is not an issue. The frame rate is
only dependent on the underlying SNN performance,
since the proposed 1D convolutions add negligible ex-
tra cost.
Future works include investigating more power-
ful kernel learning approaches for temporal series, in-
cluding LSTM and deep neural networks. There is
the possibility of developing specific neural network
models for learning the convolution filters. Further-
more, adaptive filter learning seems to be a promis-
ing approach, albeit it is a very challenging task. The
use of more memories seems promising in contexts
with complex interactions between objects of inter-
est. Also, occlusion detection strategies are very im-
portant to improve the performance on the OTB50
dataset.
ACKNOWLEDGEMENTS
Authors thank CAPES, FAPEMIG (grant CEX-
APQ-01744-15), FAPESP (grants #2017/09160-1 and
#2017/12646-3), CNPq (grant #305169/2015-7) for
the financial support, and NVIDIA Corporation for
the donation of two Titan Xp (GPU Grant Program).
REFERENCES
Ahmad, S. and Antoniou, A. (2006). Cascade-form multi-
plierless fir filter design using orthogonal genetic al-
gorithm. In IEEE International Symposium on Signal
Processing and Information Technology, pages 932–
937.
Bertinetto, L., Valmadre, J., Henriques, J. F., Vedaldi, A.,
and Torr, P. H. (2016). Fully-convolutional siamese
networks for object tracking. In European Conference
on Computer Vision, pages 850–865. Springer.
Bromley, J., Guyon, I., LeCun, Y., S
¨
ackinger, E., and Shah,
R. (1994). Signature verification using a” siamese”
time delay neural network. In Advances in Neural In-
formation Processing Systems, pages 737–744.
Cemes, R. and Ait-Boudaoud, D. (1993). Genetic approach
to design of multiplierless fir filters. Electronics Let-
ters, 29(24):2090–2091.
Danelljan, M., Bhat, G., Khan, F. S., Felsberg, M., et al.
(2017). Eco: Efficient convolution operators for track-
ing. In Computer Vision and Pattern Recognition, vol-
ume 1, page 3.
Danelljan, M., Robinson, A., Khan, F. S., and Felsberg, M.
(2016). Beyond correlation filters: Learning continu-
ous convolution operators for visual tracking. In Euro-
pean Conference on Computer Vision, pages 472–488.
Dey, A. K., Saha, S., Saha, A., and Ghosh, S. (2010). A
method of genetic algorithm for fir filter construction:
design and development with newer approaches in
neural network platform. International Journal of Ad-
vanced Computer Science and Applications, 1(6):87–
90.
Guo, Q., Feng, W., Zhou, C., Huang, R., Wan, L., and
Wang, S. (2017). Learning dynamic siamese network
for visual object tracking. In IEEE International Con-
ference on Computer Vision.
Huang, Z. (2017). An investigation of deep tracking meth-
ods. In Conference on Technologies and Applications
of Artificial Intelligence, pages 58–61. IEEE.

Kalal, Z., Mikolajczyk, K., et al. (2012). Tracking-learning-
detection. IEEE Transactions on Pattern Analysis and
Machine Intelligence, 34(7):1409.
Koch, G., Zemel, R., and Salakhutdinov, R. (2015).
Siamese neural networks for one-shot image recogni-
tion. In ICML Deep Learning Workshop, volume 2.
Kristan, M., Leonardis, A., Matas, J., Felsberg, M.,
Pfugfelder, R., Zajc, L., Vojir, T., Bhat, G., Lukezic,
A., Eldesokey, A., et al. (2018). The sixth visual
object tracking vot2018 challenge results. In Euro-
pean Conference on Computer Vision Workshops, vol-
ume 3, page 8.
Kristan, M., Leonardis, A., Matas, J., Felsberg, M.,
Pfugfelder, R., Zajc, L., Vojir, T., et al. (2017).
The visual object tracking vot 2017 challenge results.
1(1):1452 – 1459.
Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012). Im-
agenet classification with deep convolutional neural
networks. In Advances in Neural Information Pro-
cessing Systems, pages 1097–1105.
Manocha, P., Badlani, R., Kumar, A., Shah, A., Elizalde, B.,
and Raj, B. (2018). Content-based representations of
audio using siamese neural networks. In IEEE Inter-
national Conference on Acoustics, Speech and Signal
Processing, pages 3136–3140. IEEE.
Nanni, L., Ghidoni, S., and Brahnam, S. (2017). Hand-
crafted vs. non-handcrafted features for computer vi-
sion classification. Pattern Recognition, 71:158–172.
Rout, L., Mishra, D., Gorthi, R. K. S. S., et al. (2018). Rota-
tion adaptive visual object tracking with motion con-
sistency. In IEEE Winter Conference on Applications
of Computer Vision, pages 1047–1055. IEEE.
Taigman, Y., Yang, M., Ranzato, M., and Wolf, L. (2014).
Deepface: Closing the gap to human-level perfor-
mance in face verification. In IEEE Conference
on Computer Vision and Pattern Recognition, pages
1701–1708.
Tao, R., Gavves, E., and Smeulders, A. W. (2016). Siamese
instance search for tracking. In IEEE Conference
on Computer Vision and Pattern Recognition, pages
1420–1429.
Valmadre, J., Bertinetto, L., Henriques, J., Vedaldi, A., and
Torr, P. H. (2017). End-to-end representation learn-
ing for correlation filter based tracking. In Computer
Vision and Pattern Recognition, pages 5000–5008.
IEEE.
Wang, N. and Yeung, D.-Y. (2013). Learning a deep
compact image representation for visual tracking. In
Advances in Neural Information Processing Systems,
pages 809–817.
Zhang, S. (2017). A python+tensorflow implementation
of siamese-fc. https://github.com/www0wwwjs1/
tensorflow-siamese-fc.